Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants and Test Procedure
2.2. Instrumentation
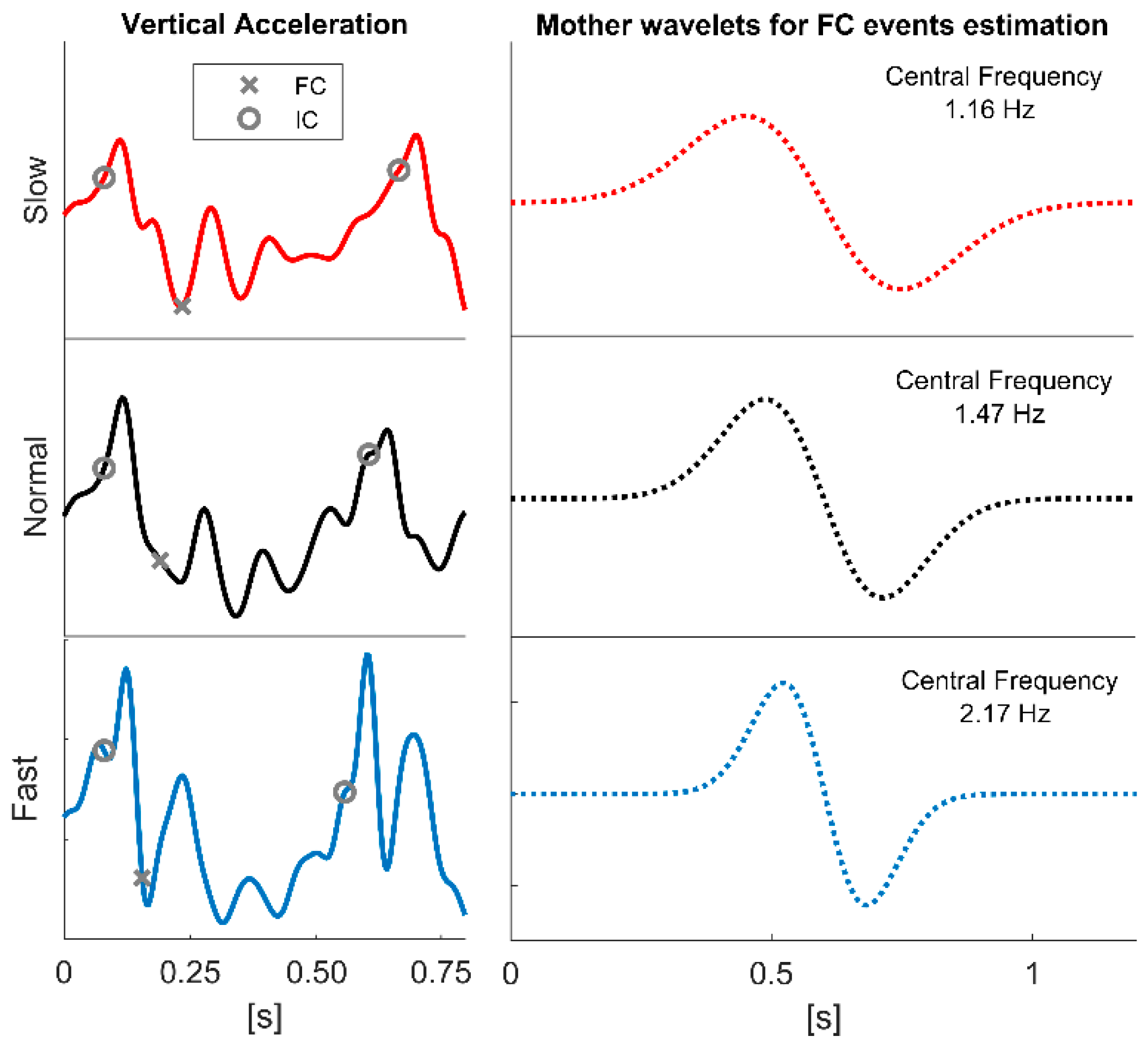
2.3. Data Processing
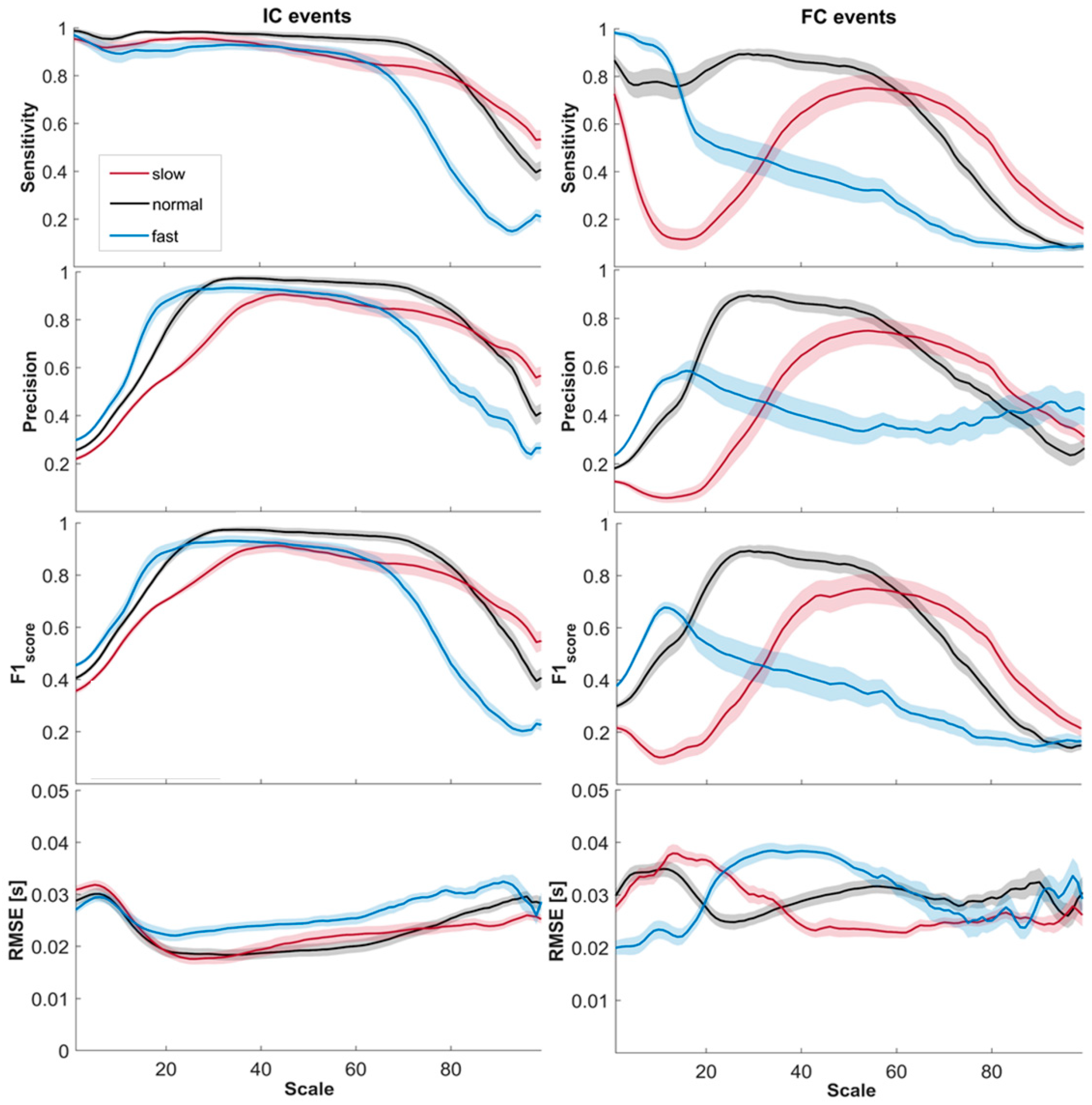
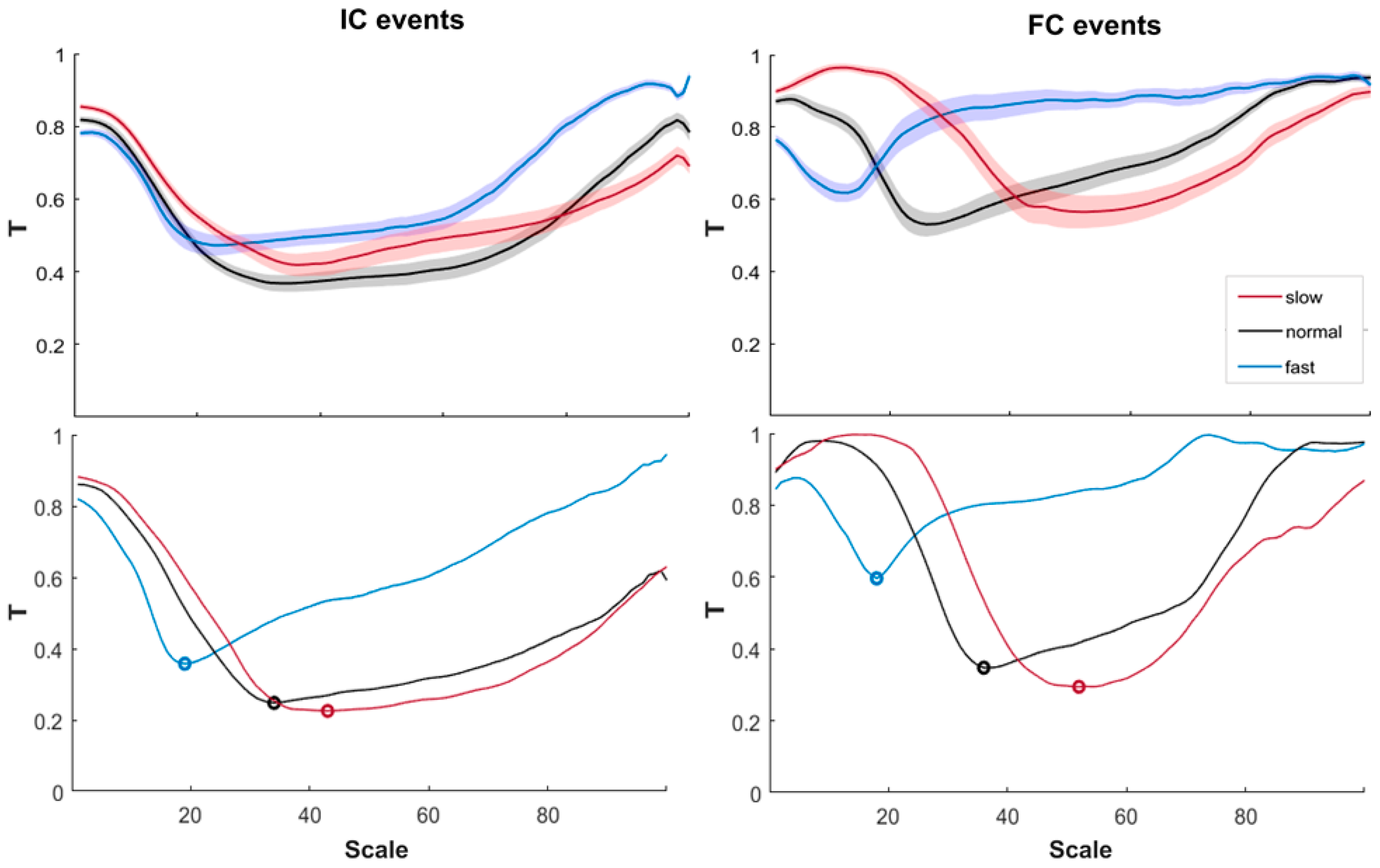
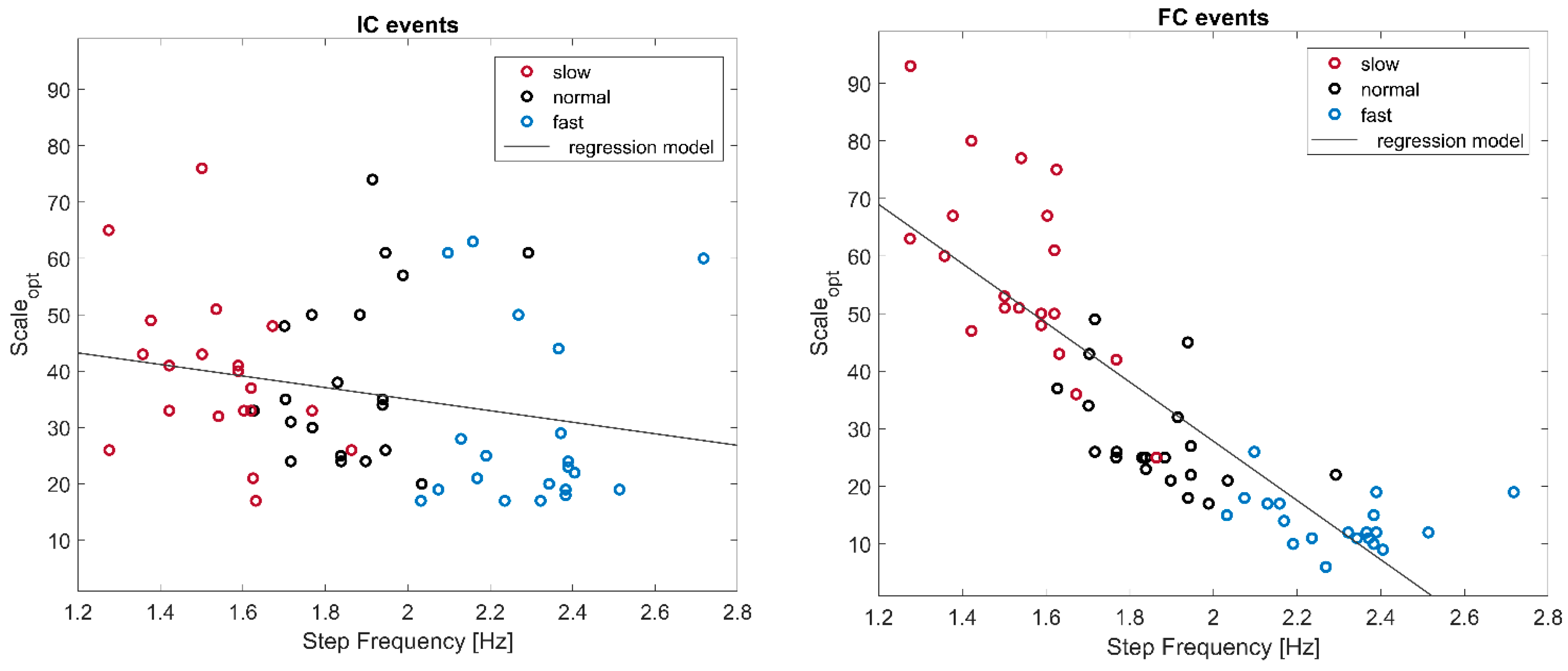
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ebersbach, G.; Sojer, M.; Valldeoriola, F.; Wissel, J.; Müller, J.; Tolosa, E.; Poewe, W. Comparative analysis of gait in Parkinson’s disease, cerebellar ataxia and subcortical arteriosclerotic encephalopathy. Brain 1999, 122, 1349–1355. [Google Scholar] [CrossRef] [PubMed]
- Caramia, C.; Torricelli, D.; Schmid, M.; Munoz, A.; Gonzalez, J.; Grandas, F.; Pons, L. IMU-based Classification of Parkinson’s Disease from Gait: A Sensitivity Analysis on Sensor Location and Feature Selection. IEEE J. Biomed. Health Inform. 2018. [Google Scholar] [CrossRef]
- Teufl, W.; Lorenz, M.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters. Sensors 2019, 19, 38. [Google Scholar] [CrossRef] [PubMed]
- Prince, F.; Corriveau, H.; Hebert, R.; Winter, D.A. Gait in the elderly. Gait Posture 1997, 5, 128–135. [Google Scholar] [CrossRef]
- Caramia, C.; Bernabucci, I.; D’Anna, C.; De Marchis, C.; Schmid, M. Gait parameters are differently affected by concurrent smartphone-based activities with scaled levels of cognitive effort. PLoS ONE 2017. [Google Scholar] [CrossRef]
- Bond, J.M.; Morris, M. Goal-directed secondary motor tasks: Their effects on gait in subjects with Parkinson disease. Arch. Phys. Med. Rehabil. 2000, 81, 110–116. [Google Scholar] [CrossRef]
- Moe-Nilssen, R.; Helbostad, J.L. Estimation of gait cycle characteristics by trunk accelerometry. J. Biomech. 2004, 37, 121–126. [Google Scholar] [CrossRef]
- Liu, T.; Inoue, Y.; Shibata, K. Development of a wearable sensor system for quantitative gait analysis. Measurement 2009, 42, 978–988. [Google Scholar] [CrossRef]
- Mariani, B.; Hoskovec, C.; Rochat, S.; Büla, C.; Penders, J.; Aminian, K. 3D gait assessment in young and elderly subjects using foot-worn inertial sensors. J. Biomech. 2010, 43, 2999–3006. [Google Scholar] [CrossRef]
- Yun, X.; Bachmann, E.R.; Moore, H.; Calusdian, J. Self-contained position tracking of human movement using small inertial/magnetic sensor modules. In Proceedings of the International Conference on Robotics and Automation of the IEEE, Rome, Italy, 10–14 April 2007; pp. 2526–2533. [Google Scholar]
- Trojaniello, D.; Cereatti, A.; Della Croce, U. Accuracy, sensitivity and robustness of five different methods for the estimation of gait temporal parameters using a single inertial sensor mounted on the lower trunk. Gait Posture 2014, 40, 487–492. [Google Scholar] [CrossRef]
- Avvenuti, M.; Carbonaro, N.; Cimino, M.; Cola, G.; Tognetti, A.; Vaglini, G. Smart Shoe-Assisted Evaluation of Using a Single Trunk/Pocket-Worn Accelerometer to Detect Gait Phases. Sensors 2018, 18, 3811. [Google Scholar] [CrossRef]
- Veltink, P.H.; Slycke, P.; Hemssems, J.; Buschman, R.; Bultstra, G.; Hermens, H. Three dimensional inertial sensing of foot movements for automatic tuning of a two-channel implantable drop-foot stimulator. Med. Eng. Phys. 2003, 25, 21–28. [Google Scholar] [CrossRef]
- Iosa, M.; Fusco, A.; Marchetti, F.; Morone, G.; Caltagirone, C.; Paolucci, S.; Peppe, A. The golden ratio of gait harmony: Repetitive proportions of repetitive gait phases. BioMed Res. Int. 2013, 2013, 918642. [Google Scholar] [CrossRef]
- Zijlstra, W.; Hof, L. Assessment of spatio-temporal gait parameters from trunk accelerations during human walking. Gait Posture 2003, 18, 1–10. [Google Scholar] [CrossRef]
- González, R.C.; Alvarez, D.; López, A.M.; Alvarez, J.C. Modified pendulum model for mean step length estimation. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Lion, France, 22–26 August 2007; pp. 1371–1374. [Google Scholar]
- González, R.C.; López, A.M.; Rodriguez-Uría, J.; Alvarez, D.; Alvarez, J.C. Real-time gait event detection for normal subjects from lower trunk accelerations. Gait Posture 2010, 31, 322–325. [Google Scholar] [CrossRef] [PubMed]
- McCamley, J.; Donati, M.; Grimpampi, E.; Mazzà, C. An enhanced estimate of initial contact and final contact instants of time using lower trunk inertial sensor data. Gait Posture 2012, 36, 316–318. [Google Scholar] [CrossRef]
- Khandelwal, S.; Wickstrom, N. Identification of gait events using expert knowledge and continuous wavelet transform analysis. In Proceedings of the 7th International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS 2014), Angers, France, 3–6 March 2014; pp. 197–204. [Google Scholar]
- Aminian, K.; Najafi, B.; Bula, C.; Leyvraz, P.F.; Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Caramia, C.; Bernabucci, I.; D’Anna, C.; De Marchis, C.; Scorza, A.; Schmid, M. Wavelet-based detection of gait events from inertial sensors: Analysis of sensitivity to scale choice. In Proceedings of the International Symposium on Medical Measurements and Applications of the IEEE, MeMeA, Rome, Italy, 11–13 June 2018; pp. 1–5. [Google Scholar]
- Riaz, Q.; Vögele, A.; Krüger, B.; Weber, A. One small step for a man: Estimation of gender, age and height from recordings of one step by a single inertial sensor. Sensors 2015, 15, 31999–32019. [Google Scholar] [CrossRef] [PubMed]
- Schwesig, R.; Leuchte, S.; Fischer, D.; Ullmann, R.; Kluttig, A. Inertial sensor based reference gait data for healthy subjects. Gait Posture 2011, 33, 673–678. [Google Scholar] [CrossRef]
- Bruening, D.A.; Frimenko, R.E.; Goodyear, C.D.; Bowden, D.R.; Fullenkamp, A.M. Sex differences in whole body gait kinematics at preferred speeds. Gait Posture 2015, 41, 540–545. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.B.; Ounpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis data collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Luo, J.; Bai, J.; Shao, J. Application of the wavelet transforms on axial strain calculation in ultra sound elastography. Prog. Nat. Sci. 2006, 16, 942–947. [Google Scholar] [CrossRef]
- De Marchis, C.; Schmid, M.; Conforto, S. An optimized method for tremor detection and temporal tracking through repeated second order moment calculations on the surface EMG signal. Med. Eng. Phys. 2012, 34, 1268–1277. [Google Scholar] [CrossRef]
- Rispens, S.M.; van Schooten, K.S.; Pijnappels, M.; Daffertshofer, A.; Beek, P.J.; van Dieen, J.H. Identification of fall risk predictors in daily life measurements: Gait characteristics’ reliability and association with self-reported fall history. Neurorehabil. Neural Repair 2015, 29, 54–61. [Google Scholar] [CrossRef]
- López, A.M.; Álvarez, D.; González, R.C.; Álvarez, J.C. Validity of four gait models to estimate walked distance from vertical COG acceleration. J. Appl. Biomech. 2008, 24, 360–367. [Google Scholar] [CrossRef] [PubMed]
- Trojaniello, D.; Ravaschio, A.; Hausdorff, J.M.; Cereatti, A. Comparative assessment of different methods for the estimation of gait temporal parameters using a single inertial sensor: Application to elderly, post-stroke, Parkinson’s disease and Huntington’s disease subjects. Gait Posture 2015, 42, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Addison, P.S. Wavelet transforms and the ECG: A review. Physiol. Meas. 2005, 26, R155. [Google Scholar] [CrossRef]
- Wahid, F.; Begg, R.K.; Hass, C.J.; Halgamuge, S.; Ackland, D.C. Classification of Parkinson’s disease gait using spatial-temporal gait features. IEEE J. Biomed. Health Inform. 2015, 19, 1794–1802. [Google Scholar] [CrossRef]
- Dadashi, F.; Mariani, B.; Rochat, S.; Bula, S.; Santos-Eggimann, B.; Aminian, K. Gait and foot clearance parameters obtained using shoe-worn inertial sensors in a large-population sample of older adults. Sensors 2014, 14, 443–457. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caramia, C.; De Marchis, C.; Schmid, M. Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds. Sensors 2019, 19, 1869. https://doi.org/10.3390/s19081869
Caramia C, De Marchis C, Schmid M. Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds. Sensors. 2019; 19(8):1869. https://doi.org/10.3390/s19081869
Chicago/Turabian StyleCaramia, Carlotta, Cristiano De Marchis, and Maurizio Schmid. 2019. "Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds" Sensors 19, no. 8: 1869. https://doi.org/10.3390/s19081869
APA StyleCaramia, C., De Marchis, C., & Schmid, M. (2019). Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds. Sensors, 19(8), 1869. https://doi.org/10.3390/s19081869




