Compressive Behavior of Composite Concrete Columns with Encased FRP Confined Concrete Cores
Abstract
:1. Introduction
2. Materials and Methods
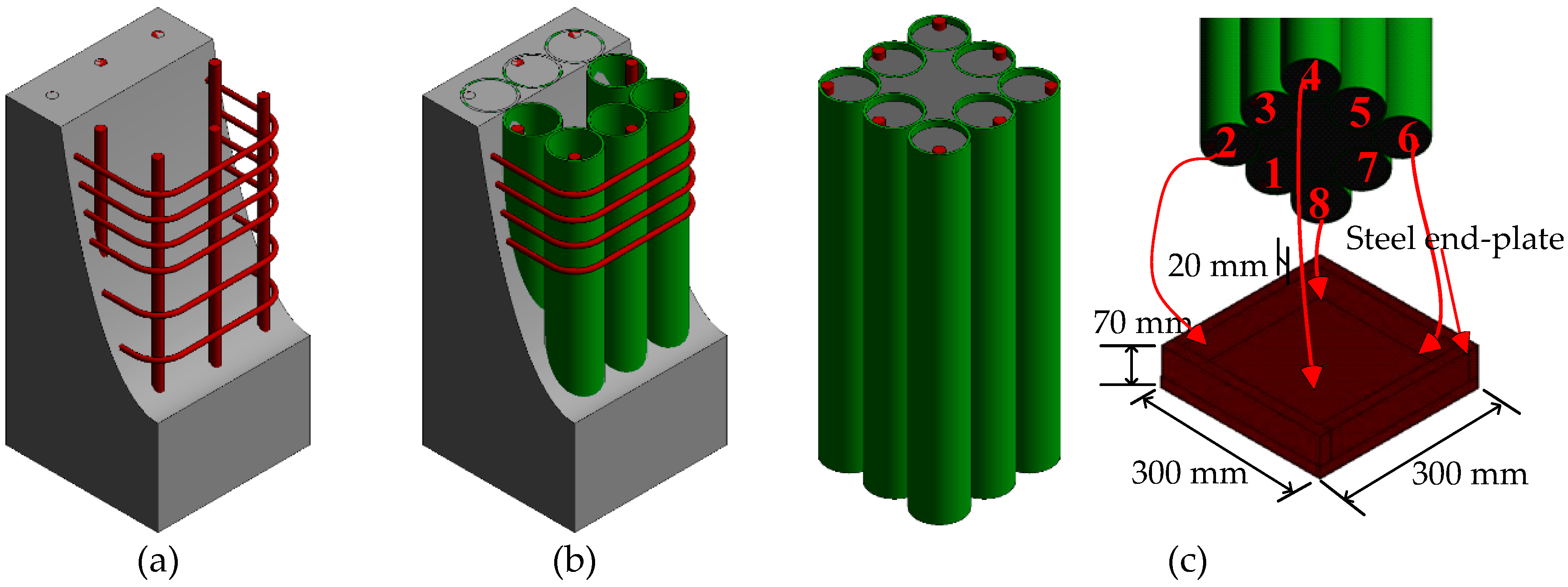
2.1. Specimens Details
- (1).
- The FCCCs were poured in the factory and transported to the laboratory;
- (2).
- The stirrups were tied into a skeleton (for specimen T8) or the position of the prefabricated steel end-plate was fixed (for specimen T8N);
- (3).
- The FCCCs were placed into the skeleton of the rebar (for specimen T8) or steel end-plates (for specimen T8N);
- (4).
- The concrete was poured into the specified location. The detailed parameters, including the size (b×h), height (H) and tube quantity, are shown in Table 1.
2.2. Material Properties
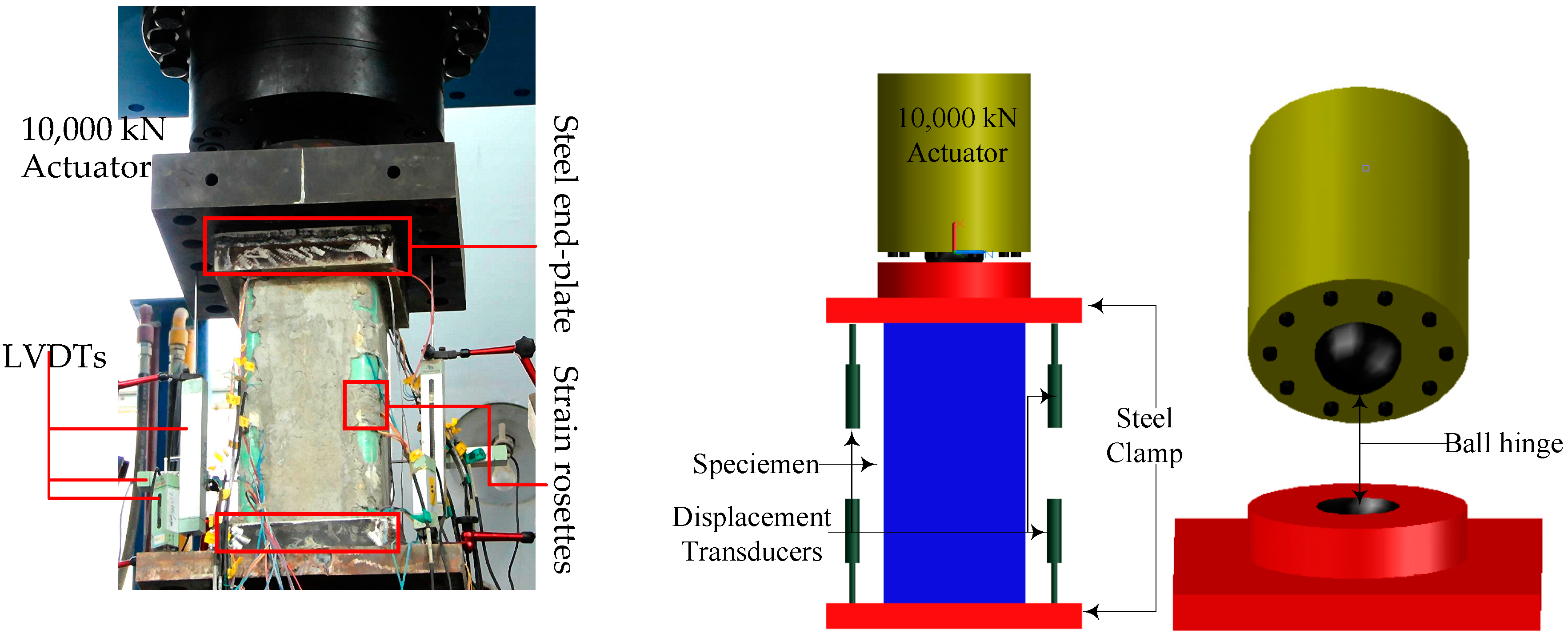
2.3. Setup and Instrumentation
3. Results
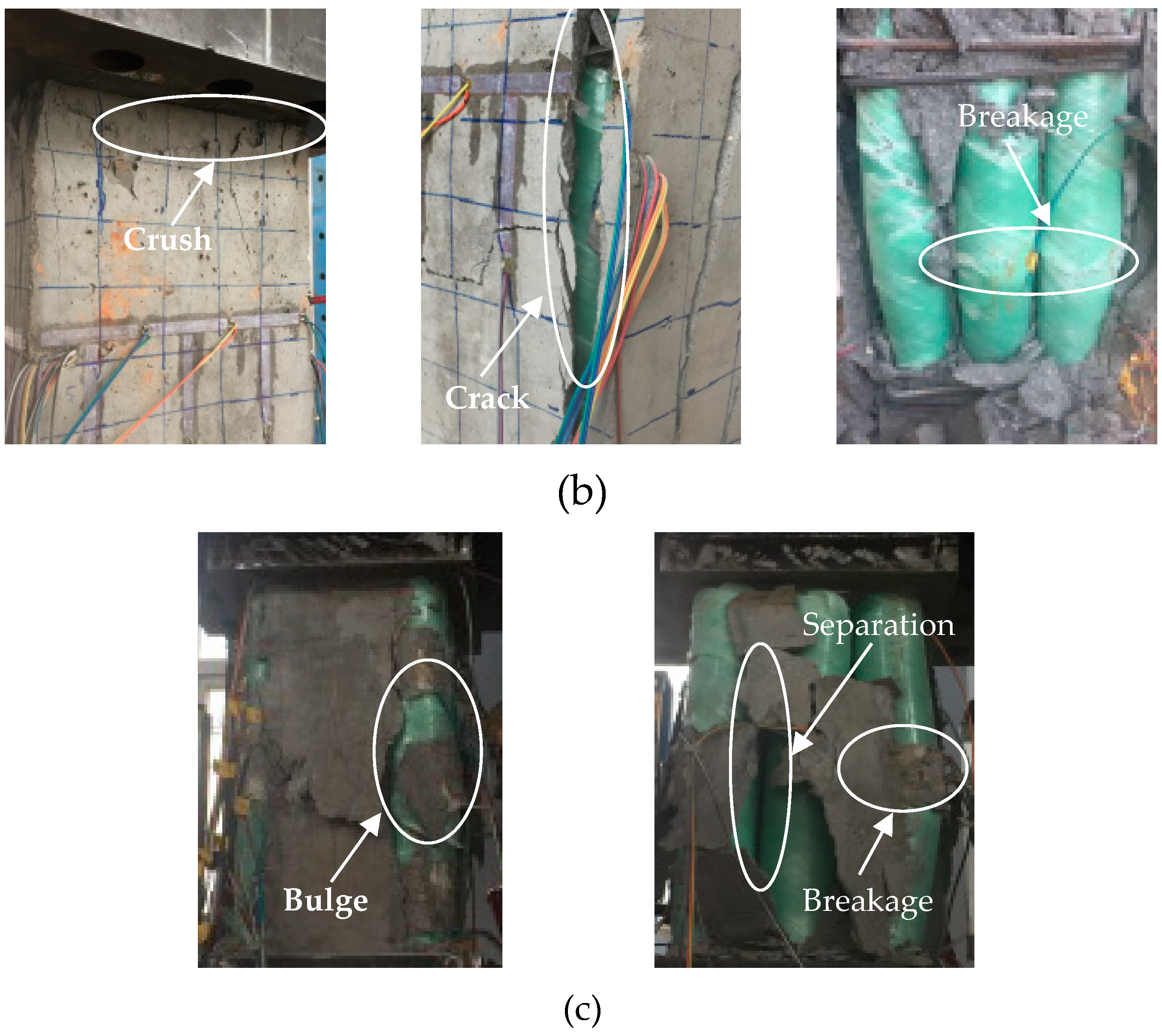
3.1. Failure Modes
3.2. Strength Analysis
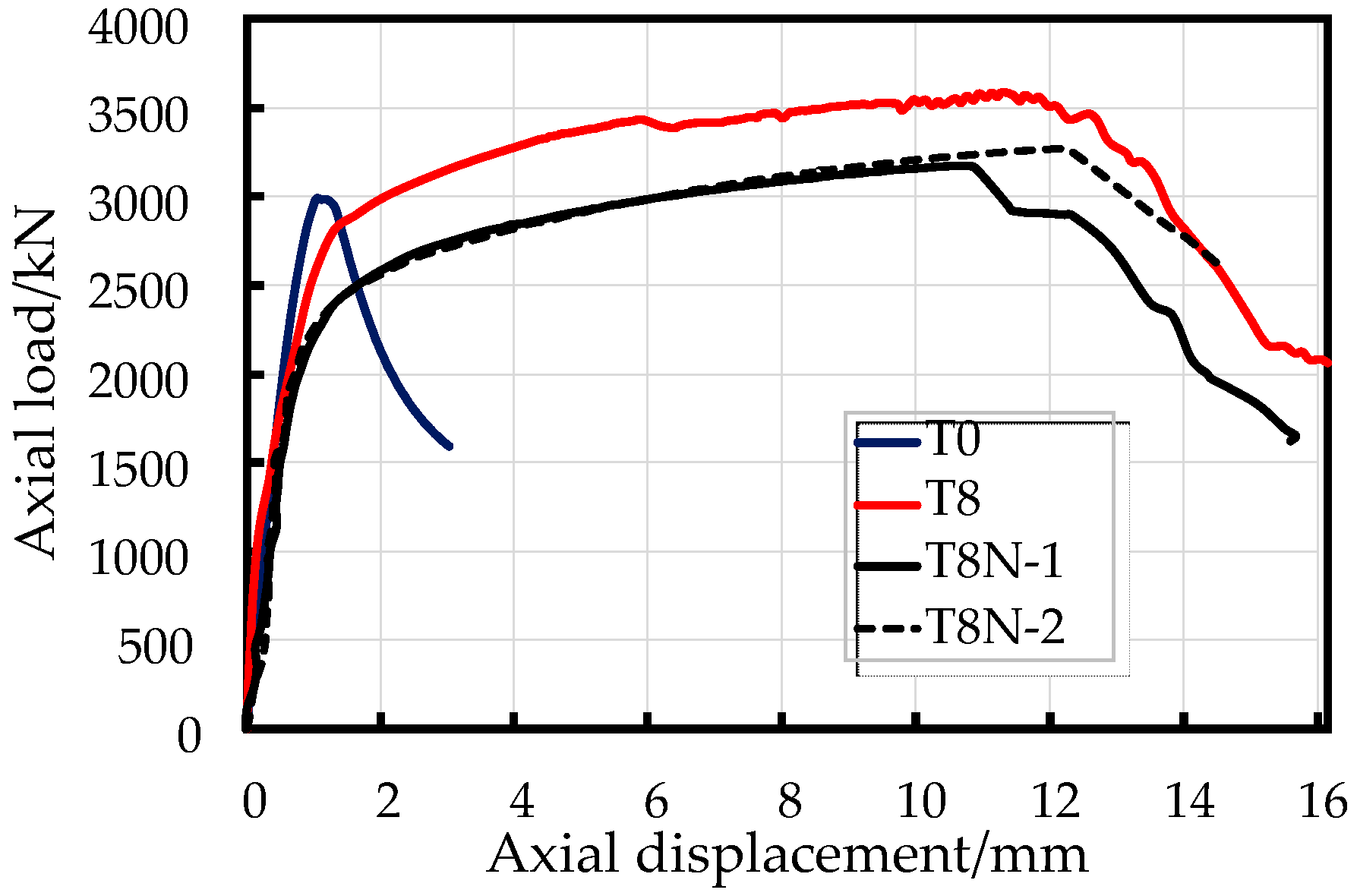
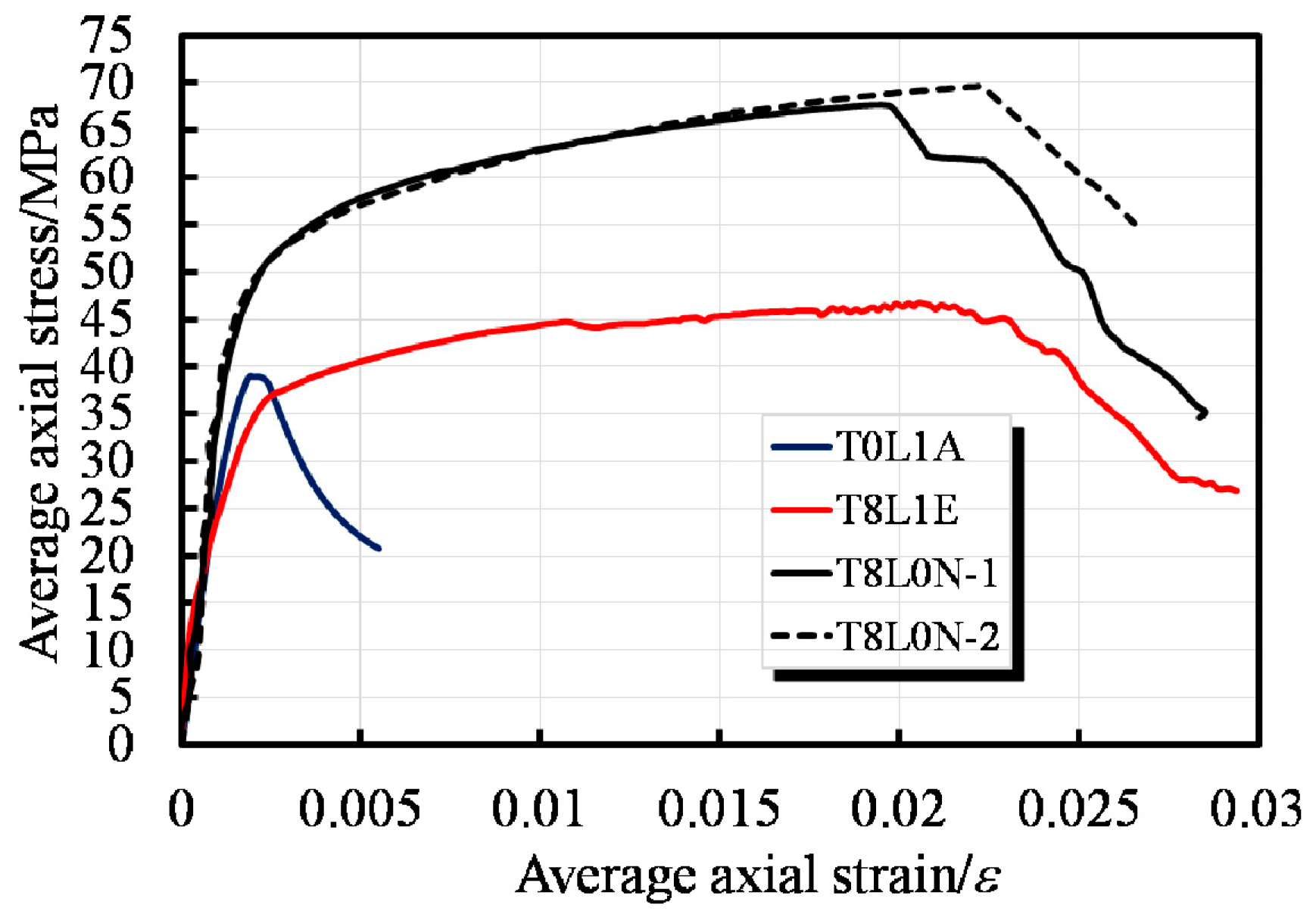
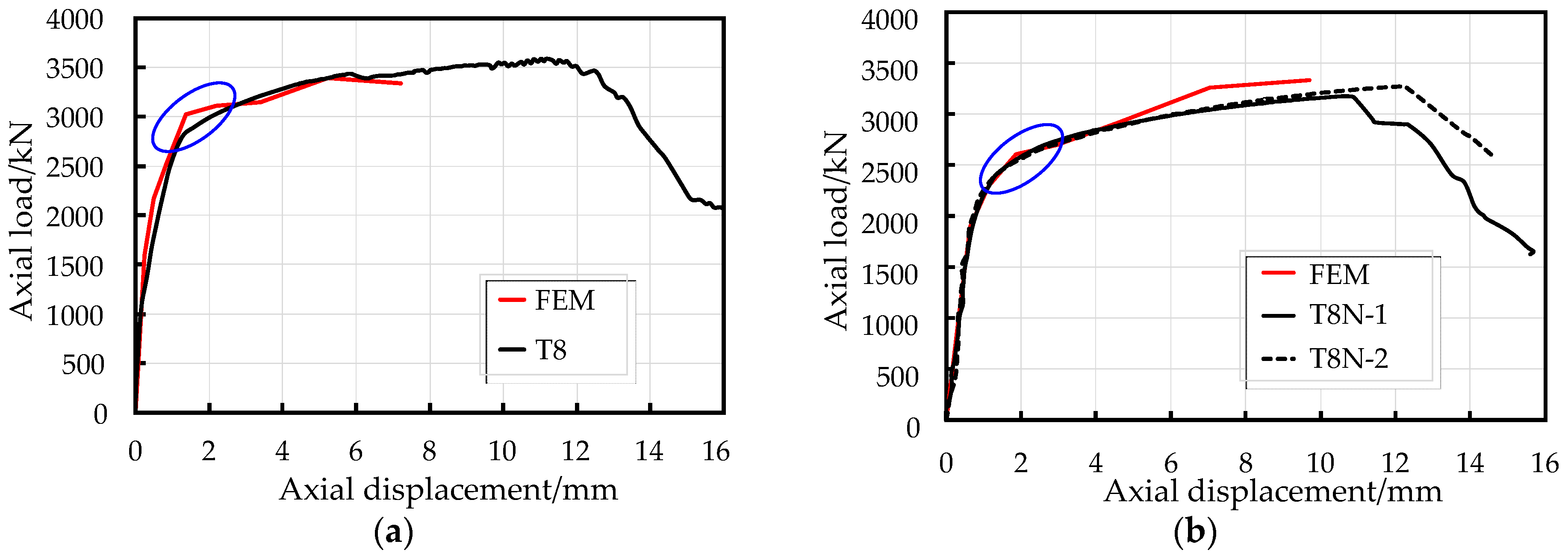
3.3. Load-Displacement Relationships
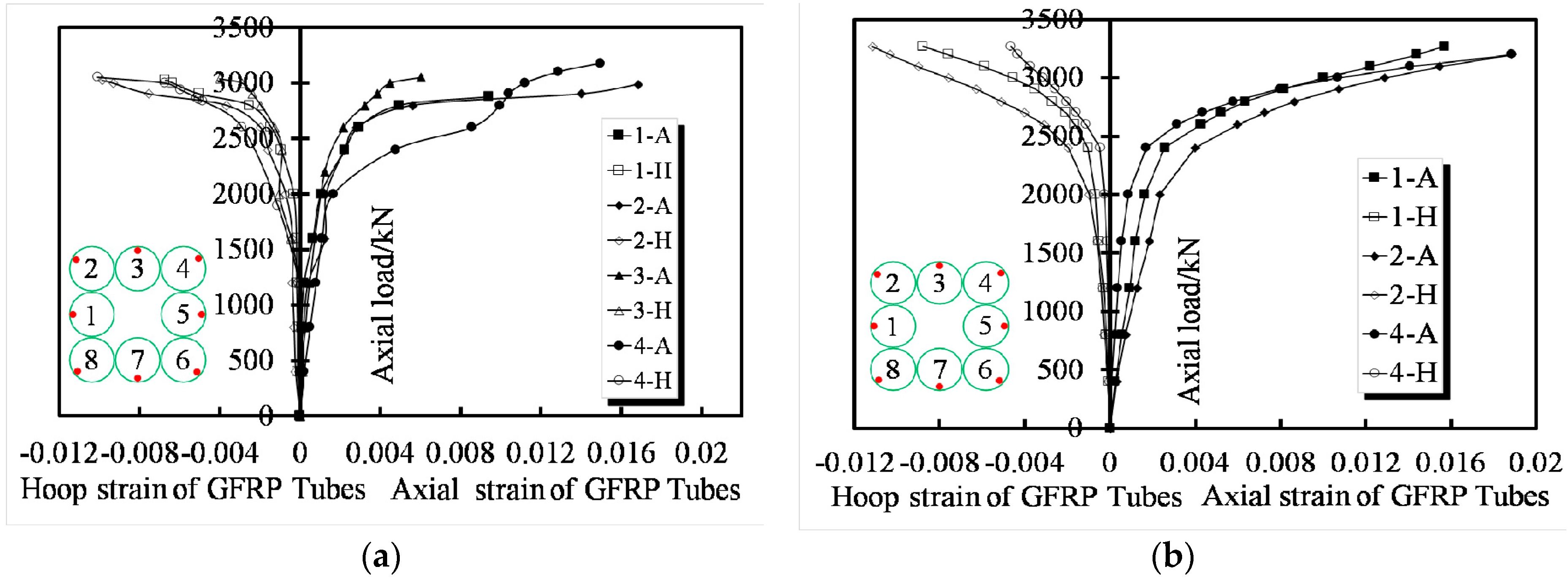
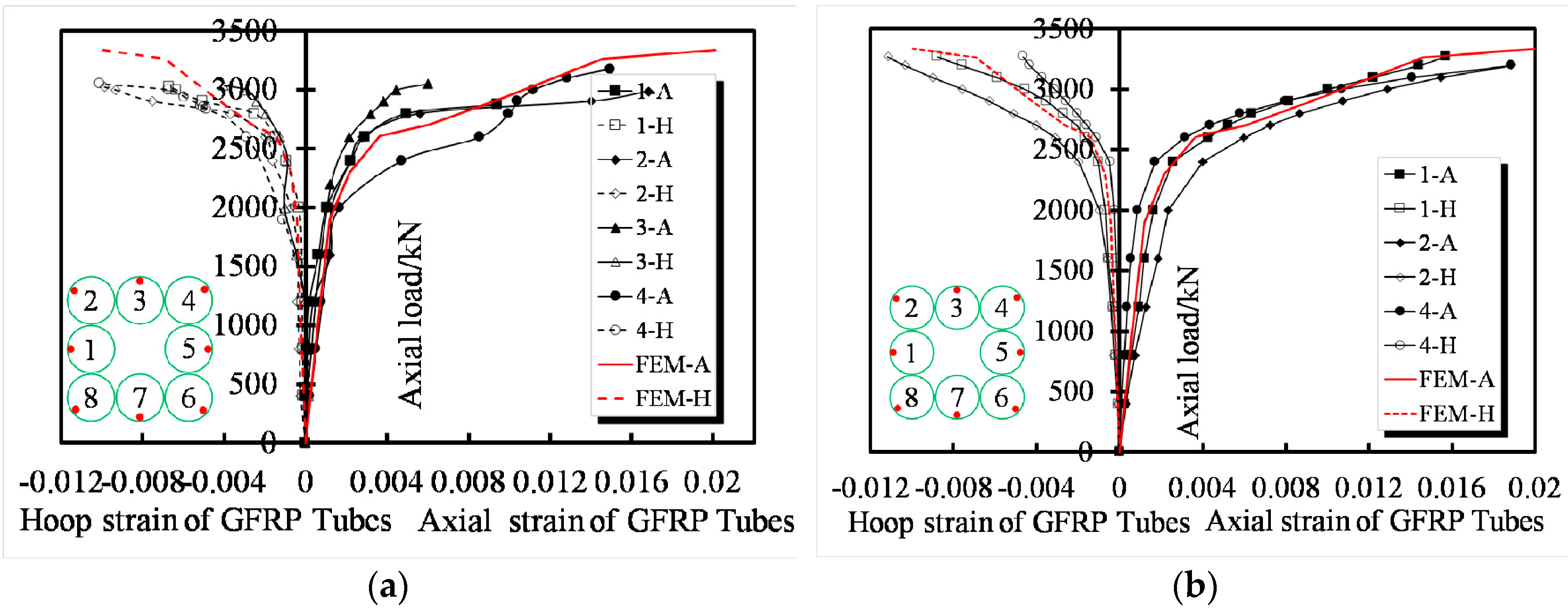
3.4. Load–Strain Response
4. Theory Analysis
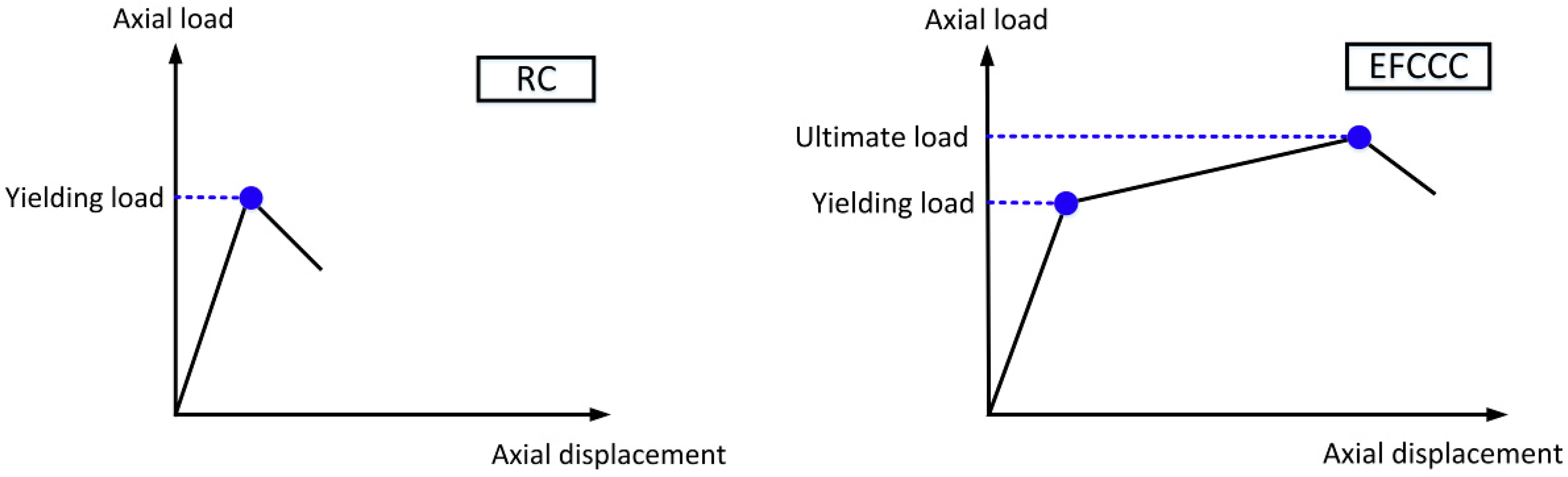
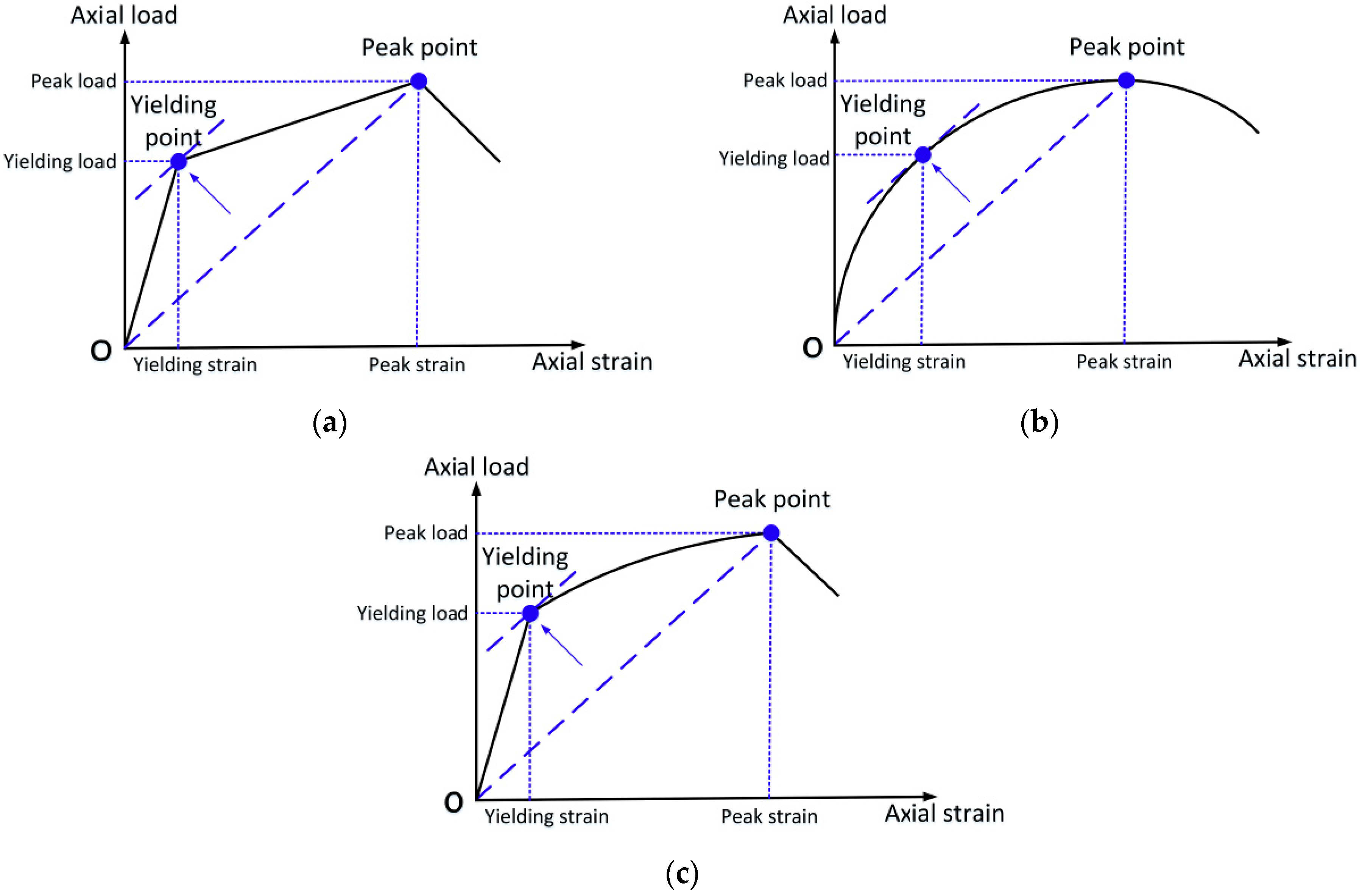
4.1. Yielding
4.2. Hardening Stage
4.3. Ductility
4.4. Theoretical Calculation
5. Numerical Simulation and Analysis
5.1. Description of the Finite Element Model (FEM)
5.2. Comparison of the Simulation Results
5.2.1. Comparison of the Failure Mode and Load–Strain Behavior
5.2.2. Comparison of Load-Displacement Behavior
6. Conclusions
- (1).
- The reduced bearing capacity of the EFCCC column is dominated by the fractures of corner tubes, and the sequential failures of the other tubes. The mechanical behavior of the EFCCC column consists of three distinct stages, namely, the first linear stage, the yielding stage, and the hardening stage.
- (2).
- Compared to specimen T8, the average yielding stress (fy) values of the T8N specimens increased by 42.89%, and the average peak stress (fu) values increased by 44.56%. These findings can be interpreted as the stress level of the unconfined outside concrete is much lower than that of the filled concrete and the core concrete. Compared to RC column, the ductility of the EFCCC column is increased by a factor of 5, and the ratio of the peak load to the yield load is also increased by a factor of 1.28–1.31, due to the effective stress redistribution caused by the built-in FCCCs.
- (3).
- An analytical model that considers the effect of the slenderness ratio on the internal FCCCs of the column was developed to predict the axial behavior of the EFCCC column. The analytical predictions were generally in good agreement with the experimental results.
- (4).
- A finite element model based on the D-P model was developed that considers nonrelated flow and hardening rules and has a satisfactory degree of agreement with the experimentally determined peak load, yielding load, and the peak load to yielding load ratio; however, the model did not accurately predict the yielding load and peak load of specimen T8N because the D-P model, which is the ideal plastic model, does not consider the cracking and damage of concrete. In future studies, many experiments with variable parameters should be conducted for the purpose of more meaningful results regarding EFCCC column.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, P.; Ye, L.P.; Huang, Y.L. Deformability and new performance indices of flexural members. Eng. Mech. 2005, 22, 28–36. [Google Scholar]
- Yuan, F.; Chen, L.P.; Chen, M.C.; Xu, K.C. Behaviour of Hybrid Steel and FRP-Reinforced Concrete—ECC Composite Columns under Reversed Cyclic Loading. Sensors 2018, 18, 4231. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Libreros, J.H.; Sneed, L.H.; D’Antino, T.; Pellegrino, C. Behavior of RC beams strengthened in shear with FRP and FRCM composites. Eng. Struct. 2017, 150, 830–842. [Google Scholar] [CrossRef]
- Oller, E.; Pujol, M.; Marí, A. Contribution of externally bonded FRP shear reinforcement to the shear strength of RC beams. Compos. Part 2019, 164, 235–248. [Google Scholar] [CrossRef]
- Shaw, I.; Andrawes, B. Repair of damaged end regions of PC beams using externally bonded FRP shear reinforcement. Constr. Build. Mater. 2017, 148, 184–194. [Google Scholar] [CrossRef]
- Chellapandian, M.; Suriya Prakash, S.; Sharma, A. Axial compression-bending interaction behavior of severely damaged RC columns rapid repaired and strengthened using hybrid FRP composites. Constr. Build. Mater. 2019, 195, 390–404. [Google Scholar] [CrossRef]
- Zoppo, M.D.; Ludovico, M.D.; Balsamo, A.; Prota, A.; Manfredi, G. FRP for seismic strengthening of shear controlled RC columns: Experience from earthquakes and experimental analysis. Compos. Part 2017, 129, 47–57. [Google Scholar] [CrossRef]
- Khorramian, K.; Sadeghian, P. Performance of high-modulus near-surface-mounted FRP laminates for strengthening of concrete columns. Compos. Part 2019, 164, 90–102. [Google Scholar] [CrossRef]
- Jiang, C.; Yuan, F.; Wu, Y.F.; Zhao, X.M. Effect of Interfacial Bond on Plastic Hinge Length of FRP-Confined RC Columns. J. Compos. Constr. 2019, 23, 04019007. [Google Scholar] [CrossRef]
- Lau, D.; Qiu, Q.W.; Zhou, A.; Chow, C.L. Long term performance and fire safety aspect of FRP composites used in building structures. Constr. Build. Mater. 2016, 126, 573–585. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented Stress–Strain Model for FRP-confined Concrete in Rectangular Columns. J. Reinf. Plast. Compos. 2003, 22, 1149–1186. [Google Scholar] [CrossRef]
- Karam, G.; Tabbara, M. Confinement Effectiveness in Rectangular Concrete Columns with Fiber Reinforced Polymer Wraps. J. Compos. Constr. 2005, 9, 388–396. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civil Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Wang, W.Q.; Sheikh, M.N.; Hadi, N.S.M.; Gao, D.Y.; Chen, G. Behaviour of concrete-encased concrete-filled FRP tube (CCFT) columns under axial compression. Eng. Struct. 2017, 147, 256–268. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Influence of fiber orientation and specimen end condition on axial compressive behavior of FRP-confined concrete. Constr. Build. Mater. 2013, 47, 814–826. [Google Scholar] [CrossRef]
- Guler, S.; Ashour, A. Review of Current Design Guidelines for Circular FRP-Wrapped Plain Concrete Cylinders. J. Compos. Constr. 2016, 20, 04015057. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M.; Samaan, M.; El Echary, H. Effect of Column Parameters on FRP-Confined Concrete. J. Compos. Constr. 1998, 2, 175–185. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Hassan, M.; Mohamed, H.; Abouzied, A.; Masmoudi, R. Axial behavior of circular CFFT long columns internally reinforced with steel or carbon and glass FRP longitudinal bars. Eng. Struct. 2018, 155, 267–278. [Google Scholar] [CrossRef]
- Khan, S.Q.; Sheikh, M.N.; Hadi, N.S.M. Concrete Filled Carbon FRP Tube (CFRP-CFFT) columns with and without CFRP reinforcing bars Axial-flexural interactions. Compos. Part 2018, 133, 42–52. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T. Compressive behavior of concrete-filled FRP tube columns Assessment of critical column parameters. Eng. Struct. 2013, 51, 188–199. [Google Scholar] [CrossRef]
- Wang, L.M.; Wu, Y.F. Effect of corner radius on the performance of CFRP-confined square concrete columns Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wei, Y.Y. Effect of cross-sectional aspect ratio on the strength of CFRP-confined rectangular concrete columns. Eng. Struct. 2010, 32, 32–45. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Moshiri, N.; Mortazavi, N. Effect of corner radius and aspect ratio on compressive behavior of rectangular concrete columns confined with CFRP. Mater. Struct. 2013, 48, 1–16. [Google Scholar] [CrossRef]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- ASTM D 2290-2012. Standard Test Method for Apparent Hoop Tensile Strength of Plastic or Reinforced Plastic Pipe by Split Disk Method; American Society for Testing and Materials: West Conshohocken, PA, USA, 2012. [Google Scholar]
- ASTM D 695-2010. Standard Test Method for Compressive Properties of Rigid Plastics; American Society for Testing and Materials: West Conshohocken, PA, USA, 2010. [Google Scholar]
- GB 50010-2010. National Standard of the People’s Republic of China. Code for Design of Concrete Structures; China Architecture and Building Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Park, R. Ductility evaluation from laboratory and analytical testing. In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]
- Lam, L.; Teng, J.G. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Feng, Y.; Niu, D. Effect of slenderness ratio on the bearing capacity of FRP-confined concrete columns. China Civil Eng. J. 2008, 41, 40–44. [Google Scholar]
- Cheng, S.; Feng, P.; Bai, Y.; Ye, L.P. Load-Strain Model for Steel-Concrete-FRP-Concrete Columns in Axial Compression. J. Compos. Constr. 2016, 20, 04016017. [Google Scholar] [CrossRef]
- Shahawy, M.; Mirmiran, A.; Beitelman, T. Tests and modeling of carbon-wrapped concrete columns. Compos. Part 2000, 31, 471–480. [Google Scholar] [CrossRef]
- Mirmiran, A.; Zagers, K.; Yuan, W. Nonlinear Finite Element Modeling of Concrete Confined by Fiber Composites; Elsevier Science Publishers: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-I Drucker-Prager type plasticity model. Eng. Struct. 2010, 32, 665–679. [Google Scholar] [CrossRef]




| Specimens | Size (b×h) (mm) | H1 (mm) | 2 (MPa) | d3 (mm) | t4 (mm) | Location of Stirrup | Location of Longitudinal Bars |
|---|---|---|---|---|---|---|---|
| T0 | 277×277 | 550 | 30 | / | / | φ8@40 φ8@70 | 8Φ16 |
| T8 | 277×277 | 550 | 30 | 77 | 3.5 | φ8@40 | 8Φ16 |
| T8N-1 | 231×231 | 550 | 30 | 77 | 3.5 | / | 8Φ16 |
| T8N-2 | 231×231 | 550 | 30 | 77 | 3.5 | / | 8Φ16 |
| Strength (MPa) | Ultimate Strain | Young’s Modulus (GPa) | Poisson’s Ratio | |
|---|---|---|---|---|
| Hoop tension | (ffrp) 365.10 | (εl) 0.030 | (El) 12.17 | (υl) 0.31 |
| Axial compression | (fac) 88.18 | (εac) 0.031 | (Eac) 2.82 | (υac) 0.33 |
| Cube Compressive Strength (MPa) | Axial Compressive Strength (MPa) | Axial Compressive Strain | Young’s Modulus (GPa) | Secant Modulus (GPa) |
|---|---|---|---|---|
| () 36.45 | () 28.80 | (εc) 0.00189 | (E0) 25.38 | (Ep) 15.22 |
| Ny (kN) | Nu (kN) | A (mm2) | fy (MPa) | fu (MPa) | ey (mm) | eu (mm) | k1 (GPa) | k2 (GPa) | γ | μ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T0 | 2600 | 2990 | 76729 | 33.86 | 38.97 | 0.72 | 1.04 | 36.11 | 3.75 | 1.03 | 1.44 |
| T8 | 2800 | 3590 | 76729 | 36.49 | 46.79 | 1.28 | 11.28 | 21.88 | 0.70 | 1.28 | 8.81 |
| T8N-1 | 2450 | 3178 | 46987 | 52.14 | 67.64 | 1.30 | 10.68 | 18.85 | 0.68 | 1.30 | 8.22 |
| T8N-2 | 2500 | 3270 | 46987 | 53.21 | 69.59 | 1.32 | 12.16 | 18.94 | 0.63 | 1.31 | 9.21 |
| Ny (kN) | NyT (kN) | NyT/Ny | Nu (kN) | NuT (kN) | NuT/Nu | |
|---|---|---|---|---|---|---|
| T8 | 2800 | 2989.56 | 1.07 | 3590 | 3723.11 | 1.18 |
| T8N-1 | 2450 | 2351.13 | 0.96 | 3178 | 2910.94 | 1.03 |
| T8N-2 | 2500 | 2351.13 | 0.94 | 3270 | 2910.94 | 1.01 |
| Avg | - | - | 0.99 | - | - | 1.07 |
| Ny (kN) | NyN (kN) | NyN/Ny | Nu (kN) | NuN (kN) | NuN/Nu | γ | γN | |
|---|---|---|---|---|---|---|---|---|
| T8 | 2800 | 3022.5 | 1.08 | 3590 | 3340.88 | 0.93 | 1.28 | 1.10 |
| T8N-1 | 2450 | 2607.0 | 1.06 | 3178 | 3336.334 | 1.05 | 1.30 | 1.27 |
| T8N-2 | 2500 | 2607.0 | 1.04 | 3270 | 3336.334 | 1.02 | 1.31 | 1.27 |
| Avg | - | - | 1.06 | - | - | 1 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Qi, Y.; Sun, Y.; Xie, Z.; Liu, W. Compressive Behavior of Composite Concrete Columns with Encased FRP Confined Concrete Cores. Sensors 2019, 19, 1792. https://doi.org/10.3390/s19081792
Wang X, Qi Y, Sun Y, Xie Z, Liu W. Compressive Behavior of Composite Concrete Columns with Encased FRP Confined Concrete Cores. Sensors. 2019; 19(8):1792. https://doi.org/10.3390/s19081792
Chicago/Turabian StyleWang, Xuxu, Yujun Qi, Yunlou Sun, Zhijin Xie, and Weiqing Liu. 2019. "Compressive Behavior of Composite Concrete Columns with Encased FRP Confined Concrete Cores" Sensors 19, no. 8: 1792. https://doi.org/10.3390/s19081792
APA StyleWang, X., Qi, Y., Sun, Y., Xie, Z., & Liu, W. (2019). Compressive Behavior of Composite Concrete Columns with Encased FRP Confined Concrete Cores. Sensors, 19(8), 1792. https://doi.org/10.3390/s19081792




