Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Experimental Protocol
2.3. Experimental Procedures
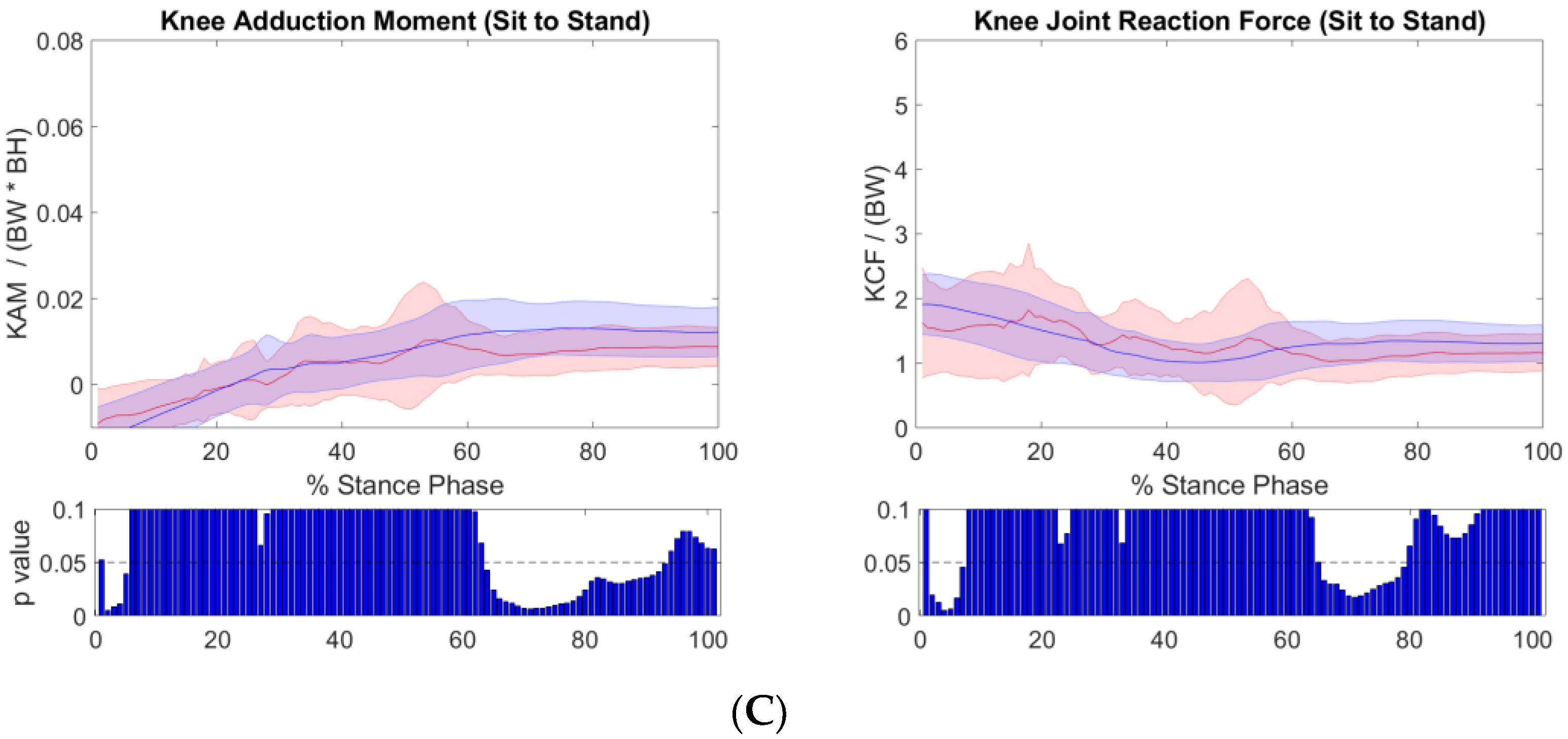
2.4. Data Analysis
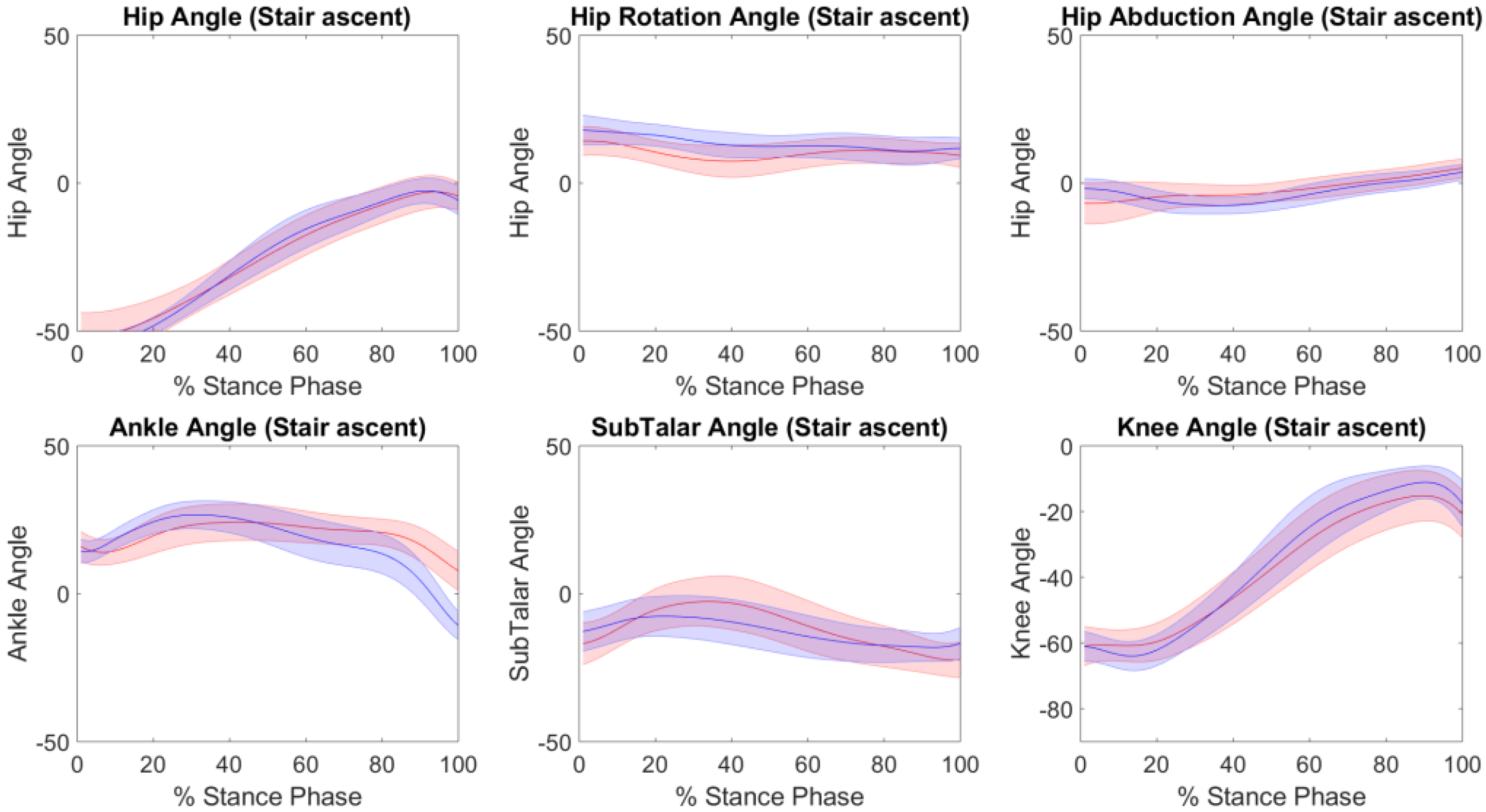
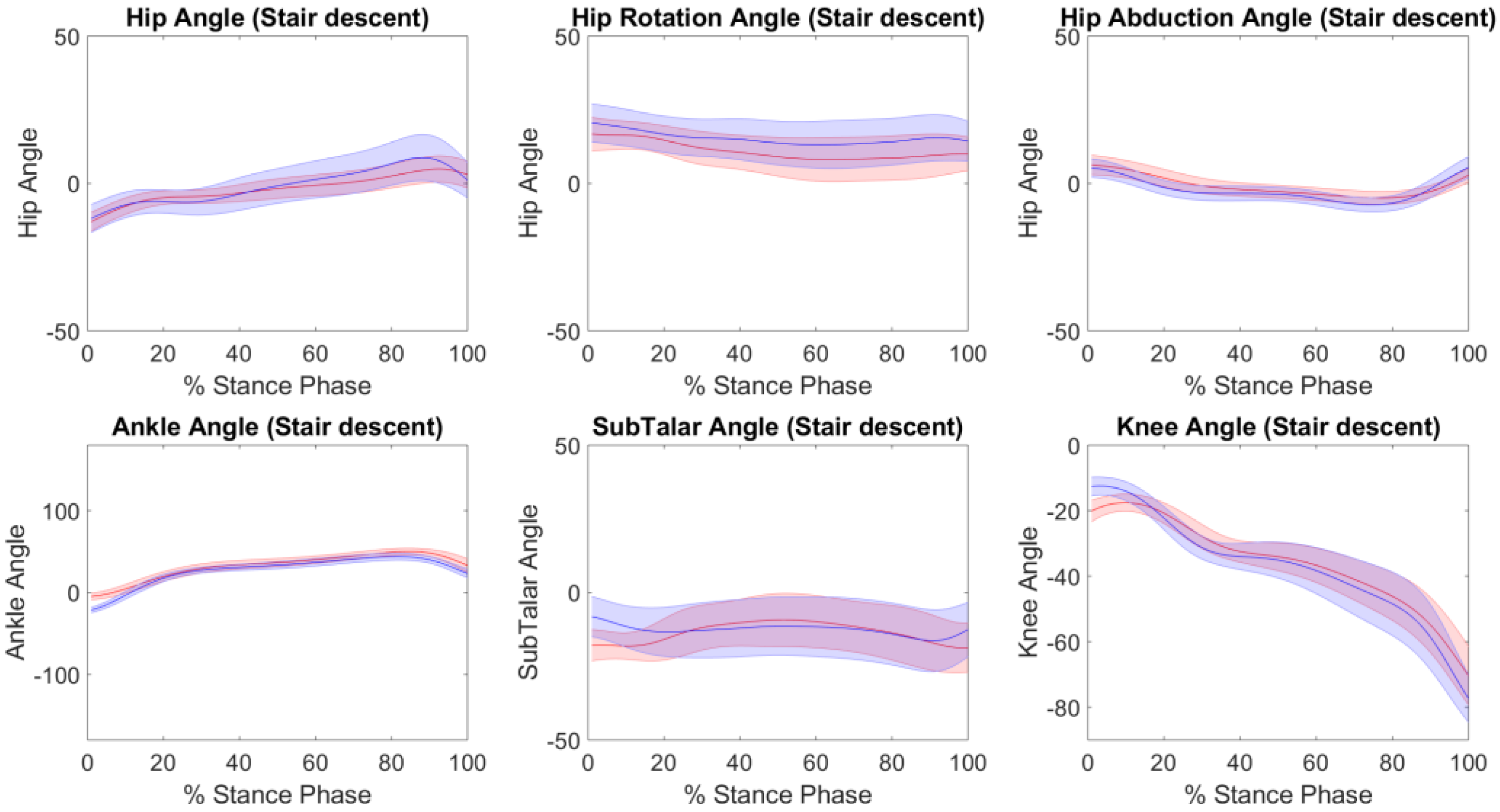
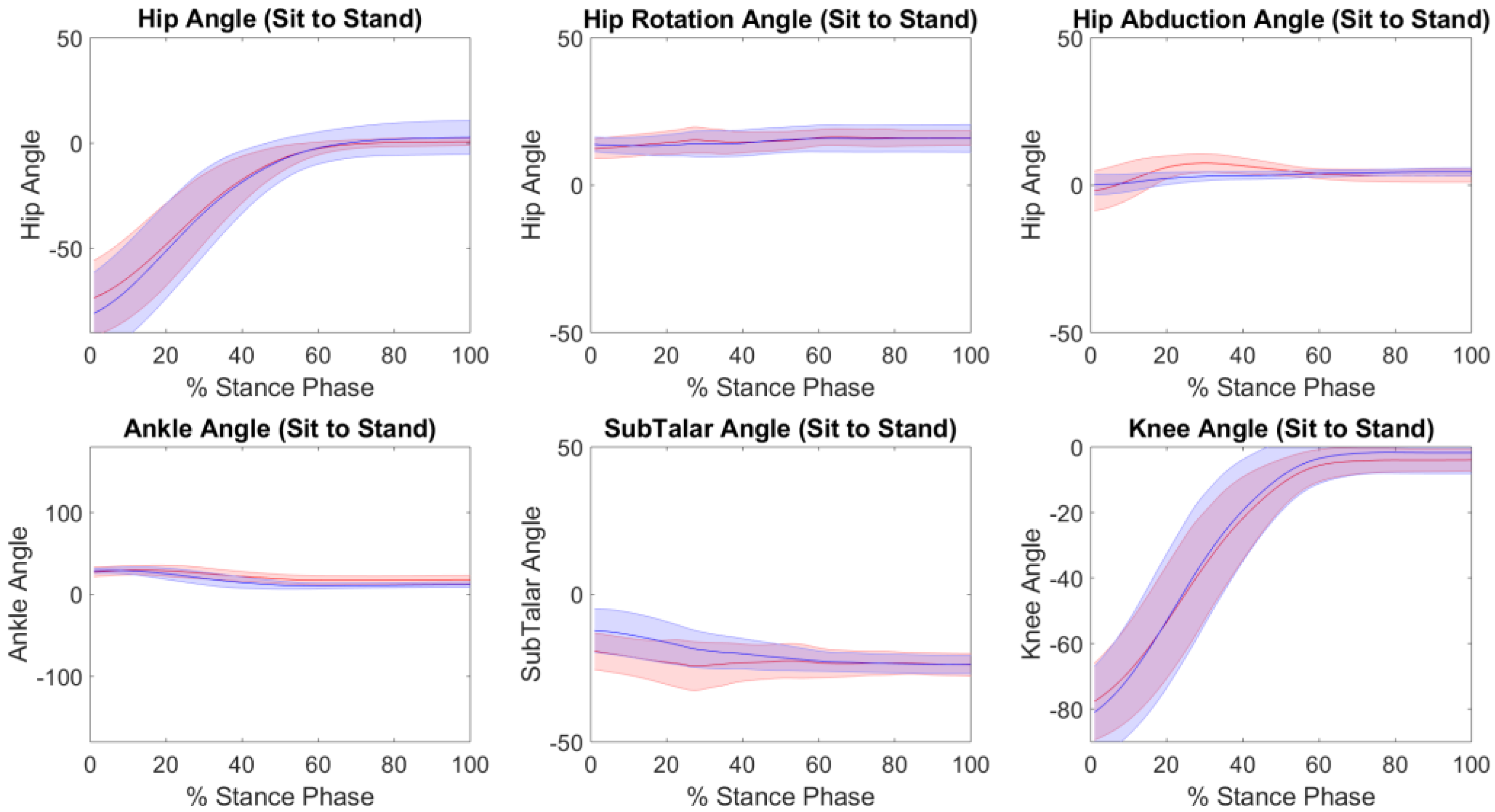
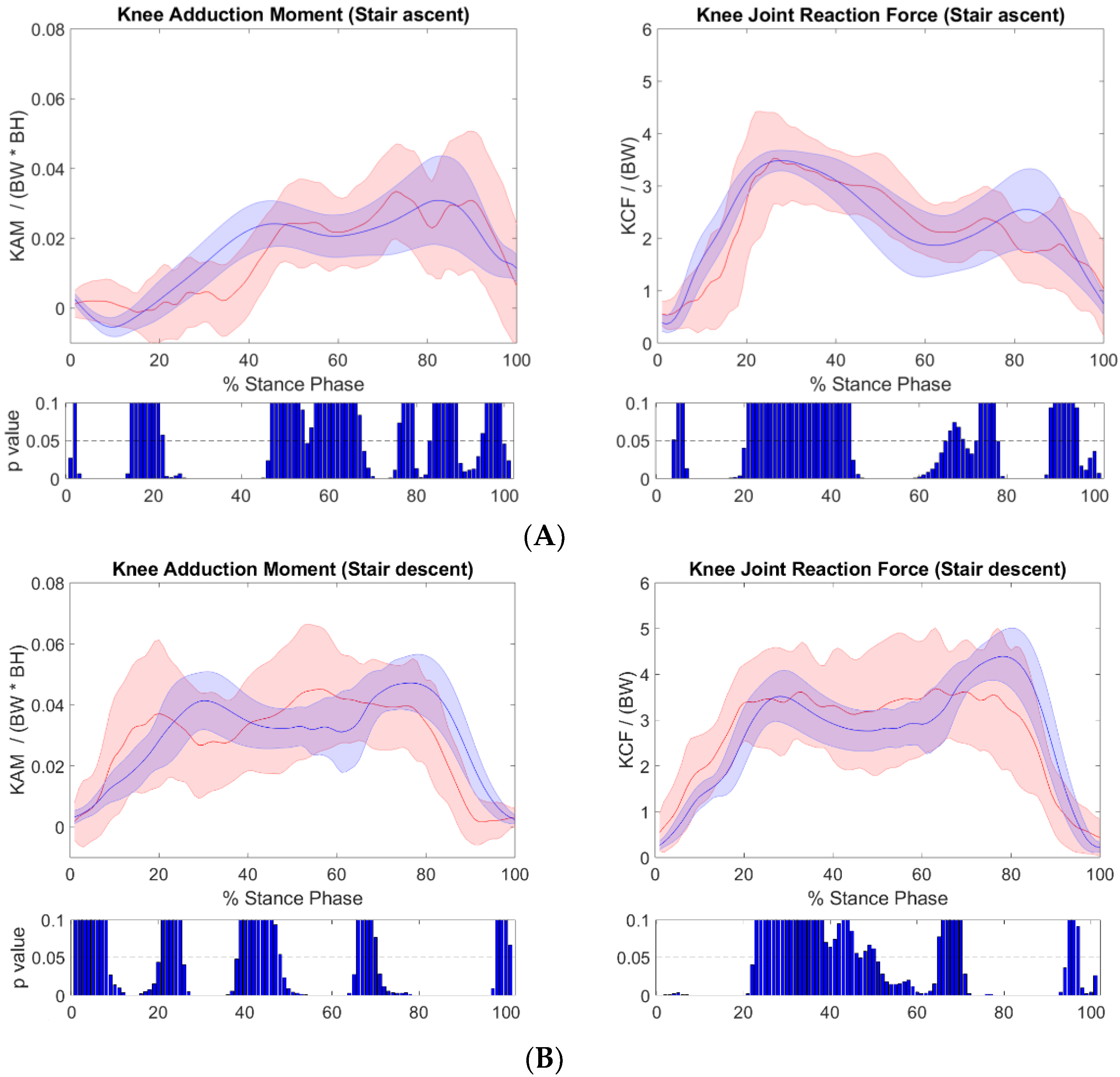
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hurley, M.V; Scott, D.L.; Rees, J.; Newham, D.J. Sensorimotor Changes and Functional Performance in Patients with Knee Osteoarthritis. Ann. Rheum. Dis. 1997, 56, 641–648. [Google Scholar] [CrossRef]
- Cicuttini, F.M.; Wluka, A.E.; Stuckey, S.L. Tibial and Femoral Cartilage Changes in Knee Osteoarthritis. Ann. Rheum. Dis. 2001, 60, 977–980. [Google Scholar] [CrossRef]
- Amin, S.; LaValley, M.P.; Guermazi, A.; Grigoryan, M.; Hunter, D.J.; Clancy, M.; Niu, J.; Gale, D.R.; Felson, D.T. The Relationship between Cartilage Loss on Magnetic Resonance Imaging and Radiographic Progression in Men and Women with Knee Osteoarthritis. Arthritis Rheum. 2005, 52, 3152–3159. [Google Scholar] [CrossRef] [PubMed]
- Felson, D.T.; McLaughlin, S.; Goggins, J.; LaValley, M.P.; Gale, M.E.; Totterman, S.; Li, W.; Hill, C.; Gale, D. Bone Marrow Edema and Its Relation to Progression of Knee Osteoarthritis. Ann. Intern. Med. 2003, 139(5_Part_1), 330–336. [Google Scholar] [CrossRef]
- Hunter, D.J.; Zhang, Y.; Niu, J.; Goggins, J.; Amin, S.; LaValley, M.P.; Guermazi, A.; Genant, H.; Gale, D.; Felson, D.T. Increase in Bone Marrow Lesions Associated with Cartilage Loss: A Longitudinal Magnetic Resonance Imaging Study of Knee Osteoarthritis. Arthritis Rheum. Off. J. Am. Coll. Rheumatol. 2006, 54, 1529–1535. [Google Scholar] [CrossRef] [PubMed]
- Andriacchi, T.P.; Mündermann, A. The Role of Ambulatory Mechanics in the Initiation and Progression of Knee Osteoarthritis. Curr. Opin. Rheumatol. 2006, 18, 514–518. [Google Scholar] [CrossRef]
- Ghafari, A.S.; Meghdari, A.; Vossoughi, G.R. Muscle-Driven Forward Dynamics Simulation for the Study of Differences in Muscle Function during Stair Ascent and Descent. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2009, 223, 863–874. [Google Scholar] [CrossRef] [PubMed]
- Riener, R.; Rabuffetti, M.; Frigo, C. Stair Ascent and Descent at Different Inclinations. Gait Posture 2002, 15, 32–44. [Google Scholar] [CrossRef]
- Rowe, P.J.; Myles, C.M.; Walker, C.; Nutton, R. Knee Joint Kinematics in Gait and Other Functional Activities Measured Using Flexible Electrogoniometry: How Much Knee Motion Is Sufficient for Normal Daily Life? Gait Posture 2000, 12, 143–155. [Google Scholar] [CrossRef]
- Brown, K.; Kachelman, J.; Topp, R.; Quesada, P.M.; Nyland, J.; Malkani, A.; Swank, A.M. Predictors of Functional Task Performance among Patients Scheduled for Total Knee Arthroplasty. J. Strength Cond. Res. 2009, 23, 436–443. [Google Scholar] [CrossRef]
- Asay, J.L.; Mündermann, A.; Andriacchi, T.P. Adaptive Patterns of Movement during Stair Climbing in Patients with Knee Osteoarthritis. J. Orthop. Res. 2009, 27, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Hicks-Little, C.A.; Peindl, R.D.; Hubbard, T.J.; Scannell, B.P.; Springer, B.D.; Odum, S.M.; Fehring, T.K.; Cordova, M.L. Lower Extremity Joint Kinematics during Stair Climbing in Knee Osteoarthritis. Med. Sci. Sport. Exerc. 2011, 43, 516–524. [Google Scholar] [CrossRef] [PubMed]
- Foroughi, N.; Smith, R.; Vanwanseele, B. The Association of External Knee Adduction Moment with Biomechanical Variables in Osteoarthritis: A Systematic Review. Knee 2009, 16, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Sharma, L.; Hurwitz, D.E.; Thonar, E.J.-M.; Sum, J.A.; Lenz, M.E.; Dunlop, D.D.; Schnitzer, T.J.; Kirwan-Mellis, G.; Andriacchi, T.P. Knee Adduction Moment, Serum Hyaluronan Level, and Disease Severity in Medial Tibiofemoral Osteoarthritis. Arthritis Rheum. 1998, 41, 1233–1240. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and Orientation in Space of Bones during Movement: Anatomical Frame Definition and Determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M.; Zaciorskij, V.M. Kinetics of Human Motion; Human Kinetics: Champaign, IL, USA, 2002. [Google Scholar]
- Winby, C.R.; Lloyd, D.G.; Besier, T.F.; Kirk, T.B. Muscle and External Load Contribution to Knee Joint Contact Loads during Normal Gait. J. Biomech. 2009, 42, 2294–2300. [Google Scholar] [CrossRef]
- Schepers, H.M.; Koopman, H.F.J.M.; Veltink, P.H. Ambulatory Assessment of Ankle and Foot Dynamics. IEEE Trans. Biomed. Eng. 2007, 54, 895–902. [Google Scholar] [CrossRef]
- Karatsidis, A.; Bellusci, G.; Schepers, H.M.; de Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of Ground Reaction Forces and Moments during Gait Using Only Inertial Motion Capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef] [PubMed]
- Fluit, R.; Andersen, M.S.; Kolk, S.; Verdonschot, N.; Koopman, H.F.J.M. Prediction of Ground Reaction Forces and Moments during Various Activities of Daily Living. J. Biomech. 2014, 47, 2321–2329. [Google Scholar] [CrossRef]
- Luinge, H.J.; Veltink, P.H. Measuring Orientation of Human Body Segments Using Miniature Gyroscopes and Accelerometers. Med. Biol. Eng. Comput. 2005, 43, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors. Xsens Motion Technol. BV Tech. Rep. 2009, 1. Available online: https://www.researchgate.net/profile/Per_Slycke/publication/239920367_Xsens_MVN_Full_6DOF_human_motion_tracking_using_miniature_inertial_sensors/links/0f31752f1f60c20b18000000/Xsens-MVN-Full-6DOF-human-motion-tracking-using-miniature-inertial-sensors.pdf (accessed on 8 April 2019).
- Felson, D.T.; Zhang, Y.; Hannan, M.T.; Naimark, A.; Weissman, B.; Aliabadi, P.; Levy, D. Risk Factors for Incident Radiographic Knee Osteoarthritis in the Elderly. The Framingham Study. Arthritis Rheum. 1997, 40, 728–733. [Google Scholar] [CrossRef] [PubMed]
- Schepers, M.; Giuberti, M.; Bellusci, G. Xsens MVN: Consistent Tracking of Human Motion Using Inertial Sensing. Available online: https://www.researchgate.net/profile/Martin_Schepers/publication/324007368_Xsens_MVN_Consistent_Tracking_of_Human_Motion_Using_Inertial_Sensing/links/5ab8be2f0f7e9b68ef51f7ba/Xsens-MVN-Consistent-Tracking-of-Human-Motion-Using-Inertial-Sensing.pdf (accessed on 8 April 2019).
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; De Zee, M. Analysis of Musculoskeletal Systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Horsman, M.D.K.; Koopman, H.F.J.M.; van der Helm, F.C.T.; Prosé, L.P.; Veeger, H.E.J. Morphological Muscle and Joint Parameters for Musculoskeletal Modelling of the Lower Extremity. Clin. Biomech. 2007, 22, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Veeger, H.E.J.; Yu, B.; An, K.-N.; Rozendal, R.H. Parameters for Modeling the Upper Extremity. J. Biomech. 1997, 30, 647–652. [Google Scholar] [CrossRef]
- De Zee, M.; Hansen, L.; Wong, C.; Rasmussen, J.; Simonsen, E.B. A Generic Detailed Rigid-Body Lumbar Spine Model. J. Biomech. 2007, 40, 1219–1227. [Google Scholar] [CrossRef]
- Andersen, M.S.; Damsgaard, M.; Rasmussen, J. Kinematic Analysis of Over-Determinate Biomechanical Systems. Comput. Methods Biomech. Biomed. Engin. 2009, 12, 371–384. [Google Scholar] [CrossRef]
- Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H.; Andersen, M.S. Musculoskeletal Model-Based Inverse Dynamic Analysis under Ambulatory Conditions Using Inertial Motion Capture. Med. Eng. Phys. 2019, 65, 68–77. [Google Scholar] [CrossRef]
- Skals, S.; Jung, M.K.; Damsgaard, M.; Andersen, M.S. Prediction of Ground Reaction Forces and Moments during Sports-Related Movements. Multibody Syst. Dyn. 2017, 39, 175–195. [Google Scholar] [CrossRef]
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A Subject-Specific Musculoskeletal Modeling Framework to Predict in Vivo Mechanics of Total Knee Arthroplasty. J. Biomech. Eng. 2015, 137, 20904. [Google Scholar] [CrossRef]
- Andersen, M.S.; Benoit, D.L.; Damsgaard, M.; Ramsey, D.K.; Rasmussen, J. Do Kinematic Models Reduce the Effects of Soft Tissue Artefacts in Skin Marker-Based Motion Analysis? An in Vivo Study of Knee Kinematics. J. Biomech. 2010, 43, 268–273. [Google Scholar]
- Schwartz, M.H.; Trost, J.P.; Wervey, R.A. Measurement and Management of Errors in Quantitative Gait Data. Gait Posture 2004, 20, 196–203. [Google Scholar] [CrossRef]
- Bergmann, J.H.M.; Mayagoitia, R.E.; Smith, I.C.H. A Portable System for Collecting Anatomical Joint Angles during Stair Ascent: A Comparison with an Optical Tracking Device. Dyn. Med. 2009, 8, 3. [Google Scholar] [CrossRef]
- Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H.; Andersen, M.S. Predicting Kinetics Using Musculoskeletal Modeling and Inertial Motion Capture. Available online: https://arxiv.org/pdf/1801.01668.pdf (accessed on 8 April 2019).
- Karatsidis, A.; Richards, R.E.; Konrath, J.M.; van den Noort, J.C.; Schepers, H.M.; Bellusci, G.; Harlaar, J.; Veltink, P.H. Validation of Wearable Visual Feedback for Retraining Foot Progression Angle Using Inertial Sensors and an Augmented Reality Headset. J. Neuroeng. Rehabil. 2018, 15, 78. [Google Scholar] [CrossRef]
- Bachmann, E.R. Inertial and Magnetic Tracking of Limb Segment Orientation for Inserting Humans into Synthetic Environments. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2000. [Google Scholar]
- Guo, M.; Axe, M.J.; Manal, K. The Influence of Foot Progression Angle on the Knee Adduction Moment during Walking and Stair Climbing in Pain Free Individuals with Knee Osteoarthritis. Gait Posture 2007, 26, 436–441. [Google Scholar] [CrossRef]
- Taylor, W.R.; Heller, M.O.; Bergmann, G.; Duda, G.N. Tibio-Femoral Loading during Human Gait and Stair Climbing. J. Orthop. Res. 2004, 22, 625–632. [Google Scholar] [CrossRef]
- Costigan, P.A.; Deluzio, K.J.; Wyss, U.P. Knee and Hip Kinetics during Normal Stair Climbing. Gait Posture 2002, 16, 31–37. [Google Scholar] [CrossRef]
- Kutzner, I.; Heinlein, B.; Graichen, F.; Bender, A.; Rohlmann, A.; Halder, A.; Beier, A.; Bergmann, G. Loading of the Knee Joint during Activities of Daily Living Measured in Vivo in Five Subjects. J. Biomech. 2010, 43, 2164–2173. [Google Scholar] [CrossRef]
- D’Lima, D.D.; Patil, S.; Steklov, N.; Slamin, J.E.; Colwell, C.W., Jr. Tibial Forces Measured in Vivo after Total Knee Arthroplasty. J. Arthroplasty 2006, 21, 255–262. [Google Scholar] [CrossRef]
- Mündermann, A.; Dyrby, C.O.; D’lima, D.D.; Colwell Jr, C.W.; Andriacchi, T.P. In Vivo Knee Loading Characteristics during Activities of Daily Living as Measured by an Instrumented Total Knee Replacement. J. Orthop. Res. 2008, 26, 1167–1172. [Google Scholar] [CrossRef]
- Rasnick, R.; Standifird, T.; Reinbolt, J.A.; Cates, H.E.; Zhang, S. Knee Joint Loads and Surrounding Muscle Forces during Stair Ascent in Patients with Total Knee Replacement. PLoS ONE 2016, 11, e0156282. [Google Scholar] [CrossRef]

| Stair Up | Stair Down | Sit to Stand | ||||
|---|---|---|---|---|---|---|
| Corr | RMSE | Corr | RMSE | Corr | RMSE | |
| Kinematics | ||||||
| SubTalar Eversion | 0.87 | 8 ± 4 | 0.256 | 6 ± 3 | 0.97 | 5 ± 3 |
| Ankle Plantar/Dorsi Flexion | 0.78 | 6 ± 2 | 0.98 | 6 ± 2 | 0.97 | 7 ± 3 |
| Knee Flexion/Extension | 0.99 | 4 ± 3 | 0.99 | 3 ± 2 | 0.99 | 4 ± 3 |
| Hip Flexion/Extension | 0.99 | 6 ± 4 | 0.95 | 4 ± 2 | 0.99 | 6 ± 2 |
| Hip Abduction | 0.77 | 3 ± 1 | 0.91 | 2 ± 1 | 0.53 | 3 ± 1 |
| Hip Rotation | 0.51 | 5 ± 2 | 0.96 | 4 ± 2 | 0.68 | 3 ± 2 |
| Kinetics | ||||||
| Knee Adduction Moment | 0.86 | 0.01 ± 0.003 | 0.74 | 0.014 ± 0.005 | 0.98 | 0.006 ± 0.002 |
| Knee Joint Reaction Force | 0.86 | 0.89 ± 0.32 | 0.85 | 0.9 ± 0.3 | 0.92 | 0.4 ± 0.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konrath, J.M.; Karatsidis, A.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Andersen, M.S. Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture. Sensors 2019, 19, 1681. https://doi.org/10.3390/s19071681
Konrath JM, Karatsidis A, Schepers HM, Bellusci G, de Zee M, Andersen MS. Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture. Sensors. 2019; 19(7):1681. https://doi.org/10.3390/s19071681
Chicago/Turabian StyleKonrath, Jason M., Angelos Karatsidis, H. Martin Schepers, Giovanni Bellusci, Mark de Zee, and Michael S. Andersen. 2019. "Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture" Sensors 19, no. 7: 1681. https://doi.org/10.3390/s19071681
APA StyleKonrath, J. M., Karatsidis, A., Schepers, H. M., Bellusci, G., de Zee, M., & Andersen, M. S. (2019). Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture. Sensors, 19(7), 1681. https://doi.org/10.3390/s19071681







