Variational Bayesian Based Adaptive Shifted Rayleigh Filter for Bearings-Only Tracking in Clutters
Abstract
1. Introduction
2. The Shifted Rayleigh Filter Algorithm
2.1. The Bearing Model
2.2. The Treatment of Clutter
3. Variational Bayesian Filtering
3.1. Conjugate Exponential Model
3.2. VB Approximation Method
- (1)
- The VB expectation step yields:
- (2)
- The VB maximization step yields that is conjugate and of the formwhere, and are the hyper-parameters, andwhere n is the dimension of the measurement.
4. VB Based Adaptive Shifted Rayleigh Filter with Unknown Clutter Probability
- (1)
- Optimization of for fixed .
- (2)
- Optimization of for fixed .
| Algorithm 1 : VB-SRF. |
(1) Initialization: , , , , , , (2) Prediction: where is the scale factor and . (3) Update: the update of VB-SRF utilizes iterate filtering framework. (3.a) First set: , , , , (3.b) Calculate state estimation and its covariance using SRF when the measurement is from the target: (3.c) For , iterate the following N (N denotes iterated times) steps: Calculate the fused state estimation and its covariance: where is a normalization term, and can be obtained using (A6). Update parameters: End for and set , , , , . |
5. Simulation Results
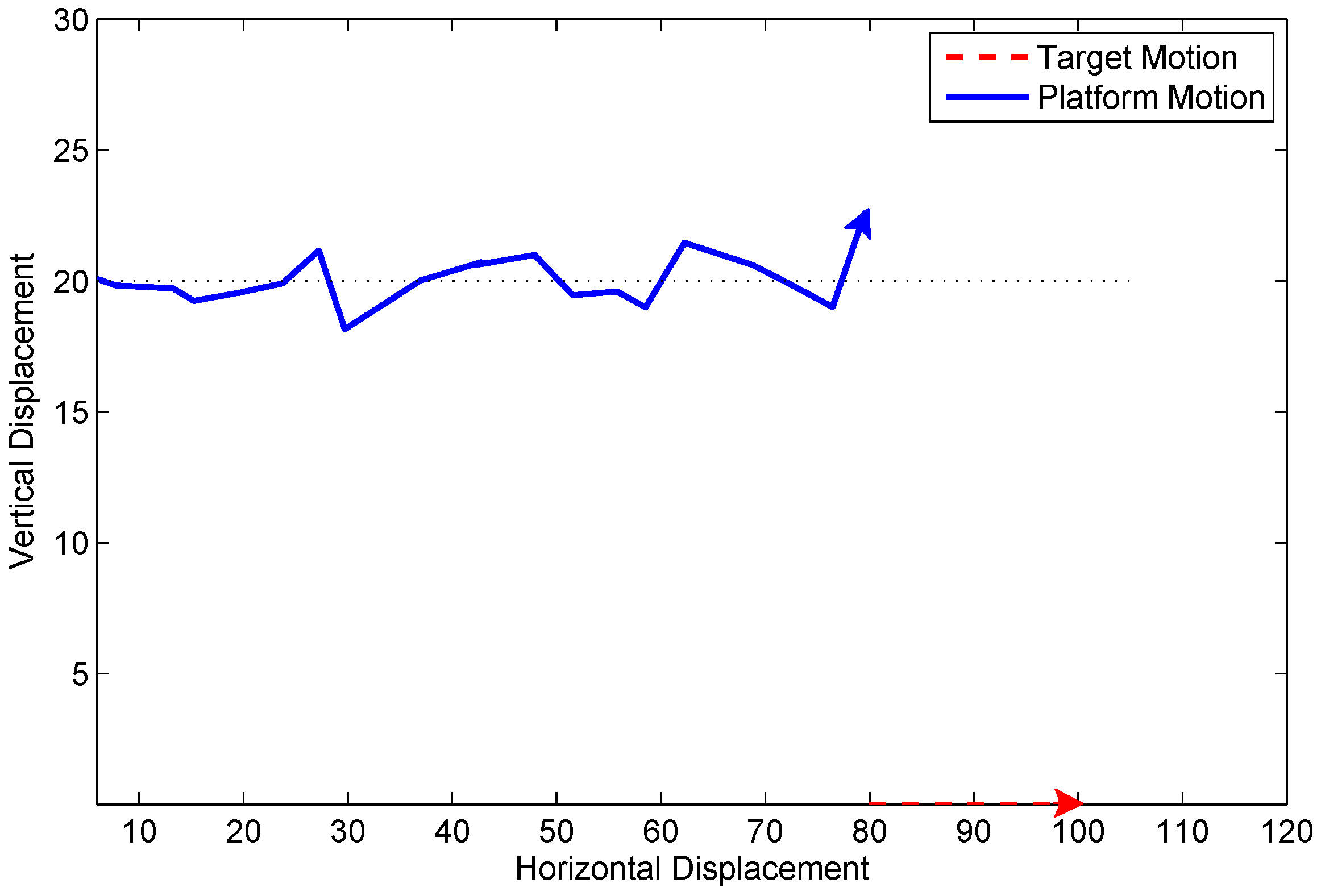
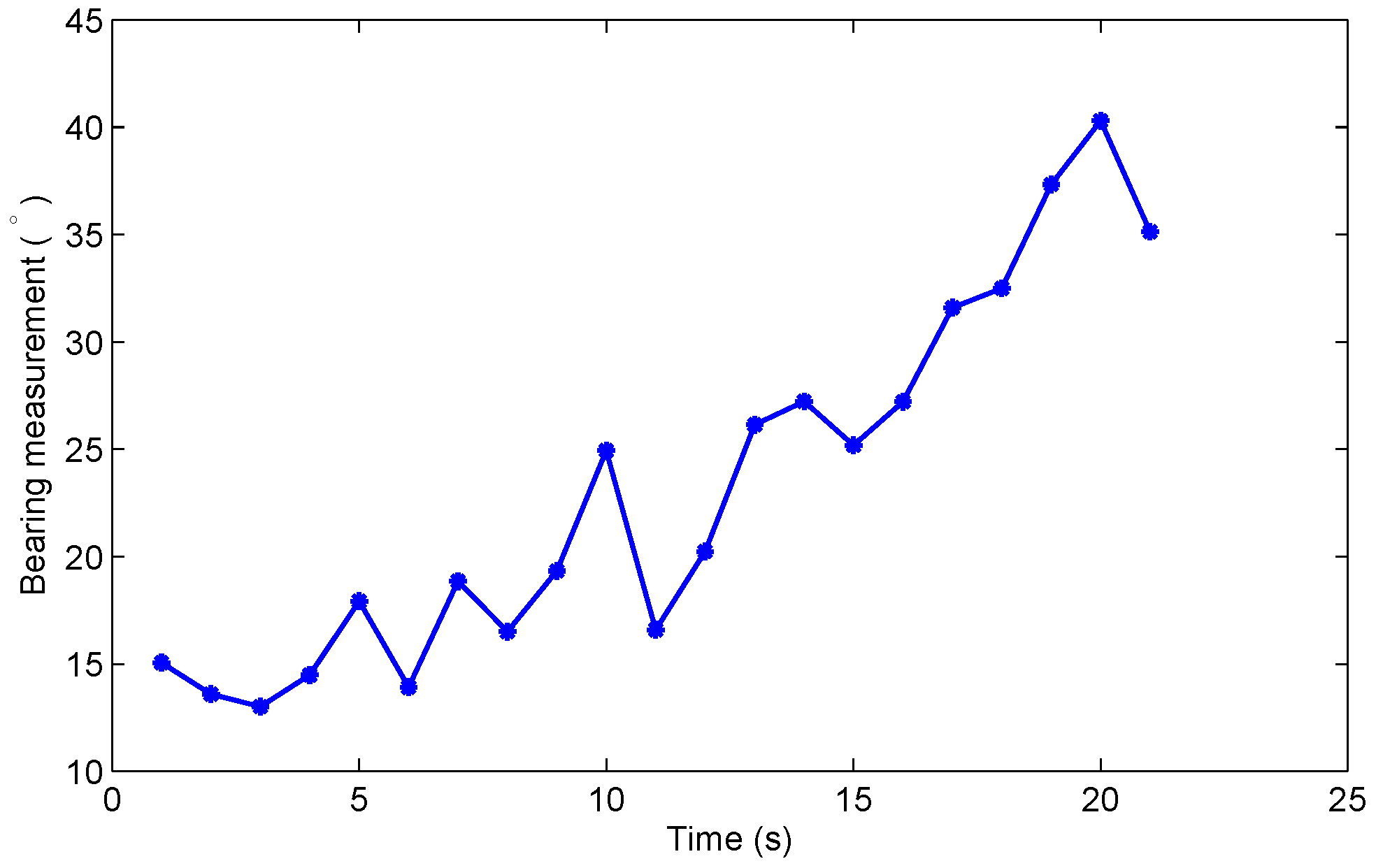
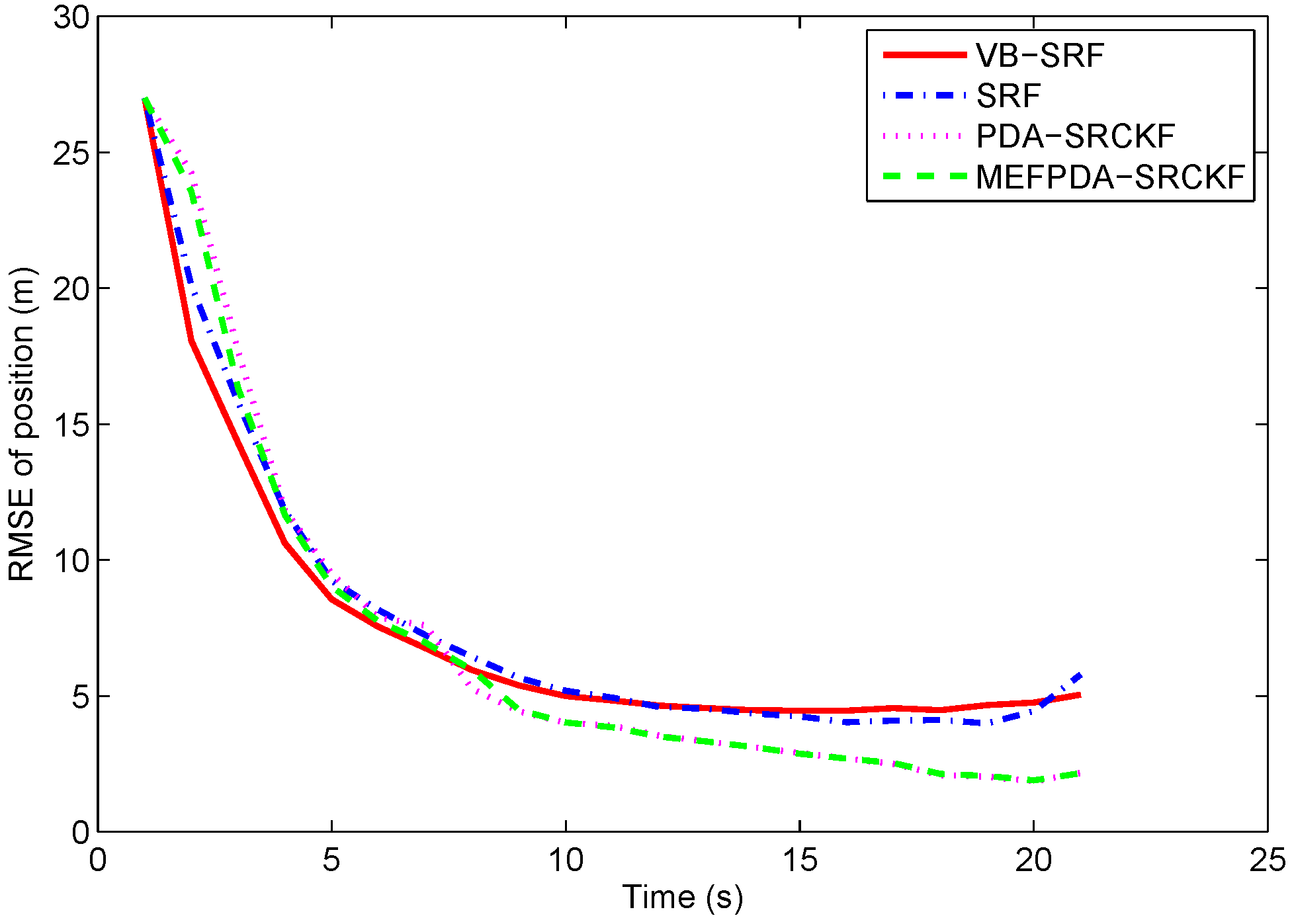
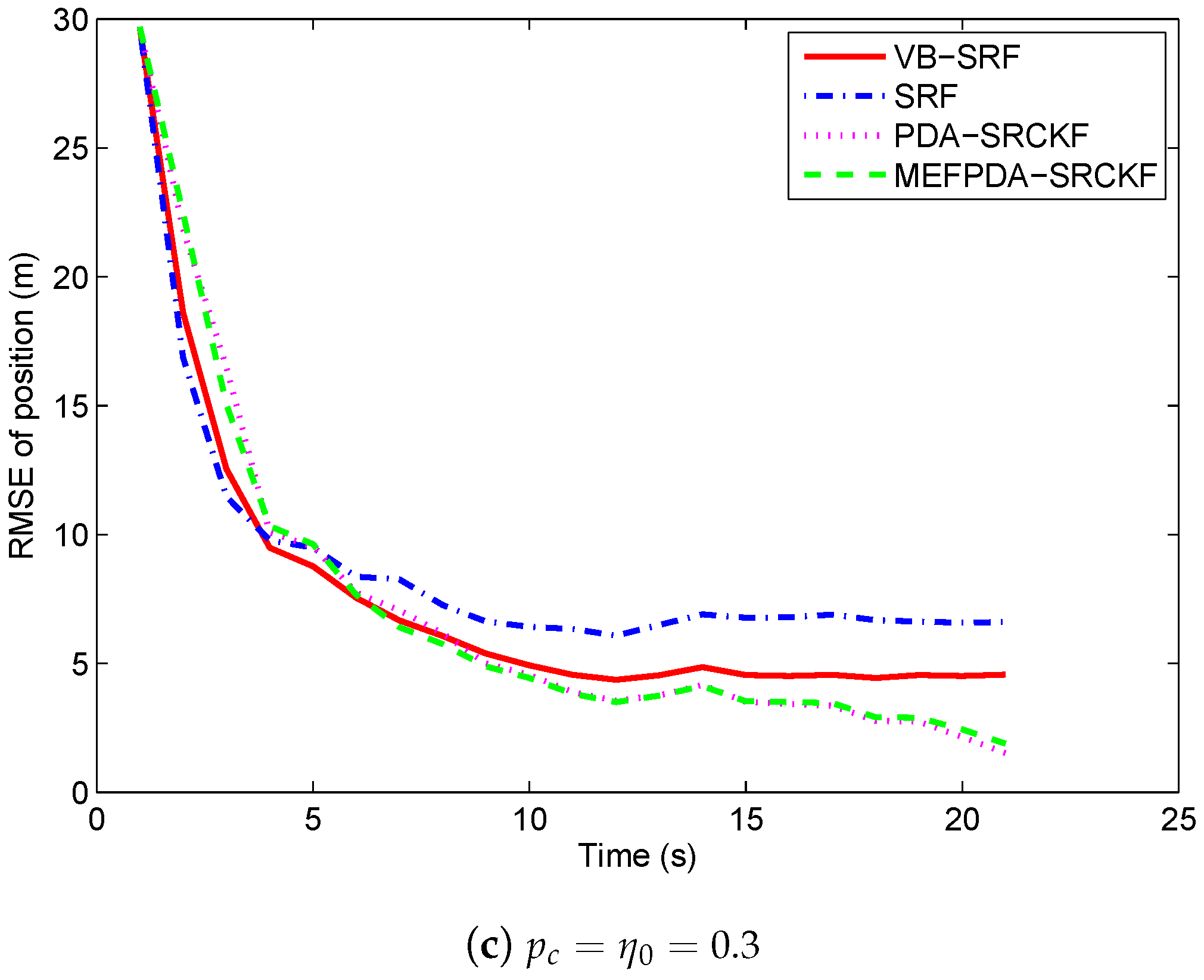
5.1. Scenario 1
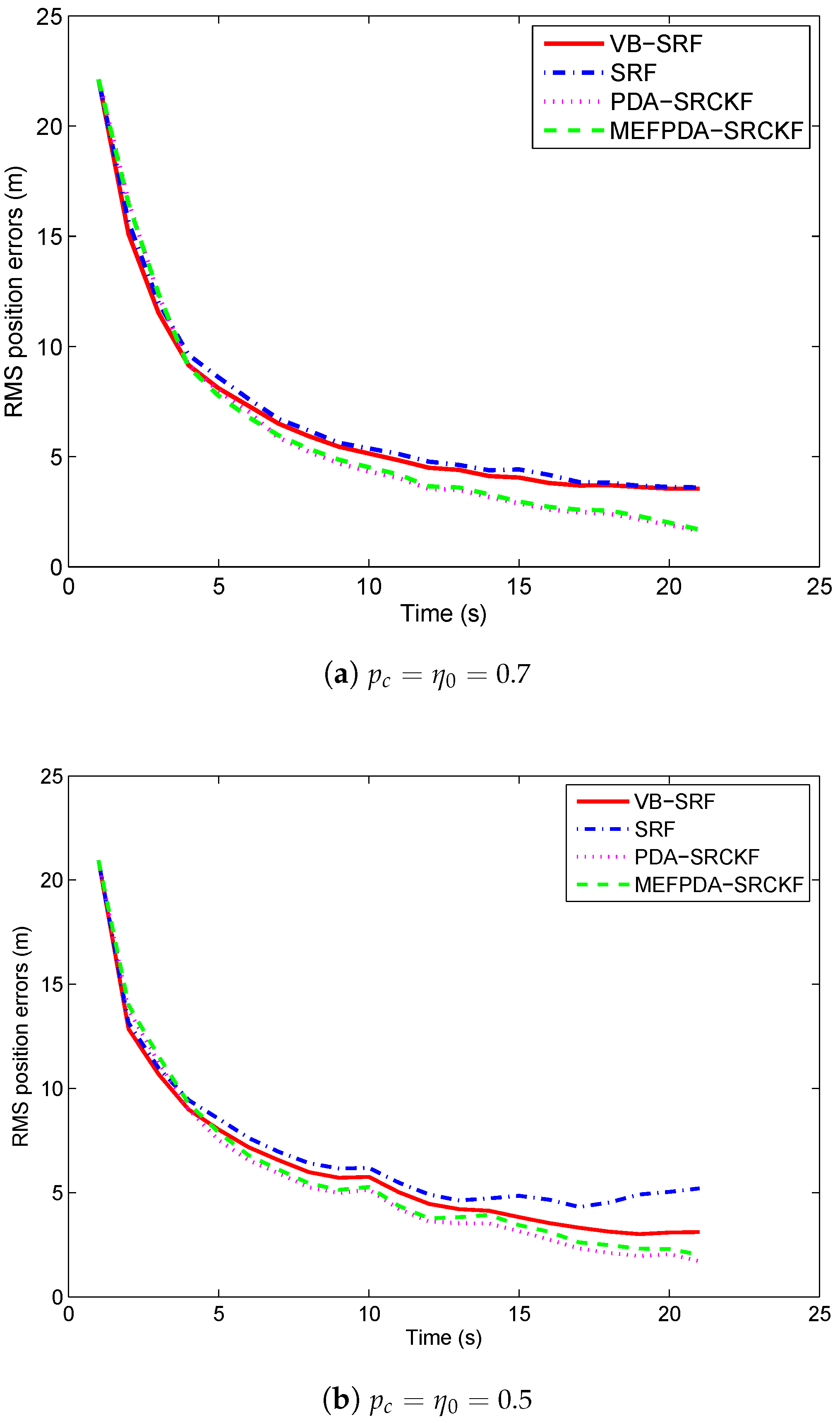
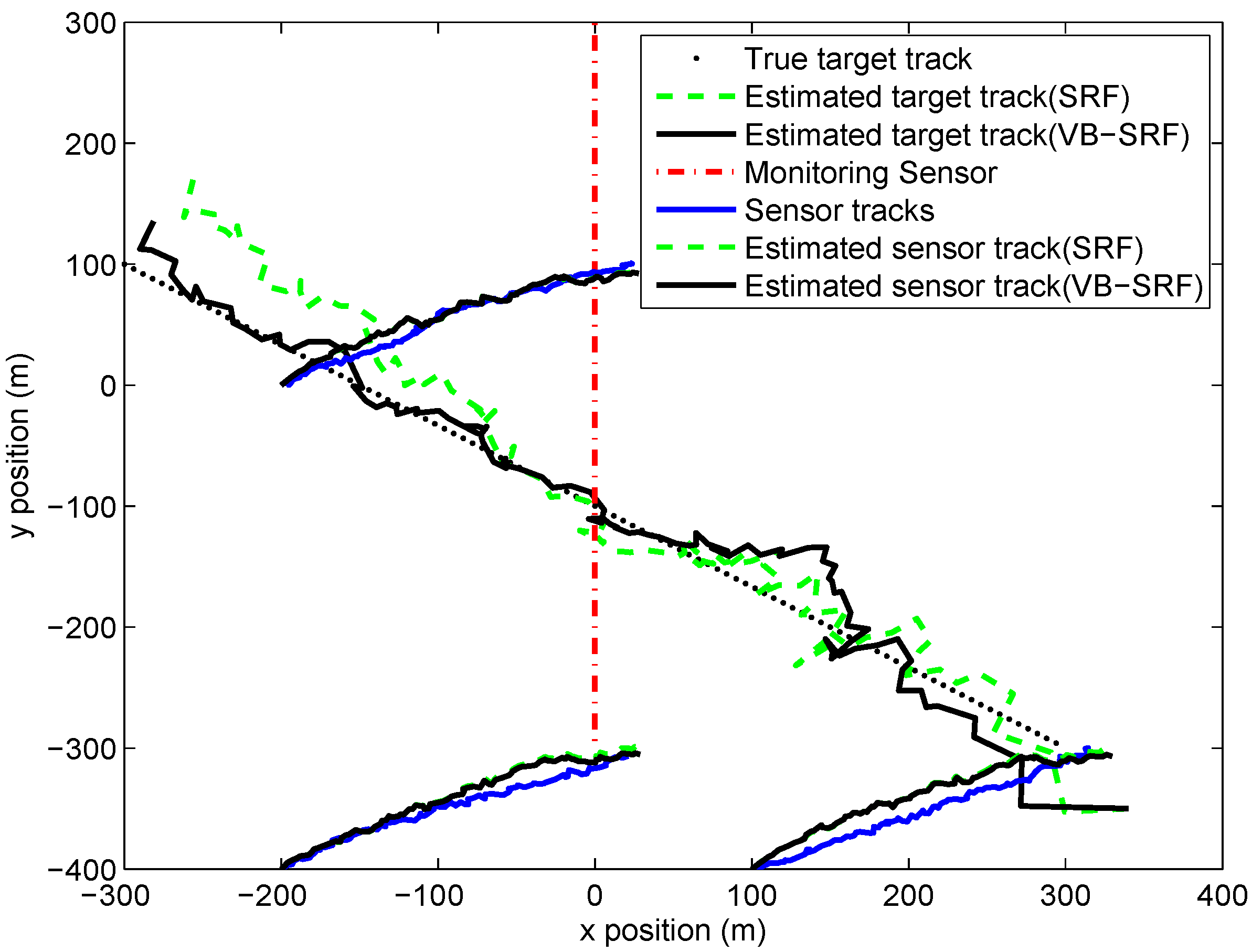
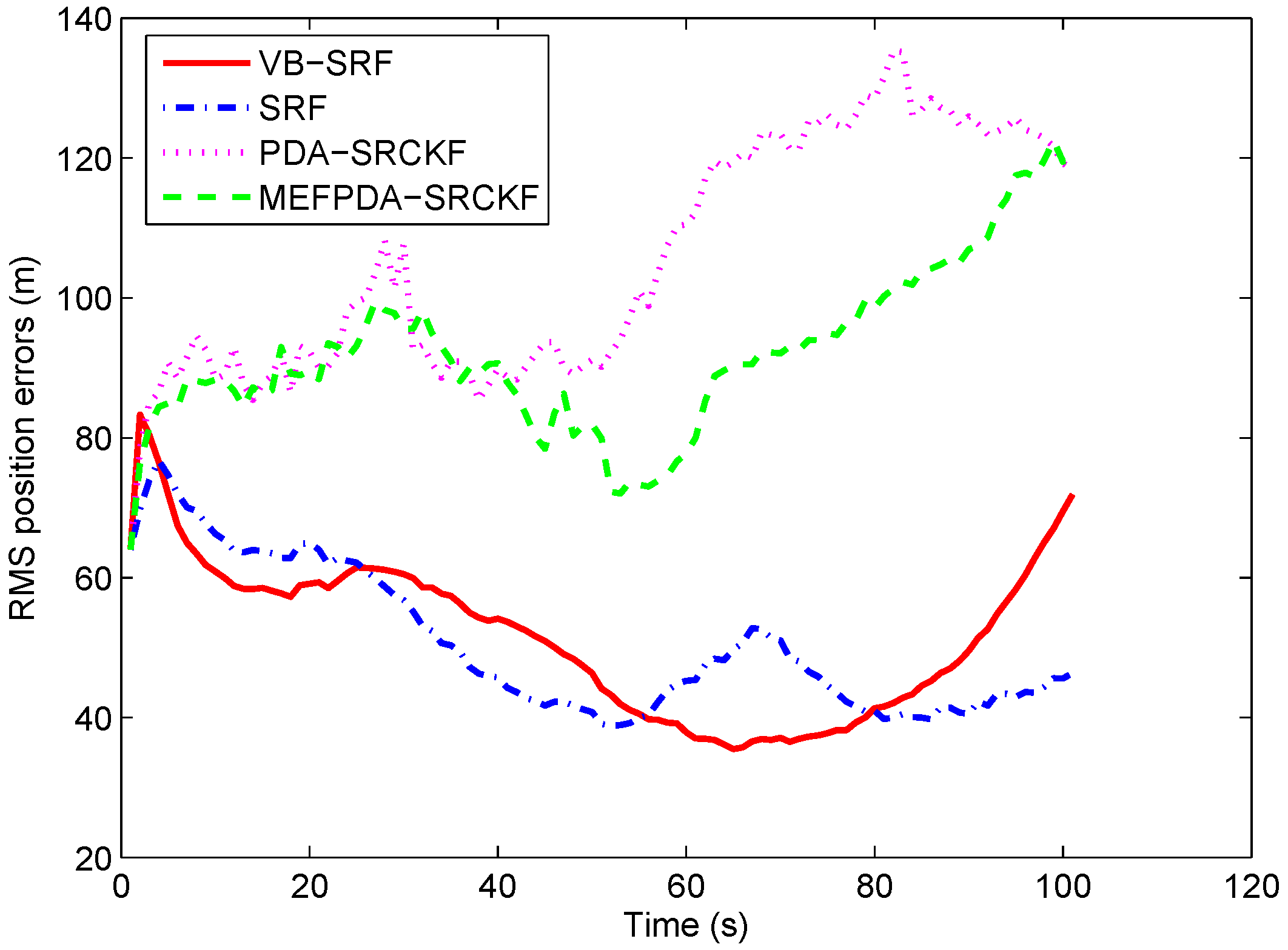
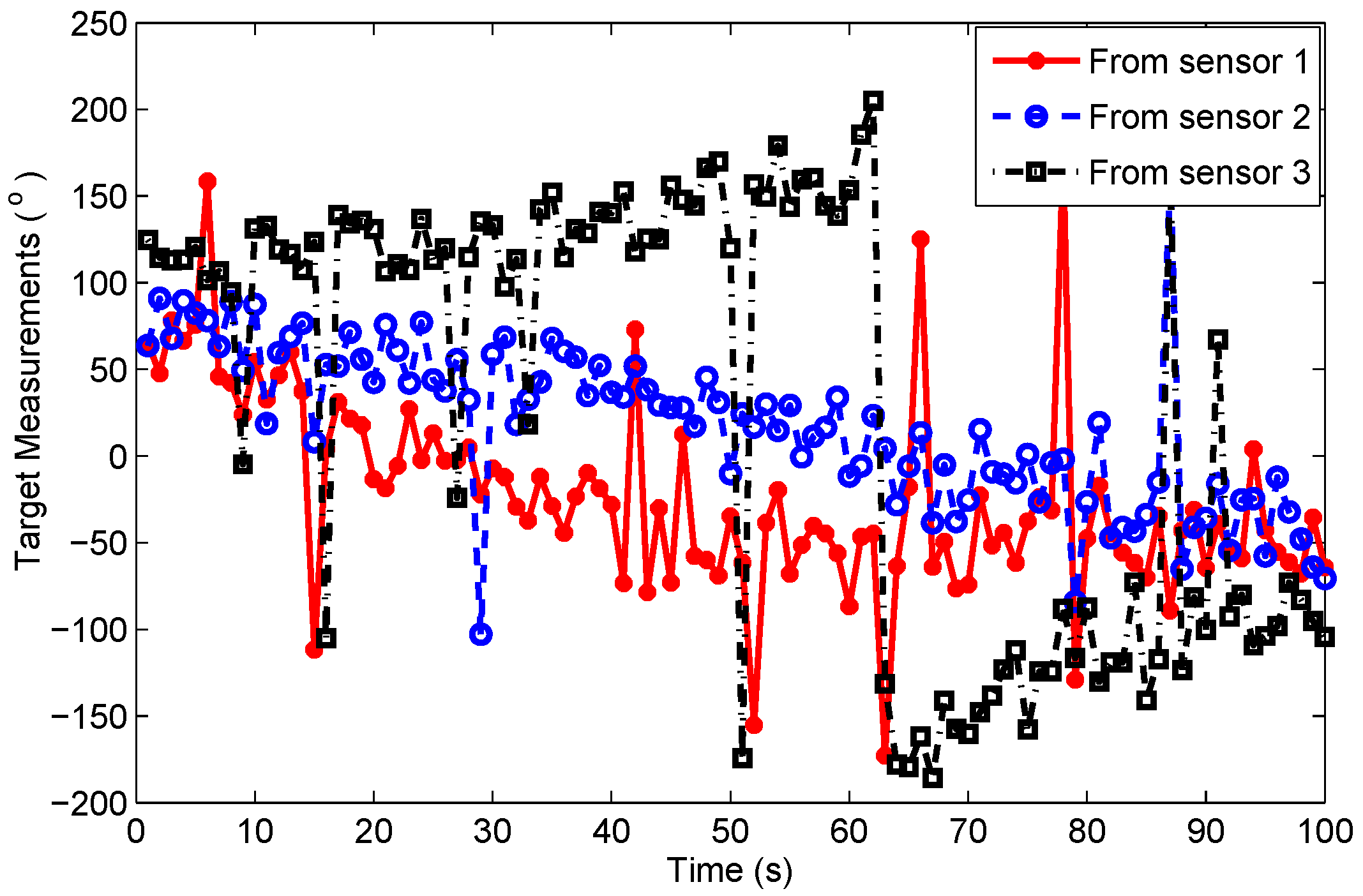
5.2. Scenario 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| VB | Variational Bayesian |
| SRF | Shifted Rayleigh Filter |
| PDA | Probability Data Association |
| EKF | Extended Kalman Filter |
| MPEKF | Polar Coordinate EKF |
| PLE | Pseudo-Linear Estimator |
| UKF | Unscented Kalman Filter |
| CKF | Cubature Kalman Filter |
| PF | Particle Filter |
| MEFPDA | Maximum Entropy Fuzzy Probabilistic Data Association |
| SCKF | Square-root Cubature Kalman Filter |
| CE | Conjugate Exponential |
| KL | Kullback- Leibler |
| EM | Expectation-Maximum |
| RMS | Root Mean Square |
Appendix A. Derivation of f(θk|xk)
Appendix B. Derivation of f(θk|z1:k−1)
References
- Leong, P.H.; Arulampalam, S.; Lamahewa, T.A.; Abhayapala, T.D. A Gaussian-sum based cubature Kalman filter for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1161–1176. [Google Scholar] [CrossRef]
- Aidala, V.J. Kalman filter behavior in bearings-only tracking applications. IEEE Trans. Aerosp. Electron. Syst. 1979, 15, 29–39. [Google Scholar] [CrossRef]
- Aidala, V.J.; Hammel, S. Utilization of modified polar coordinates for bearings-only tracking. IEEE Trans. Autom. Control 1983, 28, 283–294. [Google Scholar] [CrossRef]
- Aidala, V.J.; Nardone, S.C. Biased estimation properties of the pseudo linear tracking filter. IEEE Trans. Aerosp. Electron. Syst. 1982, 18, 432–441. [Google Scholar] [CrossRef]
- Doğançay, K. On the efficiency of a bearings-only instrumental variable estimator for target motion analysis. Signal Process. 2005, 85, 481–490. [Google Scholar] [CrossRef]
- Doğançay, K. Bias compensation for the bearings-only pseudolinear target track estimator. IEEE Trans. Signal Process. 2006, 54, 59–68. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Doğançay, K. Improved pseudolinear Kalman filter algorithms for bearings-only target tracking. IEEE Trans. Signal Process. 2017, 65, 6119–6134. [Google Scholar] [CrossRef]
- Wang, W.P.; Liao, S.; Xing, T.W. The unscented Kalman filter for state estimation of 3-dimension bearing-only tracking. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009; pp. 1–5. [Google Scholar]
- Yang, R.; Ng, G.W.; Bar-Shalom, Y. Bearings-only tracking with fusion from heterogenous passive sensors: ESM/EO and acoustic. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 1810–1816. [Google Scholar]
- Hong, S.H.; Shi, Z.G.; Chen, K.S. Novel roughening algorithm and hardware architecture for bearings-only tracking using particle filter. J. Electromagn. Waves Appl. 2008, 22, 411–422. [Google Scholar] [CrossRef]
- Chang, D.C.; Fang, M.W. Bearing-only maneuvering mobile tracking with nonlinear filtering algorithms in wireless sensor networks. IEEE Syst. J. 2014, 8, 160–170. [Google Scholar] [CrossRef]
- Clark, J.M.C.; Vinter, R.B.; Yaqoob, M.M. The shifted Rayleigh filter for bearings only tracking. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; pp. 93–100. [Google Scholar]
- Clark, J.M.C.; Vinter, R.B.; Yaqoob, M.M. Shifted Rayleigh filter: A new algorithm for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1373–1384. [Google Scholar] [CrossRef]
- Arulampalam, S.; Clark, M.; Vinter, R. Performance of the shifted Rayleigh filter in single-sensor bearings-only tracking. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–6. [Google Scholar]
- Mei, D.; Liu, K.; Wang, Y. MEFPDA-SCKF for underwater single observer bearings-only target tracking in clutter. In Proceedings of the 2013 OCEANS—San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–6. [Google Scholar]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Hu, B. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, J.; Li, X.R. State estimation for systems with unknown inputs based on variational Bayes method. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 983–990. [Google Scholar]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Dissertation, Gatsby Computational Neuroscience Unit, University College London, London, UK, 2003. [Google Scholar]
- Hou, J. jaylin254/VB-SRF1. Available online: https://github.com/jaylin254/VB-SRF1 (accessed on 23 March 2019).
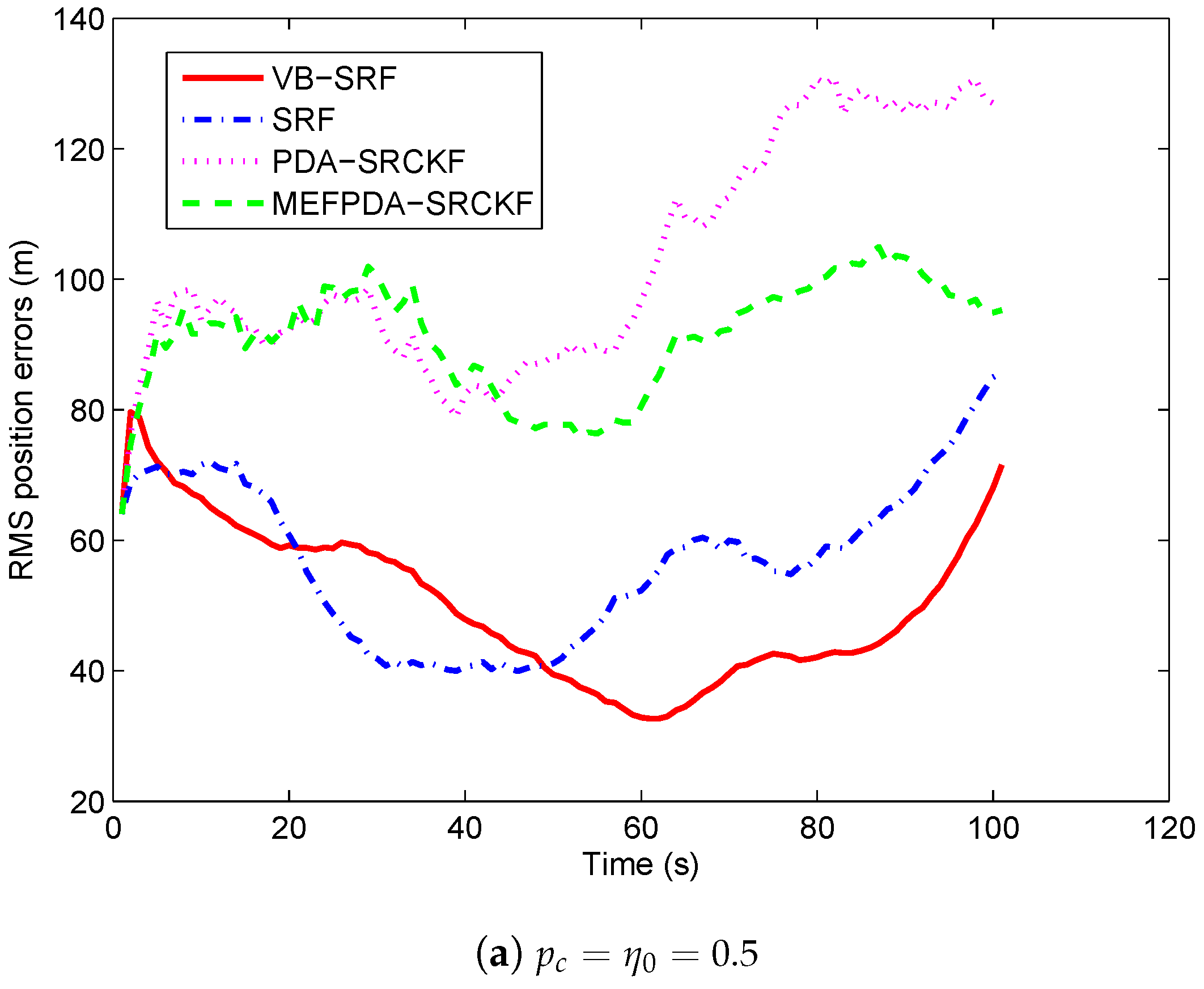
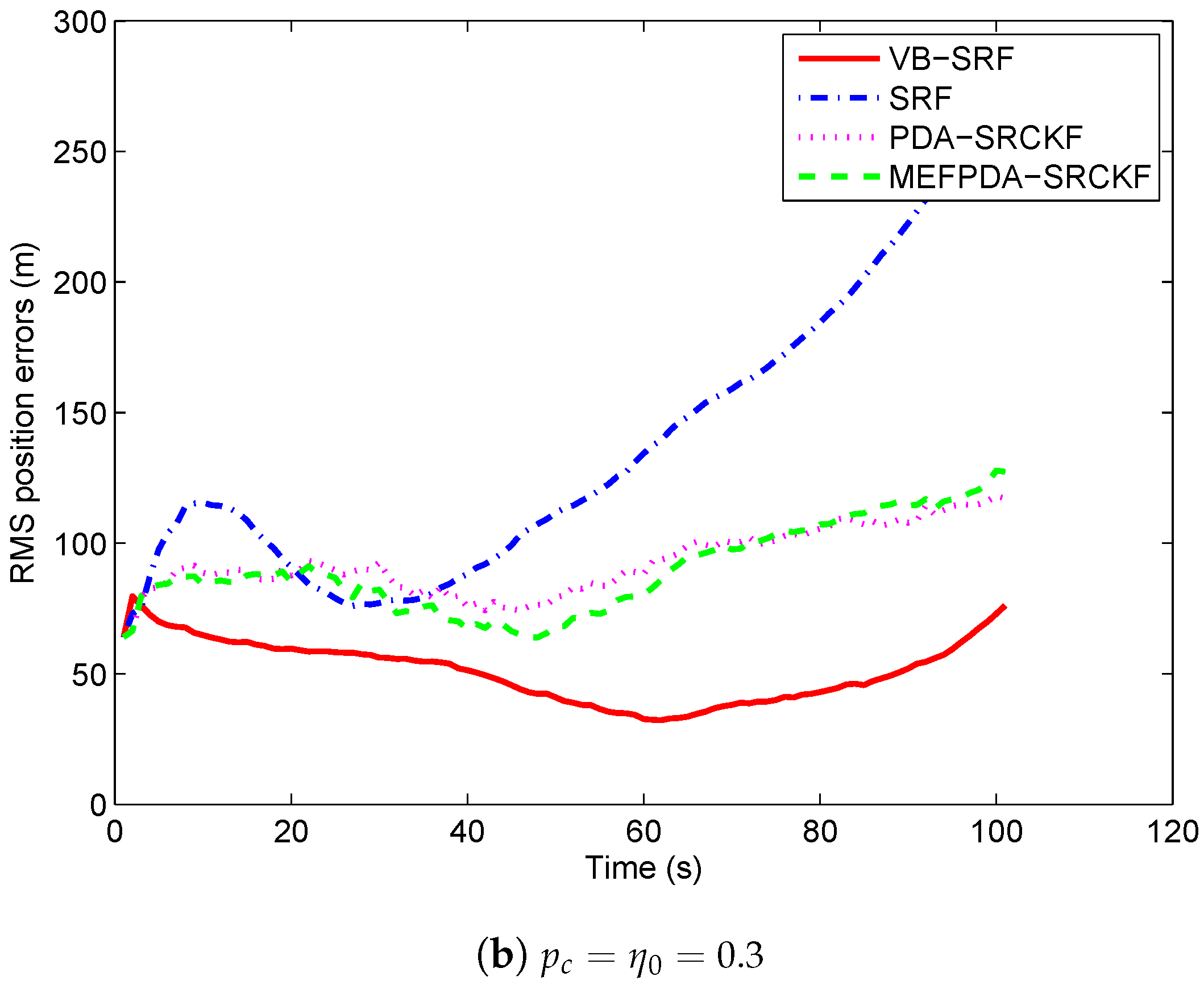
| Scenario 1 | Scenario 2 | |||||
|---|---|---|---|---|---|---|
| VB-SRF | 0 | 0 | 0.1% | 0 | 0 | 0 |
| SRF | 0.9% | 1.6% | 2.9% | 0 | 0 | 2.7% |
| MEFPDA-SCKF | 0 | 0 | 0 | 13.5% | 13.3% | 14.2% |
| PDA-SCKF | 0 | 0 | 0 | 20.1% | 20.8% | 22.4% |
| Scenario 1 | Scenario 2 | |
|---|---|---|
| VB-SRF | 0.7406 s | 1.0236 s |
| SRF | 0.3690 s | 0.5779 s |
| MEFPDA-SCKF | 0.2066 s | 0.3314 s |
| MEFPDA-SCKF | 0.2092 s | 0.3128 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Yang, Y.; Gao, T. Variational Bayesian Based Adaptive Shifted Rayleigh Filter for Bearings-Only Tracking in Clutters. Sensors 2019, 19, 1512. https://doi.org/10.3390/s19071512
Hou J, Yang Y, Gao T. Variational Bayesian Based Adaptive Shifted Rayleigh Filter for Bearings-Only Tracking in Clutters. Sensors. 2019; 19(7):1512. https://doi.org/10.3390/s19071512
Chicago/Turabian StyleHou, Jing, Yan Yang, and Tian Gao. 2019. "Variational Bayesian Based Adaptive Shifted Rayleigh Filter for Bearings-Only Tracking in Clutters" Sensors 19, no. 7: 1512. https://doi.org/10.3390/s19071512
APA StyleHou, J., Yang, Y., & Gao, T. (2019). Variational Bayesian Based Adaptive Shifted Rayleigh Filter for Bearings-Only Tracking in Clutters. Sensors, 19(7), 1512. https://doi.org/10.3390/s19071512





