Improving Quality-of-Service in Cloud/Fog Computing through Efficient Resource Allocation †
Abstract
1. Introduction
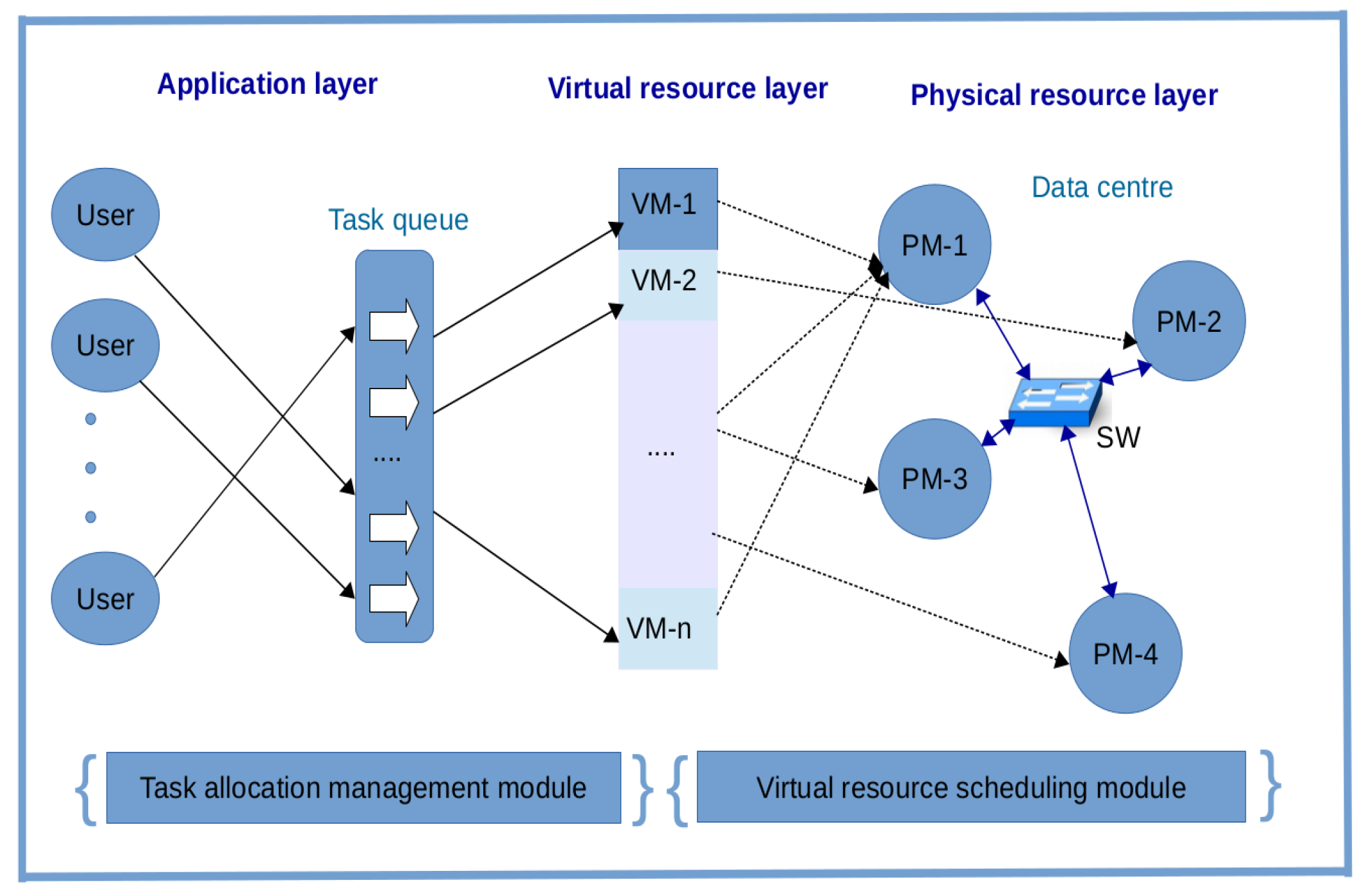
1.1. Cloud/Fog Computing Resource Management Framework
- A physical resource layer which is composed of data centres that host PMs in the form of host machines. The PMs are interconnected by switches (SWs).
- A virtual resource layer which lies above the physical resource layer to virtualize the physical resources as VMs for better resource management.
- An application layer which lies above the virtual resource layer to provide a variety of services to users. These include SaaS, PaaS and IaaS.
- A virtual resource scheduling module, where a mapping between physical machines and the virtual machines is made. We assume in this paper that each physical machine (host machine) provides at least one virtual machine.
- A task allocation management module enabling the virtual resources to be allocated to the users in a cost effective way.
1.2. Contributions
- Problem formulation: The task allocation and VM placement problem models in the cloud computing environment are formulated and presented. These models aim to minimize the resource allocation cost in a setting where multiple cloud user requests have to be processed on a limited number of physical resources.
- A task assignment strategy: We propose the Hungarian Algorithm Based Binding Policy (HABBP) as a heuristic solution to the linear programming problem, and use the algorithm to implement a novel assignment strategy for the famous CloudSim simulator. We also propose the assignment strategy module as a contributed module to CloudSim which includes: (i) A graphical user interface as a front-end component which enables cloud users to interact and communicate with CloudSim and to configure the tasks, VM and PM parameters from the interface, rather than embedding parameter values in the CloudSim source code and (ii) a novel assignment strategy as a back-end component.
- VMs placement solution: We propose a Genetic Algorithm Based Virtual Machine Placement (GABVMP) to solve and optimize the VM placement problem in the cloud computing environment.
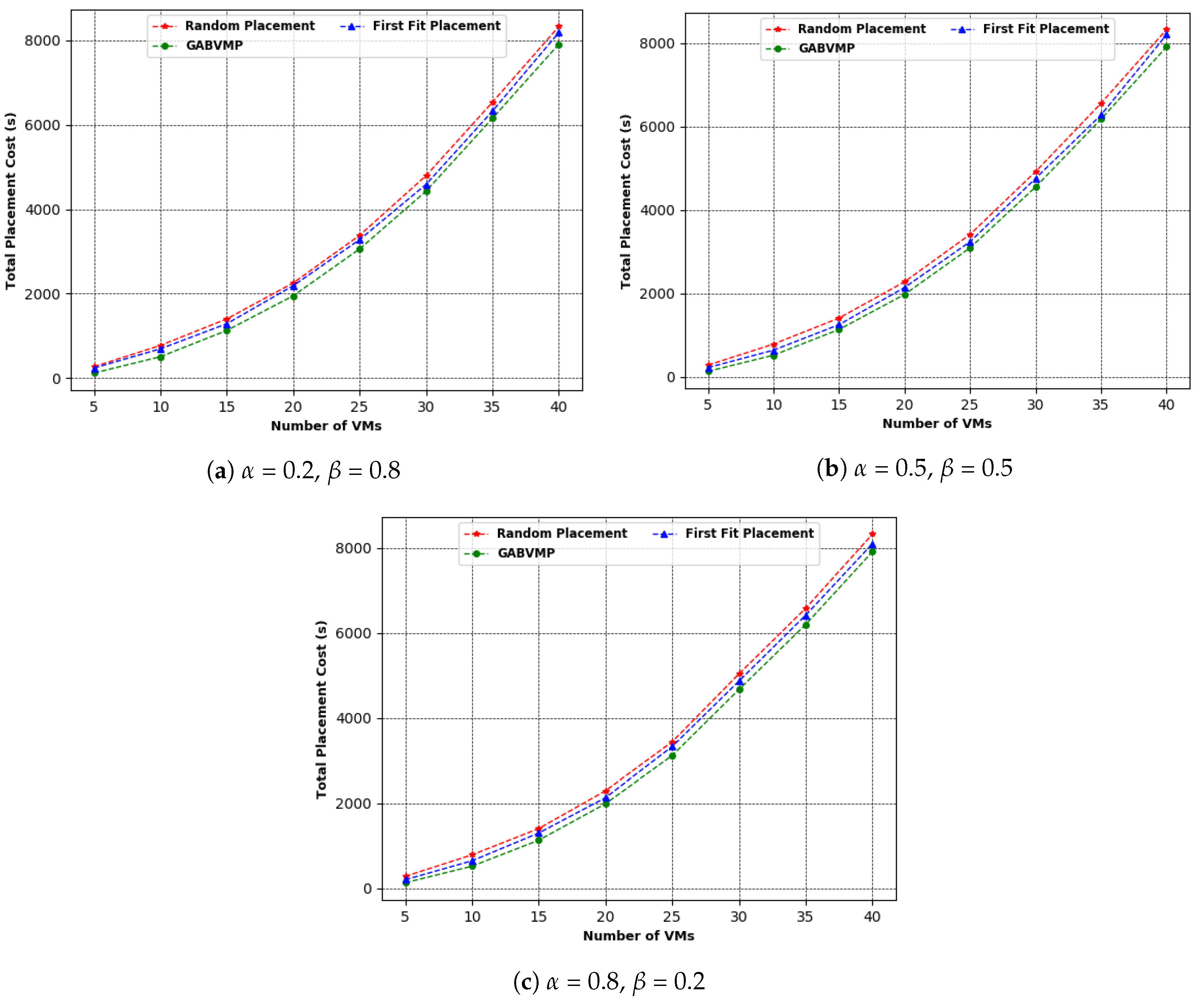
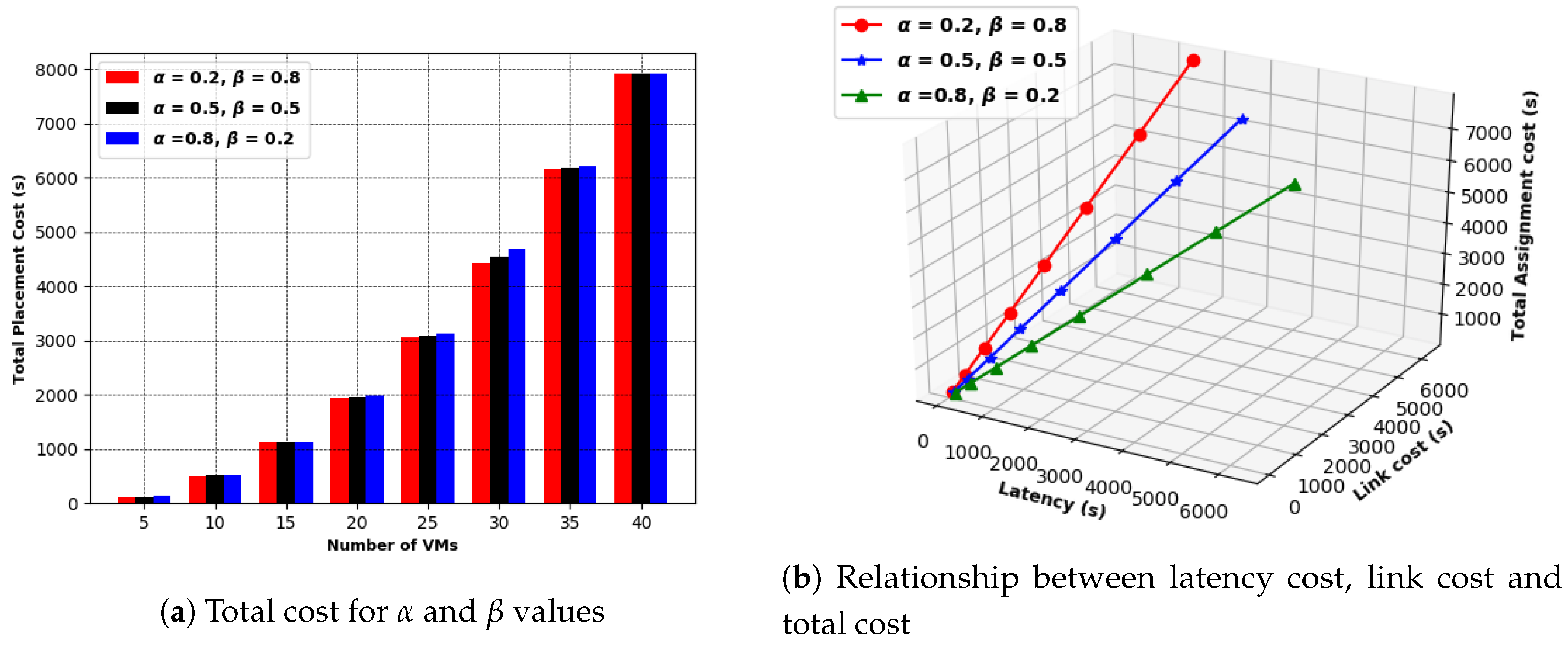
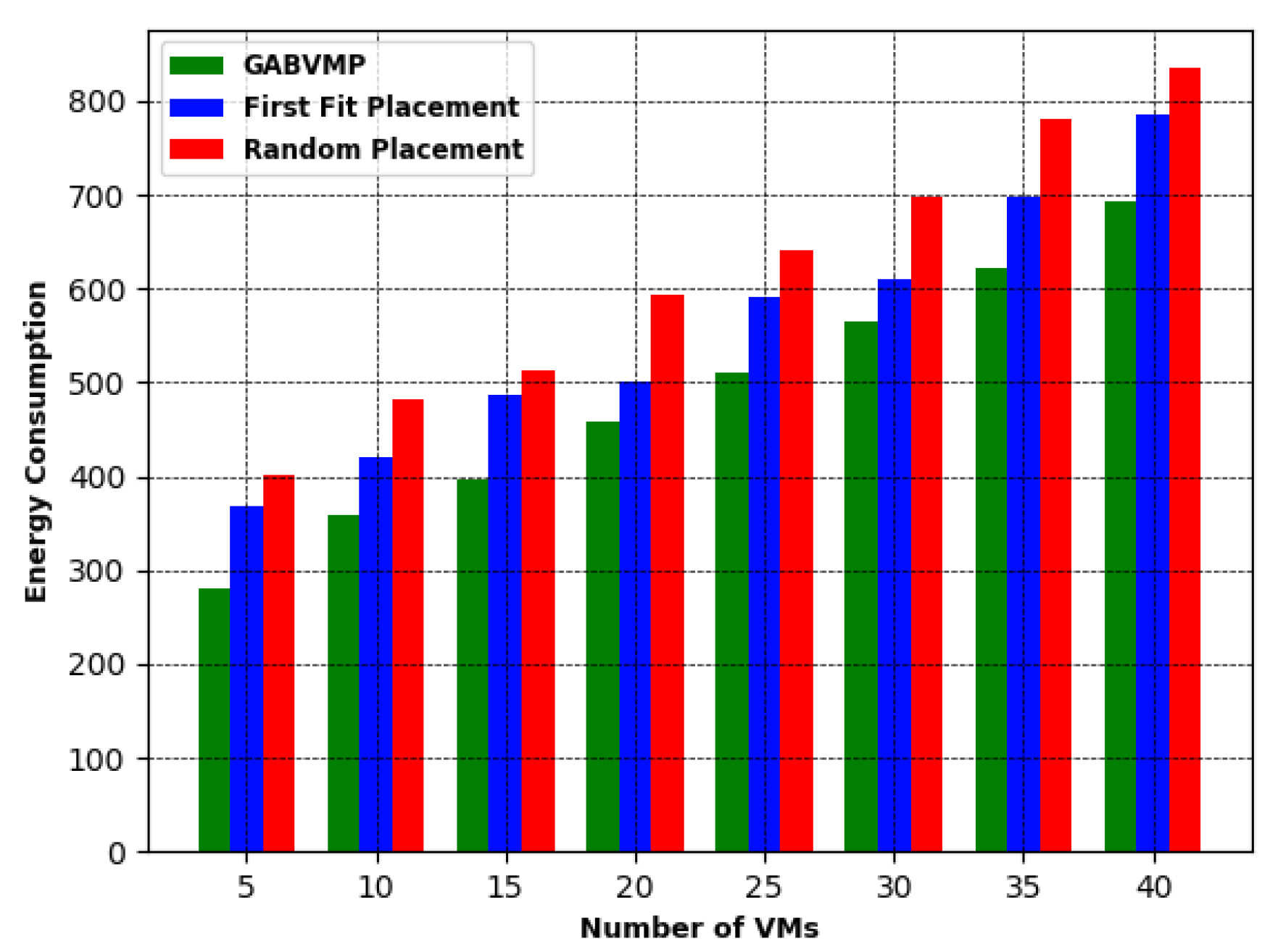
- Analysis of experimental results: We evaluate and compare the performance of the proposed binding policy with the conventional binding policy implemented by the CloudSim simulator and benchmark both solutions against the Simplex algorithm commonly used as a linear programming solver. The proposed GABVMP solution is also compared with the greedy heuristics: Random Placement and First Fit Placement.
1.3. Paper Organization
2. Related Work
3. Task Allocation Problem Model
4. Task Allocation Algorithmic Solution
4.1. Notation and Preliminaries
- Given a cost-matrix of size ,
- n is the number of VMs,
- m is the number of cloudlets,
- represents the time required to complete by .
4.2. Procedures of the Algorithm
| Algorithm 1: Computation of the total assignment cost C. |
 |
4.3. Illustration
5. Virtual Machine Placement Problem
5.1. Parameters
- P = is a set of PMs.
- V = is a set of VM requests.
- S = is a set of switches.
- is the latency between and .
- is the bandwidth for link.
- represents MIPS of each .
- represents MIPS of each .
- represents utilization of .
- is the power consumed by when it is doing nothing but powered on.
- is the power consumed when the is fully loaded/utilized or at the peak load.
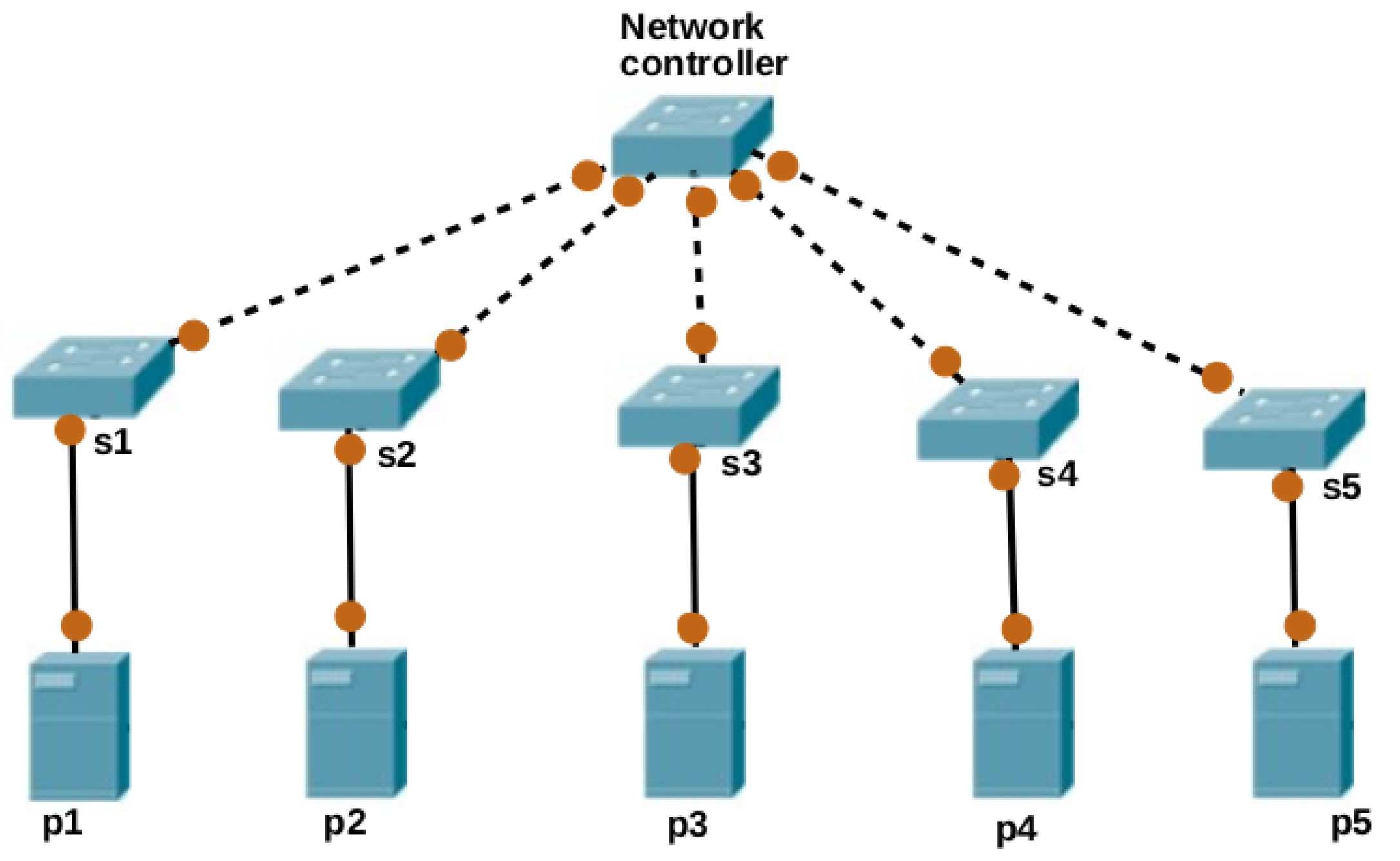
5.2. Assumptions
- Each PM has different latency to all SWs in the network.
- Each PM has one and only one link to the SW in the network.
- Each PM can accommodate more than one VM depending on the capacity of the PM.
- Each link between PMs and SWs has enough capacity and there is no congestion on the links.
- The number of VMs, PMs and SWs are equal i.e., .
5.3. The Mathematical Model
6. Virtual Machine Placement Algorithmic Solution
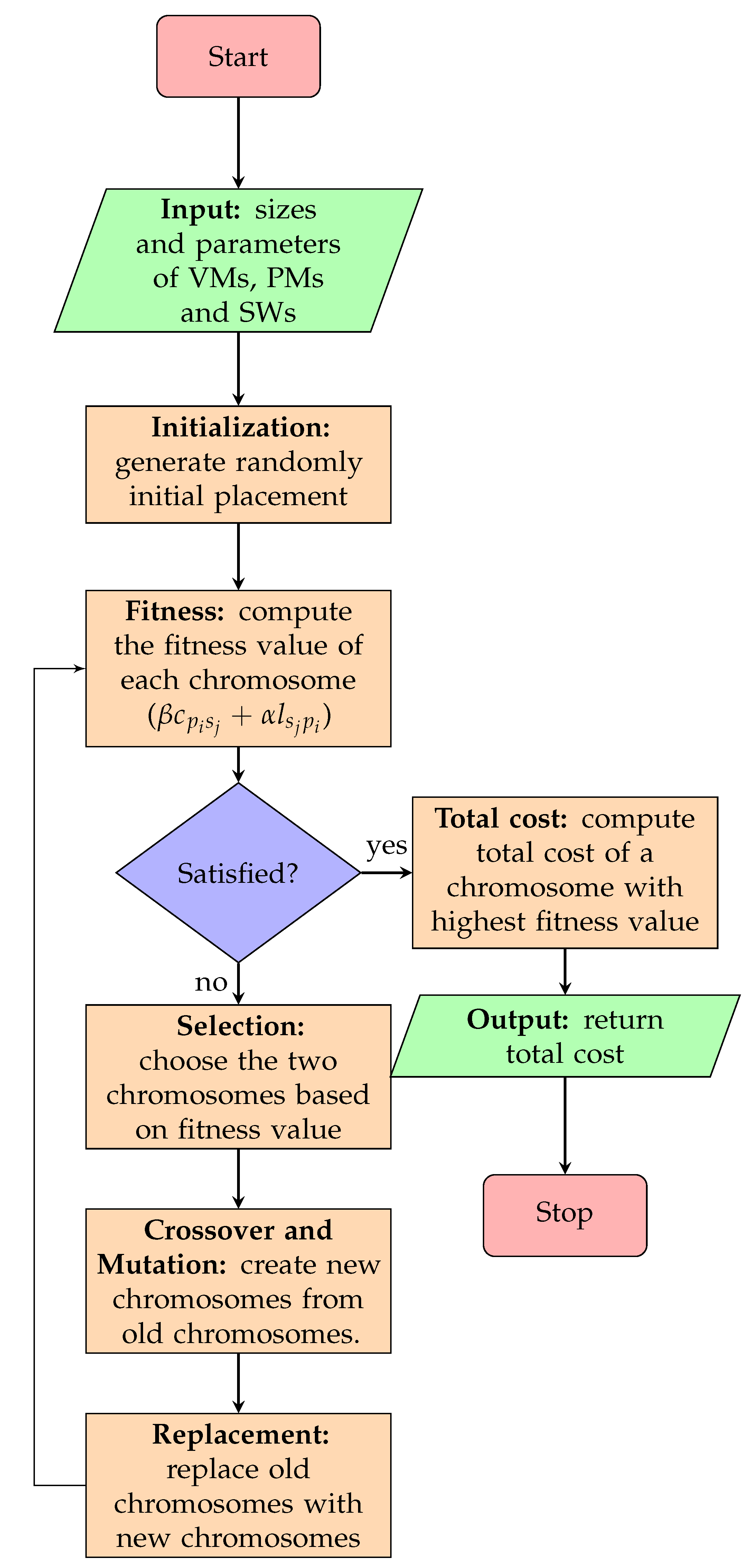
6.1. Genetic Algorithm Based Virtual Machine Placement
6.2. Initialization
| Algorithm 2: Initial population algorithm. |
 |
6.3. Fitness Evaluation
6.4. Generating the Next Population
6.4.1. Selection Process
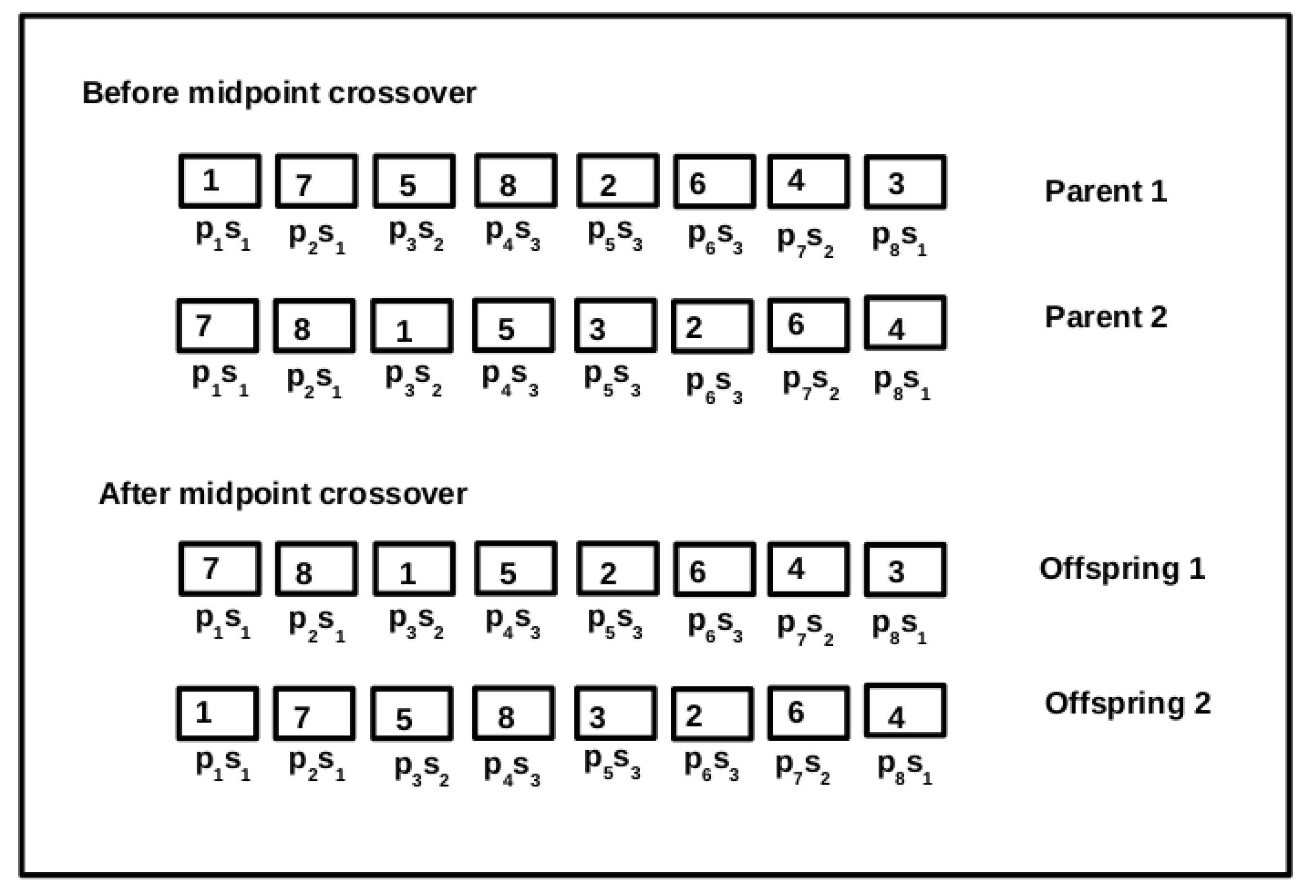
6.4.2. Crossover Operator
| Algorithm 3: Crossover function. |
| input: , : two parent chromosomes output: , : two offspring chromosomes 1 = 2 = ; 3 mid cross point; 4 = 5 = 6 return , . |
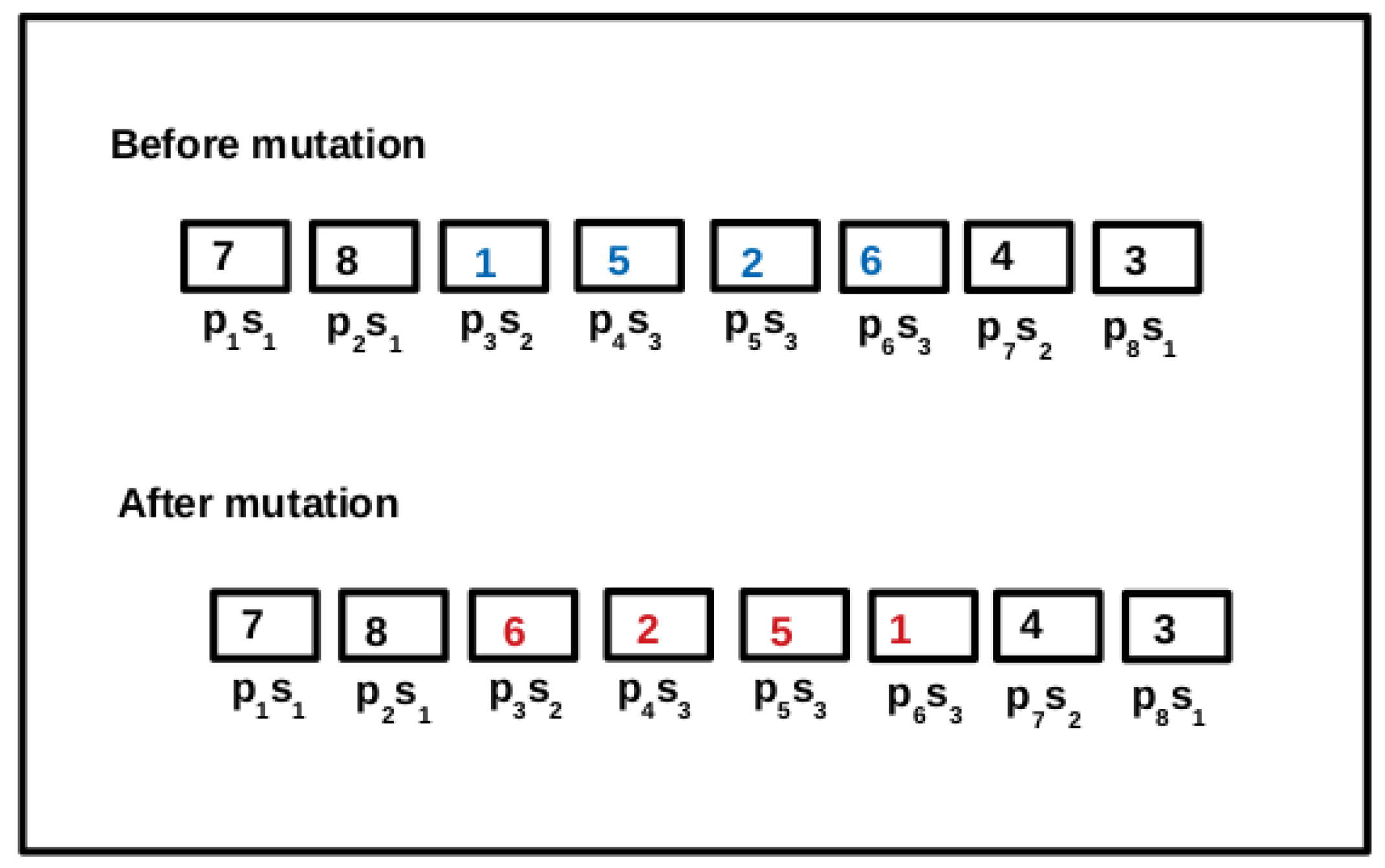
6.4.3. Mutation Operator
6.4.4. Replacement
6.4.5. Stopping Criterion
7. Experimental Results
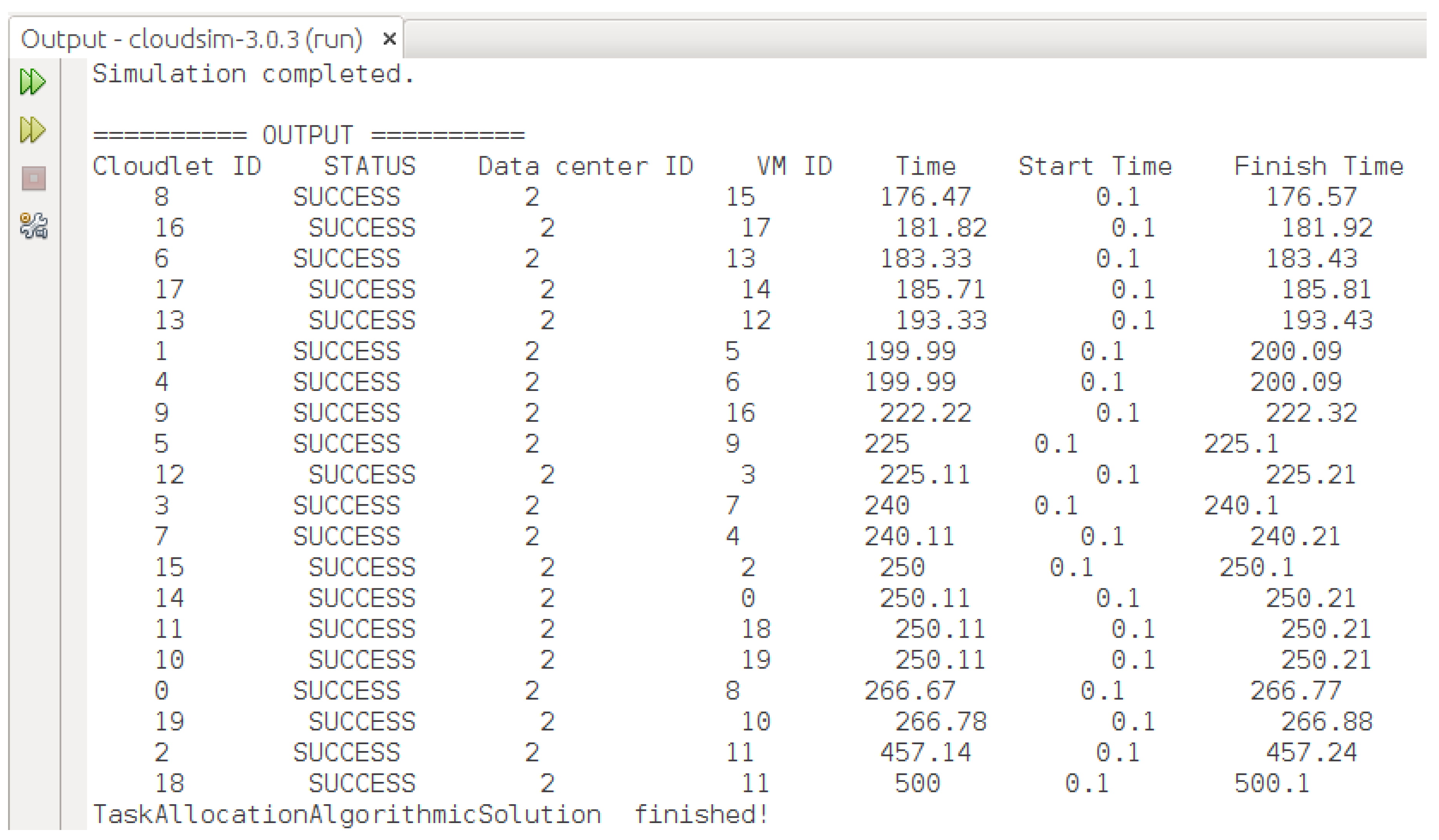
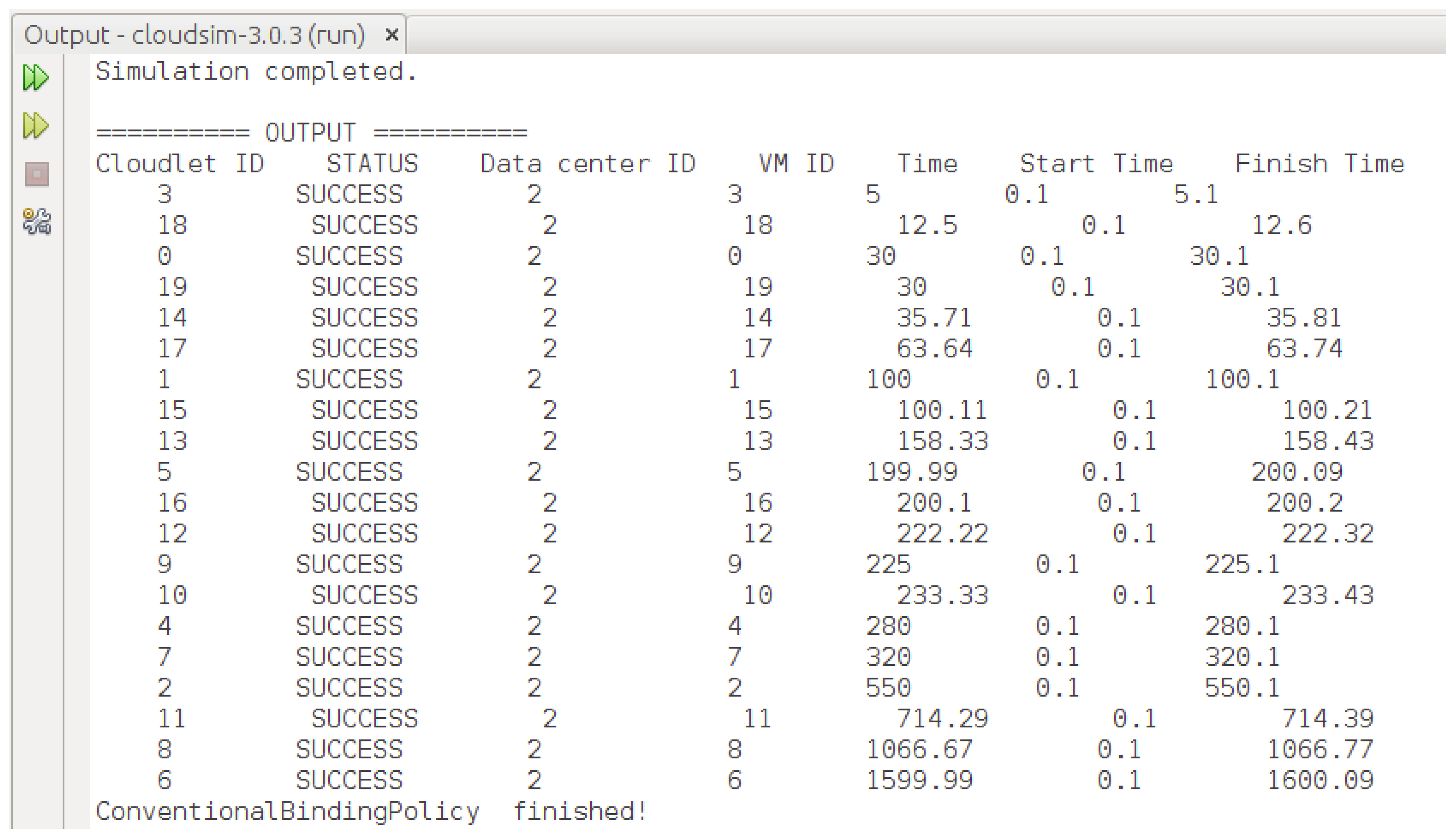
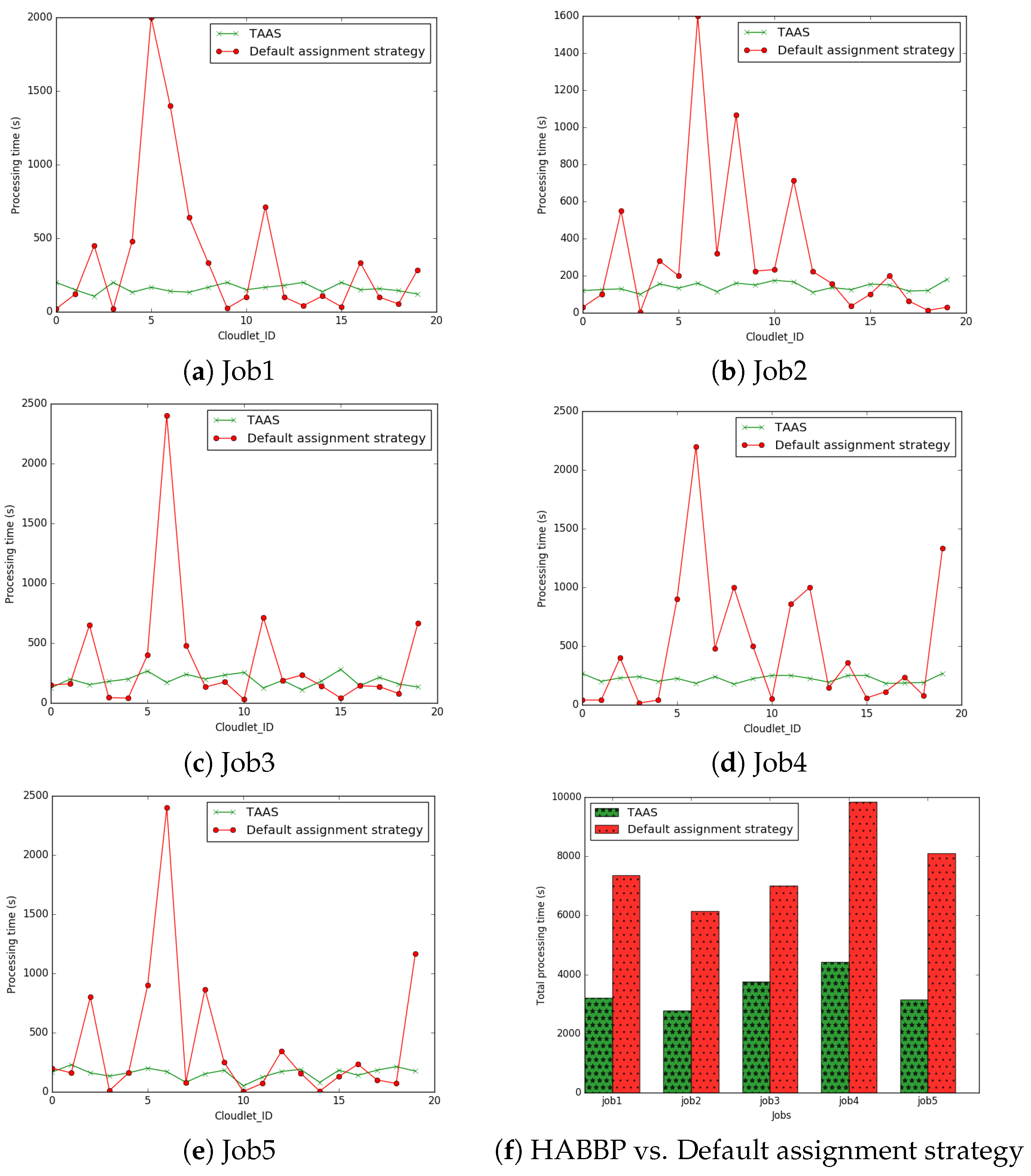
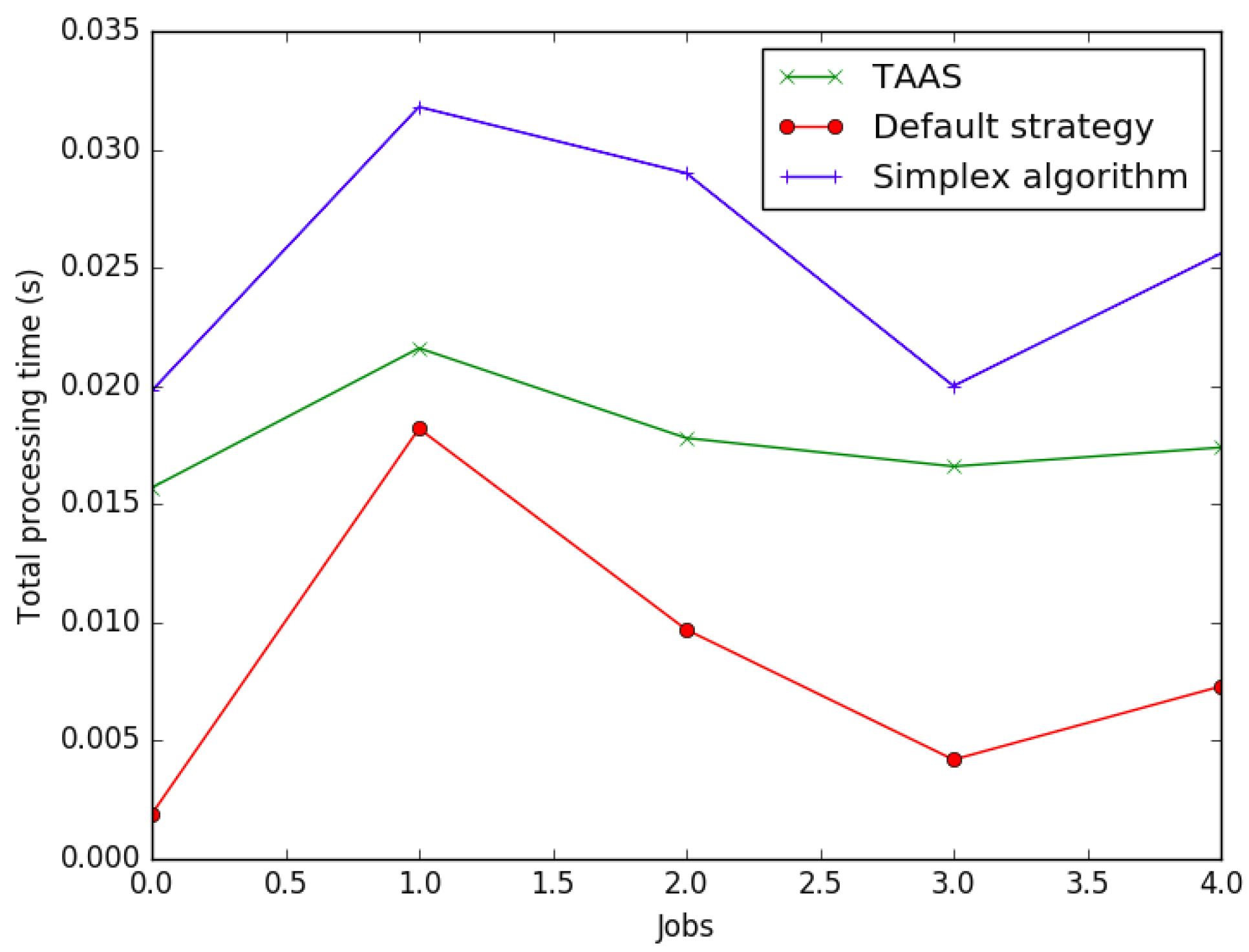
7.1. Implementation of the Proposed HABBP
7.2. Implementation of the Proposed GABVMP
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. Available online: http://www.nist.gov/itl/cloud (accessed on 19 October 2015).
- Rimal, B.P.; Choi, E.; Lumb, I. A taxonomy and survey of cloud computing systems. In Proceedings of the Fifth International Joint Conference on INC, IMS and IDC, Seoul, Korea, 25–27 August 2009; pp. 44–51. [Google Scholar]
- Assante, D.; Castro, M.; Hamburg, I.; Martin, S. The Use of Cloud Computing in SMEs. J. Inf. Technol. Manag. 2016, 83, 1207–1212. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, L.; Boutaba, R. Cloud computing: State-of-the-art and research challenges. J. Internet Serv. Appl. 2010, 1, 7–18. [Google Scholar] [CrossRef]
- Chaudhary, V.; Minsuk, C.; Walters, J.P.; Guercio, S.; Gallo, S. A Comparison of Virtualization Technologies for HPC. In Proceedings of the 22nd International Conference on Advanced Information Networking and Applications (AINA 2008), Okinawa, Japan, 25–28 March 2008; pp. 861–868. [Google Scholar]
- Buyya, R.; Yeo, C.; Venugopal, S.; Broberg, J.; Brandic, I. Cloud computing and emerging IT platforms: Vision, hype, and reality for delivering computing as the 5th utility. Future Gener. Comput. Syst. 2009, 25, 599–616. [Google Scholar] [CrossRef]
- Maguluri, S.T.; Srikant, R.; Ying, L. Stochastic models of load balancing and scheduling in cloud computing clusters. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 702–710. [Google Scholar]
- Baker, T.; MacKay, M.; Randles, M.; Taleb-Bendiab, A. Intention-oriented programming support for runtime adaptive autonomic cloud-based applications. Comput. Electr. Eng. 2013, 39, 2400–2412. [Google Scholar] [CrossRef]
- Al-khafajiy, M.; Baker, T.; Waraich, A.; Al-Jumeily, D.; Hussain, A. IoT-Fog Optimal Workload via Fog Offloading. In Proceedings of the 2018 IEEE/ACM International Conference on Utility and Cloud Computing Companion (UCC Companion), Auckland, New Zealand, 2–5 December 2018. [Google Scholar]
- Lin, C.T. Comparative based analysis of scheduling algorithms for RM in cloud computing environment. Int. J. Comput. Sci. Eng. 2013, 1, 17–23. [Google Scholar]
- Liu, Z.; Qu, W.; Liu, W.; Li, Z.; Xu, Y. Resource preprocessing and optimal task scheduling in cloud computing environments. Concurr. Comput. Pract. Exp. 2014, 27, 3461–3482. [Google Scholar] [CrossRef]
- Zhang, L.; Zhuang, Y.; Zhu, W. Constraint Programming Based Virtual Cloud Resources Allocation Model. Int. J. Hybrid Inf. Technol. 2013, 6, 333–344. [Google Scholar] [CrossRef]
- Dupont, C.; Giuliani, G.; Hermenier, F.; Schulze, T.; Somov, A. An energy aware framework for virtual machine placement in cloud federated data centres. In Proceedings of the Future Energy Systems: Where Energy, Computing and Communication Meet (e-Energy), Madrid, Spain, 9–11 May 2012; pp. 1–10. [Google Scholar]
- Kanagavelu, R.; Bu-Sung, L.; DatLe, N.T.; NgMingjie, L.; MiAung, K.M. Virtual machine placement with two-path traffic routing for reduced congestion in data center networks. J. Comput. Commun. 2014, 53, 1–12. [Google Scholar] [CrossRef]
- Li, X.; Qiana, Z.; Lu, S.; Wub, J. Energy efficient virtual machine placement algorithm with balanced and improved resource utilization in a data center. J. Math. Comput. Model. 2013, 58, 1222–1235. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, H.; Qi, Z.; Hou, Y.; Liu, L. A multi-objective ant colony system algorithm for virtual machine placement in cloud computing. J. Comput. Syst. Sci. 2013, 79, 1230–1242. [Google Scholar] [CrossRef]
- Pascual, J.; Lorido-Botran, T.; Miguel-Alonso, J.; Lozano, J. Towards a greener cloud infrastructure management using optimized placement policies. J. Grid Comput. 2014, 13, 375–389. [Google Scholar] [CrossRef]
- Ebrahimirad, V.; Goudarzi, M.; Rajabi, A. Energy-aware scheduling for precedence-constrained parallel virtual machines in virtualized data centers. J. Grid Comput. 2015, 13, 233–253. [Google Scholar] [CrossRef]
- Georgiou, S.; Delis, K.T.A. Exploiting network-topology awareness for vm placement in iaas clouds. In Proceedings of the 2013 International Conference on Cloud and Green Computing, Karlsruhe, Germany, 30 September–2 October 2013; pp. 151–158. [Google Scholar]
- Meng, X.; Pappas, V.; Zhang, L. Improving the scalability of data center networks with traffic-aware virtual machine placement. In Proceedings of the 2010 IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Breitgand, D.; Epstein, A.; Glikson, A.; Israel, A.; Raz, D. Network aware virtual machine and image placement in a cloud. In Proceedings of the 9th International Conference on Network and Service Management (CNSM 2013), Zurich, Switzerland, 14–18 October 2013; pp. 9–17. [Google Scholar]
- Vakilinia, S.; Heidarpour, B.; Cheriet, M. Energy Efficient Resource Allocation in Cloud Computing Environments. IEEE Access 2016, 4, 8544–8557. [Google Scholar] [CrossRef]
- Mohamed, H.K.; Alkabani, Y.; Selmy, H. Energy Efficient Resource Management for Cloud Computing Environment. In Proceedings of the 9th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 22–23 December 2014; Volume 1. [Google Scholar]
- Kuhn, H.W. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Konig, D. Grafok es matrixok. matematikai es fizikai lapok. Matematikai Es Fizikai Lapok 1931, 38, 116–119. [Google Scholar]
- Dantzig, G.B. Programming in a Linear Structure; USAF: Washington, DC, USA, 1948. [Google Scholar]
- Dantzig, G.B. Linear Programming and Extensions; Princeton University Press: Princeton, NJ, USA, 2016; Volume 4. [Google Scholar]
- Lee, Y.; Zomaya, A. Energy efficient utilization of resources in cloud computing systems. J. Supercomput. 2012, 60, 268–280. [Google Scholar] [CrossRef]
- Holland, J. The Grid: Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Su, F.; Zhu, F.; Yin, Z.; Yao, H.; Wang, Q.; Dong, W. New Crossover Operator of Genetic Algorithms for the TSP. In Proceedings of the 2009 International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009; Volume 1, pp. 666–669. [Google Scholar] [CrossRef]
- Calheiros, R.N.; Ranjan, R.; Beloglazov, A.; De Rose, C.A.F.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Exp. 2011, 41, 23–50. [Google Scholar] [CrossRef]
- Garg, S.K.; Buyya, R. NetworkCloudSim: Modelling parallel applications in cloud simulations. In Proceedings of the Fourth IEEE International Conference on Utility and Cloud Computing (UCC), Victoria, Australia, 5–8 December 2011; pp. 105–113. [Google Scholar]
- Masinde, M.; Bagula, A. A framework for predicting droughts in developing countries using sensor networks and mobile phones. In Proceedings of the 2010 Conference of the South African Institute of Computer Scientists and Information Technologists, Bela Bela, South Africa, 11–13 October 2010; pp. 390–399. [Google Scholar]
- Masinde, M.; Bagula, A.; Muthama, T.N. The role of ICTs in downscaling and upscaling integrated weather forecasts for farmers in sub-Saharan Africa. In Proceedings of the Fifth International Conference on Information and Communication Technologies and Development, Atlanta, GA, USA, 12–15 March 2012; pp. 122–129. [Google Scholar]
- Bagula, A.; Mandava, M.; Bagula, H. A Framework for Supporting Healthcare in Rural and Isolated Areas. Elsevier J. Netw. Commun. Appl. 2018. [Google Scholar] [CrossRef]
- Bagula, A.; Lubamba, C.; Mandava, M.; Bagula, H.; Zennaro, M.; Pietrosemoli, E. Cloud Based Patient Prioritization as Service in Public Health Care. In Proceedings of the ITU Kaleidoscope 2016, Bangkok, Thailand, 14–16 November 2016. [Google Scholar]
- Bagula, A. Hybrid Traffic Engineering: The Least Path Interference Algorithm. In Proceedings of the SAICSIT 2004, Cape Town, South Africa, 4–6 October 2004; pp. 89–96. [Google Scholar]
- Chavula, J.; Suleman, H.; Bagula, A. Quantifying the Effects of Circuitous Routes on the Latency of Intra-Africa Internet Traffic: A Study of Research and Education Networks. In Proceedings of the e-Infrastructure and e-Services for Developing Countries, Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Cham, Switzerland, 2014; Volume 147, pp. 64–73. [Google Scholar]
- Chiaraviglio, L.; Blefari-Melazzi, N.; Liu, W.; Gutiérrez, J.A.; van de Beek, J.; Birke, R.; Chen, L.; Idzikowski, F.; Kilper, D.; Monti, P.; et al. Bringing 5g into rural and low-income areas: Is it feasible? IEEE Commun. Stand. Mag. 2017, 1, 50–57. [Google Scholar] [CrossRef]

| id | 0 | 1 | 2 |
| file-size | 500 | 1000 | 1000 |
| length | 40,000 | 80,000 | 120,000 |
| output-size | 500 | 2048 | 2048 |
| id | 0 | 1 | 2 |
| size | 1000 | 1000 | 1000 |
| mips | 400 | 1000 | 500 |
| ram | 2048 | 2048 | 2048 |
| pes-number | 1 | 2 | 2 |
| bandwidth | 500 | 500 | 500 |
| 100 | 200 | 300 | |
| 40 | 80 | 120 | |
| 80 | 160 | 240 |
| 0 | 100 | 200 | |
| 0 | 40 | 80 | |
| 0 | 80 | 160 |
| 0 | 60 | 120 | |
| 0 | 0 | 0 | |
| 0 | 40 | 80 |
| 0 | 20 | 80 | |
| 0 | 0 | 0 | |
| 0 | 0 | 40 |
| Cloudlets | Virtual Machines |
|---|---|
| Tableau | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | −1 | −1 | −1 | −1 | −1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | |||||||||||||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | −1 | 0 | 0 | −1 | −1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | −1 | −1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | −1 | −1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | −1 | −1 | −1 | −1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | −1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | −1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 0 |
| Tableau | −100 | −200 | −300 | −40 | −80 | −120 | −80 | −160 | −240 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | |||||||||||
| −200 | 0 | 0 | 1 | 1 | −1 | 0 | 0 | −1 | 0 | 0 | |
| −240 | 0 | 0 | 0 | 1 | −1 | −1 | 0 | 0 | 0 | 1 | |
| −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| −160 | 1 | 0 | 0 | −1 | 1 | 1 | 0 | 1 | 1 | 0 | |
| −100 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| −120 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |
| −380 | 0 | 0 | 20 | 100 | 40 | 0 | 20 | 0 | 0 |
| Paper | Latency-Aware | Energy-Aware | Network-Aware | Internal Traffic | Flow Path Allocation | Method Adopted |
|---|---|---|---|---|---|---|
| [18] | No | Yes | No | Yes | No | Scheduling algorithms |
| [14] | No | No | Yes | Yes | Yes | Greedy method |
| [15] | No | Yes | No | No | No | EAGLE algorithm |
| [16] | No | Yes | No | No | No | Ant-colony based algorithm |
| [20] | No | No | Yes | Yes | Yes | Cluster-and-Cut algorithm |
| [17] | No | Yes | Yes | Yes | No | Multi-objective evolutionary algorithms |
| [19] | No | No | Yes | Yes | Yes | Virtual Infrastructure Opportunistic fit (VIO) and VIcinity-BasEd Search (VIBES) |
| [21] | Yes | No | Yes | Yes | No | Local search algorithm |
| [22] | No | Yes | No | No | No | Column generation method, cut-and-solve-based algorithm and the call back method |
| [23] | No | Yes | No | No | No | Neural networks, Self Organizing Map (SOM) and K-Mean Clustering algorithms |
| GABVMP | Yes | Yes | Yes | Yes | Yes | Genetic algorithm |
| job1 | job2 | job3 | job4 | job5 | |
|---|---|---|---|---|---|
| () | () | () | () | () | |
| 0 | 20,000 | 30,000 | 150,000 | 40,000 | 200,000 |
| 1 | 60,000 | 50,000 | 80,000 | 20,000 | 80,000 |
| 2 | 90,000 | 110,000 | 130,000 | 80,000 | 160,000 |
| 3 | 40,000 | 10,000 | 90,000 | 30,000 | 20,000 |
| 4 | 120,000 | 70,000 | 10,000 | 10,000 | 40,000 |
| 5 | 200,000 | 20,000 | 40,000 | 90,000 | 90,000 |
| 6 | 70,000 | 80,000 | 120,000 | 110,000 | 120,000 |
| 7 | 80,000 | 40,000 | 60,000 | 60,000 | 10,000 |
| 8 | 50,000 | 160,000 | 20,000 | 150,000 | 130,000 |
| 9 | 10,000 | 90,000 | 70,000 | 200,000 | 100,000 |
| 10 | 150,000 | 350,000 | 45,000 | 75,000 | 5000 |
| 11 | 250,000 | 250,000 | 250,000 | 300,000 | 25,000 |
| 12 | 45,000 | 100,000 | 85,000 | 450,000 | 155,000 |
| 13 | 25,000 | 95,000 | 140,000 | 87,000 | 95,000 |
| 14 | 75,000 | 25,000 | 100,000 | 250,000 | 4000 |
| 15 | 30,000 | 85,000 | 35,000 | 50,000 | 110,000 |
| 16 | 300,000 | 180,000 | 130,000 | 100,000 | 210,000 |
| 17 | 55,000 | 35,000 | 75,000 | 130,000 | 55,000 |
| 18 | 65,000 | 15,000 | 95,000 | 95,000 | 85,000 |
| 19 | 85,000 | 9000 | 200,000 | 400,000 | 350,000 |
| 0 | 1000 |
| 1 | 500 |
| 2 | 200 |
| 3 | 2000 |
| 4 | 250 |
| 5 | 100 |
| 6 | 50 |
| 7 | 125 |
| 8 | 150 |
| 9 | 400 |
| 10 | 1500 |
| 11 | 350 |
| 12 | 450 |
| 13 | 600 |
| 14 | 700 |
| 15 | 850 |
| 16 | 900 |
| 17 | 550 |
| 18 | 1200 |
| 19 | 300 |
| job1 | job2 | job3 | job4 | job5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| proc. time | proc. time | proc. time | proc. time | proc. time | ||||||
| 0 | 0 | 20 | 0 | 30 | 0 | 150 | 0 | 40 | 0 | 200 |
| 1 | 1 | 120 | 1 | 100 | 1 | 160 | 1 | 40 | 1 | 160 |
| 2 | 2 | 450 | 2 | 550 | 2 | 650 | 2 | 400 | 2 | 800 |
| 3 | 3 | 20 | 3 | 5 | 3 | 45 | 3 | 15 | 3 | 10 |
| 4 | 4 | 480 | 4 | 280 | 4 | 40 | 4 | 40 | 4 | 160 |
| 5 | 5 | 2000 | 5 | 200 | 5 | 400 | 5 | 900 | 5 | 900 |
| 6 | 6 | 1400 | 6 | 1600 | 6 | 2400 | 6 | 2200 | 6 | 2400 |
| 7 | 7 | 640 | 7 | 320 | 7 | 480 | 7 | 480 | 7 | 80 |
| 8 | 8 | 333 | 8 | 1066 | 8 | 133 | 8 | 1000 | 8 | 866 |
| 9 | 9 | 25 | 9 | 225 | 9 | 175 | 9 | 500 | 9 | 250 |
| 10 | 10 | 100 | 10 | 233 | 10 | 30 | 10 | 50 | 10 | 3 |
| 11 | 11 | 714 | 11 | 714 | 11 | 714 | 11 | 857 | 11 | 71 |
| 12 | 12 | 100 | 12 | 222 | 12 | 189 | 12 | 1000 | 12 | 344 |
| 13 | 13 | 42 | 13 | 158 | 13 | 233 | 13 | 145 | 13 | 158 |
| 14 | 14 | 107 | 14 | 36 | 14 | 143 | 14 | 357 | 14 | 6 |
| 15 | 15 | 35 | 15 | 100 | 15 | 41 | 15 | 59 | 15 | 129 |
| 16 | 16 | 333 | 16 | 200 | 16 | 144 | 16 | 111 | 16 | 233 |
| 17 | 17 | 100 | 17 | 64 | 17 | 136 | 17 | 236 | 17 | 100 |
| 18 | 18 | 54 | 18 | 13 | 18 | 79 | 18 | 79 | 18 | 71 |
| 19 | 19 | 283 | 19 | 30 | 19 | 667 | 19 | 1333 | 19 | 1167 |
| total processing time | 7356 | 6147 | 7009 | 9842 | 8109 | |||||
| job1 | job2 | job3 | job4 | job5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| proc. time | proc. time | proc. time | proc. time | proc. time | ||||||
| 0 | 5 | 200 | 4 | 120 | 18 | 125 | 8 | 267 | 18 | 167 |
| 1 | 9 | 150 | 9 | 125 | 9 | 200 | 5 | 200 | 11 | 229 |
| 2 | 15 | 106 | 15 | 129 | 15 | 153 | 11 | 229 | 0 | 160 |
| 3 | 2 | 200 | 5 | 100 | 1 | 180 | 7 | 240 | 8 | 133 |
| 4 | 16 | 133 | 12 | 156 | 6 | 200 | 6 | 200 | 4 | 160 |
| 5 | 18 | 167 | 8 | 133 | 8 | 267 | 9 | 225 | 12 | 200 |
| 6 | 1 | 140 | 1 | 160 | 14 | 171 | 13 | 183 | 14 | 171 |
| 7 | 13 | 133 | 11 | 114 | 4 | 240 | 4 | 240 | 7 | 80 |
| 8 | 19 | 167 | 0 | 160 | 5 | 200 | 15 | 176 | 15 | 153 |
| 9 | 6 | 200 | 13 | 150 | 19 | 233 | 16 | 222 | 17 | 182 |
| 10 | 0 | 150 | 3 | 175 | 2 | 255 | 19 | 250 | 5 | 50 |
| 11 | 10 | 167 | 10 | 167 | 3 | 125 | 18 | 250 | 2 | 125 |
| 12 | 4 | 180 | 16 | 111 | 12 | 189 | 3 | 225 | 16 | 172 |
| 13 | 7 | 200 | 14 | 136 | 0 | 110 | 12 | 193 | 1 | 190 |
| 14 | 17 | 136 | 2 | 125 | 17 | 182 | 0 | 250 | 6 | 80 |
| 15 | 8 | 200 | 17 | 155 | 7 | 280 | 2 | 250 | 13 | 183 |
| 16 | 3 | 150 | 18 | 150 | 16 | 144 | 17 | 182 | 10 | 140 |
| 17 | 11 | 157 | 19 | 117 | 11 | 214 | 14 | 186 | 19 | 183 |
| 18 | 12 | 144 | 7 | 120 | 13 | 158 | 11 | 190 | 9 | 213 |
| 19 | 14 | 121 | 6 | 180 | 10 | 133 | 10 | 267 | 3 | 175 |
| total processing time | 3201 | 2783 | 3759 | 4425 | 3146 | |||||
| HABBP | Default Assignment Strategy | Simplex Algorithm |
|---|---|---|
| 0.0157 | 0.0019 | 0.0198 |
| 0.0216 | 0.0182 | 0.0318 |
| 0.0178 | 0.0097 | 0.0290 |
| 0.0166 | 0.0042 | 0.0200 |
| 0.0174 | 0.0073 | 0.0256 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akintoye, S.B.; Bagula, A. Improving Quality-of-Service in Cloud/Fog Computing through Efficient Resource Allocation. Sensors 2019, 19, 1267. https://doi.org/10.3390/s19061267
Akintoye SB, Bagula A. Improving Quality-of-Service in Cloud/Fog Computing through Efficient Resource Allocation. Sensors. 2019; 19(6):1267. https://doi.org/10.3390/s19061267
Chicago/Turabian StyleAkintoye, Samson Busuyi, and Antoine Bagula. 2019. "Improving Quality-of-Service in Cloud/Fog Computing through Efficient Resource Allocation" Sensors 19, no. 6: 1267. https://doi.org/10.3390/s19061267
APA StyleAkintoye, S. B., & Bagula, A. (2019). Improving Quality-of-Service in Cloud/Fog Computing through Efficient Resource Allocation. Sensors, 19(6), 1267. https://doi.org/10.3390/s19061267





