Design of Non-Uniform Antenna Arrays for Improved Near-Field MultiFocusing
Abstract
:1. Introduction
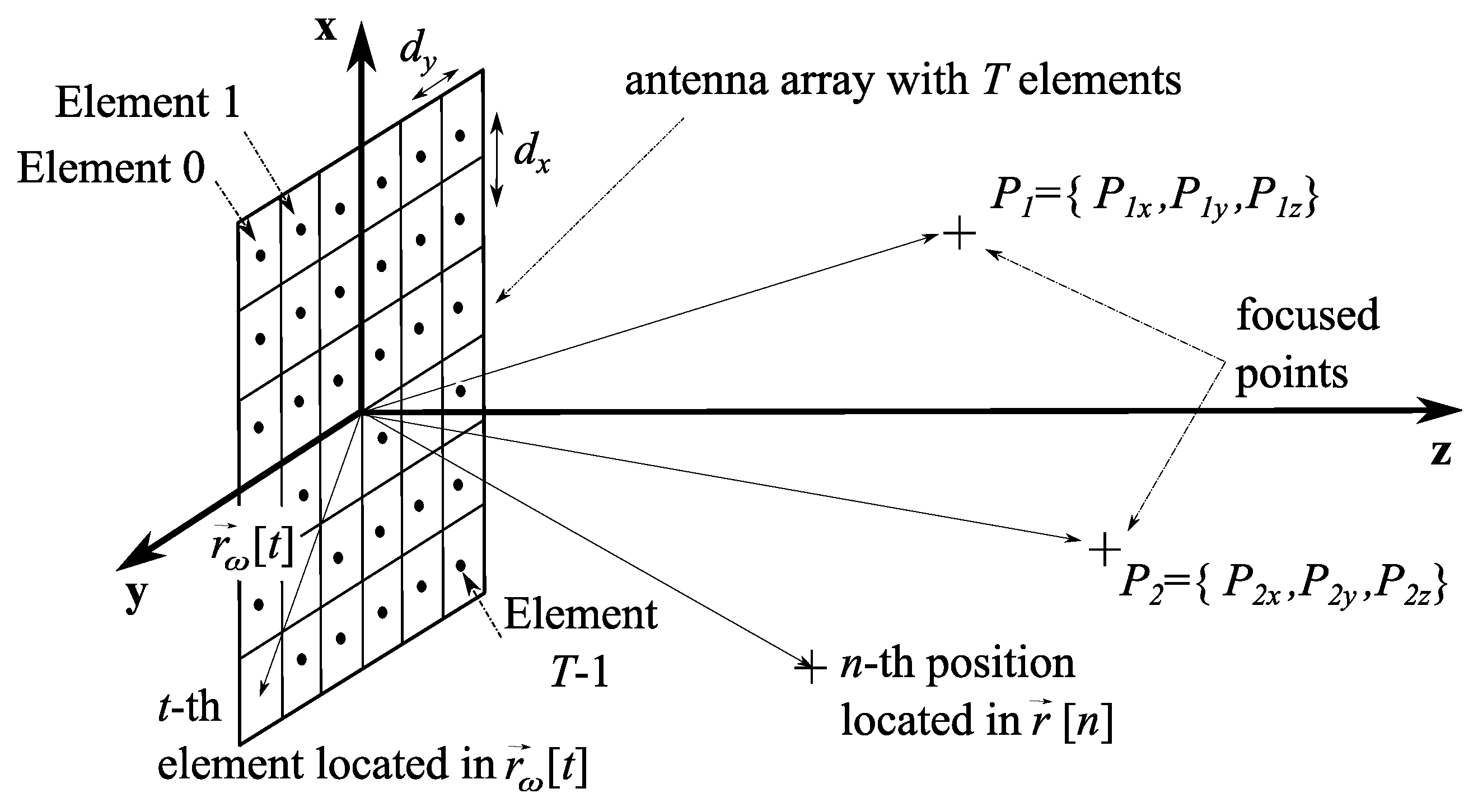
2. Near Field Multifocusing on Antenna Arrays
3. NF-MF Framework Including Position Optimization
3.1. Cost Function Definition
3.2. Magnitude-Phase-Position and Phase-Position Synthesis
3.3. Selection of Array Parameters to be Synthesized
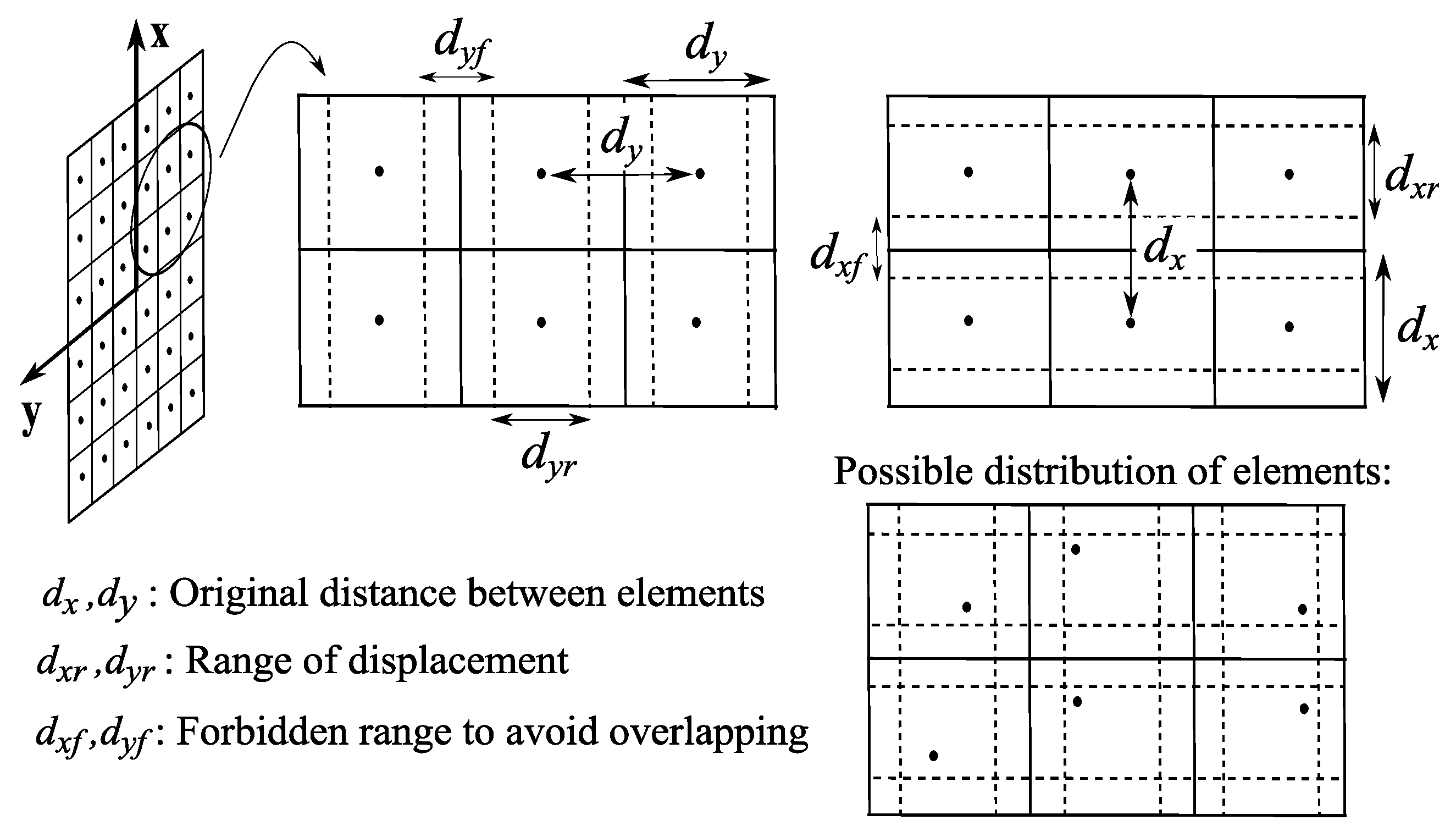
- Planar array antennas with irregular mesh. If planar array antennas are considered, the optimization of positions can be limited to , avoiding the modification of coordinates ; thus, and ( and unknowns, respectively). A possible scheme which represents the limits in the allowed locations of the elements in the plane is represented in Figure 4. Note the non-uniform mesh allowed in both directions .
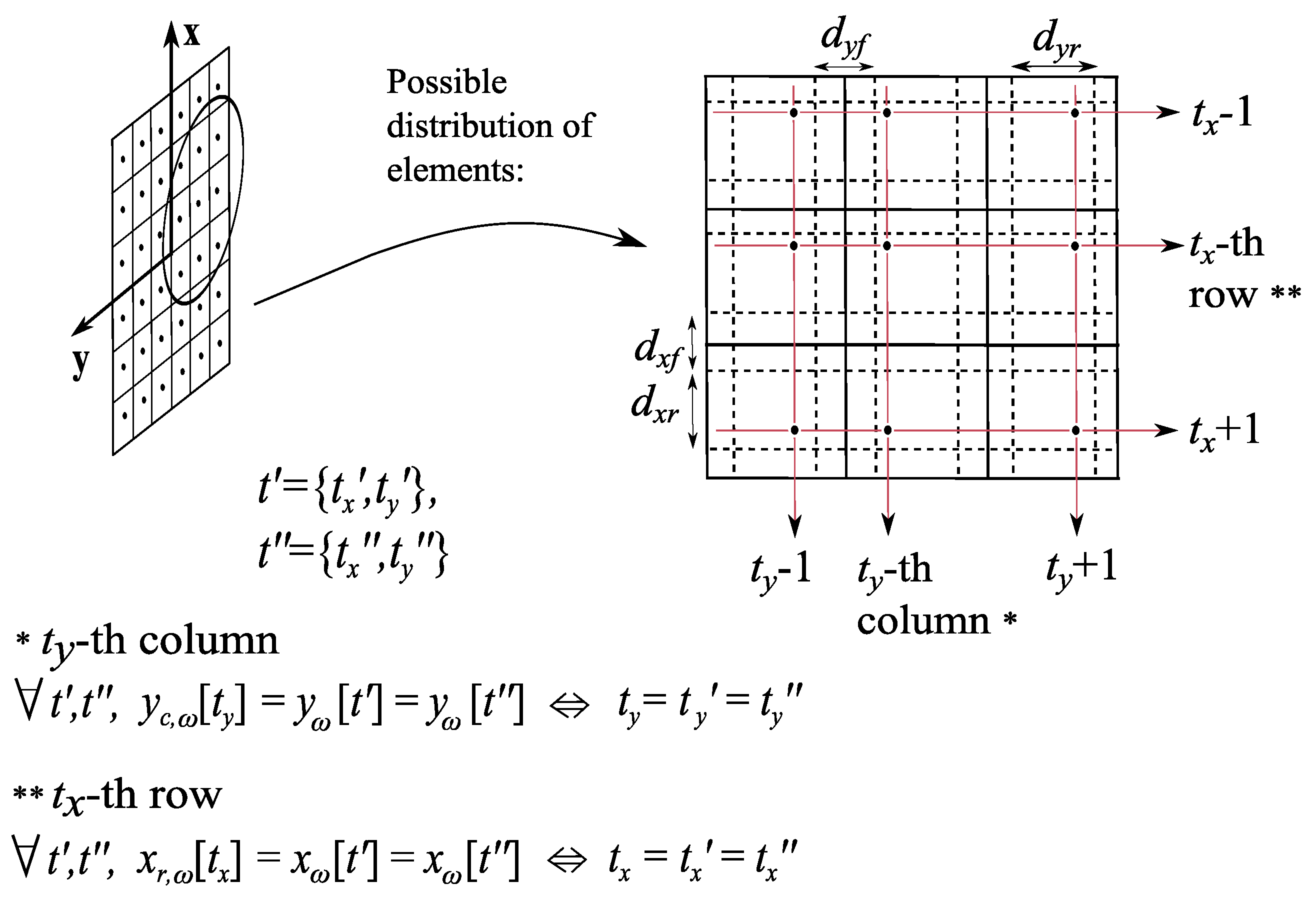
- Planar array antennas keeping the distribution in rows and columns. In order to simplify the previous mesh, NF-MF algorithm may be modified to optimize positions maintaining the original distribution in rows and columns (i.e., only the location of each row and column is to be optimized), as it is depicted in Figure 5. This option highly reduces temporal costs, since the number of variables considered in the position synthesis is lower (only the number of rows and columns, i.e., ). Moreover, the fabrication issues are simplified with respect to the previous case; in contrast, the NF performance of the resulting array may decrease, since the number of degrees of freedom in the solutions is reduced, and hence the focusing capability of the system is also reduced (It will be assessed in Section 4). Considering the description shown in Figure 5, the solution vector for this option is defined as:where . Thus, the dimension of and is and respectively. The partial derivatives required in (9) are defined as the sum of the ones shown in (12) for each row or column:where .
- Elements follow certain model or mathematical function. The position of elements may be distributed according to a certain function, which is determined by a set of coefficients or hyperparameters. Generally, this set is smaller than the original number of positions, so the number of variables involved in the optimization is reduced. As an example, a paraboloid function may be used to model the array structure as:Considering fixed , the optimization is limited to , hence modifying . Thus, only two parameters are used in the optimization, in order to modify the curve of the array (component ) instead of positions :As a result, the optimization process is faster without degrading the array capabilities of focusing; in contrast, the fabrication tasks become more complex. An example is depicted in Figure 6. The partial derivatives are defined as:
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NF | Near-Field |
| NFF | Near-Field Focusing |
| CP | Conjugate-Phase |
| NF-MF | Near-Field Multifocusing |
| WPT | Wireless Power Transfer |
| WPIT | Wireless Power and Information Transfer |
| IoT | Internet of Things |
| LS | Least Squares |
| LM | Levenberg-Marquardt |
| MP | Magnitude-Phase |
| PO | Phase-Only |
| MPP | Magnitude-Phase-Position |
| PP | Phase-Position |
References
- Buffi, A.; Serra, A.A.; Nepa, P.; Chou, H.T.; Manara, G. A Focused Planar Microstrip Array for 2.4 GHz RFID Readers. IEEE Trans. Antennas Propag. 2010, 58, 1536–1544. [Google Scholar] [CrossRef]
- Buffi, A.; Nepa, P.; Manara, G. Design Criteria for Near-Field-Focused Planar Arrays. IEEE Antennas Propag. Mag. 2012, 54, 40–50. [Google Scholar] [CrossRef]
- Chou, H.T.; Hung, T.M.; Wang, N.N.; Chou, H.H.; Tung, C.; Nepa, P. Design of a Near-Field Focused Reflectarray Antenna for 2.4 GHz RFID Reader Applications. IEEE Trans. Antennas Propag. 2011, 59, 1013–1018. [Google Scholar] [CrossRef]
- Chou, H.; Hung, K.; Chou, H. Design of Periodic Antenna Arrays With the Excitation Phases Synthesized for Optimum Near-Field Patterns via Steepest Descent Method. IEEE Trans. Antennas Propag. 2011, 59, 4342–4345. [Google Scholar] [CrossRef]
- Monti, G.; Costanzo, A.; Mastri, F.; Mongiardo, M.; Tarricone, L. Rigorous design of matched wireless power transfer links based on inductive coupling. Radio Sci. 2016, 51, 858–867. [Google Scholar] [CrossRef]
- Costanzo, A.; Masotti, D. Smart Solutions in Smart Spaces: Getting the Most from Far-Field Wireless Power Transfer. IEEE Microw. Mag. 2016, 17, 30–45. [Google Scholar] [CrossRef]
- Alvarez, J.; Ayestaran, R.G.; Leon, G.; Herran, L.F.; Arboleya, A.; Lopez-Fernandez, J.A.; Las-Heras, F. Near field multifocusing on antenna arrays via non-convex optimisation. IET Microw. Antennas Propag. 2014, 8, 754–764. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Bevacqua, M.T.; Crocco, L.; Isernia, T. 3-D Field Intensity Shaping via Optimized Multi-Target Time Reversal. IEEE Trans. Antennas Propag. 2018, 66, 4380–4385. [Google Scholar] [CrossRef]
- Nepa, P.; Buffi, A. Near-Field-Focused Microwave Antennas: Near-field shaping and implementation. IEEE Antennas Propag. Mag. 2017, 59, 42–53. [Google Scholar] [CrossRef]
- Gee, W.; Lee, S.W.; Bong, N.K.; Cain, C.A.; Mittra, R.; Magin, R.L. Focused Array Hyperthermia Applicator: Theory and Experiment. IEEE Trans. Biomed. Eng. 1984, BME-31, 38–46. [Google Scholar] [CrossRef]
- Sheen, D.M.; McMakin, D.L.; Hall, T.E. Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 2001, 49, 1581–1592. [Google Scholar] [CrossRef]
- Yu, S.; Liu, H.; Li, L. Design of Near-Field Focused Metasurface for High Efficient Wireless Power Transfer with Multi-Focus Characteristics. IEEE Trans. Ind. Electron. 2018, 66, 3993–4002. [Google Scholar] [CrossRef]
- Gomez-Tornero, J.L.; Quesada-Pereira, F.; Alvarez-Melcon, A.; Goussetis, G.; Weily, A.R.; Guo, Y.J. Frequency Steerable Two Dimensional Focusing Using Rectilinear Leaky-Wave Lenses. IEEE Trans. Antennas Propag. 2011, 59, 407–415. [Google Scholar] [CrossRef]
- Gomez-Tornero, J.L.; Weily, A.R.; Guo, Y.J. Rectilinear Leaky-Wave Antennas With Broad Beam Patterns Using Hybrid Printed-Circuit Waveguides. IEEE Trans. Antennas Propag. 2011, 59, 3999–4007. [Google Scholar] [CrossRef]
- Martínez-Ros, A.J.; Gómez-Tornero, J.L.; Clemente-Fernández, F.J.; Monzó-Cabrera, J. Microwave Near-Field Focusing Properties of Width-Tapered Microstrip Leaky-Wave Antenna. IEEE Trans. Antennas Propag. 2013, 61, 2981–2990. [Google Scholar] [CrossRef]
- Ayestarán, R.G. Fast Near-Field Multifocusing of Antenna Arrays Including Element Coupling Using Neural Networks. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1233–1237. [Google Scholar] [CrossRef]
- Alvarez, J.; Ayestaran, R.G.; Las-Heras, F. Design of antenna arrays for near-field focusing requirements using optimisation. Electron. Lett. 2012, 48, 1323–1325. [Google Scholar] [CrossRef]
- Lero, D.A.M.; Crocco, L.; Isernia, T. Advances in 3-D electromagnetic focusing: Optimized time reversal and optimal constrained power focusing. Radio Sci. 2017, 52, 166–175. [Google Scholar]
- Bellizzi, G.G.; Iero, D.A.M.; Crocco, L.; Isernia, T. Three-Dimensional Field Intensity Shaping: The Scalar Case. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 360–363. [Google Scholar] [CrossRef]
- Hansen, R. Focal region characteristics of focused array antennas. IEEE Trans. Antennas Propag. 1985, 33, 1328–1337. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Capozzoli, A.; Curcio, C.; Iavazzo, E.; Liseno, A.; Migliorelli, M.; Toso, G. Phase-only synthesis of a-periodic reflectarrays. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; pp. 987–991. [Google Scholar]
- Ridwan, M.; Abdo, M.; Jorswieck, E. Design of non-uniform antenna arrays using genetic algorithm. In Proceedings of the 13th International Conference on Advanced Communication Technology (ICACT2011), Seoul, Korea, 13–16 Feburary 2011; pp. 422–427. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design; Wiley-Interscience: New York, NY, USA, 2005. [Google Scholar]
- Alvarez, J.; Ayestaran, R.G.; Laviada, J.; Las-Heras, F. Support vector regression for near-field multifocused antenna arrays considering mutual coupling. Int. J. Numer. Model. Electron. Netw. Devices Fields 2016, 29, 146–156. [Google Scholar]
- Harrington, R.F. Field Computation by Moment Methods; Wiley-IEEE Press: New York, NY, USA, 1993. [Google Scholar]











| Mesh | ||||||||
|---|---|---|---|---|---|---|---|---|
| Planar array | 1.54 | 0.944 | 0.852 | |||||
| Planar array (col/row) | 1.54 | 0.10 | 0.969 | 0.841 | ||||
| Paraboloid function | 1.89 | 0.10 | 0.947 | 0.785 | ||||
| Best MP 8 × 8 uniform array in [7] | 1.70 | 0.13 | 0.873 | 0.698 |
| Mesh | ||||||||
|---|---|---|---|---|---|---|---|---|
| Planar array | 0.12 | 0 | 1 | 0.952 | ||||
| Planar array (col/row) | 0.12 | 0 | 1 | 0.963 | ||||
| Paraboloid function | 0.40 | 0 | 1 | 0.873 | ||||
| Best PO 16 × 16 uniform array in [7] | 0.67 | 0.972 | 0.6981 |
| Optimization Case | Time per Iteration | Iterations |
|---|---|---|
| MP | 18 s | 45 |
| PO | 22 s | 32 |
| MPP | 25 s | 120 |
| PP | 31 s | 80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Ayestarán, R.; Álvarez, J.; Las-Heras, F. Design of Non-Uniform Antenna Arrays for Improved Near-Field MultiFocusing. Sensors 2019, 19, 645. https://doi.org/10.3390/s19030645
González-Ayestarán R, Álvarez J, Las-Heras F. Design of Non-Uniform Antenna Arrays for Improved Near-Field MultiFocusing. Sensors. 2019; 19(3):645. https://doi.org/10.3390/s19030645
Chicago/Turabian StyleGonzález-Ayestarán, Rafael, Jana Álvarez, and Fernando Las-Heras. 2019. "Design of Non-Uniform Antenna Arrays for Improved Near-Field MultiFocusing" Sensors 19, no. 3: 645. https://doi.org/10.3390/s19030645
APA StyleGonzález-Ayestarán, R., Álvarez, J., & Las-Heras, F. (2019). Design of Non-Uniform Antenna Arrays for Improved Near-Field MultiFocusing. Sensors, 19(3), 645. https://doi.org/10.3390/s19030645






