An Evaluation Framework for Spectral Filter Array Cameras to Optimize Skin Diagnosis
Abstract
1. Introduction
- comparison framework of spectral filter array cameras for skin imaging and medical diagnosis
- illustrate the impact of spectral reflectance reconstruction using a specialized training set for SFA camera applications in skin imaging.
- recommendation of commercially available SFA cameras for monitoring of vital functions and diagnosis.
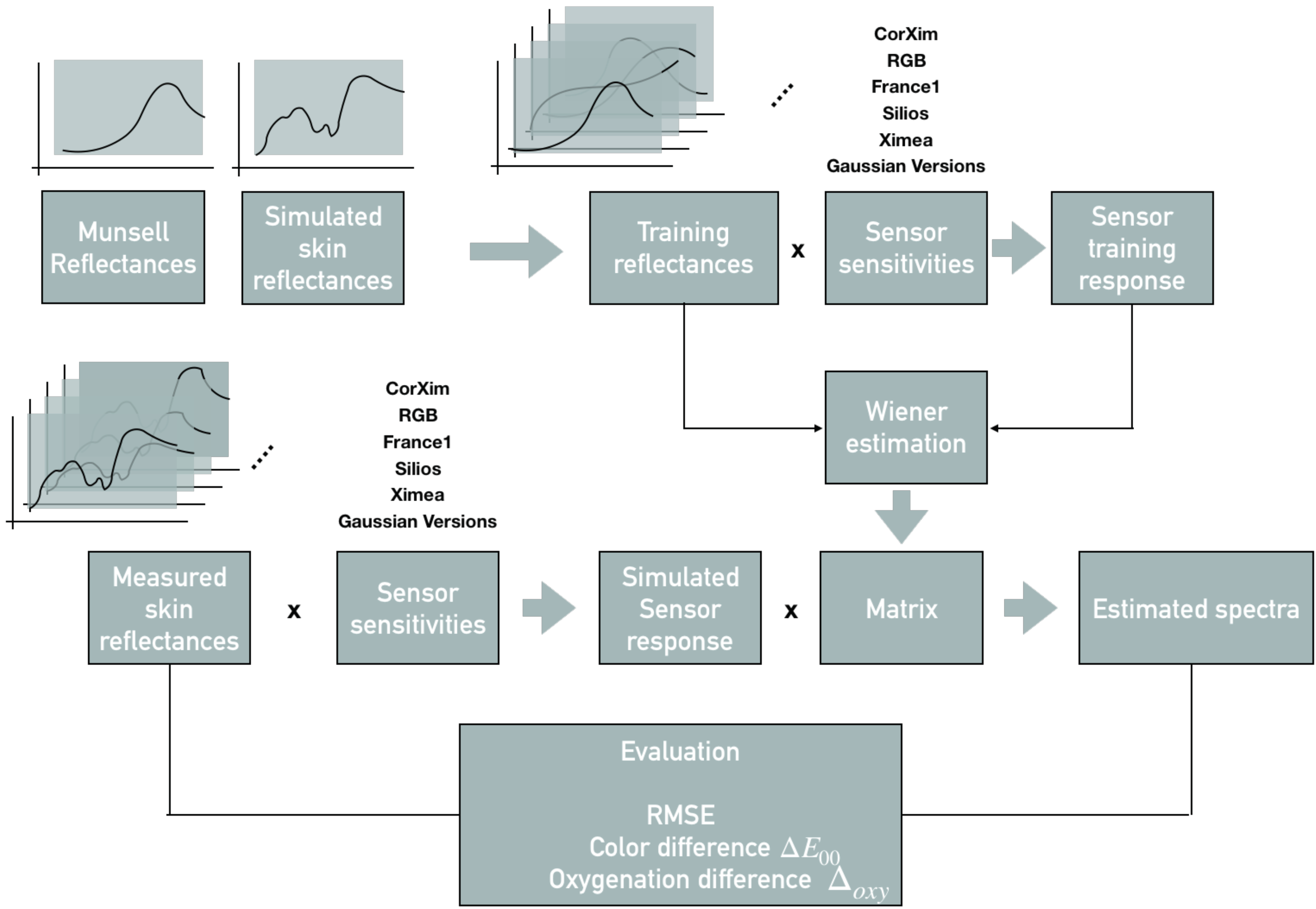
2. The Proposed Framework
3. Prerequisites
3.1. Spectral Imaging Model and Spectral Reconstruction
3.2. Sensors
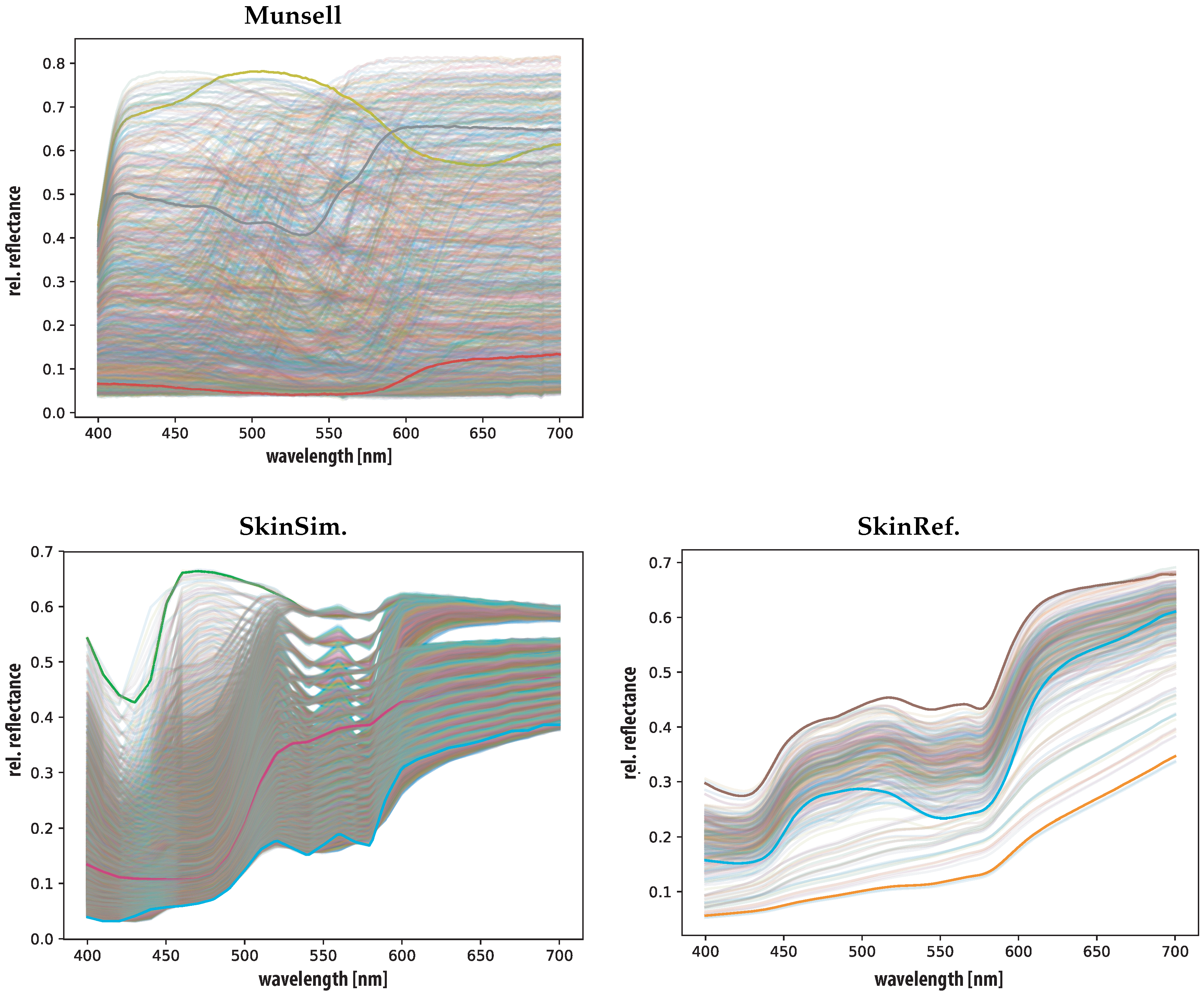
3.3. Training and Test Set
3.4. Evaluation Metrics
3.5. Application-Specific Metric and Oxygenation Level Estimation
4. Experimental Setup
4.1. Sensors
4.2. Generating a Training Set
5. Results and Discussion
5.1. Training Set Validation
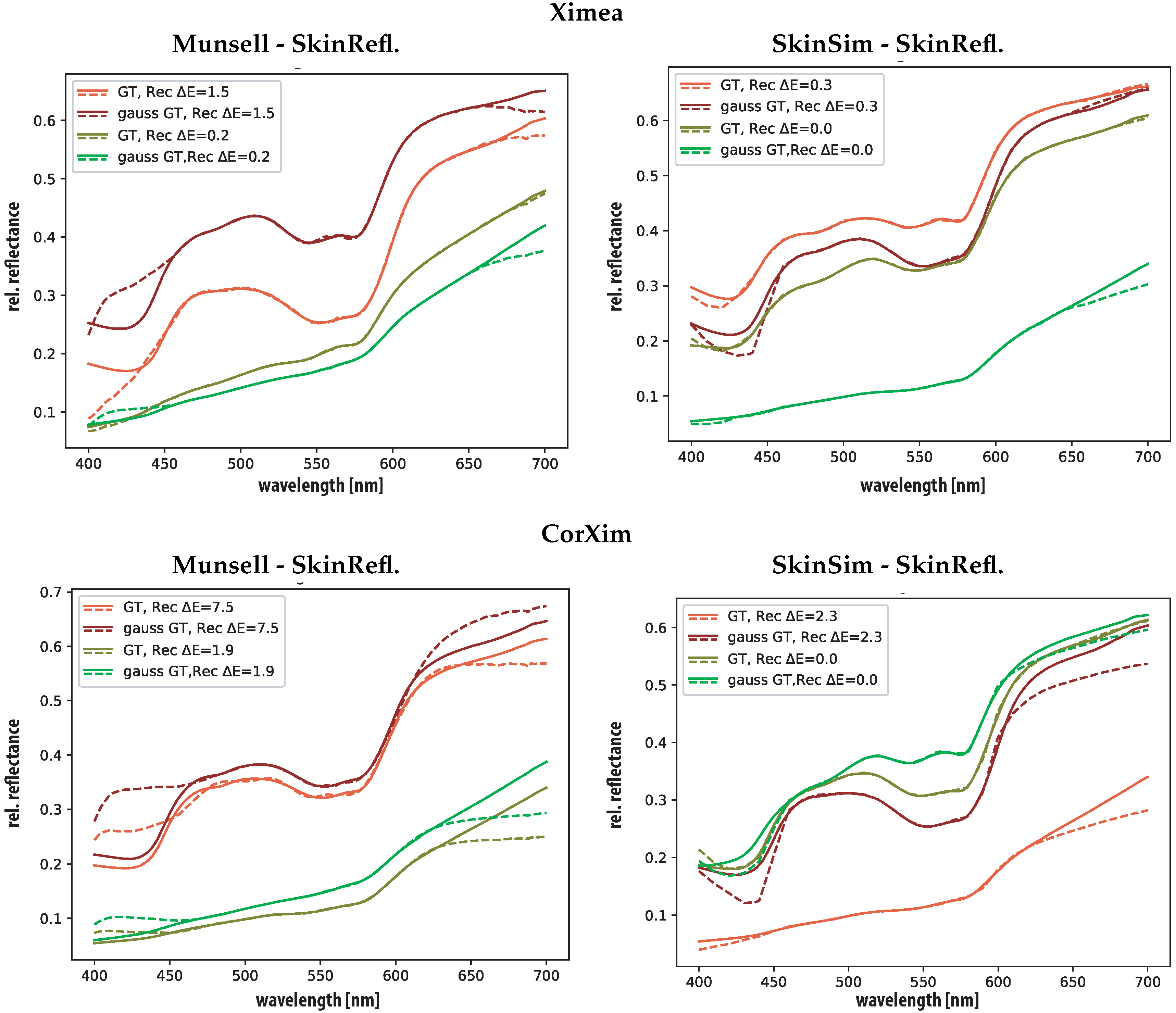
5.2. Spectral Reconstruction
5.3. Oxygenation Level Estimation
5.4. Summary and Conclusions
- Spectral shapes of the filters should be adapted application-specific
- Careful choice of the spectral bands should be adapted application-specific
- Selecting an optimal training set for spectral reflectances reconstruction improves the results for SFAs with narrow spectral sensitivities
- GSB improve spectral reconstruction considering color differences and RMSE
- GSB have a small impact on oxygenation level estimation if the bands are not close to the ideal wavelength for oxygen estimation
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SFA | spectral filter array |
| GFC | goodness of fit coefficient |
| RMSE | root mean square error |
| sRGB | standard RGB |
| MCML | Monte Carlo modelling of light transport in multi-layered tissues |
| GSB | gaussian spectral bands |
References
- Lapray, P.J.; Wang, X.; Thomas, J.B.; Gouton, P. Multispectral filter arrays: Recent advances and practical implementation. Sensors 2014, 14, 21626–21659. [Google Scholar] [CrossRef] [PubMed]
- Ewerlöf, M.; Larsson, M.; Salerud, E.G. Spatial and temporal skin blood volume and saturation estimation using a multispectral snapshot imaging camera. Proc. SPIE 2017. [Google Scholar] [CrossRef]
- Thomas, J.B.; Lapray, P.J.; Gouton, P.; Clerc, C. Spectral Characterization of a Prototype SFA Camera for Joint Visible and NIR Acquisition. Sensors 2016, 16, 993. [Google Scholar] [CrossRef] [PubMed]
- Ximea. Hyperspectral Cameras. 2018. Available online: https://www.ximea.com (accessed on 2 December 2018).
- IMEC. Hyperspectral-Imaging. 2018. Available online: https://www.imec-int.com (accessed on 2 December 2018).
- SILIOS. Multispectral-Imaging. 2018. Available online: https://www.silios.com (accessed on 2 December 2018).
- Pedersen, M.; Hardeberg, J.Y. Full-reference image quality metrics: Classification and evaluation. Found. Trends® Comput. Graph. Vis. 2012, 7, 1–80. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Chandler, D.M. Seven Challenges in Image Quality Assessment: Past, Present, and Future Research. ISRN Signal Process. 2013, 2013, 1–53. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H.; Ramanath, R.; Snyder, W.E. Binary tree-based generic demosaicking algorithm for multispectral filter arrays. IEEE Trans. Image Process. 2006, 15. [Google Scholar] [CrossRef]
- Monno, Y.; Tanaka, M.; Okutomi, M. Multispectral demosaicking using adaptive kernel upsampling. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 3157–3160. [Google Scholar]
- Wang, C.; Wang, X.; Hardeberg, J.Y. A Linear Interpolation Algorithm for Spectral Filter Array Demosaicking. In Image and Signal Processing; Springer International Publishing: Cham, Switzerland, 2014; pp. 151–160. [Google Scholar]
- Wang, X.; Thomas, J.B.; Hardeberg, J.Y.; Gouton, P. A Study on the Impact of Spectral Characteristics of Filters on Multispectral Image Acquisition. In Proceedings of the 12th Congress of the International Colour Association, Newcastle Gateshead, UK, 8–12 July 2013; Volume 4, pp. 1765–1768. [Google Scholar]
- Park, C.; Kang, M. Color Restoration of RGBN Multispectral Filter Array Sensor Images Based on Spectral Decomposition. Sensors 2016, 16, 719. [Google Scholar] [CrossRef]
- Nazari, R.M. Denoising and Demosaicking of Color Images. Ph.D. Thesis, Université d’Ottawa/University of Ottawa, Ottawa, ON, Canada, 2017. [Google Scholar]
- Bersha, K.S. Spectral Imaging and Analysis of Human Skin. Master’s Thesis, University of Estern Finland, Joensuu, Finnland, 2010. [Google Scholar]
- Kuzmina, I.; Diebele, I.; Jakovels, D.; Spigulis, J.; Valeine, L.; Kapostinsh, J.; Berzina, A. Towards noncontact skin melanoma selection by multispectral imaging analysis. J. Biomed. Opt. 2011, 16, 060502. [Google Scholar] [CrossRef]
- Nishidate, I.; Tanaka, N.; Kawase, T.; Maeda, T.; Yuasa, T.; Aizu, Y.; Yuasa, T.; Niizeki, K. Noninvasive imaging of human skin hemodynamics using a digital red-green-blue camera. J. Biomed. Opt. 2011, 16, 086012. [Google Scholar] [CrossRef]
- Jakovels, D.; Spigulis, J. RGB imaging device for mapping and monitoring of hemoglobin distribution in skin. Lith. J. Phys. 2012, 52, 50–54. [Google Scholar] [CrossRef]
- Jakovels, D.; Kuzmina, I.; Berzina, A.; Spigulis, J. RGB imaging system for monitoring of skin vascular malformation’s laser therapy. Proc. SPIE 2012, 8427, 842737. [Google Scholar]
- Kumar, A.; Dhawan, A.P.; Relue, P.; Chaudhuri, P.K. Multi-spectral optical imaging of skin to diagnose malignant melanoma. In Proceedings of the Engineering in Medicine and Biology, Atlanta, GA, USA, 13–16 October 1999; Volume 2, p. 1098. [Google Scholar]
- Cotton, S.; Claridge, E.; Hall, P. A skin imaging method based on a colour formation model and its application to the diagnosis of pigmented skin lesions. In Proceedings of the Medical Image Understanding and Analysis, BMVA, Oxford, UK, 19–20th July 1999; pp. 49–52. [Google Scholar]
- Tsumura, N.; Kawabuchi, M.; Haneishi, H.; Miyake, Y. Mapping Pigmentation in Human Skin by Multi-Visible-Spectral Imaging by Inverse Optical Scattering Technique. Color Imaging Conf. 2000, 2000, 81–84. [Google Scholar]
- Balas, C.; Themelis, G.; Papadakis, A.; Vasgiouraki, E. A novel hyper-spectral imaging system: Application on in-vivo detection and grading of cervical precancers and of pigmented skin lesions. In Proceedings of the IEEE Computer Society Workshop on Computer Vision Beyond the Visible Spectrum, Kauai, HI, USA, 14 December 2001. [Google Scholar]
- Kerekes, J.; Subramanian, N.; Kearney, K.; Schad, N. Spectral imaging of skin: Experimental observations and analyses. Proc. SPIE 2006, 6142, 61423V. [Google Scholar]
- Randeberg, L.L.; Baarstad, I.; Løke, T.; Kaspersen, P.; Svaasand, L.O. Hyperspectral imaging of bruised skin. Proc. SPIE 2006, 6078, 6078. [Google Scholar] [CrossRef]
- Klaessens, J.H.G.M.; Noordmans, H.J.; de Roode, R.; Verdaasdonk, R.M. Non-invasive skin oxygenation imaging using a multi-spectral camera system: Effectiveness of various concentration algorithms applied on human skin. Proc. SPIE 2009, 7174. [Google Scholar] [CrossRef]
- Spigulis, J.; Jakovels, D.; Rubins, U. Multi-spectral skin imaging by a consumer photo-camera. Proc. SPIE 2010, 7557. [Google Scholar] [CrossRef]
- Huang, J. Multispectral Imaging of Skin Oxygenation. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2013. [Google Scholar]
- Poxon, I.; Wilkinson, J.; Herrick, A.; Dickinson, M.; Murray, A. Pilot study to visualise and measure skin tissue oxygenation, erythema, total haemoglobin and melanin content using index maps in healthy controls. Proc. SPIE 2014, 8951, 89510X. [Google Scholar]
- Van Gastel, M.; Stuijk, S.; De Haan, G. New principle for measuring arterial blood oxygenation, enabling motion-robust remote monitoring. Sci. Rep. 2016, 6, 38609. [Google Scholar] [CrossRef]
- Bauer, J.R.; van Beekum, K.; Klaessens, J.H.G.M.; Noordmans, H.J.; Boer, C.; Hardeberg, J.Y.; Verdaasdonk, R.M. Towards real-time non contact spatial resolved oxygenation monitoring using a multi spectral filter array camera in various light conditions. Proc. SPIE 2018, 10489. [Google Scholar] [CrossRef]
- Preece, S.J.; Claridge, E. Spectral filter optimization for the recovery of parameters which describe human skin. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 913–922. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Gutiérrez, J.; Pardo, A.; Real, E.; López-Higuera, J.; Conde, O.M. Custom Scanning Hyperspectral Imaging System for Biomedical Applications: Modeling, Benchmarking, and Specifications. Sensors 2019, 19, 1692. [Google Scholar] [CrossRef] [PubMed]
- Saager, R.B.; Baldado, M.L.; Rowland, R.A.; Kelly, K.M.; Durkin, A.J. Method using in vivo quantitative spectroscopy to guide design and optimization of low-cost, compact clinical imaging devices: Emulation and evaluation of multispectral imaging systems. J. Biomed. Opt. 2018, 23, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, J.; Scully, T.; Barbosa, N.; Donner, C.; Alvarez, X.; Vieira, T.; Matts, P.; Orvalho, V.; Gutierrez, D.; Weyrich, T. A practical appearance model for dynamic facial color. ACM Trans. Graph. (Proc. SIGGRAPH Asia) 2010, 29, 141:1–141:10. [Google Scholar]
- Iglesias-Guitian, J.A.; Aliaga, C.; Jarabo, A.; Gutierrez, D. A Biophysically-Based Model of the Optical Properties of Skin Aging. Comput. Graph. Forum 2015, 34, 45–55. [Google Scholar] [CrossRef]
- Lapray, P.J.; Thomas, J.B.; Gouton, P. High Dynamic Range Spectral Imaging Pipeline For Multispectral Filter Array Cameras. Sensors 2017, 17, 1281. [Google Scholar] [CrossRef] [PubMed]
- Delgado Atencio, J.A.; Jacques, S.L.; Montiel, S.V. Monte Carlo Modeling of Light Propagation in Neonatal Skin; InTech: London, UK, 2011. [Google Scholar]
- Hiltunen, J. Munsell Book of Color: Matte Finish Collection Measured by J. Hiltunen. 2019. Available online: https://www.uef.fi/web/spectral/munsell-colors-matt-spectrofotometer-measured (accessed on 2 December 2018).
- Munsell Color. Munsell Book of Color: Matte Finish Collection; Munsell Color: Baltimore, MD, USA, 1976. [Google Scholar]
- Cooksey, C.C.; Allen, D.W.; Tsai, B.K. Reference Data Set of Human Skin Reflectance. J. Res. Natl. Inst. Stand. Technol. 2017, 122, 1–5. [Google Scholar] [CrossRef]
- Publication, CIE. CIE 15: Technical Report: Colorimetry, 3rd ed.; CIE Cent. Bur.: Vienna, Austria, 2004; Volume 3. [Google Scholar]
- Hardeberg, J.Y. Acquisition and Reproduction of Color Images: Colorimetric and Multispectral Approaches. Ph.D. Thesis, Ecole Nationale Supérieure des Télécommunications, Paris, France, 1999. [Google Scholar]
- Imai, F.H.; Berns, R.S. Spectral estimation using trichromatic digital cameras. In Proceedings of the International Symposium on Multispectral Imaging and Color Reproduction for Digital Archives, Chiba, Japan, 21–22 October 1999; Volume 42, pp. 1–8. [Google Scholar]
- Shimano, N.; Terai, K.; Hironaga, M. Recovery of spectral reflectances of objects being imaged by multispectral cameras. J. Opt. Soc. Am. A 2007, 24, 3211. [Google Scholar] [CrossRef]
- Shimano, N.; Hironaga, M. Recovery of spectral reflectances of imaged objects by the use of features of spectral reflectances. J. Opt. Soc. Am. A 2010, 27, 251–258. [Google Scholar] [CrossRef]
- Stigell, P.; Miyata, K.; Hauta-Kasari, M. Wiener estimation method in estimating of spectral reflectance from RGB images. Pattern Recognit. Image Anal. 2007, 17, 233–242. [Google Scholar] [CrossRef]
- Nishidate, I.; Maeda, T.; Niizeki, K.; Aizu, Y. Estimation of Melanin and Hemoglobin Using Spectral Reflectance Images Reconstructed from a Digital RGB Image by the Wiener Estimation Method. Sensors 2013, 13, 7902–7915. [Google Scholar] [CrossRef] [PubMed]
- Heikkinen, V.; Lenz, R.; Jetsu, T.; Parkkinen, J.; Hauta-Kasari, M.; Jääskeläinen, T. Evaluation and unification of some methods for estimating reflectance spectra from RGB images. J. Opt. Soc. Am. A 2008, 25, 2444–2458. [Google Scholar] [CrossRef] [PubMed]
- Lapray, P.J.; Thomas, J.B.; Gouton, P.; Ruichek, Y. Energy balance in Spectral Filter Array camera design. J. Eur. Opt. Soc.-Rapid Publ. 2017, 13, 1. [Google Scholar] [CrossRef]
- Thomas, J.B. Illuminant estimation from uncalibrated multispectral images. In Proceedings of the 2015 Colour and Visual Computing Symposium (CVCS), Gjøvik, Norway, 25–26 August 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Thomas, J.B.; Hardeberg, J.Y.; Gouton, P. Multispectral imaging: Narrow or wide band filters? JAIC J. Int. Colour Assoc. 2014, 12, 44–51. [Google Scholar]
- Khan, H.A.; Thomas, J.B.; Hardeberg, J.Y.; Laligant, O. Illuminant estimation in multispectral imaging. J. Opt. Soc. Am. A 2017, 34, 1085–1098. [Google Scholar] [CrossRef]
- Randeberg, L.L.; Winnem, A.; Blindheim, S.; Haugen, O.; Svaasand, L. Optical classification of bruises. Proc. SPIE 2004, 5312, 54–64. [Google Scholar] [CrossRef]
- Humphreys, K.; Ward, T.; Markham, C. A CMOS camera-based pulse oximetry imaging system. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 3494–3497. [Google Scholar]
- Kong, L.; Yi, D.; Sprigle, S.; Wang, F.; Wang, C.; Liu, F.; Adibi, A.; Tummala, R. Single sensor that outputs narrowband multispectral images. J. Biomed. Opt. 2010, 15. [Google Scholar] [CrossRef]
- Spigulis, J.; Oshina, I.; Berzina, A.; Bykov, A. Smartphone snapshot mapping of skin chromophores under triple-wavelength laser illumination. J. Biomed. Opt. 2017, 22, 091508. [Google Scholar] [CrossRef]
- Bauer, J.R.; Bruins, A.A.; Hardeberg, J.Y.; Verdaasdonk, R.M. A Spectral Filter Array Camera for Clinical Monitoring and Diagnosis: Proof of Concept for Skin Oxygenation Imaging. J. Imaging 2019, 5. [Google Scholar] [CrossRef]
- Day, D. Spectral Sensitivities of the Sinarback 54 Camera; Technical Report; Munsell Color Science Laboratory, Chester F. Carlson Center for Imaging Science, Rochester Institute of Technology: Rochester, NY, USA, 2003. [Google Scholar]
- Bauer, J.R.; Pedersen, M.; Hardeberg, J.Y.; Verdaasdonk, R. Skin color simulation - review and analysis of available Monte Carlo-based photon transport simulation models. Color Imaging Conf. 2017, 2017, 165–170. [Google Scholar]
- Jacques, S. Origins of tissue optical properties in the UVA, visible, and NIR regions. Adv Opt Imaging Photon Migr. 1996, 2, 364–369. [Google Scholar]
- Jacques, S.L.; Prahl, S.A. A Collaboration of Oregon Health & Science University, Portland State University, and the Oregon Institute of Technology. Optical Spectra. 2015. Available online: https://www.omlc.org (accessed on 2 December 2018).
- IEC. International Standard: International Electrotechnical Commission; IEC 61966-2-1:1999; IEC: Geneva, Switzerland, 1999. [Google Scholar]
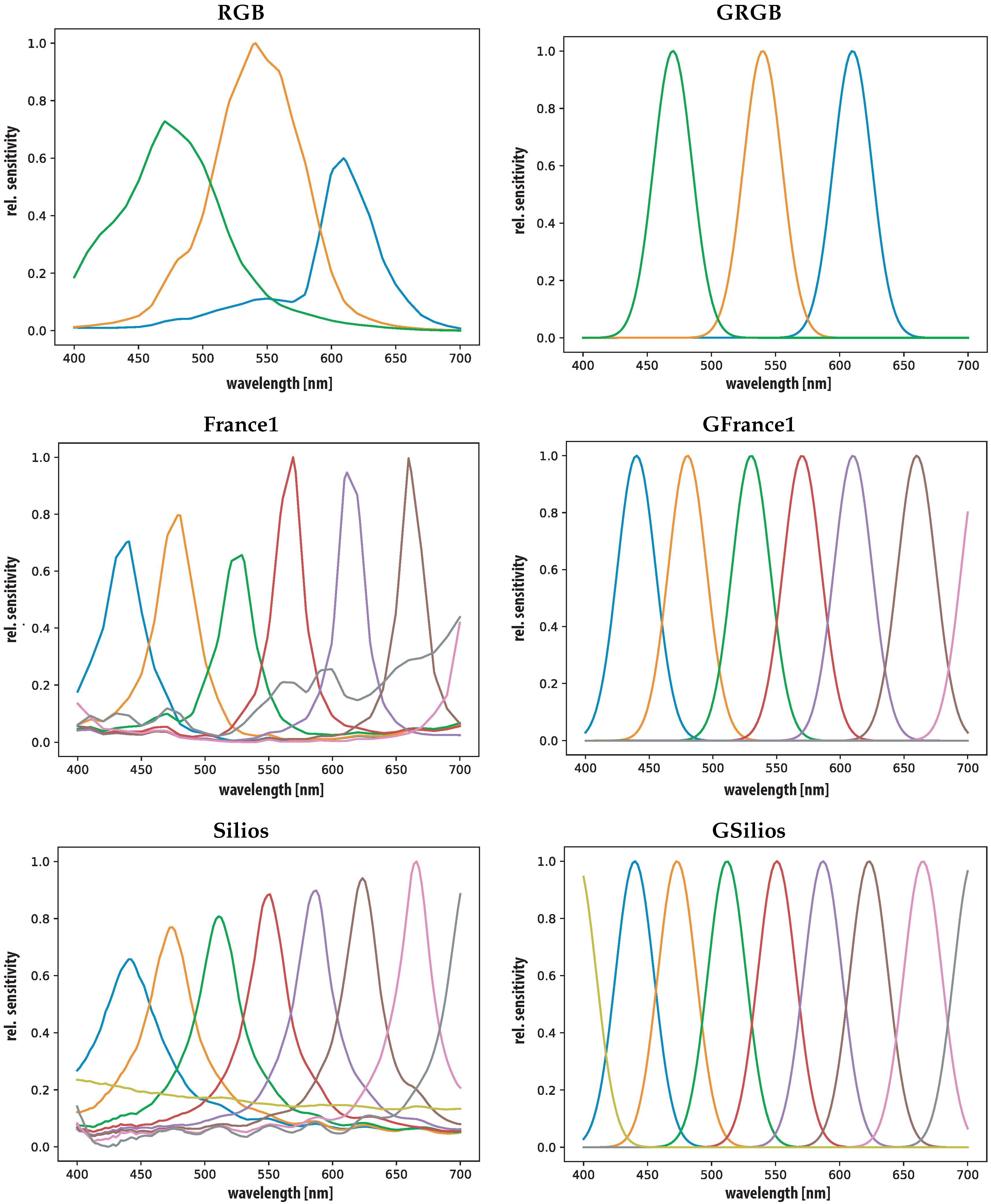
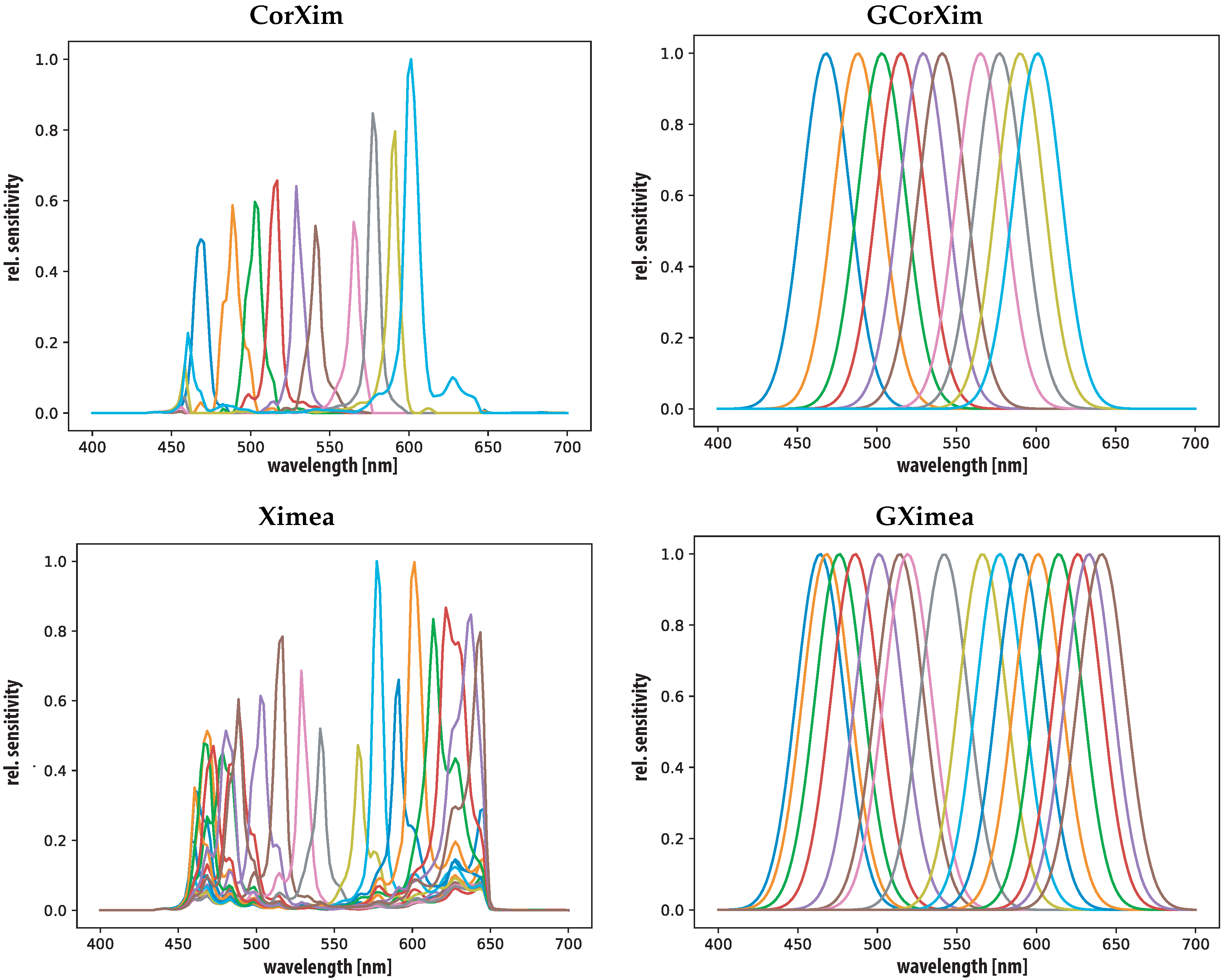
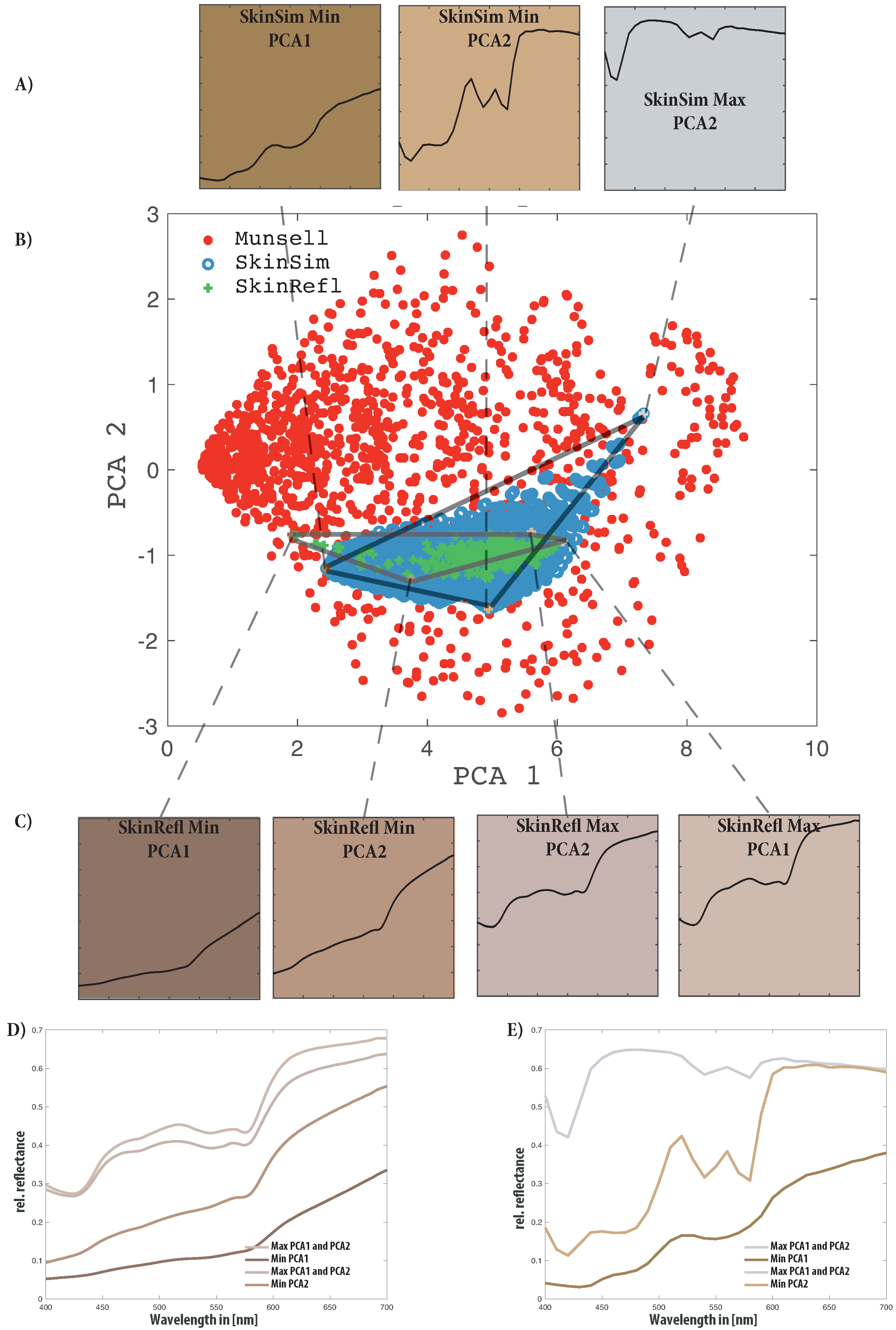
| Property | RGB | France1 | Silios | CorXim | Ximea |
|---|---|---|---|---|---|
| spectral bands | 3 | 8 | 9 | 10 | 16 |
| spectral peak range [nm] | 480–610 | 440–850 | 445–710 | 465–630 | 465–630 |
| frame rate [Hz] | 60 | 60 | 60 | 170 | 170 |
| resolution per band | |||||
| size [mm] | NA |
| Parameter | Level: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% | |
| 0.1% | 0.2% | 0.3% | 0.4% | 0.5% | 0.6% | 0.7% | 0.8% | 0.9% | 1% | |
| 0.0 | 0.025 | 0.05 | 0.075 | 0.1 | 0.125 | 0.15 | 0.175 | 0.2 | 0.225 | |
| 0 | 2% | 3% | 4 % | 5% | 6% | 7% | 8% | 9% | 10% |
| PCA | Munsell | SkinSim | SkinRefl | Combined |
|---|---|---|---|---|
| 1 | 76.8 | 87.1 | 96.0 | 74.7 |
| 2 | 15.8 | 7.7 | 2.1 | 17.0 |
| 3 | 6.0 | 4.3 | 1.5 | 4.8 |
| 4 | 0.8 | 0.5 | 0.2 | 2.1 |
| Parameter | Max PCA1 and PCA2 | Min PCA1 | Min PCA2 |
|---|---|---|---|
| 10% | 100 % | 10% | |
| 0.1% | 1% | 1% | |
| 0.225 | 0.0 | 0.225 | |
| 0.0 % | 10% | 10% |
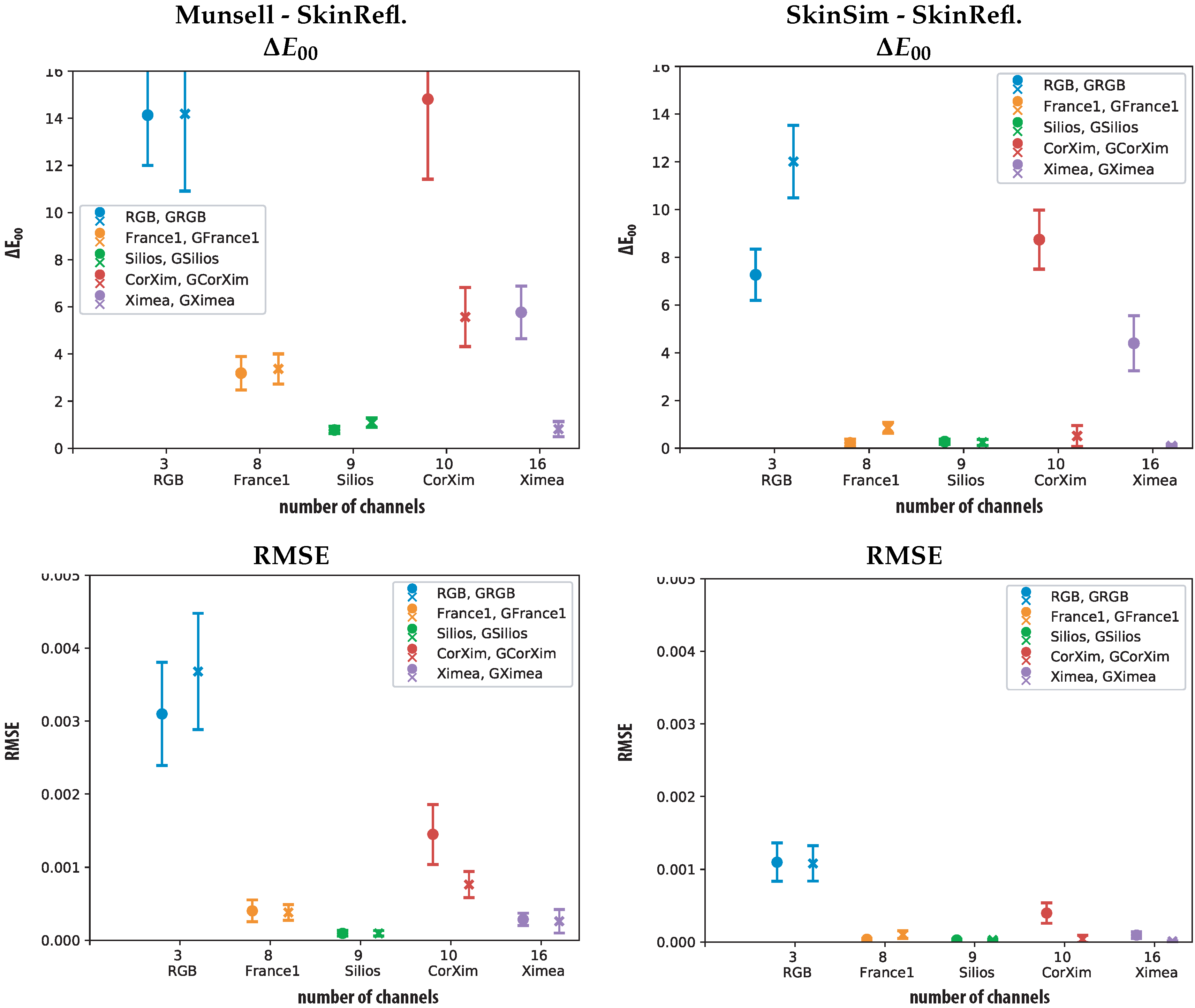
| Sensor | Min | Max | Mean | Std | 98% | Min | Max | Mean | Std | 98% | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RGB | 5.04 | 11.03 | 7.27 | 1.08 | 9.20 | GRGB | 8.89 | 16.76 | 12.01 | 1.52 | 14.87 | |
| France1 | 0.02 | 0.93 | 0.22 | 0.15 | 0.68 | GFrance1 | 0.40 | 1.50 | 0.86 | 0.23 | 1.35 | |
| Silios | 0.04 | 0.66 | 0.28 | 0.11 | 0.49 | GSilios | 0.03 | 0.75 | 0.25 | 0.12 | 0.51 | |
| CorXim | 5.82 | 11.99 | 8.74 | 1.24 | 11.50 | GCorXim | 0.02 | 2.27 | 0.51 | 0.44 | 2.18 | |
| Ximea | 0.89 | 6.81 | 4.40 | 1.16 | 6.38 | GXimea | 0.00 | 0.30 | 0.09 | 0.07 | 0.25 | |
| RMSE | ||||||||||||
| Sensor | Min | Max | Mean | Std | 98% | Min | Max | Mean | Std | 98% | ||
| RGB | 0.000647 | 0.002112 | 0.001099 | 0.000263 | 0.001717 | GRGB | 0.00067 | 0.00194 | 0.00108 | 0.00024 | 0.00180 | |
| France1 | 0.00001 | 0.00009 | 0.00004 | 0.00001 | 0.00007 | GFrance1 | 0.00003 | 0.00037 | 0.00010 | 0.00005 | 0.00022 | |
| Silios | 0.000003 | 0.00006 | 0.00003 | 0.00001 | 0.00005 | GSilios | 0.000003 | 0.00006 | 0.00003 | 0.00001 | 0.00006 | |
| CorrXim | 0.000184 | 0.00099 | 0.00040 | 0.00014 | 0.00081 | GCorXim | 0.000004 | 0.00028 | 0.00004 | 0.00005 | 0.00026 | |
| Ximea | 0.000007 | 0.00028 | 0.00010 | 0.00004 | 0.00020 | GXimea | 0.000002 | 0.00003 | 0.00001 | 0.00001 | 0.00003 | |
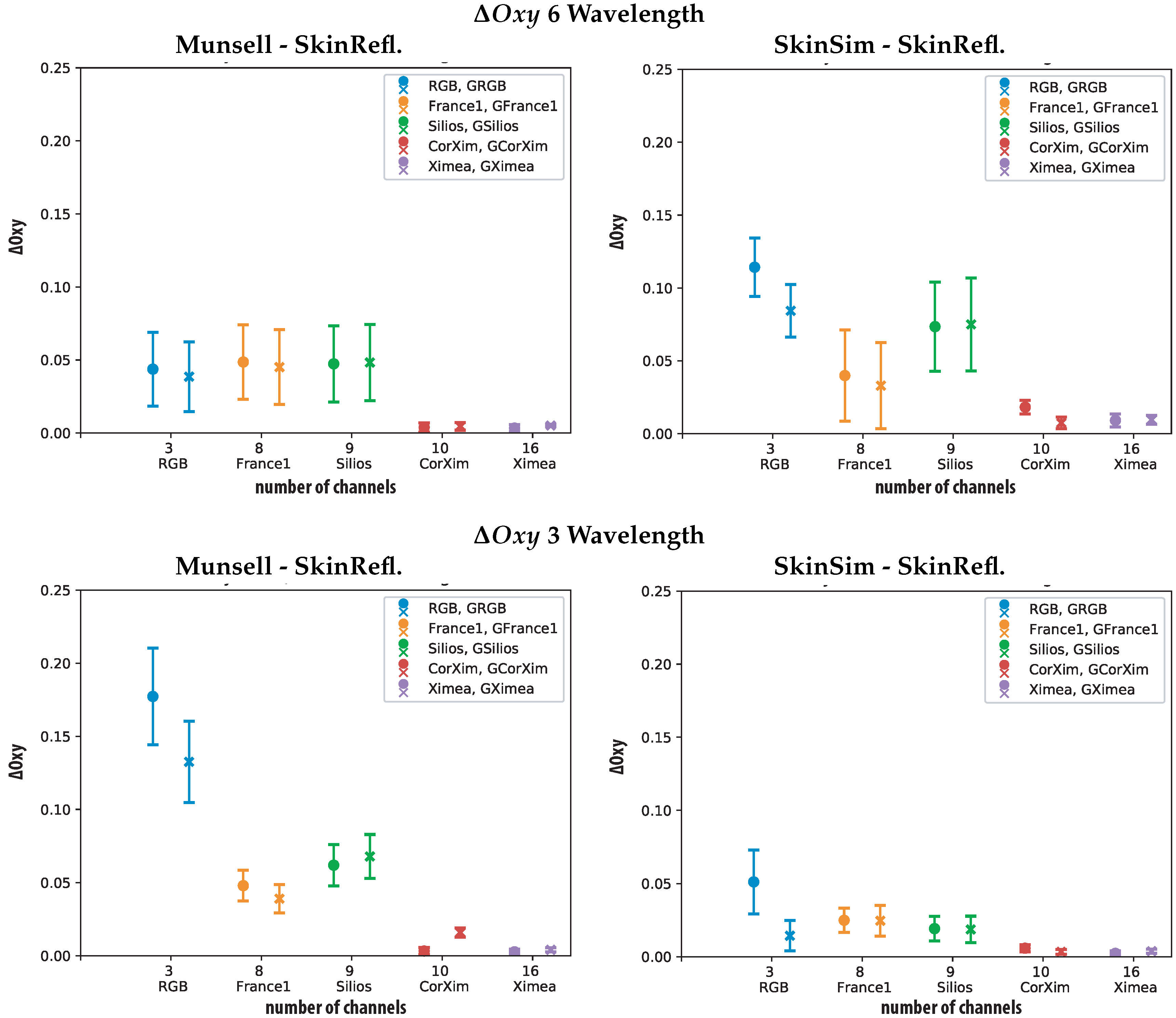
| Oxyg. Metric 6wvl | ||||||||||||
| Sensor | Min | Max | Mean | Std | 98% | Min | Max | Mean | Std | 98% | ||
| RGB | 0.070 | 0.169 | 0.114 | 0.020 | 0.155 | GRGB | 0.051 | 0.125 | 0.084 | 0.018 | 0.119 | |
| France1 | 0.001 | 0.150 | 0.040 | 0.031 | 0.109 | GFrance1 | 0.0001 | 0.145 | 0.033 | 0.030 | 0.102 | |
| Silios | 0.002 | 0.140 | 0.073 | 0.031 | 0.131 | GSilios | 0.006 | 0.151 | 0.075 | 0.032 | 0.134 | |
| CorXim | 0.001 | 0.028 | 0.018 | 0.005 | 0.027 | GCorXim | 0.0002 | 0.017 | 0.007 | 0.004 | 0.016 | |
| Ximea | 0.000 | 0.019 | 0.009 | 0.004 | 0.018 | GXimea | 00.002 | 0.017 | 0.009 | 0.003 | 0.016 | |
| Oxyg. Metric 3wvl | ||||||||||||
| Sensor | Min | Max | Mean | Std | 98% | Min | Max | Mean | Std | 98% | ||
| RGB | 0.010 | 0.132 | 0.051 | 0.022 | 0.090 | GRGB | 0.0001 | 0.051 | 0.014 | 0.010 | 0.044 | |
| France1 | 0.001 | 0.041 | 0.025 | 0.008 | 0.038 | GFrance1 | 0.002 | 0.048 | 0.025 | 0.010 | 0.043 | |
| Silios | 0.001 | 0.043 | 0.019 | 0.008 | 0.035 | GSilios | 0.001 | 0.048 | 0.019 | 0.009 | 0.036 | |
| CorXim | 0.00004 | 0.011 | 0.006 | 0.002 | 0.010 | GCorXim | 0.0001 | 0.008 | 0.003 | 0.002 | 0.007 | |
| Ximea | 0.001 | 0.041 | 0.025 | 0.008 | 0.038 | GXimea | 0.00001 | 0.007 | 0.004 | 0.001 | 0.006 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bauer, J.R.; Thomas, J.-B.; Hardeberg, J.Y.; Verdaasdonk, R.M. An Evaluation Framework for Spectral Filter Array Cameras to Optimize Skin Diagnosis. Sensors 2019, 19, 4805. https://doi.org/10.3390/s19214805
Bauer JR, Thomas J-B, Hardeberg JY, Verdaasdonk RM. An Evaluation Framework for Spectral Filter Array Cameras to Optimize Skin Diagnosis. Sensors. 2019; 19(21):4805. https://doi.org/10.3390/s19214805
Chicago/Turabian StyleBauer, Jacob Renzo, Jean-Baptiste Thomas, Jon Yngve Hardeberg, and Rudolf M. Verdaasdonk. 2019. "An Evaluation Framework for Spectral Filter Array Cameras to Optimize Skin Diagnosis" Sensors 19, no. 21: 4805. https://doi.org/10.3390/s19214805
APA StyleBauer, J. R., Thomas, J.-B., Hardeberg, J. Y., & Verdaasdonk, R. M. (2019). An Evaluation Framework for Spectral Filter Array Cameras to Optimize Skin Diagnosis. Sensors, 19(21), 4805. https://doi.org/10.3390/s19214805






