1. Introduction
Quality of media content can be evaluated using different types of measures. The most reliable way of doing this is by conducting visual experiments under controlled conditions, in which human observers grade the quality of the multimedia contents under evaluation [
1]. Unfortunately, such experiments are time-consuming and costly, making the search for alternative quality estimation methods an important research topic. A much simpler approach is to use some computable objective measure that equates quality degradation with the (numerical) error between the original and the distorted media [
2,
3]. Every objective quality measure has as its aim approximating the human quality perception (or human visual system, HVS) as closely as possible, meaning that good correlation with subjective measures (mean opinion score, MOS) is sought. Objective quality measures for image and video can be generally divided into three categories according to the reference information they use, as follows:
full-reference (FR) quality measures;
reduced-reference (RR) quality measures;
no-reference (NR) quality measures.
FR quality measures require the original undistorted or unprocessed signal. NR quality measures require only the processed/degraded signal. RR quality measures need information derived from the original signal [
3].
In this paper, we present no-reference video quality measure for frame freezing degradations called NR-FFM (no-reference frame–freezing measure). This type of degradation often occurs during video transmission in different types of TV broadcasting (internet, mobile), with low SNR (signal to noise ratio) margin. It will be shown that the proposed measure achieves high correlation with MOS and that it can be used in cases where only this type of degradation is expected or in combination with other degradation types, so that NR-FFM is combined with some other FR or RR objective measure.
This paper is organized as follows:
Section 2 describes related work,
Section 3 describes the test of the laboratory for image and video engineering (LIVE) mobile database,
Section 4 describes the development of the proposed NR-FFM measure,
Section 5 presents the experimental results,
Section 6 provides the discussion, and
Section 7 draws the conclusions.
2. Related Work
A survey that classifies and compares current objective video quality assessment algorithms can be found in [
4]. Generally, any image quality measure can be extended to video sequence analysis by computing the quality difference of each image of the distorted video to its corresponding image in the original video (or by computing the quality of each image of the distorted video alone, for NR measures). These measures include the well-known PSNR (peak signal-to-noise ratio) [
5], SSIM (structural similarity index) [
6], VSNR (visual signal to noise ratio) [
7], and reduced reference image quality assessment meter (IQAM) [
8], among others. Because these image-based measures are not able to capture temporal distortions, different full reference or reduced reference video quality measures for simultaneous capturing of spatial and temporal distortions have been developed. These measures include MOVIE (motion-based video integrity evaluation) [
9], VQM (video quality measure) [
10], STRRED (spatio-temporal reduced reference entropic differences) [
11], and RVQM (reduced video quality measure) [
12], among others. VQM accounting for variable frame delay distortions (VQM-VFD) have been also proposed in [
13].
Because frame-freezes produce video sequences that may have a total play time longer than reference video sequence (e.g., in the case of stored video delivery), it is unclear how to compare such video sequences by using full or reduced reference quality measures. Also, by matching segments of the degraded sequence to corresponding segments of the reference, usual quality measures would always be perfect (because the sequences tested, from the LIVE mobile database, have no other degradations besides frame freezing).
The paper [
14] presents a subjective test that estimates the quality of video subject to frame freeze and frame skip distortions, showing that they impact the video quality differently. The paper [
15] describes a no-reference temporal quality measure to model the effect of frame freezing impairments on perceived video quality; however, their subjective tests results are not available, preventing comparison with our proposed measure NR-FFM. In the paper [
16], a new objective video quality measure based on spatiotemporal distortion is described. However, this measure also takes into account other degradations besides frame freezes and so the quality estimate reflects the combination of these effects. For sequences with frame freezing degradation only, this measure would calculate the same objective grade (even with different AFR (affected frame rate) for frame freezing degradations). The paper [
17] tested video quality model (VQM) that accounts for the perceptual impact of variable frame delays (VFD) in videos. VQM-VFD demonstrated top performance on the laboratory for image and video engineering (LIVE) mobile video quality assessment (VQA) database [
18].
There are also other algorithms for the detection of dropped video frames. In one of the state-of-the-art algorithms [
19], the author proposed a jerkiness measure that is also a NR method. Jerkiness is a perceptual degradation that includes both jitter (repeating of frames and dropping frames) and freezing (exceedingly long display of frames). The jerkiness measure takes two variables into consideration: the display time and the motion intensity. It is a sum of the product of relative display time and a monotone function of display time, as well as a monotone function of motion intensity over all frame times. This measure is also applicable to a variety of video resolutions. In [
20], the motion energy of videos is used in order to detect dropped video frames. The algorithm calculates temporal perceptual information (TI) and compares it to a dynamic threshold in order to detect long and short duration of frame repetition. However, the problem with this NR algorithm is the periods of low motion causing false-positive results, which is the reason why the RR version is better to apply. The authors in [
21] use algorithms from [
20] and [
15] for comparison and in terms per frame computation times, their algorithm outperforms the mentioned NR methods. This algorithm uses two separate thresholds for videos with high and low motion content. The NR algorithm in [
22], aside from [
20] and [
15], uses the algorithm in [
19] for comparison. However, the comparison with [
15] did not show good results in cases of freeze duration less than 0.5 s, and thus the focus was put on [
20] and [
19]. This algorithm [
22] showed better performance in terms of estimating the impact of multiple frame freezing impairments and is closer to subjective test results. The new NR method in [
23] that measures the impact of frame freezing due to packet loss and delay in video streaming network is based on [
21] with a few modifications. This method was also tested on three more databases and detailed comparison is given for the algorithm in [
20]. The study in [
24] showed that the algorithm in [
20] has better performance. A recent work from [
25] is a novel temporal jerkiness quality metric that uses the algorithm from [
20] and neural network for mapping between features (number of freezes, freeze duration statistics, inter-freeze distance statistics, frame difference before and after the freeze, normal frame difference, and the ratio of them) and subjective test scores. In recent papers [
26,
27], algorithms were tested on UHD (ultra high definition) videos. In [
26], the histogram-based freezing artifacts detection algorithm (HBFDA) is proposed. HBFDA methodology includes comparison of consecutive video frames which consist of splitting a frame into regions and then comparing the regions’ consecutive frame histograms. The HBFDA algorithm adapts its parameters in real-time and can process 75 frames per second. The authors of [
27] propose a new real-time no-reference freezing detection algorithm, called the RTFDA. A detailed comparison of results is given for the algorithm in [
20]. RTFDA has a high detection rate of video freezing artefacts (in videos of different content type, resolution, and compression norm) with low false-positive rate in comparison to other commonly used freezing detection algorithms. It achieves real-time performance on 4K UHD videos by processing 216 frames per second.
In this study, we developed a no-reference measure for frame-freezing degradations (NR-FFM) on the basis of AFR and spatial information of the video content. NR-FFM can be used to quantify frame freezing degradations alone, or in combination with other measures to calculate quality in the presence of different types of degradations. LIVE mobile database [
18] was used for NR-FFM evaluation. Additionally, the VQEG (Video Quality Experts Group) HD5 dataset [
28] was also used to further test NR-FFM measures using a new set of video sequences.
Compared to the existing measures, contributions in this paper are:
NR-FFM measure based on overall frame duration, number of frame freezings, and spatial information of the tested video sequence;
NR-FFM obtains best correlation among other tested frame freezing objective measures in LIVE mobile dataset and similar correlation in VQEG HD5 dataset as other tested measures;
NR-FFM can be combined with other objective measures designed for other degradation types, tested on LIVE mobile dataset with five degradation types, and combined with RVQM and STRRED as reduced reference measures.
4. NR-FFM Measure Development
To be able to further analyze video content, we used spatial and temporal activity indicators, the spatial information (SI), and the temporal information (TI) for all degraded video sequences. SI and TI are defined as follows [
30]:
where
Fn represents luminance plane at time
n,
Sobel represents the Sobel operator and by convolvingwith 3 × 3 kernel, calculation of the SI is defined as maximal value of all Sobel-filtered frames standard deviation (
stdspace ) values. By default, Sobel operator should be calculated for both horizontal and vertical edges. However, we later calculated SI for only horizontal (later described as SI
H), only vertical (later described as SI
V), and both horizontal and vertical edges (later described as SI
H,V):
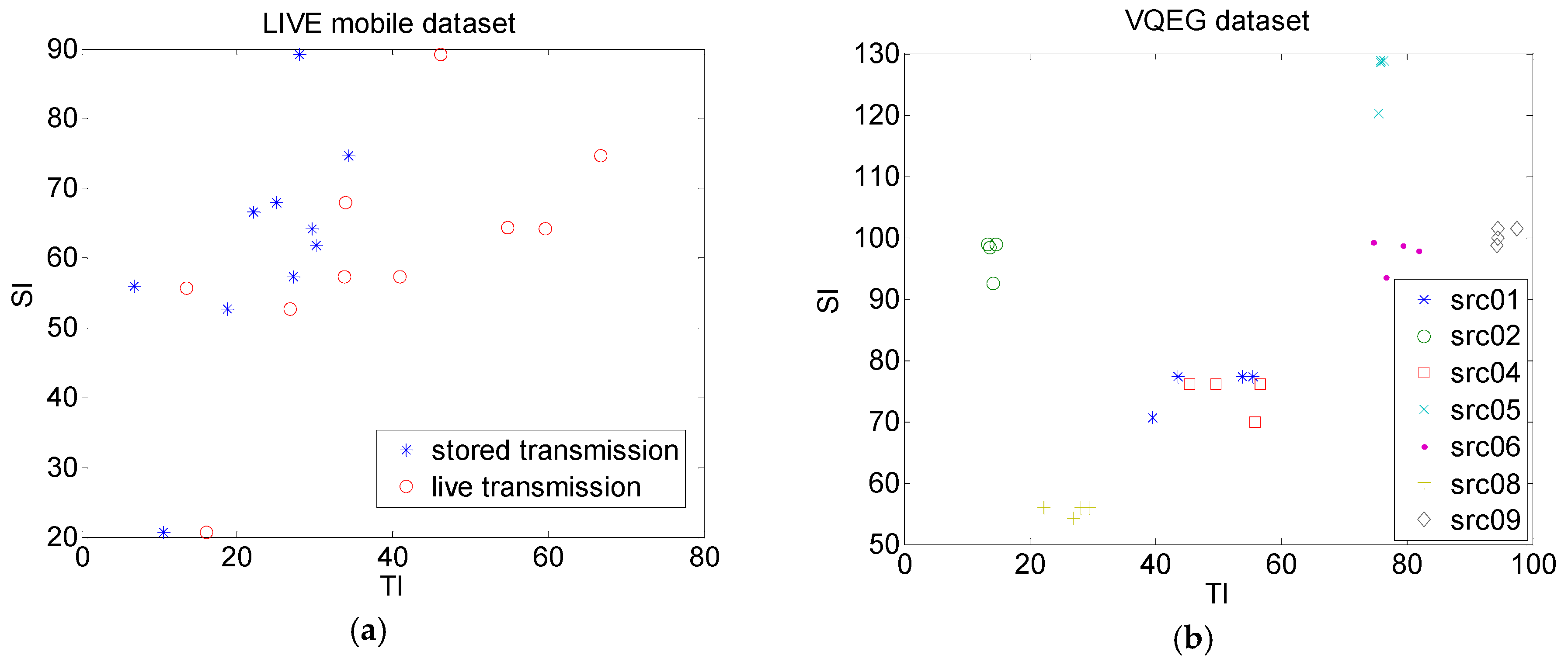
Results of TI versus SI are presented in
Figure 3 for the LIVE mobile dataset and the VQEG dataset. For the LIVE mobile dataset, these were presented separately for the first three degradations (stored transmission) and fourth degradation (live transmission) separately. It can be seen that TI in the case of live transmission scenario was higher than in the case of the stored scenario. For the VQEG dataset, generally SI and TI characteristics were grouped for each video sequence. Also, it can be seen that the VQEG dataset was more diverse in terms of their dynamic characteristics when compared to the LIVE dataset. Later in this study, VQEG is used to compare proposed NR-FFM measure and several existing objective quality measures.
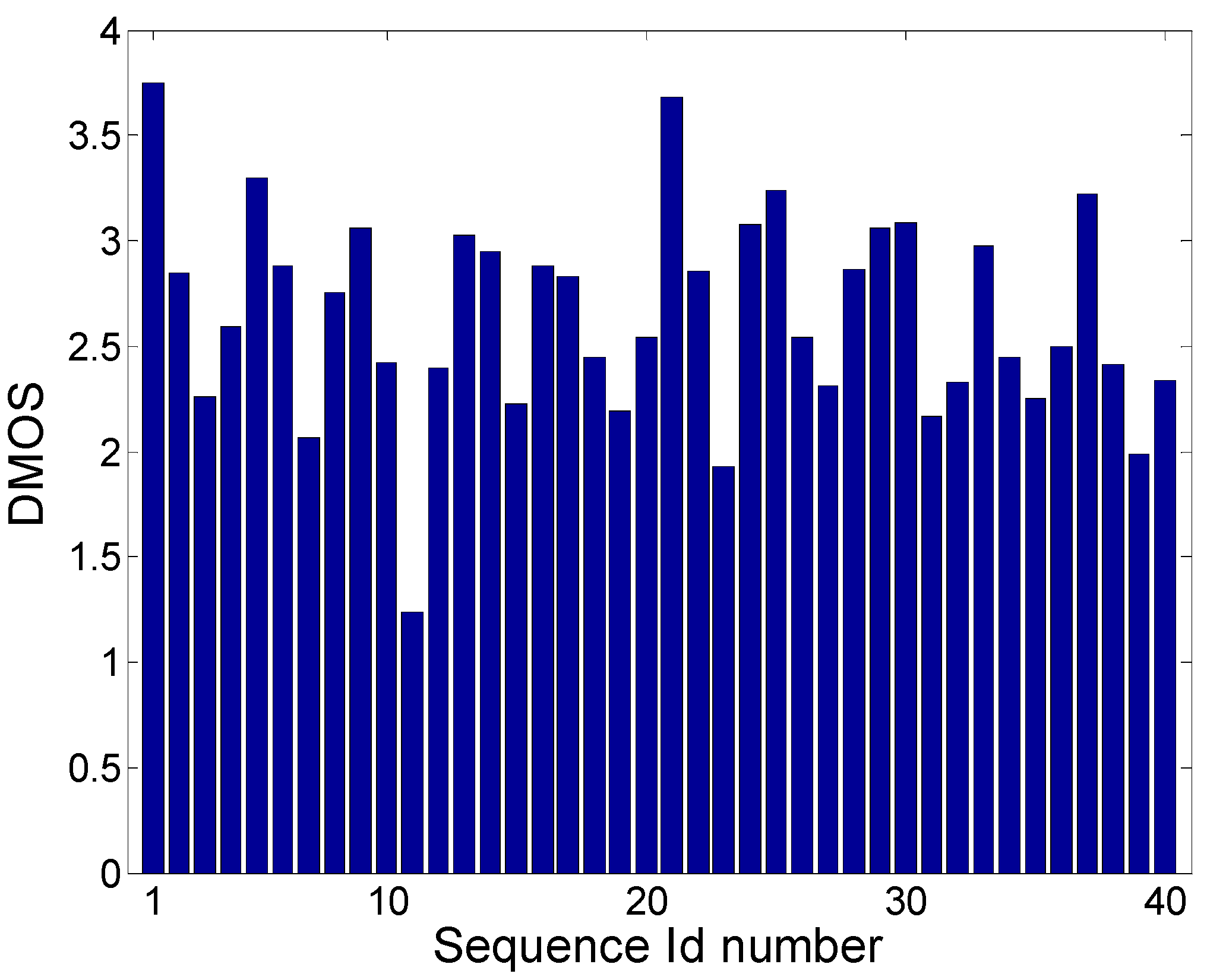
Firstly, we tried to find if there was a relationship between spatial information (SI), temporal information (TI), and DMOS scores, of all the 40 degraded sequences in the LIVE dataset. A genetic algorithm (GA) [
31] was used to find a relationship between the four observed degradation types with the goal of maximizing Spearman’s correlation (GA population size was set to 50).
We then hypothesized the following form for the reference frame freezing measure (NR-FFM) for degraded video sequence j (j ∈ {1,40}):
where higher value means worse quality and
n is number of freezes in one sequence
j, NFD(
i,
j) is normalized frame duration of one freezing (normalized by sequence frame length), SI(
j) and TI(
j) are spatial and temporal information of the whole sequence
j (according to the Equation (1)), respectively, and coefficients
α,
β, and
γ were optimized using a GA to maximize Spearman’s correlation. Coefficient
α takes into account impact of the duration of one frame freeze as well as overall frame freeze duration on final video quality. It should be expected that 0 <
α < 1.
α < 1 means that one freezing event with longer duration will have a better (lower) objective grade than few shorter freezing events (with same overall duration as one longer freezing event), which is in accordance with
Figure 2. Also,
α > 0 means that a longer frame freeze will have a higher impact (worse, higher objective grade) on video quality than a shorter frame freeze. Coefficients
β and
γ show the impact of spatial and temporal information on video quality. It would be expected that
β and
γ were higher than 0, meaning that higher spatial or temporal activity will have a higher influence on video quality.
6. Discussion
In this paper we developed no reference objective measure NR-FFM and tested it using two different datasets, LIVE mobile and VQEG-HD5. NR-FFM measure was also compared with some existing objective measures for frame freezing degradations named Borer (no-reference), FDF (no-reference), Quanhuyn (no-reference), and FDF-RR (reduced reference). In the LIVE mobile dataset, NR-FFM gave the best correlation results between all tested measures (
Table 12). In the VQEG-HD5 dataset, NR-FFM (which was trained on the LIVE mobile dataset) had the best Pearson’s correlation for Q1, Q2, and Q3 fitting functions (
Table 13). Borer and FDF-RR measures obtained somewhat higher Spearman’s and Kendall’s correlations (
Table 13).
The main difference between LIVE mobile frame freezing degradations and VQEG-HD5 frame freezing degradations were the type and overall duration of the freezing occurrences. In the LIVE mobile dataset, there were online degradations (due to, for example, packet losses), which resulted in frame drops and offline degradations (due to, for example, packet delay), where no frame was actually lost, only delayed. Also, in the LIVE mobile dataset, overall freezing duration was generally the same—in offline frame freezing 8 × 1 s long, 4 × 2 s long, and 2 × 4 s long. Only online freezing had one 4 s long freeze and one 2 s long freeze. In the VQEG-HD5 dataset, all freezing frames were online degradations, resulting in frame drops. Also, higher packet loss ratio (PLR) resulted in longer frame freezes and, consequently, more lost frames. This meant that overall frame freezing duration was different for different degradation types (in the VQEG-HD5 dataset this was due to the different PLR ratio). Probably because of this, the NR measures FDF and Borer had lower correlation in the LIVE mobile dataset compared to the VQEG-HD5 dataset. Also, motion intensity or temporal information (or any other measure that would take differences between consecutive frames into account) did not have a higher value in offline frame freezing compared to the original video sequence (and that degradation was present only in the LIVE mobile dataset). NR-FFM measure had the best correlation in the LIVE mobile dataset compared to the other tested measures, probably also because it was calculated only on the basis of frame freezing duration and spatial information. NR-FFM measure also had different values for the equal overall frame freezing, but with different numbers of occurrences (see Equation (7)). Nonetheless, in the VQEG-HD5 dataset, NR-FFM had similar correlation to Borer and FDF measures without pretrained values on the VQEG-HD5 dataset.
When comparing online degradation (e.g., stored video sequences) and offline degradation (e.g., live video sequences) types in the LIVE mobile dataset (
Table 6), offline degradation had higher correlation. However, in online degradation there were only 10 video sequences with equal degradation type—two equally spaced frame drops that were 4 and 2 s long (3–7 and 13–15 s in each video sequence); thus, these correlation coefficients had lower confidence. Also, compared with
Table 13, also with only an online degradation type, NR-FFM had in this case a higher correlation for the tested VQEG-HD5 dataset, probably due to the different degradation levels for each video sequence (4 video sequences), as well as more tested video sequences (28 video sequences overall).
NR-FFM measure was also tested using both the LIVE mobile (40 video sequences) and LIVE tablet study (20 video sequences) and was trained/tested using another dataset, showing similar fitting coefficients and correlations in both cases (trained on the LIVE mobile and tested on the LIVE tablet and vice versa).
Furthermore, we combined the proposed NR-FFM measure with some existing reduced-reference measures (RVQM and STRRED) and tested it using all video sequences from the LIVE mobile/tablet dataset. Results have shown that it is possible to obtain similar correlation for the overall combined objective measure using all five degradation types in the LIVE mobile dataset (
Table 10 and
Table 11).