Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles
Abstract
1. Introduction
2. Fusion Systems Literature Review
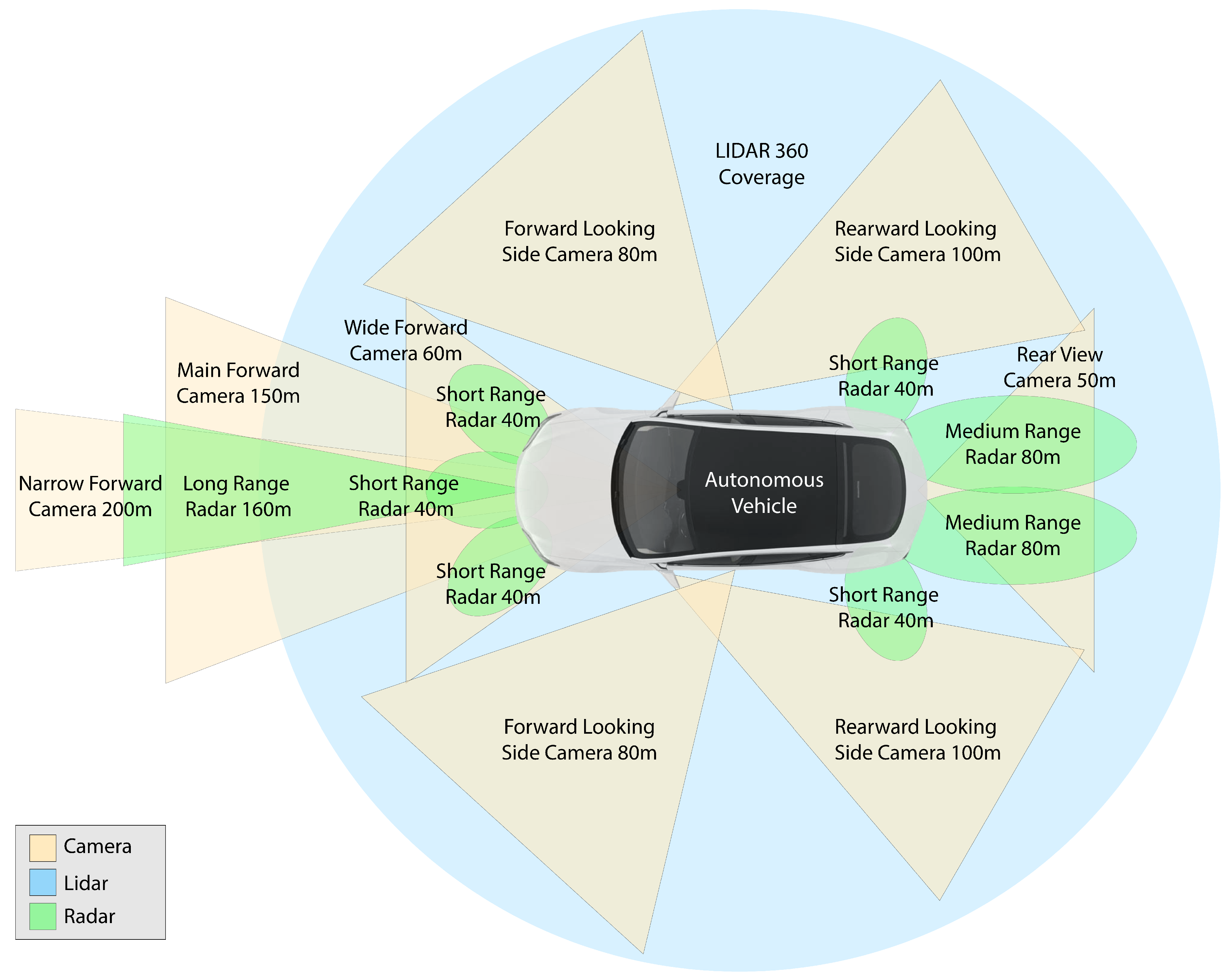
3. Autonomous Vehicle Perception Sensors
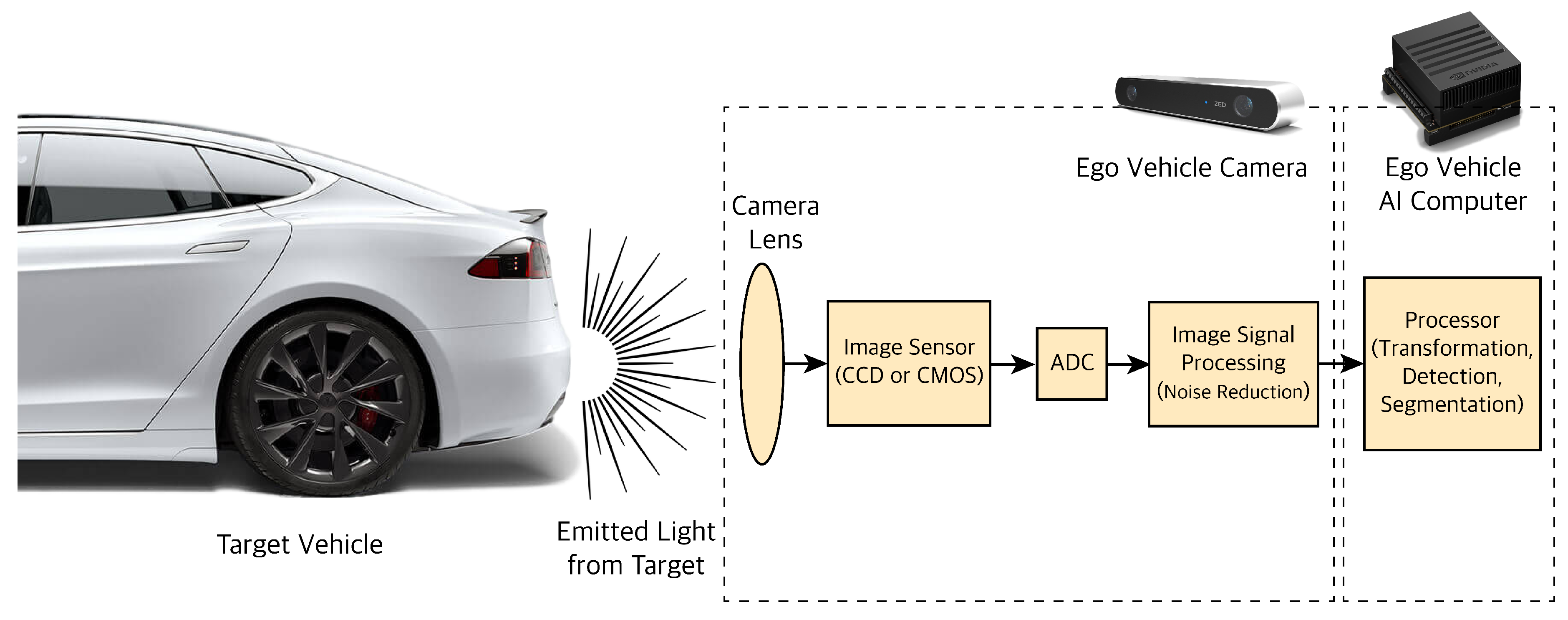
3.1. Camera
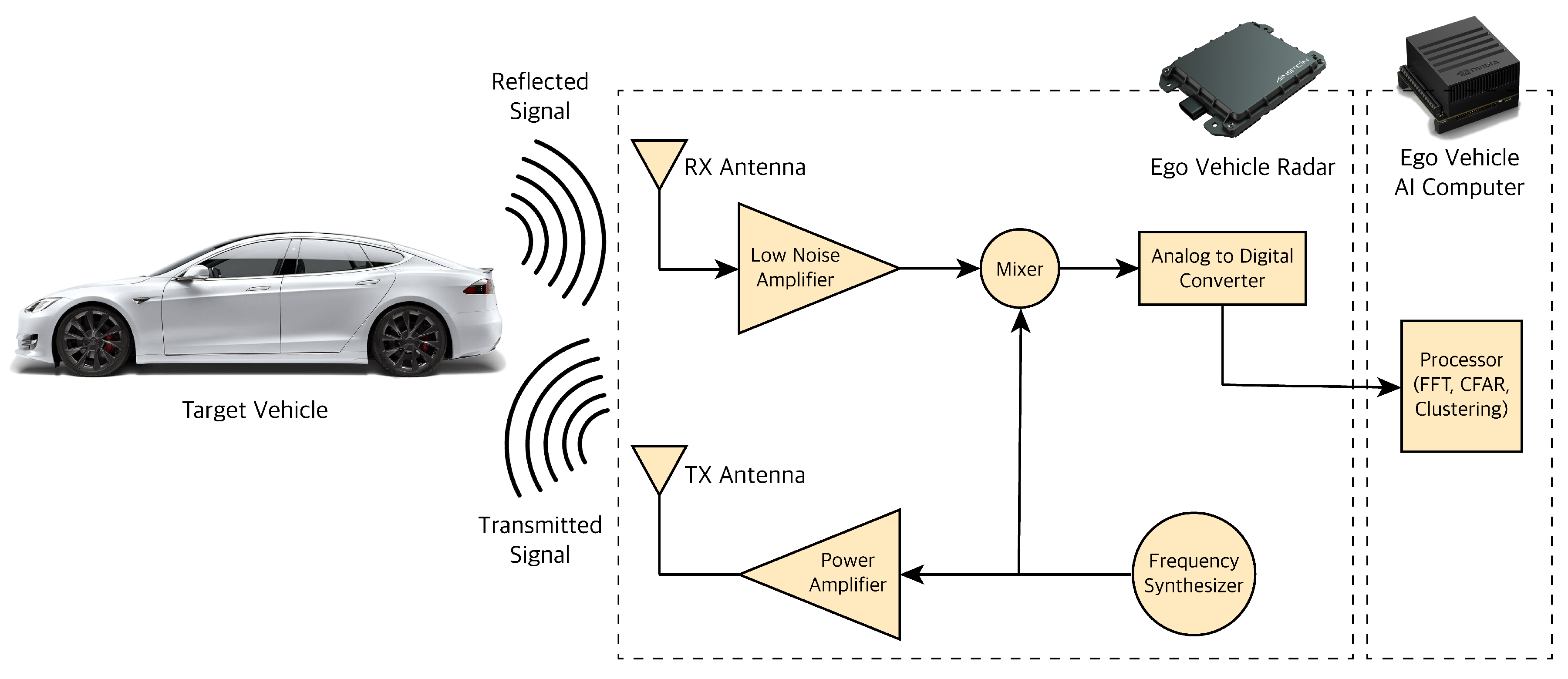
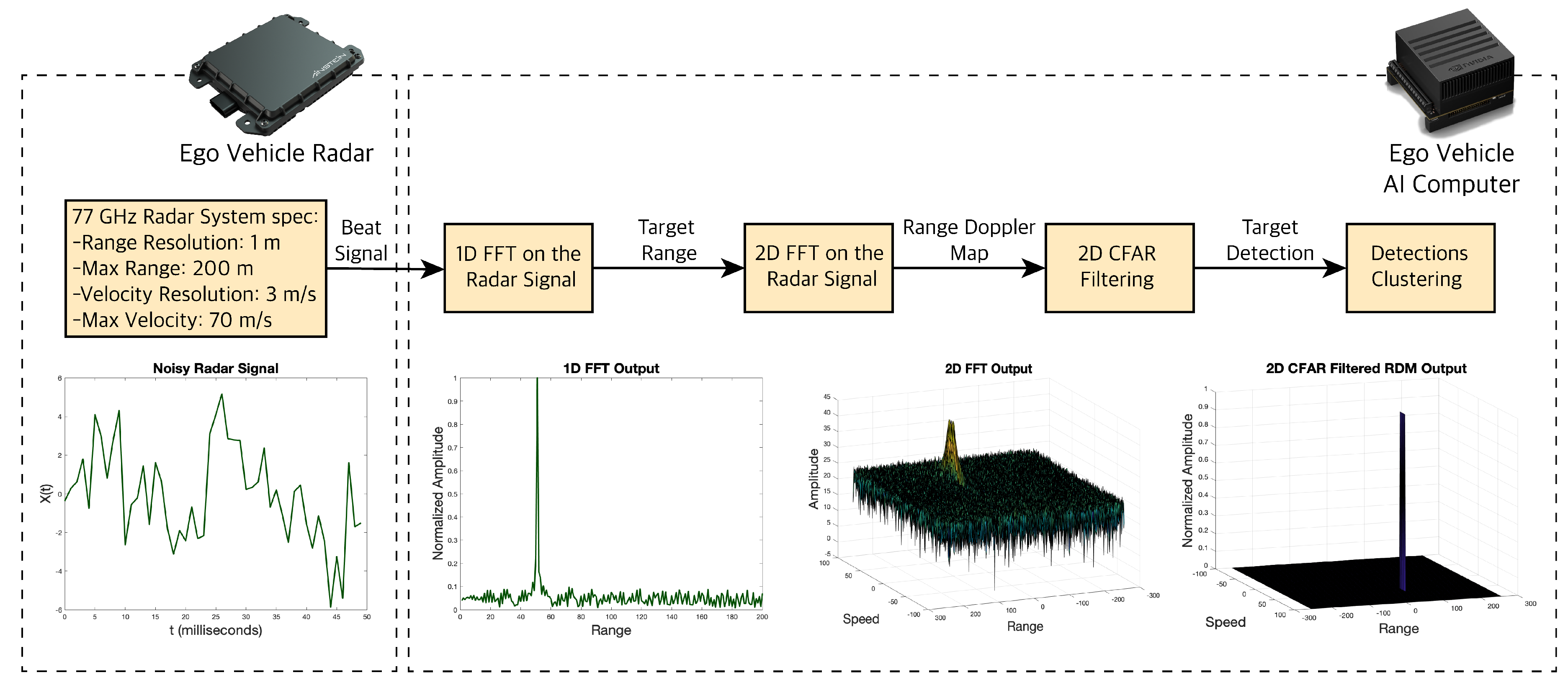
3.2. RADAR
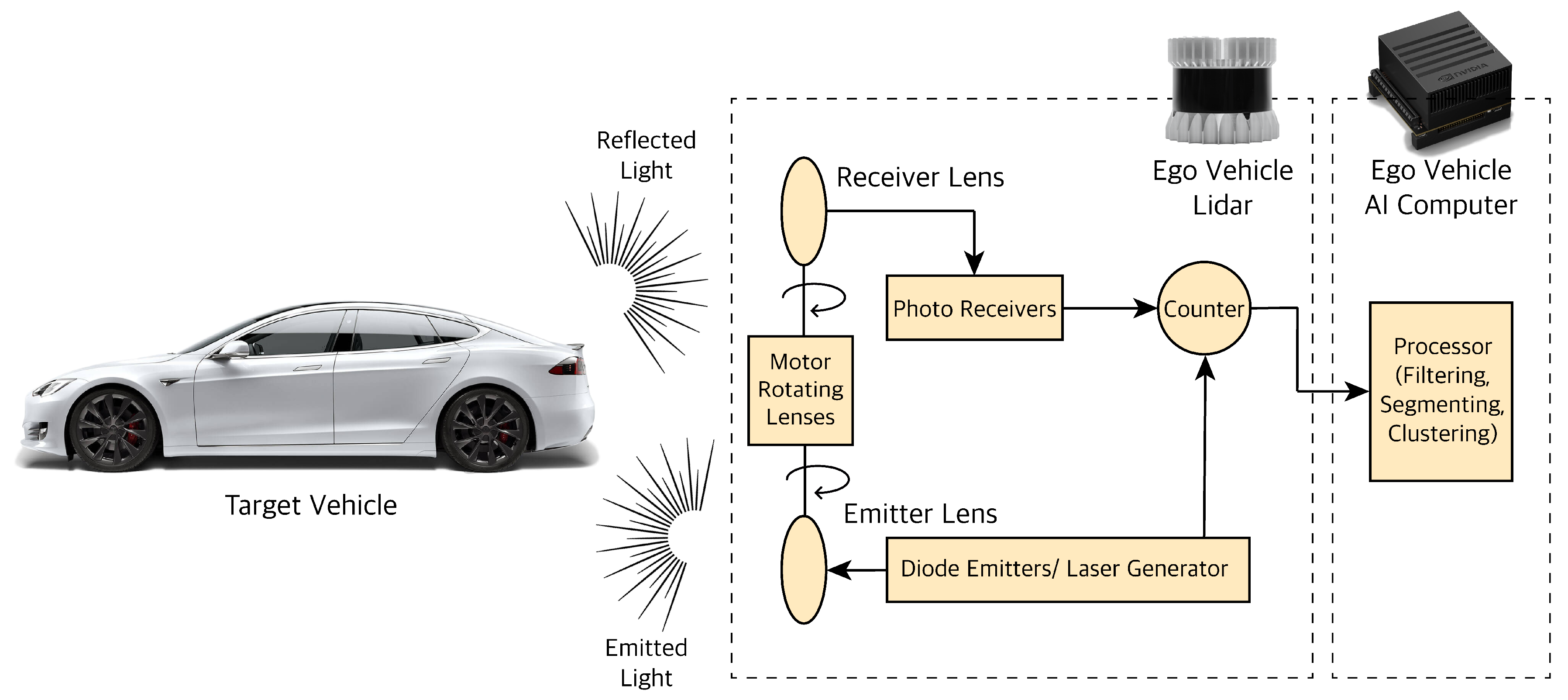
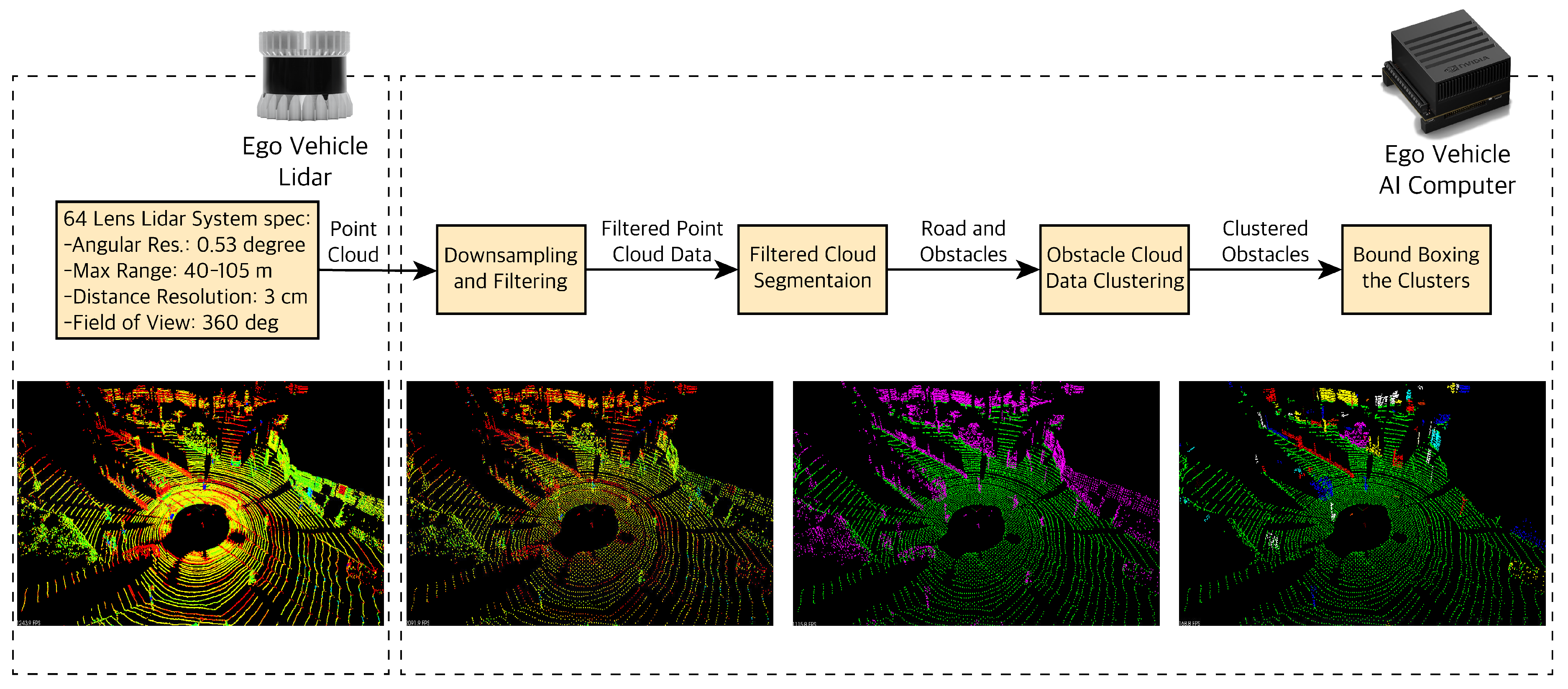
3.3. LiDAR
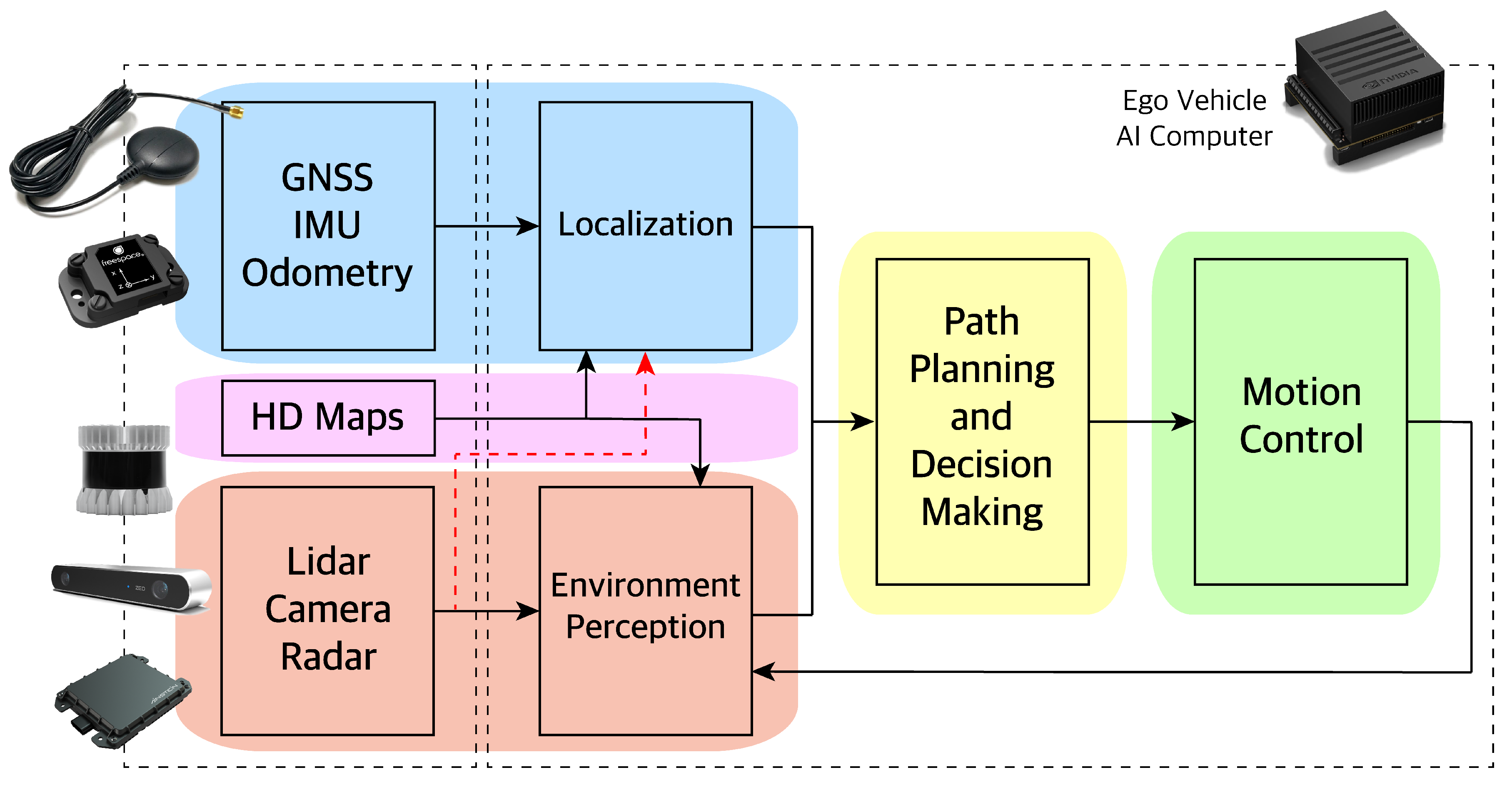
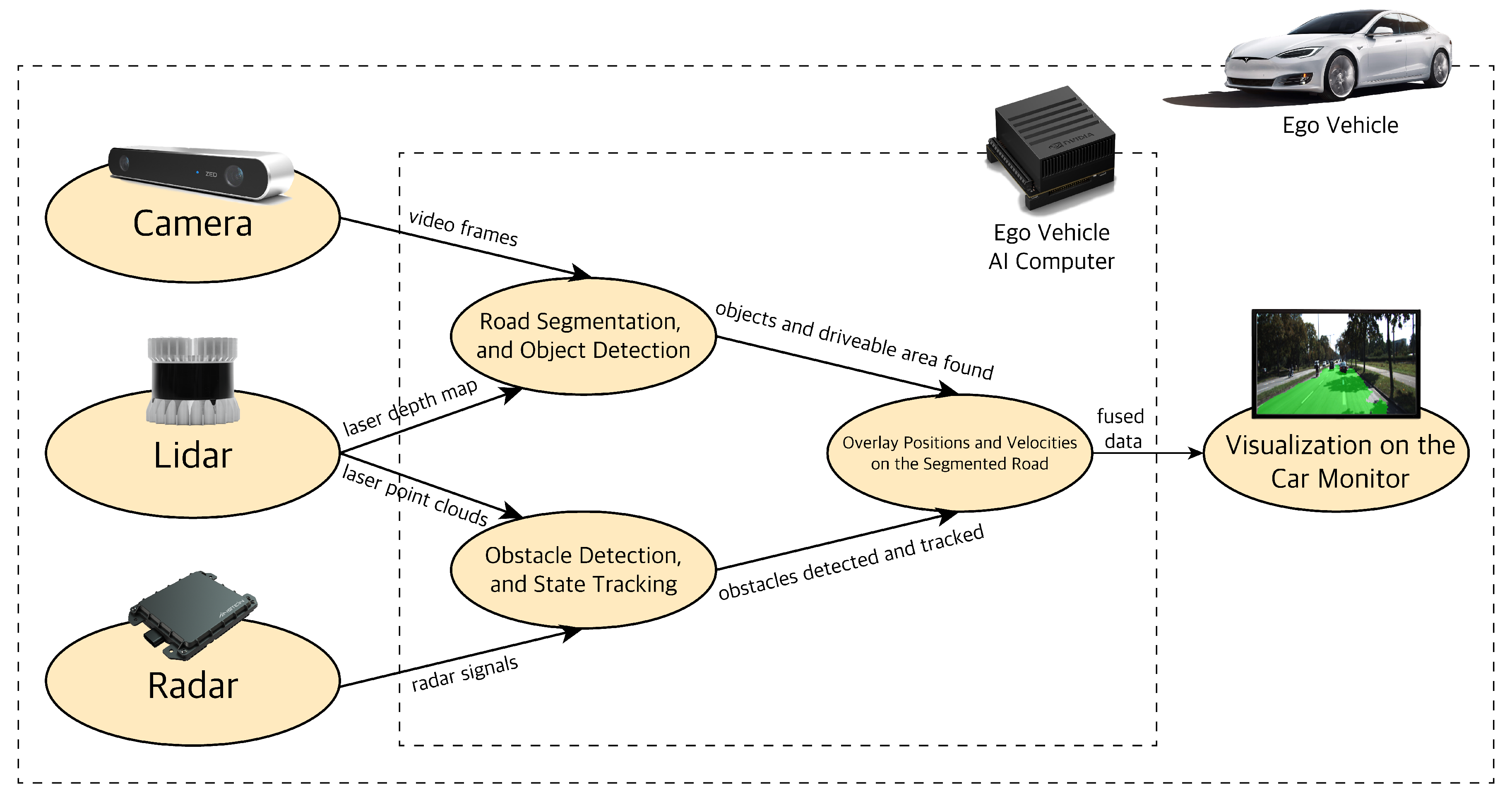
4. Hybrid Sensor Fusion Algorithm Overview
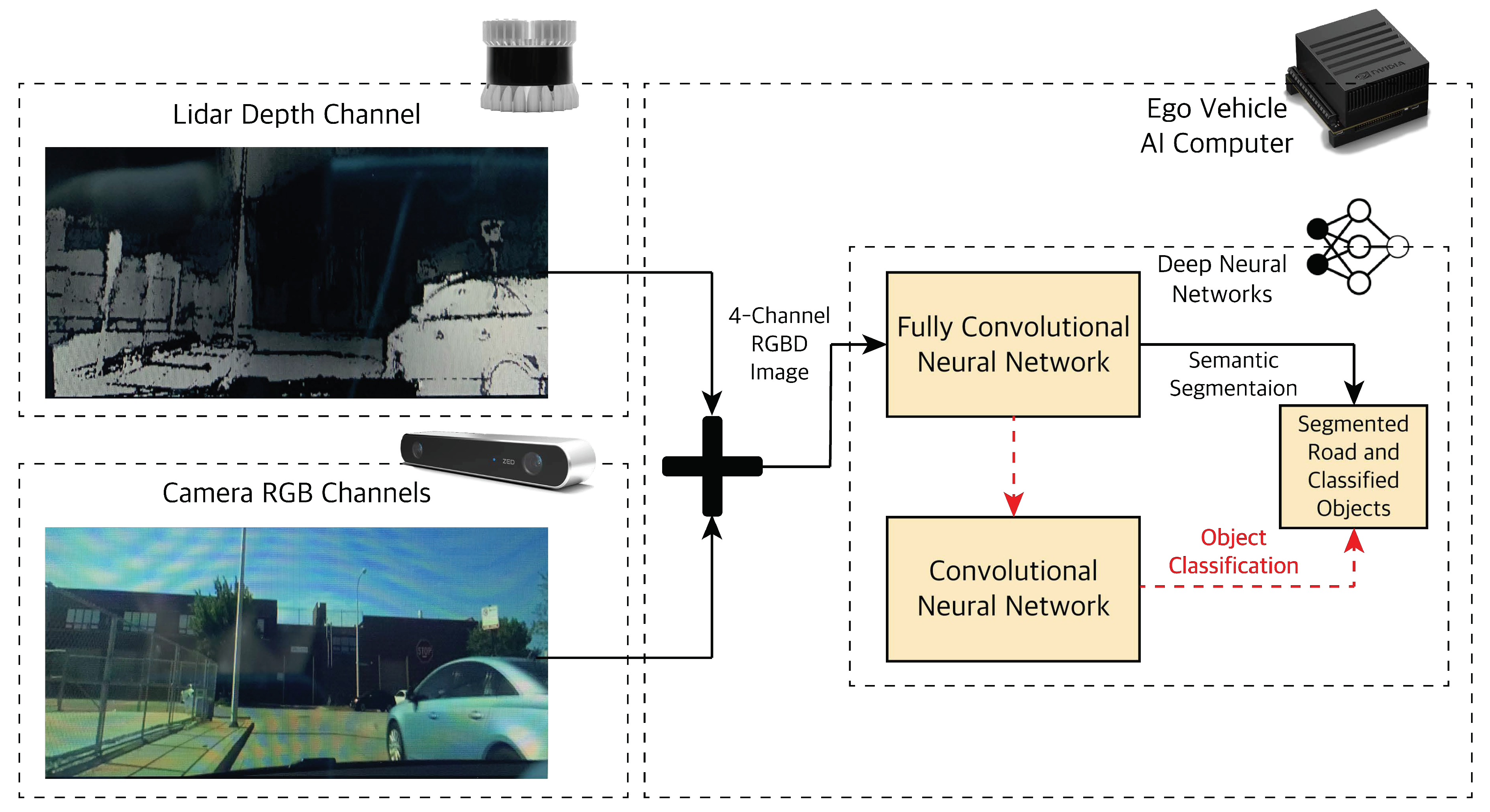
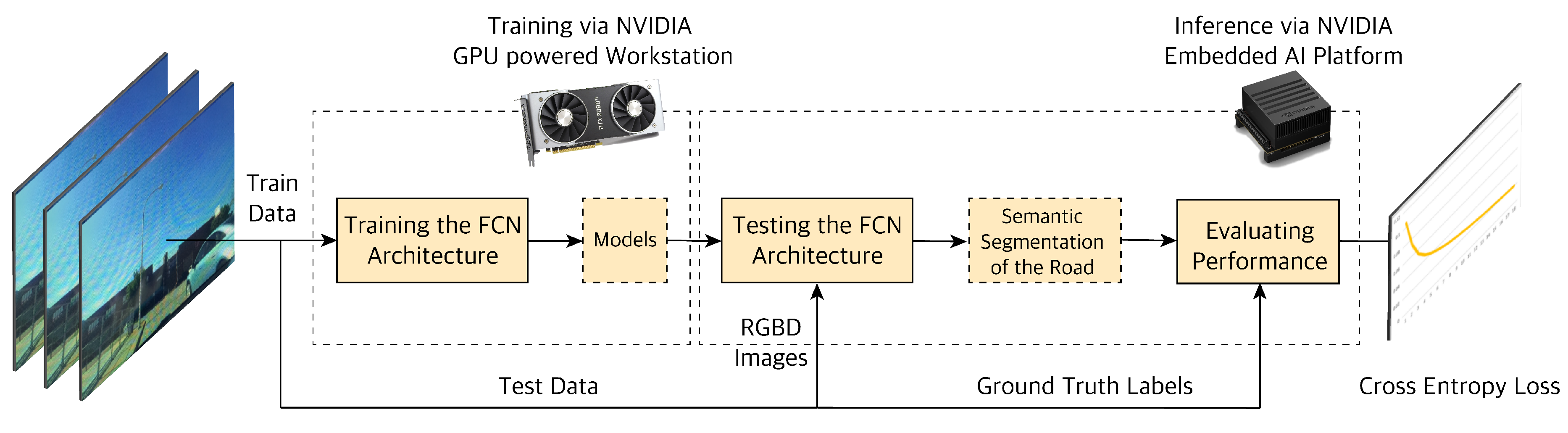
4.1. Object Classification and Road Segmentation Using Deep Learning
4.1.1. Camera-LiDAR Raw Data Fusion
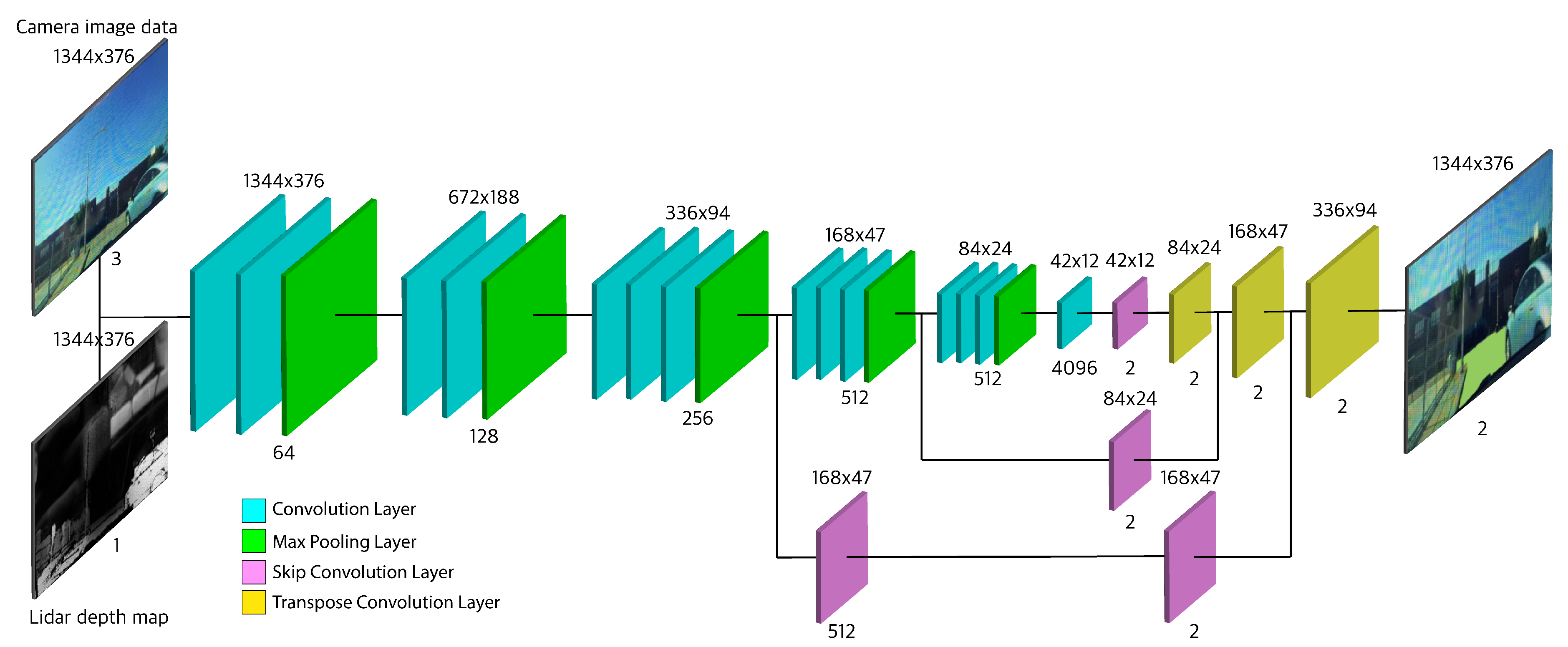
4.1.2. Proposed Fully Convolutional Network (FCNx) Architecture
4.2. Testing Obstacle Detection and Tracking using Kalman Filtering
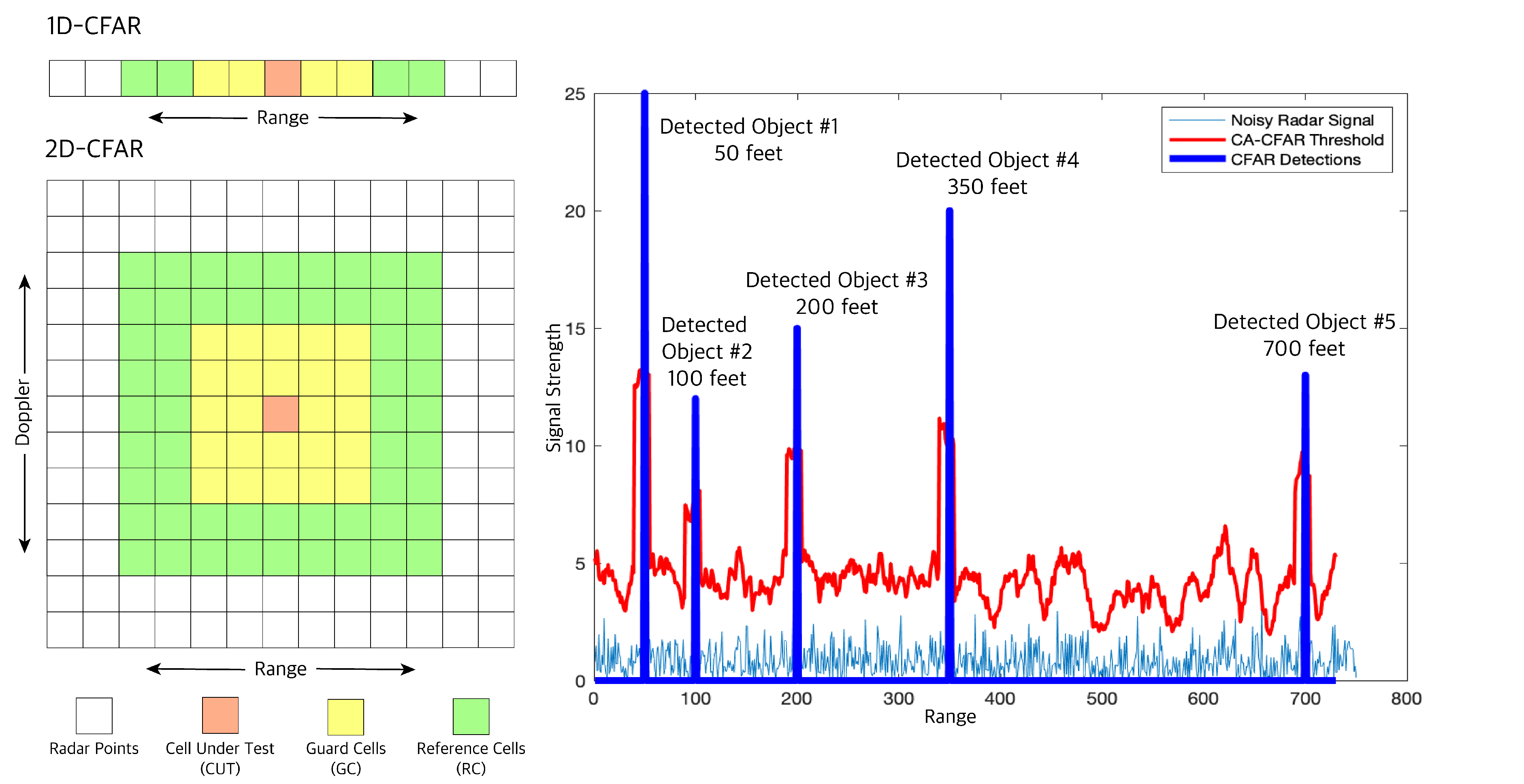
4.2.1. Radar Beat Signal Data Processing
4.2.2. LiDAR Point Cloud Data Processing
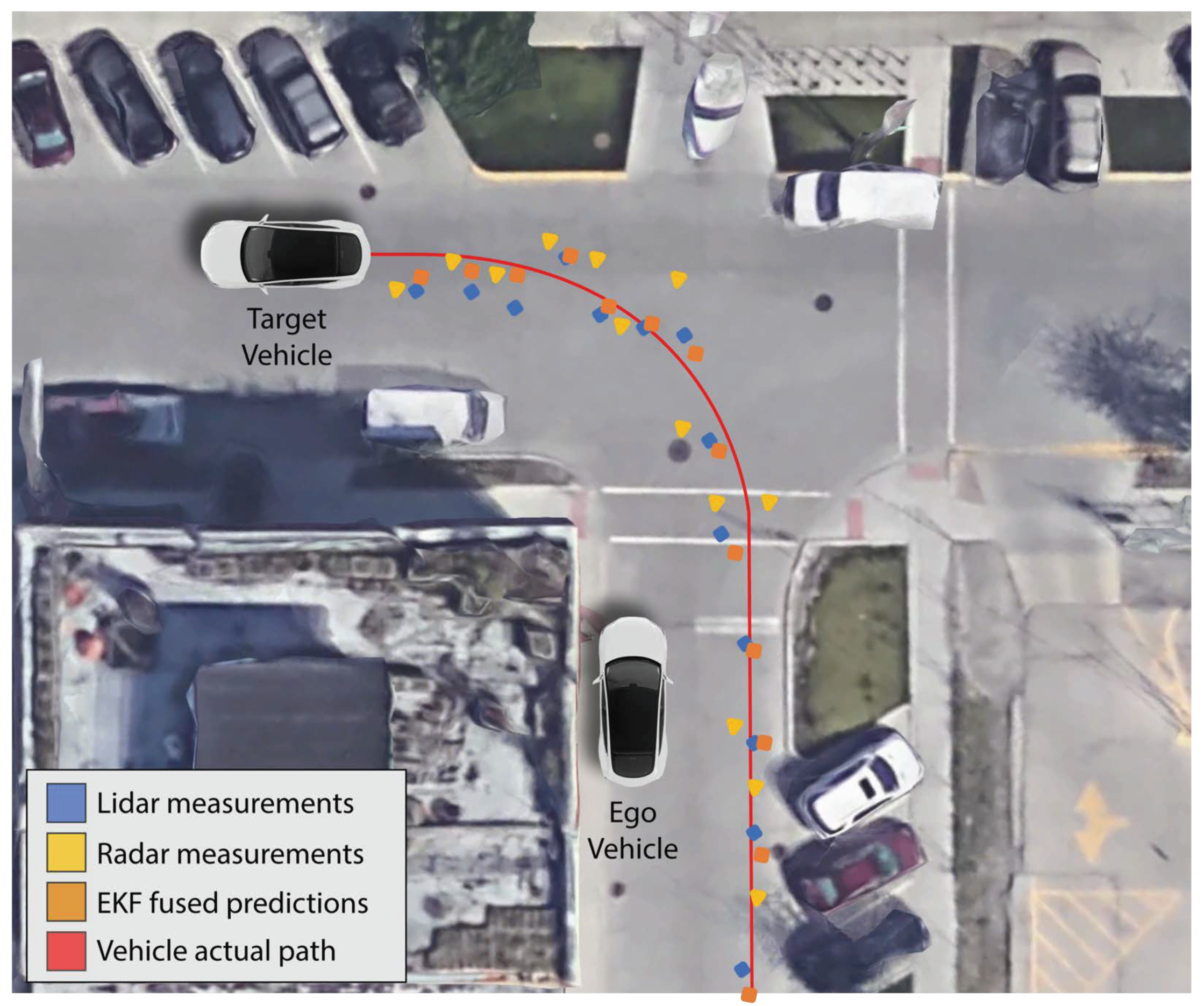
4.2.3. Extended Kalman Filtering
5. Experiments Procedure Overview
6. Experimental Results and Discussion
- Camera sensor failure: In this case, the pipelines free navigation space segmentation is affected, but it is still able to properly segment using LiDAR depth map alone. Detecting and tracking objects is unaffected and done via the late fused (object level) LiDAR and radar data with the EKF algorithm.
- Radar sensor failure: In this case, LiDAR can measure the speed of the objects via the range and ToF measurements. However this is slightly less accurate, but still usable for EKF to track the state of objects detected. The road segmentation and object classification remain unaffected.
- LiDAR sensor failure will not fail the framework. Since the camera and radar essentially are doing the segmentation and tracking tasks on their own, not having LiDAR data will not completely derail or disturb the fusion flow. However, not having LiDAR depth map or point cloud position coordinates information can reduce the segmentation quality as well as tracking accuracy.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, L.; Wang, R.; Dai, B.; Fang, Y.; Liu, D.; Wu, T. Hybrid conditional random field based camera-LIDAR fusion for road detection. Inf. Sci. 2018, 432, 543–558. [Google Scholar] [CrossRef]
- Xiao, L.; Dai, B.; Liu, D.; Hu, T.; Wu, T. Crf based road detection with multi-sensor fusion. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 192–198. [Google Scholar]
- Broggi, A. Robust real-time lane and road detection in critical shadow conditions. In Proceedings of the International Symposium on Computer Vision-ISCV, Coral Gables, FL, USA, 21–23 November 1995; pp. 353–358. [Google Scholar]
- Teichmann, M.; Weber, M.; Zoellner, M.; Cipolla, R.; Urtasun, R. Multinet: Real-time joint semantic reasoning for autonomous driving. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1013–1020. [Google Scholar]
- Sobh, I.; Amin, L.; Abdelkarim, S.; Elmadawy, K.; Saeed, M.; Abdeltawab, O.; Gamal, M.; El Sallab, A. End-To-End multi-modal sensors fusion system for urban automated driving. In Proceedings of the 2018 NIPS MLITS Workshop: Machine Learning for Intelligent Transportation Systems, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Eitel, A.; Springenberg, J.T.; Spinello, L.; Riedmiller, M.; Burgard, W. Multimodal deep learning for robust RGB-D object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 681–687. [Google Scholar]
- John, V.; Nithilan, M.; Mita, S.; Tehrani, H.; Konishi, M.; Ishimaru, K.; Oishi, T. Sensor Fusion of Intensity and Depth Cues using the ChiNet for Semantic Segmentation of Road Scenes. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 585–590. [Google Scholar]
- Garcia, F.; Martin, D.; De La Escalera, A.; Armingol, J.M. Sensor fusion methodology for vehicle detection. IEEE Intell. Transp. Syst. Mag. 2017, 9, 123–133. [Google Scholar] [CrossRef]
- Nada, D.; Bousbia-Salah, M.; Bettayeb, M. Multi-sensor data fusion for wheelchair position estimation with unscented Kalman Filter. Int. J. Autom. Comput. 2018, 15, 207–217. [Google Scholar] [CrossRef]
- Jagannathan, S.; Mody, M.; Jones, J.; Swami, P.; Poddar, D. Multi-sensor fusion for Automated Driving: Selecting model and optimizing on Embedded platform. In Proceedings of the Autonomous Vehicles and Machines 2018, Burlingame, CA, USA, 28 January–2 February 2018; pp. 1–5. [Google Scholar]
- Shahian-Jahromi, B.; Hussain, S.A.; Karakas, B.; Cetin, S. Control of autonomous ground vehicles: A brief technical review. IOP Conf. Ser. Mater. Sci. Eng. 2017, 224, 012029. [Google Scholar]
- Zhu, H.; Yuen, K.V.; Mihaylova, L.; Leung, H. Overview of environment perception for intelligent vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2584–2601. [Google Scholar] [CrossRef]
- Kocić, J.; Jovičić, N.; Drndarević, V. Sensors and sensor fusion in autonomous vehicles. In Proceedings of the 2018 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 420–425. [Google Scholar]
- Caltagirone, L.; Scheidegger, S.; Svensson, L.; Wahde, M. Fast LIDAR-based road detection using fully convolutional neural networks. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Redondo Beach, CA, USA, 11–14 June 2017; pp. 1019–1024. [Google Scholar]
- Aeberhard, M.; Kaempchen, N. High-level sensor data fusion architecture for vehicle surround environment perception. In Proceedings of the 8th International Workshop on Intelligent Transportation (WIT 2011), Hamburg, Germany, 22–23 March 2011. [Google Scholar]
- Caltagirone, L.; Bellone, M.; Svensson, L.; Wahde, M. LIDAR-camera fusion for road detection using fully convolutional neural networks. Rob. Autom. Syst. 2018. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L.; Sun, H.; Xin, J.; Zheng, N. On-road vehicle detection and tracking using MMW radar and monovision fusion. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2075–2084. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Clarke, D.; Knoll, A. Vehicle detection based on LiDAR and camera fusion. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1620–1625. [Google Scholar]
- Verma, S.; Eng, Y.H.; Kong, H.X.; Andersen, H.; Meghjani, M.; Leong, W.K.; Shen, X.; Zhang, C.; Ang, M.H.; Rus, D. Vehicle Detection, Tracking and Behavior Analysis in Urban Driving Environments Using Road Context. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 20–25 May 2018. [Google Scholar]
- Cho, H.; Seo, Y.W.; Kumar, B.V.; Rajkumar, R.R. A multi-sensor fusion system for moving object detection and tracking in urban driving environments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 1836–1843. [Google Scholar]
- Wagner, J.; Fischer, V.; Herman, M.; Behnke, S. Multispectral Pedestrian Detection using Deep Fusion Convolutional Neural Networks. In Proceedings of the 24th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), Bruges, Belgium, 27–29 April 2016. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision And Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Las Condes, Chile, 11–18 December 2015. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. arXiv 2015, arXiv:1505.07293. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R.B. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.B.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- York, T.; Jain, R. Fundamentals of Image Sensor Performance. Available online: https://www.cse.wustl.edu/~jain/cse567-11/ftp/imgsens/ (accessed on 10 August 2019).
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Mukhtar, A.; Xia, L.; Tang, T.B. Vehicle Detection Techniques for Collision Avoidance Systems: A Review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2318–2338. [Google Scholar] [CrossRef]
- Sun, Z.; Bebis, G.; Miller, R. On-Road Vehicle Detection: A Review. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 694–711. [Google Scholar] [PubMed]
- Barowski, T.; Szczot, M.; Houben, S. Fine-Grained Vehicle Representations for Autonomous Driving. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 3797–3804. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Shafiee, M.J.; Chywl, B.; Li, F.; Wong, A. Fast YOLO: A fast you only look once system for real-time embedded object detection in video. arXiv 2017, arXiv:1709.05943. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, Netherlands, 6–8 October 2016; pp. 21–37. [Google Scholar]
- Kabakchiev, C.; Doukovska, L.; Garvanov, I. Cell averaging constant false alarm rate detector with Hough transform in randomly arriving impulse interference. Cybern. Inf. Tech. 2006, 6, 83–89. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Ljung, L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems. IEEE Trans. Autom. Control 1979, 24, 36–50. [Google Scholar] [CrossRef]
- Yu, F.; Xian, W.; Chen, Y.; Liu, F.; Liao, M.; Madhavan, V.; Darrell, T. Bdd100k: A diverse driving video database with scalable annotation tooling. arXiv 2018, arXiv:1805.04687. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Rob. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015. [Google Scholar]
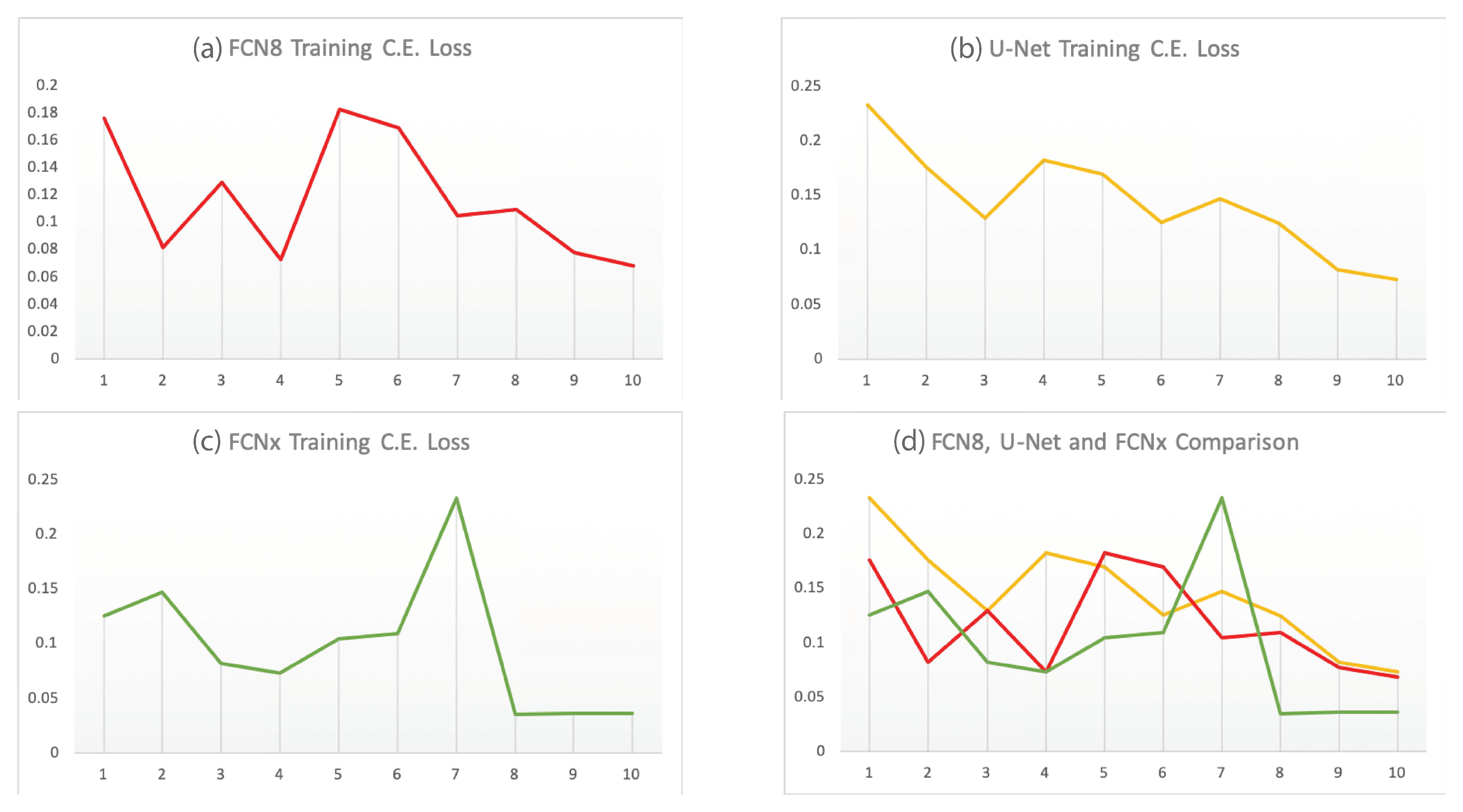


| Network | Architecture | Skip Connection Operation | Residual Connections | |
|---|---|---|---|---|
| FCN8 [23] | Asymmetrical encoder-decoder base | Skip connections between the encoder and the decoder using element-wise sum operator | Three convolution groups for three downsampling layers before the upsampling path | |
| U-Net [43] | Symmetrical encoder-decoder base | Skip connections between the encoder and the decoder using concatenation operator | All downsampling layers information is passed to the upsampling path | |
| FCNx (Our model) | Asymmetrical encoder-decoder base | Skip connections between the encoder and the decoder using element-wise sum operator | Four convolution groups for three downsampling layers before the upsampling path |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahian Jahromi, B.; Tulabandhula, T.; Cetin, S. Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles. Sensors 2019, 19, 4357. https://doi.org/10.3390/s19204357
Shahian Jahromi B, Tulabandhula T, Cetin S. Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles. Sensors. 2019; 19(20):4357. https://doi.org/10.3390/s19204357
Chicago/Turabian StyleShahian Jahromi, Babak, Theja Tulabandhula, and Sabri Cetin. 2019. "Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles" Sensors 19, no. 20: 4357. https://doi.org/10.3390/s19204357
APA StyleShahian Jahromi, B., Tulabandhula, T., & Cetin, S. (2019). Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles. Sensors, 19(20), 4357. https://doi.org/10.3390/s19204357






