Prediction of Motor Failure Time Using An Artificial Neural Network
Abstract
1. Introduction
2. Related Works
2.1. Data Predicting with ANN
2.2. ANN in Engines Failure Prediction Systems
3. Proposed Method
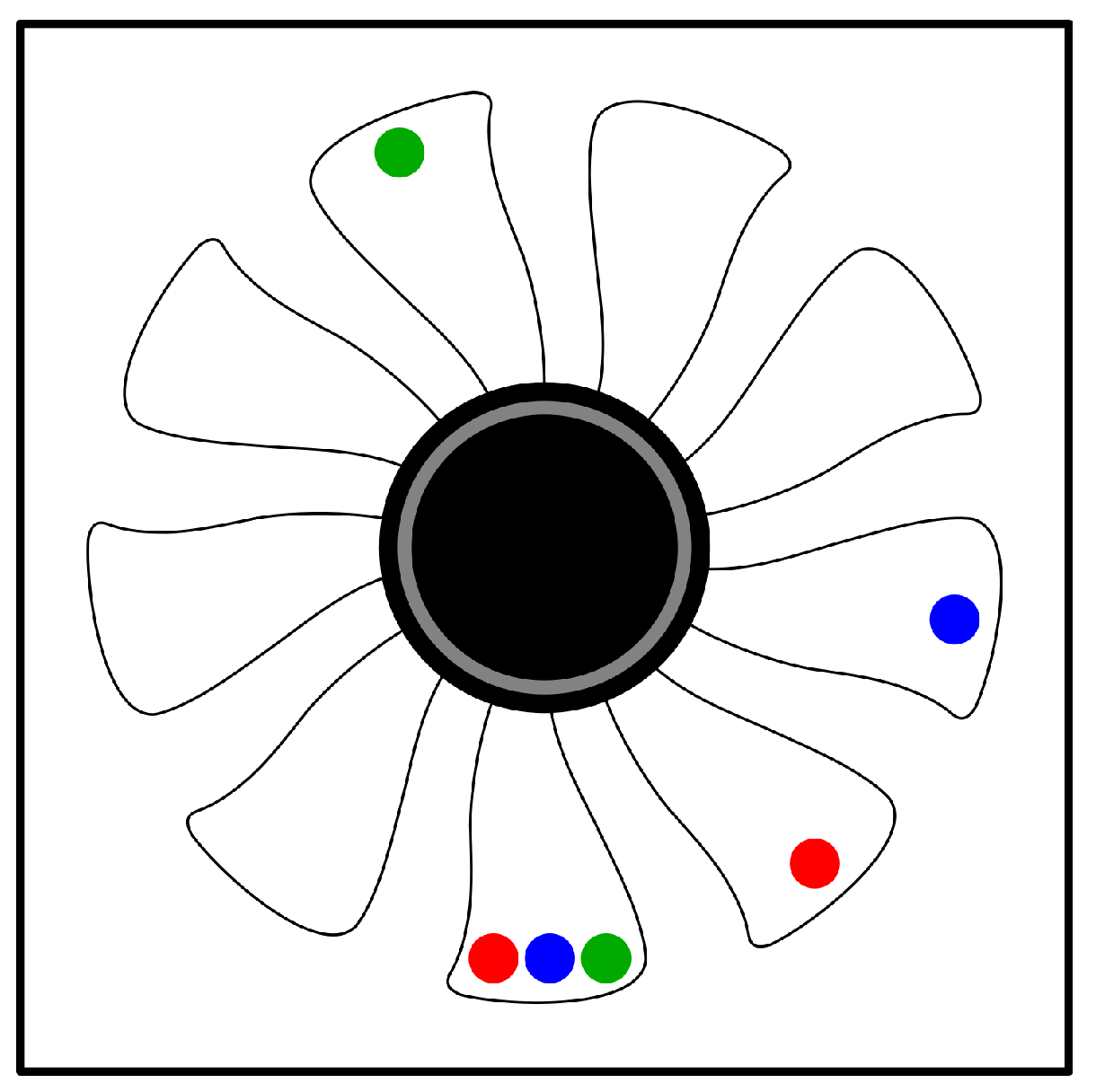
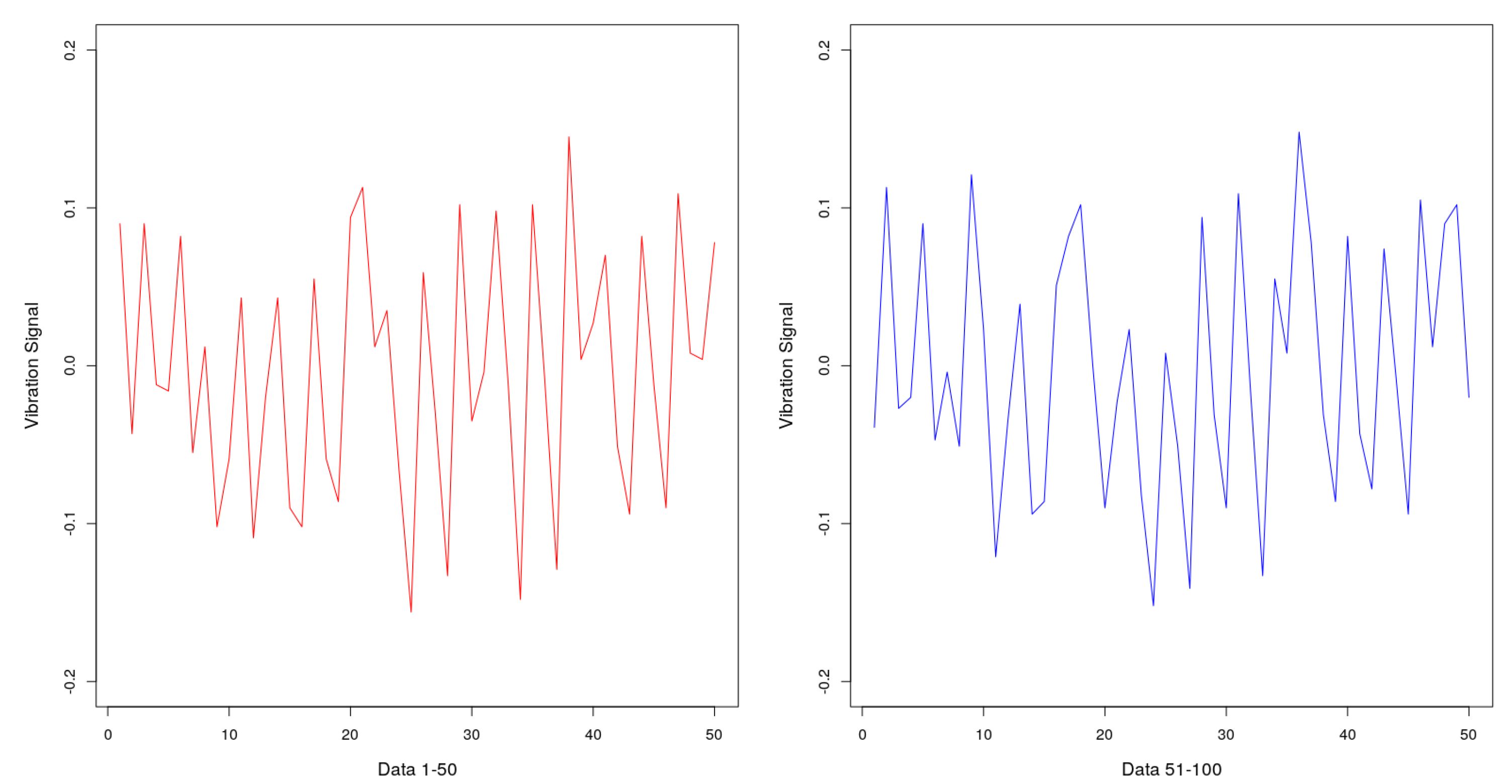
3.1. Data Collection and Data Processing
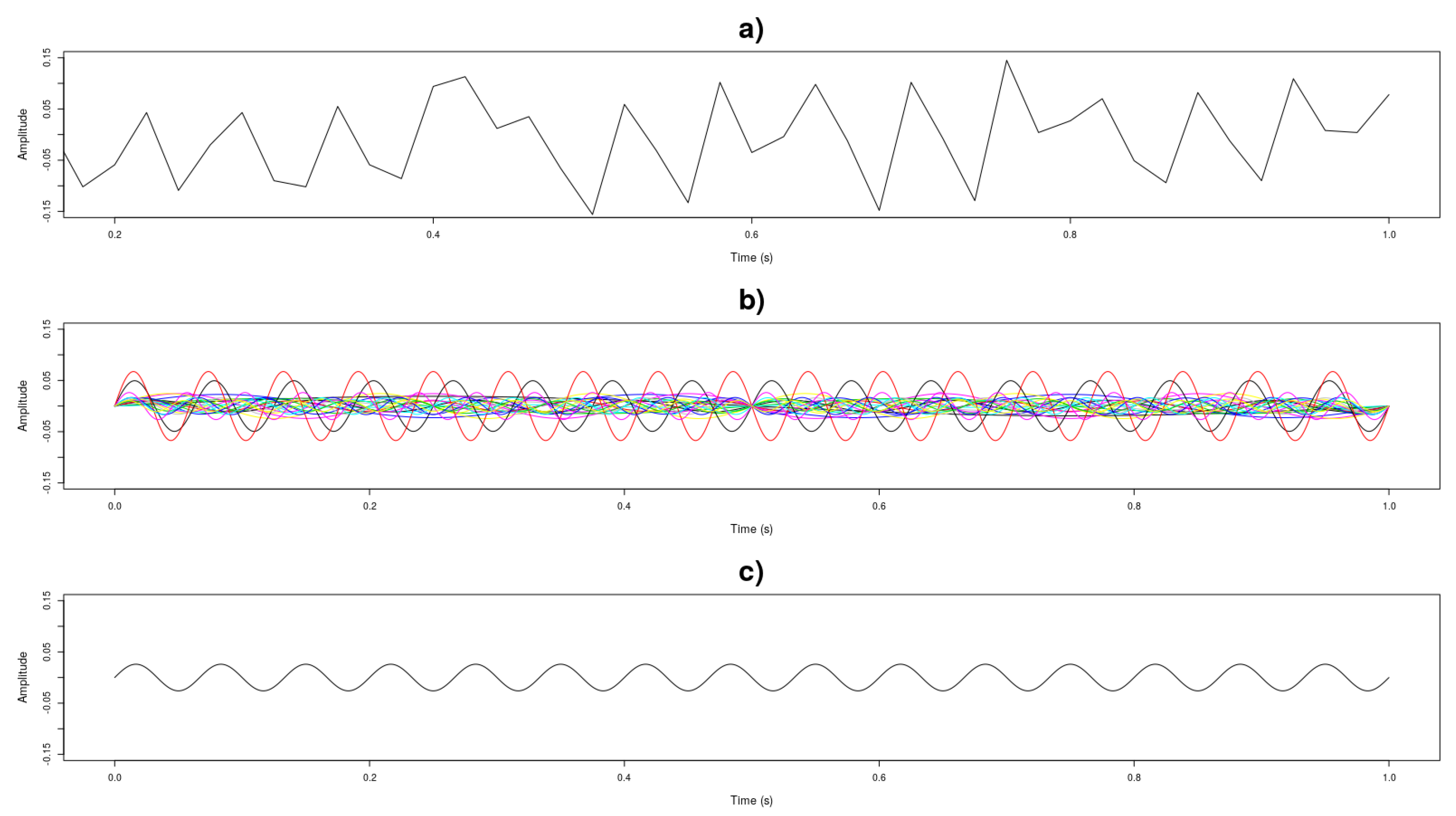
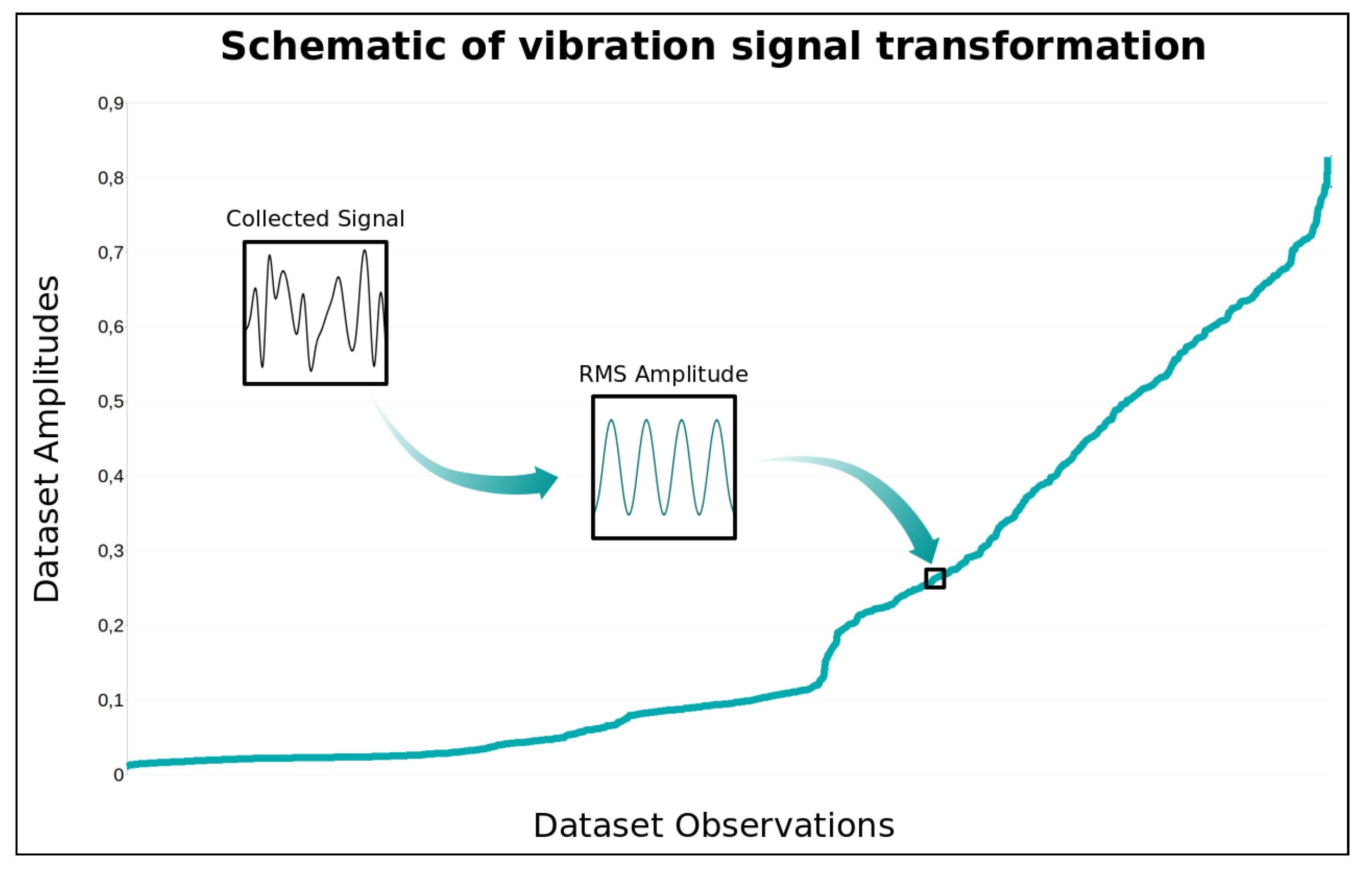
3.2. Performance Index
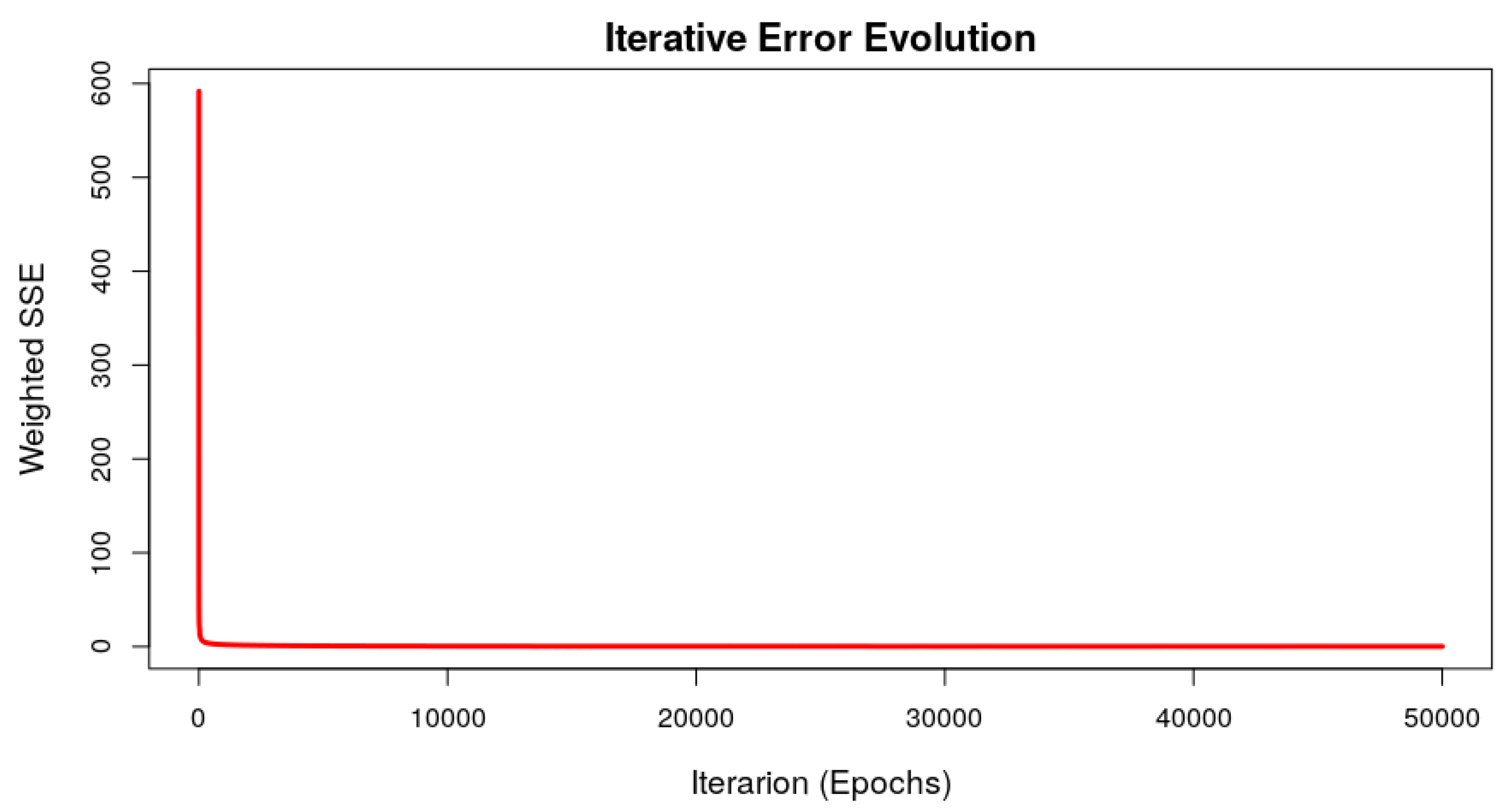
3.3. ANN Training
3.4. Comparing with Other Machine Learning Techniques
4. Prediction Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Networks |
| FDS | Fault Diagnosis System |
| Inter-Integrated Circuit | |
| MLP | Multilayer Perceptron |
| RF | Random Forest |
| RT | Regression Tree |
| RMS | Root Mean Square |
| RMSE | Root Mean Square Error |
| SG | Smart Grid |
| SVM | Suport Vector Machine |
References
- Patan, K.; Korbicz, J.; Głowacki, G. DC motor fault diagnosis by means of artificial neural networks. In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, Angers, France, 9–12 May 2007; pp. 11–18. [Google Scholar] [CrossRef]
- Gongora, W.S.; Silva, H.V.D.; Goedtel, A.; Godoy, W.F.; da Silva, S.A.O. Neural approach for bearing fault detection in three phase induction motors. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013. [Google Scholar] [CrossRef]
- Kouki, M.; Dellagi, S.; Achour, Z.; Erray, W. Optimal integrated maintenance policy based on quality deterioration. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Bandar Sunway, Malaysia, 9–12 December 2014. [Google Scholar] [CrossRef]
- Amihai, I.; Gitzel, R.; Kotriwala, A.M.; Pareschi, D.; Subbiah, S.; Sosale, G. An Industrial Case Study Using Vibration Data and Machine Learning to Predict Asset Health. In Proceedings of the 2018 IEEE 20th Conference on Business Informatics (CBI), Vienna, Austria, 11–14 July 2018. [Google Scholar] [CrossRef]
- Wang, N.; Sun, S.; Si, S.; Li, J. Research of predictive maintenance for deteriorating system based on semi-markov process. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009. [Google Scholar] [CrossRef]
- Gao, B.; Guo, L.; Ma, L.; Wang, K. Corrective maintenance process simulation algorithm research based on process interaction. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference (PHM), Beijing, China, 23–25 May 2012. [Google Scholar] [CrossRef]
- Plante, T.; Nejadpak, A.; Yang, C.X. Faults detection and failures prediction using vibration analysis. In Proceedings of the 2015 IEEE AUTOTESTCON, National Harbor, Maryland, 2–5 Novermber 2015. [Google Scholar] [CrossRef]
- Yildirim, M.; Sun, X.A.; Gebraeel, N.Z. Sensor-Driven Condition-Based Generator Maintenance Scheduling—Part I: Maintenance Problem. IEEE Trans. Power Syst. 2016, 31, 4253–4262. [Google Scholar] [CrossRef]
- Yildirim, M.; Sun, X.A.; Gebraeel, N.Z. Sensor-Driven Condition-Based Generator Maintenance Scheduling—Part II: Incorporating Operations. IEEE Trans. Power Syst. 2016, 31, 4263–4271. [Google Scholar] [CrossRef]
- Mathew, V.; Toby, T.; Singh, V.; Rao, B.M.; Kumar, M.G. Prediction of Remaining Useful Lifetime (RUL) of turbofan engine using machine learning. In Proceedings of the 2017 IEEE International Conference on Circuits and Systems (ICCS), Batumi, Georgia, 5–8 December 2017. [Google Scholar] [CrossRef]
- Verbert, K.; Schutter, B.D.; Babuška, R. A Multiple-Model Reliability Prediction Approach for Condition- Based Maintenance. IEEE Trans. Reliab. 2018, 67, 1364–1376. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R. Classification and Regression Trees, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bird, J. Engineering Mathematics, 5th ed.; Newnes-Elsevier: Oxford, UK, 2007. [Google Scholar]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed; Pearson: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Zheng, C.; Malbasa, V.; Kezunovic, M. Regression tree for stability margin prediction using synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 1978–1987. [Google Scholar] [CrossRef]
- Bae, K.Y.; Jang, H.S.; Sung, D.K. Hourly Solar Irradiance Prediction Based on Support Vector Machine and Its Error Analysis. IEEE Trans. Power Syst. 2016. [Google Scholar] [CrossRef]
- Shevchik, S.A.; Saeidi, F.; Meylan, B.; Wasmer, K. Prediction of Failure in Lubricated Surfaces Using Acoustic Time–Frequency Features and Random Forest Algorithm. IEEE Trans. Ind. Inform. 2017, 13, 1541–1553. [Google Scholar] [CrossRef]
- Wang, X. Ladle furnace temperature prediction model based on large-scale data with random forest. IEEE/CAA J. Autom. Sin. 2017, 4, 770–774. [Google Scholar] [CrossRef]
- Zhang, B.; Wei, Z.; Ren, J.; Cheng, Y.; Zheng, Z. An Empirical Study on Predicting Blood Pressure Using Classification and Regression Trees. IEEE Access 2018, 6, 21758–21768. [Google Scholar] [CrossRef]
- Ababei, C.; Moghaddam, M.G. A Survey of Prediction and Classification Techniques in Multicore Processor Systems. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 1184–1200. [Google Scholar] [CrossRef]
- Tian, Z.; Zuo, M.J. Health Condition Prediction of Gears Using a Recurrent Neural Network Approach. IEEE Trans. Reliab. 2010, 59, 700–705. [Google Scholar] [CrossRef]
- Li, C.; Liu, S.; Zhang, H.; Hu, Y. Machinery condition prediction based on wavelet and support vector machine. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Sichuan, China, 15–18 July 2013. [Google Scholar] [CrossRef]
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef]
- Huang, J.; Chen, G.; Shu, L.; Wang, S.; Zhang, Y. An Experimental Study of Clogging Fault Diagnosis in Heat Exchangers Based on Vibration Signals. IEEE Access 2016, 4, 1800–1809. [Google Scholar] [CrossRef]
- Ntalampiras, S. Fault Diagnosis for Smart Grids in Pragmatic Conditions. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Alippi, C.; Ntalampiras, S.; Roveri, M. Model-Free Fault Detection and Isolation in Large-Scale Cyber-Physical Systems. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 61–71. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Daoud, M.; Mayo, M. A survey of neural network-based cancer prediction models from microarray data. Artif. Intell. Med. 2019, 97, 204–214. [Google Scholar] [CrossRef]
- Brand, L.; Patel, A.; Singh, I.; Brand, C. Real Time Mortality Risk Prediction: A Convolutional Neural Network Approach. In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies, SCITEPRESS—Science and Technology Publications, Funchal, Madeira, Portugal, 19–21 January 2018. [Google Scholar] [CrossRef]
- Hao, Y.; Usama, M.; Yang, J.; Hossain, M.S.; Ghoneim, A. Recurrent convolutional neural network based multimodal disease risk prediction. Future Gener. Comput. Syst. 2019, 92, 76–83. [Google Scholar] [CrossRef]
- Stubbemann, J.; Treiber, N.A.; Kramer, O. Resilient Propagation for Multivariate Wind Power Prediction. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, SCITEPRESS—Science and and Technology Publications, Lisbon, Portugal, 10–12 January 2015. [Google Scholar] [CrossRef]
- Ak, R.; Fink, O.; Zio, E. Two Machine Learning Approaches for Short-Term Wind Speed Time-Series Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1734–1747. [Google Scholar] [CrossRef]
- Li, F.; Ren, G.; Lee, J. Multi-step wind speed prediction based on turbulence intensity and hybrid deep neural networks. Energy Convers. Manag. 2019, 186, 306–322. [Google Scholar] [CrossRef]
- Yilboga, H.; Eker, O.F.; Guclu, A.; Camci, F. Failure prediction on railway turnouts using time delay neural networks. In Proceedings of the 2010 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Taranto, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Shebani, A.; Iwnicki, S. Prediction of wheel and rail wear under different contact conditions using artificial neural networks. Wear 2018, 406–407, 173–184. [Google Scholar] [CrossRef]
- Arora, Y.; Singhal, A.; Bansal, A. PREDICTION & WARNING. ACM SIGSOFT Softw. Eng. Notes 2014, 39, 1–5. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Y.; Yan, J. Neural Network Based Movie Rating Prediction. In Proceedings of the 2018 International Conference on Big Data and Computing—ICBDC, Shenzhen, China, 28–30 April 2018. [Google Scholar] [CrossRef]
- Muradkhanli, L. Neural Networks for Prediction of Oil Production. IFAC-PapersOnLine 2018, 51, 415–417. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual Life Predictions From Vibration-Based Degradation Signals: A Neural Network Approach. IEEE Trans. Ind. Electron. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Wen, P. Vibration Analysis and Prediction of Turbine Rotor Based Grey Artificial Neural Network. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Hunan, China, 11–12 April 2009. [Google Scholar] [CrossRef]
- Günnemann, N.; Pfeffer, J. Predicting Defective Engines using Convolutional Neural Networks on Temporal Vibration Signals. In Proceedings of the First International Workshop on Learning with Imbalanced Domains: Theory and Applications, ECML-PKDD, Skopje, Macedonia, 22 September 2017; Volume 74, pp. 92–102. [Google Scholar]
- Arduino. About Us. Available online: https://www.arduino.cc/en/Main/AboutUs (accessed on 8 July 2019).
- Akasa. 12cm Viper Fan. Available online: http://www.akasa.com.tw/search.php?seed=AK-FN059 (accessed on 8 July 2019).
- Freescale Semiconductor. Technical Data: Xtrinsic MMA8452Q 3-Axis,12-bit/8-bit Digital Accelerometer. Available online: https://cdn.sparkfun.com/datasheets/Sensors/Accelerometers/MMA8452Q-rev8.1.pdf (accessed on 8 July 2019).
- NXP Semiconductor. UM10204 I2C-Bus Specification and User Manual. Available online: https://www.nxp.com/docs/en/user-guide/UM10204.pdf (accessed on 8 July 2019).
- Processing. Home. Available online: https://processing.org/ (accessed on 8 July 2019).
- Lathi, B.P. Linear Systems and Signals, 2nd ed.; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Skiena, S.S. The Data Science Design Manual (Texts in Computer Science); Springer: Cham, Switzerland, 2017. [Google Scholar]
- Inc., W.R. Root-Mean-Square. Available online: http://mathworld.wolfram.com/Root-Mean-Square.html (accessed on 8 July 2019).
- Foundation, T.R. The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 8 July 2019).
- DataCamp. The R Documentation. Available online: https://www.rdocumentation.org (accessed on 8 July 2019).
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]


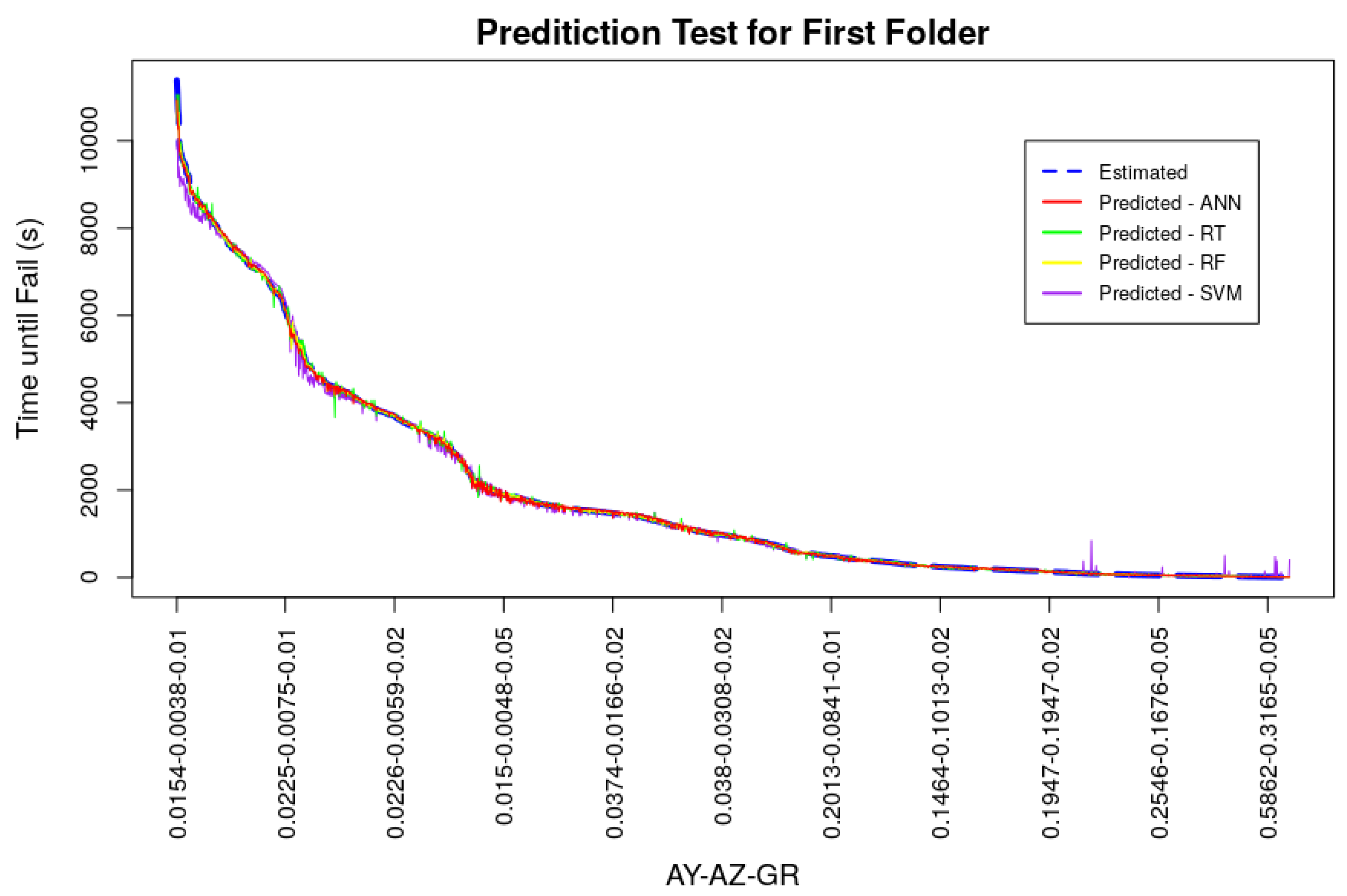
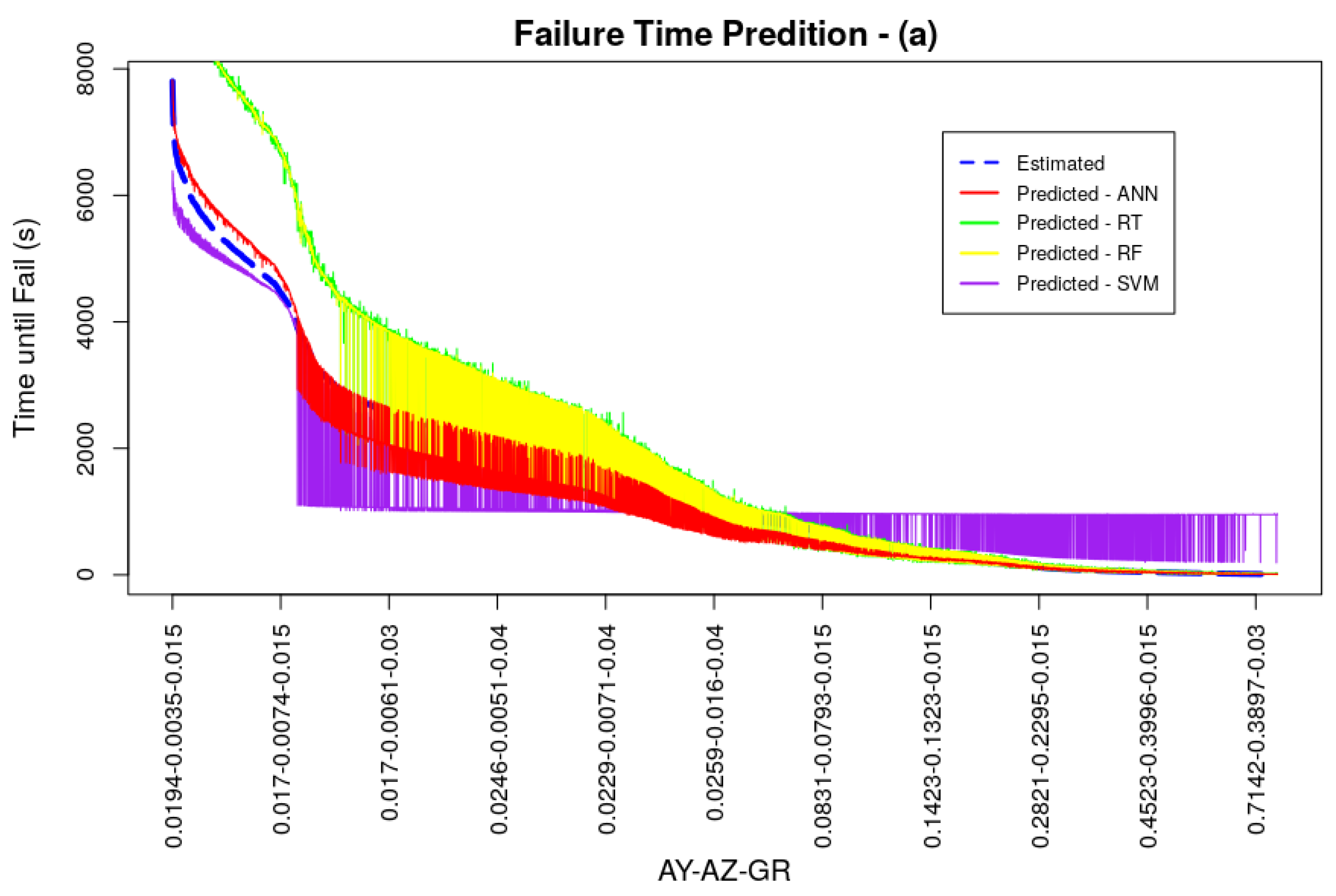

| ANN | RF | ||
|---|---|---|---|
| 50,000 | |||
| RT | SVM | ||
| Folder | ANN | RT | RF | SVM |
|---|---|---|---|---|
| 1 | 0.0039 | 0.0047 | 0.0025 | 0.0106 |
| 2 | 0.0035 | 0.0054 | 0.0035 | 0.0129 |
| 3 | 0.0028 | 0.0051 | 0.0022 | 0.0105 |
| 4 | 0.0041 | 0.0052 | 0.0024 | 0.0120 |
| 5 | 0.0049 | 0.0052 | 0.0026 | 0.0123 |
| Average | 0.0038 | 0.0051 | 0.0026 | 0.0117 |
| Gen. | ANN | RT | RF | SVM |
|---|---|---|---|---|
| a | 0.0313 | 0.0922 | 0.0920 | 0.0696 |
| b | 0.1184 | 0.1417 | 0.1430 | 0.1237 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scalabrini Sampaio, G.; Vallim Filho, A.R.d.A.; Santos da Silva, L.; Augusto da Silva, L. Prediction of Motor Failure Time Using An Artificial Neural Network. Sensors 2019, 19, 4342. https://doi.org/10.3390/s19194342
Scalabrini Sampaio G, Vallim Filho ARdA, Santos da Silva L, Augusto da Silva L. Prediction of Motor Failure Time Using An Artificial Neural Network. Sensors. 2019; 19(19):4342. https://doi.org/10.3390/s19194342
Chicago/Turabian StyleScalabrini Sampaio, Gustavo, Arnaldo Rabello de Aguiar Vallim Filho, Leilton Santos da Silva, and Leandro Augusto da Silva. 2019. "Prediction of Motor Failure Time Using An Artificial Neural Network" Sensors 19, no. 19: 4342. https://doi.org/10.3390/s19194342
APA StyleScalabrini Sampaio, G., Vallim Filho, A. R. d. A., Santos da Silva, L., & Augusto da Silva, L. (2019). Prediction of Motor Failure Time Using An Artificial Neural Network. Sensors, 19(19), 4342. https://doi.org/10.3390/s19194342





