A Computationally Efficient Labeled Multi-Bernoulli Smoother for Multi-Target Tracking †
Abstract
:1. Introduction
2. Background
2.1. Notation
2.2. GLMB and LMB RFS
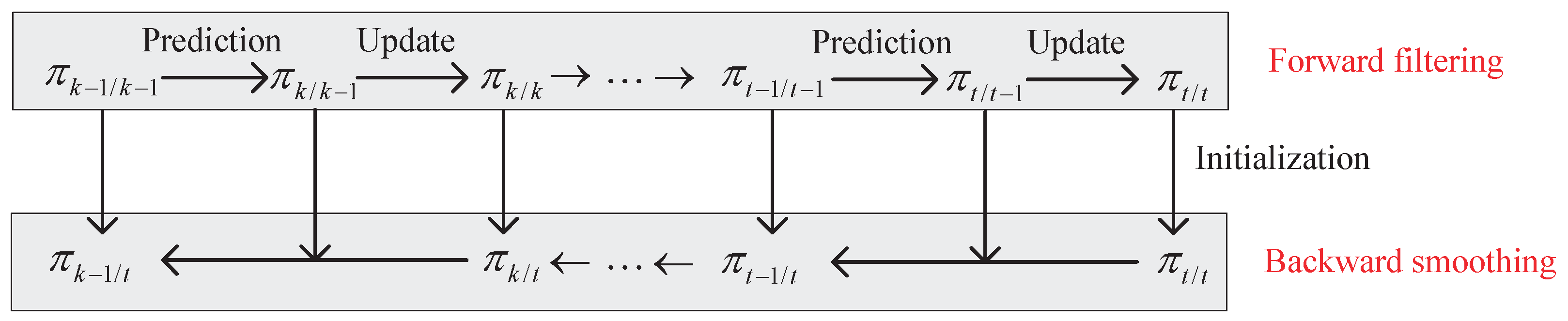
2.3. Multi-Target Bayes Forward–Backward Smoother
2.4. Multi-Target Motion and Measurement Models
3. LMB Smoother
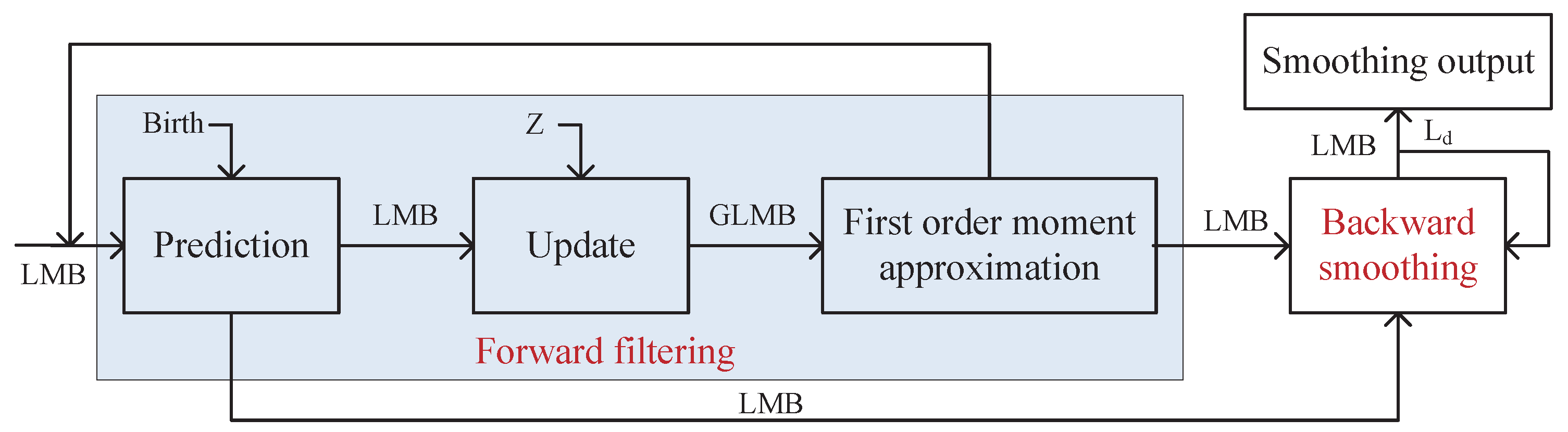
3.1. Forward LMB Filtering
3.1.1. Prediction
3.1.2. Update
3.2. Backward LMB Smoothing
4. SMC Implementation and Algorithm Analysis
4.1. SMC Implementation
4.2. Backward Smoothing and State Extraction
| Algorithm 1: The proposed backward LMB smoothing algorithm. |
| Input: lag at time t, , ; |
| initialize with ; |
| for k=t:-1:max(,1)+1 |
| ; |
| for q = 1:size(,2) |
| compute according to (33); |
| for j=1: |
| estimate according to (51); |
| end |
| for i=1: |
| compute according to (48)–(49); |
| ; |
| end |
| end |
| end |
| Output: . |
4.3. Algorithm Complexity
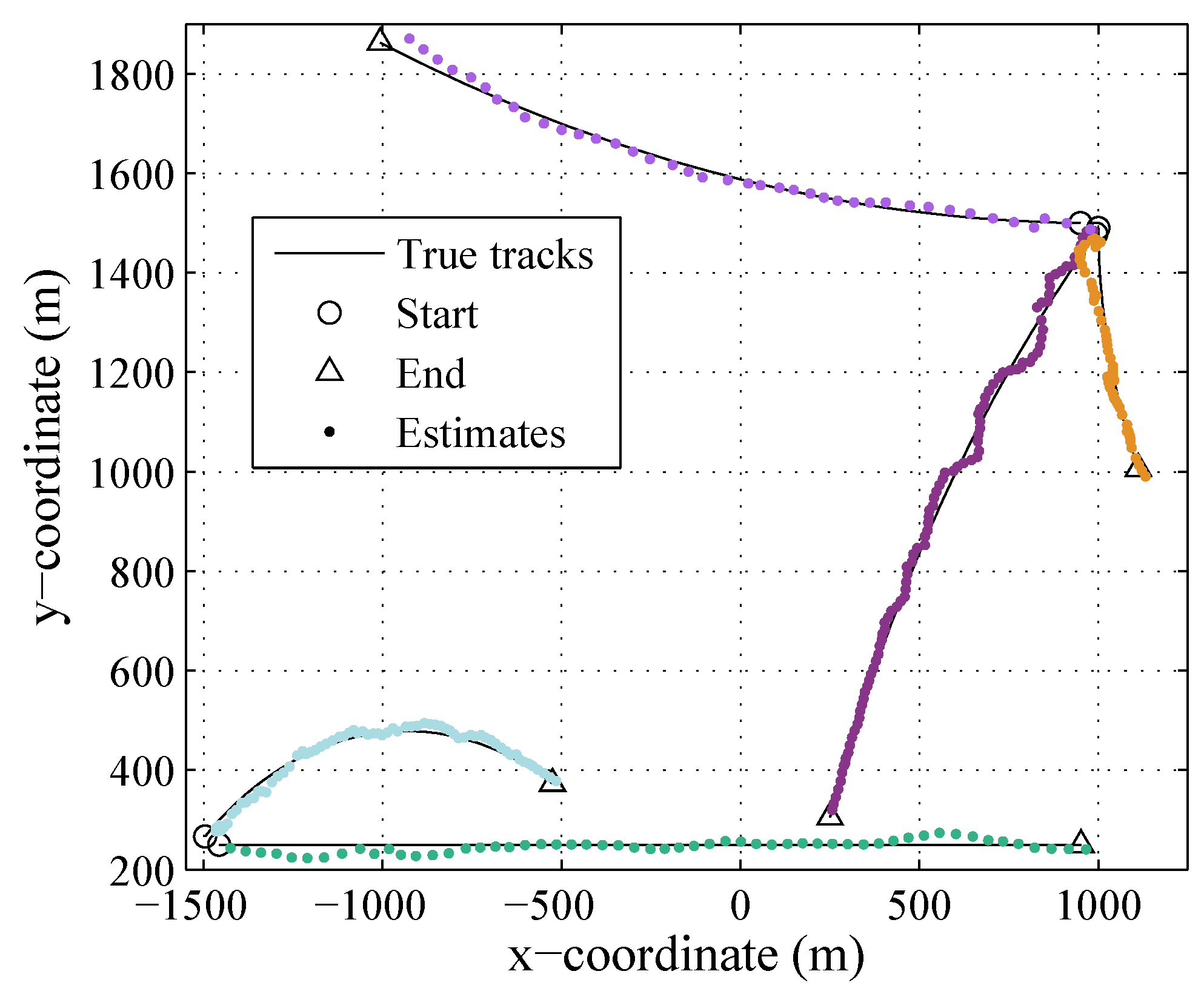
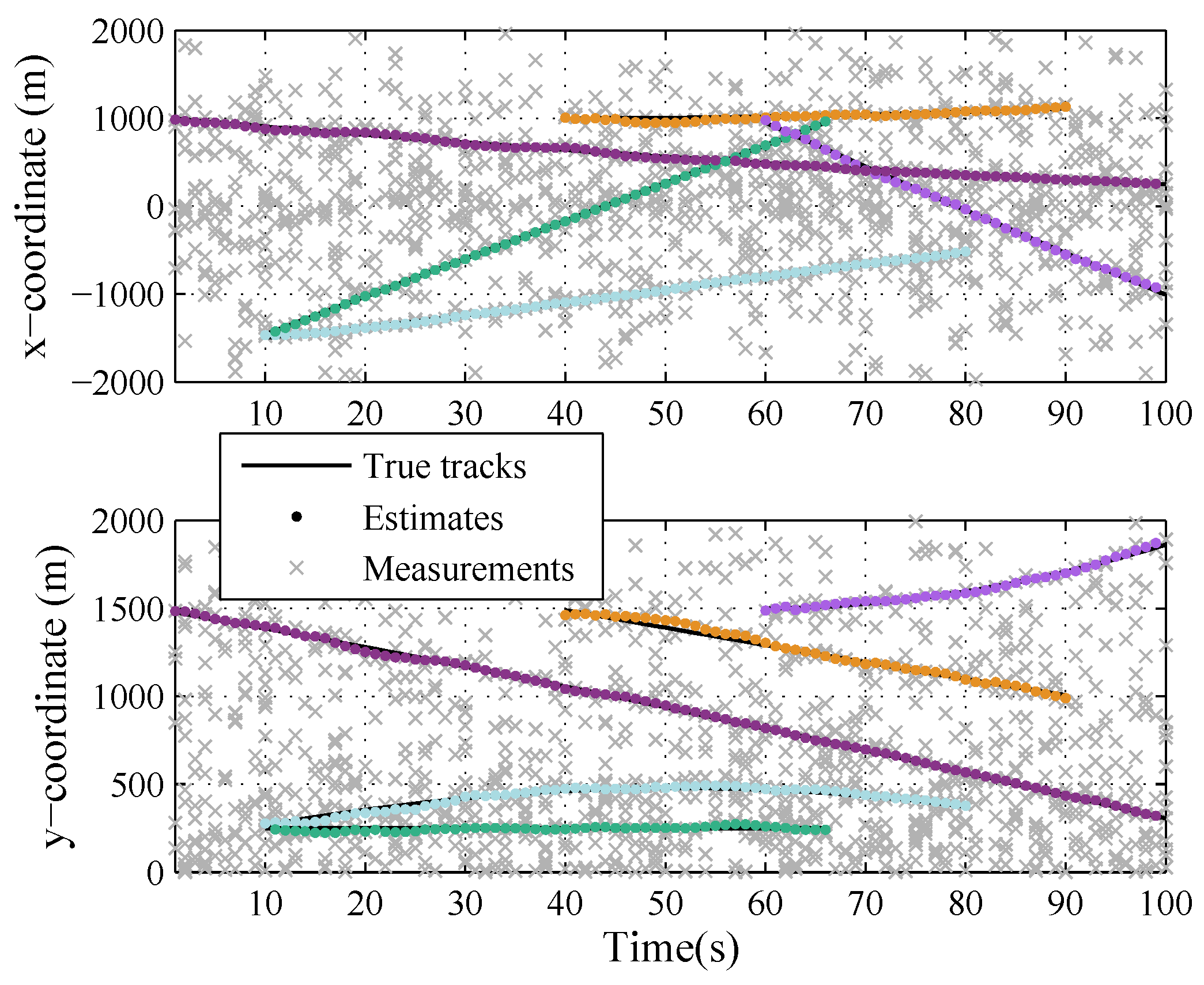
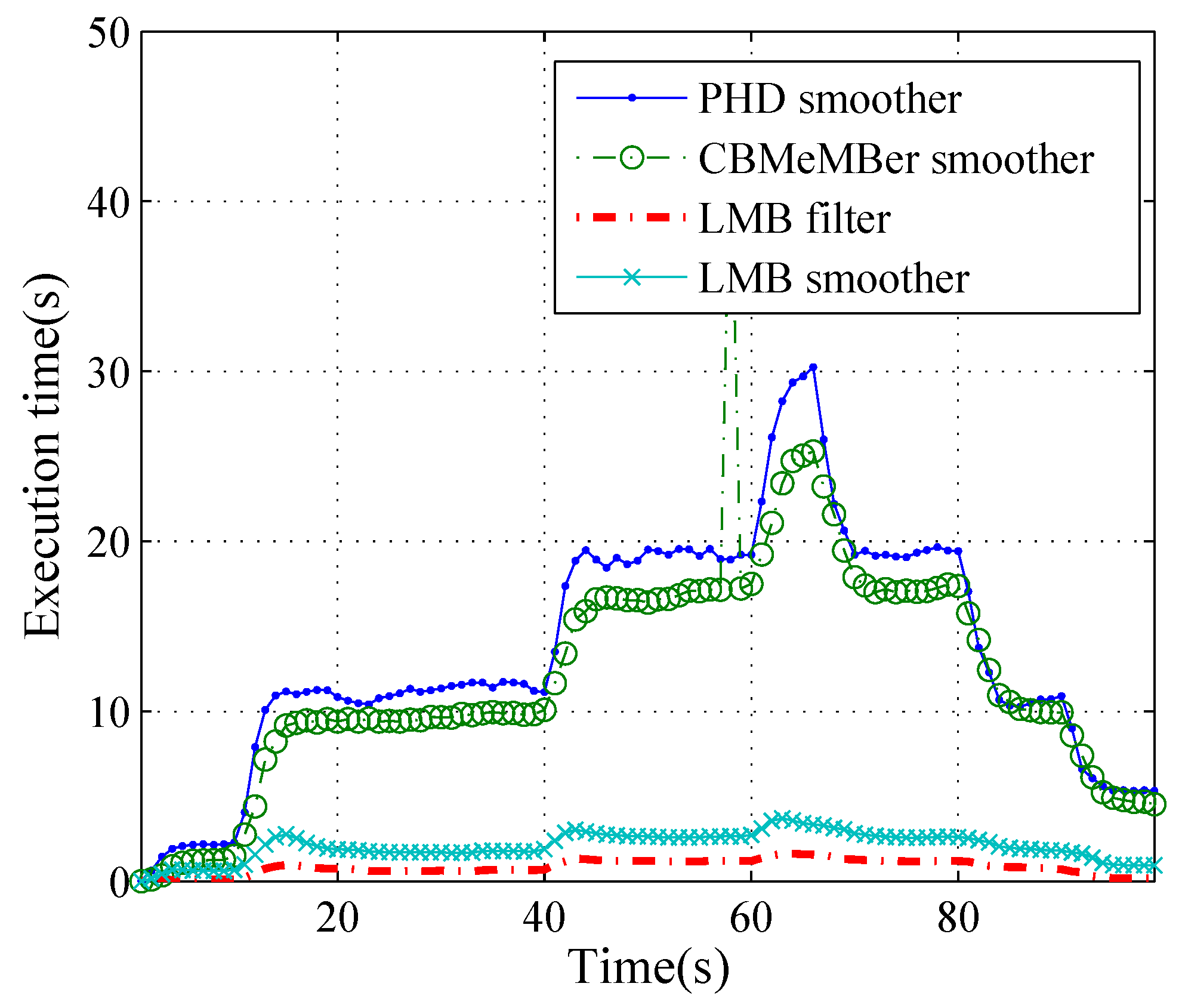
5. Simulation Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Bar-Shalom, Y.; Willett, P.; Tian, X. Tracking and Data Fusion: A Handbook of Algorithms; YBS Publishing: Storrs, CT, USA, 2001. [Google Scholar]
- Mahler, R.P.S. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Vo, B.N.; Mallick, M.; Bar-shalom, Y.; Coraluppi, S.; Osborne, R.; Mahler, R.P.S.; Vo, B.T. Multitarget Tracking. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wang, X.; Li, T.; Sun, S.; Corchado, J.M. A Survey of Recent Advances in Particle Filters and Remaining Challenges for Multitarget Tracking. Sensors 2017, 17, 2707. [Google Scholar] [CrossRef] [PubMed]
- Meyer, F.; Kropfreiter, T.; Williams, J.L.; Lau, R.; Hlawatsch, F.; Braca, P.; Win, M.Z. Message Passing Algorithms for Scalable Multitarget Tracking. Proc. IEEE 2018, 106, 221–259. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Willett, P.; Ruan, Y.; Streit, R. PMHT: Problems and some solutions. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 738–754. [Google Scholar] [CrossRef]
- Mahler, R.P.S. ”Statistics 103” for Multitarget Tracking. Sensors 2019, 19, 202. [Google Scholar] [CrossRef] [PubMed]
- Mahler, R.P.S. Multitarget Bayes Filtering via First-Order Multitarget Moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Yang, F.; Tang, W.; Liang, Y. A novel track initialization algorithm based on random sample consensus in dense clutter. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef] [Green Version]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Vo, B.T.; Vo, B.N. Labeled Random Finite Sets and Multi-Object Conjugate Priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef] [Green Version]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Arnaud Doucet, A.M.J. A Tutorial on Particle Filtering and Smoothing: Fifteen years later. In The Oxford Handbook of Nonlinear Filtering; Crisan, D., Rozovskii, B., Eds.; Oxford University Press: Oxford, UK, 2008; pp. 656–704. [Google Scholar]
- Mahler, R.P.S.; Vo, B.T. Forward-Backward Probability Hypothesis Density Smoothing. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 707–728. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Mahler, R.P.S. Closed-form solutions to forward-backward smoothing. IEEE Trans. Signal Process. 2011, 60, 2–17. [Google Scholar] [CrossRef]
- Li, T.; Chen, H.; Sun, S.; Corchado, J.M. Joint Smoothing and Tracking Based on Continuous-Time Target Trajectory Function Fitting. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1476–1483. [Google Scholar] [CrossRef]
- Vo, B.T.; Clark, D.; Vo, B.N.; Ristic, B. Bernoulli Forward-Backward Smoothing for Joint Target Detection and Tracking. IEEE Trans. Signal Process. 2011, 59, 4473–4477. [Google Scholar] [CrossRef]
- Wong, S.; Vo, B.T.; Papi, F. Bernoulli Forward-Backward Smoothing for Track-Before-Detect. IEEE Signal Process. Lett. 2014, 21, 727–731. [Google Scholar] [CrossRef]
- Nadarajah, N.; Kirubarajan, T.L.T. Multitarget Tracking using Probability Hypothesis Density Smoothing. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2344–2360. [Google Scholar] [CrossRef]
- Nagappa, S.; Clark, D.E. Fast Sequential Monte Carlo PHD Smoothing. In Proceedings of the International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1819–1825. [Google Scholar]
- He, X.; Liu, G. Improved Gaussian mixture probability hypothesis density smoother. Signal Process. 2016, 120, 56–63. [Google Scholar] [CrossRef]
- Nagappa, S.; Delande, E.D.; Clark, D.E.; Houssineau, J. A Tractable Forward-Backward CPHD Smoother. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 201–217. [Google Scholar] [CrossRef]
- Clark, D.E. First-moment multi-object forward-backward smoothing. In Proceedings of the International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–6. [Google Scholar]
- Dong, L.; Hou, C.; Yi, D. Multi-Bernoulli smoother for multi-target tracking. Aerosp. Sci. Technol. 2016, 48, 234–245. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Gia, H. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Papi, F.; Vo, B.T.; Vo, B.N.; Fantacci, C.; Beard, M. Generalized Labeled Multi-Bernoulli approximation of Multi-object densities. IEEE Trans. Signal Process. 2015, 63, 5487–5497. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N.; Arulampalam, S. Void probabilities and Cauchy-Schwarz divergence for Generalized Labeled Multi-Bernoulli models. IEEE Trans. Signal Process. 2017, 65, 5047–5061. [Google Scholar] [CrossRef]
- Li, S.; Wei, Y.; Hoseinnezhad, R.; Wang, B.; Kong, L.J. Multi-object Tracking for Generic Observation Model Using Labeled Random Finite Sets. IEEE Trans. Signal Process. 2018, 66, 368–383. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. Generalised labelled multi-Bernoulli forward-backward smoothing. In Proceedings of the International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016; pp. 1–7. [Google Scholar]
- Chen, L. From labels to tracks: It’s complicated. Proc. SPIE 2018, 10646. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T. A Multi-Scan Labeled Random Finite Set Model for Multi-Object State Estimation. IEEE Trans. Signal Process. 2019, 67, 4948–4963. [Google Scholar] [CrossRef] [Green Version]
- Li, T. Single-Road-Constrained Positioning Based on Deterministic Trajectory Geometry. IEEE Commun. Lett. 2019, 23, 80–83. [Google Scholar] [CrossRef]
- Li, T.; Wang, X.; Liang, Y.; Yan, J.; Fan, H. A Track-oriented Approach to Target Tracking with Random Finite Set Observations. In Proceedings of the ICCAIS 2019, Chengdu, China, 23–26 October 2019. [Google Scholar]
- Liu, R.; Fan, H.; Xiao, H. A forward-backward labeled Multi-Bernoulli smoother. In Proceedings of the International Conference on Distributed Computing and Artificial Intelligence, Avila, Spain, 26–28 June 2019; pp. 253–261. [Google Scholar]
- Li, T.; Su, J.; Liu, W.; Corchado, J.M. Approximate Gaussian conjugacy: Recursive parametric filtering under nonlinearity, multimodality, uncertainty, and constraint, and beyond. Front. Inf. Technol. Electron. Eng. 2017, 18, 1913–1939. [Google Scholar] [CrossRef]
- Li, T.; Bolic, M.; Djuric, P. Resampling methods for particle filtering: Classification, Implementation, and Strategies. IEEE Signal Process. Mag. 2015, 32, 70–86. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
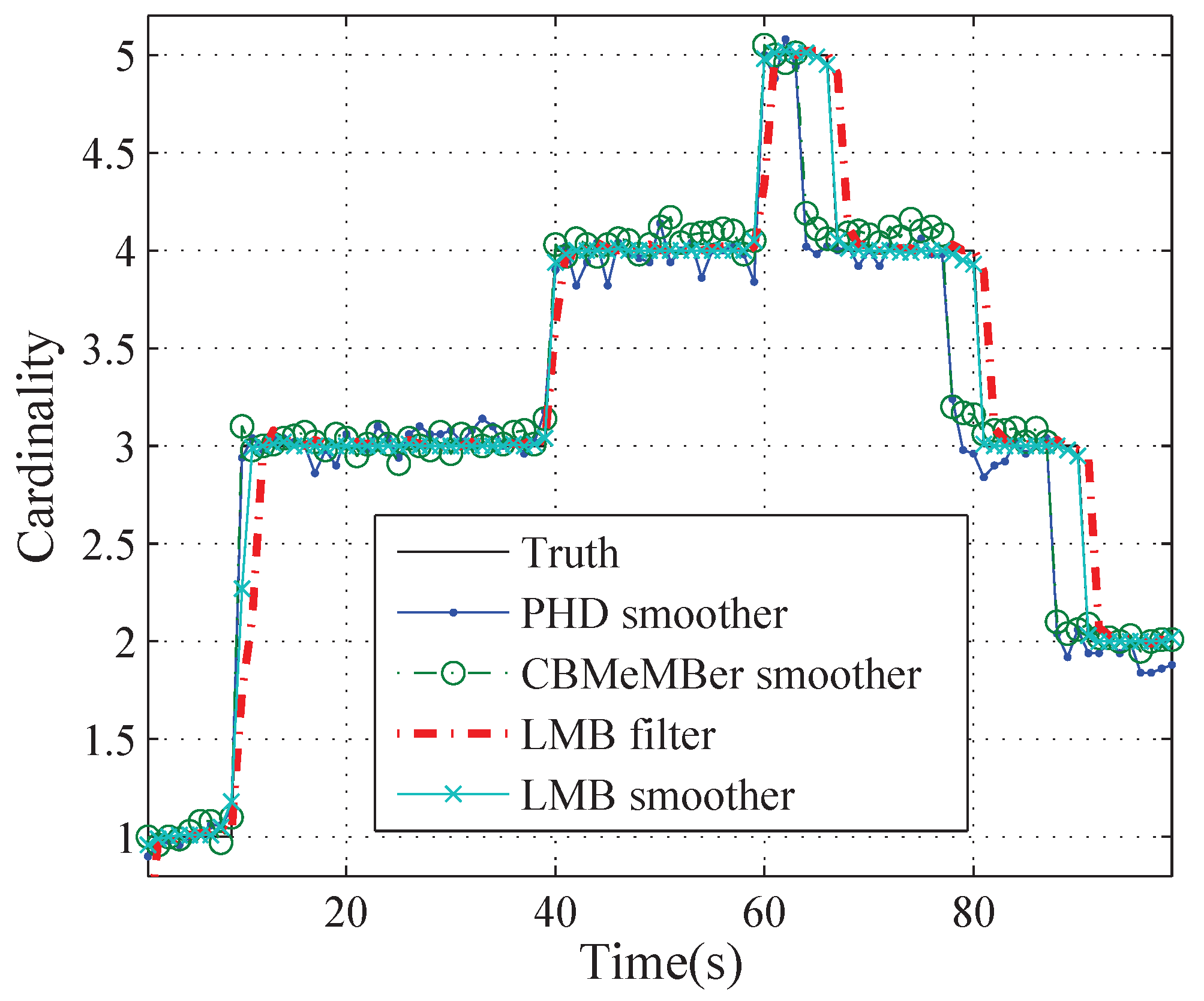
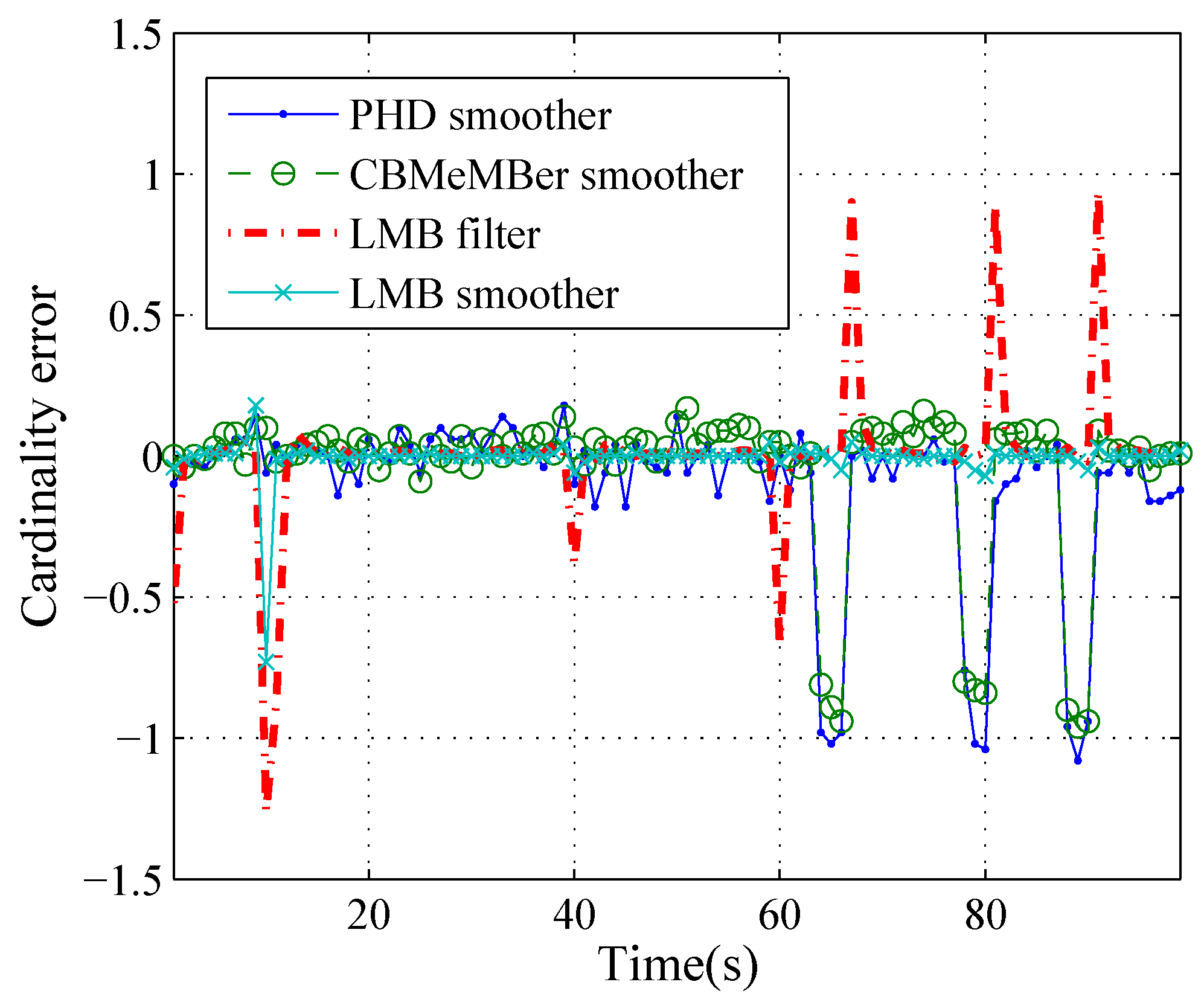
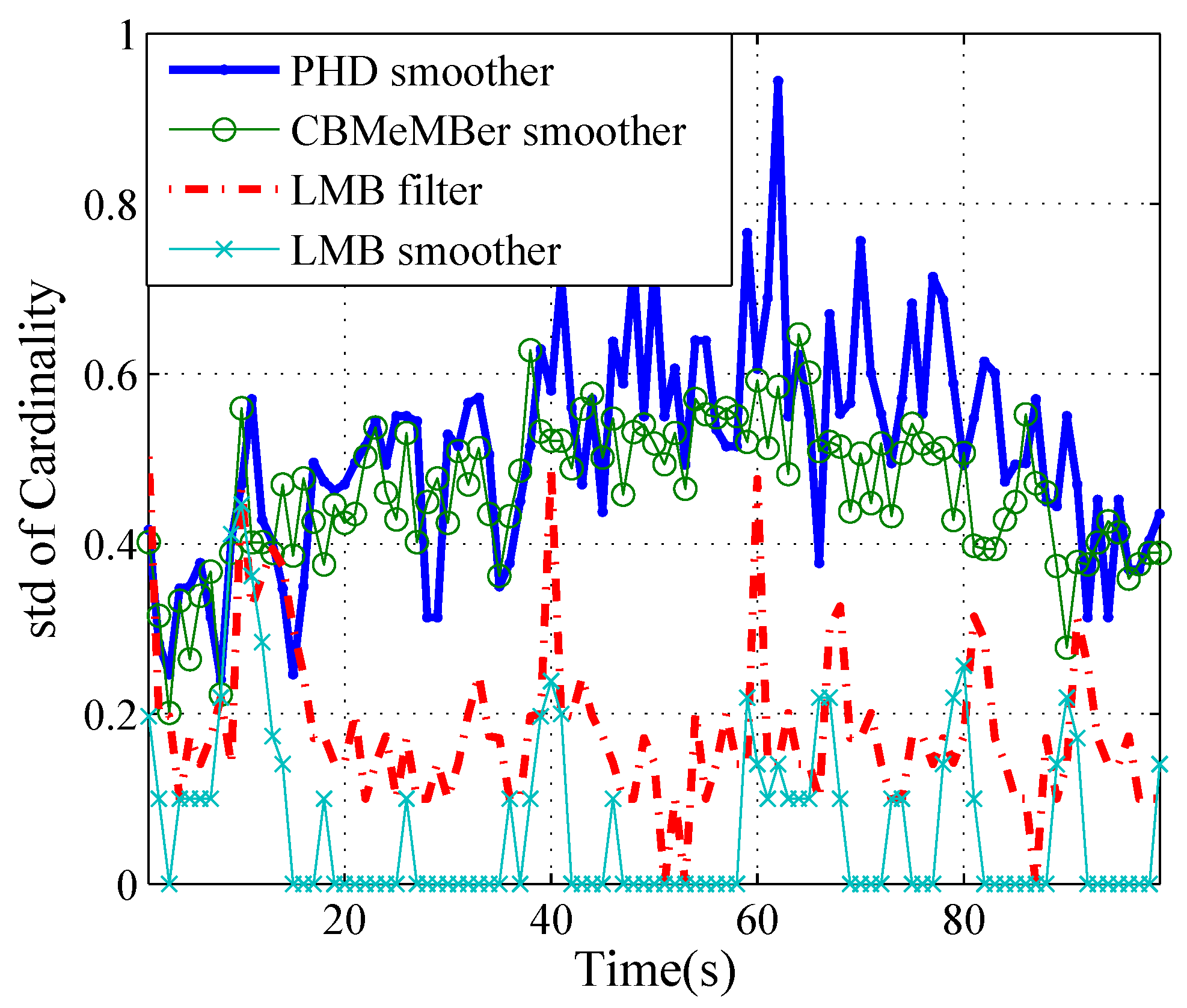
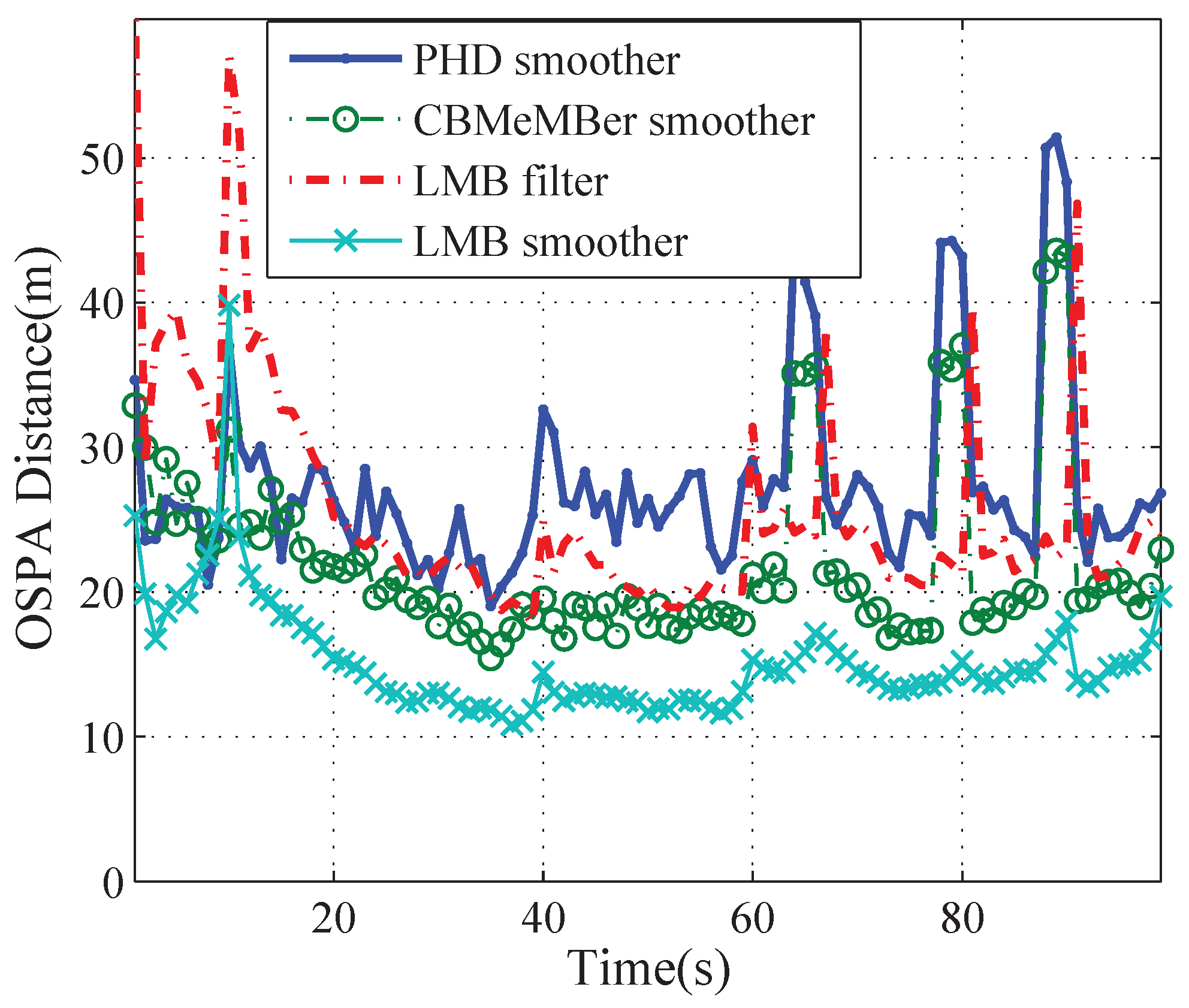
| Method | Total | Localization | Cardinality |
|---|---|---|---|
| OSPA (m) | Component (m) | Component (m) | |
| PHD filter | 34.3821 | 26.4094 | 7.9727 |
| PHD smoother | 27.3199 | 18.6526 | 8.6673 |
| CBMeMBer filter | 30.2842 | 22.3566 | 7.9276 |
| MeMBer smoother | 22.0721 | 14.6664 | 7.4056 |
| LMB filter | 25.6800 | 22.6574 | 3.0226 |
| LMB smoother | 15.1762 | 14.4932 | 0.6830 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Fan, H.; Li, T.; Xiao, H. A Computationally Efficient Labeled Multi-Bernoulli Smoother for Multi-Target Tracking. Sensors 2019, 19, 4226. https://doi.org/10.3390/s19194226
Liu R, Fan H, Li T, Xiao H. A Computationally Efficient Labeled Multi-Bernoulli Smoother for Multi-Target Tracking. Sensors. 2019; 19(19):4226. https://doi.org/10.3390/s19194226
Chicago/Turabian StyleLiu, Rang, Hongqi Fan, Tiancheng Li, and Huaitie Xiao. 2019. "A Computationally Efficient Labeled Multi-Bernoulli Smoother for Multi-Target Tracking" Sensors 19, no. 19: 4226. https://doi.org/10.3390/s19194226





