Indirect Time-of-Flight Depth Sensor with Two-Step Comparison Scheme for Depth Frame Difference Detection

Abstract

A depth sensor with integrated frame difference detection is proposed. Instead of frame difference detection using light intensity, which is vulnerable to ambient light, the difference in depth between successive frames can be acquired. Because the conventional time-of-flight depth sensor requires two frames of depth-image acquisition with four-phase modulation, it has large power consumption, as well as a large area for external frame memories. Therefore, we propose a simple two-step comparison scheme for generating the depth frame difference in a single frame. With the proposed scheme, only a single frame is needed to obtain the frame difference, with less than half of the power consumption of the conventional depth sensor. Because the frame difference is simply generated by column-parallel circuits, no access of the external frame memory is involved, nor is a digital signal processor. In addition, we used an over-pixel metal–insulator–metal capacitor to store temporary signals for enhancing the area efficiency. A prototype chip was fabricated using a 90 nm backside illumination complementary metal–oxide–semiconductor (CMOS) image sensor process. We measured the depth frame difference in the range of 1–2.5 m. With a 10 MHz modulation frequency, a depth frame difference of >10 cm was successfully detected even for objects with different reflectivity. The maximum relative error from the difference of the reflectivity (white and wooden targets) was <3%.

1. Introduction

In both three-dimensional (3D) and conventional two-dimensional (2D) imaging, acquiring digital image signals with full spatial resolution is redundant, particularly when the image is utilized only for the recognition of objects and the activation of functions. Instead, the frame difference can be acquired for the recognition and tracking of moving objects, as well as for motion-triggered awakening [1,2,3]. Specifically, acquiring the frame difference suppresses the transmission of redundant information through the identification of moving objects and the elimination of repetitive frames in surveillance systems [4]. In machine vision, successive functions such as the tracking of moving objects can be activated by the frame difference [5]. Another application of the frame difference is the optic-flow sensor for the navigation of micro-vehicles [6]. The on-chip optic-flow generation firstly requires the detection of the frame difference in order to provide the pattern of motion of objects.

For 2D imaging, several image sensors with integrated frame difference detection were reported [1,2,3,4,5,6]. The sensors generate the frame difference by simply subtracting signals of successive frames. However, the frame difference is determined by simply calculating the change in light intensity, which varies according to the ambient light. Thus, the absolute difference for moving objects cannot be acquired. A more critical problem is that the frame difference cannot be detected under dark conditions. Additionally, the optic-flow sensor reported in Reference [6] generates only a 2D optic flow based on the frame difference of the light intensity, which is inaccurate when the ambient light intensity is extremely low or extremely high in outdoor applications.

Three-dimensional imaging that provides depth information, as well as 2D shape information, can be implemented with a variety of methods such as structured light projection (SLP), direct time-of-flight (dTOF), and indirect time-of-flight (iTOF) methods. These 3D imaging methods have the advantage of being immune to ambient light because they involve the detection of infrared (IR) light. Moreover, the 3D movement of objects can be detected. The SLP method provides high depth accuracy but involves complex post-processing in order to calculate the depth from the pattern matching [7]. Even though the dTOF method offers simple post processing, it requires photodetectors with high sensitivity (such as avalanche photodiodes and single-photon avalanche diodes) and a large form factor in order to measure the time-of-flight with a small number of incident photons in a single measurement [8,9]. Therefore, high spatial resolution is difficult to be implemented. Among the 3D imaging methods, the iTOF method provides high depth accuracy, simple post processing, and high spatial resolution using small photodetectors (such as pinned photodiodes or photogates) that are widely used in 2D image sensors [10,11,12,13]. In the iTOF depth sensor, the four-phase modulation scheme is usually used to provide an accurate depth regardless of the reflectivity of objects while suppressing the offset from ambient lights. However, this four-phase modulation scheme requires two frames of modulation for acquisition of a single-frame depth image, power consuming modulation and analog-to-digital (A/D) conversion in two frames, and huge frame memory to store intermediate signals, which is illustrated in Section 2.

In this paper, we propose a two-step comparison scheme for detecting an accurate depth frame difference regardless of the reflectivity. Without power-consuming four-phase modulation, A/D conversion, digital readout, and image signal processing, a depth frame difference can be simply generated via two-phase modulation with only column-parallel circuits in a single frame. Moreover, instead of frame memory, we implemented an over-pixel metal–insulator–metal (MIM) capacitor to store previous frame signals. Owing to the backside illumination (BSI) complementary metal–oxide–semiconductor (CMOS) image sensor (CIS) process [3,14], the over-pixel MIM capacitor as an analog memory (AM) did not reduce the sensitivity. Additionally, we reused the existing column-parallel amplifier circuit for the gain amplification of signals and reused the comparator of the column-parallel A/D converter (ADC) for acquiring the depth frame difference without a significant area overhead.

The remainder of this paper is organized as follows: Section 2 introduces conventional four-phase modulation scheme. Section 3 describes the operation principle of the proposed two-step comparison scheme for acquiring the depth frame difference. Section 4 describes the structure and operation of the circuit. Section 5 presents the experimental results. The paper is concluded in Section 6.

2. Conventional Four-Phase Modulation Scheme

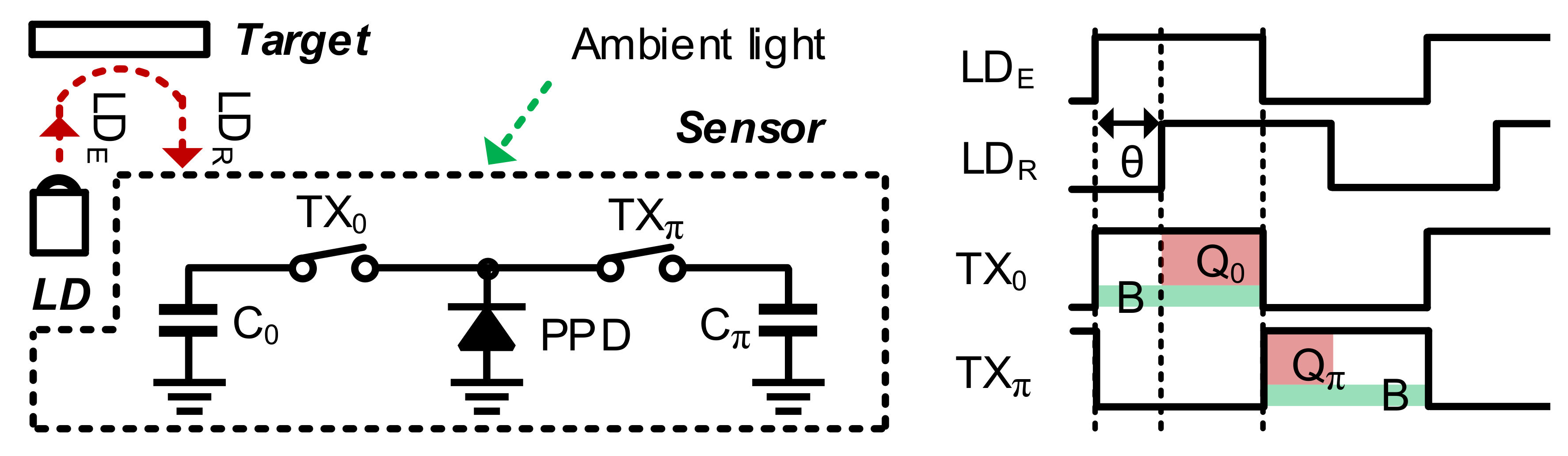
As shown in Figure 1, an IR laser diode (LD) emits modulated light. The iTOF sensor calculates the depth according to the phase difference θ between the emitted light LD_E and reflected light LD_R. Two electronic shutters TX₀ and TX_π in a pixel are modulated in-phase (synchronized with the LD) and out-of-phase, respectively. The typical modulation frequency is >10 MHz. The sensor detects a photogenerated current (I_PIX) in a pinned photodiode (PPD), which is integrated to obtain the charges Q₀ from TX₀ and Q_π from TX_π. Then, θ can be calculated as follows:

$$\theta =\pi ·\frac{A{Q}_{\pi }}{A{Q}_0+A{Q}_{\pi }}=\frac{Q_{\pi }}{Q_0+Q_{\pi }}=\pi ·\frac{Q_{\pi }}{Q_{TOT}},$$

(1)

where A represents the gain from different reflectivities and distances of the object. The total charge Q_TOT that is the sum of Q₀ and Q_π varies according to the distance and the reflectivity. However, the ratio Q_π/Q_TOT depends only on the distance. This operation is called two-phase modulation. Unfortunately, there is a strong background signal from ambient light, particularly in outdoor applications. This strong ambient light provides a common direct-current (DC) offset (BG) to Q₀ and Q_π, as shown in Figure 1. Accordingly, θ becomes erroneous, as shown in Equation (2).

$$\theta +error=\pi ·\frac{A{Q}_{\pi }+BG}{A{Q}_0+BG+A{Q}_{\pi }+BG}=\pi ·\frac{A{Q}_{\pi }+BG}{A{Q}_{TOT}+2BG}.$$

(2)

Therefore, in the conventional iTOF sensor, four-phase modulation is commonly used. To cancel the background signal BG, ΔQ₀ = AQ₀ − AQ_π is acquired. To cancel the gain term A, we obtain another signal ΔQ_π/2 = AQ_π/2 − AQ_3π/2 in the next frame. Finally, we can obtain the exact distance regardless of the reflectivity and ambient light [13] by calculating the following ratio:

$$\theta =\frac{\pi }{2}\times \left(1-\frac{\mathrm{\Delta }{Q}_{\pi /2}}{\left|\Delta Q_0\right|+\left|\Delta Q_{\pi /2}\right|}\right).$$

(3)

To calculate the depth frame difference, we must calculate and store θ₍₁₎ in Frame #1, calculate θ₍₂₎ in Frame #2, and then detect their difference. However, we have three critical problems. Firstly, we need two frames to obtain θ₍₁₎ (and also θ₍₂₎) for the four-phase modulation. This two-frame operation (for each θ_(k)) requires a large power consumption, particularly for the modulation of pixels. Additionally, the calculation of θ involves a digital readout of 10-bit signals and image signal processing, including division, which requires additional power consumption. Secondly, significant motion blur arises because of the two-frame operation, particularly for fast-moving objects. Thirdly, a frame memory with large area is needed to store the ΔQ₀ and ΔQ_π/2 generated from the previous frame. In Section 3, we illustrate the proposed two-step comparison scheme that generates the depth frame difference in a single frame without area overhead from the frame memories and power consumption overhead from the modulation in two frames.

3. Two-Step Comparison Scheme for Acquiring Depth Frame Difference

The main purpose of the proposed scheme is to provide on-chip depth frame difference regardless of reflectivity of objects. In ideal case, we can detect the depth frame difference by measuring only intensity of the reflected light from a single object because the light intensity decreases according to the distance. However, more than two objects with different reflectivities provide different intensity (according to the reflectivity). Therefore, a simple measurement of light intensity like a conventional proximity sensor in mobile devices will induce an error for calculating the absolute difference of depth in successive frames. Instead of light intensity, we can calculate the depth itself using the four-phase modulation scheme that is commonly used in an iTOF depth sensor. However, as mentioned in Section 2, significant overhead of area, power consumption, and speed arise. Therefore, we propose the two-step comparison scheme to generate on-chip depth frame difference in a single frame without any additional memory and power consumption overhead from the modulation.

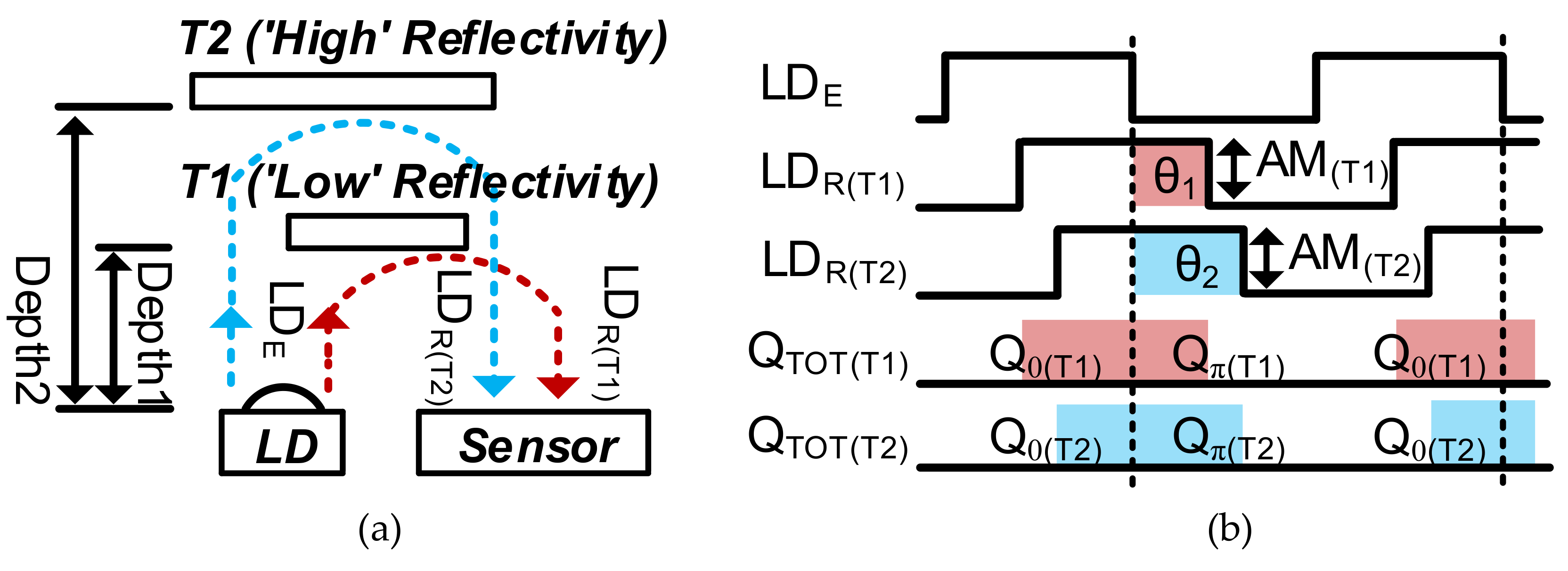
Figure 2 shows the operation principles of the proposed method for acquiring the depth frame difference. The main idea is that the change of Q_π/Q_TOT in successive frames is detected if the depth frame difference occurs. Because Q_TOT varies according to the reflectivity, as well as the distance, Q_TOT (and also Q_π) is linearly adjusted to the fixed reference first. Then, the depth frame difference can be detected by simply detecting the change in Q_π because the denominator Q_TOT was adjusted to the fixed reference. For illustration, we assumed a special case in which Targets 1 (T1) and 2 (T2) are present in the first and second frames, respectively, as shown in Figure 2a. The targets have different reflectivities and depths. We assumed this special case to show that the proposed scheme works regardless of the reflectivity of the objects. Assuming that the amplitude (AM_(T1)) of reflected light (LDR_(T1)) from T1 and the amplitude (AM_(T2)) of reflected light LDR_(T2) from T2 are equal, the total integrated charges Q_TOT(T1) and Q_TOT(T2) are the same, as shown in Figure 2c. In the illustration of Figure 2c, we describe the integrated charge at each sub-integration time T_SUB, where T_SUB is evenly divided over the whole integration time. The situation illustrated in Figure 2c can occur even with different distances, because of differences in reflectivity. In this case, we cannot detect the depth difference by just calculating the change in the light intensity (Q_TOT) even though Q_TOT varies according to the distance, because the Q_TOT values in successive frames are equal owing to reflectivity. However, using the proposed two-step comparison scheme, we can detect the depth difference for T1 and T2 without depth calculation in Equation (1) regardless of the Q_TOT values. Assuming that Q_TOT(T1) and Q_TOT(T2) are different, as shown in case 2 of Figure 2d, we equalize Q_TOT(T1) and Q_TOT(T2) using two phase operations. In the first phase, we integrate charges until Q_TOT reaches the fixed reference Q_REF for equalizing Q_TOT(T1) and Q_TOT(2). For this equalization process, the total integration time is divided into N sub-integration times (N·T_SUB). Each T_SUB consists of the modulation time (T_MOD) for accumulating photogenerated charge in the pixel and the accumulation time for accumulating the pixel output into the AM, as illustrated in detail in Section 4. Therefore, the total charges integrated in the pixel (Q_TOT(N·T_SUB)) can be expressed as follows:

$$Q_{TOT}\left(N·T_{SUB}\right)={\displaystyle \sum }_{T_{SUB}=0}^N{I}_{PIX}·T_{MOD},$$

(4)

where I_PIX represents the photocurrent in a pixel. At each T_SUB, Q_TOT is compared with Q_REF. The integration of Q_TOT is continued until the k-th T_SUB (k·T_SUB) that has a larger Q_TOT than Q_REF is reached. We can then obtain

$$A·Q_{TOT\left(T1\right)} = B·Q_{TOT\left(T2\right)} = Q_{REF},$$

(5)

where A and B are proportionality factors (PFs) based on the controlled integration time. This equalization process involves comparison in each T_SUB. We call this process the first comparison phase. In the second comparison phase, the values of A·Q_π(T1) and B·Q_π(T2) scaled with same PF used in the first comparison phase are compared. They have hte same PF because Q_π experiences the same controlled integration time (k·T_SUB) as Q_TOT. According to the adjusted integration in the first comparison phase, we already have A·Q_π(T1) and B·Q_π(T2). Because the denominator Q_TOT in Equation (1) is a constant in the first comparison phase, a simple comparison of the two Q_π values provides the same result as a comparison of the θ values. Therefore, we can effectively compare the ratios Q_π(T1)/Q_TOT(T1) and Q_π(T2)/Q_TOT(T2), where the reflectivity in both the numerator and denominator can be divided and cancelled. The Q_π(1) and Q_π(2) from Frames #1 and #2, respectively, are simply compared to determine whether a significant frame difference of the depth occurs, as follows:

$$\left|A·Q_{\pi \left(1\right)}-B·Q_{\pi \left(2\right)}\right|>Q_{th} \left(\mathrm{second} \mathrm{comparison}\right),$$

(6)

where Q_th is the threshold of the depth frame difference. Using this two-step comparison scheme, we can simply generate the depth frame difference without accessing the A/D-converted digital signal and calculating the ratio in the image signal processor. More significantly, the two-phase modulation is sufficient; the power-consuming (and slow) four-phase modulation is not necessary.

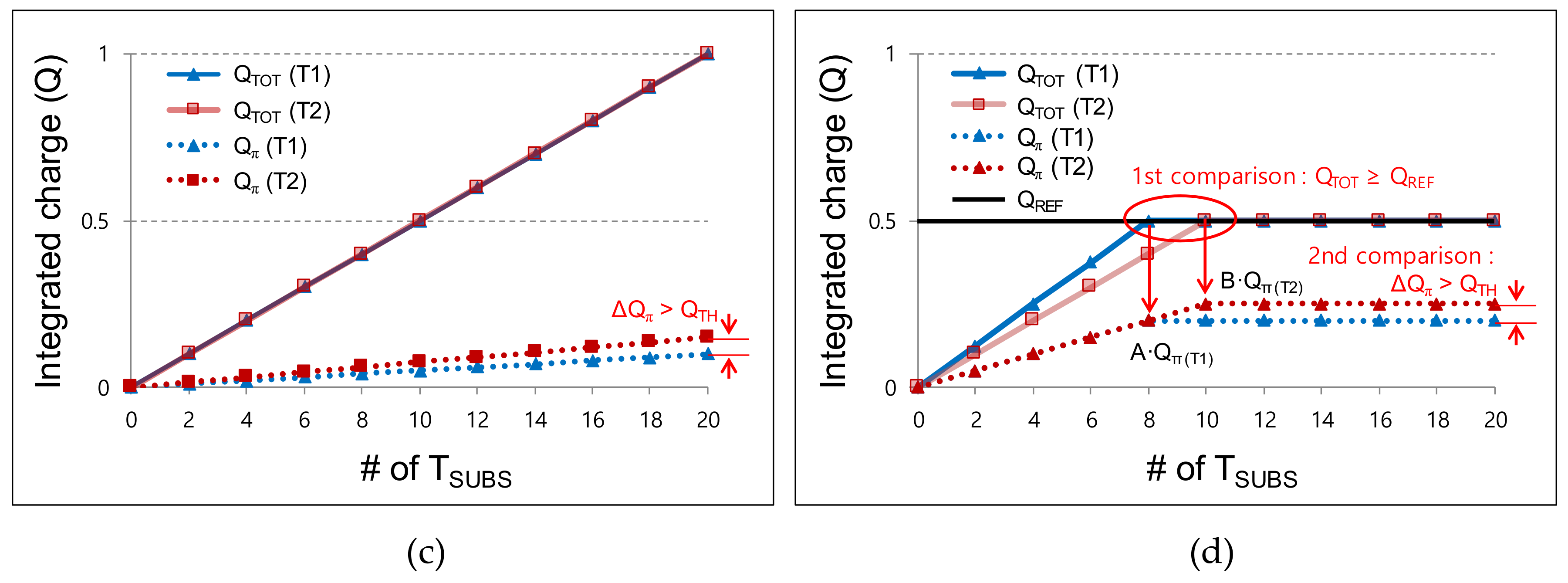
However, the proposed two-step comparison scheme can induce an error because the integrated charge decreases significantly along the distance, particularly for a short distance, as shown in Figure 3a. To illustrate this error, in Figure 3b, we assume that the Q_TOT(1) (marked with a blue line) of the first frame reaches Q_REF (= 0.5) at the second T_SUB and that the Q_TOT(2) of the second frame is exactly equal to Q_TOT(1). Additionally, we assume that the Q_π (marked with a blue dotted line) in both frames is half of the Q_TOT. In this case, no frame difference should be detected. However, if Q_TOT(2) is judged as a smaller value than Q_REF in the second T_SUB owing to noise, Q_TOT(2) is decided as 0.75 in the third T_SUB. In this case, Q_π(2) is 0.375 owing to the error, whereas Q_π(1) is 0.25. With this error (ΔQ_{π_err} = 0.125), if Q_TH is set as 0.1, the wrong frame difference (0.375 − 0.25 > 0.1) is detected, even though no frame difference occurs. In summary, Q_TOT can be integrated with one more T_SUB via random noise or quantization noise during the first comparison phase. This induces significant error, particularly at a short distance, because Q decreases significantly with an increase in the distance, as shown in Figure 3b.

To suppress this error, we must reduce the increment of Q in each T_SUB only for the short distance that induces significant error. This can be achieved by using the adaptive modulation time AF·T_MOD, where AF is an adaptive factor. Therefore, the decrement of Q is reduced at a short distance, whereas the decrement of Q is maintained (or increased) at a long distance. This effect is also shown in Figure 3a,b. The increment of Q (marked with a solid red line for Q_TOT and a dotted red line for Q_π) in each T_SUB is reduced by applying AF·T_MOD/N in each T_SUB, where AF < 1. Then, Q_π(2) is 0.28125 in the ninth T_SUB (owing to the error), and Q_π(1) (0.25·T_MOD) is 0.25 in the eighth T_SUB. The depth frame difference (0.28125 − 0.25 < 0.1) is not detected, as desired.

Figure 4a shows the integrated Q_TOT along the sub-integration time. Both the cases with and without the adaptive modulation time are shown. We reduce the increment of Q for the first 24 T_SUBs by applying a small AF (T_MOD/4), because the integrated Q_TOT generated from the short-distance objects has an abrupt transition along the distance. In this case, we have a large error that arises from the difference between the integrated Q_TOT (at the 24th T_SUB) and the reference Q_REF (Q_TOT − Q_REF). By reducing the T_MOD to T_MOD/4, the error can be suppressed owing to the decreased increment of Q. However, for the long-distance objects, the rate of the charge integration is too low because of the reduced T_MOD. Therefore, from the 25th T_SUB to the 128th T_SUB, we gradually increase the T_MOD from T_MOD/2 to 2·T_MOD such that the integration of the small Q reaches Q_REF. Note that only the first T_SUB has a large AF (14.25). This is because the large initial Q (integrated in the 1st T_SUB) accelerates the time to reach Q_REF within 128·T_SUB. Without a large AF in the first T_SUB, the integration of the small Q (in the case of long-distance objects) does not reach Q_REF.

Figure 4b illustrates the PF·ΔQ_π according to the distance. Using the proposed two-step comparison scheme, we acquire PF·Q_TOT first (first comparison) from N·T_SUB. The maximum Q_TOT is set as 1 for simple illustration, as shown in Figure 4a. As shown in Figure 3a, Q_TOT decreases proportionally to the square of the distance. Then, the PF·Q_TOT and the resultant PF·ΔQ_π are acquired according to the distance. We use ΔQ_π (= Q₀ + BG − Q_π − BG = Q₀ − Q_π) instead of Q_π in this calculation because we actually use ΔQ_π in the prototype chip in order to cancel out the background term BG, as in the four-phase modulation. As illustrated in Figure 4b, allocating a larger number of T_SUBs in a given frame suppresses the depth error because the T_SUB is the effective resolution that determines ΔQ_π. With the allocation of 128·T_SUB, the deviation in each T_SUB is suppressed. Without the adaptive modulation time, the error at the short distance (<1.5 m) is large (5.5% at maximum) because of the large decrement of Q_TOT. Using the adaptive modulation time shown in Figure 4a, the large decrement can be suppressed, and the error rate is reduced to 2.2% (maximum) over all distances. Thus, we can detect a frame difference larger than a certain threshold regardless of the distance of the objects. In this way, we suppress the nonlinearity-induced error using the adaptive modulation time and the allocation of 128·T_SUB.

In summary, the depth frame difference can be calculated in a single frame using the proposed two-step comparison scheme without generating four-phase images in two frames. Even though finite error in the depth calculation occurs owing to the quantization, the error can be suppressed below 2.2 % (<3.3 cm) by aid of the adaptive modulation. Because of the single-frame operation, no additional memory and power consumption overhead for the four-phase modulation are required. The detailed circuit implementation of the two-step comparison scheme is illustrated in the next section.

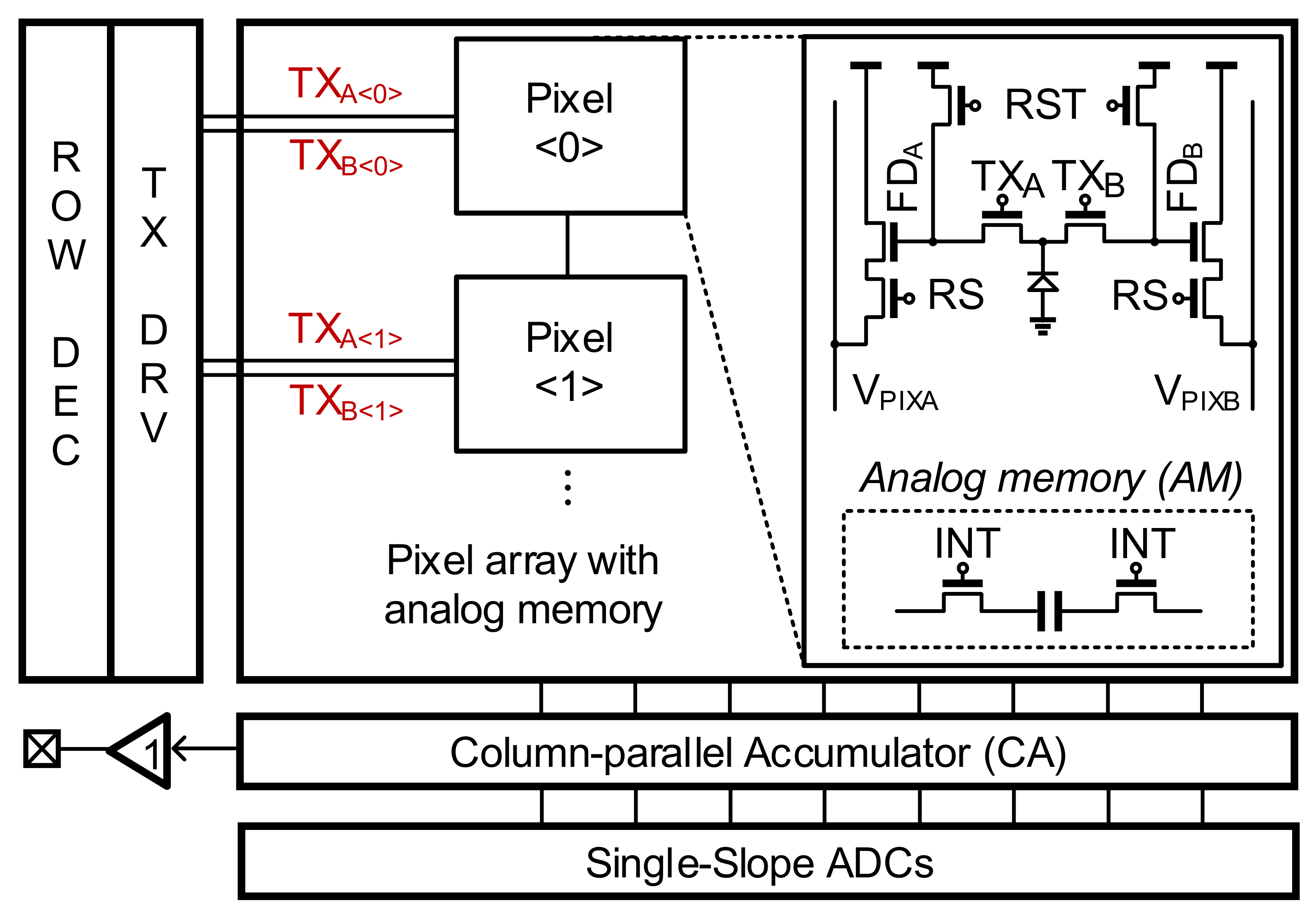
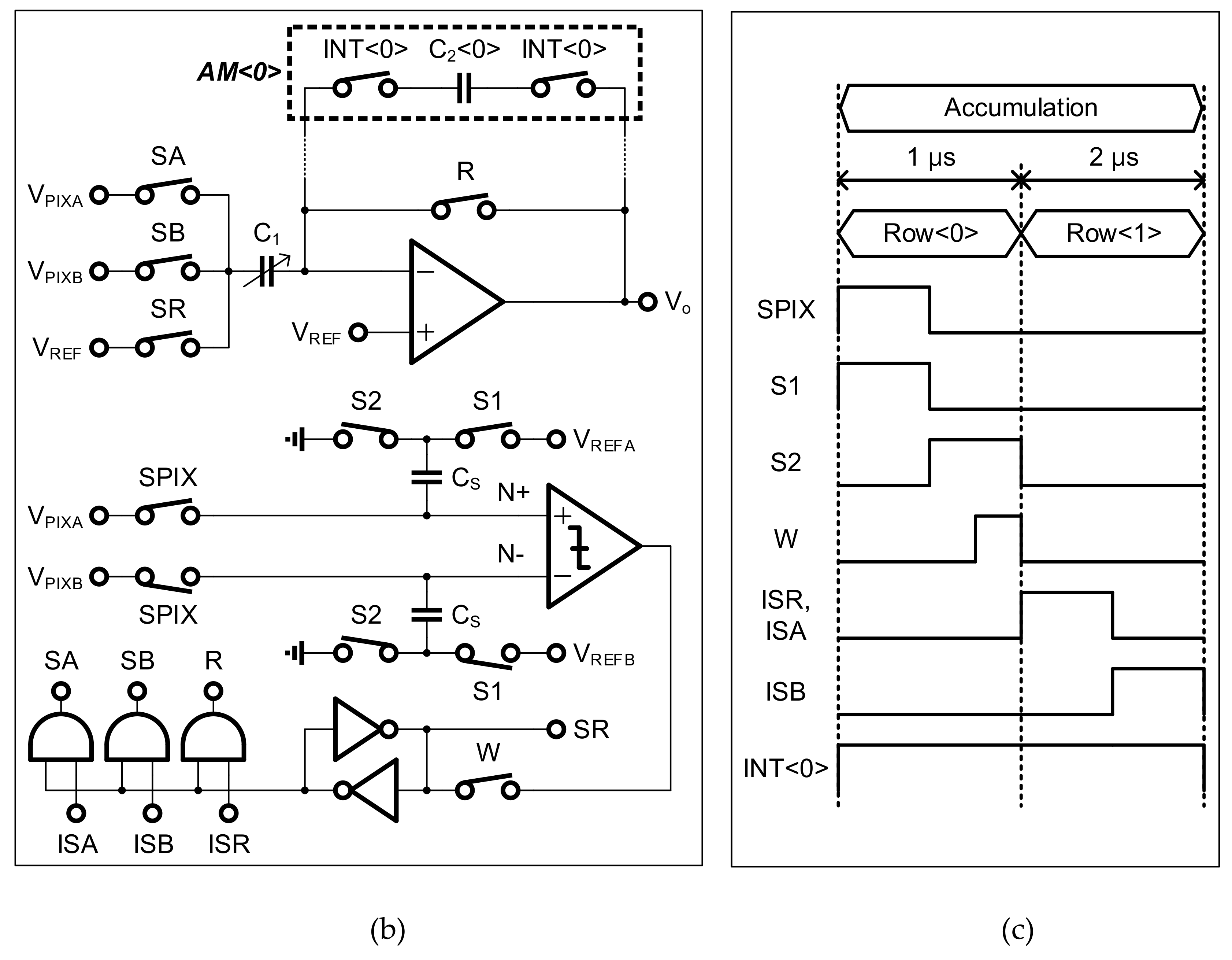
4. Circuit Implementation

Figure 5 shows the overall architecture of the proposed sensor chip. The sensor chip consists of an array of pixels with an over-pixel AM, a TX driver, and a row decoder for driving and selecting pixels, a column-parallel accumulator (CA) for accumulating charges from the pixels into the AM, and a unity-gain buffer for the output. The pixel consists of a PPD, two reset transistors (RST), two row-selection transistors (RS), two source follower transistors, and two electronic shutters (TX₀ and TX_π). Additionally, the AM (including one capacitor and two access transistors) is placed to store an intermediate Q during the integration time. After the overall operation is finished in a frame, this AM stores the acquired ΔQ_π in a given frame, which becomes the previous frame signal in the next frame.

The proposed two-step comparison scheme requires comparing the values of Q_TOT and Q_π. However, with strong ambient light, the DC offset BG is added, as indicated by Equation (2). Therefore, instead of acquiring Q_TOT and Q_π, we must obtain ΔQ_TOT = (Q_TOT + BG) − (0 + BG) and ΔQ_π = (Q₀ + BG) − (Q_π + BG) in a single frame. Both Q_π and ΔQ_π provide phase information according to the depth [2]. Therefore, the first comparison is performed as ΔQ_TOT > ΔQ_REF, and the second comparison is performed as |A·ΔQ_π(1) − B·ΔQ_π(2)| > ΔQ_TH.

For a two-step comparison scheme, we grouped two adjacent pixels. The pixel<0> generates ΔQ_TOT, and the pixel<1> generates ΔQ_π. As shown in Figure 6a, the modulation period of TX in pixel<1> is twice that of the even pixels, such that ΔQ_TOT is generated in a single frame. Each pixel has an AM, i.e., AM<0> to AM<1>. The ΔQ_π(1)s from Frame #1 are stored in AM<0>, and the ΔQ_π(2)s from Frame #2 are stored in AM<1>.

Figure 6b shows the CA circuit that accumulates the pixel output into the AM and reads the stored signal in the AM. The CA consists of an analog multiplexer, an amplifier, a static random-access memory (SRAM), and an input capacitor bank (C₁) for providing a high gain of >8. The comparator circuit that is originally used for the single-slope ADC is reused for the two-step comparison scheme. Additionally, the amplifier originally used for the column-parallel programmable-gain amplifier is reused for area efficiency.

The timing diagram of Figure 6a illustrates the operation in a single T_SUB in one frame. Each T_SUB consists of two operation phases: (1) modulation, and (2) accumulation and the first comparison. The detailed operation is as follows: the first phase is the modulation phase, where Q₀, Q_π, and Q_TOT are integrated in the floating-diffusion (FD) nodes of pixels by modulating the electronic shutters TX_A and TX_B. After the modulation phase, four signals (Q₀ + BG, Q_π + BG, Q_TOT + BG, BG) are generated. These signals are stored in the FD nodes FD_A and FD_B of the two pixels. The second phase is the accumulation and first comparison phase. In the second phase, the integrated ΔQ_TOT (from pixel<0>) until the current T_SUB and ΔQ_REF are compared. If ΔQ_TOT is larger than ΔQ_REF, ΔQ_π (from pixel<1>) is stored in the AM. In this case, ΔQ_π is no longer stored in the AM from the next T_SUB. Therefore, the ΔQ_π acquired when ΔQ_TOT reaches ΔQ_REF is preserved in the AM. When ΔQ_TOT is smaller than ΔQ_REF, ΔQ_π is still stored in the AM. However, in this case, a new ΔQ_π is stored in the AM in the next T_SUB. After 128∙T_SUB (= 1 frame), the ΔQ_π stored in the current frame and the ΔQ_π stored in the previous frame are accessed through the amplifier to be compared.

The circuit operation, along with a timing diagram, is shown in Figure 6c. At t₁, even pixels (row<0>) are selected. The switches SA and SAD are enabled. Then, two outputs of the source followers (V_PIXA and V_PIXB) are sampled on C_S. At this time, V_PIXA is V_RST − BG/C_FD, and V_PIXB is V_RST − (Q_TOT + BG)/C_FD. At t₂, the switch SB is enabled. Then, the comparator inputs N+ and N− experience voltage drops based on V_REFA and V_REFB. We set V_REFB as V_REFA + Q_REF/C_FD, such that the comparator compares Q_TOT with Q_REF. Therefore, if Q_TOT > Q_REF, the comparator generates an output of “1”. At t₃, the switch SE is enabled to store the comparator output in the SRAM. At t₄, odd pixels (row<1>) are selected. Additionally, AM<0> is selected by enabling the INT<0>. Then, the switches RINT and ISM1 are enabled. If the SRAM is storing “0”, the accumulation of ΔQ_π to the AM is required, because Q_TOT has not reached Q_REF yet. In this case, V_PIXA (= V_RST − (Q_π + BG)/C_FD) is sampled on C₁ for the accumulation. Simultaneously, the C₂ for AM<0> is reset by unity-gain feedback. If the SRAM is storing “0”, no accumulation of ΔQ_π is required, because Q_TOT already reached Q_REF in the previous T_SUB, and the final ΔQ_π is already stored in the AM. In this case, the reference voltage V_REF is sampled on C₁ instead of sampling the V_PIXA. By fixing the input as a constant V_REF, no accumulation is performed in the accumulator. Moreover, the AM is not reset, for preserving the stored ΔQ_π. At t₅, ISM2 is enabled for the accumulation. Simultaneously, V_PIXB (= V_RST − (Q₀ + BG)/C_FD) is input to the capacitor C₁. This accumulation is performed only when the SRAM is storing “1”. Finally, the output of the CA is

$$V_o=V_{REF}+\frac{C_1}{C_2}\frac{\left(Q_0-Q_{\pi }\right)}{C_{FD}}=V_{REF}+\frac{C_1}{C_2}\frac{\Delta Q_{\pi }}{C_{FD}}.$$

(7)

This operation is repeated during 128 sub-integration times. In this manner, ΔQ_π is stored in one AM (AM<0>) out of the two AMs in the first frame. The other AM (AM<1>) is used for storing the next frame signals. After 128·T_SUB, both the stored A·ΔQ_π(1) in AM<0> and B·ΔQ_π(2) in AM<1> are read out through the unity-gain buffer, which is used only for testing purposes, such that the second comparison of the values of |A·ΔQ_π(1) − B·ΔQ_π(2)| > ΔQ_TH can be performed in the external logic circuit. Even though we used the buffer circuit to read ΔQ_π and performed the second comparison off-chip for the purpose of characterization, the second comparison can be easily performed using the existing comparator of the single-slope ADC. It is noteworthy that the binary quantization in the second comparison is mainly for simple post processing, e.g., optic-flow estimation [6] or motion-triggered awakening [1] that use binary information of the frame difference. In the case that analog frame difference is required to generate accurate 3D motion vectors, A·ΔQ_π(1) − B·ΔQ_π(2) can be simply generated through an additional amplifier circuit that is similar as the one used in the column amplifier.

5. Experimental Results

A prototype chip was fabricated using a 90-nm BSI CIS process. The core size was 3.8 × 2.8 mm². The light source, which was composed of IR light-emitting diodes (LEDs), was modulated at 10 MHz with a power of 40 mW for each LED. This prototype chip was originally implemented to have a split pixel array for characterizing various PPDs and pixel layouts. The pixel split was performed in a row-by-row manner. To characterize the proposed two-step comparison scheme, we implemented the accumulator with comparison logic circuits only in one column, as shown in Figure 7. The output of the accumulator was read through the unity-gain buffer.

Table 1. Chip characteristics.

Parameter	Value
Process	90-nm BSI CMOS image sensor
Core size	3.8 × 2.8 mm2
Pixel size	8 × 8 μm2 (fill factor: 39%)
Frame rate	20 fps
Powers supply voltage	2.8 V (pixel), 1.8 V (analog), 1.2 V (digital)
Power consumption/ frame (per column)	4 μW (at 128 sub-integration times)
Power [μW]	8.8
Range	1–2.5 m
(De)modulation frequency	10 MHz
Light source	850-nm IR LED
Demodulation contrast	74%

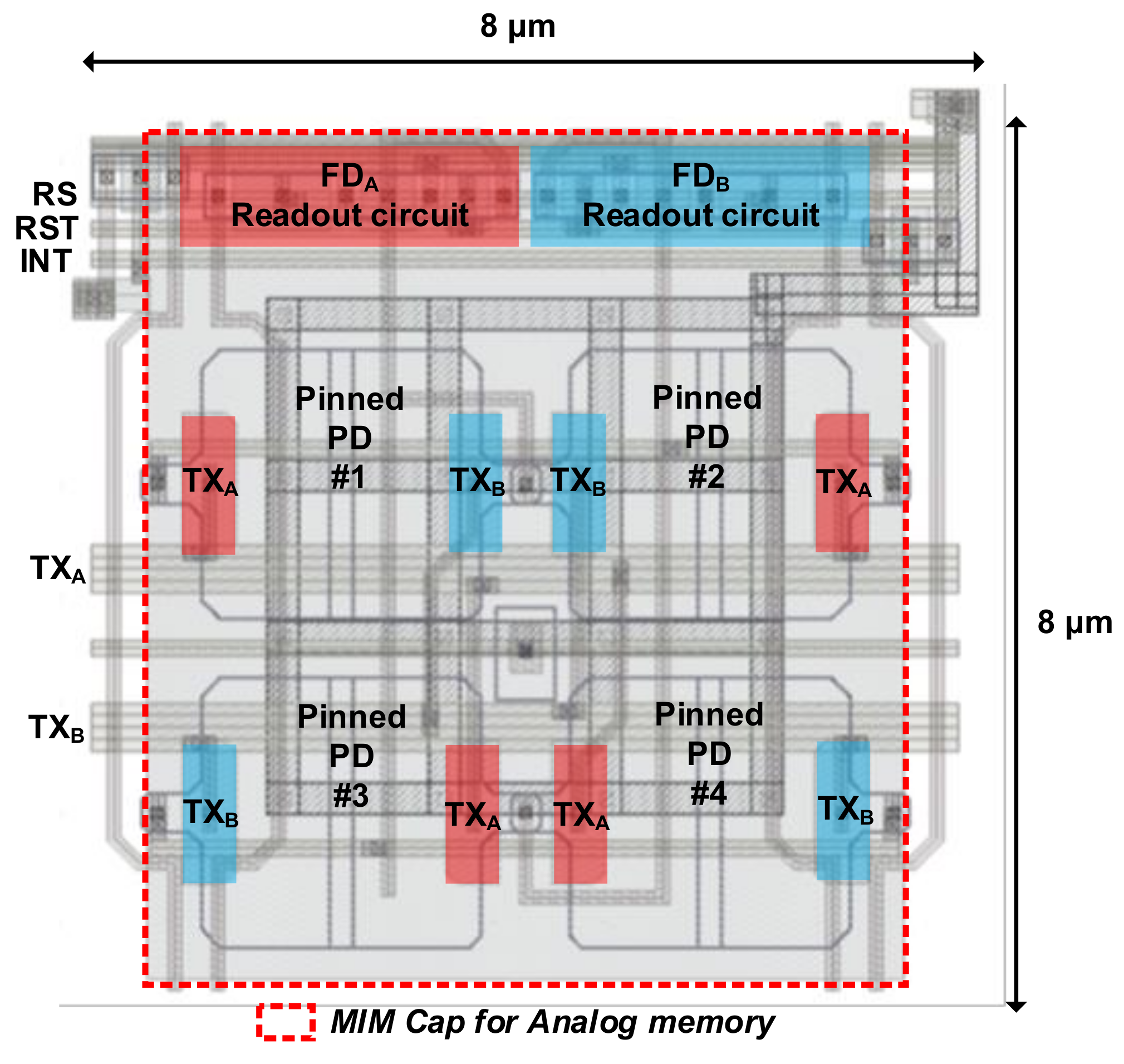
presents the chip characteristics. Figure 8 shows the pixel layout with an AM. To minimize the distance of charge transfer in the PPD within a short modulation period, the size of the PPD should be small enough while guaranteeing high sensitivity. Therefore, four small PPDs were shared to provide higher sensitivity [15]. The size of each PPD was 2.3 × 2.3 μm². Because the AM was implemented with an MIM capacitor using the BSI CIS process, the AM on the front side did not degrade the sensitivity. In the proposed two-step comparison scheme, the AM must be accessed 128 times using a column amplifier. However, the column amplifier was designed with a low bias current of 2 μA for power-efficient operation. The average power consumption in a column was measured as 4 μW at 20 fps, which is even smaller than the power consumption in the column-parallel ADC of conventional image sensors [16,17,18].

As illustrated in Figure 6b, the AM operates as a feedback capacitor when ΔQ_π is read out through the CA. Because of the gain amplification of 8 in the CA, the capacitance variation of the AM (C₁) affects gain term (C₁/C₂) in Equation (7) and induces gain fixed-pattern noise (FPN) in a column. Because the gain error from the gain FPN provides an error in the second comparison that compares the amplified ΔQ_π, the result of the second comparison becomes erroneous. In order to suppress the gain FPN, the AM should be designed to have enough size such that mismatch between rows (and also between columns) are suppressed. The size of the MIM capacitor was designed to be 6.2 × 7 μm². The capacitance was 278 fF. In order to prove that the gain FPN does not provide significant error if enough capacitance is used, we measured the gain FPN in the test column. The measurement result shows 0.42% FPN that corresponds to an error of the depth frame difference below 0.1 cm.

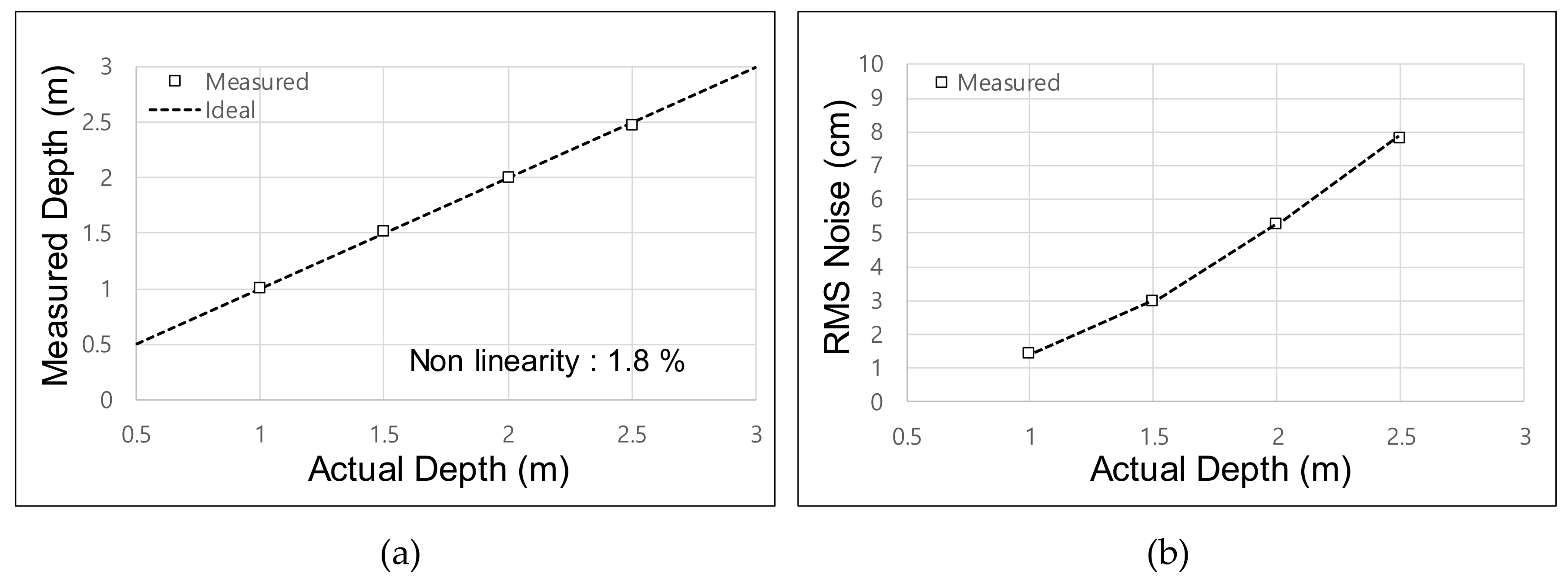
Figure 9a shows the measured depth over the range of 1–2.5 m. For the four-phase operation of depth acquisition, we had to acquire ΔQ_π in the first frame and ΔQ_π/2 in the second frame. Therefore, the effective frame rate was set as 10 fps for the depth-acquisition experiment. The measured nonlinearity was 1.8%. The minimum root-mean-square (RMS) noise was measured as 1.42 cm at a distance of 1 m, as shown in Figure 9b. The frame rate of 10 fps was used only for the depth acquisition using the four-phase operation. The depth frame difference using the proposed two-step comparison scheme was measured at 20 fps because only a single frame of integration was needed to acquire ΔQ. We allocated a modulation time of 25 ms for all 128 sub-integration times. Reducing the modulation time enhances the frame rate but degrades the depth accuracy. The frame rate is expected to be improved by optimizing the responsivity of the PPD in further research.

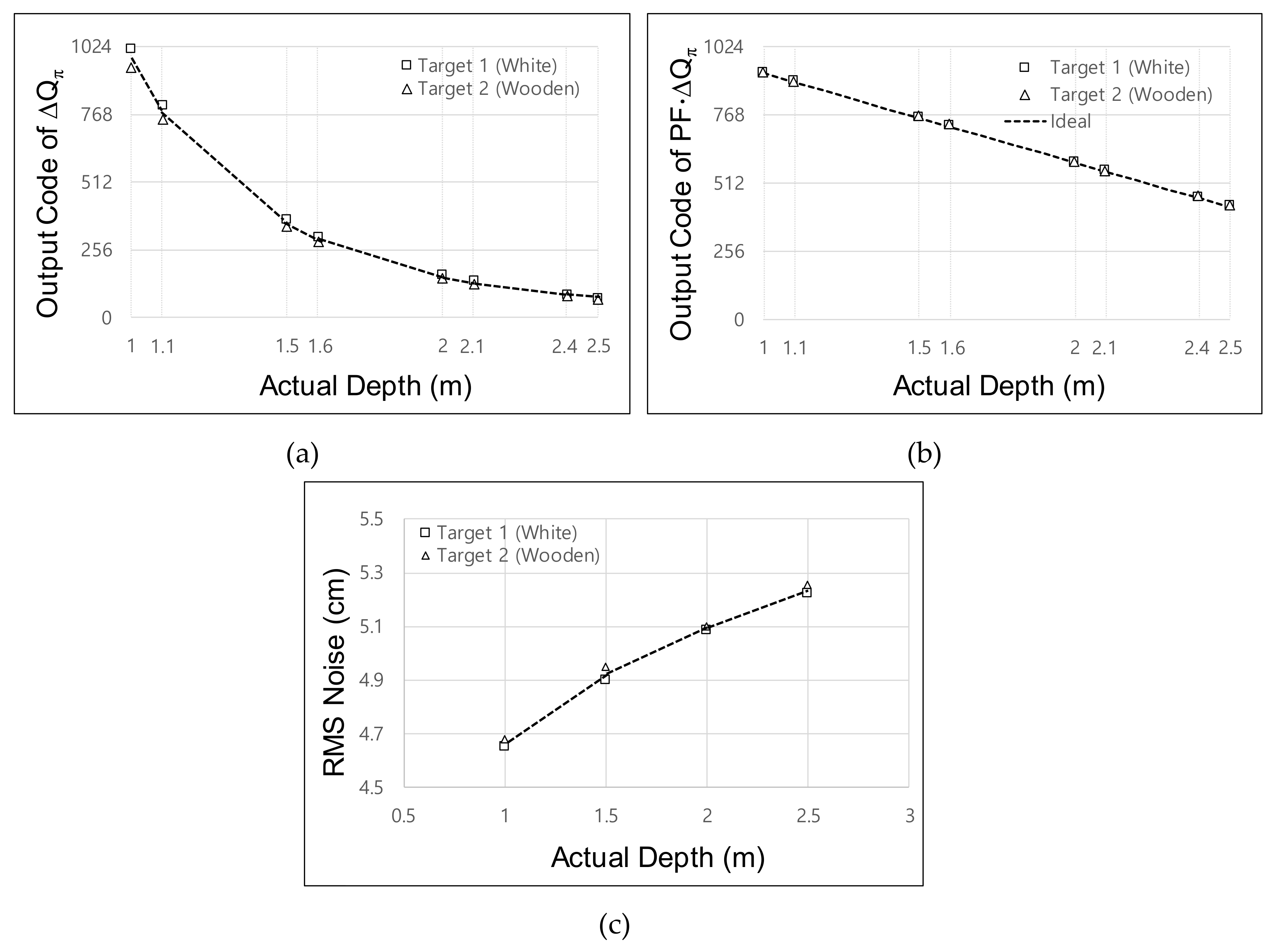
Figure 10 shows the measured ΔQ_π for acquisition of the depth frame difference. To prove that the depth frame difference can be reliably acquired regardless of the reflectivity, we measured two target objects with different reflectivities. As shown in Figure 10a, ΔQ_π had a nonlinear response without the application of the two-step comparison scheme. This measured curve is similar to the curve illustrated in Figure 3a. Therefore, the accurate depth frame difference could not be detected, because even a small depth difference provided an abrupt change of ΔQ_π at a short distance, whereas a large depth difference was needed to provide a sufficient change of ΔQ_π at a long distance. Moreover, differences in reflectivity induced the variation of ΔQ_π. Figure 10b shows the ΔQ_π measured using the two-step comparison scheme. With this scheme, the output PF·ΔQ_π exhibited a linear response regardless of the reflectivity. The maximum relative error between the ideal PF·ΔQ_π and the measured PF·ΔQ_π was 1.5% at a distance of 2.5 m. Figure 10c shows the RMS noise of the ΔQ_π. Considering that the RMS error of ΔQ_π can be increased by up to 5.25 cm at a 2.5-m distance, the RMS error of the depth frame difference ΔQ_π(1) − ΔQ_π(2) was <10 cm (= $\sqrt{{5.25}^2+{5.25}^2}$). Thus, the targeted resolution of the depth frame difference was 7.4 cm. In the experiment, the location of the object was adjusted in increments of 10 cm from a distance of 1 m to 2.5 m. It is noteworthy that the RMS error of ΔQ_π is quite constant over the whole range of distances, whereas the RMS error of the depth measured using the conventional four-phase modulation increases along with the distance. This is because the charge is integrated up to the Q_REF in the two-step comparison scheme, where Q_REF cannot be set as a high value considering the maximum range of the distance. Therefore, the two-step comparison scheme provides more error in the short range, whereas it provides a similar error in the long range compared with the four-phase modulation scheme. Even though the two-step comparison scheme using the single reference Q_REF provides constant error under 7.4 cm in the prototype sensor, we expect that the error can be further suppressed by using dual references, i.e., using high Q_REF1 for short range and low Q_REF2 for long range such that a small error can be achieved in the short range. This dual reference can be implemented spatially (implemented in dual pixels) or temporally (implemented in dual frames).

Figure 11 shows the testing environment and captured images from the fabricated sensor. As shown in Figure 11a, we used the hardboard with different reflectivities as a target object. Figure 11b shows the IR image of ΔQ_π without the two-step comparison scheme. As illustrated in Figure 10a, output values are different owing to the reflectivity. The depth image using conventional four-phase modulation scheme is also shown in Figure 11c. No differences between reflectivities were measured, as expected. Note that the images have row patterns because the pixel split with slightly different layout was performed in a row-by-row manner for characterization purposes.

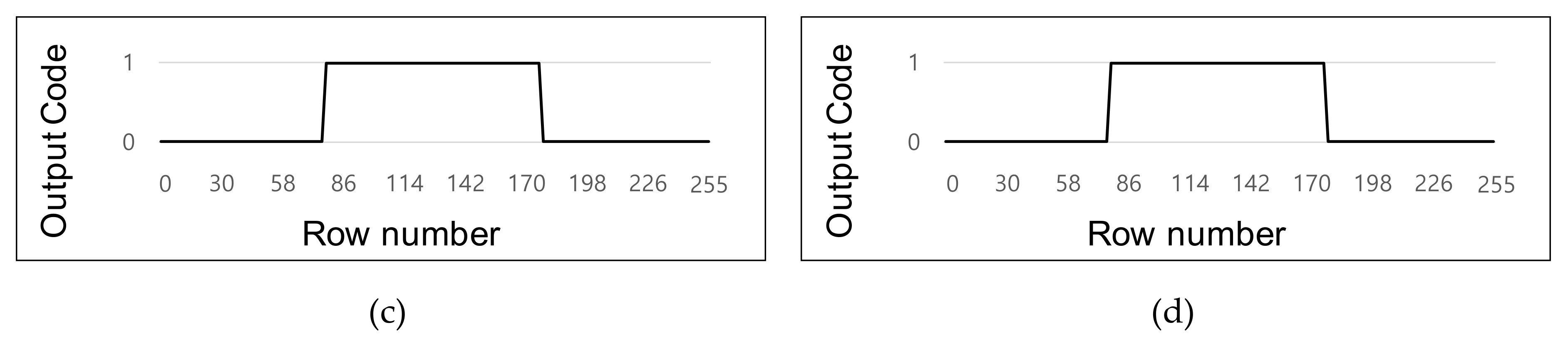
Figure 12a,b show the line images of the depth frame difference that were generated from the test column with application of the four-phase modulation scheme and the proposed two-step comparison scheme, respectively. Figure 12c,d show the result of binary quantization. The threshold of the binary detection was set as 10 cm. In both results, no detection error was found regardless of the reflectivity.

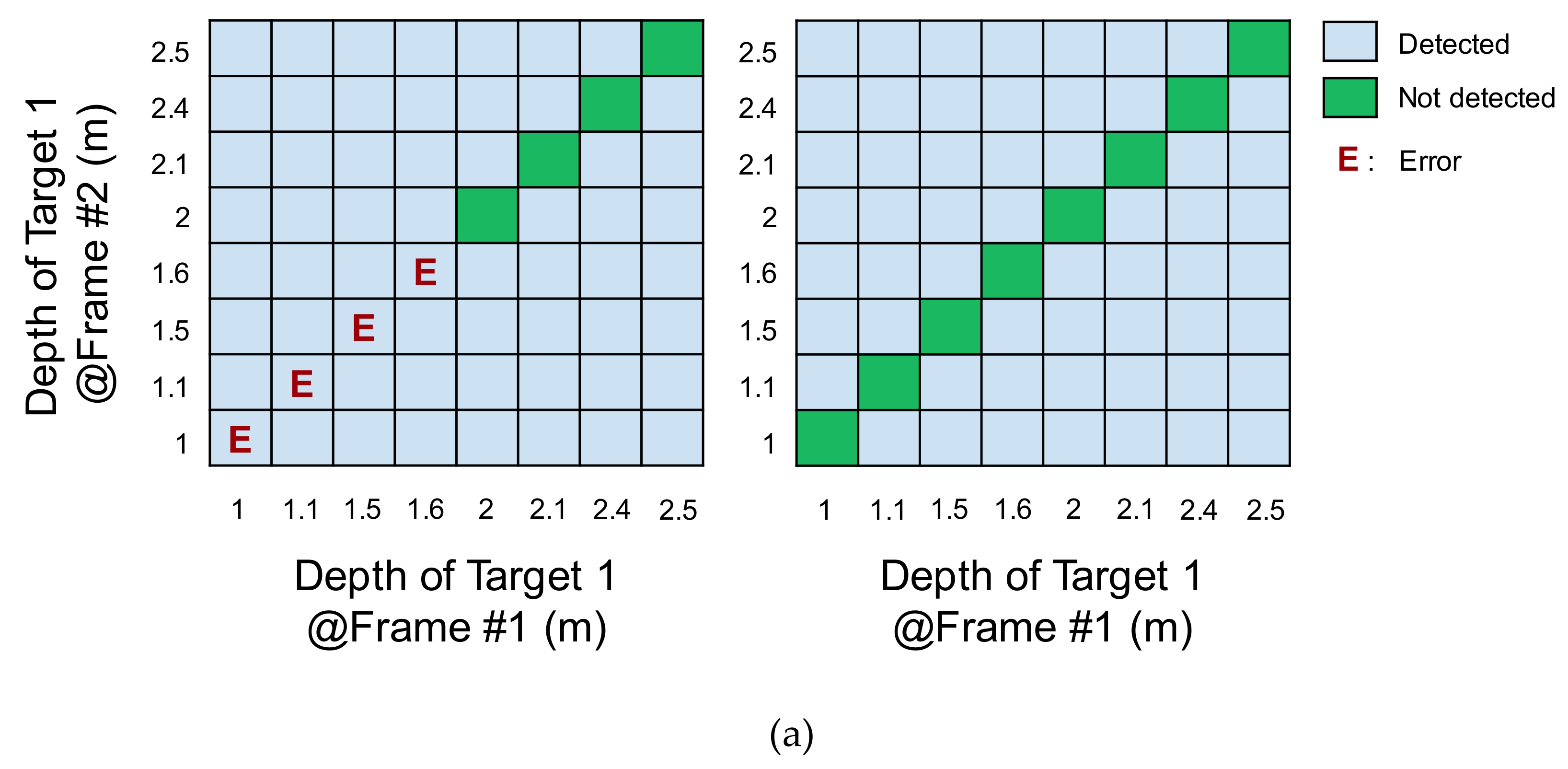
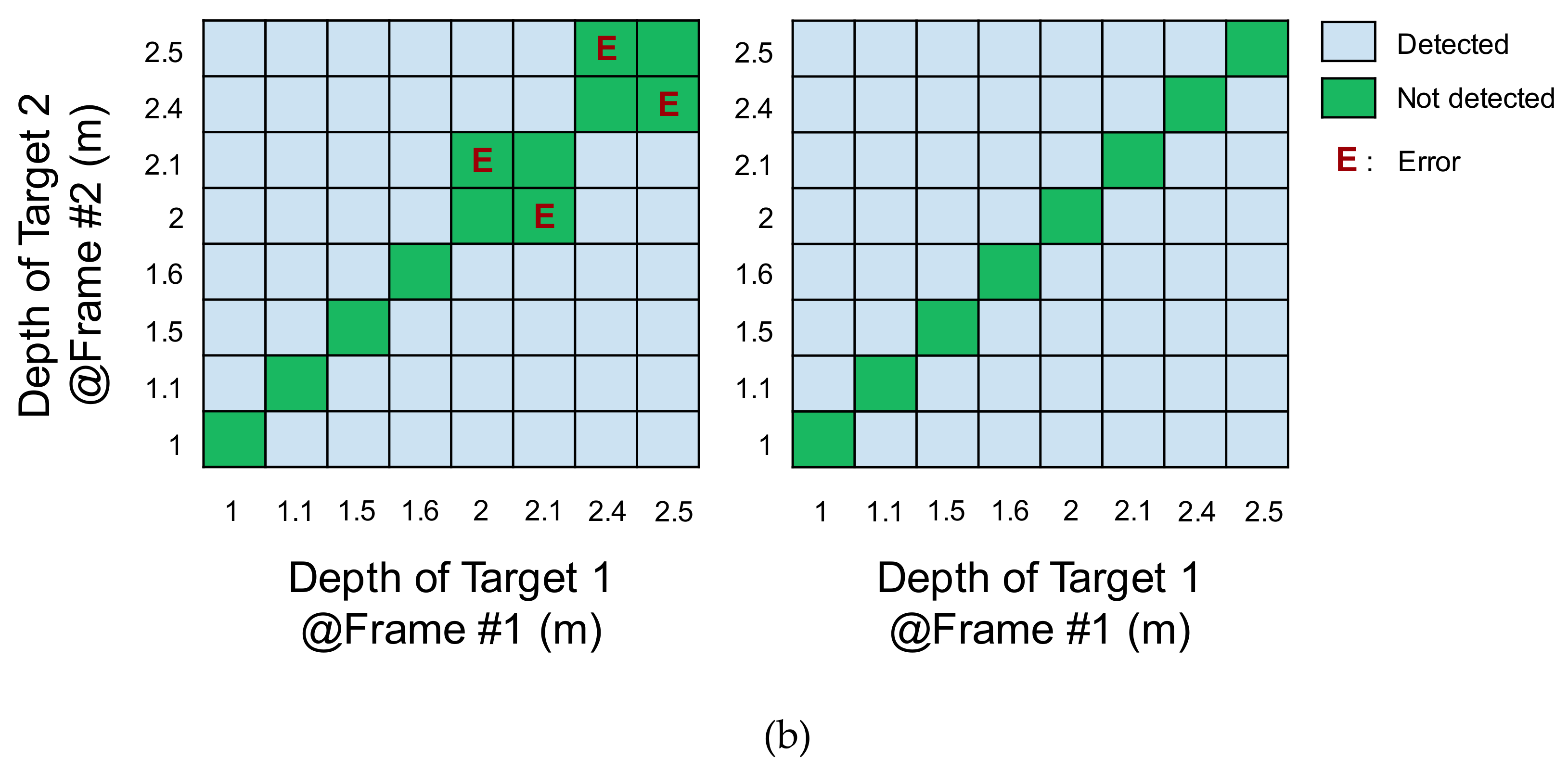
Figure 13 summarizes the result for the depth frame difference. Without the two-step comparison scheme, the frame difference was not detected in a significant portion of the range. Moreover, the detection results exhibited differences due to the different reflectivities. With the two-step comparison scheme, the frame difference was successfully detected in the entire range for both target objects with different reflectivities.

Table 2. Comparison of conventional depth sensors with a four-phase modulation scheme.

Parameter	[19], JSSC 2018	[20], TCAS I 2019	[13], JSSC 2014	This Work
				4 Phase Operation	2 Step Comparison Operation
Process	90 nm	350 nm	110 nm	90 nm
Demodulation Frequency	100 MHz	5 MHz	12.5 MHz	10 MHz
Demodulation contrast	85%	64%	50%	74%
Pixel	10 × 10 μm2	48 × 48 μm2	5.9 × 5.9 μm2	8 × 8 μm2
Fill factor	>80% (w/microlens)	17.40%	24%	39%
Range	-	0.5 m ~ 2 m	0.75 m ~ 4 m	1 m ~ 2.5 m
Integrated depth frame difference	×	×	×	×	○
Resolution	320 × 240	24 × 24	84 × 64	336 × 256	1 × 128
Frame-rate	-	100	10	10	20
External memory	-	-	-	○	×
Image Signal Processor	-	-	-	○	×
Illumination power	-	500 mW	650 μW/cm2 @ 1m	240 mW	120 mW

shows a comparison of conventional depth sensors with a four-phase modulation scheme. Regarding the performance of the depth sensor itself, our prototype sensor includes non-optimized pixels in terms of the demodulation contrast, modulation frequency, and so on. However, with a given pixel, the proposed two-step comparison scheme offers three advantages to generate on-chip depth frame difference compared with the conventional four-phase modulation scheme. Firstly, the frame rate can be doubled. In order to calculate the depth (D) using a four-phase modulation scheme, we have to acquire four signals Q₀, Q_π, Q_π/2, and Q_3π/2 in two frames. For calculating the depth frame difference, four frames of images are required. Therefore, the frame rate is reduced by half compared with the proposed two-step comparison scheme. This is disadvantageous because of motion blur for detecting moving objects. Secondly, memory requirement is reduced by half. In each frame of the depth acquisition with the four-phase modulation, two delta charges (ΔQ_π and ΔQ_π/2) should be stored in the frame memory in order to calculate the depth. Therefore, we need two 10-bit frame memories per pixel to store ΔQ₀ and ΔQ_π/2. The two-step comparison scheme reduces the requirement into a single 10-bit frame memory that stores only ΔQ_π. Moreover, we used the over-pixel MIM capacitor as a frame memory without any area overhead. Thirdly, power consumption can be significantly saved. For the four-phase modulation, both the light source (LD) and pixels should be modulated with high frequency over 10 MHz in two frames. This modulation power that occurs in the two-frame modulation can be saved by the single-frame modulation of the two-step comparison scheme. In summary, the proposed depth sensor can provide both power and area efficiency while providing sufficient resolution of the depth frame difference; thus, the sensor is applicable to gesture sensors, object trackers, motion-triggered surveillance, vacuum robot navigators, etc.

6. Conclusions

An iTOF depth sensor with integrated circuits that detects the depth frame difference was proposed. To detect the accurate difference of the depth in successive frames regardless of the reflectivity, we proposed a two-step comparison scheme with an amplifier-based accumulator and an over-pixel AM. To suppress the error arising from the nonlinear response of light-dependent charges, we used adaptive modulation times and 128 sub-integration times. According to experimental results, a 10-cm depth frame difference was successfully detected at a 2.5-m distance with 3% relative error according to the difference in the reflectivity. Owing to the single-frame operation, the measured power consumption was 10.7 μW for each column, and the power consumption of the modulation driver circuits was 6.7 μW for each column. Additionally, compact implementation of <3.8 × 2.8 mm² was possible without external frame memories. Therefore, the proposed iTOF sensor can be utilized in a variety of applications, including surveillance, gesture recognition, object tracking, and navigation.