Abstract
In this research, the dynamic walking of a legged robot in underwater environments is proposed. For this goal, the underwater zero moment point (Uzmp) is proposed in order to generate the trajectory of the centre of the mass of the robot. Also, the underwater zero moment point auxiliary (Uzmp aux.) is employed to stabilize the balance of the robot before it undergoes any external perturbations. The concept demonstration of a legged robot with hydraulic actuators is developed. Moreover, the control that was used is described and the hydrodynamic variables of the robot are determined. The results demonstrate the validity of the concepts that are proposed in this article, and the dynamic walking of the legged robot in an underwater environment is successfully demonstrated.
1. Introduction
As oceans occupy a huge part of the Earth [1], submarine robots are under constant development [2,3,4] for exploration, construction, mining and even aquaculture. However, the constant movement of the water causes instability in such robots. For this reason, legged robots are proposed as an alternative to achieve more stable exploration in an underwater environment.
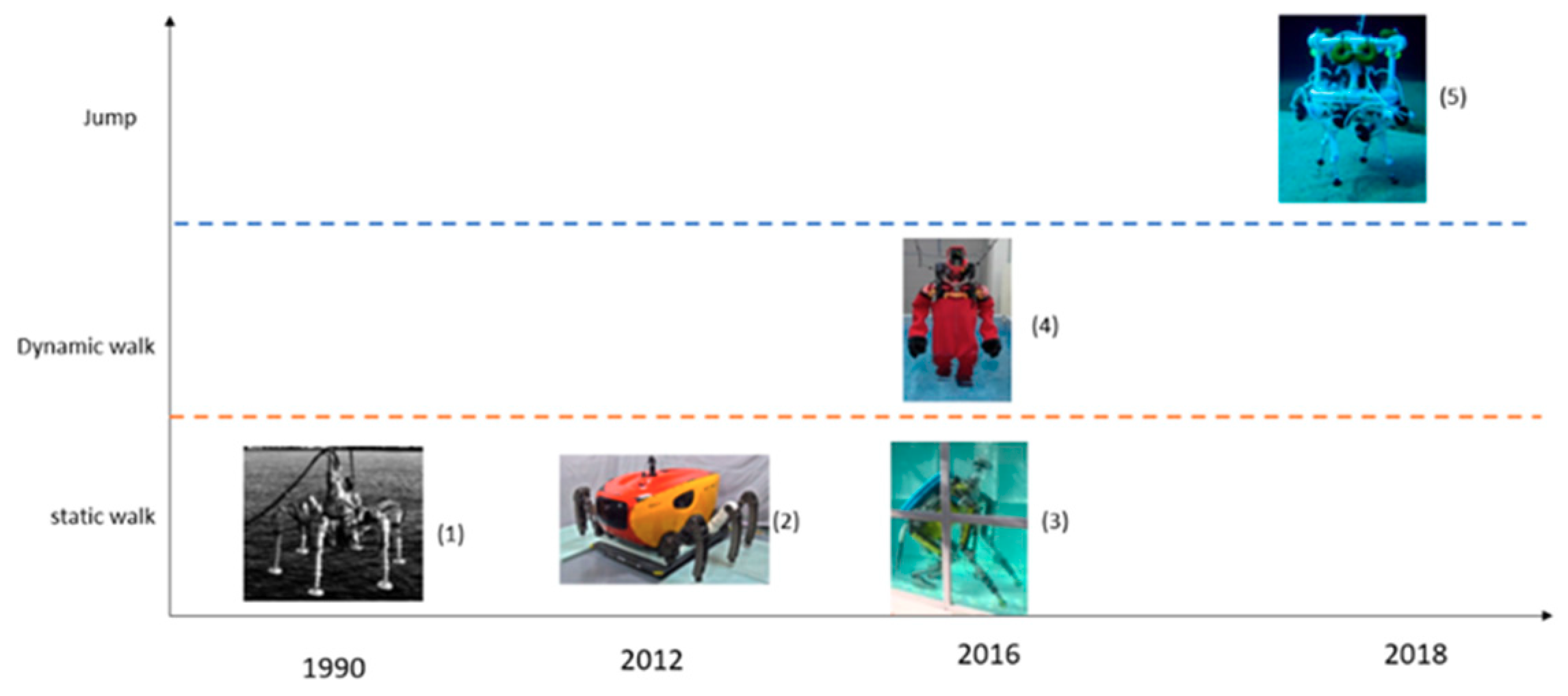
To better understand the contribution of this article, Figure 1 shows the development of underwater locomotion, wherein the vertical axis indicates the type of locomotion (static walking, dynamic walking, jumping), and the horizontal axis shows the year of publication of these developments.
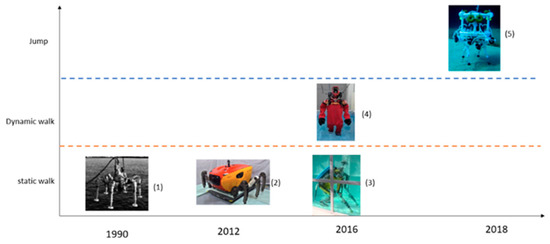
Figure 1.
Development of underwater locomotion, where the locomotion types are represented on the vertical axis, and the year in which they were developed on the horizontal axis.
Concerning static walking, which is based on a centre of mass that is within the support polygon, you can see three important developments for underwater environments: (1) a six-legged underwater robot proposed by the researchers Junichi et al. [5]; (2) the Crabster CR200 robot, also with six legs, but with a more hydrodynamic structure [6,7,8]; and (3) a quadruped, humanoid robot proposed by researchers Roque Saltarén et al. [9].
On the concept of dynamic walking, there has been very little development. Yuta Kojio et al. [10] proposed the dynamic walking of a semi-submerged robot, as observed in (4). Being semi-submerged, the centre of mass is out of the water, so they did not make variations to the zero moment point. Moreover, hydrodynamic variables such as hydrodynamic mass are not considered. However, as noted in our investigation, this has great relevance in underwater dynamic walking.
In regard to jumping, the robot SILVER (5) was proposed by researchers Giacomo Picardi et al. [11,12]. This robot was designed with the aim of jumping in underwater environments. The interesting thing about their research is that they proposed the U-SLIP model (Underwater Spring Loaded Inverted Pendulum), a spring–mass model, which allows the development of jump control in underwater environments.
Noting the lack of development in the field of underwater walking dynamics, in this article the dynamic walking of an underwater legged robot is proposed. In order to reach this goal, a new concept is introduced: the underwater zero moment point (Uzmp). This is used to generate the centre of mass trajectory in such way that the robot can keep balance in the walking process. Additionally, knowing that underwater environments are constantly disturbed by the movement of water, the underwater zero moment point auxiliary (Uzmp aux.) is proposed. This is used to generate each step of the robot for stabilization in the event of water disturbance.
For the demonstration of the proposed concepts, a prototype of a planar bipedal robot was developed with a hydraulic actuator and a mechanical sensor that measures the velocity of the fluid relative to the centre of mass of the robot. The theoretical foundation and experimental validation of the sensor are found in [13,14].
2. Materials and Methods
2.1. Underwater Inverted Pendulum (UIP)
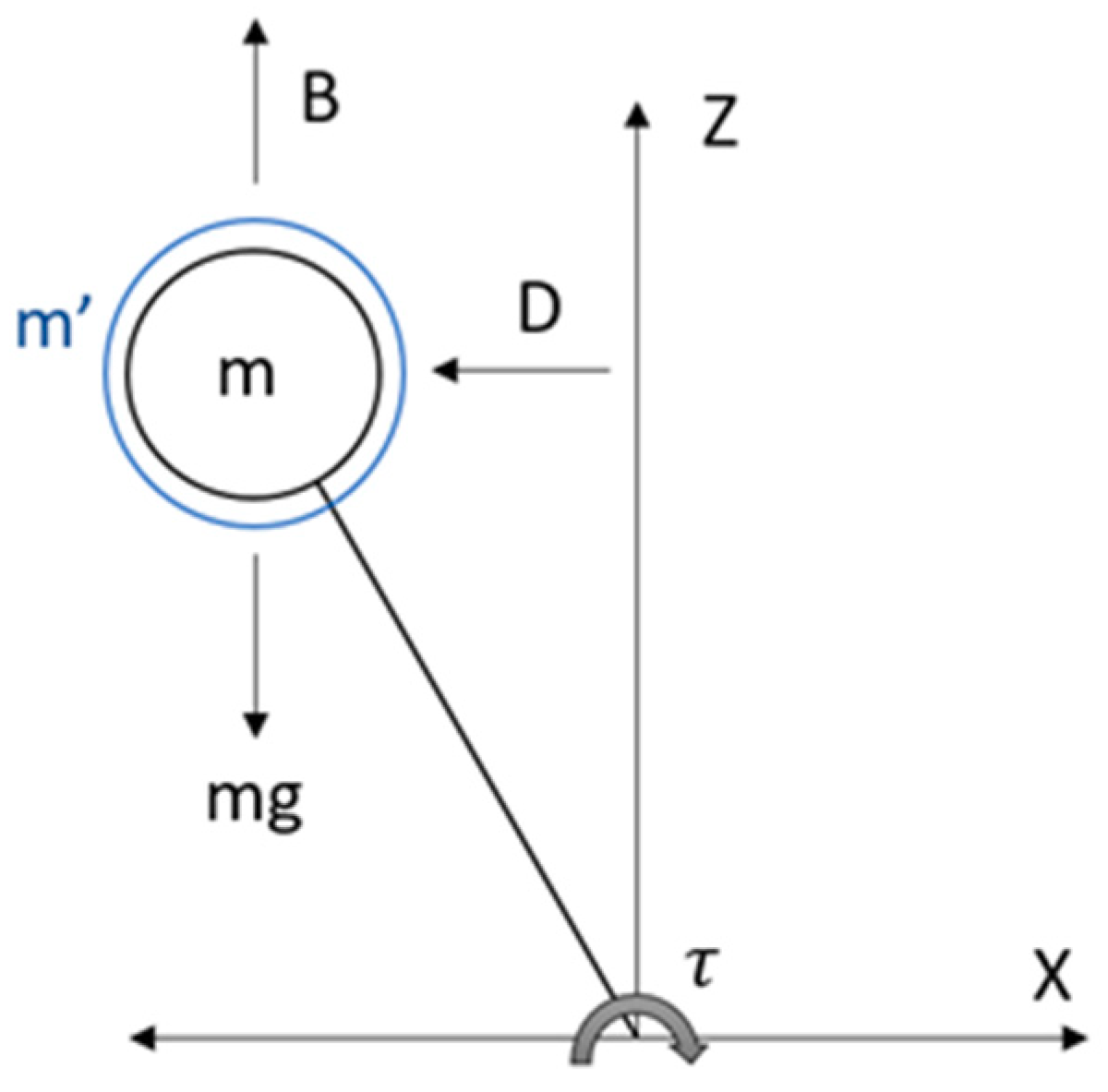
Figure 2 shows the Underwater Inverted Pendulum (UIP) model. It can be seen that the forces that affect a pendulum underwater are weight (mg), buoyancy (B), hydrodynamic mass (m’) and hydrodynamic damping (D).
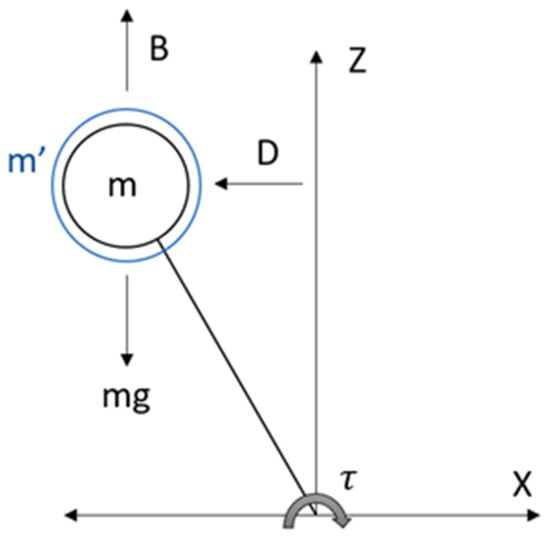
Figure 2.
Inverted pendulum model in an underwater environment. Here, m’ is the hydrodynamic mass of the water, m is the mass of the robot trunk, D is the hydraulic damping force, mg is the weight, B is the buoyancy of the body and τ is the resulting torque.
2.1.1. Simplification of Buoyant Force
The fluids generate a pushing force. The resultant force between the weight and that force can be resolved using [15]
where is the resulting force due to buoyancy, is the mass of the body, is the gravity, is the density of the fluid and V is the volume of the body. Clearing mass and gravity, we obtain
where is the density of the body. We can see that the relationship between the densities is a constant. Hence, to simplify the Equation, it can be replaced by a constant in such a way that the resulting force is expressed as
2.1.2. Hydrodynamic Damping
Hydrodynamic damping depends on two variables—linear damping and quadratic damping—as shown in the following equation [16,17].
where is the velocity of the centre of mass, is the constant of the linear damping, and is the constant of quadratic damping.
Applying the sum of moments in the pendulum, we obtain the following.
Clearing , we obtain the Underwater Inverted Pendulum model:
where is the acceleration of the centre of mass, is the velocity, and is its position, the mass of the pendulum, is its height, is the hydrodynamic mass of the pendulum, is the constant of the quadratic damping, and is the constant of the linear damping. Lastly, is the torque generated at the point of support.
2.2. Underwater Zero Moment Point
The torque generated in the Underwater Inverted Pendulum must be equal to the torque generated by the location, as shown in Equation (7).
Therefore, replacing Equation (7) in Equation (6), we obtain the underwater zero moment point as follows
Walking Pattern Generation
For the generation of the walking path, the Kajita method [18] with a model predictive control (MPC) should be used. To use this method, it is first necessary to linearize the of Equation (8), obtaining the following.
where is the constant linearization velocity at which the centre of mass moves.
Let us define a new variable as the input of Equation (9),
and the state space,
For the output matrix, it is necessary to use Equation (9).
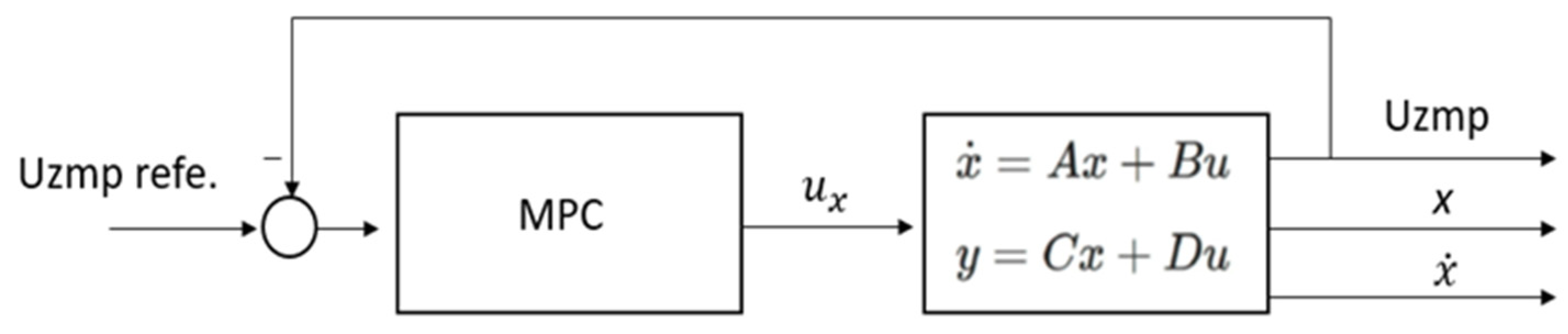
In this way, it is possible to obtain the output variables , , and . Finally, a predictive control was used, and the position of the centre of mass (x) and its velocity () were obtained, as seen in Figure 3.
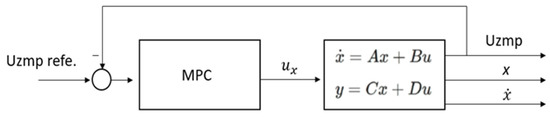
Figure 3.
Model Predictive control for the calculation of the position and velocity of the centre of mass.
2.3. Reaction Step for Balance Recovery
Underwater environments are subject to constant disturbances, such as waves, currents, etc. For this reason, it is important to implement an underwater zero moment point auxiliary () so as to compensate the balance of the robot.
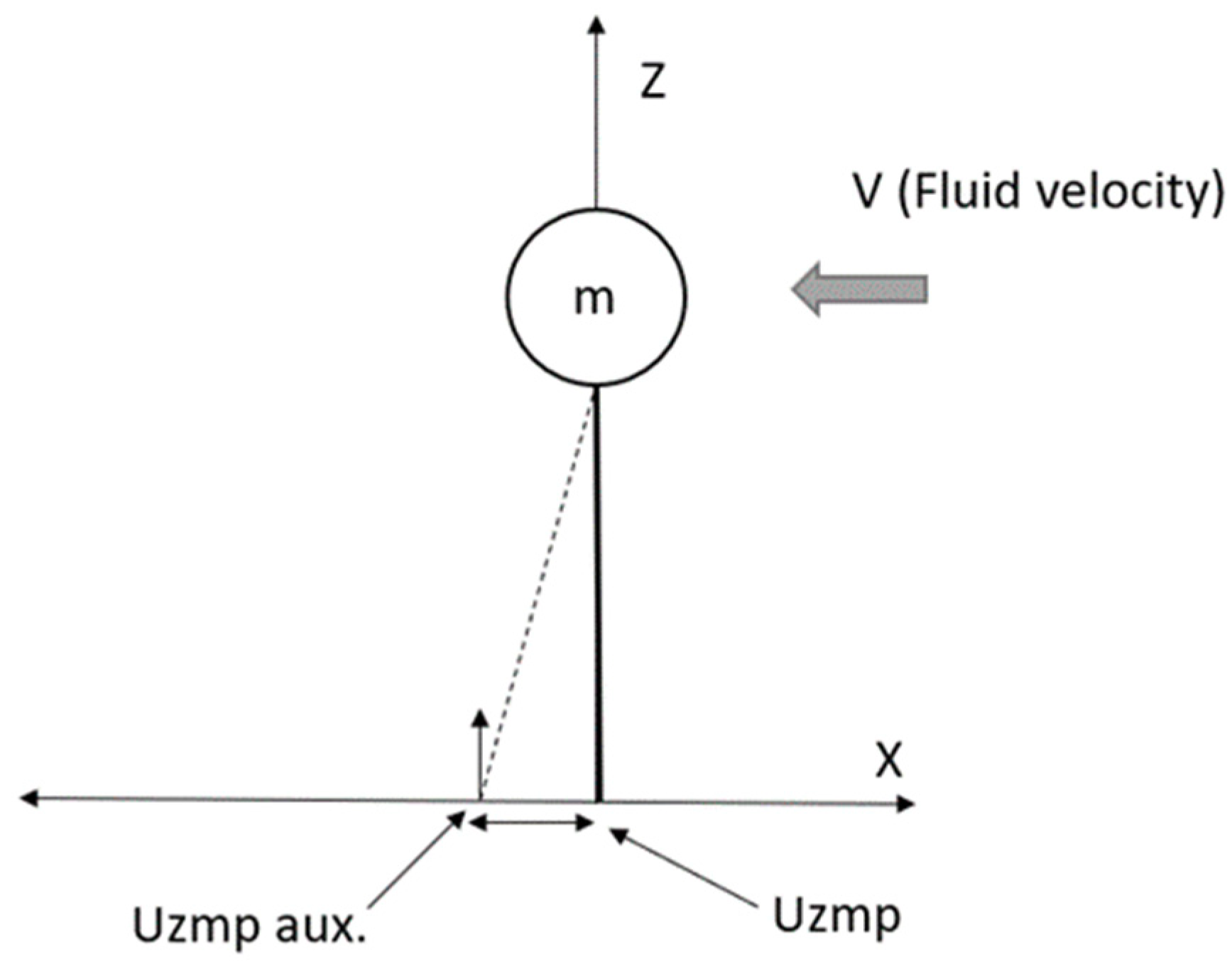
Figure 4 shows the inverted underwater pendulum, this time with the fluid in motion (V).
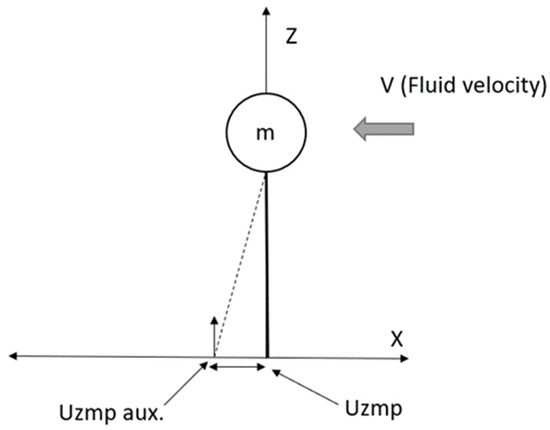
Figure 4.
Displacement of the Uzmp when the inverted pendulum is disturbed by the movement of the fluid (V).
Figure 4 shows the displacement, due to the fluid disturbance, this variation is defined by the following Equation;
Clearing (auxiliary underwater zero moment point), we obtain
where is the fluid velocity, which is measured by the mechanical sensor of the robot. When this variable is measured during the first 0.5 s, the maximum value is used to generate the reference.
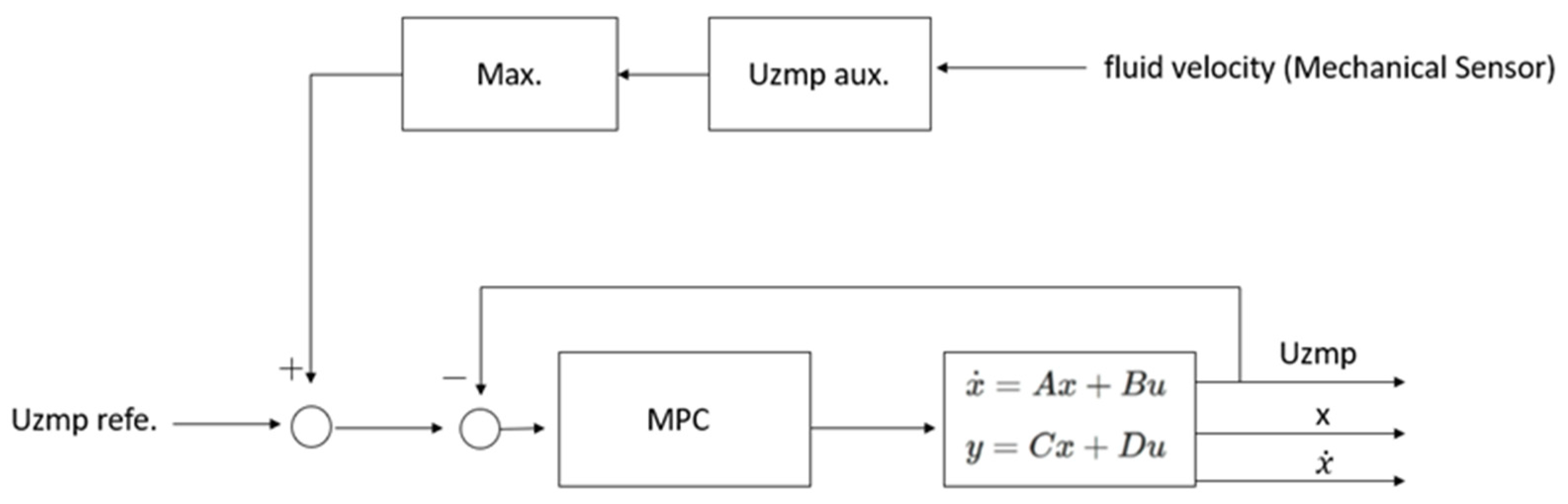
This reference adds to the initial reference of the Uzmp of walking, and then the MPC is employed to generate the trajectory of the centre of mass (see Figure 5).
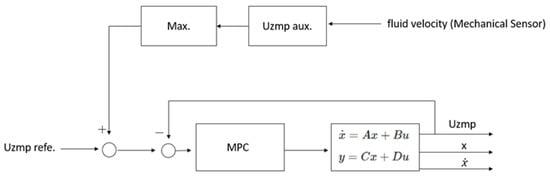
Figure 5.
Reaction model step to recover balance.
2.4. Dynamic and Control Position
2.4.1. Inverse Dynamic
The inverse dynamics of the legged robot in an underwater environment [19] are defined by the following Equation.
where is the inertial matrix including the terms of hydrodynamic mass; is the Coriolis and centripetal matrix; is the hydrodynamic damping matrix; is the vector of gravity and buoyancy; is the vector of torques and forces generated in each actuator; , , and are the vectors of the accelerations, speeds, and positions of the actuators, respectively; is the Jacobian transpose of the leg; and is the vector of the reaction forces between the robot foot and the ground.
These reaction forces of the legged robot can be calculated by the following Equation [20].
where is the vector between the CoM (centre of mass) and the foot i, I is the unitary matrix, is the forces vector of the reaction in the foot i, and and are the forces vectors and the torques, respectively, that are applied in the centre of mass of the robot. In the case of an underwater environment, these vectors are defined by the following Equation.
where is the vector of the accelerations in the three axes of the centre of mass. Note that the third vector in the z-axis is multiplied by , which is the buoyancy factor shown in Equation (3). is the inertial matrix of the robot body and is the vector of angular accelerations in the three axes. is the vector of the relative velocity in the three axes of the fluid with the trunk of the robot; this value is calculated by the robot’s mechanical sensor.
Depending on the number of feet in contact with the ground, Equation (16) may or may not have multiple solutions. To solve this problem, the criterion of the friction force is used, in which forces must satisfy the following Equation.
where , , and are the reaction forces in each foot and is the coefficient of the static friction of the ground.
2.4.2. Control Position
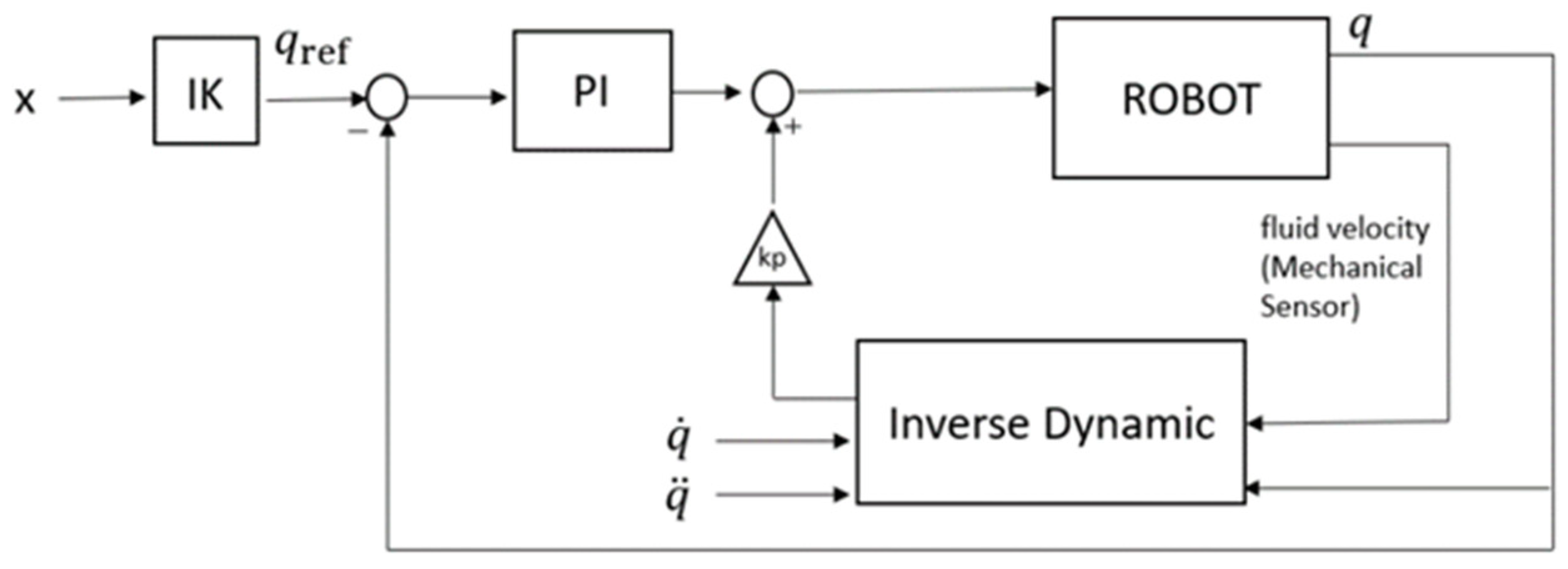
The control strategy that was used in the robot is a model of dynamic compensation control. As shown in Figure 6, a proportional–integral controller (PI) [21] was used. It is compensated [22,23] by the torques, which are calculated by the inverse dynamics. This value is multiplied by the value of Kp, which is easily adjustable in the robot. This method allows the control to be more adaptive, since during the period in which the foot of the robot is on the ground, the torques and forces increase drastically. This method allows such variability to be compensated during the calculation of the inverse dynamics.
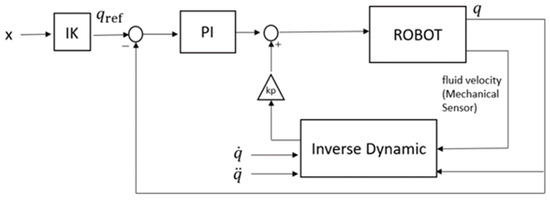
Figure 6.
Position control by dynamic compensation.
2.5. Description of Prototype
For the experimental test, a planar bipedal robot was built. The advantage of using this type of robot is that it allows you to test two-dimensional models [24,25,26,27], such as . Figure 7 shows some planar bipedal robots.

Figure 7.
(a) A biped robot used by MIT’s leg laboratory, (b) the Mabel robot of the University of Michigan, (c) Atrias of the Oregon State University’s Dynamic Robotics Laboratory and (d) Rabbit of Laboratoire de Grenoble Automatique.
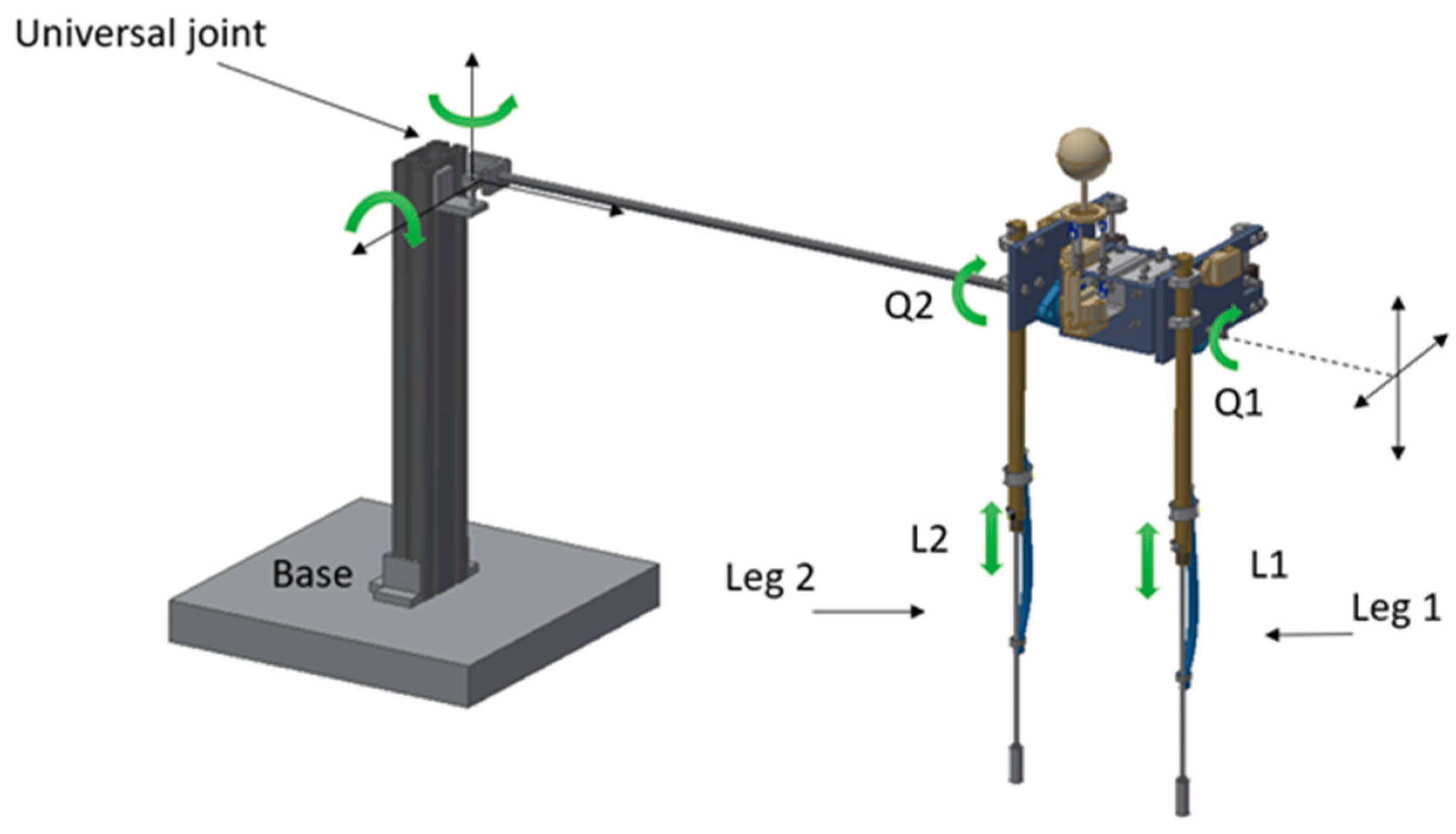
Figure 8 shows the degrees of freedom of our underwater planar bipedal robot. As can be seen, it has two legs (leg1, leg2) with two degrees of freedom, one rotational (Q1, Q2), and another linear (L1, L2). This is tied to an axis attached to a base through a universal joint, allowing the robot to have two degrees of spatial freedom.
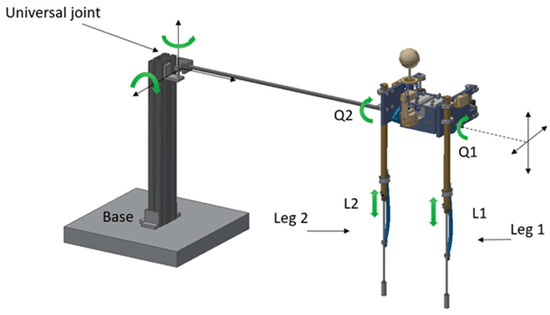
Figure 8.
Planar bipedal robot for underwater walking.
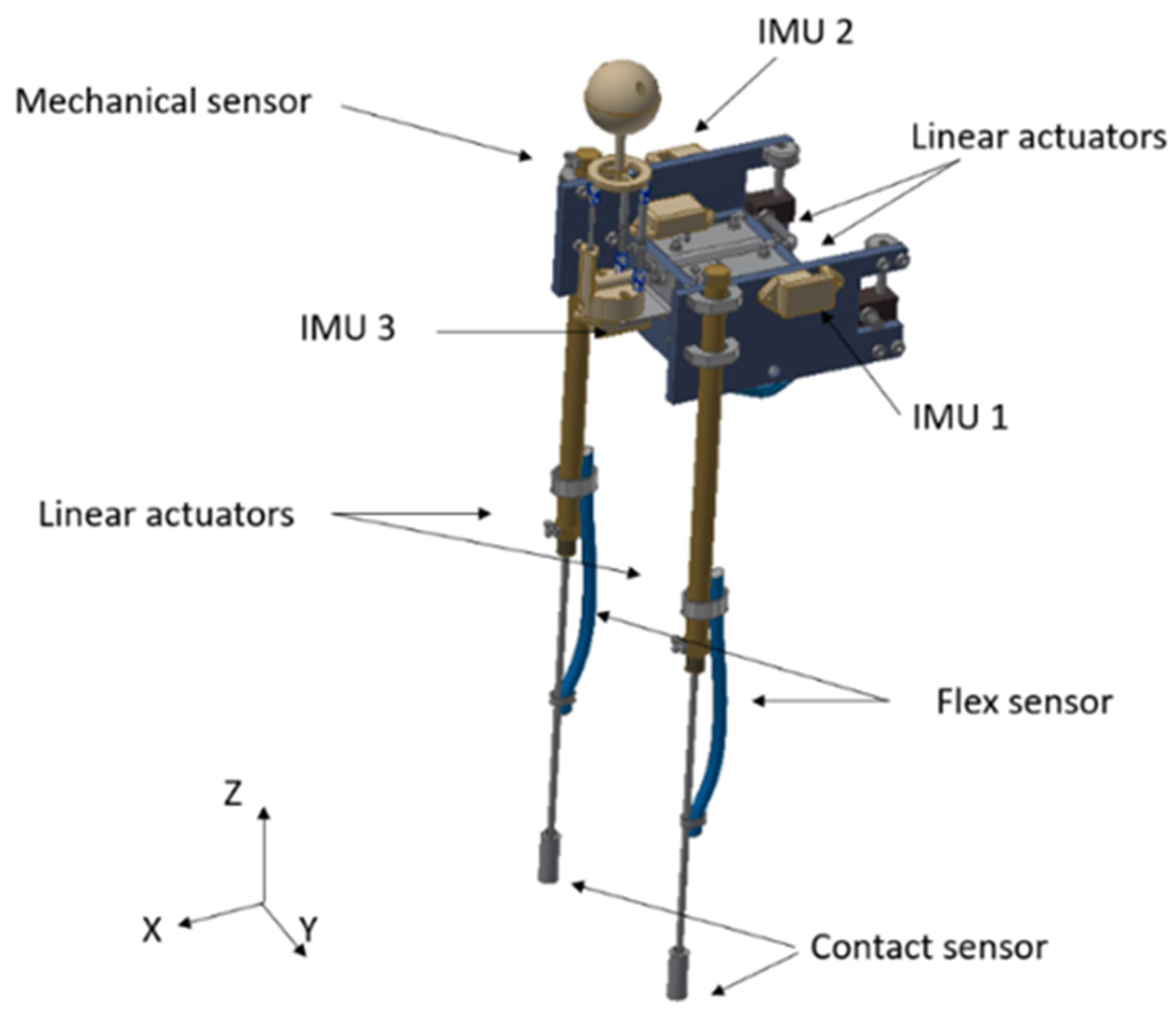
Figure 9 shows a biped robot with four hydraulic actuators, which work at a hydraulic pressure of 20 bars. This robot has a height of 90 cm, a width of 22.2 cm and weighs 4 kg. The mechanical sensor was developed by our research group, and it is made to measure the fluid velocity in all three directions. The robot has three inertial measurement unit (IMU) sensors; one in the centre of mass in order to calculate the linear accelerations, angular positions and speeds, and another in each leg in order to calculate the angular position. Moreover, it has two flexible resistive sensors; by their deformation it is possible to measure the displacement of the linear actuators in the legs. Also, there are two contact sensors in each foot. This type of sensor was chosen because it is waterproof, as each of them is covered with resin.
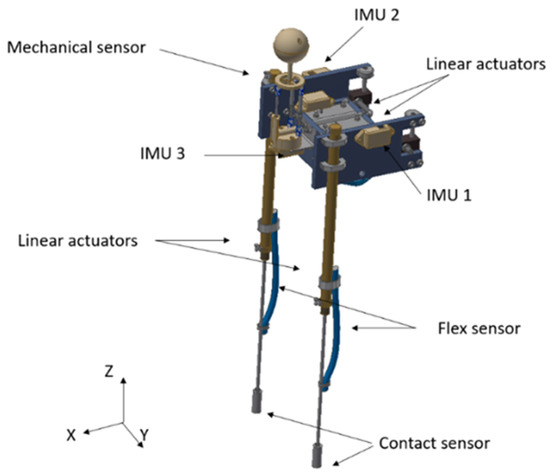
Figure 9.
Bipedal robot sensors and actuators.
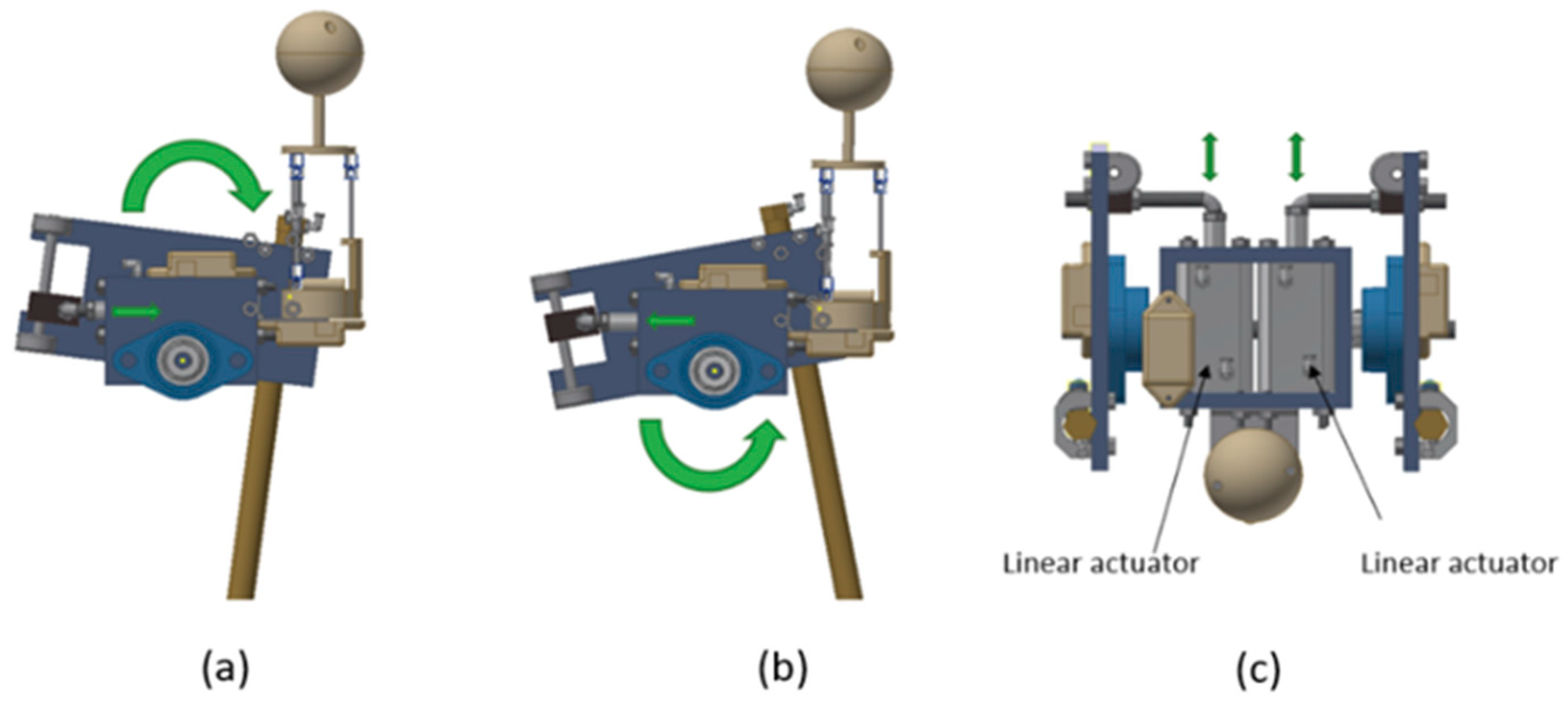
Figure 10 shows the mechanism that was used to transform the linear movement of the actuators into a rotational movement to rotate the leg. The mechanism is based on a sliding mechanism perpendicular to the line actuator; when the cylinder bar is introduced, this rotates the leg clockwise (see Figure 10a), and when it is it comes out, the leg rotates counterclockwise (see Figure 10b). This mechanism of action is applied to each leg (see Figure 10c).
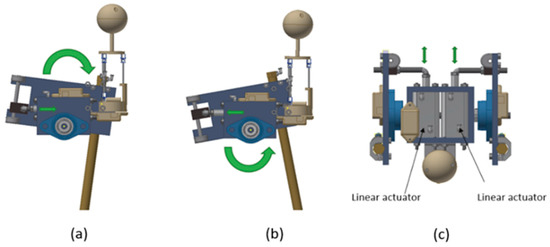
Figure 10.
Leg rotation mechanism, (a) cylinder bar introduced, this rotates the leg clockwise, (b) cylinder bar outside, this rotates the leg counterclockwise, (c) top view of each actuator.
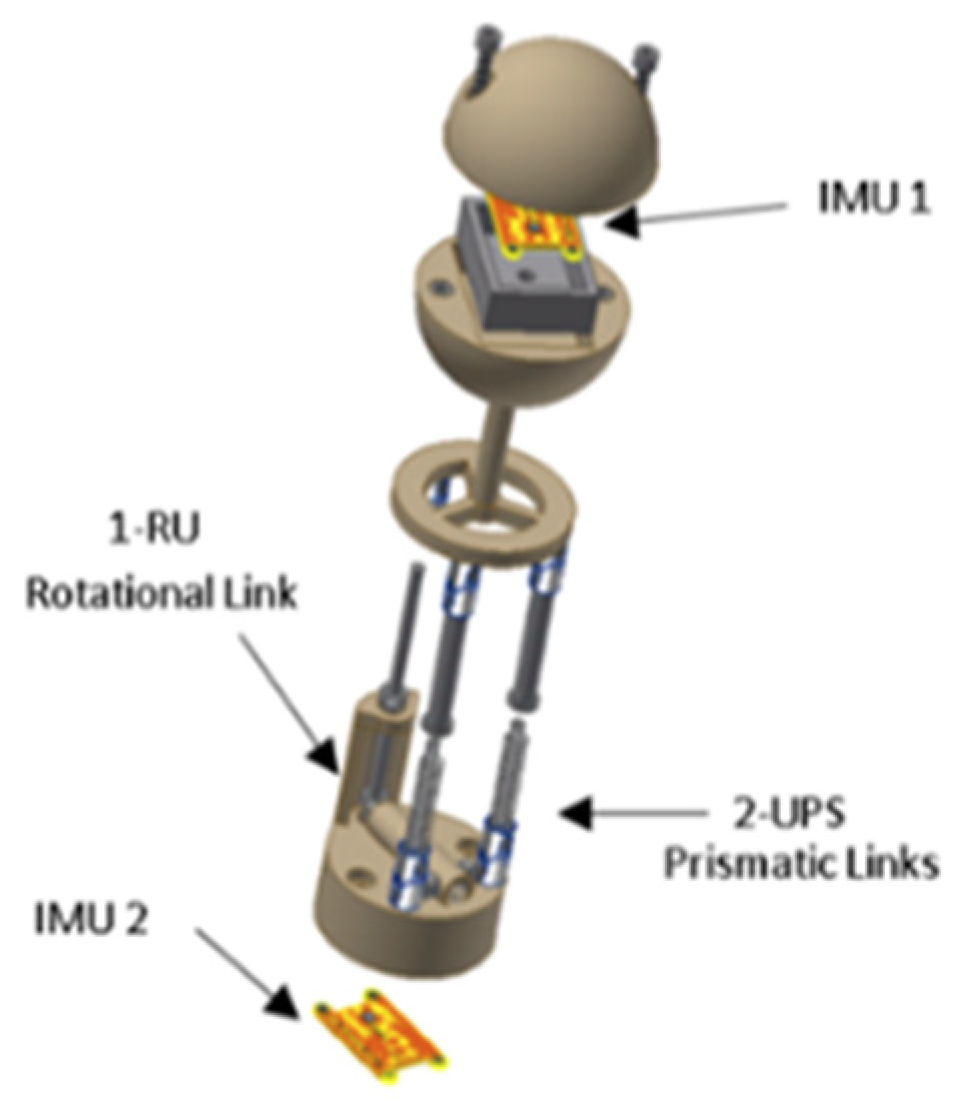
The mechanical sensor measures the velocity and direction of the fluid through the parallel mechanism [28,29,30,31] (see Figure 11), which uses passive actuators (springs). The platform of the mechanism is connected to a spherical body. Within this body, there is an inertial measurement unit (IMU). When the fluid collides with the sphere, the parallel mechanism is deformed, from which it is possible to determine the angles of the platform and the acceleration of the sphere by using the IMU. Using inverse kinematics, the deformation of the springs is calculated. From the deformation of the springs, the force of each actuator can be determined. Then, using dynamics, the drag force in the sphere is calculated. Finally, the velocity of the fluid is calculated by the hydrodynamic Equation of the drag force. The theoretical explanation of this sensor is shown in the paper by the authors of [13] and the demonstration experiment is shown in the paper by the authors of [14].
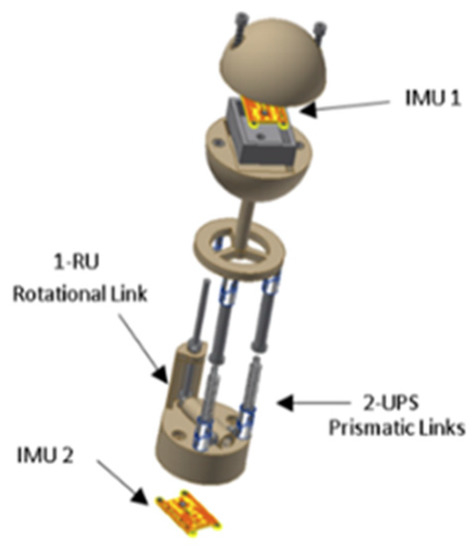
Figure 11.
CAD design of the sensor. Inertial measurement unit 1 (IMU1) is in the sphere of the sensor, and IMU2 is in the base of the sensor. Also, the 2-UPS prismatic links and 1-RU rotational link are shown.
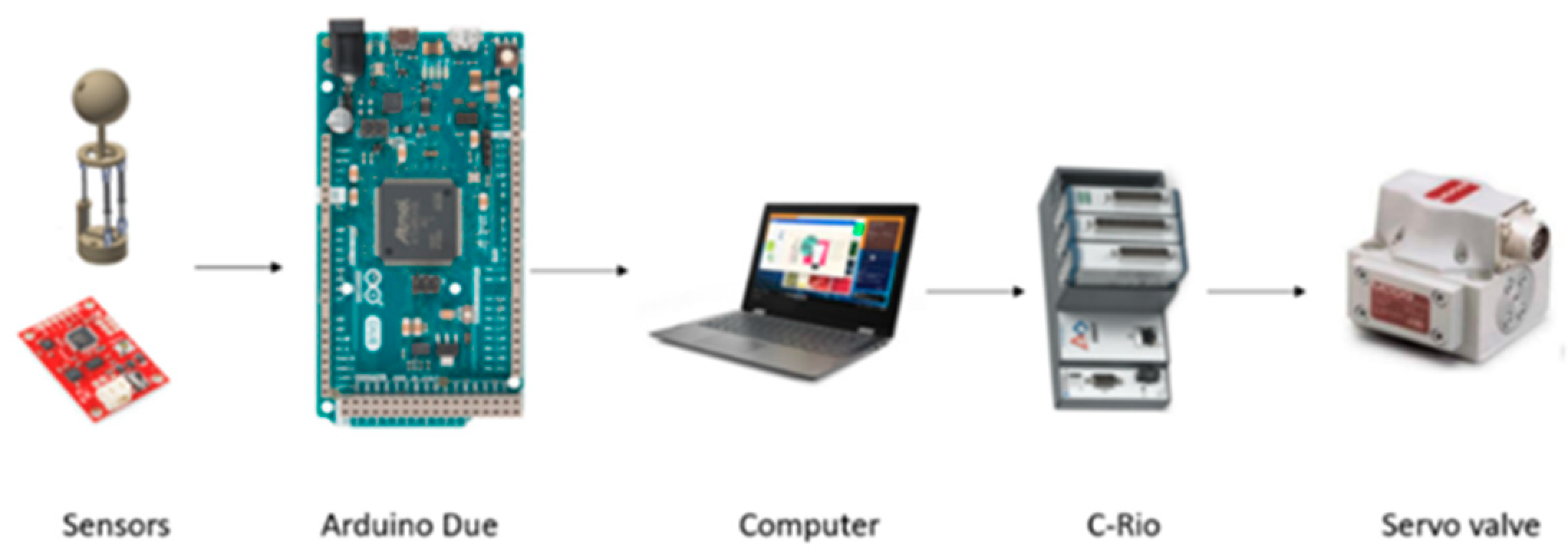
The robot control software was developed in LabVIEW and the hardware architecture is shown in Figure 12. Using an Arduino DUE, the data of the sensors were extracted and transferred to a computer by a USB cable. In this way, high-level control is executed and the positions of each actuator are sent to the C-Rio, where the low-level control described in Section 2.4.2 is executed. Also, it generates the voltage signals, which are sent to the current converter, and activates the servo valves.
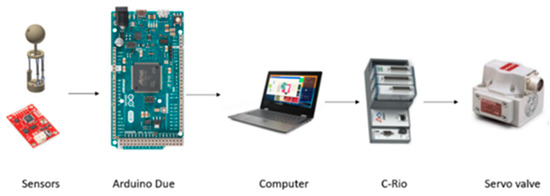
Figure 12.
Hardware architecture of the legged robot.
Figure 13 shows the submerged robot in an underwater environment at a depth of 4 m. It can be observed that this is supported by the axis that is connected by a universal connection to the metal base. In addition, it is possible to see the hydraulic hoses and the Arduino DUE, which is covered with resin.

Figure 13.
Legged robot in an underwater environment at a depth of 4 m.
2.5.1. Hydrodynamic Mass
Because the computational methods for calculating hydrodynamic mass are still in development, the method that was used to determine the hydrodynamic mass is the Small Oscillation Method, by means of mass-spring free vibration [32]. This is an experimental method which has been shown to have good results with scale models [33,34,35].
Figure 14 shows the experiment. The robot’s hip model at 0.5 scale can be seen submerged in water. This model and a weight of 0.5 kg are suspended by a spring, while a linear sensor measures the displacement of vibration.

Figure 14.
Experiment model for the determination of hydrodynamic mass.
The hydrodynamic mass of a body is determined by the following Equation [36].
where is the hydrodynamics mass coefficient, is the density of the water and is the volume of the body.
The Equation of motion is determined as follows [37]
where is the amplitude, is the maximum amplitude, is the damping factor, is the oscillation frequency and is the time. The oscillation frequency is determined by the following Equation [37].
where is the natural frequency without damping. Since is normally small compared with unity, the damped natural angular frequency, , can be approximated to , the undamped natural angular frequency [37],
where [36],
where K is the stiffness of the spring (120 N/m), m’ is the hydrodynamic mass, and m is the mass of the model with the weight addition of 0.5 kg. By using a linear encoder, the displacements can be measured and the natural frequency can be calculated. In this way, it is possible to determine the hydrodynamic mass of the model and then to calculate by Equation (19).
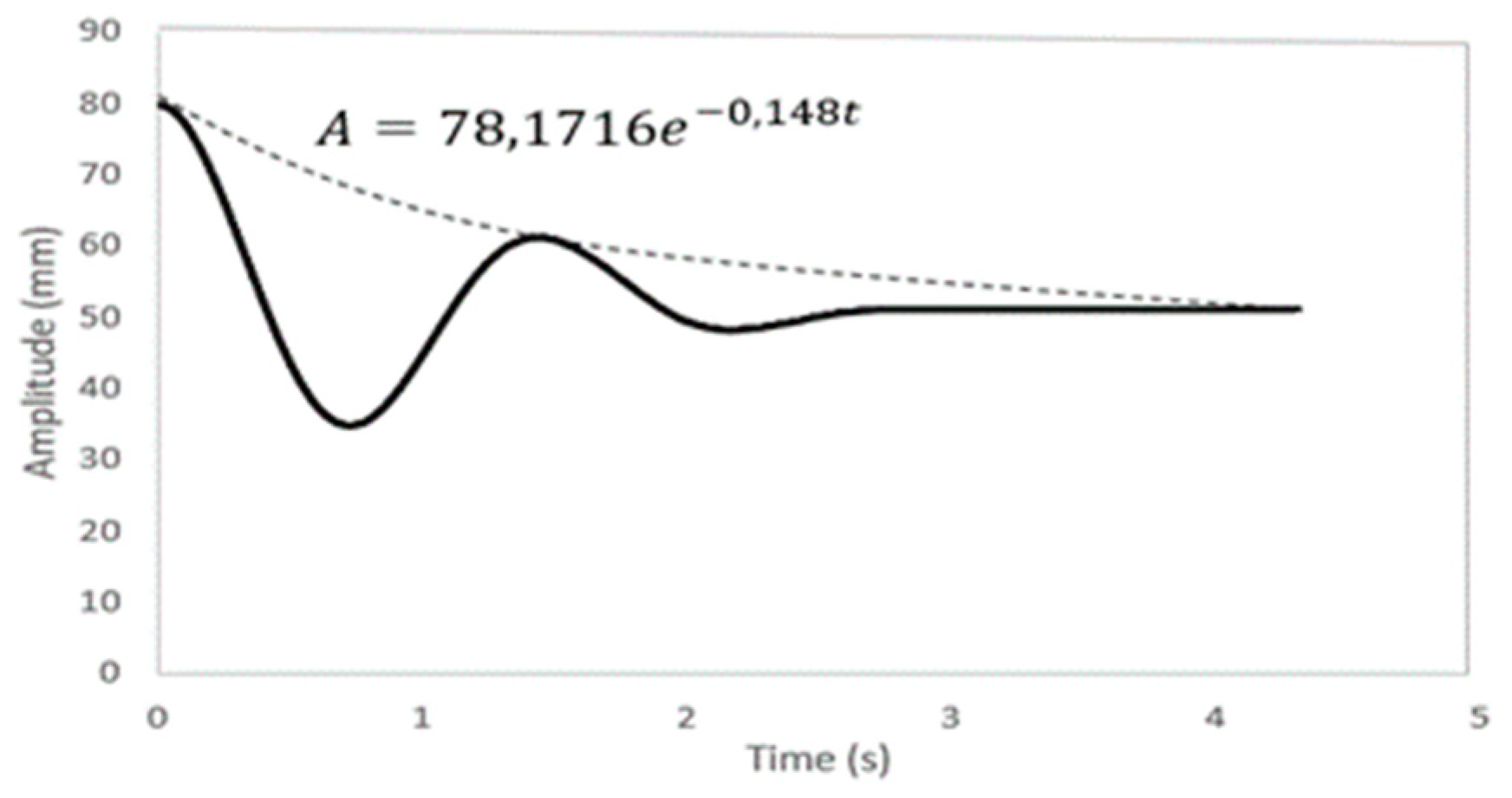
Figure 15 shows a free fall experiment, where the amplitude decays exponentially. By equating the amplitude Equation shown in the figure with Equation (26), the values and can be obtained. The damping factor value was observed to be quite low, indicating that the vibration frequency can approximate very well to the natural frequency.
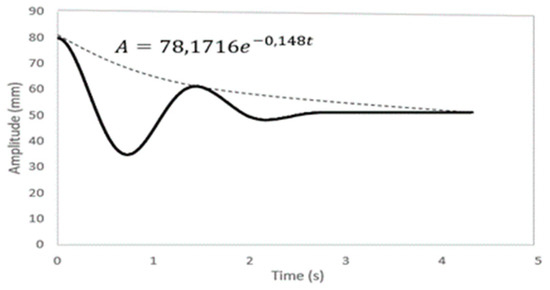
Figure 15.
Oscillating movement of the free fall experiment.
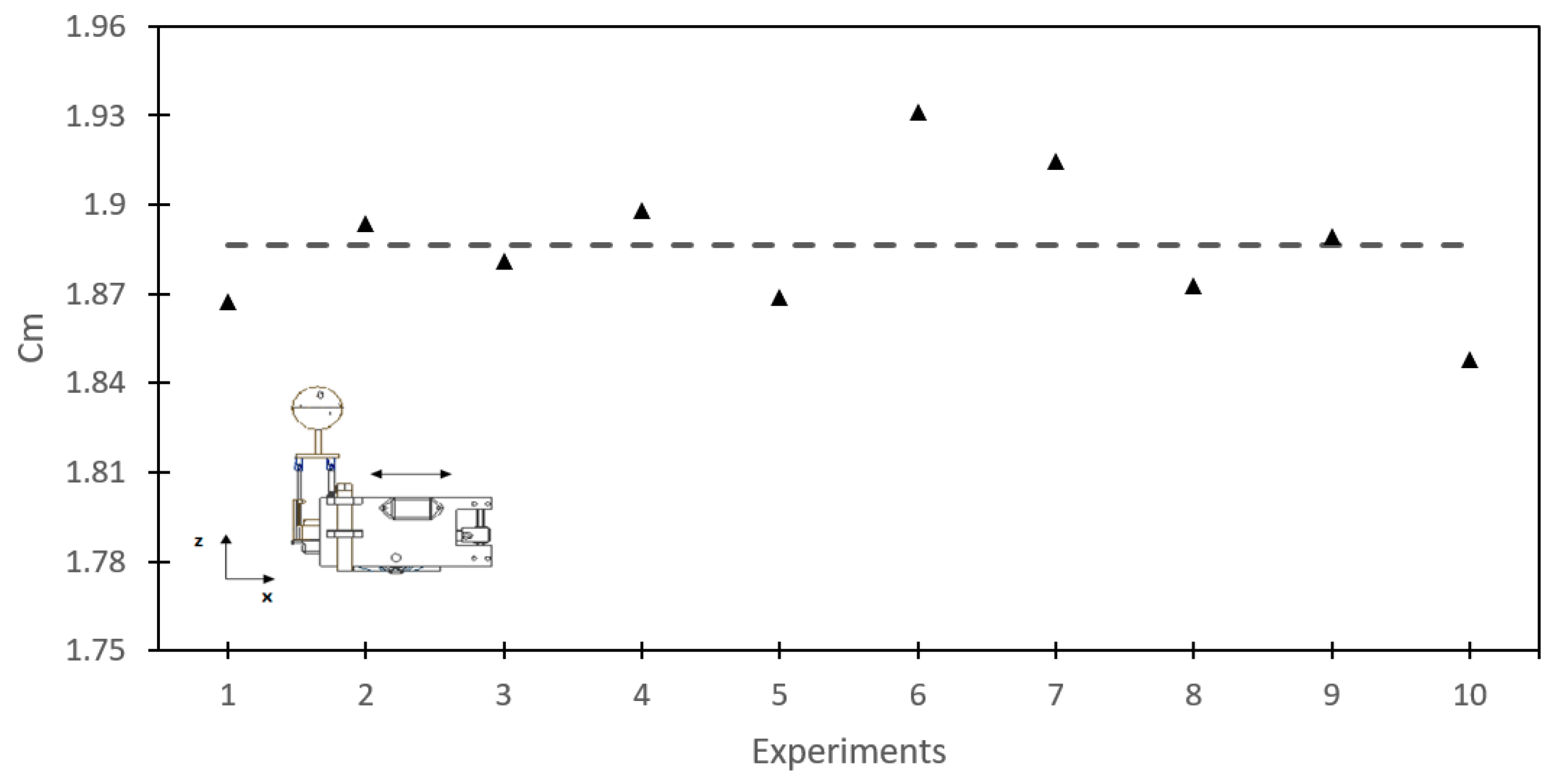
Figure 16 shows the results of that were obtained in 10 experiments. The mean value of was found to be 1.89. This value is replaced in Equation (19) with the real volume of the robot to obtain the hydrodynamic mass of 4.2 kg.
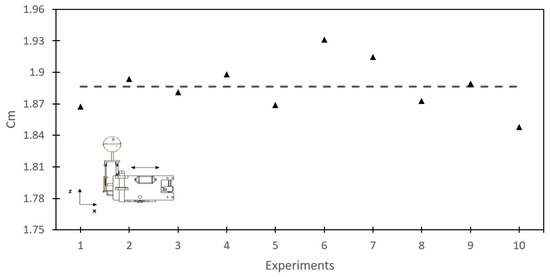
Figure 16.
Hydrodynamic mass coefficients obtained in each experiment.
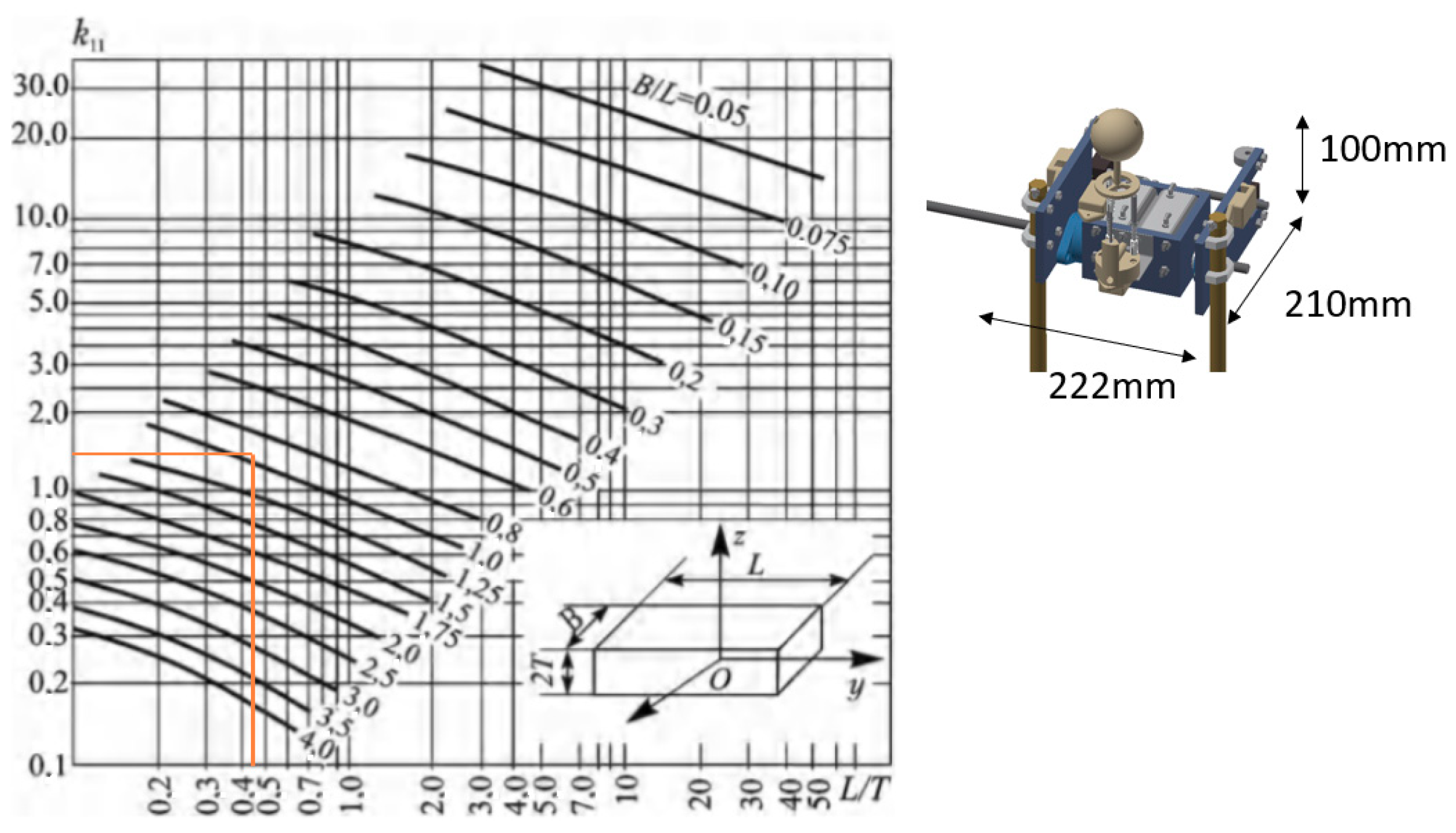
To verify that our experimental results are correct, we approximated the geometry of the robot’s hip to a parallelepiped. Figure 17 shows the hydrodynamic mass coefficient for a parallelepiped that is in motion on the x-axis [32]. At the right-hand side, the dimensions of the robot’s hip are shown, approximating it to a parallelepiped. Using the table with the given dimensions, we obtained , which is very close to the value we found through the experiment (), being reasonably higher since the geometry is more complex. Therefore, we can ensure that the value of found by the experiment is correct.
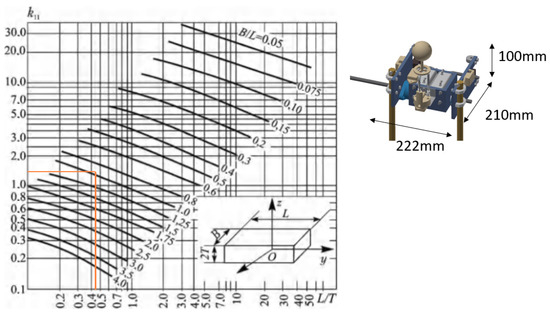
Figure 17.
Hydrodynamic mass of a parallelepiped moving on the x-axis, where .
In order to determine the hydrodynamic mass of the legs and axis, the geometry that was assumed is the geometry of the cylinder; the hydrodynamic mass coefficient of the cylinder is [36]. Table 1 shows the mass and the hydrodynamic mass of each body.

Table 1.
Added mass of each body.
In Table 1, it is possible to see that the total mass of the hip represents 77.7% of the total mass of the robot. Taking into account that the hip has the highest accelerations, for our model only the value of the hip is considered.
2.5.2. Damping Coefficients
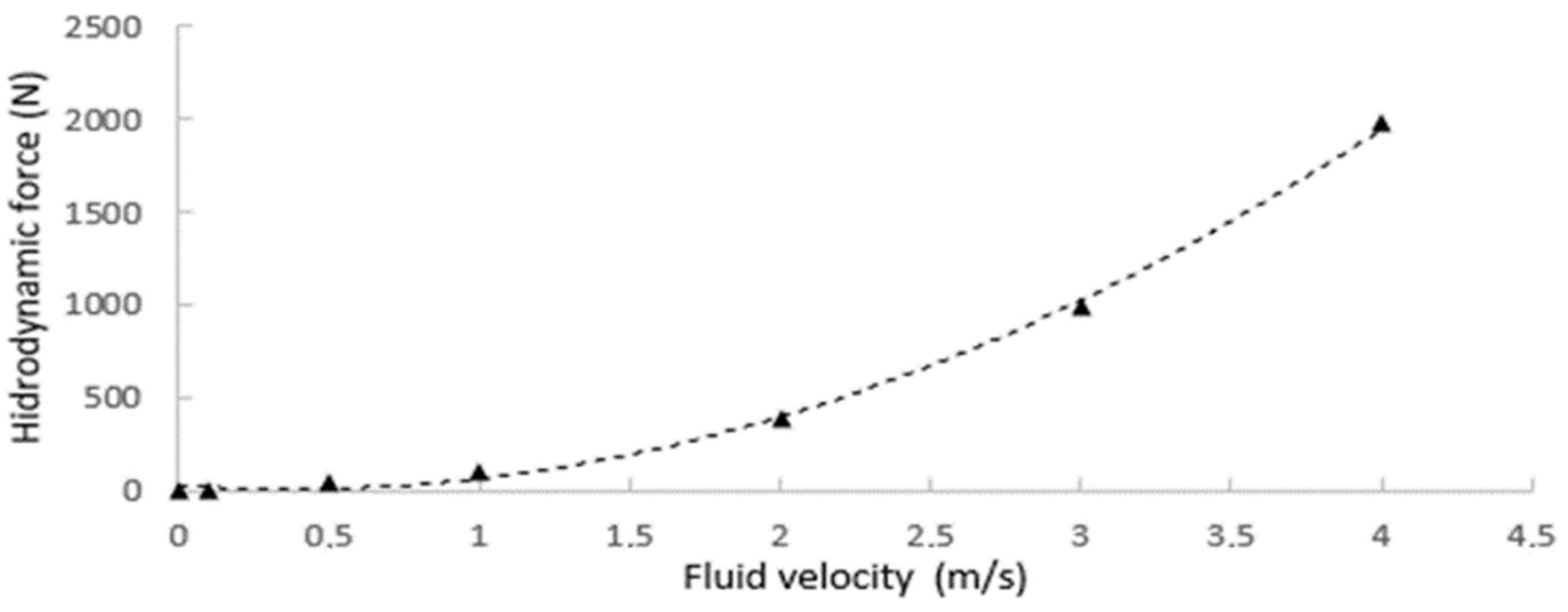
The hydrodynamic damping coefficients [38,39] of the robot were obtained by CFD (computational fluid dynamics) with a series of experiments by varying the fluid speed, as shown in Figure 18. First, the applied hydrodynamic forces in the body of the robot are obtained. By performing a regression, the quadratic Equation is obtained, from which it is possible to deduce the quadratic coefficient and linear coefficient .
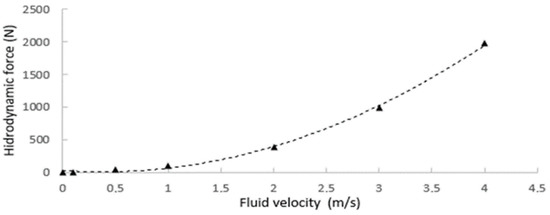
Figure 18.
Hydrodynamic forces that are obtained by each fluid velocity to determine the damping constants.
2.6. Experiment
Two experiments were carried out; walking for a period of 54 s and a reaction step for balance recovery. In last experiment, two perturbations in the fluid were generated by a square aluminium plate of 30 cm. The constants used in the experiments are shown in Table 2.

Table 2.
Constants used in the experiment.
3. Results
3.1. Walking
Figure 19 shows a series of photographs of the walking period during 54 s (see Supplementary Materials).

Figure 19.
Photographic series of the walking process.
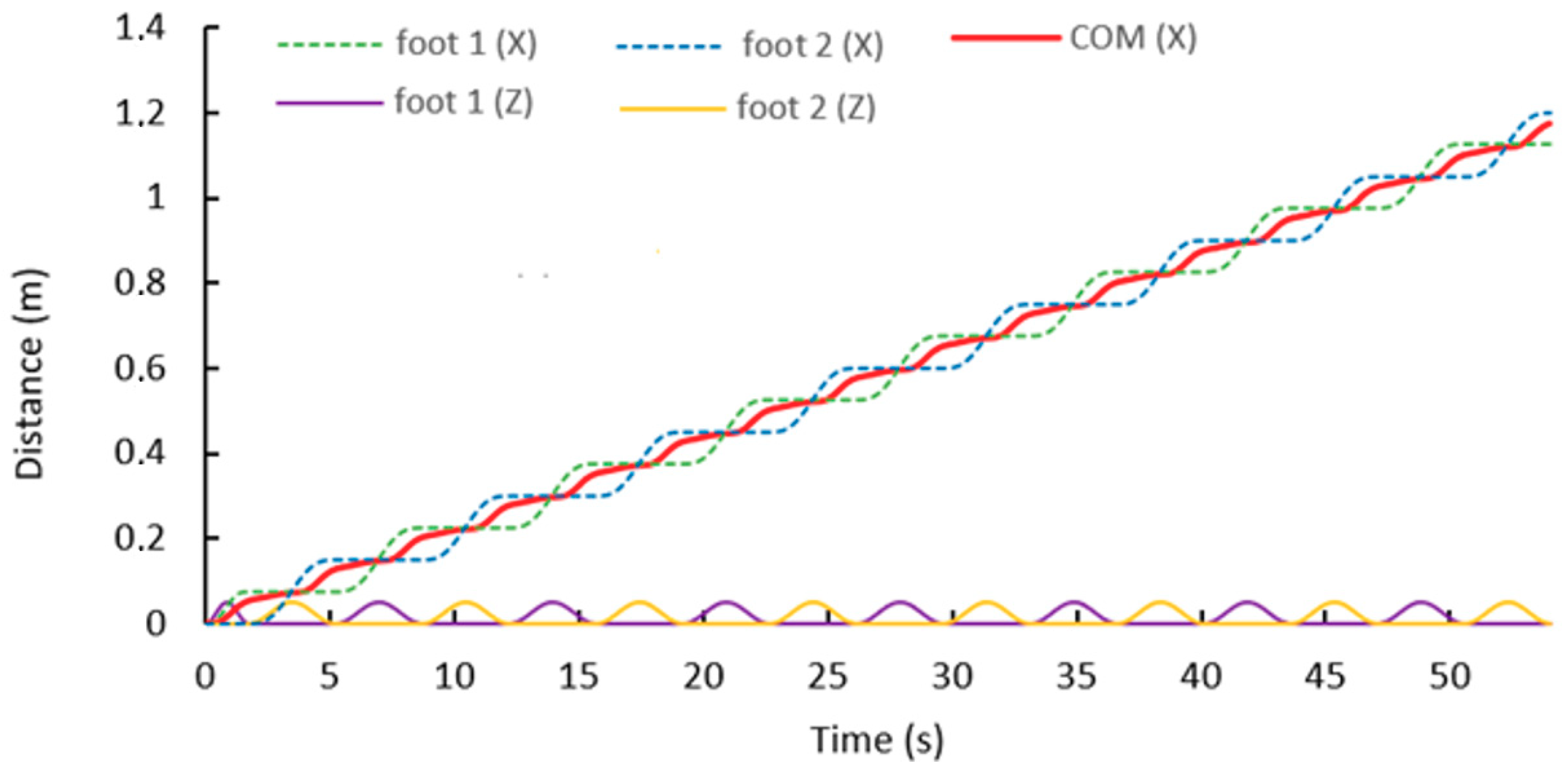
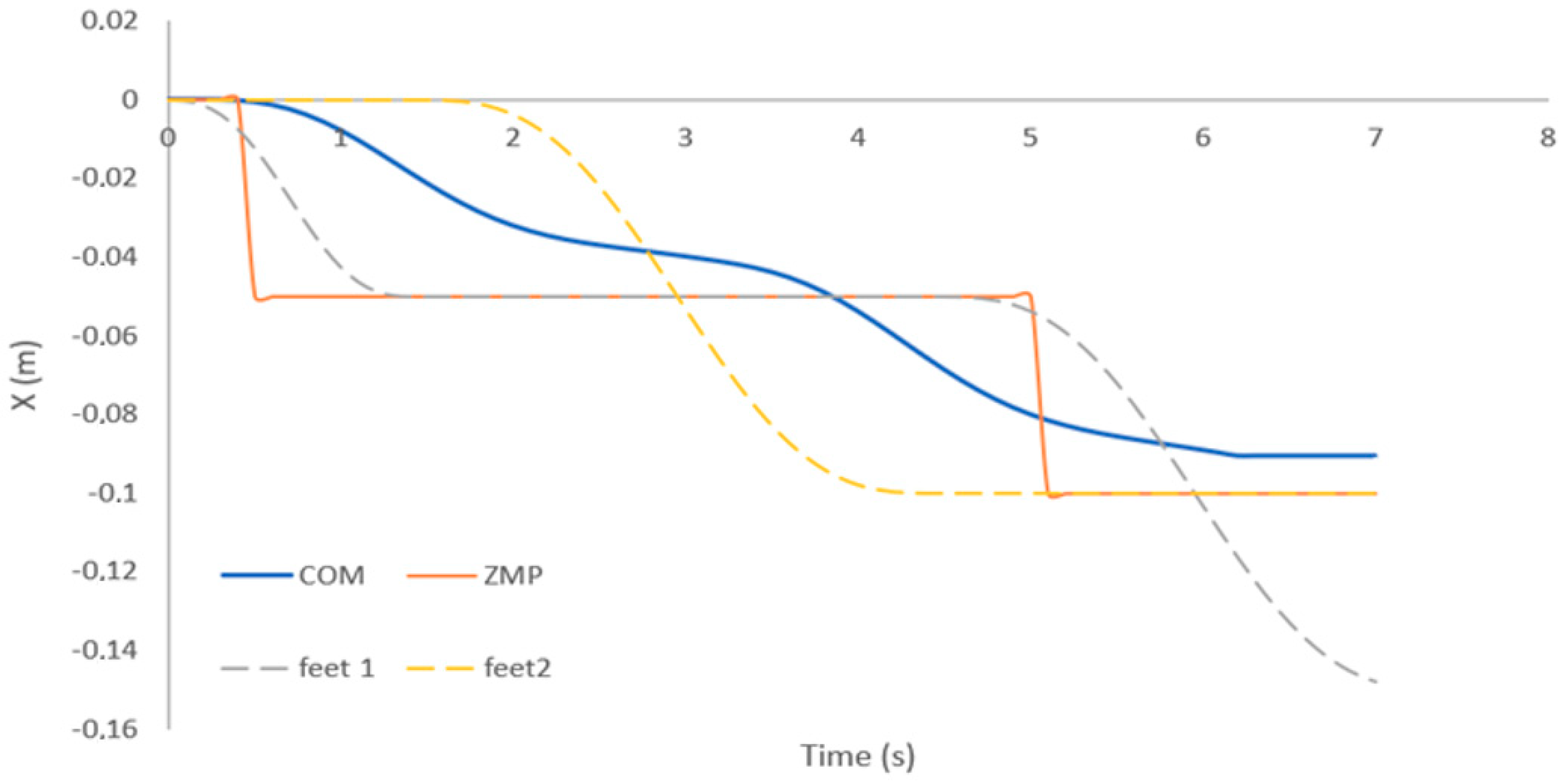
Figure 20 shows the trajectory of the CoM (red line) that is generated by the MPC and Uzmp. The feet trajectory of the robot is also shown along the x-axis and the z-axis.
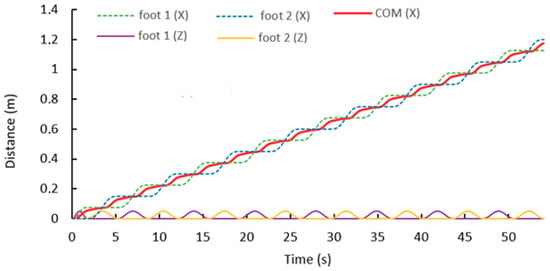
Figure 20.
Trajectory of the centre of mass generated by the Uzmp and MPC.
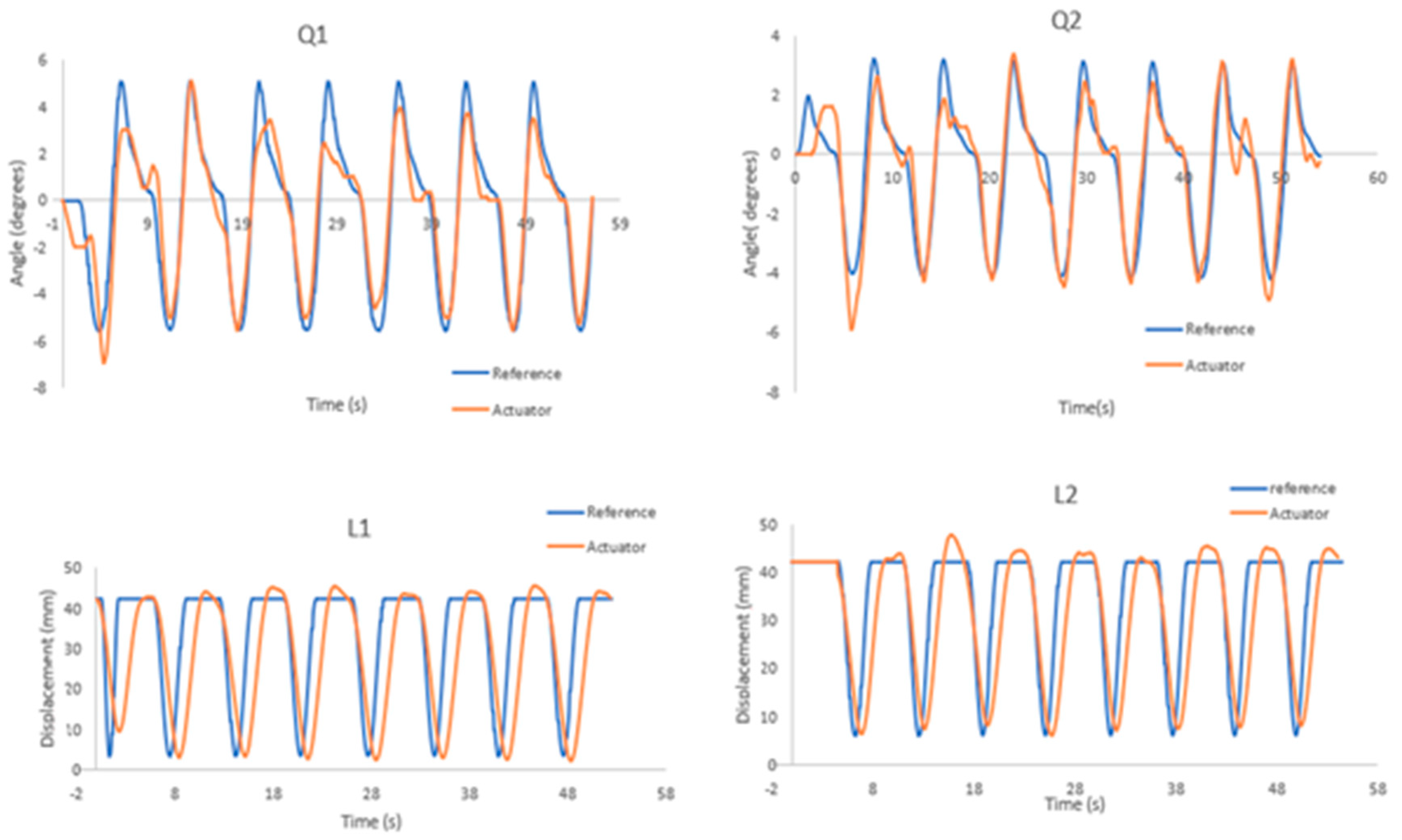
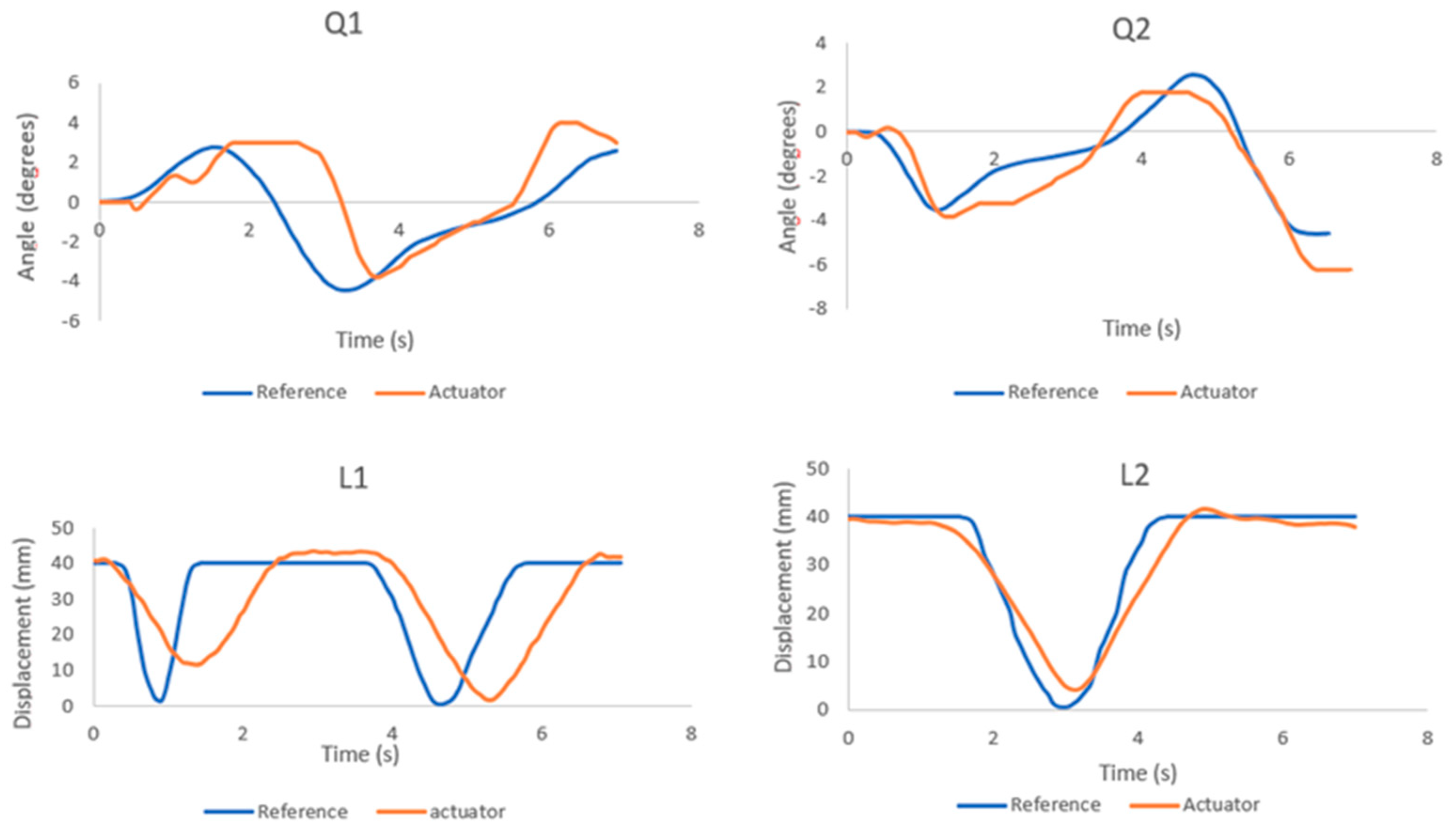
Figure 21 shows the position control results of each actuator, where the blue line is the reference position and the orange line is the position obtained by the actuator.
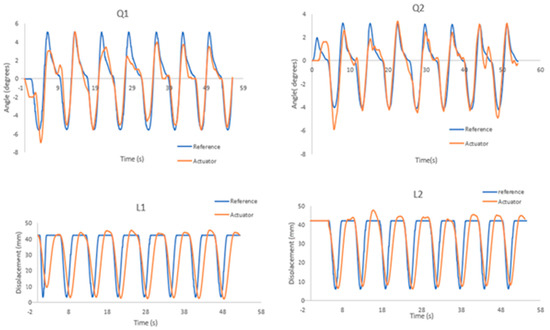
Figure 21.
Position actuators in the walking process.
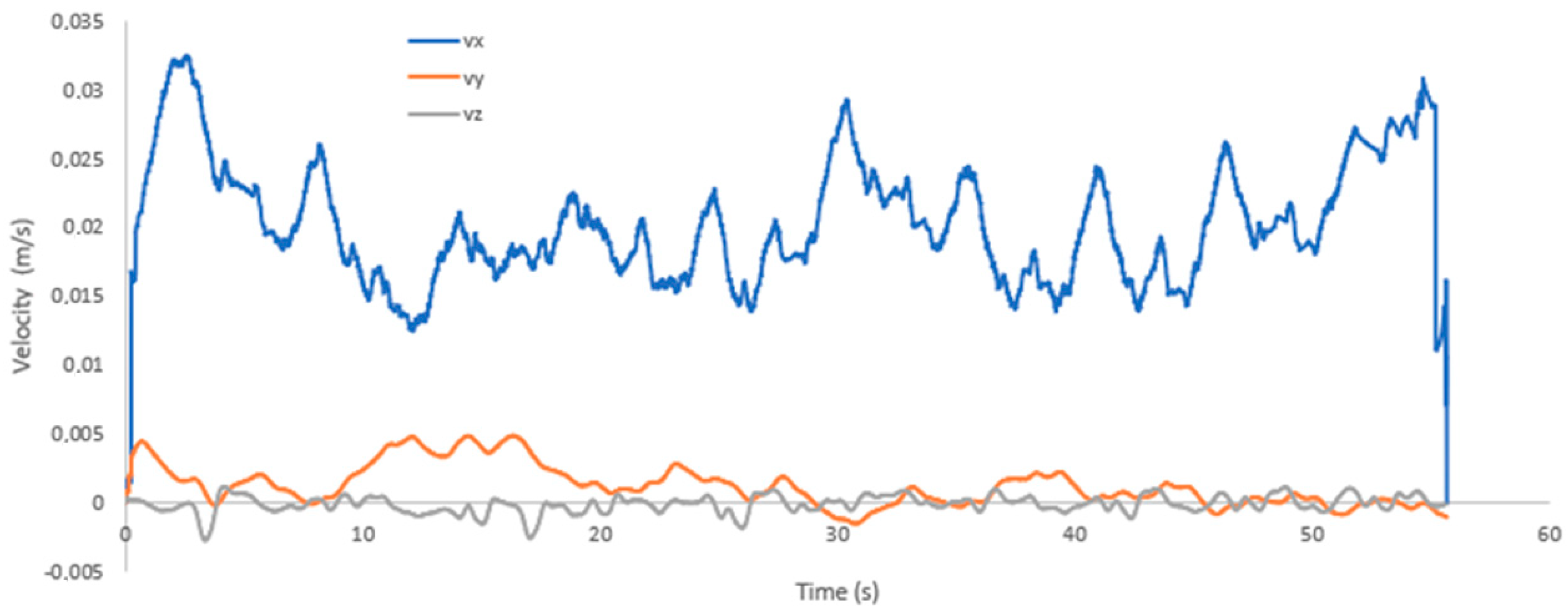
Figure 22 shows the results of the velocities in the three directions that were sensed by the mechanical sensor. It can be seen that the velocity along the x-axis maintains an average of 0.02 m/s. The y-axis velocity has an average of 0.003 m/s, much smaller than the velocity along the x-axis. However, it is greater than the velocity along the z-axis, due to the fact that the robot is walking in a circular manner. So even if the sensor moves with the robot, there is a y-direction component due to the centrifugal force. The speed along the z-axis is very small since the robot does not move or at least avoids moving in that direction. Hence, these velocity measurements are a product of disturbances in the environment that are caused by walking.
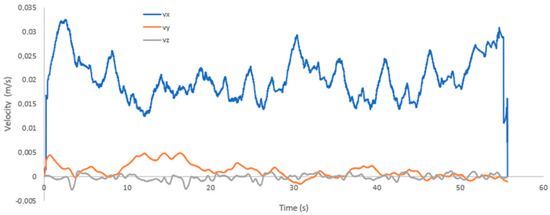
Figure 22.
Speeds measured by the mechanical sensor in the walking process.
3.2. Reaction Step for Balance Recovery
Figure 23 shows a photographic series of the experimentation process for the reaction of the step to recover the balance of the robot (see Supplementary Materials). In the first photograph, the aluminium plate is observed in the yellow circle to generate the disturbance and the yellow arrow indicates its movement. The blu, e arrow indicates the movement of the fluid that is generated to disturb the robot. Two disturbances were made; the first a time of 0 s reaches stability at 4 s. Then another disturbance is generated at 5 s and the robot regains its stability at 7 s.

Figure 23.
Photographic series of the reaction step experiment for balance recovery.
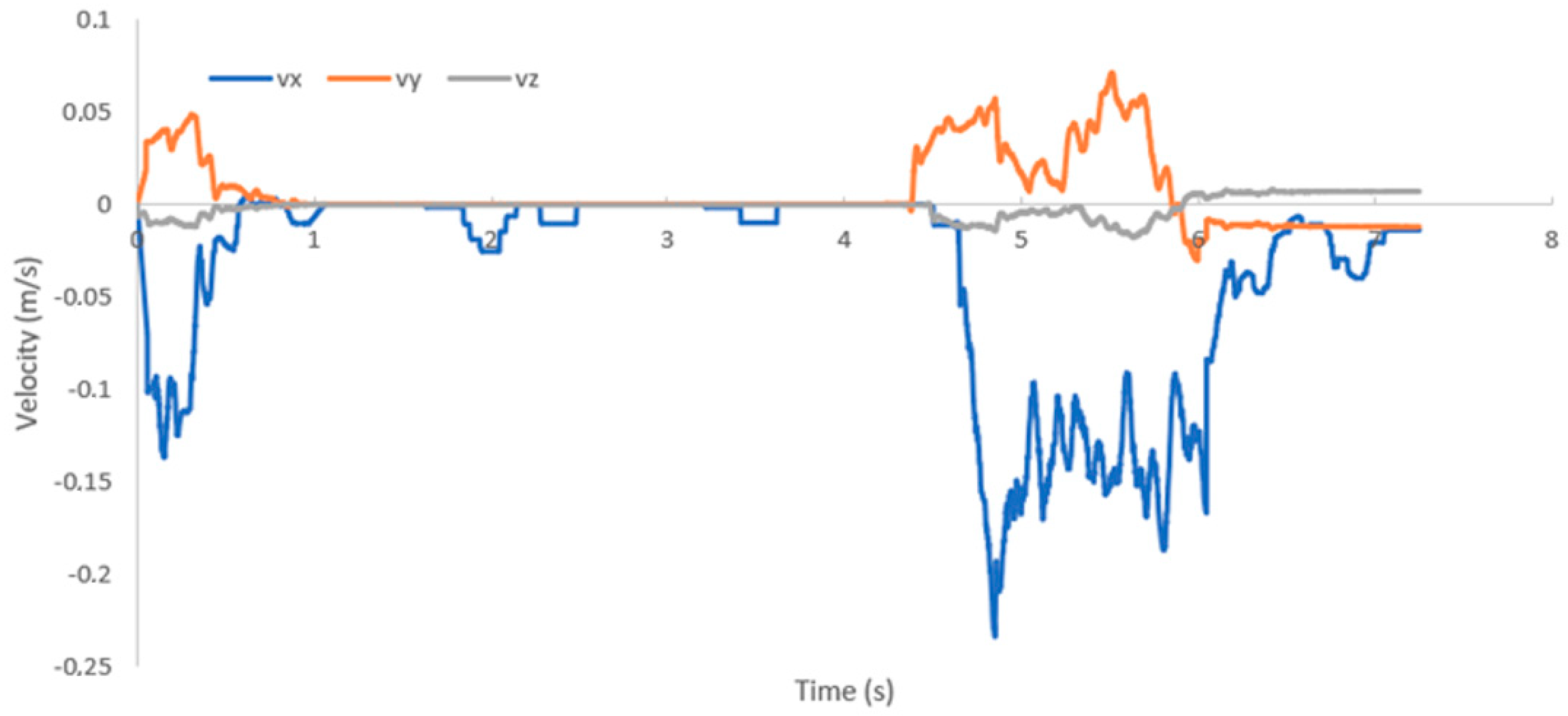
Figure 24 shows the velocity that is measured by the mechanical sensor. Two disturbances can be clearly seen—the first generated a velocity along the x-axis of up to −0.15 m/s (the negative value is because the sensor also measures the direction of the fluid), and the second disturbance caused the fluid velocity to reach an average of −0.2 m/s. The disturbances were also generated along the y- and z-axes.
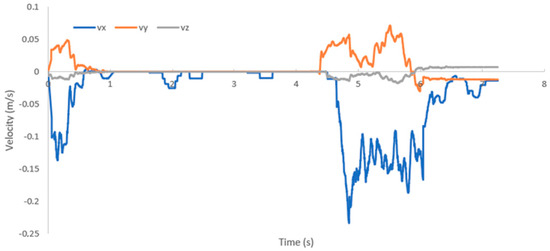
Figure 24.
Fluid velocities that are measured by the mechanical sensor at the time of water disturbance.
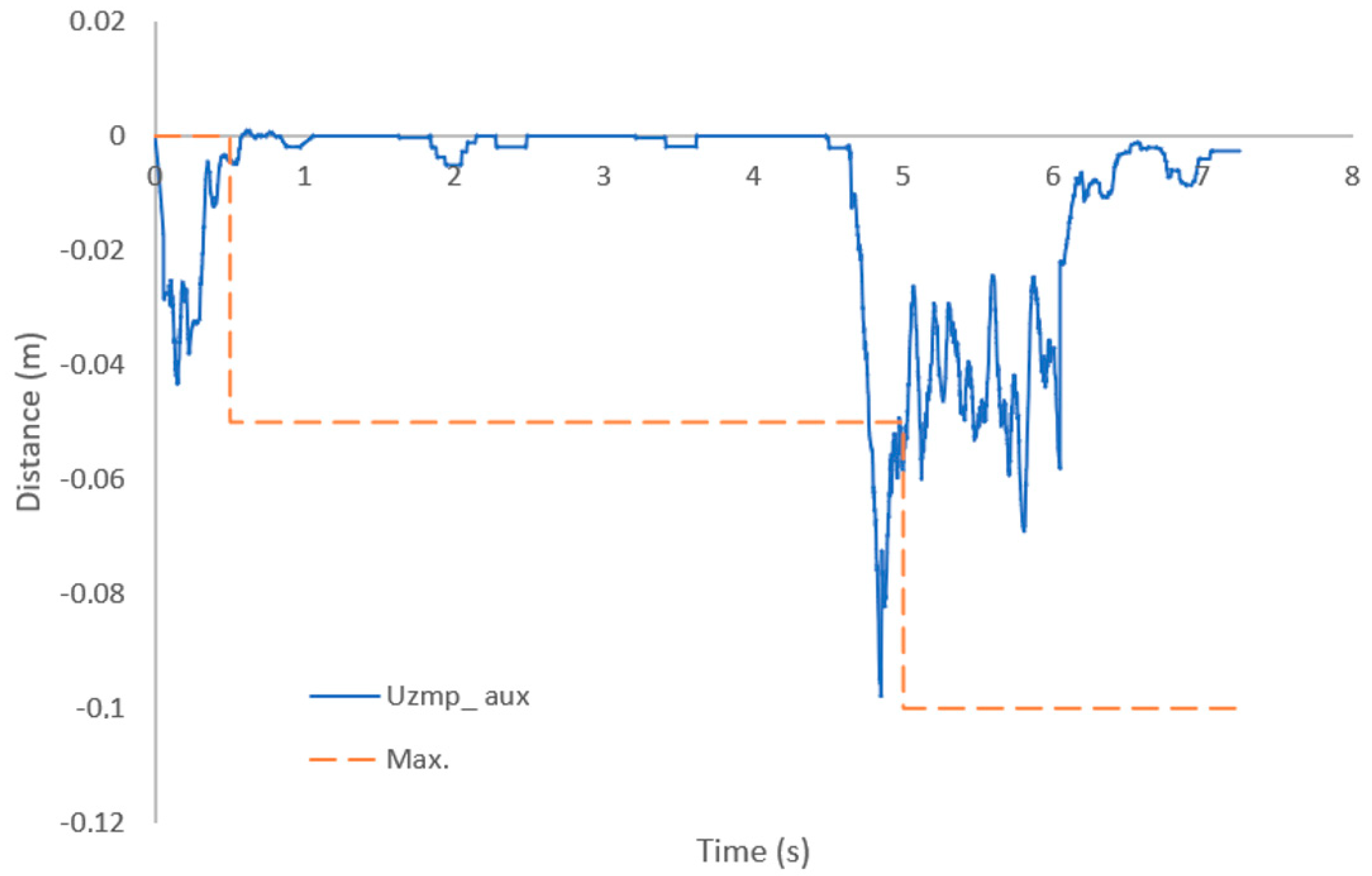
Figure 25 shows the Uzmp aux (blue line), which is calculated by Equation (14). The orange line is the reference generated with the maximum value of the Uzmp aux; at the beginning a maximum reference value of −0.05 m was generated and in the second case a value of −0.1 m was obtained.
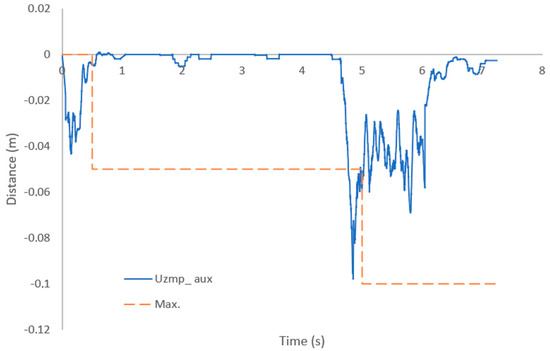
Figure 25.
Underwater zero moment point auxiliar (line blue) and reference (orange line).
Once the reference of the Uzmp is defined, the MPC can be used to generate the trajectory of the centre of mass, as shown in Figure 26. In this case, the value is negative, so it is understood that the robot steps back in order to recover its balance.
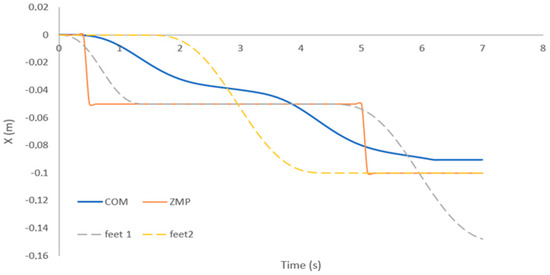
Figure 26.
Trajectory of the centre of mass, generated by the MPC, in reaction to a disturbance.
Figure 27 shows the reference positions of each actuator (blue line) at the moment of the reaction, obtained from the inverse kinematics. Also, from the positions of the actuators (orange line), it can be seen that in the case of Q1 and L1, the first one has a larger error. This situation is normal because at that moment the disturbance is taking place.
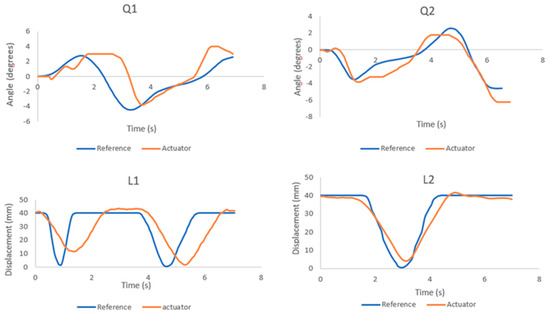
Figure 27.
Position actuators in the balance recovery process.
4. Discussion
Figure 20 shows the path generated by the Uzmp. First, a low speed is generated for walking, approximately , as shown by the measurement of the mechanical sensor. There are two main reasons why a low speed is obtained: First, as seen in the Uzmp Equation, is that the inertial force increases due to the hydrodynamic mass acquired by the robot, which is quite considerable as demonstrated in the experiment. On the other hand, the gravitational force decreases due to the buoyancy of the body; this makes the pendulum escape velocity very low, decreasing the maximum walking speed, and causes a transition to trotting or jumping. This analysis of a robot with terrestrial legs was performed with the Froude number. According to Alexander’s research [40] on walking bipeds and quadrupeds, walking gaits are abandoned at Froude numbers greater than about 0.5. Therefore, the same analysis should be done by proposing a Froude number for underwater environments. This would enable a better understanding of the maximum walking and transition speeds, which depend on hydrodynamic constants such as the hydrodynamic mass and buoyancy.
The walking speed is also limited due to the reaction force in the plane. Due to the buoyancy, the force in the z-direction of the foot decreases, reducing the limit of the reaction force. To prevent the robot from sliding, this reaction force in the plane must be greater than the force generated by the damping of the water, which depends on the hydrodynamic constants and the speed of the robot. Equating Equation (18) with Equation (4), we obtain the following.
Solving this inequality in the case of our planar robot, the centre of mass velocity must be . At velocities greater than this speed, the robot would slide. Obviously, this is a theoretical value, but it is still very low. In the real experiment, at the speed of , the robot did not present a slide. Upon increasing the speed, the robot could walk but presented a slide in certain areas. In order to overcome this speed limit, the hydrodynamic constants would have to be reduced, which could be achieved more hydrodynamic designs.
Regarding the proposal of Uzmp for walking underwater, researchers Yuta Kojio et al. [10] presented a proposal for a humanoid robot to walk semi-submerged. They proposed using the terrestrial ZMP plus an auxiliary variable, which only depends on the quadratic damping, without taking into account the hydrodynamic mass. However, we determined that this variable cannot be neglected, since its value is important; in our case, it causes the mass of the robot to double. On the other hand, not taking into account the linear damping at low speeds (less than 1 m/s) could also lead to error since, as Fossen [39] mentioned, linear damping at low speeds may be greater than quadratic damping. For this reason, both should always be taken into account.
The auxiliary Uzmp managed to generate a reference to absorb the hydrodynamic force of the fluid, as observed in Figure 25, causing the robot to step back in order to recover balance. There are different proposals for the absorption of external forces for terrestrial robots; these methods are mainly based on measuring the acceleration of the centre of mass of the robot. This makes sense in terrestrial environments, since it is very difficult to estimate the force of the disturbance before it affects the body. However, with our method we can estimate the force by measuring the speed of the fluid, and that can be done with either our proposed sensor or other more advanced sensors which could even estimate the speed of the fluid before it reaches the robot, such as Doppler effect sensors. This would allow the generation of the reference step before the water disturbance affected the robot.
Figure 21 and Figure 27 demonstrate that the control strategy applied in this investigation works. Compensation control is nothing new, but the fact that it is feedback based on the fluid velocity contributes a lot. The current robots with underwater legs do not measure the speed of the fluid, but rather assume at all times that the fluid is not in motion. This only has a limited range of application, as we know that fluid is always in motion, and that the robot is sensitive to small disturbances. Thus, it is necessary to know the relative velocity of the fluid surrounding the body; this is why the development of the mechanical sensor for the measurement of fluid velocity was important.
5. Conclusions
It can be concluded that the Uzmp proposed in this article gives satisfactory results, as it enables the robot to remain stable during walking. Furthermore, the Uzmp aux. was shown to be able to calculate the stabilization point of the robot in the face of disturbances, generating the trajectory of the centre of mass to react and not to fall. The mechanical sensor developed by our research group was also shown to be of great importance, both for the Uzmp and for the control of the robot. As seen in the Equations, the relative speed of the fluid surrounding the robot is an important variable to measure in order to achieve robot locomotion in underwater environments.
For future research, an underwater inverted pendulum model with thrusters could be proposed, so that the robot’s speed is not limited by the reaction force, compensating for either the hydrodynamic damping force or the buoyancy. It is very likely that future robots with underwater legs will have thrusters for navigation, though they can also be used for locomotion.
Supplementary Materials
The following are available online at https://www.mdpi.com/1424-8220/19/16/3588/s1. Video S1: Dynamic Walking of a Legged Robot in Underwater Environments.
Author Contributions
G.P. contributed to the concept, development of the mathematical model, design, construction and experimentation of the robot, resources, as well as the writing of the article; R.S. contributed to the concept, resources, supervision, project administration and review of the article; F.M.d.E. contributed to the supervision; A.R.B., J.C. and O.Y. reviewed the article.
Funding
This work was supported in part by the Spanish Government Projects under Grant DPI2014-57220-C2-1-P and Grant PGC2018-095939-B-I00, in part by the “RoboCity2030 DIH-CM Madrid Robotics Digital Innovation Hub, S2018/NMT-4331, funded by the ”Programas Actividades I + D en la Comunidad de Madrid”, and in part by Structural Funds of the EU.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Neauman, G. Ocean Currents; Elsevier: New York, NY, USA, 1968. [Google Scholar]
- Duecker, D.A.; Geist, A.R.; Kreuzer, E.; Solowjow, E. Learning Environmental Field Exploration with Computationally Constrained Underwater Robots: Gaussian Processes Meet Stochastic Optimal Control. Sensors 2019, 19, 2094. [Google Scholar] [CrossRef] [PubMed]
- Bonin-Font, F.; Massot-Campos, M.; Negre-Carrasco, P.L.; Oliver-Codina, G.; Beltran, J.P. Inertial Sensor Self-Calibration in a Visually-Aided Navigation Approach for a Micro-AUV. Sensors 2015, 15, 1825–1860. [Google Scholar] [CrossRef] [PubMed]
- Landa-Torres, I.; Manjarres, D.; Bilbao, S.; Del Ser, J. Underwater Robot Task Planning Using Multi-Objective Meta-Heuristics. Sensors 2017, 17, 762. [Google Scholar] [CrossRef] [PubMed]
- Junichi, A.; Mineo, I.; Takashi, N.; Asamu, A. Field test of aquatic walking robot for underwater inspection. In Proceedings of the 7th International Symposium on Automation and Robotics in Construction (ISARC), Bristol, UK, 5 June 1990. [Google Scholar]
- Kang, H.; Shim, H.; Jun, B.H.; Lee, P.M. Design of the underwater link-joint system for the multi-legged underwater robot “CR200”. In Proceedings of the 2012 Oceans—Yeosu, Yeosu, Korea, 21–24 May 2012; pp. 1–6. [Google Scholar]
- Kim, B.; Shim, H.; Seong, Y.; Gyeong, L.; Jun, B.; Lee, P. Control architecture for stable gait of a six-legged subsea robot CR200 2013. In Proceedings of the 2013 OCEANS—San Diego, San Diego, CA, USA, 23–27 September 2013; pp. 1–4. [Google Scholar]
- Jun, B. Preliminary design of the multi-legged underwater walking robot CR200. In Proceedings of the 2012 Oceans—Yeosu, Yeosu, Korea, 21–24 May 2012; pp. 1–4. [Google Scholar]
- Saltaren, R.; Barroso, A.; Yakrangi, O. Robotics for Seabed Teleoperation: Part-1–Conception and Practical Implementation of a Hybrid Seabed Robot. IEEE Access 2018, 6, 60559–60569. [Google Scholar] [CrossRef]
- Kojio, Y.; Karasawa, T.; Kojima, K.; Koyama, R.; Sugai, F.; Nozawa, S.; Inaba, M. Walking control in water considering reaction forces from water for humanoid robots with a waterproof suit. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Calisti, M.; Falotico, E.; Laschi, C. Hopping on Uneven Terrains with an Underwater One-Legged Robot. IEEE Robot. Autom. Lett. 2016, 1, 461–468. [Google Scholar] [CrossRef]
- Picardi, G.; Laschi, C.; Calisti, M. Model-based open loop control of a multigait legged underwater robot. Mechatronics 2018, 55, 162–170. [Google Scholar] [CrossRef]
- Saltarén, R.; Portilla, G.; Barroso, A.; Cely, J. A sensor based on a spherical parallel mechanism for the measurement of fluid velocity: Physical modelling and computational analysis. Sensors 2018, 18, 2867. [Google Scholar] [CrossRef] [PubMed]
- Portilla, G.; Saltarén, R.; Barroso, A.R.; Cely, J.; Yakrangi, O. A Sensor Based on a Spherical Parallel Mechanism for the Measurement of Fluid Velocity: Experimental Development. IEEE Access 2019, 7, 16145–16154. [Google Scholar] [CrossRef]
- Franz, Z. Mechanics of Solids and Fluids; Springer: New York, NY, USA, 2012; pp. 225–256. [Google Scholar]
- Antonelli, G. Underwater Robots; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fossen, T.I. Marine control system-guidance, navigation and control of ships, rigs and underwater vehicles. Mar. Cybemet. 2002, 1, 74. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Biped walking pattern generation by using preview control of zero-moment point. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 1620–1626. [Google Scholar]
- Feastherstone, R. Rigid Body Dynamics Algorithms; Springer: Sydney, Australia, 2008. [Google Scholar]
- Gehring, C.; Coros, S.; Hutter, M.; Bloesch, M.; Hoepflinger, M.A.; Siegwart, R. Control of dynamic gaits for a quadrupedal robot. In Proceedings of the 2013 IEEE international conference on Robotics and automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3287–3292. [Google Scholar]
- Ogata, K. Ingeniería de Control Moderna, 5th ed.; Pearson Educación: Madrid, Spain, 2010. [Google Scholar]
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems: Modelling, Identification and Control; Springer Science & Business: London, UK, 2012. [Google Scholar]
- Konami, S.; Nishiumi, T. Hydraulic Control Systems; World Scientific Publishing Company: Singapore, 2016. [Google Scholar]
- Raibert, M. Legged Robots that Balance; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Sreenath, K.; Park, H.; Poulakakis, I.; Grizzle, J. A compliant hybrid zero dynamics controller for stable, efficient and fast bipedal walking on MABEL. Int. J. Robot. Res. 2011, 30, 1170–1193. [Google Scholar] [CrossRef]
- Ramezani, A.; Hurst, J.; Hamed, K.; Grizzle, J. Performance analysis and feedback control of ATRIAS, a three-dimensional bipedal robot. J. Dyn. Syst. 2014, 136, 021012. [Google Scholar] [CrossRef]
- Chevallereau, C.; Abba, G.; Aoustin, Y.; Plestan, F.; Westervelt, E.; Wit, C.; Grizzle, J. Rabbit: A Testbed for Advanced Control Theory. IEEE Control Syst. Mag. 2003, 23, 57–79. [Google Scholar]
- Gough, V.; Whitehall, S. Universal Tyre Testing Machine; International Technical Congress FISITA: London, UK, 1962. [Google Scholar]
- Stewart, D. Platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. The optimum kinematic design of a spherical three-degree-of-freedom parallel manipulator. J. Mech. Transm. Autom. 1989, 111, 202–207. [Google Scholar] [CrossRef]
- Merlet, J. Parallel Robots, 2nd ed.; Springer: Dordrecht, The Nertherlands, 2006. [Google Scholar]
- Korotkin, A.I. Added Masses of Ship Structures; Springer Science & Business: Petersburg, Russia, 2008. [Google Scholar]
- Eng, Y.; Lau, W.; Low, E. Identification of the hydrodynamics coefficients of an underwater vehicle using free decay pendulum motion. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 19–21 March 2008. [Google Scholar]
- Ross, A.; Fossen, T.; Johansen, T. Identification of underwater vehicle hydrodynamic coefficients using free decay tests. IFAC Proc. Vol. 2004, 37, 363–368. [Google Scholar] [CrossRef]
- Morrison, A.; Yoerger, D. Determination of the hydrodynamic parameters of an underwater vehicle during small scale, nonuniform, 1-dimensional translation. In Proceedings of the OCEANS, Victoria, BC, Canada, 18–21 October 1993; p. II277. [Google Scholar]
- Sumer, B.M.; Fredsoe, J. Hydrodynamics around Cylindrical Structures; World Scientific Publishing: Singapore, 1997. [Google Scholar]
- Thomson, W.T. Theory of Vibration with Applications; CRC Press: New York, NY, USA, 1993. [Google Scholar]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer Science & Business: London, UK, 2009. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Alexander, R. The gaits of bipedal and quadrupedal animals. Int. J. Robot. Res. 1984, 3, 49–59. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).