Time-Frequency Characteristics of In-Home Radio Channels Influenced by Activities of the Home Occupant
Abstract
1. Introduction
1.1. Background
1.2. Motivation and Contribution
2. Measurement Methodology
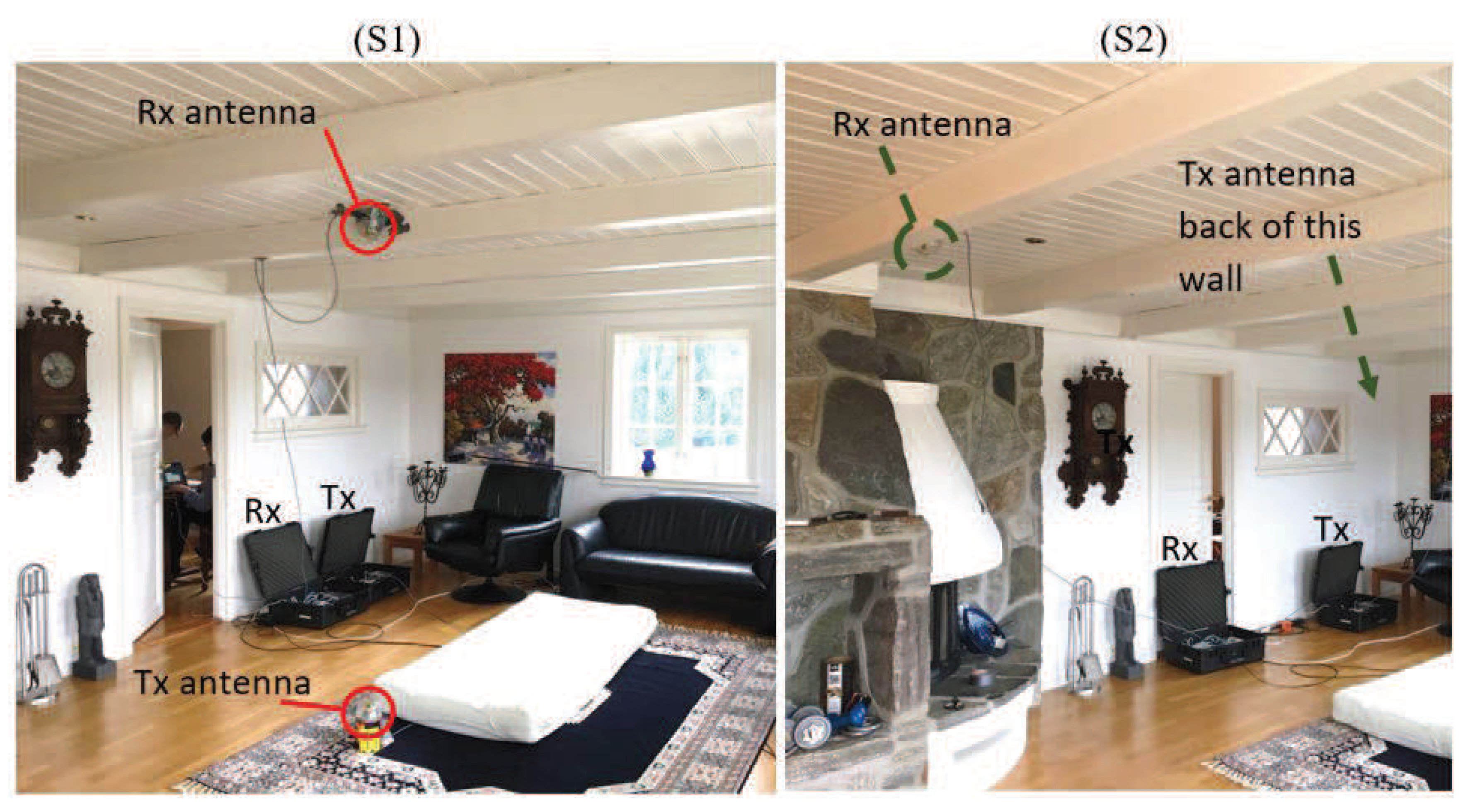
2.1. Equipment
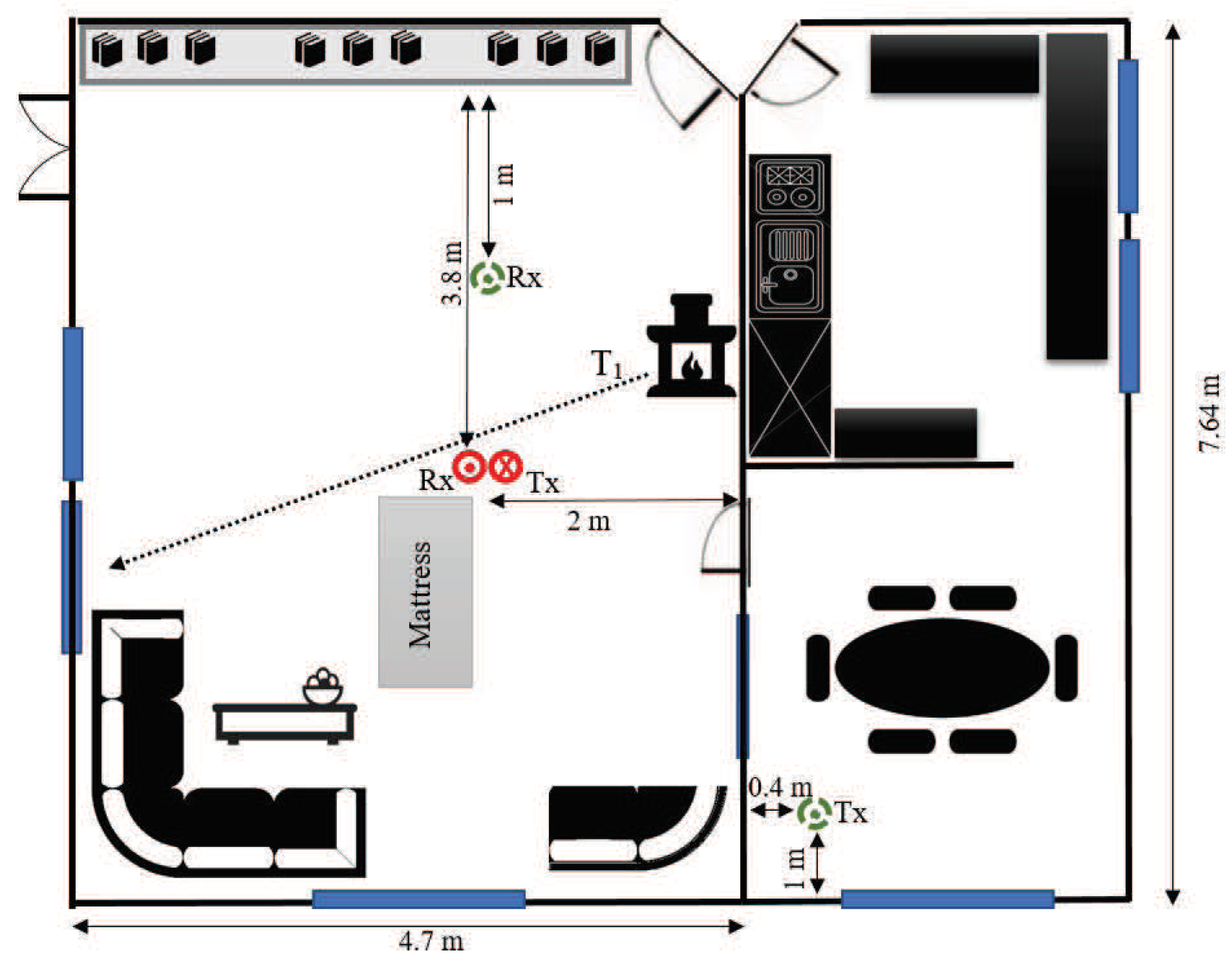
2.2. Propagation Environment
2.3. Scenarios
- (a)
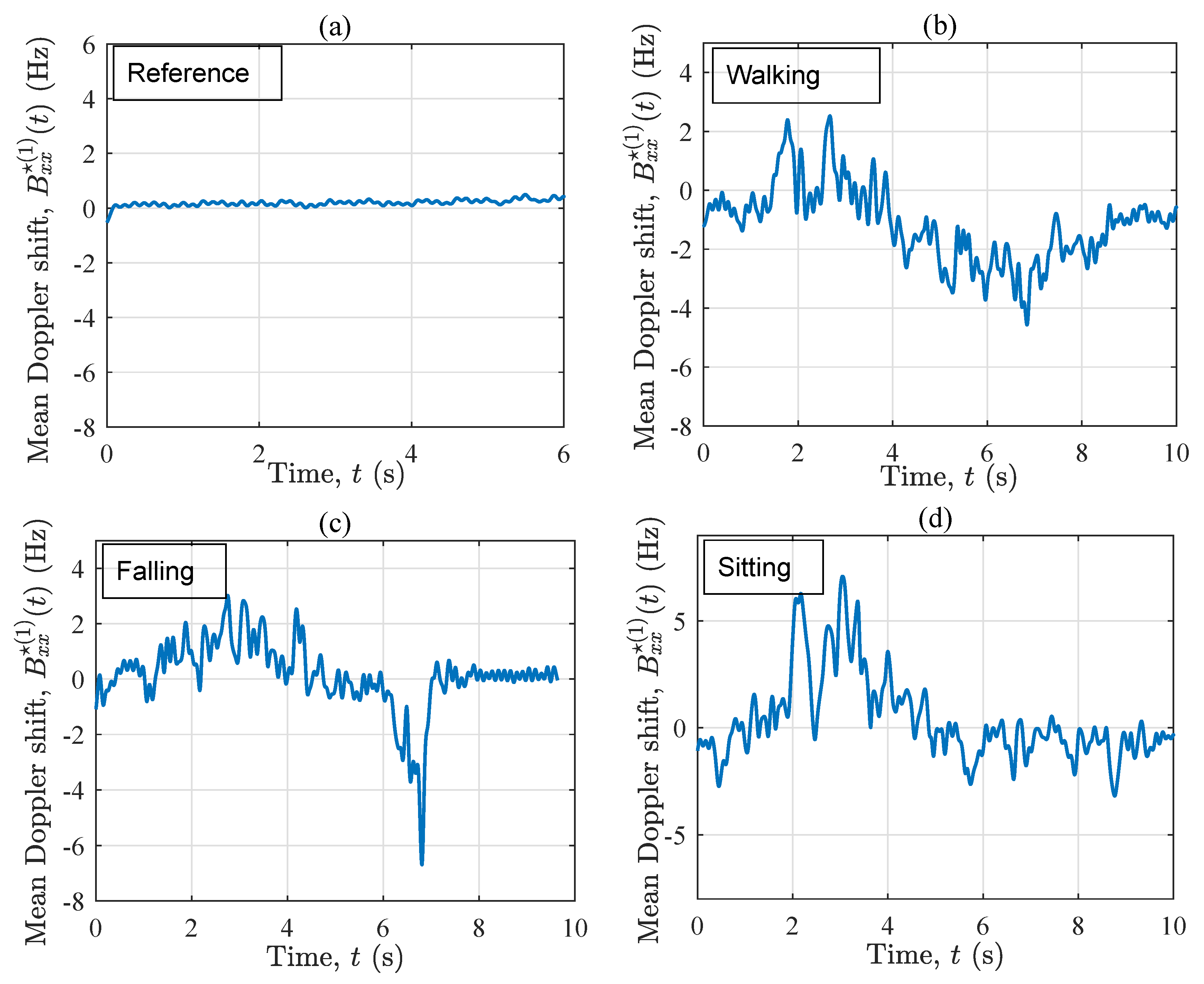
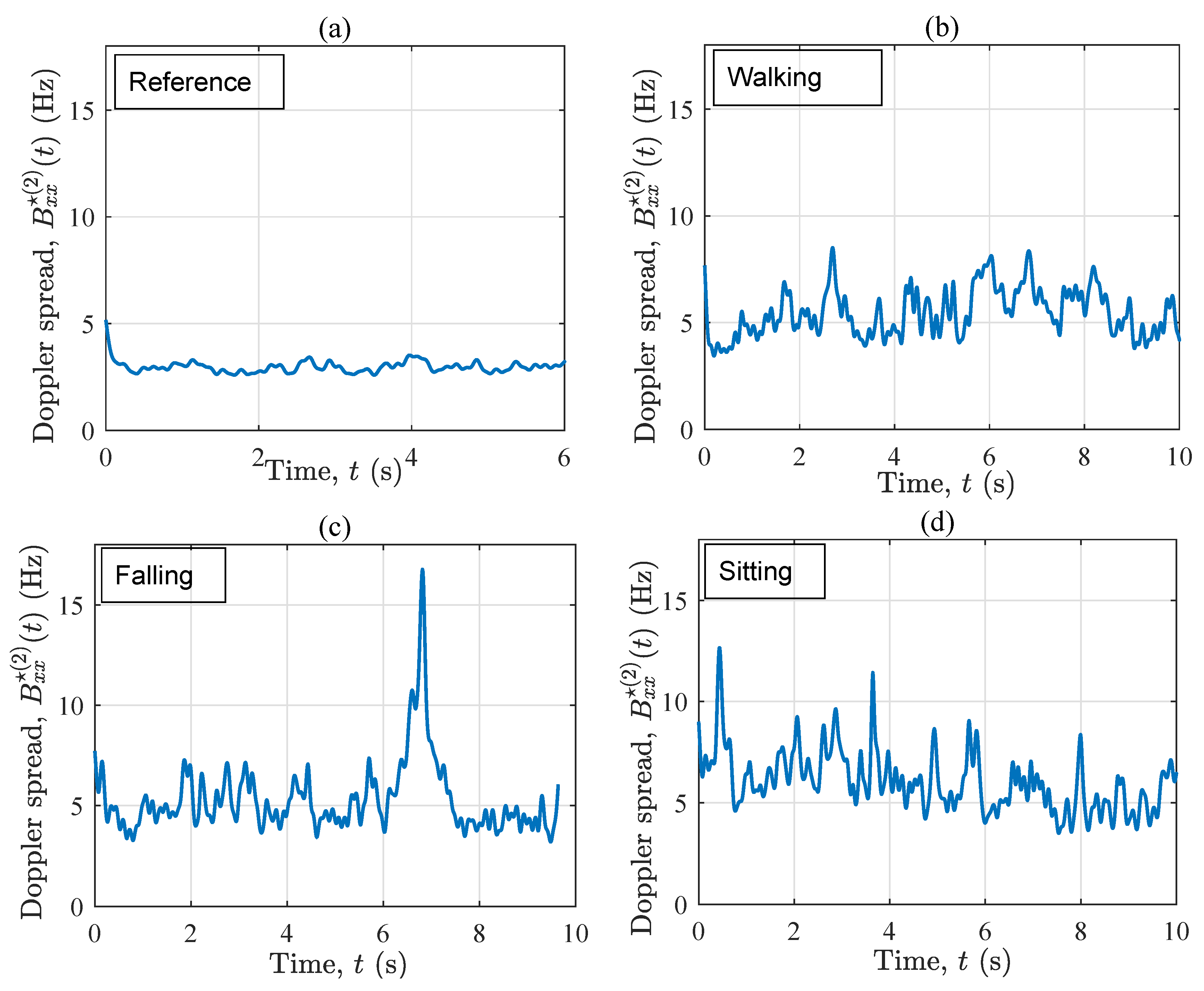
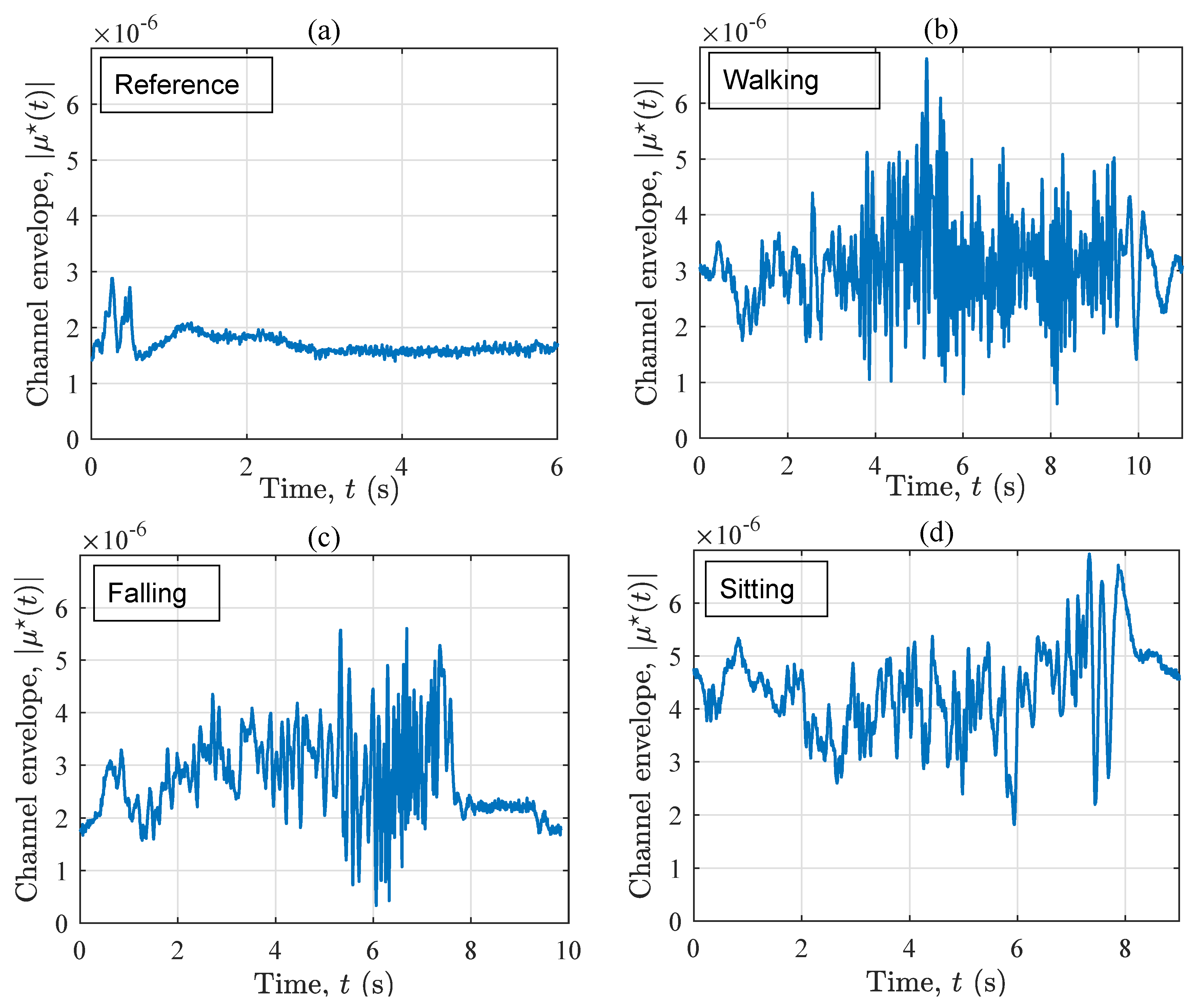
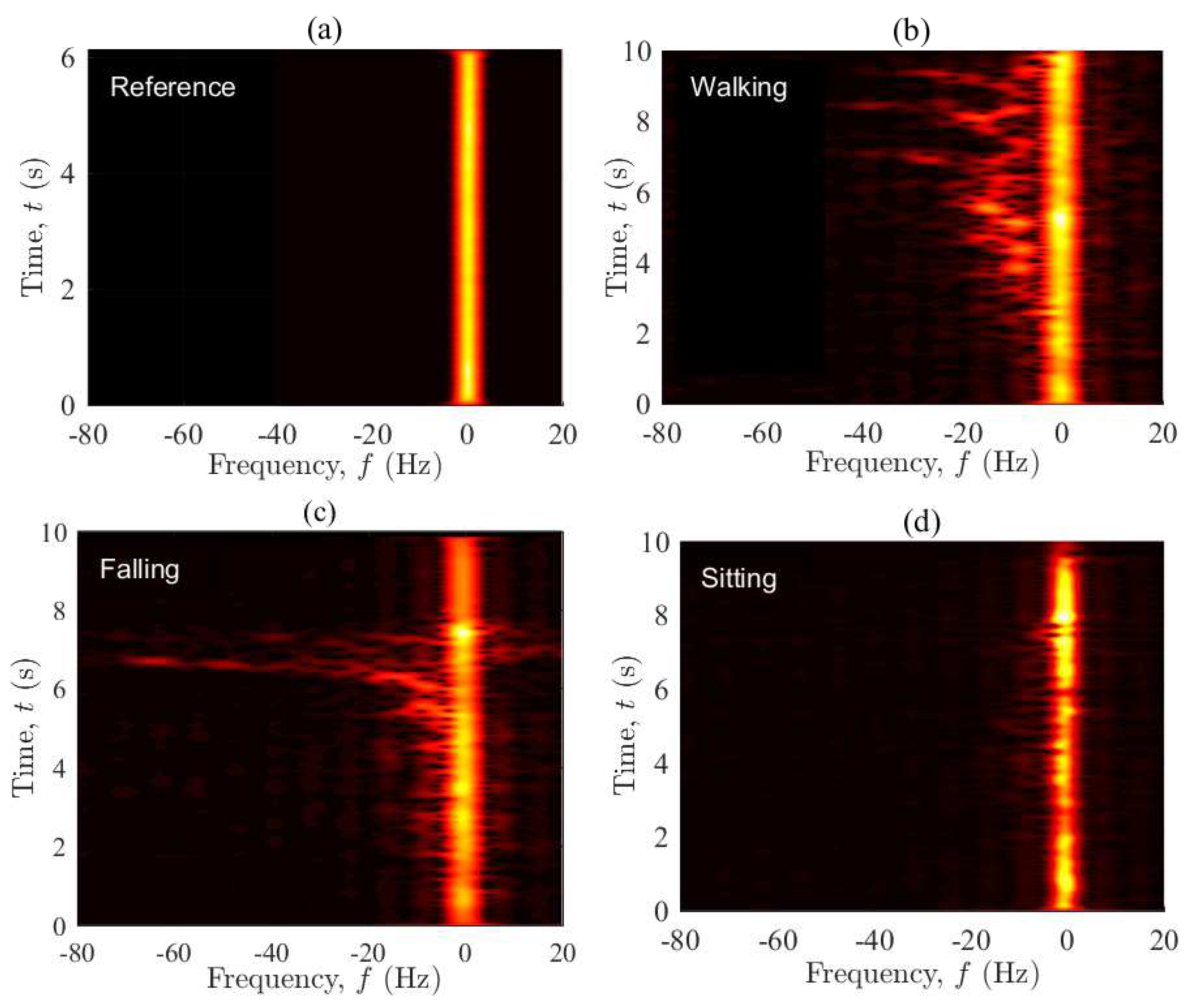
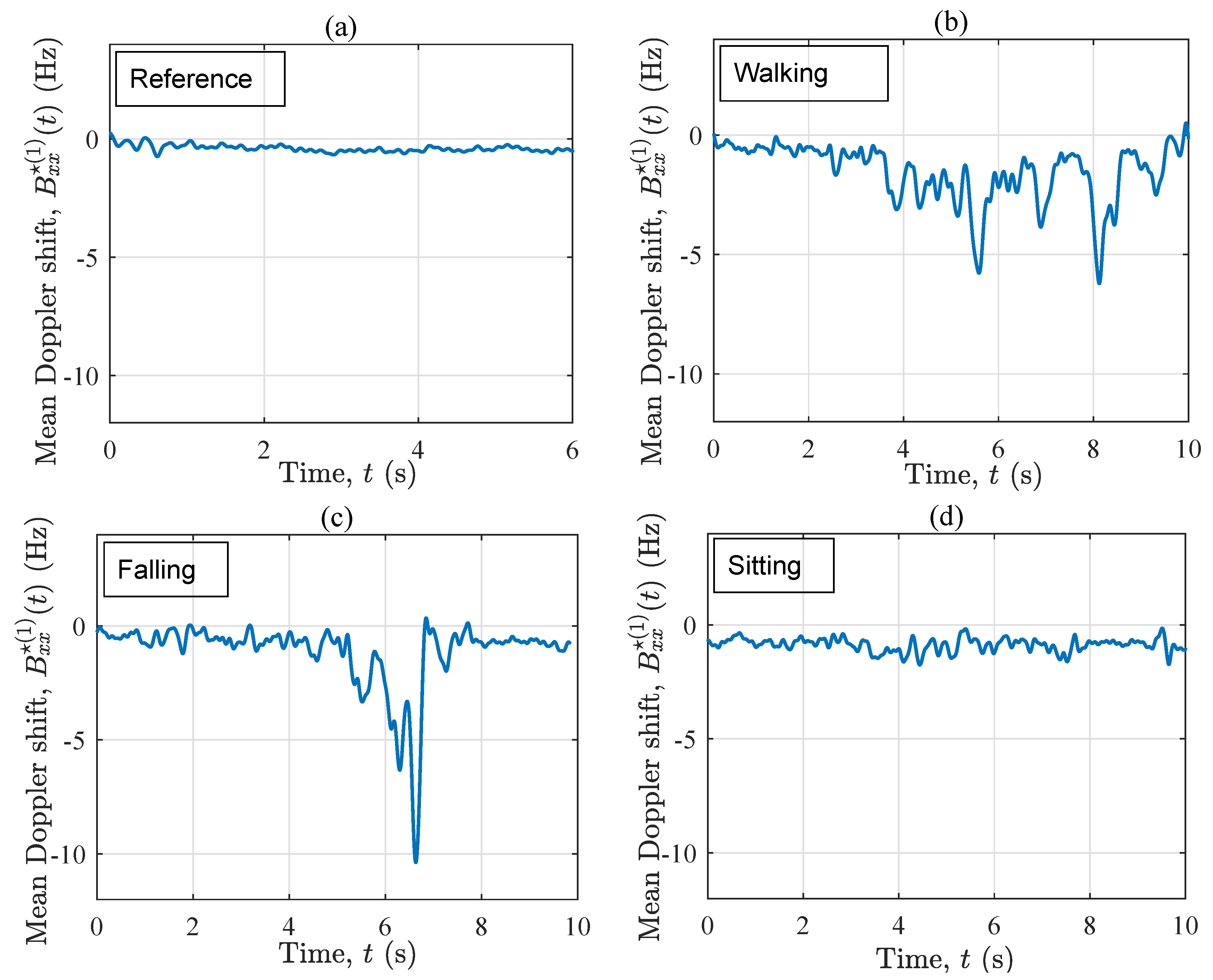
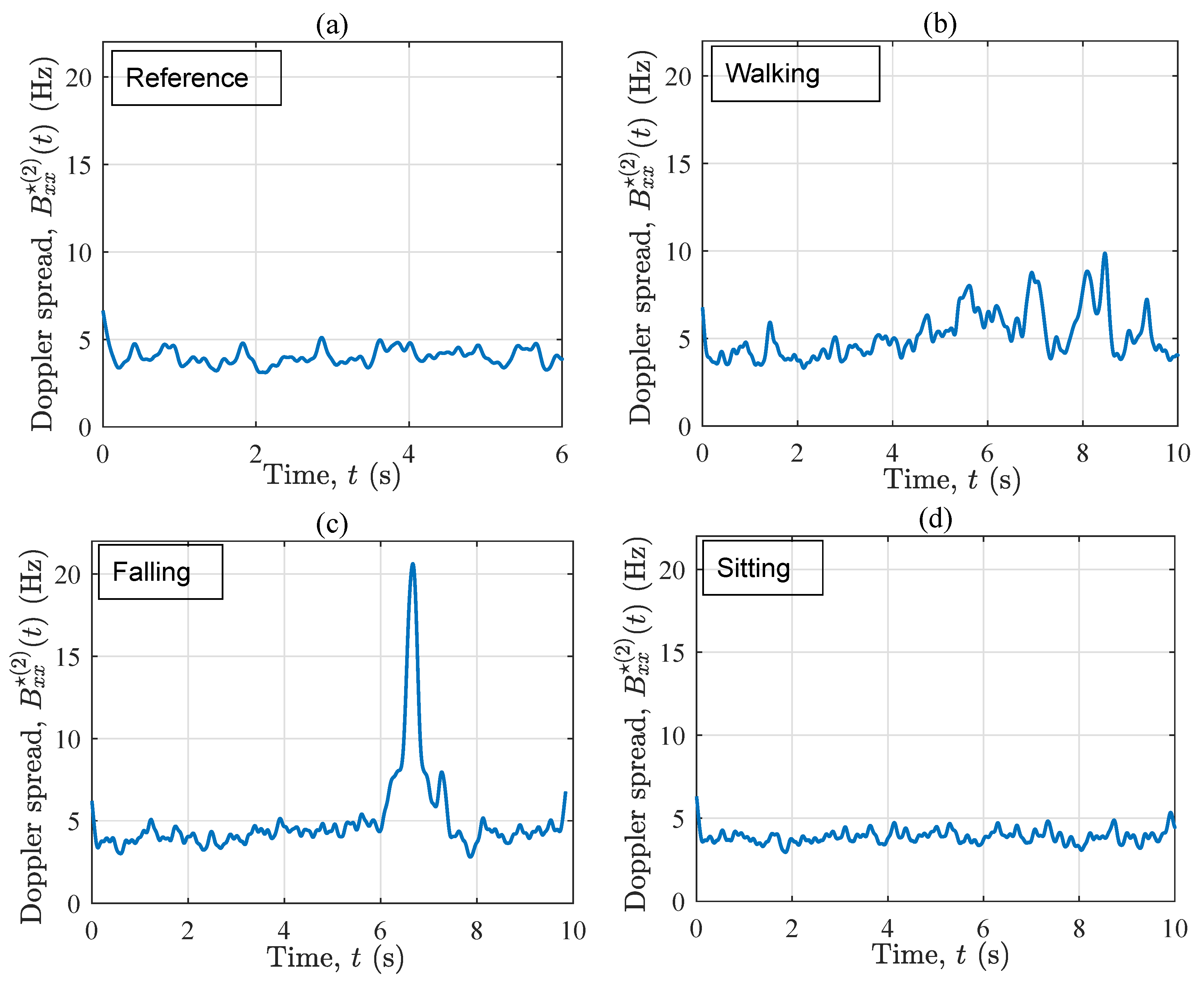
- Reference: Stay out of the living area without any physical activities.This scenario gives a benchmark for comparing the properties of the stationary channel with those of the non-stationary channels (associated with the following activities).
- (b)
- Walking: Walk slowly along the trajectory towards the window (see Figure 2) and stop at the destination point.This scenario is designed to analyze the influence of the normal walking of an elderly person on the channel characteristics.
- (c)
- Falling: Walk slowly along to the mattress, simulate a relatively fast fall (less than a second) on the mattress, then lie motionless on the mattress.In this scenario, the impact of rapid movement variations on the channel characteristics is investigated.
- (d)
- Sitting: Walk slowly along and sit slowly down on a wooden chair (not shown in Figure 1 and Figure 2), where the mattress was previously placed.The impact of slow motions of the home occupant on the channel characteristics is studied in this scenario. Moreover, it is intended to see if the impact of the last two action plans on the time-frequency behavior of the channel is distinguishable.
3. Analysis Methodology
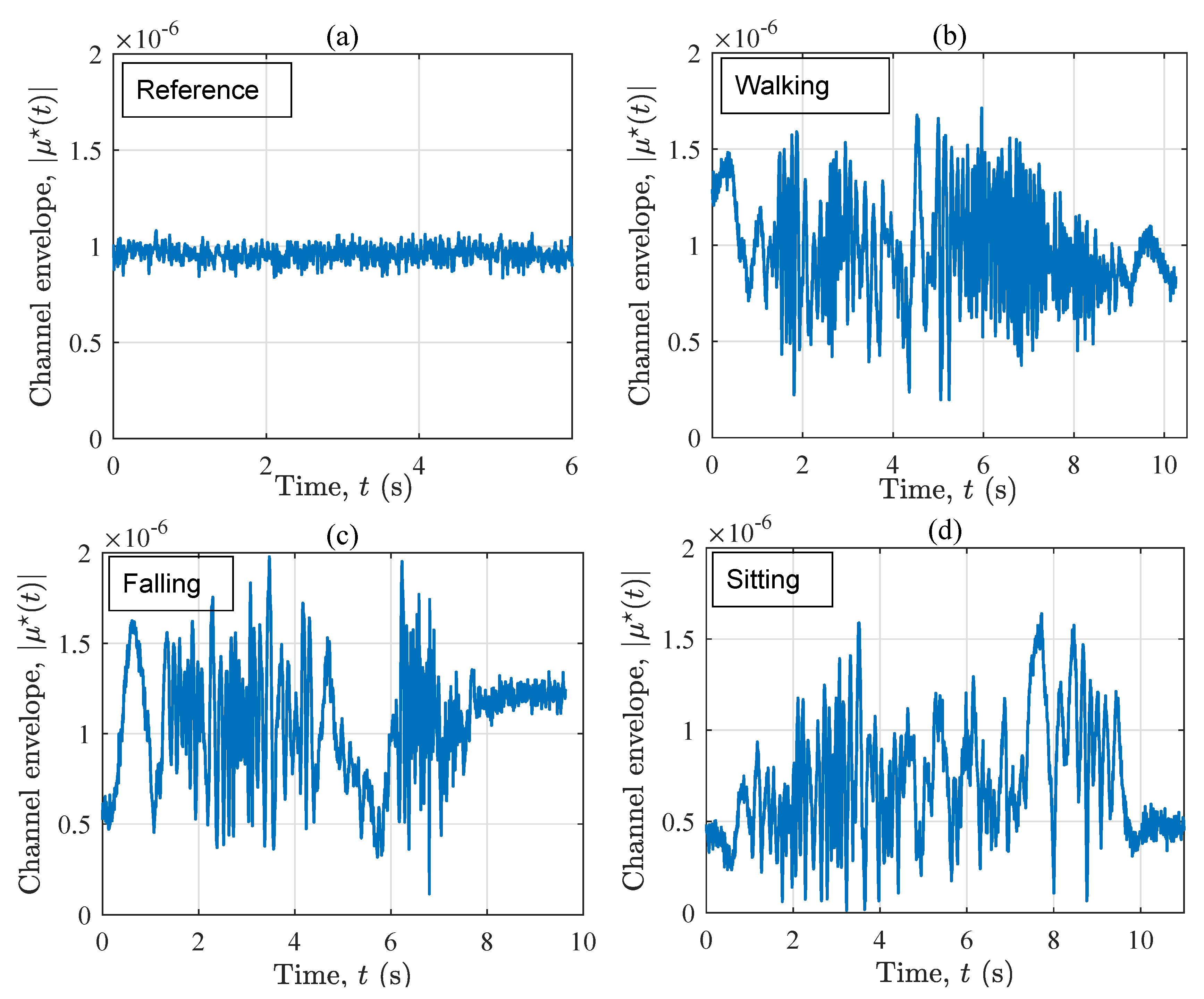
3.1. Complex Channel Gain
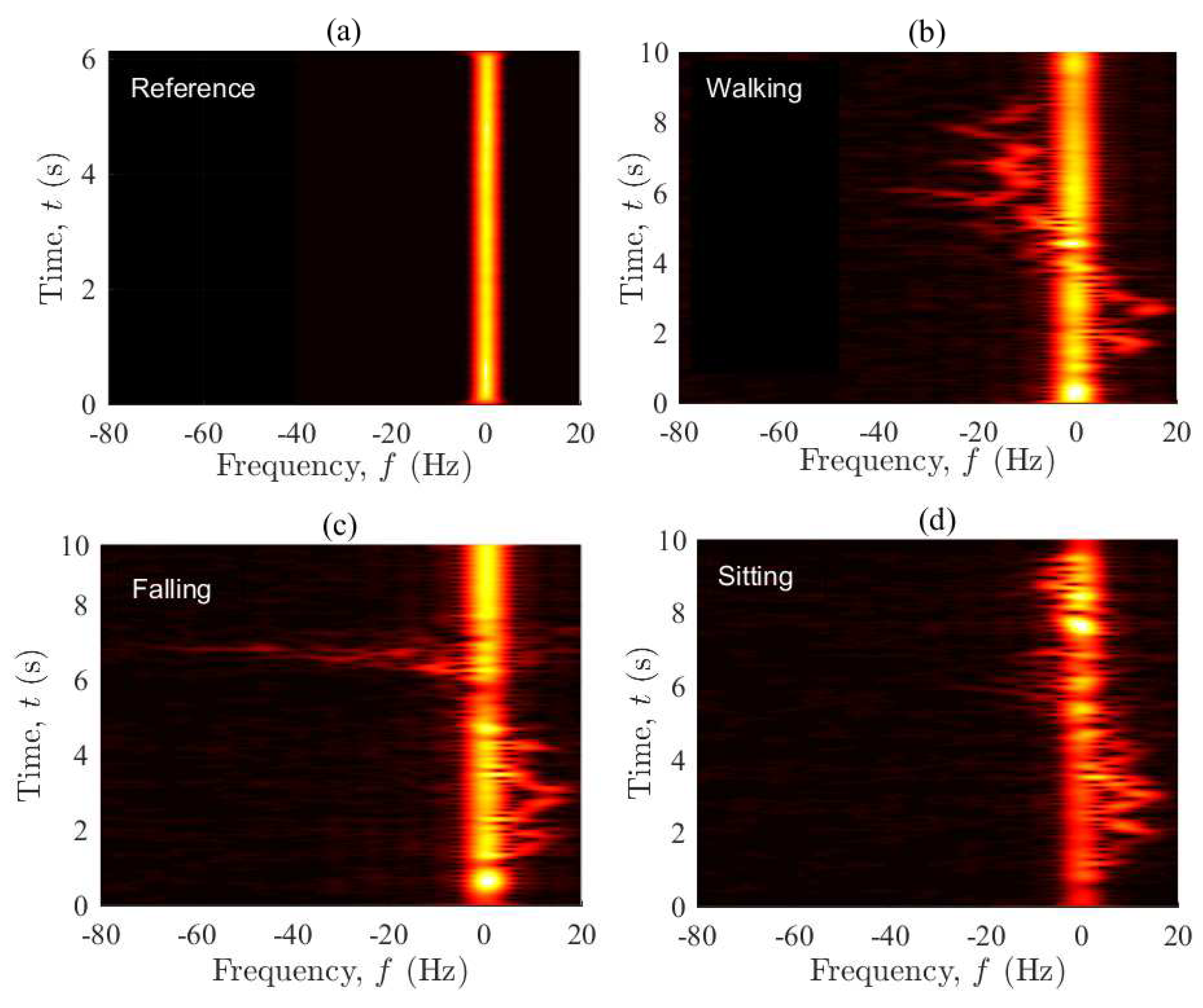
3.2. Spectrogram
3.3. Instantaneous Doppler Characteristics
4. Measurement Results
4.1. LOS Condition (S1)
4.2. OLOS Condition (S2)
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kalache, A. WHO Global Report on Falls Prevention in Older Age; Department of Ageing and Life Course: Geneva, Switzerland, 2007. [Google Scholar]
- Houry, D.; Florence, C.; Baldwin, G.; Stevens, J.; McClure, R. The CDC Injury Center’s Response to the Growing Public Health Problem of Falls Among Older Adults. Am. J. Lifestyle Med. 2016, 10, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Erol, B.; Amin, M.G. Fall motion detection using combined range and Doppler features. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 2075–2080. [Google Scholar] [CrossRef]
- Rougier, C.; Meunier, J.; St-Arnaud, A.; Rousseau, J. Robust Video Surveillance for Fall Detection Based on Human Shape Deformation. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 611–622. [Google Scholar] [CrossRef]
- Zhang, Z.; Conly, C.; Athitsos, V. A Survey on Vision-based Fall Detection. In Proceedings of the 8th ACM International Conference on PErvasive Technologies Related to Assistive Environments, PETRA’15, Corfu, Greece, 1–3 July 2015; ACM: New York, NY, USA, 2015; pp. 46:1–46:7. [Google Scholar] [CrossRef]
- Rimminen, H.; Lindström, J.; Linnavuo, M.; Sepponen, R. Detection of falls among the elderly by a floor sensor using the electric near field. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1475–1476. [Google Scholar] [CrossRef] [PubMed]
- Mubashir, M.; Shao, L.; Seed, L. A survey on fall detection: Principles and approaches. Neurocomputing 2013, 100, 144–152, Special issue: Behaviours in video. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, P.; Pan, A.; Guo, J.; Sun, W.; Wang, L.; Chen, X.; Liu, Z. A Survey of Fall Detection Algorithm for Elderly Health Monitoring. In Proceedings of the 2015 IEEE Fifth International Conference on Big Data and Cloud Computing, Dalian, China, 26–28 August 2015; pp. 270–274. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A Survey on Human Activity Recognition using Wearable Sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Delahoz, Y.S.; Labrador, M.A. Survey on Fall Detection and Fall Prevention Using Wearable and External Sensors. Sensors 2014, 14, 19806–19842. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Y.D.; Tao, W.; Amin, M.G. Radar-based fall detection based on Doppler time-frequency signatures for assisted living. IET Radar Sonar Navig. 2015, 9, 164–172. [Google Scholar] [CrossRef]
- Su, B.Y.; Ho, K.C.; Rantz, M.J.; Skubic, M. Doppler Radar Fall Activity Detection Using the Wavelet Transform. IEEE Trans. Biomed. Eng. 2015, 62, 865–875. [Google Scholar] [CrossRef]
- Liu, L.; Popescu, M.; Skubic, M.; Rantz, M.; Yardibi, T.; Cuddihy, P. Automatic fall detection based on Doppler radar motion signature. In Proceedings of the 2011 5th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth) and Workshops, Dublin, Ireland, 23–26 May 2011; pp. 222–225. [Google Scholar] [CrossRef]
- Hong, J.; Tomii, S.; Ohtsuki, T. Cooperative fall detection using Doppler radar and array sensor. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 3492–3496. [Google Scholar] [CrossRef]
- Rivera, L.R.; Ulmer, E.; Zhang, Y.D.; Tao, W.; Amin, M.G. Radar-based fall detection exploiting time-frequency features. In Proceedings of the 2014 IEEE China Summit International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 713–717. [Google Scholar] [CrossRef]
- Peng, Z.; Muñoz-Ferreras, J.; Gómez-García, R.; Li, C. FMCW radar fall detection based on ISAR processing utilizing the properties of RCS, range, and Doppler. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Erol, B.; Amin, M.G.; Boashash, B. Range-Doppler radar sensor fusion for fall detection. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 819–824. [Google Scholar] [CrossRef]
- Yang, T.; Cao, J.; Guo, Y. Placement selection of millimeter wave FMCW radar for indoor fall detection. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Adib, F.; Kabelac, Z.; Katabi, D.; Miller, R.C. 3D Tracking via Body Radio Reflections. In Proceedings of the 11th USENIX Conference on Networked Systems Design and Implementation, NSDI’14, Seattle, WA, USA, 2–4 April 2014; USENIX Association: Berkeley, CA, USA, 2014; pp. 317–329. [Google Scholar]
- EMERALD. From Wearables to Invisibles. Available online: http://www.emeraldinno.com/ (accessed on 20 July 2019).
- Shrestha, A.; Kernec, J.L.; Fioranelli, F.; Cippitellii, E.; Gambi, E.; Spinsante, S. Feature diversity for fall detection and human indoor activities classification using radar systems. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, UK, 23–26 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Shiba, K.; Kaburagi, T.; Kurihara, Y. Fall Detection Utilizing Frequency Distribution Trajectory by Microwave Doppler Sensor. IEEE Sens. J. 2017, 17, 7561–7568. [Google Scholar] [CrossRef]
- Yao, L.; Sheng, Q.Z.; Li, X.; Gu, T.; Tan, M.; Wang, X.; Zou, W. Compressive Representation for Device-Free Activity Recognition with Passive RFID Signal Strength. IEEE Trans. Mob. Comput. 2017, 17, 293–306. [Google Scholar] [CrossRef]
- Mokhtari, G.; Zhang, Q.; Fazlollahi, A. Non-wearable UWB sensor to detect falls in smart home environment. In Proceedings of the 2017 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kona, HI, USA, 13–17 March 2017; pp. 274–278. [Google Scholar] [CrossRef]
- Firoozi, F.; Borhani, A.; Pätzold, M. Experimental characterization of mobile fading channels aiming the design of non-wearable fall detection radio systems at 5.9 GHz. In Proceedings of the 2016 IEEE International Conference on Communication Systems (ICCS), Shenzhen, China, 14–16 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Halperin, D.; Hu, W.; Sheth, A.; Wetherall, D. Tool release: Gathering 802.11n traces with channel state information. ACM SIGCOMM Comput. Commun. Rev. 2011, 41, 53. [Google Scholar] [CrossRef]
- Ramezani, R.; Xiao, Y.; Naeim, A. Sensing-Fi: Wi-Fi CSI and accelerometer fusion system for fall detection. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 402–405. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, D.; Wang, Y.; Ma, J.; Wang, Y.; Li, S. RT-Fall: A Real-Time and Contactless Fall Detection System with Commodity WiFi Devices. IEEE Trans. Mob. Comput. 2017, 16, 511–526. [Google Scholar] [CrossRef]
- Palipana, S.; Rojas, D.; Agrawal, P.; Pesch, D. FallDeFi: Ubiquitous Fall Detection Using Commodity Wi-Fi Devices. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 1, 155:1–155:25. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Z.; Li, M. Precise Power Delay Profiling with Commodity WiFi. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, MobiCom’15, Paris, France, 7–11 September 2015; ACM: New York, NY, USA, 2015; pp. 53–64. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, K.; Ni, L.M. WiFall: Device-Free Fall Detection by Wireless Networks. IEEE Trans. Mob. Comput. 2017, 16, 581–594. [Google Scholar] [CrossRef]
- Wang, X.; Yang, C.; Mao, S. PhaseBeat: Exploiting CSI Phase Data for Vital Sign Monitoring with Commodity WiFi Devices. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 1230–1239. [Google Scholar] [CrossRef]
- Mager, B.; Patwari, N.; Bocca, M. Fall detection using RF sensor networks. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 3472–3476. [Google Scholar] [CrossRef]
- Kianoush, S.; Savazzi, S.; Vicentini, F.; Rampa, V.; Giussani, M. Leveraging RF signals for human sensing: Fall detection and localization in human-machine shared workspaces. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 1456–1462. [Google Scholar] [CrossRef]
- Kianoush, S.; Savazzi, S.; Vicentini, F.; Rampa, V.; Giussani, M. Device-Free RF Human Body Fall Detection and Localization in Industrial Workplaces. IEEE Internet Things J. 2017, 4, 351–362. [Google Scholar] [CrossRef]
- Agata, Y.; Ohtsuki, T.; Toyoda, K. Doppler Analysis Based Fall Detection Using Array Antenna. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nishimori, K.; Koide, Y.; Kuwahara, D.; Honmay, N.; Yamada, H.; Hideo, M. MIMO Sensor—Evaluation on Antenna Arrangement. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; pp. 2771–2775. [Google Scholar]
- Honma, N.; Nishimori, K.; Sato, H.; Tsunekawa, Y. Compact Antenna Arrangement for MIMO Sensor in Indoor Environment. IEICE Trans. Commun. 2013, E96.B, 2491–2498. [Google Scholar] [CrossRef]
- Ikeda, S.; Tsuji, H.; Ohtsuki, T. Indoor Event Detection with Eigenvector Spanning Signal Subspace for Home or Office Security. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Ikeda, S.; Tsuji, H.; Ohtsuki, T. Indoor Event Detection with Eigenvector Spanning Signal Subspace for Home or Office Security. IEICE Trans. Commun. 2009, E92.B, 2406–2412. [Google Scholar] [CrossRef]
- Hong, J.; Ohtsuki, T. State Classification with Array Sensor Using Support Vector Machine for Wireless Monitoring Systems. IEICE Trans. Commun. 2012, E95.B, 3088–3095. [Google Scholar] [CrossRef]
- Hong, J.; Ohtsuki, T. Signal Eigenvector-Based Device-Free Passive Localization Using Array Sensor. IEEE Trans. Veh. Technol. 2015, 64, 1354–1363. [Google Scholar] [CrossRef]
- Hanssens, B.; Tanghe, E.; Martens, L.; Oestges, C.; Joseph, W. Measurement-Based Analysis of Delay- Doppler Characteristics in an Indoor Environment. IEEE Trans. Antennas Propag. 2016, 64, 370–374. [Google Scholar] [CrossRef]
- Jiang, H.; Cai, C.; Ma, X.; Yang, Y.; Liu, J. Smart Home Based on WiFi Sensing: A Survey. IEEE Access 2018, 6, 13317–13325. [Google Scholar] [CrossRef]
- Rucco, R.; Sorriso, A.; Liparoti, M.; Ferraioli, G.; Sorrentino, P.; Ambrosanio, M.; Baselice, F. Type and Location of Wearable Sensors for Monitoring Falls during Static and Dynamic Tasks in Healthy Elderly: A Review. Sensors 2018, 18, 1613. [Google Scholar] [CrossRef] [PubMed]
- Domenico, S.D.; Pecoraro, G.; Cianca, E.; Sanctis, M.D. Trained-once device-free crowd counting and occupancy estimation using WiFi: A Doppler spectrum based approach. In Proceedings of the 2016 IEEE 12th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), New York, NY, USA, 17–19 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Borhani, A. Indoor Channel Measurement Data—5.9 GHz. Available online: https://codeocean.com/capsule/d540a905-77e7-4588-bec3-f479c2ddfc15/?ID=ac1b21d40e10497e9c48e29463b27853 (accessed on 1 May 2019).
- Abdelgawwad, A.; Pätzold, M. On the Influence of Walking People on the Doppler Spectral Characteristics of Indoor Channels. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Borhani, A.; Pätzold, M. A Non-Stationary Channel Model for the Development of Non-Wearable Radio Fall Detection Systems. IEEE Trans. Wirel. Commun. 2018, 17, 7718–7730. [Google Scholar] [CrossRef]
- Yousefi, S.; Narui, H.; Dayal, S.; Ermon, S.; Valaee, S. A Survey on Behavior Recognition Using WiFi Channel State Information. IEEE Commun. Mag. 2017, 55, 98–104. [Google Scholar] [CrossRef]
- Cai, X.; Peng, B.; Yin, X.; Perez, A. Hough-Transform-Based Cluster Identification and Modeling for V2V Channels Based on Measurements. IEEE Trans. Veh. Technol. 2018, 67, 3838–3852. [Google Scholar] [CrossRef]
- Shui, Y.; Li, F.; Yu, J.; Chen, W.; Li, C.; Yang, K.; Chang, F. Vehicle-to-Vehicle Radio Channels Characteristics for Congestion Scenario in Dense Urban Region at 5.9 GHz. Int. J. Antennas Propag. 2017, 2017, 1751869. [Google Scholar] [CrossRef]
- Borhani, A.; Pätzold, M. The Impact of Human Walking on the Time-Frequency Distribution of In-Home Radio Channels. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 920–922. [Google Scholar] [CrossRef]
- Pätzold, M. Mobile Fading Channels, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Pätzold, M.; Gutiérrez, C.A. Enhancing the resolution of the spectrogram of non-stationary mobile radio channels by using massive MIMO techniques. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017. [Google Scholar]
- Pätzold, M.; Gutiérrez, C.A. Spectrogram Analysis of Multipath Fading Channels under Variations of the Mobile Speed. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Foroughiand, H.; Alishah, M.; Pourreza, H.; Shahinfar, M. Distinguishing Fall Activities using Human Shape Characteristics. In Technological Developments in Education and Automation; Iskander, M., Kapila, V., Karim, M.A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 523–528. [Google Scholar]
- Lee, H.; Ahn, C.R.; Choi, N.; Kim, T.; Lee, H. The Effects of Housing Environments on the Performance of Activity-Recognition Systems Using Wi-Fi Channel State Information: An Exploratory Study. Sensors 2019, 19, 983. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value/Type |
|---|---|
| Carrier frequency | 5.9 GHz |
| Chirp bandwidth | 100 MHz |
| Transmitting power at the antenna port | 16 dBm |
| Maximum delay span | 25.6 s |
| Delay resolution | 10 ns |
| Maximum Doppler shift span | ±967 Hz |
| Number of TX and RX antennas | 1 |
| TX and RX antennas beamwidths | omni-direction |
| Antenna gain | 2 dBi |
| Cable loss in total | 6 dB |
| Temperature | 19 C |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borhani, A.; Pätzold, M.; Yang, K. Time-Frequency Characteristics of In-Home Radio Channels Influenced by Activities of the Home Occupant. Sensors 2019, 19, 3557. https://doi.org/10.3390/s19163557
Borhani A, Pätzold M, Yang K. Time-Frequency Characteristics of In-Home Radio Channels Influenced by Activities of the Home Occupant. Sensors. 2019; 19(16):3557. https://doi.org/10.3390/s19163557
Chicago/Turabian StyleBorhani, Alireza, Matthias Pätzold, and Kun Yang. 2019. "Time-Frequency Characteristics of In-Home Radio Channels Influenced by Activities of the Home Occupant" Sensors 19, no. 16: 3557. https://doi.org/10.3390/s19163557
APA StyleBorhani, A., Pätzold, M., & Yang, K. (2019). Time-Frequency Characteristics of In-Home Radio Channels Influenced by Activities of the Home Occupant. Sensors, 19(16), 3557. https://doi.org/10.3390/s19163557





