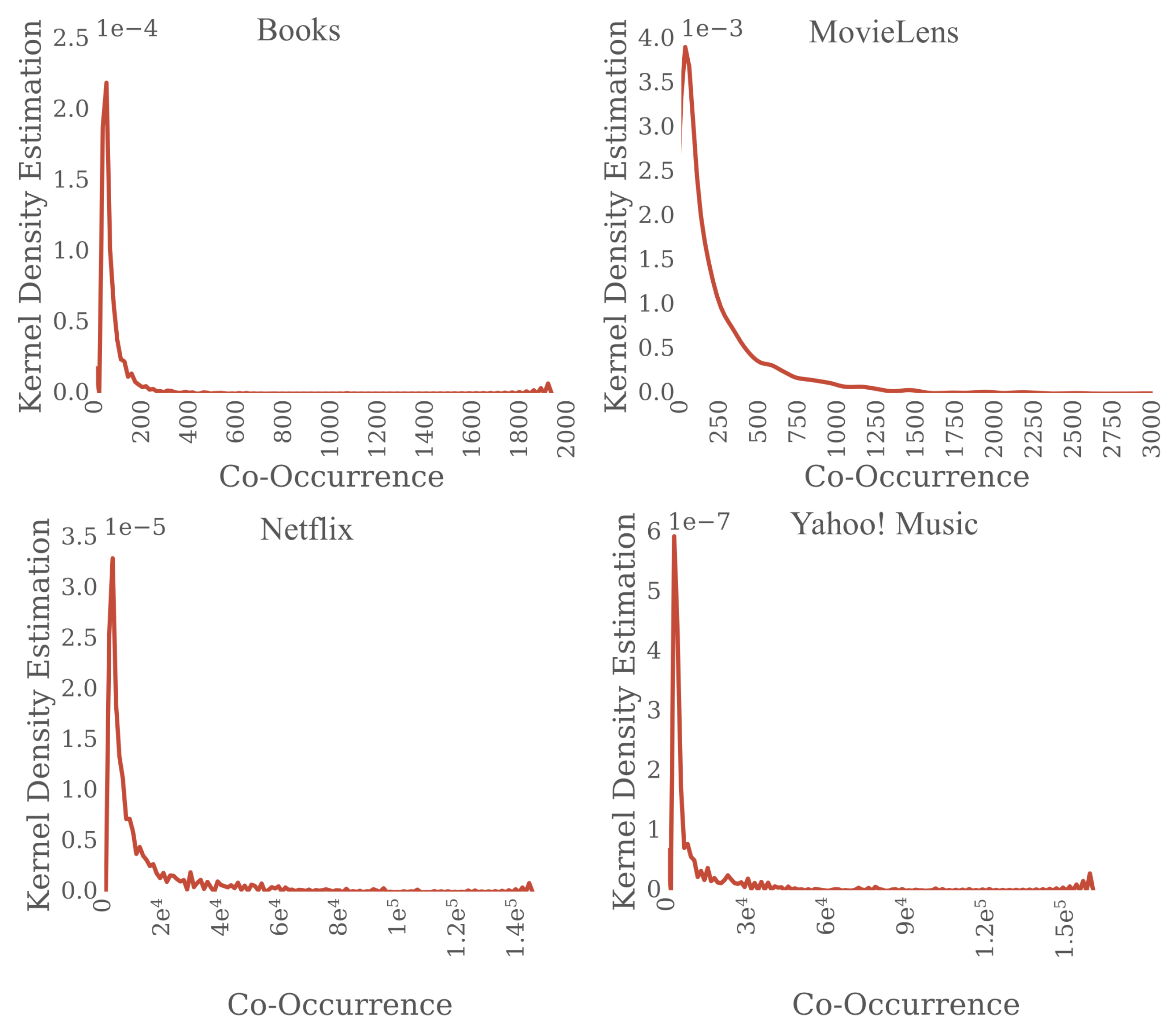
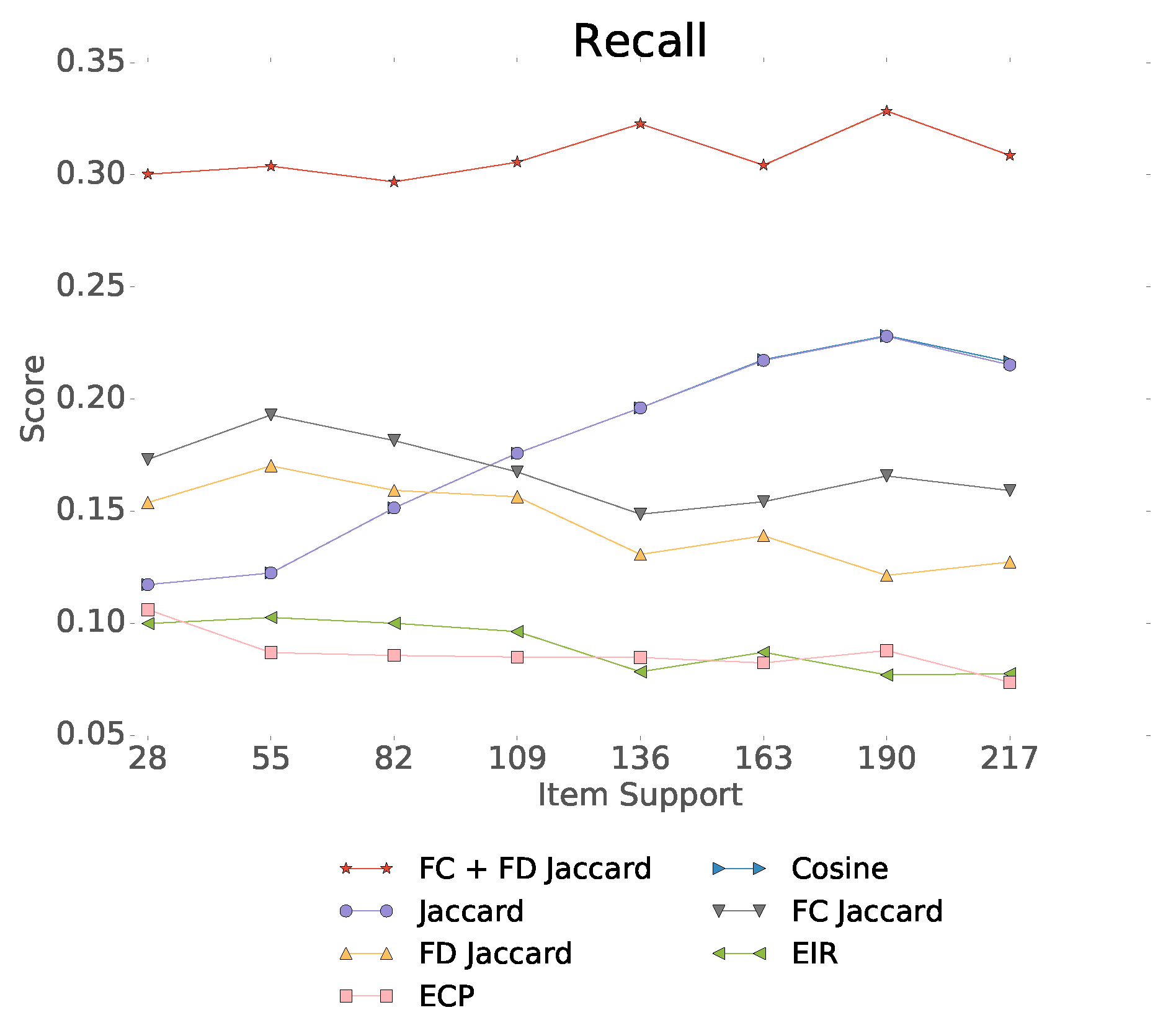
The natural way of item-to-item recommendation is to rank the next candidate items based on their similarity to the last visited item. While the idea is simple, a wide variety of methods exist to compute the distance or divergence of user feedback, content, and other potential item metadata.
In this section, first we enumerate the most common similarity measures among raw item attributes, which will also serve as the baseline in our experiments. Then we describe our new methodology that introduces an item representation in a kernel space built on top of the raw similarity values. Based on the item representation, we define three different types of “kernelized”, transformed similarity measures.
3.1. Raw Attribute Similarity Measures
First, we enumerate distance and divergence measures that directly compare the attributes of the item pair in question. We list both implicit feedback collaborative filtering and content-based measures. The raw attribute similarity formulas yield the natural baseline methods for item-to-item recommendation.
For user implicit feedback on item pairs, various joint and conditional distribution measures can be defined based on the frequencies and of items i and item pairs , as follows.
Empirical Conditional Probability (ECP), which estimates the item transition probability:
where the value 1 in the denominator is used for smoothing.
Additionally, in [
6] the authors suggest the Euclidean Item Recommender (EIR) model to approximate the transition probabilities with the following conditional probability
where
T is the set of items. They learn the item latent vectors
and biases
.
Besides item transitions, one can measure the similarity of the items based on their content (e.g., metadata, text, title). We will measure the content similarity between two items by the Cosine, Jaccard, tf-idf, and the Jensen–Shannon divergence of the bag of words representation of the metadata description.
3.3. Notion of Similarity Based on Fisher Information
In this section, we describe our new method, a feature representation of the items that augments the similarity measures of the previous section by using global information. Our representation can be the basis of performance improvement, since it relies on global structural properties rather than simple statistics between the user feedback or content of the two items in question. In addition, by starting out with multimodal similarity measures, including implicit or explicit user feedback, user independent metadata, such as text description, linkage, or even multimedia content, our machinery yields a parameter-free combination of the different item descriptions. Hence, the current section builds upon and fuses all the possible representations described in the previous sections.
Our method is based on the theory of the tangent space representation of items described in a sequence of papers with the most important steps including [
11,
12,
13]. In this section, we describe the theory and its adaptation to the item-to-item recommendation task where we process two representations, one for the previous and one for the current item.
After describing our feature representation, in the subsequent subsections we give three different distance metrics in the representing space, based on different versions of the feature representations. We start our definition of global structural similarity by considering a set of arbitrary item pair similarity measures, such as the ones listed in the previous section. We include other free model parameters , which can, for example, serve to scale the different raw attributes or the importance of attribute classes. We give a generative model of items i as a random variable . From , we infer the distance and the conditional probability of pairs of items i and j by using all information in .
To define the item similarity generative model, let us consider a certain sample of items
(e.g., most popular or recent items), and assume that we can compute the distance of any item
i from each of
. We consider our current item
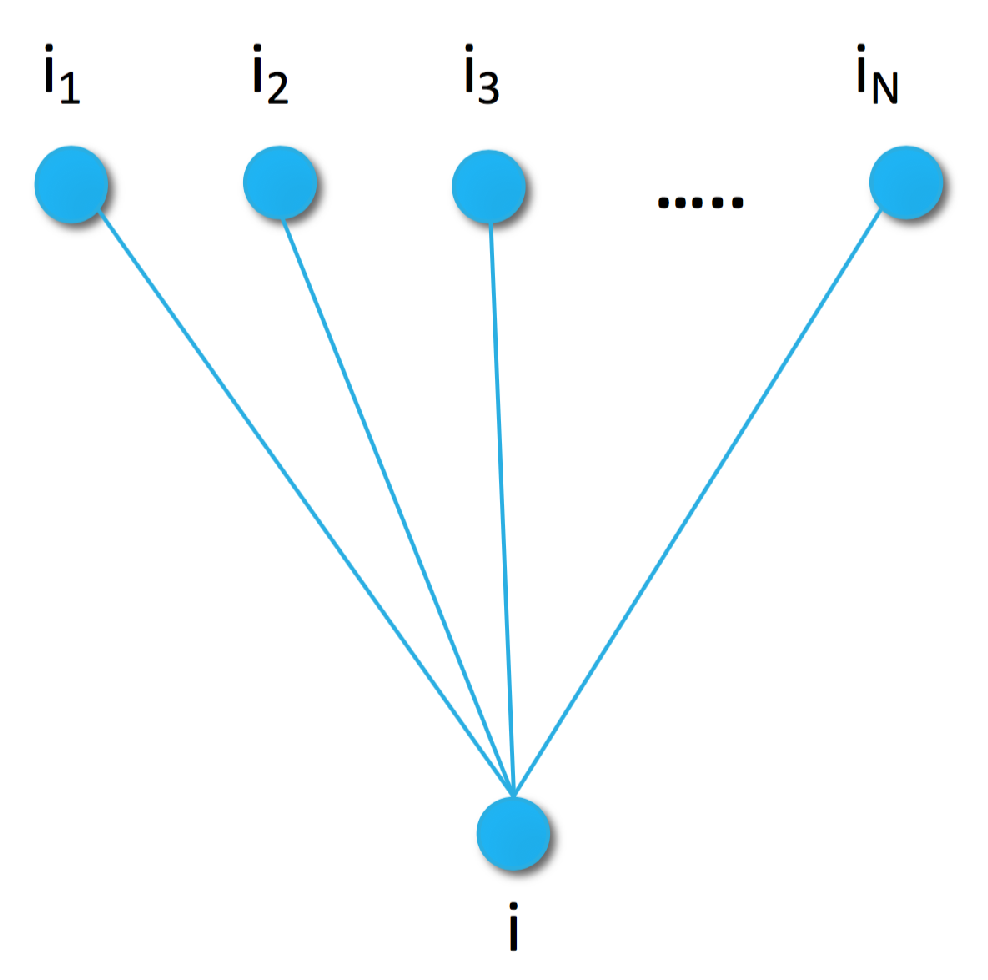
i along with its distance from each
as a random variable generated by a Markov Random Field (MRF). Random Fields are a set of (dependent) random variables. In case of MRF, the connection between the elements is described by an undirected graph satisfying the Markov property [
48]. For example, the simplest Markov Random Field can be obtained by using a graph with edges between item
i and items
, as shown in
Figure 1.
Let us assume that we are given a Markov Random Field generative model for
. By the Hammersley–Clifford theorem [
49], the distribution of
is a Gibbs distribution, which can be factorized over the maximal cliques and expressed by a potential function
U over the maximal cliques as follows:
where
is the energy function and
is the sum of the exponent of the energy function over our generative model, a normalization term called the partition function. If the model parameters are previously determined, then
is a constant.
By using the Markov Random Field defined by the graph in
Figure 1, or some more complex ones defined later, a wide variety of proper energy functions can be used to define a Gibbs distribution. The weak but necessary restrictions are that the energy function has to be positive real valued, additive over the maximal cliques of the graph, and more probable parameter configurations have to have lower energy.
We define our first energy function for (
6) based on the similarity graph of
Figure 1. Since the maximal cliques of that graph are its edges, the energy function has the form
where
is a finite sample set, dist is an arbitrary distance or divergence function of item pairs, and the hyperparameter set
is the weight of the elements in the sample set.
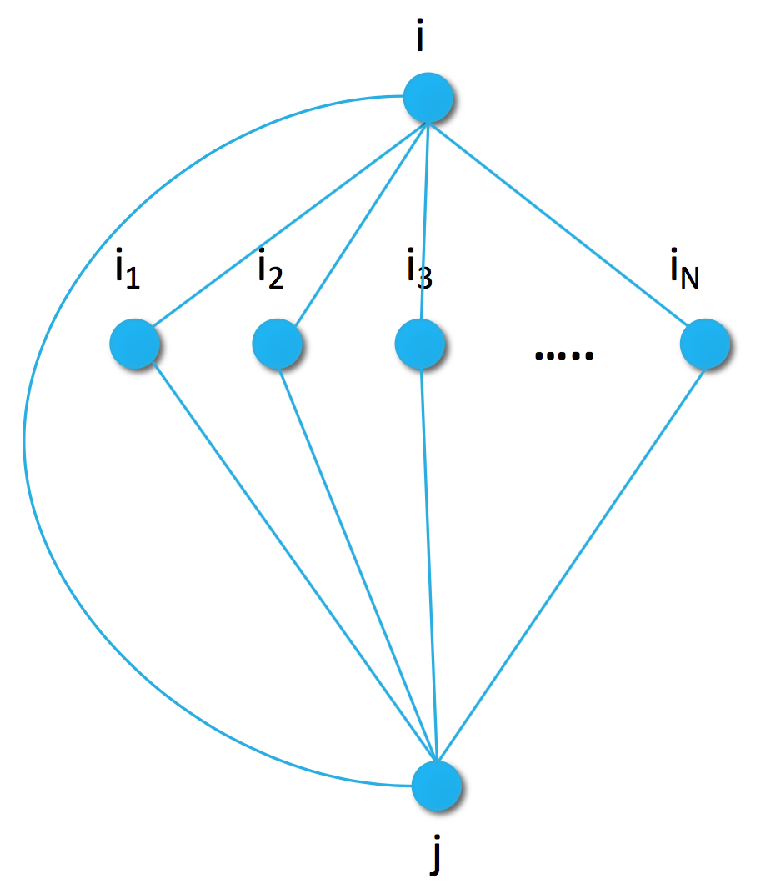
In a more complex model, we capture the connection between pairs of items by extending the generative graph model with an additional node for the previous item as shown in
Figure 2. In the pairwise similarity graph, the maximal clique size increases to three. To capture the joint energy with parameters
, we can use a heuristic approximation similar to the pseudo-likelihood method [
48]: we approximate the joint distribution of each size three clique as the sum of the individual edges by
At first glance, the additive approximation seems to oversimplify the clique potential and falls back to the form of Equation (
8). However, the three edges of clique
n share the hyperparameter
, which connects these edges in our modeling approach.
Based on either of the energy functions in Equation (
8) or (
9), we are ready to introduce the Fisher information to estimate distinguishing properties by using the similarity graphs. Let us consider a general parametric class of probability models
where
. The collection of models with parameters from a general hyperparameter space
can then be viewed as a (statistical) manifold
, provided that the dependence of the potential on
is sufficiently smooth. By [
50],
can be turned into a Riemann manifold by giving an inner product (kernel) at the tangent space of each point
where the inner product varies smoothly with
p.
The notion of the inner product over
allows us to define the so-called Fisher metric on
M. The fundamental result of Čencov [
11] states that the Fisher metric exhibits a unique invariance property under some maps, which are quite natural in the context of probability. Thus, one can view the use of Fisher kernel as an attempt to introduce a natural comparison of the items on the basis of the generative model [
12].
We start by defining the Fisher kernel over the manifold
of probabilities
as in Equation (
6), by considering the tangent space. The tangent vector, which is the row vector defined as
is called the
Fisher score of (the occurrence of) item
i. An intuitive interpretation is that
gives the direction where the parameter vector
should be changed to fit item
i the best [
13]. The
Fisher information matrix is a positive definite matrix of size
, defined as
where the expectation is taken over
, i.e.,
where
T is the set of all items. The corresponding kernel function
is called the
Fisher kernel. We further define the
Fisher vector of item
i as
so that the equation
holds (as
F is symmetric).
Thus, to capture the generative process, the gradient space of is used to derive the Fisher vector, a mathematically grounded feature representation of item i.
3.4. Item-to-Item Fisher Distance (FD)
Based on the feature representation framework of the previous section, in the next three subsections we propose three item similarity measures.
Our first measure arises as an inner product of the Fisher vectors. Any inner product can be used to obtain a metric by having . Using the Fisher kernel , the Fisher distance can be formulated as
Thus, we need to compute the Fisher kernel over our generative model as in (
12). By substituting into (
15), the recommended next item after item
i will be
The computational complexity of the Fisher information matrix estimated on the training set is
where
T is the size of the training set. To reduce the complexity to
, we can approximate the Fisher information matrix with the diagonal as suggested in [
12,
13]. Our aim is then to compute
For this, we observe that
and also that
Combining (
17) and (
18), we get
Also, since
by (
17) and (
18)
i.e., for the energy functions of Equations (
8) and (
9), the diagonal of the Fisher kernel is the standard deviation of the distances from the samples.
Finally, using this information, we are able to compute
as
which gives us the final kernel function as
The formula in (
22) involves the distance values on the right side, which are readily available, and the expected values on the left side, which can be estimated by using the training data. We note that here we make a heuristic approximation: instead of computing the expected values (e.g., by simulation), we substitute the mean of the distances from the training data.
All of the measures in
Section 3 can be used in the energy function as the distance measure after small modifications. Now, let us assume that our similarity graph (
Figure 1) has only one sample element
i, and the conditional item is also
i. The Fisher kernel will be
where
and
are the expected value and variance of distance from item
i. Therefore, if we fix
,
and
are positive constants, and the minimum of the Fisher distance is
Hence, if we measure the distance over the latent factors of EIR, the recommended items will be the same as defined by EIR, see Equation (
10) in [
6].
3.5. Item-to-Item Fisher Conditional Score (FC)
Our second item similarity measure relies on the item-item transition conditional probability
computed from the Fisher scores of Equation (
10). As the gradient corresponds to how well the model fits the sample, the easiest fit as next item
has the lowest norm; hence,
We compute
by the Bayes theorem as
To compute, we need to determine the joint and the marginal distributions
and
for a particular item pair. For an energy function as in Equation (
8), we have seen in (
19) that the Fisher score of
i has a simple form,
and it can be seen similarly for Equation (
9) that
Now, if we put (
28) and (
29) into (
27), several terms cancel out and the Fisher score becomes
Substituting the mean instead of computing the expected value as in
Section 3.4, the probabilities
. Using this information, we can simplify the above formula:
Since the second term is independent of k, it has to be calculated only once, making the computation . Thus, this method is less computationally efficient than the previous one.