A Robust Indoor Positioning Method based on Bluetooth Low Energy with Separate Channel Information
Abstract
1. Introduction
2. Related Work
3. Algorithm
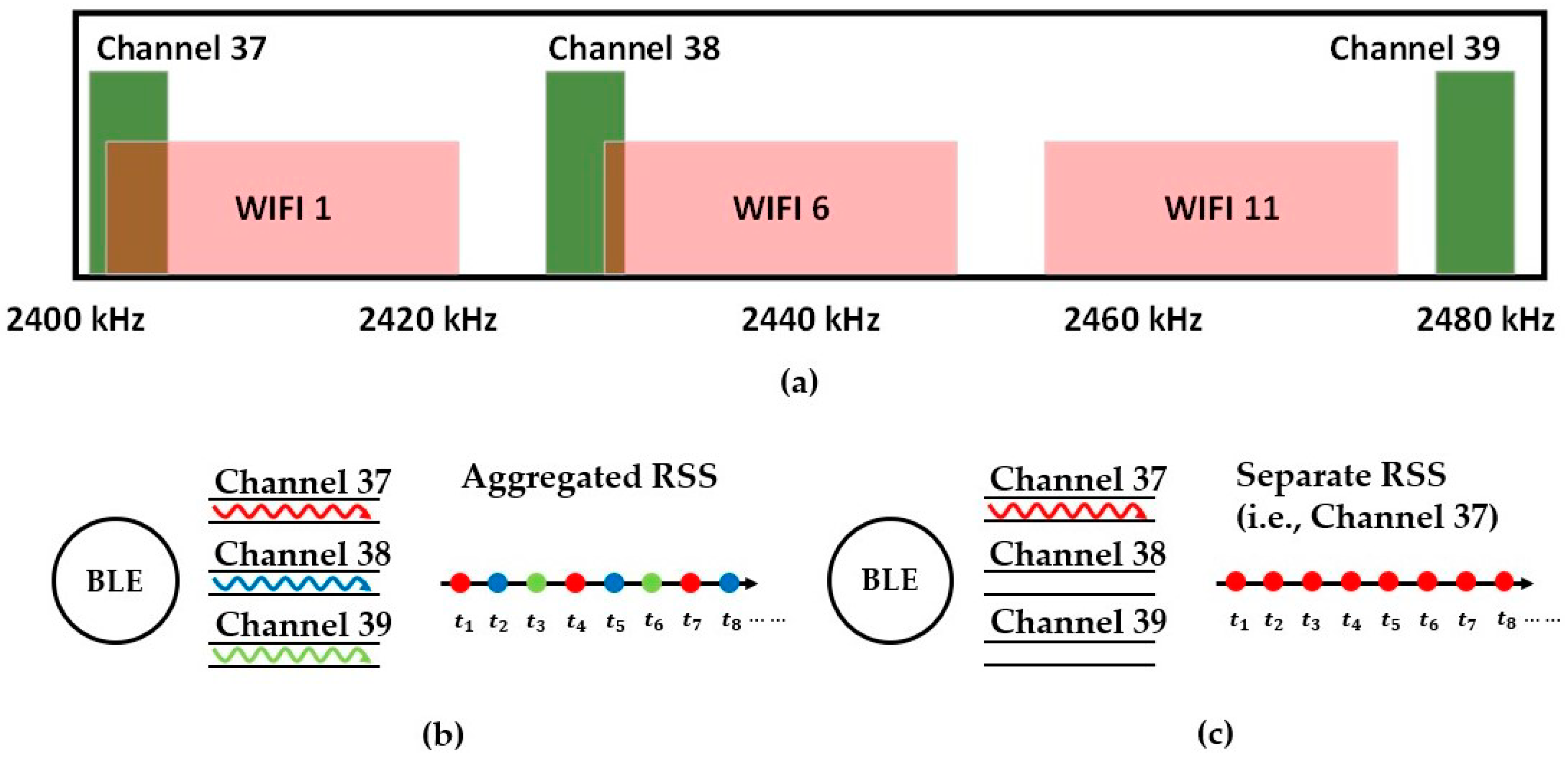
3.1. Separation of the BLE Channels for a More Stable Signal
3.2. The Distance Decision Strategy
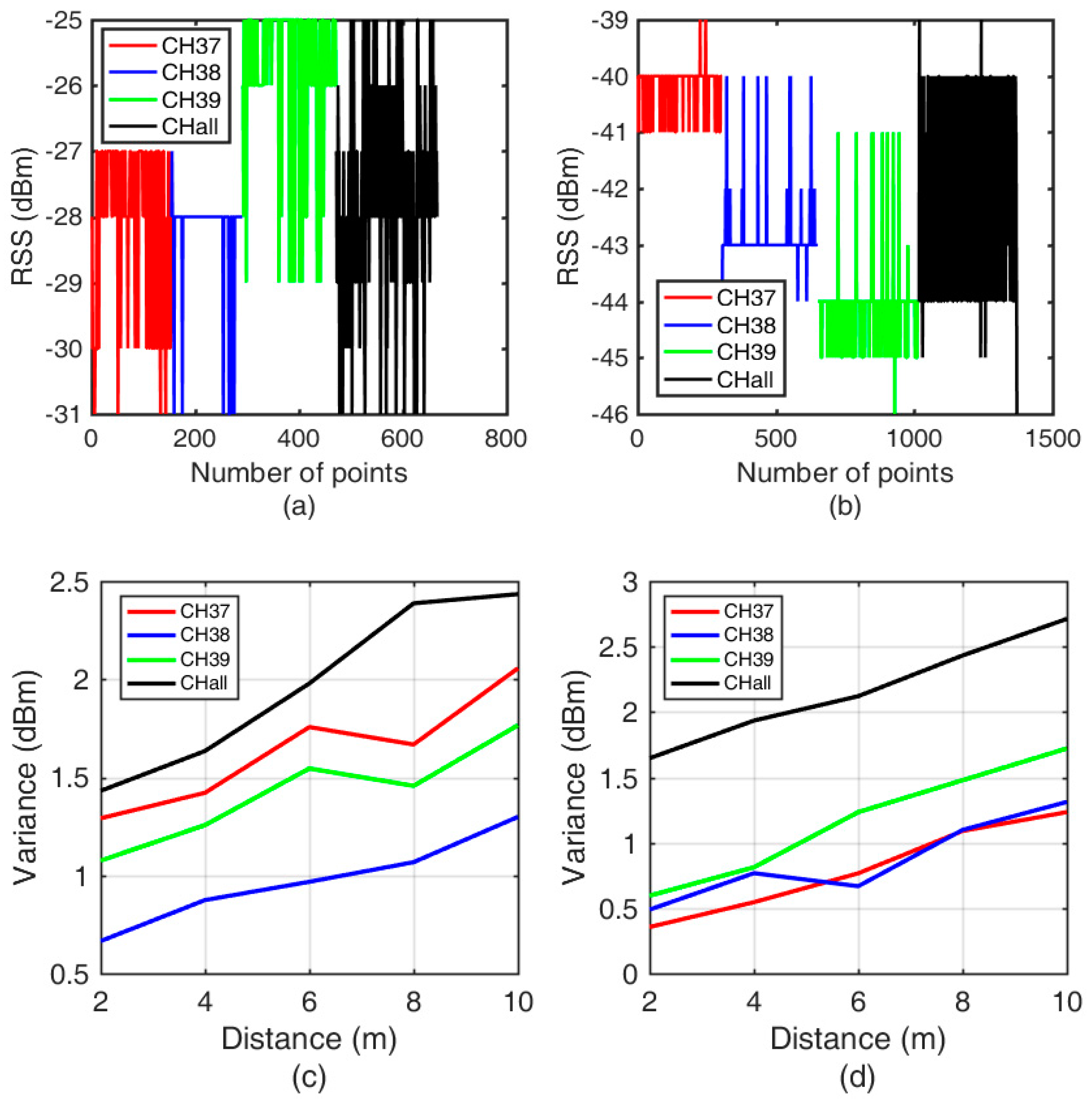
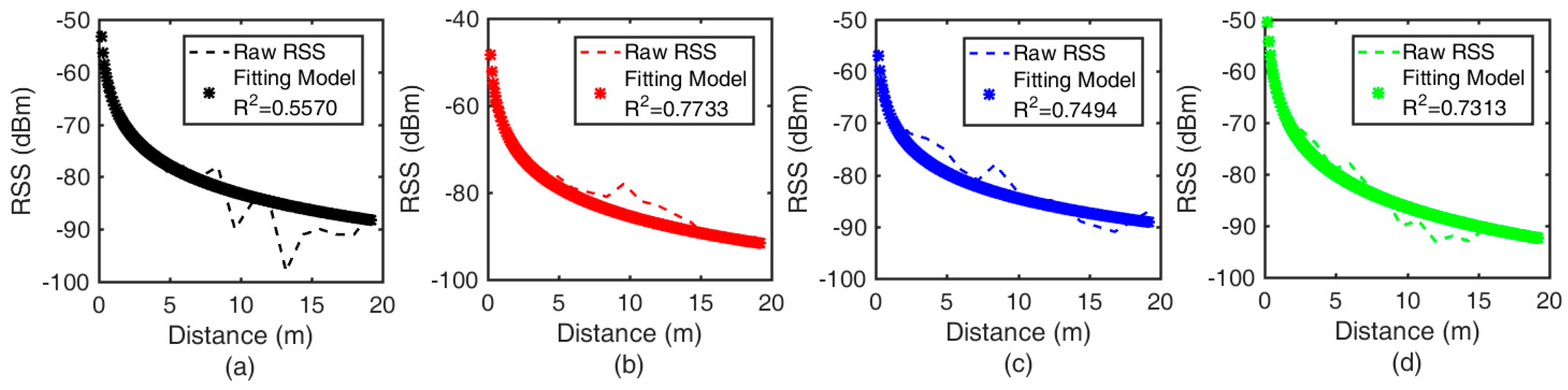
3.2.1. Separate Signal-Attenuation Models in the Offline Phase
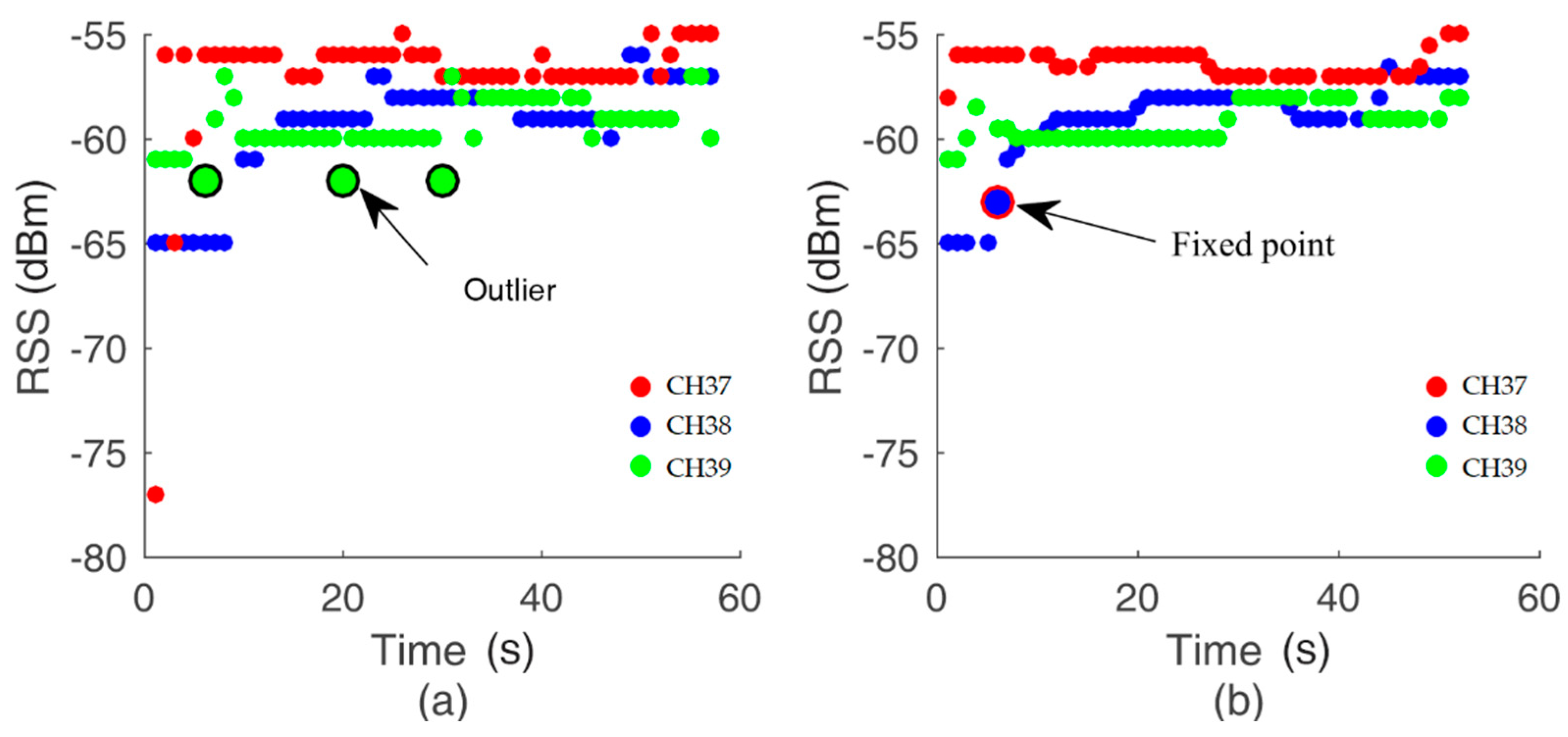
3.2.2. Data Filtering
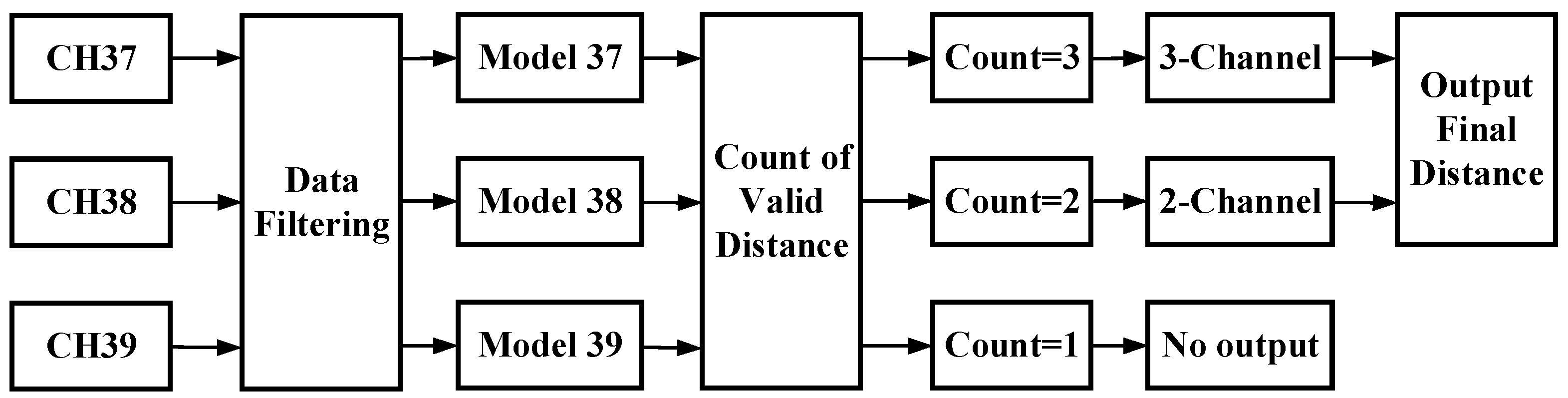
3.2.3. Distance Decision
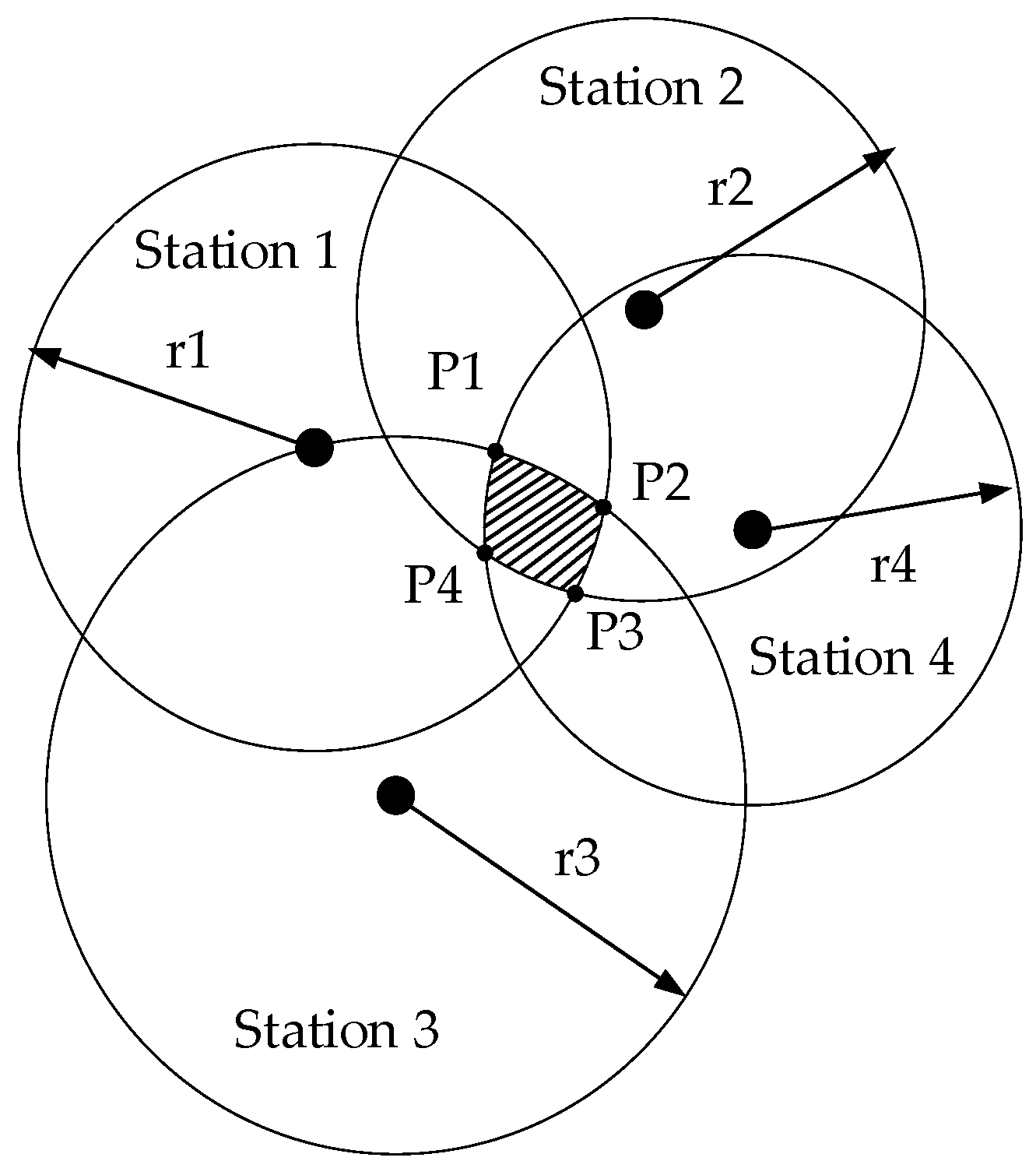
3.3. Weighted Trilateration
4. Results
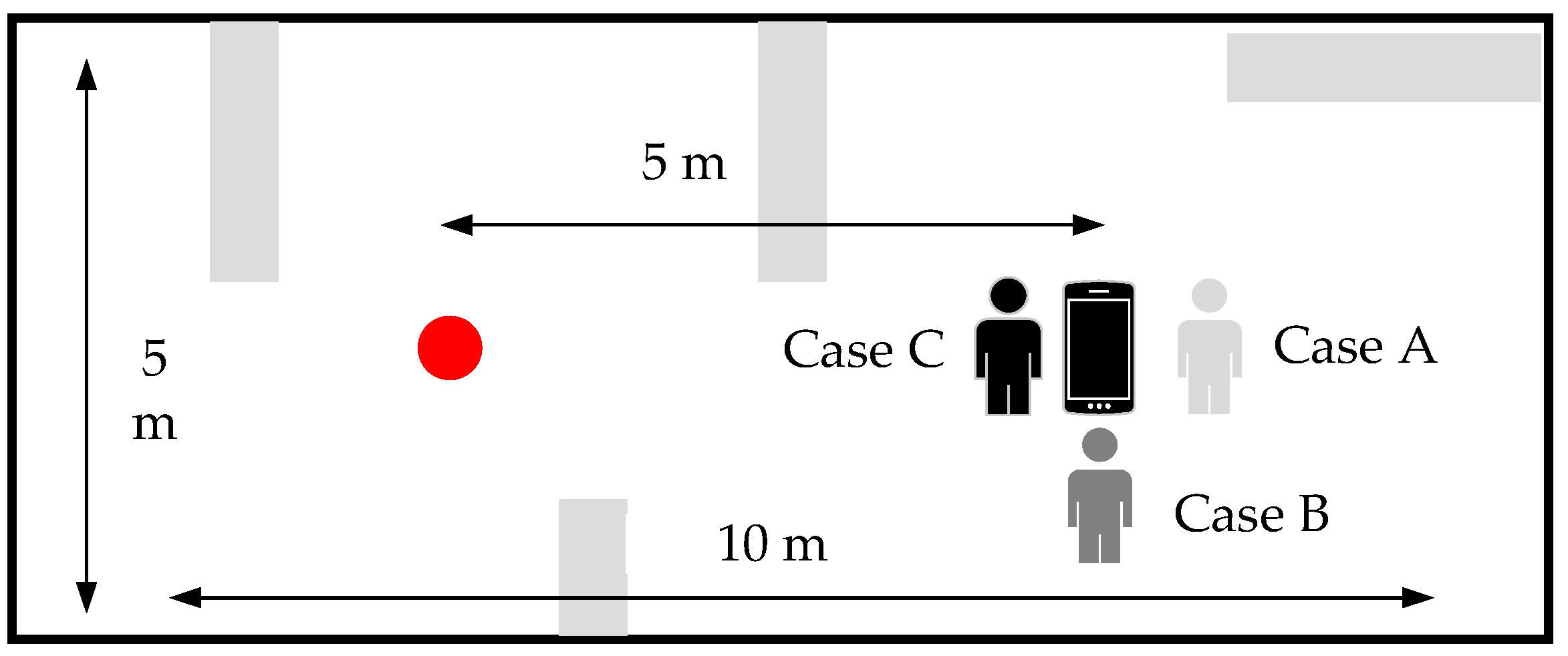
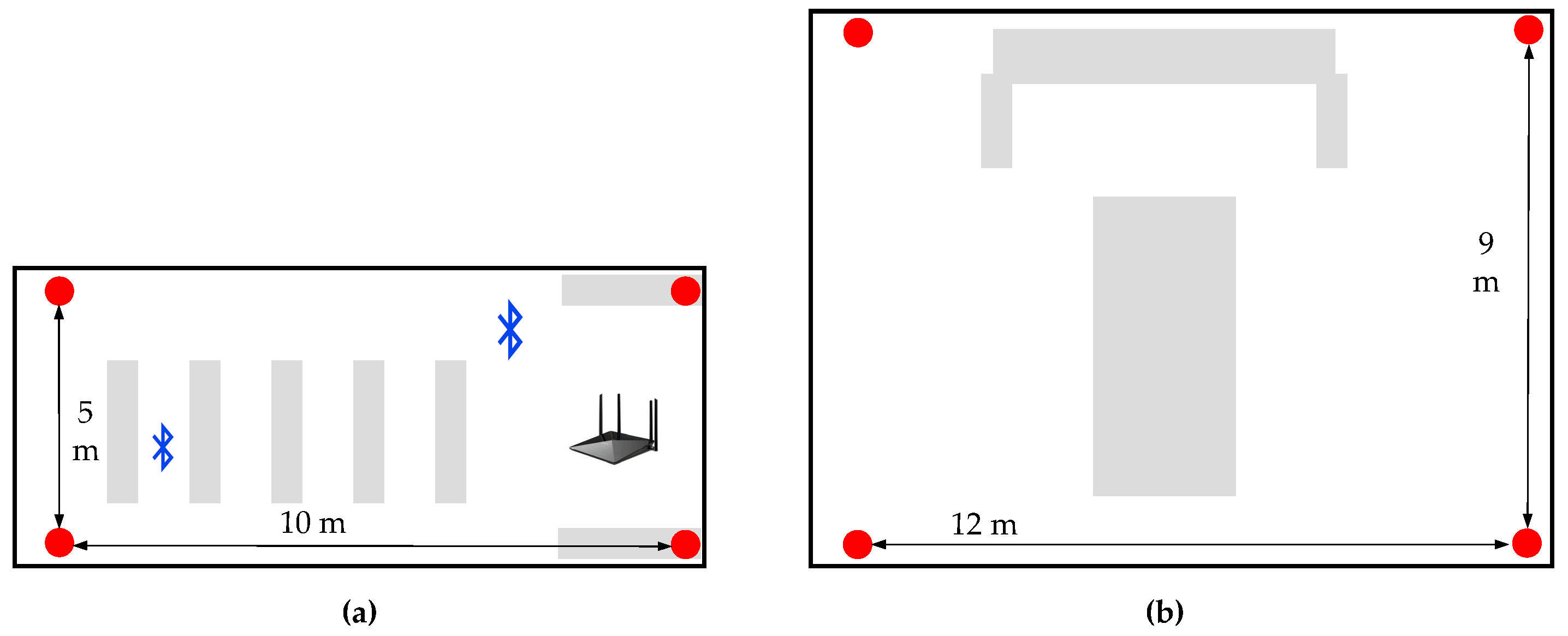
4.1. Experimental Setup
4.2. Performance of the Algorithm
4.2.1. The Distance Decision Strategy
4.2.2. The Weighted Trilateration
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Li, D.; Shen, X.; Li, D.; Li, S. On civil-military integrated space-based real-time information service system. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 1501–1505. [Google Scholar]
- Gu, Y.; Anthony, L.; Ignas, N. A survey of indoor positioning systems for wireless personal networks. IEEE Commun. Surv. Tut. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Dardari, D.; Pau, C.; Petar, M.D. Indoor tracking: Theory, methods, and technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. Part C 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Shieh, W.Y.; Hsu, C.J.; Wang, T.H. Vehicle positioning and trajectory tracking by infrared signal-direction discrimination for short-range vehicle-to-infrastructure communication systems. IEEE Trans. Intell. Transp. Syst. 2017, 19, 368–379. [Google Scholar] [CrossRef]
- Ma, F.; Liu, F.; Zhang, X.; Wang, P.; Bai, H.; Guo, H. An ultrasonic positioning algorithm based on maximum correntropy criterion extended Kalman filter weighted centroid. Signal Image Video Process. 2018, 12, 1207–1215. [Google Scholar] [CrossRef]
- Lee, N.; Ahn, S.; Han, D. AMID: Accurate magnetic indoor localization using deep learning. Sensors 2018, 18, 1598. [Google Scholar] [CrossRef]
- Liu, J.; Chen, R.; Pei, L.; Guinness, R.; Kuusniemi, H. A hybrid smartphone indoor positioning solution for mobile LBS. Sensors 2012, 12, 17208–17233. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, R.; Chen, Y.; Pei, L.; Chen, L. iParking: An intelligent indoor location-based smartphone parking service. Sensors 2012, 12, 14612–14629. [Google Scholar] [CrossRef]
- Wu, T.; Liu, J.; Li, Z.; Liu, K.; Xu, B. Accurate smartphone indoor visual positioning based on a high-precision 3D photorealistic map. Sensors 2018, 18, 1974. [Google Scholar] [CrossRef]
- Mandal, A.; Lopes, C.V.; Givargis, T.; Haghighat, A.; Jurdak, R.; Baldi, P. Beep: 3D indoor positioning using audible sound. In Proceedings of the 5th Consumer Communications and Networking Conference, Las Vegas, NV, USA, 3–6 January 2005. [Google Scholar]
- Rishabh, I.; Kimber, D.; Adcock, J. Indoor localization using controlled ambient sounds. In Proceedings of the 3rd International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, Australia, 13–15 November 2012. [Google Scholar]
- Li, Z.; Liu, J.; Yang, F.; Niu, X.; Li, L.; Wang, Z.; Chen, R. A bayesian density model based radio signal fingerprinting positioning method for enhanced usability. Sensors 2018, 18, 4063. [Google Scholar] [CrossRef] [PubMed]
- Faragher, R.; Robert, H. Location fingerprinting with Buetooth low energy beacons. IEEE J. Sel. Area. Commun. 2015, 33, 2418–2428. [Google Scholar] [CrossRef]
- Li, W.; Wei, D.; Lai, Q.; Li, X.; Yuan, H. Geomagnetism-aided indoor Wi-Fi radio-map construction via smartphone crowdsourcing. Sensors 2018, 18, 1462. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhou, Z.; Liu, Y. From RSSI to CSI: Indoor localization via channel response. Acm Comput. Surv. 2013, 46, 25. [Google Scholar] [CrossRef]
- Yang, F.; Xiong, J.; Liu, J.; Wang, C.; Li, Z.; Tong, P.; Chen, R. A pairwise SSD fingerprinting method of smartphone indoor localization for enhanced usability. Remote Sens. 2019, 11, 566. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, L.; Jiang, Z.; Chen, B.; Liu, K.; Xuan, Q.; Xiang, Y. Accurate indoor localization based on CSI and visibility graph. Sensors 2018, 18, 2549. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.B.; Huang, B.C.; Zhang, B.; Li, L.L.; Yang, F.; Zhang, Z.B.; Li, Z.; Tong, P.F. AOA estimation based on channel state information extracted from WiFi with double antenna. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 2167–2172. [Google Scholar]
- Faragher, R.; Robert, H. An analysis of the accuracy of Bluetooth low energy for indoor positioning applications. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS + 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Powar, J.; Gao, C.; Harle, R. Assessing the impact of multi-channel BLE beacons on fingerprint-based positioning. In Proceedings of the 8th International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Bernardo, L. On target localization using combined RSS and AoA measurements. Sensors 2018, 18, 1266. [Google Scholar] [CrossRef]
- Li, G.; Geng, E.; Ye, Z.; Xu, Y.; Lin, J.; Pang, Y. Indoor positioning algorithm based on the improved RSSI distance model. Sensors 2018, 18, 2820. [Google Scholar] [CrossRef]
- Hashemi, H. The indoor radio propagation channel. Proc. IEEE 1993, 81, 943–968. [Google Scholar] [CrossRef]
- Nikoukar, A.; Abboud, M.; Samadi, B.; Güneş, M.; Dezfouli, B. Empirical analysis and modeling of Bluetooth low-energy (BLE) advertisement channels. In Proceedings of the 17th Annual Mediterranean Ad Hoc Networking Workshop (Med-Hoc-Net), Capri, Italy, 20–22 June 2018. [Google Scholar]
- Kim, D.Y.; Kim, S.H.; Choi, D.; Jin, S.H. Accurate indoor proximity zone detection based on time window and frequency with Bluetooth low energy. Procedia Comput. Sci. 2015, 56, 88–95. [Google Scholar] [CrossRef]
- Ozer, A.; John, E. Improving the accuracy of Bluetooth low energy indoor positioning system using kalman filtering. In Proceedings of the 3rd International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2016. [Google Scholar]
- Ishida, S.; Takashima, Y.; Tagashira, S.; Fukuda, A. Proposal of separate channel fingerprinting using Bluetooth low energy. In Proceedings of the 5th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Kumamoto, Japan, 10–14 July 2016. [Google Scholar]
- Giovanelli, D.; Farella, E.; Fontanelli, D.; Macii, D. Bluetooth-based indoor positioning through ToF and RSSI data fusion. In Proceedings of the 9th International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018. [Google Scholar]
- Viswanathan, S.; Srinivasan, S. Improved path loss prediction model for short range indoor positioning using Bluetooth low energy. Proceedings of 14th IEEE Sensors Conference, Busan, Korea, 1–4 November 2015. [Google Scholar]
- Yu, N.; Zhan, X.; Zhao, S.; Wu, Y.; Feng, R. A precise dead reckoning algorithm based on Bluetooth and multiple sensors. IEEE Internet Things J. 2017, 5, 336–351. [Google Scholar] [CrossRef]
- Cantón, P.V.; Calveras, A.A.; Paradells, A.J.; Pérez, B.M. A Bluetooth low energy indoor positioning system with channel diversity, weighted trilateration and kalman filtering. Sensors 2017, 17, 2927. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Yang, J. Smartphone-based indoor localization with Bluetooth low energy beacons. Sensors 2016, 16, 596. [Google Scholar] [CrossRef] [PubMed]
- Perreault, S.; Hébert, P. Median filtering in constant time. IEEE Trans. Image Process. 2007, 16, 2389–2394. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.J.; Kim, S. Indoor smartphone localization based on LOS and NLOS identification. Sensors 2018, 18, 3987. [Google Scholar] [CrossRef] [PubMed]
- Jian, Y.Z.; Hai, Y.L.; Zi, L.C.; Zhao, H.L. RSSI based Bluetooth low energy indoor positioning. Proceedings of 5th International Conference on Indoor Positioning & Indoor Navigation, Busan, Korea, 27–30 October 2014. [Google Scholar]
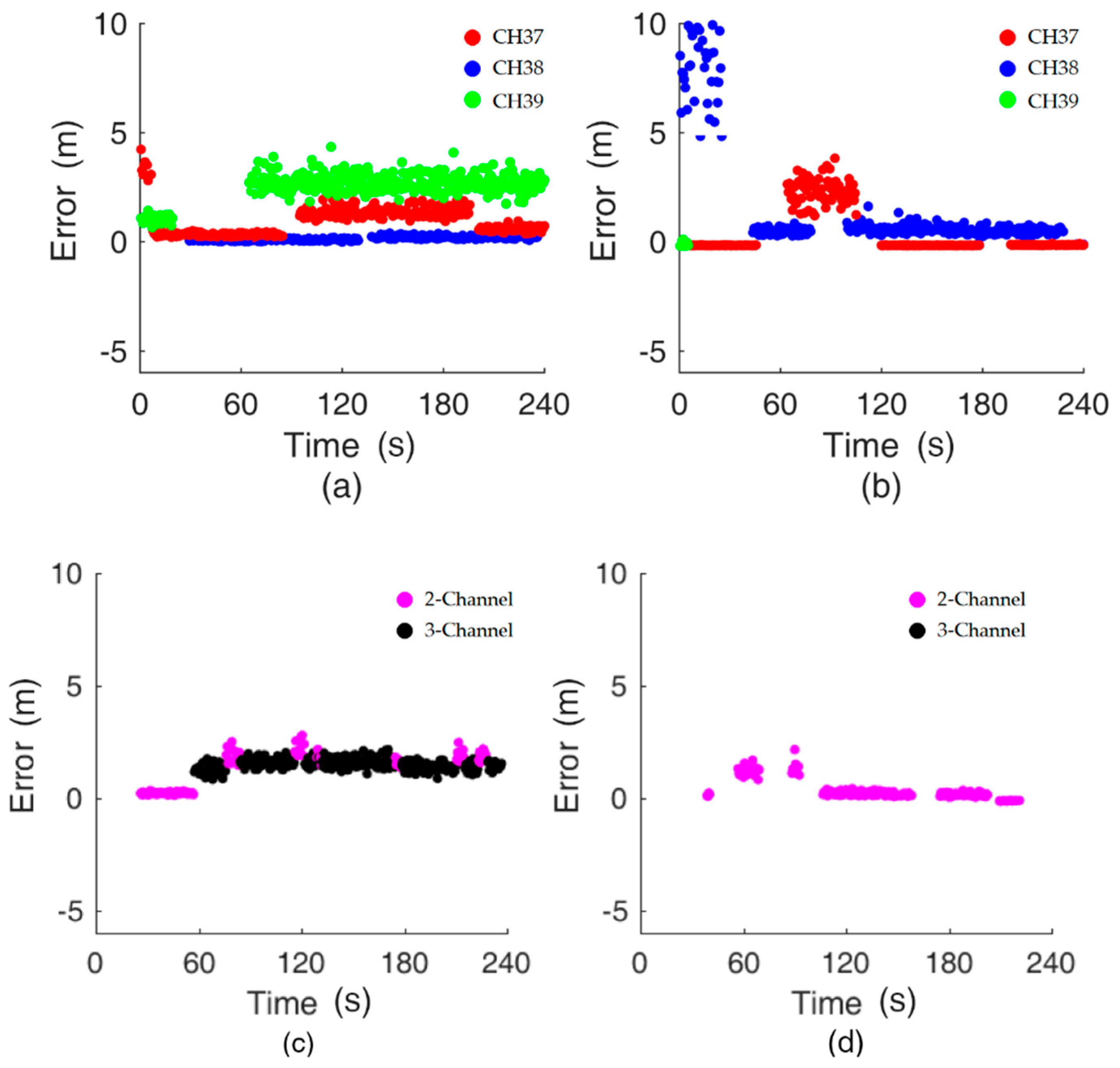
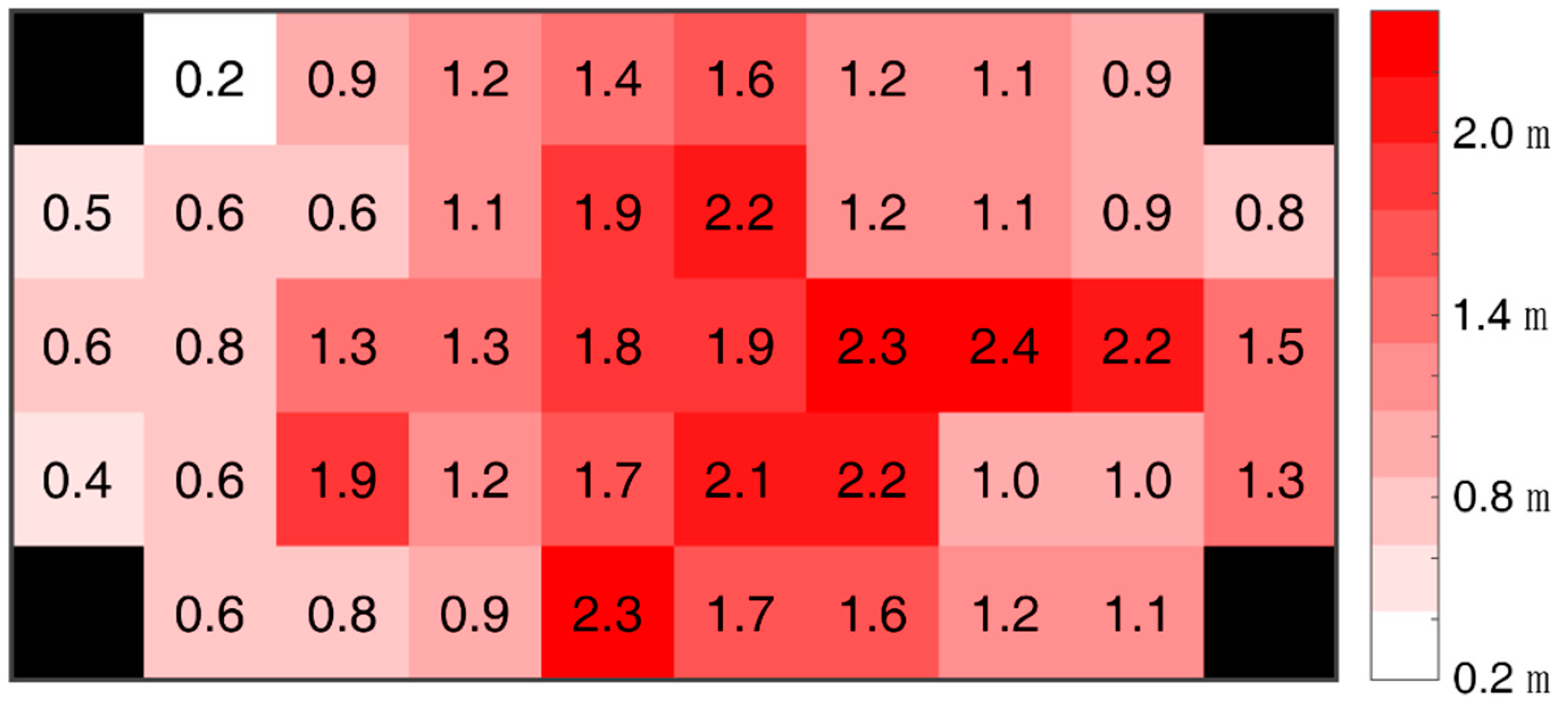
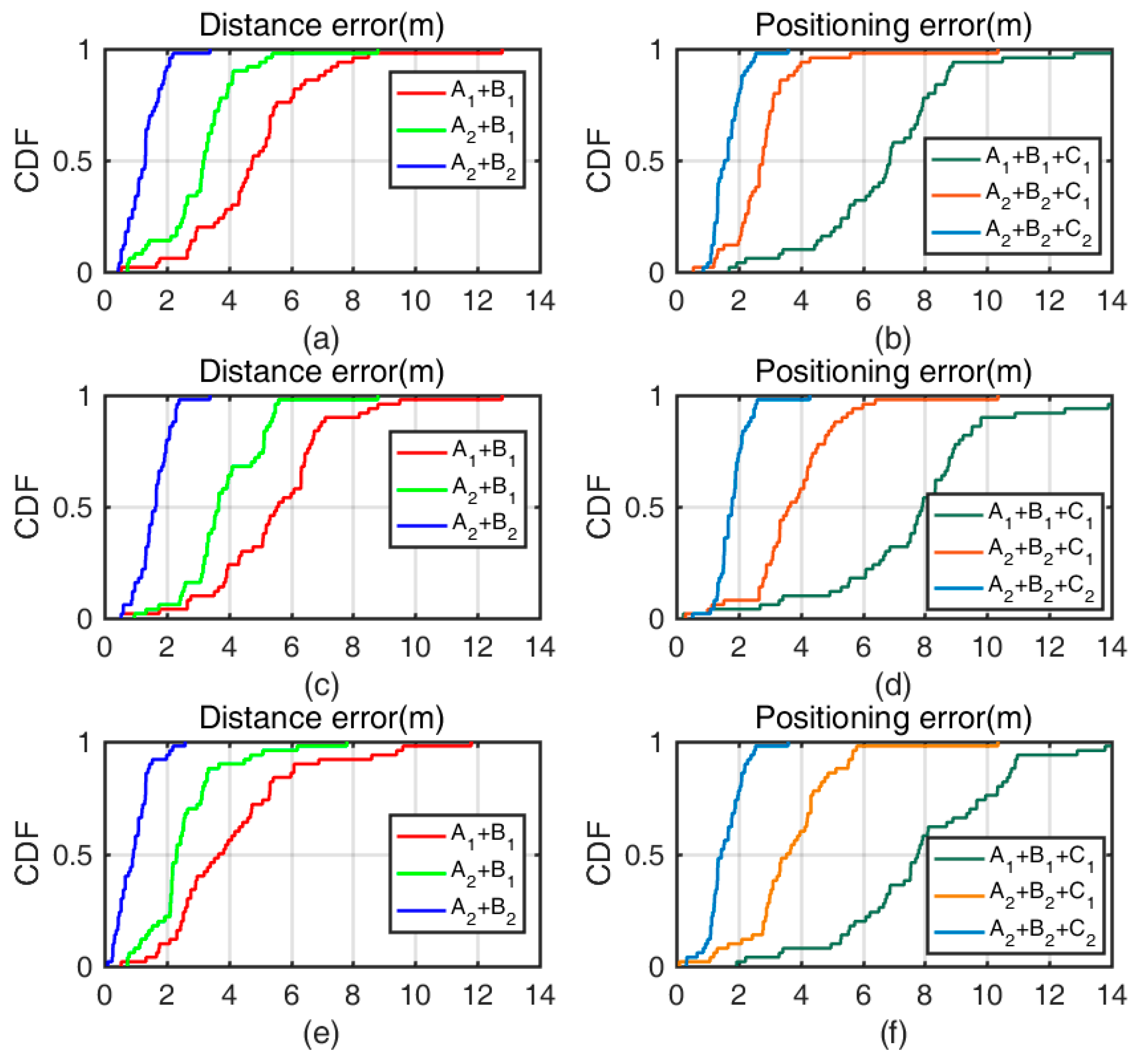
| Channel ID | 30% of Time in Error (m) | 60% of Time in Error (m) | 90% of Time in Error (m) |
|---|---|---|---|
| CH 37 | 2.0 | 3.5 | 5.2 |
| CH 38 | 1.6 | 2.6 | 4.6 |
| CH 39 | 1.1 | 1.9 | 4.0 |
| Case | A | B | C |
|---|---|---|---|
| Number of Tests | 10 | 10 | 10 |
| Number of Empty Outputs | 1 | 6 | 10 |
| Dist. (m) | 0.2 | 1.4 | 2.6 | 3.8 | 5.0 | 6.2 | 7.4 | 8.6 | 9.8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error (m) | ||||||||||
| Google Pixel 3 L | 0.1 | 0.2 | 0.8 | 1.1 | 1.2 | 1.5 | 1.2 | 1.9 | 2.0 | |
| Huawei P20 | 0.1 | 0.4 | 0.1 | 1.4 | 1.3 | 1.5 | 1.3 | 1.8 | 2.3 | |
| Algorithm | Symbol |
|---|---|
| Aggregate Channel | |
| Separate Channel | |
| Normal Distance Decision | |
| Proposed Distance Decision | |
| Traditional Trilateration | |
| Weighted Trilateration |
| Mean Absolute Error | Algorithm | 90% | 98% |
|---|---|---|---|
| Distance Error | (Tradition) | 7.1 | 8.5 |
| (Test) | 4.6 | 5.2 | |
| (Proposed) | 2.0 | 2.2 | |
| Positioning Error | (Tradition) | 8.8 | 12.8 |
| (Test) | 3.6 | 4.3 | |
| (Proposed) | 2.2 | 2.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Liu, J.; Sun, W.; Yang, F. A Robust Indoor Positioning Method based on Bluetooth Low Energy with Separate Channel Information. Sensors 2019, 19, 3487. https://doi.org/10.3390/s19163487
Huang B, Liu J, Sun W, Yang F. A Robust Indoor Positioning Method based on Bluetooth Low Energy with Separate Channel Information. Sensors. 2019; 19(16):3487. https://doi.org/10.3390/s19163487
Chicago/Turabian StyleHuang, Baichuan, Jingbin Liu, Wei Sun, and Fan Yang. 2019. "A Robust Indoor Positioning Method based on Bluetooth Low Energy with Separate Channel Information" Sensors 19, no. 16: 3487. https://doi.org/10.3390/s19163487
APA StyleHuang, B., Liu, J., Sun, W., & Yang, F. (2019). A Robust Indoor Positioning Method based on Bluetooth Low Energy with Separate Channel Information. Sensors, 19(16), 3487. https://doi.org/10.3390/s19163487





