Hough Transform-Based Large Dynamic Reflection Coefficient Micro-Motion Target Detection in SAR
Abstract
1. Introduction
2. Signal Model
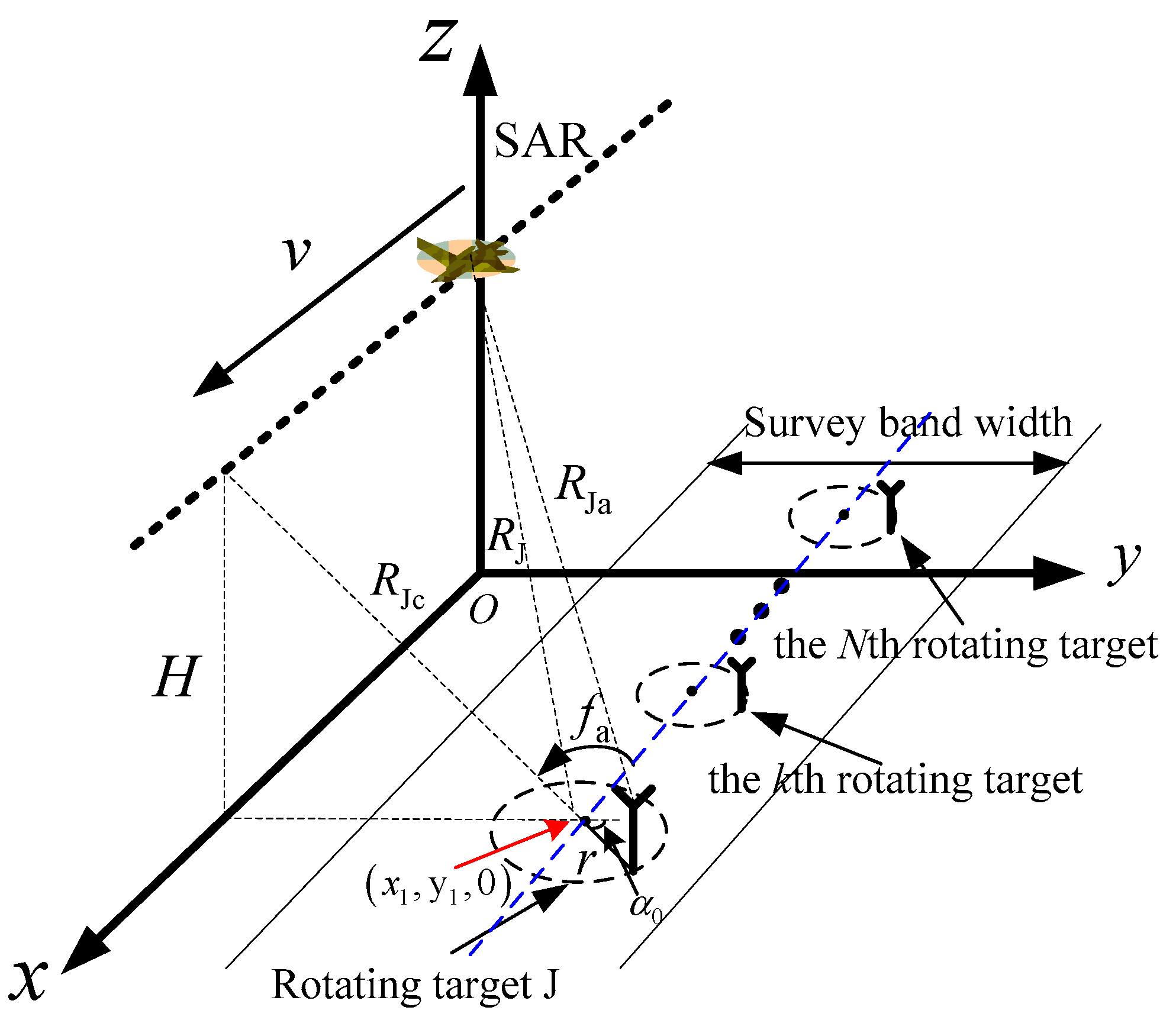
2.1. Rotating-Target Geometry
2.2. SAR Azimuth Echo
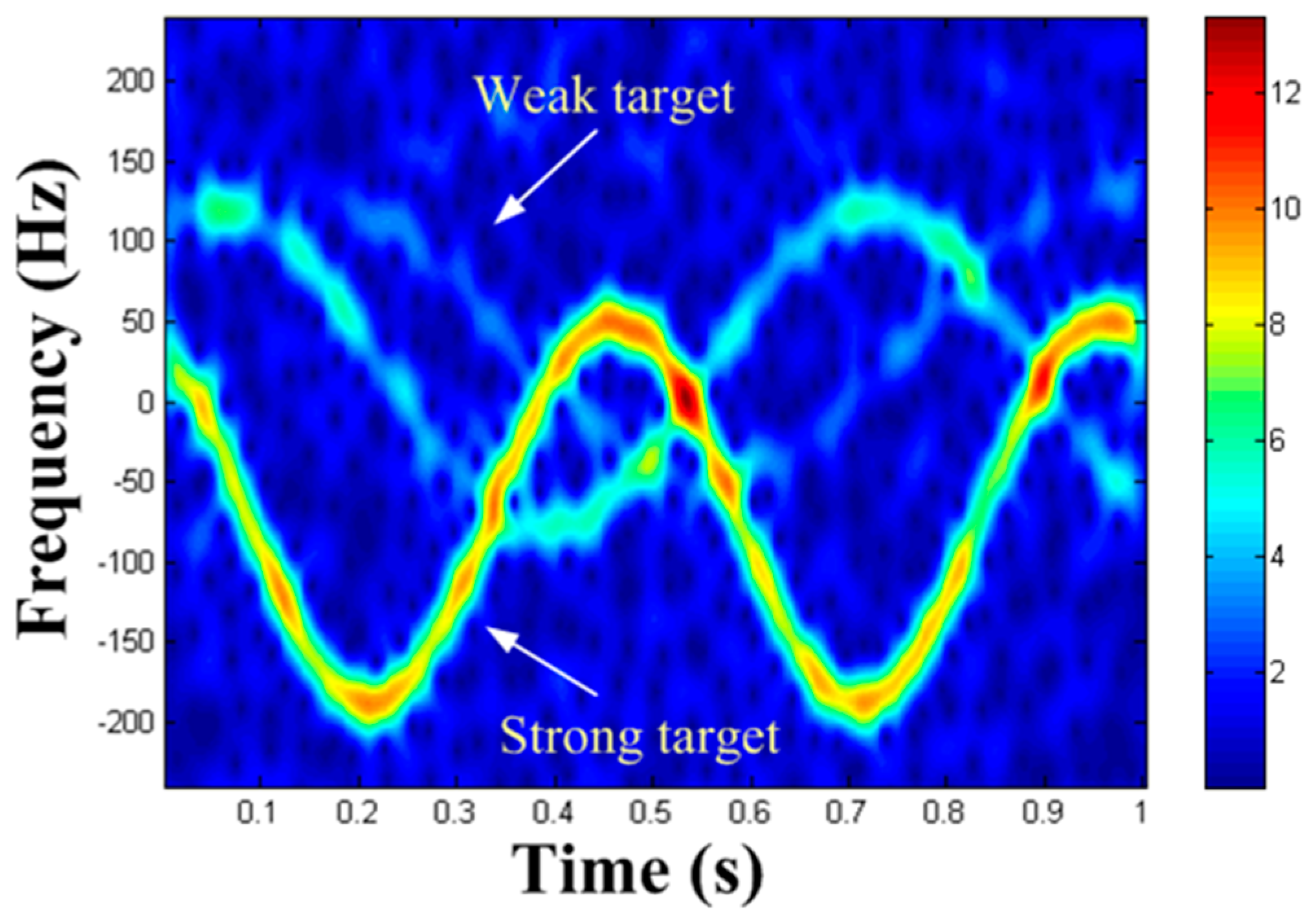
2.3. Masking Phenomenon of Weak MM Targets
3. Detection Algorithm for Large Dynamic Reflection Coefficient MM Targets
3.1. Principles
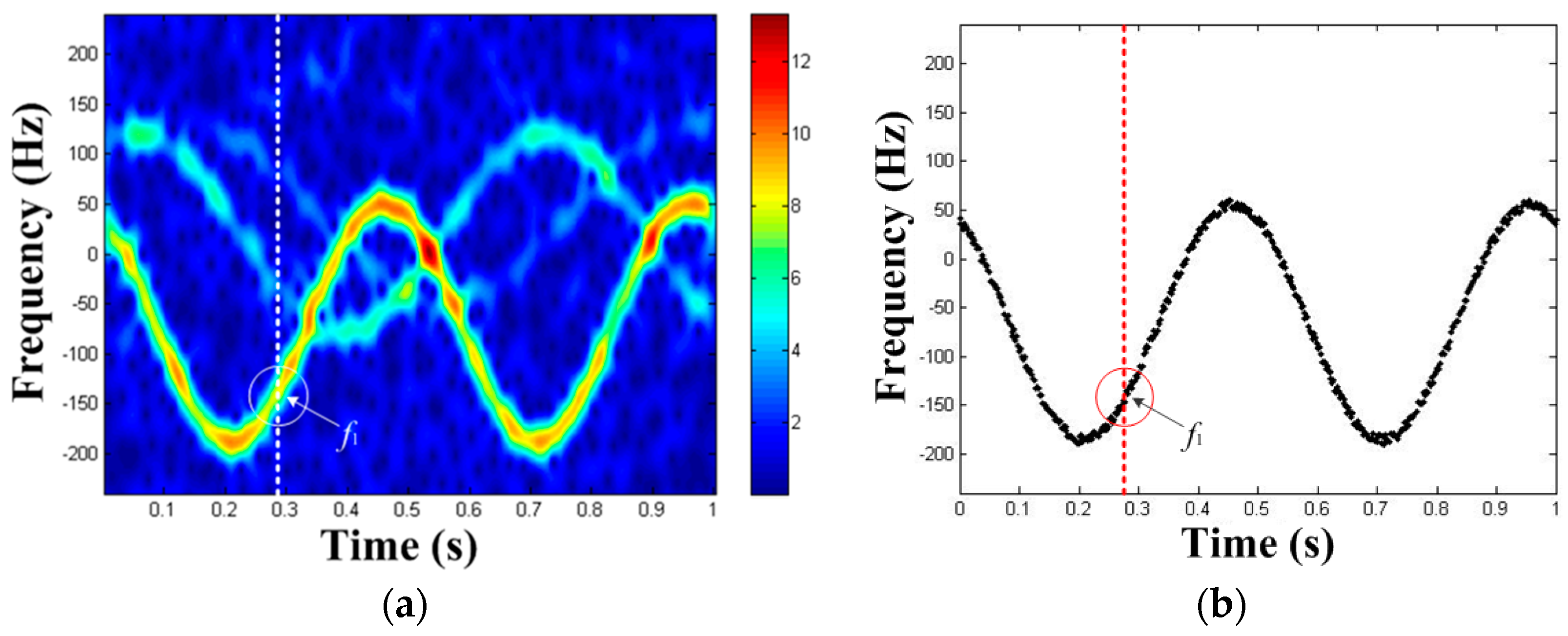
3.2. TF Curve Extraction
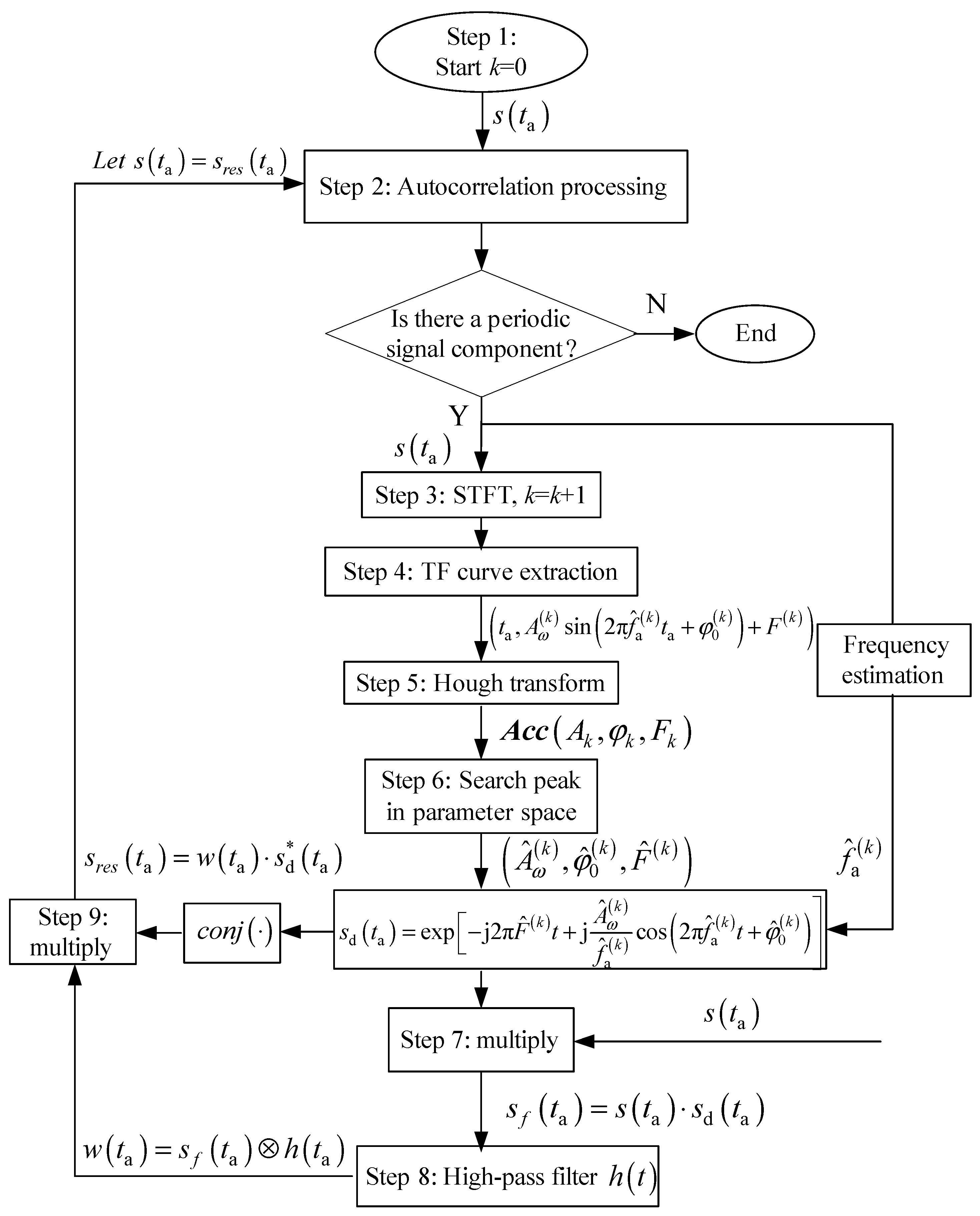
3.3. Algorithm Steps
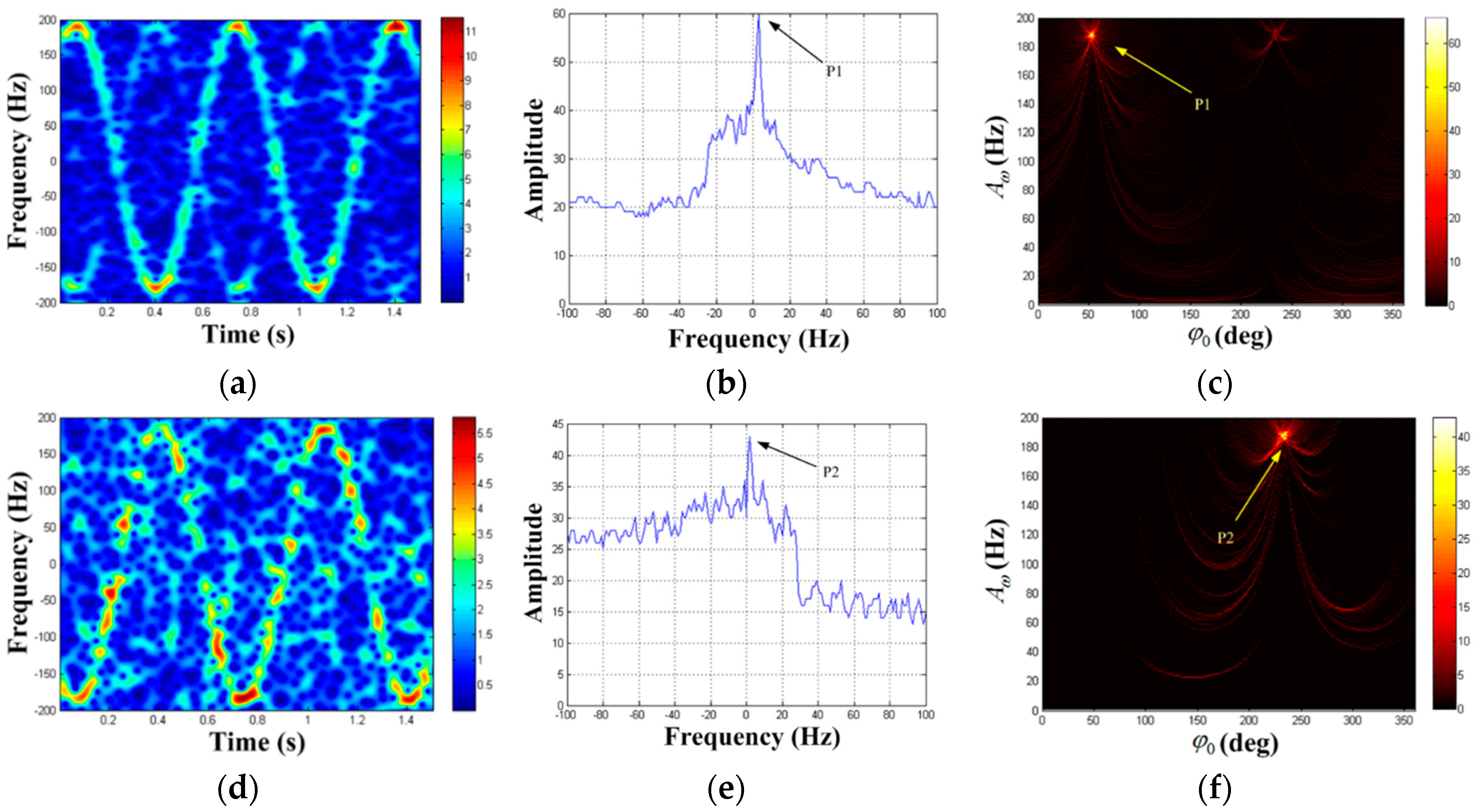
4. Simulation and Field Experiment Data Research
4.1. Algorithm Step Simulations
4.2. Algorithm Performance Analysis
4.2.1. Computational Load Analysis
4.2.2. SNR Analysis
4.2.3. The Ideal Peak Search Performance
4.2.4. The Maximum Number of Targets and Maximum Dynamic Range of the Method
4.2.5. Limitations of the Algorithm
4.3. Field Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Maurice, R.; Erich, M.; Daniel, N. Vibration and rotation in millimeter-wave SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 293–304. [Google Scholar]
- Li, X.; Deng, B.; Qin, Y.L.; Wang, H.Q.; Li, Y. The influence of target micromotion on SAR and GMTI. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2738–2751. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Yuan, N.; Zhu, F.; Gu, F. Three-dimensional precession feature extraction of space targets. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1313–1329. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F.; Bao, Z. High-Resolution Three-Dimensional Imaging of Space Targets in Micromotion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 8, 3428–3440. [Google Scholar] [CrossRef]
- Pan, X.Y.; Liu, J.; Xu, L.T.; Ai, X.; Xie, Q.; Yu, B.; Li, C. Extraction of micro-Doppler frequency from HRRPs of rotating targets. IEEE Access 2017, 5, 26163–26174. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Qiu, C.W.X.; Liang, J.; Li, K.M. Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency chirp signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2087–2098. [Google Scholar]
- Sadjadi, F.A. Target classification via labeling of subtarget motion patterns. Aerospace/defense Sensing, Simulation, & Controls. SPIE 2001, 4379, 308–316. [Google Scholar]
- Gaunaurd, G.C.; Hans, C.S. Signal analysis by means of time-frequency (Wigner-type) distributions-applications to sonar and radar echoes. Proc. IEEE 1996, 84, 1231–1248. [Google Scholar] [CrossRef]
- Li, G.; Varshney, P.K. Micro-Doppler Parameter Estimation via Parametric Sparse Representation and Pruned Orthogonal Matching Pursuit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4937–4948. [Google Scholar] [CrossRef]
- Suresh, P.; Thayaparan, T.; Obulesu, T.; Venkataramaniah, K. Extracting Micro-Doppler Radar Signatures from Rotating Targets Using Fourier-Bessel Transform and Time-Frequency Analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3204–3210. [Google Scholar] [CrossRef]
- Igor, D.; Vesna, P.B.; Marko, S. The STFT-Based Estimator of Micro-Doppler Parameters. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1273–1283. [Google Scholar]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Zhang, Q.; Yeo, T.S.; Tan, H.S.; Luo, Y. Imaging of a moving target with rotating parts based on the Hough transform. IEEE Trans. Geosci. Remote Sens. 2008, 46, 291–299. [Google Scholar] [CrossRef]
- Zhou, Y.; Bi, D.P.; Shen, A.G.; Wang, X.P. Hough transform-based large micro-motion target detection and estimation in synthetic aperture radar. IET Radar Sonar Navig. 2019, 13, 558–565. [Google Scholar] [CrossRef]
- Stankovic, L.; Dakovic, M.; Thayaparan, T.; Popovic-Bugarin, V. Inverse radon transform based micro-Doppler analysis from a reduced set of observations. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1155–1169. [Google Scholar] [CrossRef]
- Thayaparan, T.; Abrol, S.; Riseborough, E. Analysis of radar micro-Doppler signatures from experimental helicopter and human data. IET Radar Sonar Navig. 2007, 1, 289–299. [Google Scholar] [CrossRef]
- Deng, B.; Wang, H.Q.; Li, X.; Qin, Y.L. Generalised likelihood ratio test detector for micro-motion targets in SAR raw signals. IET Radar Sonar Navig. 2011, 5, 528–535. [Google Scholar] [CrossRef]
- Peng, B.; Wei, X.Z.; Deng, B.; Chen, H.; Liu, Z.; Li, X. A sinusoidal frequency modulation Fourier transform for radar-based vehicle vibration estimation. IEEE Trans. Geosci. Remote Sens. 2014, 63, 2188–2199. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, B.; Wang, H.; Qin, Y.; Ding, W. Doppler aliasing free micro-motion parameter estimation algorithm based on the spliced time-frequency image and inverse Radon transform. In Proceedings of the 2014 International Conference on Information and Communications Technologies (ICT 2014), Nanjing, China, 16–18 May 2014; pp. 1–6. [Google Scholar]
- Krishnan, S.; Rangayyan, R.M. Detection of nonlinear frequency-modulated components in the time-frequency plane using an array of accumulators. In Proceedings of the 1998 IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Pittsburgh, PA, USA, 6–9 October 1998; pp. 557–560. [Google Scholar]
- Sun, Z.; Li, B.; Lu, Y. Research on Micro-Motion and Micro-Doppler of Ballistic Targets. In Proceedings of the 2009 IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Xu, L.; Oja, E. Randomized Hough Transform (RHT): Basic Mechanisms, Algorithms, and Computational Complexities. CVGIP Image Underst. 1993, 57, 131–154. [Google Scholar] [CrossRef]
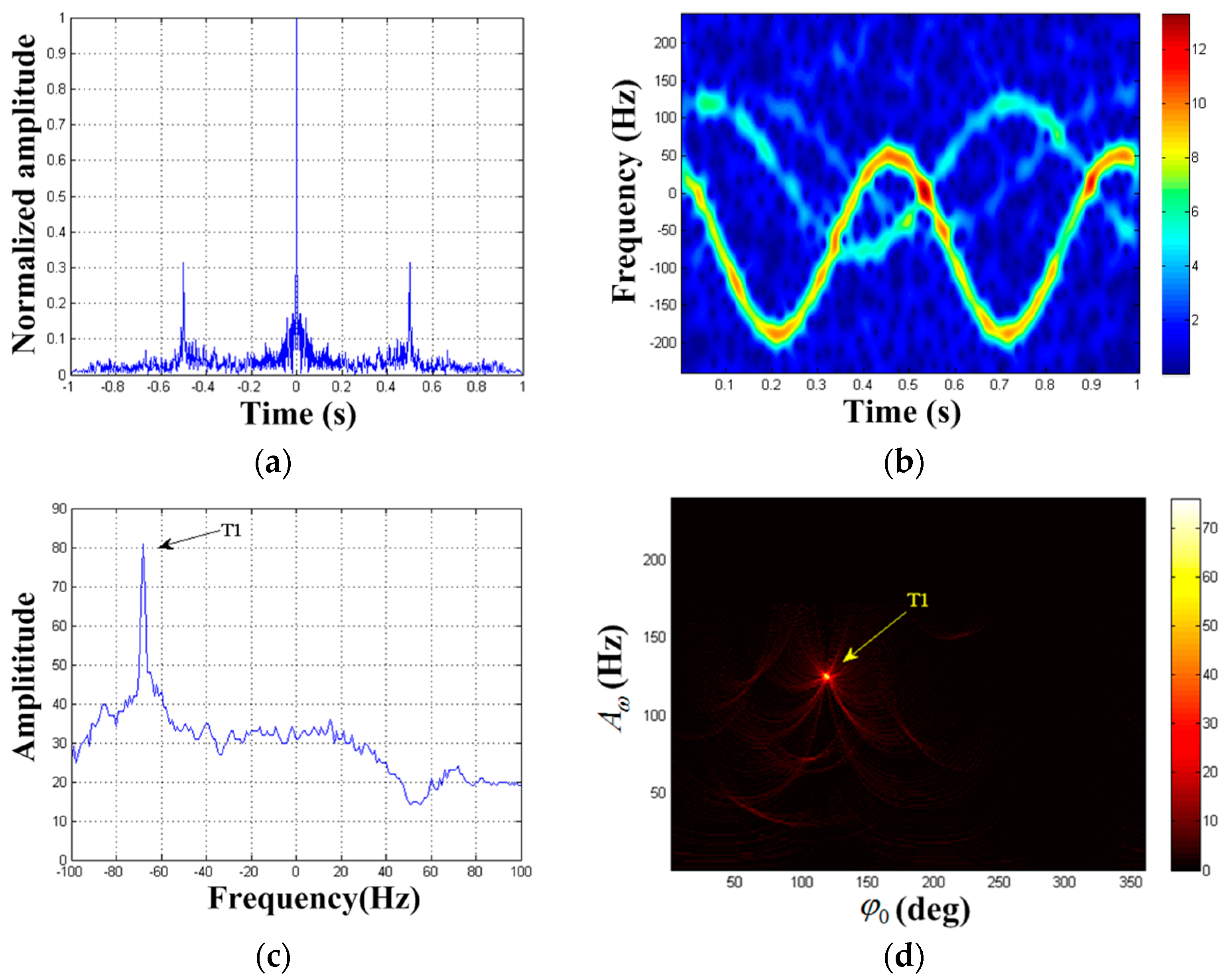
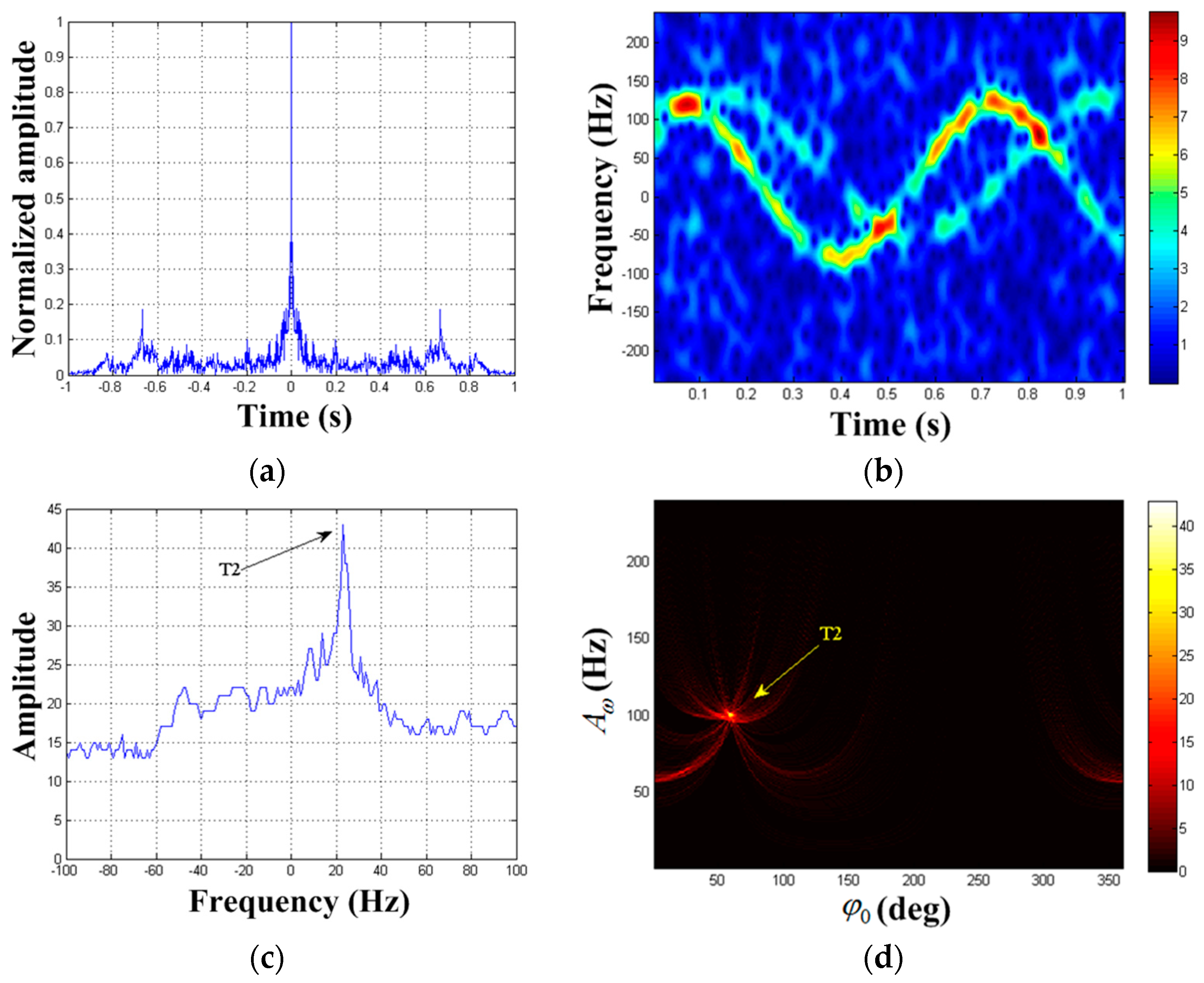
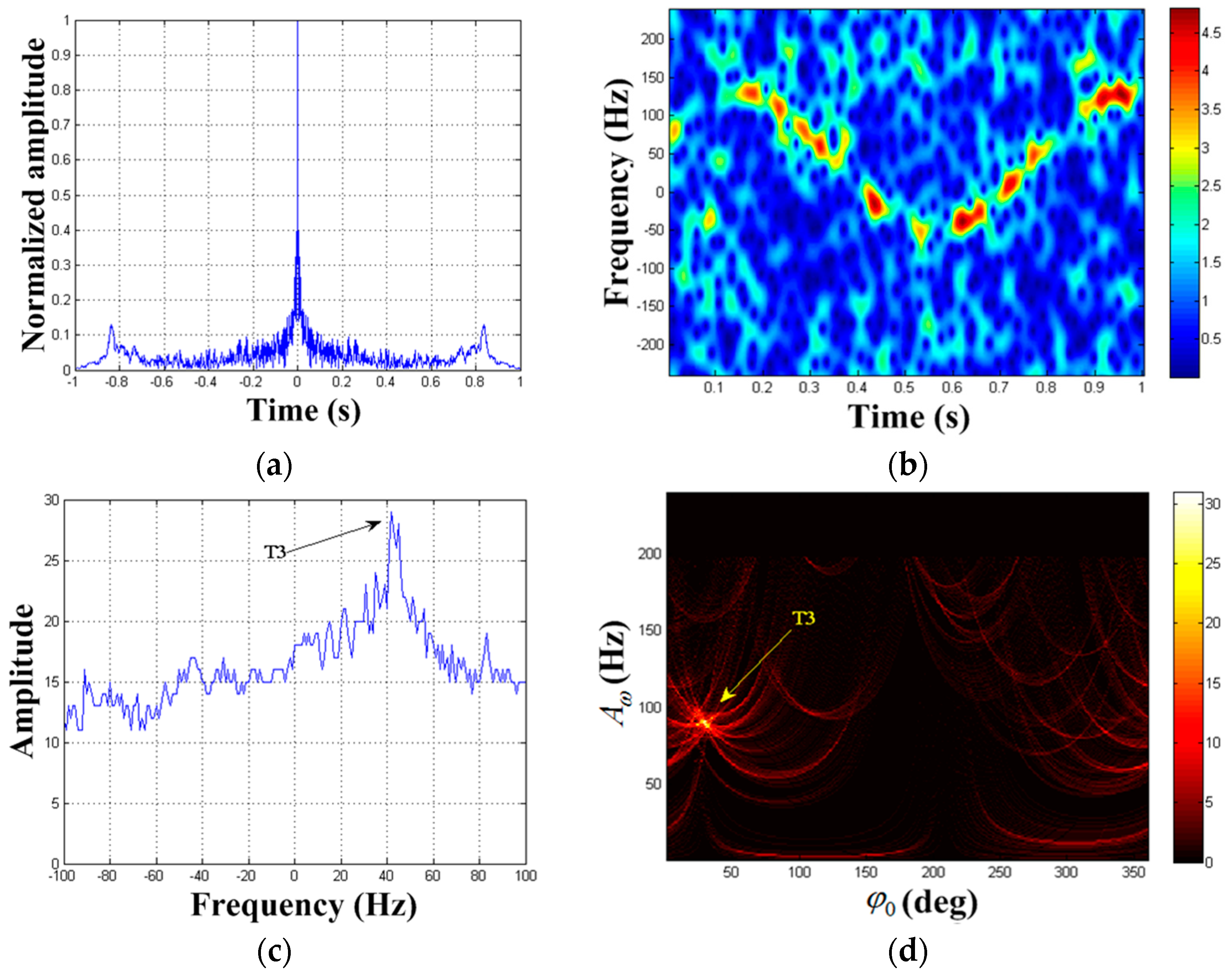
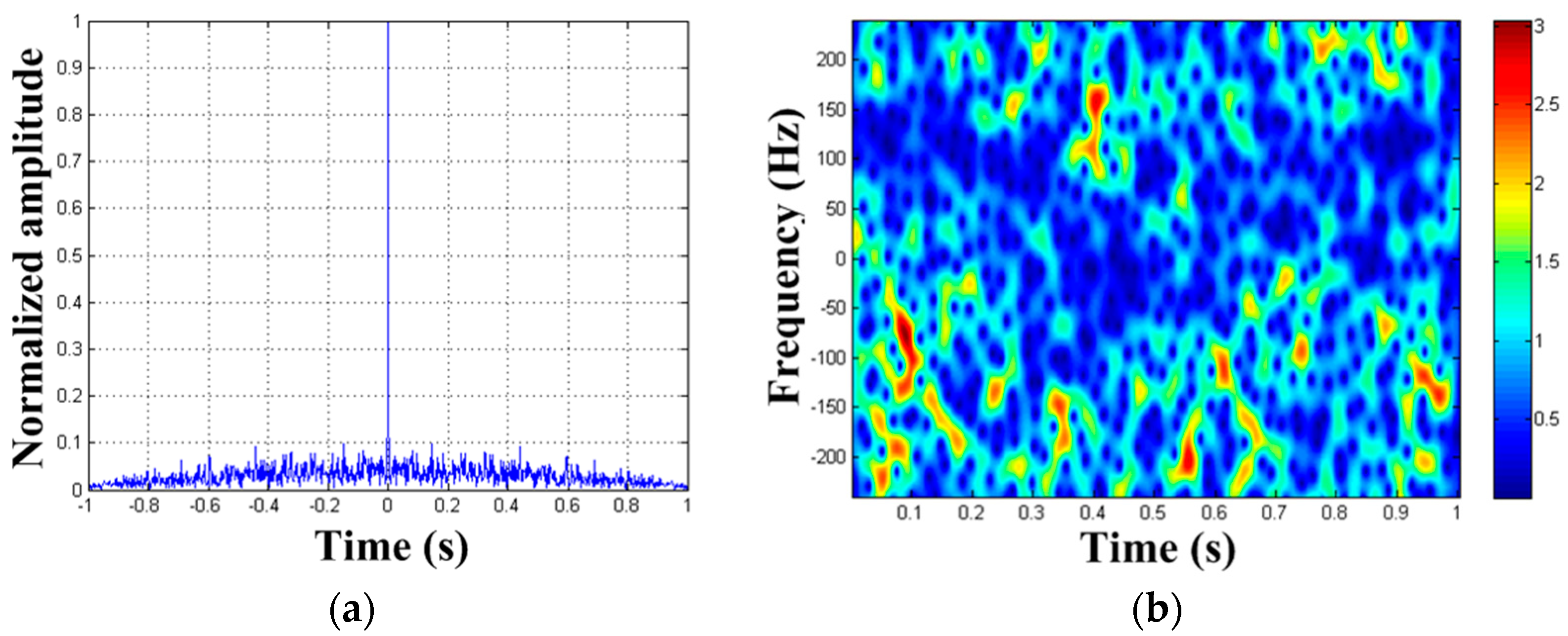
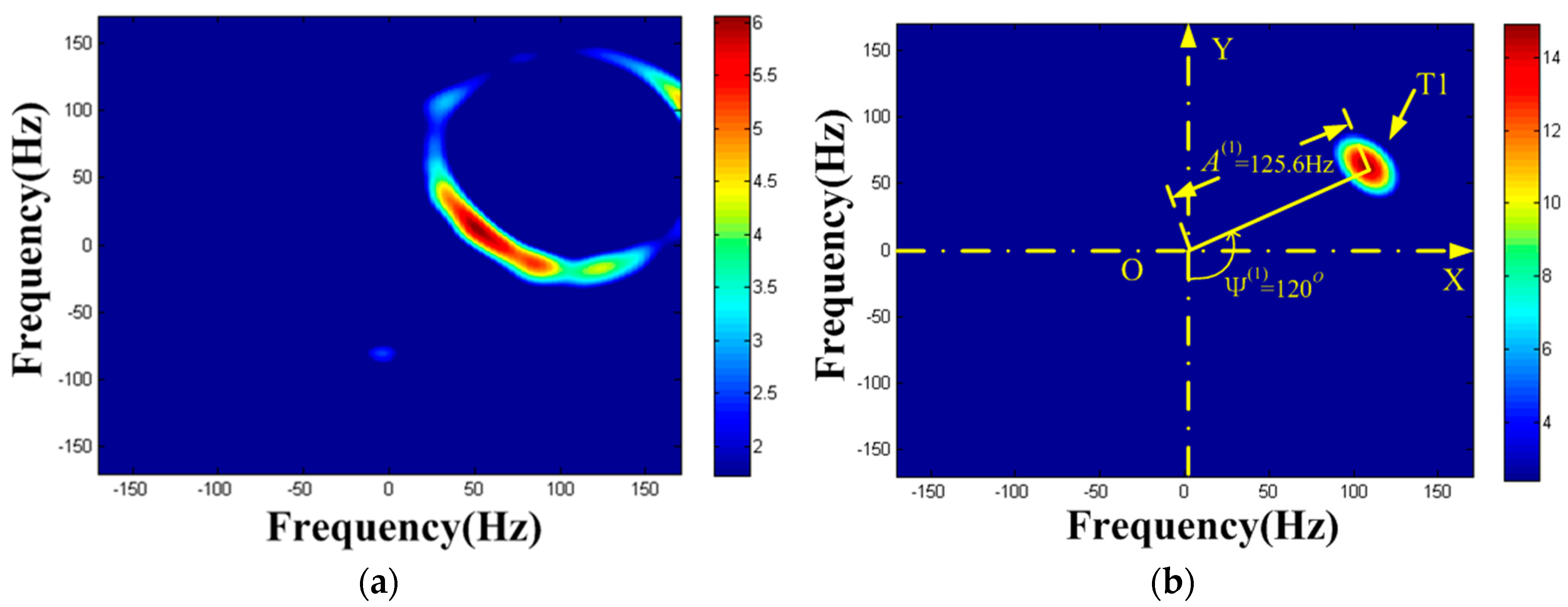
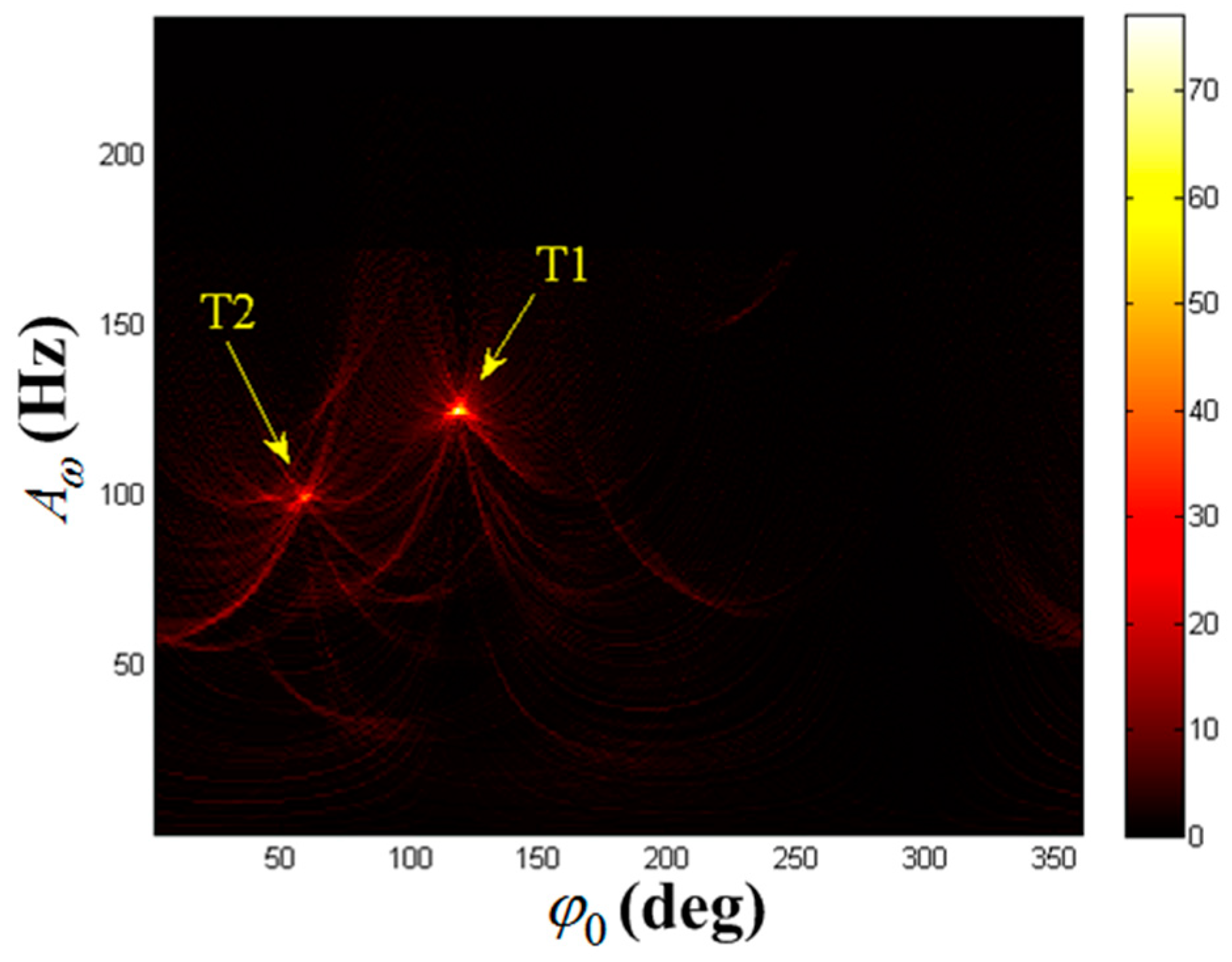
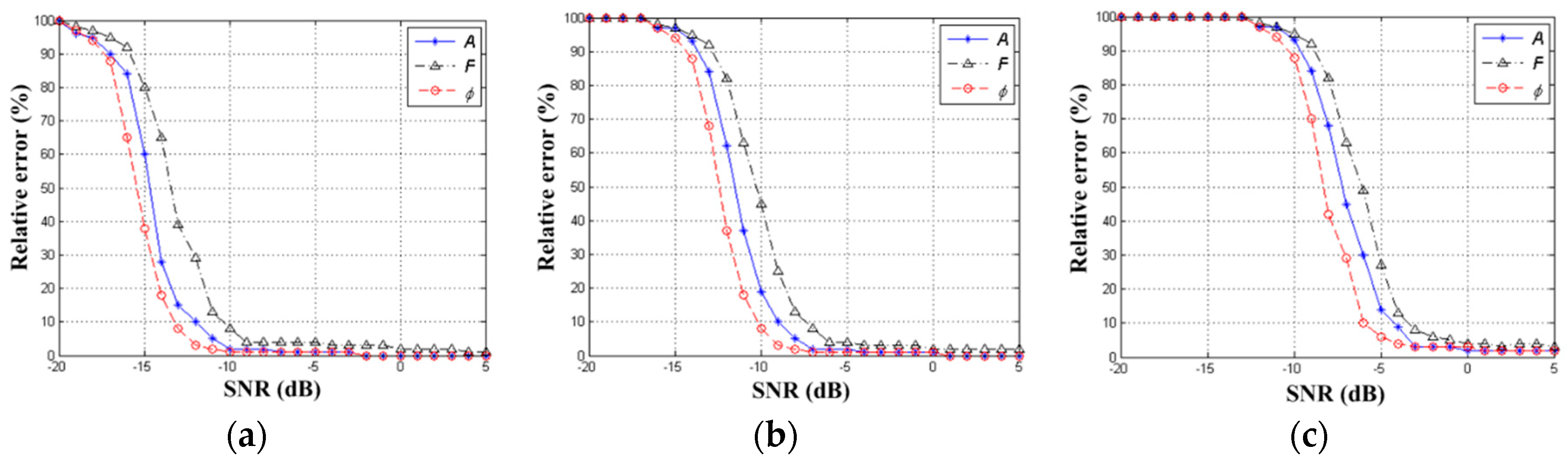


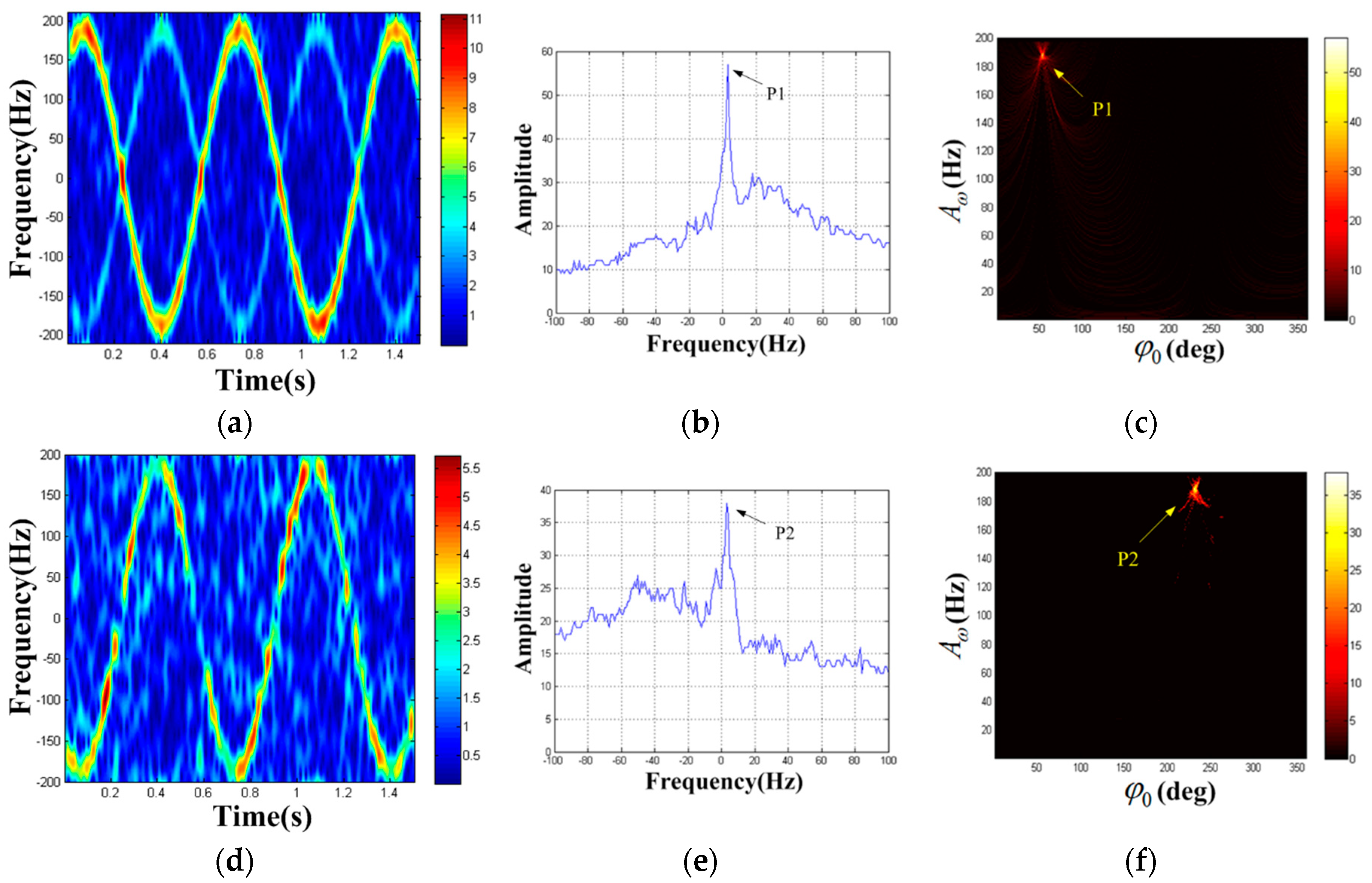
| Target | Reflection Coefficient | Rotational Frequency/Hz | Effective Radius/m | Initial Phase | Rotation Center Coordinate |
|---|---|---|---|---|---|
| T1 | 2.4 | 2 | 0.15 | 120° | |
| T2 | 1.2 | 1.5 | 0.16 | 60° | |
| T3 | 0.7 | 1.2 | 0.18 | 30° |
| Targets | Parameters | Theoretical Values | Estimated Values | Relative Errors |
|---|---|---|---|---|
| 0.48% | ||||
| 120° | 120° | |||
| 2.1% | ||||
| 0.49% | ||||
| 60° | 60° | |||
| 5% | ||||
| 1.5% | ||||
| 30° | 30° | 3.3% | ||
| 7.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Bi, D.; Shen, A.; Wang, X.; Wang, S. Hough Transform-Based Large Dynamic Reflection Coefficient Micro-Motion Target Detection in SAR. Sensors 2019, 19, 3227. https://doi.org/10.3390/s19143227
Zhou Y, Bi D, Shen A, Wang X, Wang S. Hough Transform-Based Large Dynamic Reflection Coefficient Micro-Motion Target Detection in SAR. Sensors. 2019; 19(14):3227. https://doi.org/10.3390/s19143227
Chicago/Turabian StyleZhou, Yang, Daping Bi, Aiguo Shen, Xiaoping Wang, and Shuliang Wang. 2019. "Hough Transform-Based Large Dynamic Reflection Coefficient Micro-Motion Target Detection in SAR" Sensors 19, no. 14: 3227. https://doi.org/10.3390/s19143227
APA StyleZhou, Y., Bi, D., Shen, A., Wang, X., & Wang, S. (2019). Hough Transform-Based Large Dynamic Reflection Coefficient Micro-Motion Target Detection in SAR. Sensors, 19(14), 3227. https://doi.org/10.3390/s19143227




