Monocular Robust Depth Estimation Vision System for Robotic Tasks Interventions in Metallic Targets †
Abstract
1. Introduction
1.1. State of the Art
1.2. Problem Formulation
2. Preliminary Experiments
2.1. Tracking Algorithms Comparison
- The Boosting algorithm [30] uses a set of techniques that mixes several weak classifiers algorithms to create a more robust solution. It showed the fastest performance when evaluating the features, while presenting a very low accuracy.
- Babenko et al. [31] present a robust object tracking Multiple Instance Learning (MIL)-based algorithm [32], which, although it was showing high precision, the computational time was higher too, due to the fact that it considers a set of training samples that can be ambiguous, as a single object can have many alternative instances that describe it.
- The Tracking-Learning-Detection (TLD) algorithm [33] tries to localise all the similarities within the scene. Thanks to this behaviour, it is capable of facing temporal occlusions, but it obtains a large number of miss-detections in scenarios with metallic parts, as well as higher computational time consumption.
- A version of the Kernelized Correlation Filters (KCF) algorithm [34] has been implemented. This algorithm, which is based on Histogram of Oriented Gradients (HOG) [35,36], has shown good computational performance and the greatest accuracy by tracking different kinds of objects. This is the algorithm that has been used as the basis for the solution implementation presented in this paper.
2.2. Camera Calibration
- Intrinsic parameters: The OpenCV solution [41] was used for this purpose, by applying the classical black-white chessboard, obtaining the distortion coefficient and the camera matrix (see Equation (1)).Although the well-known distortion present in current pinhole cameras, this does not present an issue for the aim of this work, as it is possible to discard the distortion coefficient. However, the camera matrix provides the essential values for this aim, where and are the focal length in X and Y axis, respectively, and and are the optical centres expressed in pixels coordinates.
- Extrinsic parameters: Unlike the intrinsic parameters, this calibration provides the camera position and orientation in regards to the frame (i.e., the base of the robot). In Reference [42] a fast technique to carry out the task is presented, which is fully implemented in the ViSP library [43]. Due to the fact that the robotic system has been designed to be modular and easily re-configurable, including tools, actuators and sensors re-positioning, this calibration technique has been demonstrated to be very appropriate, due to the fact that the camera selection, as well as its position, changes assiduously (see Table 2).
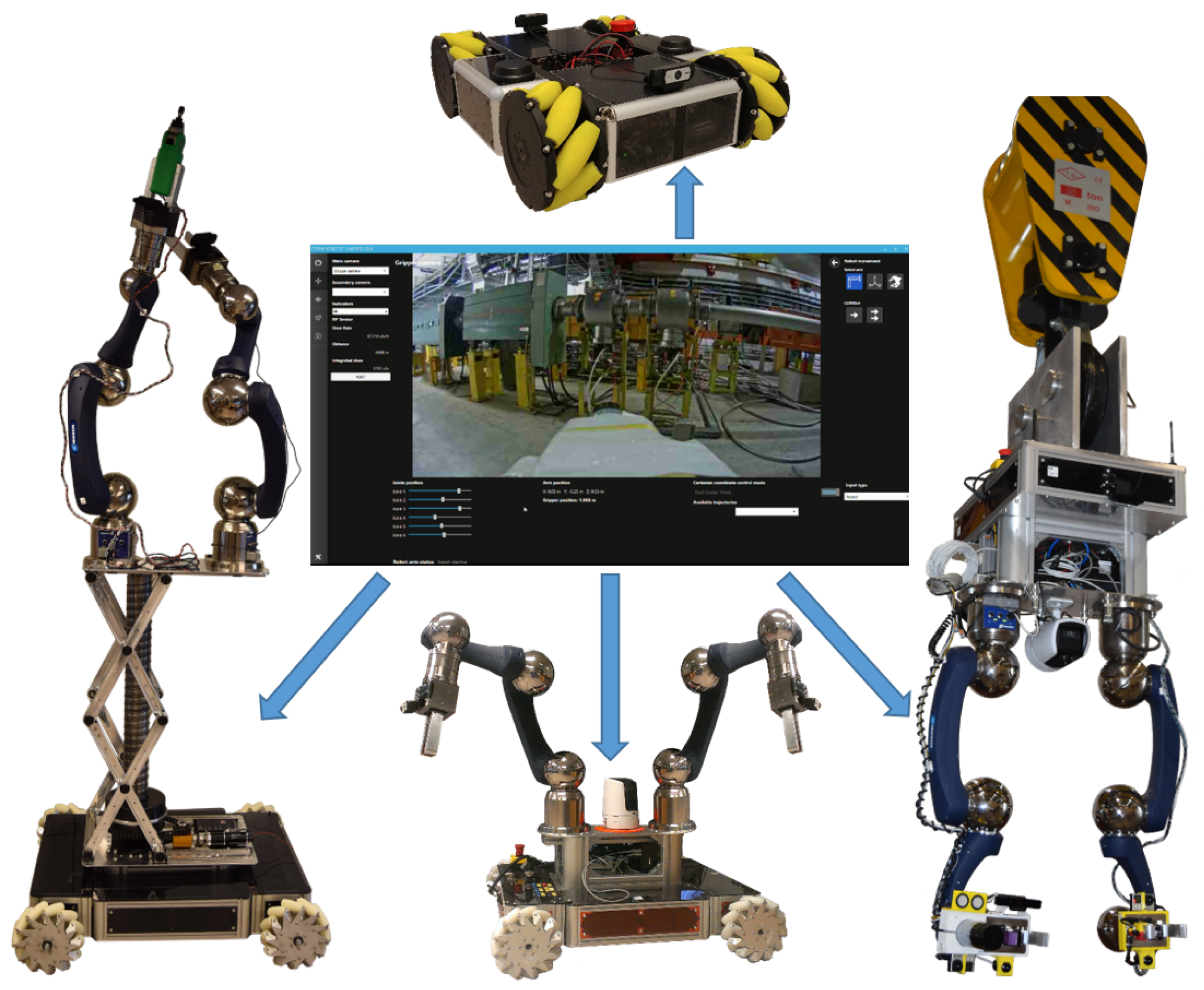
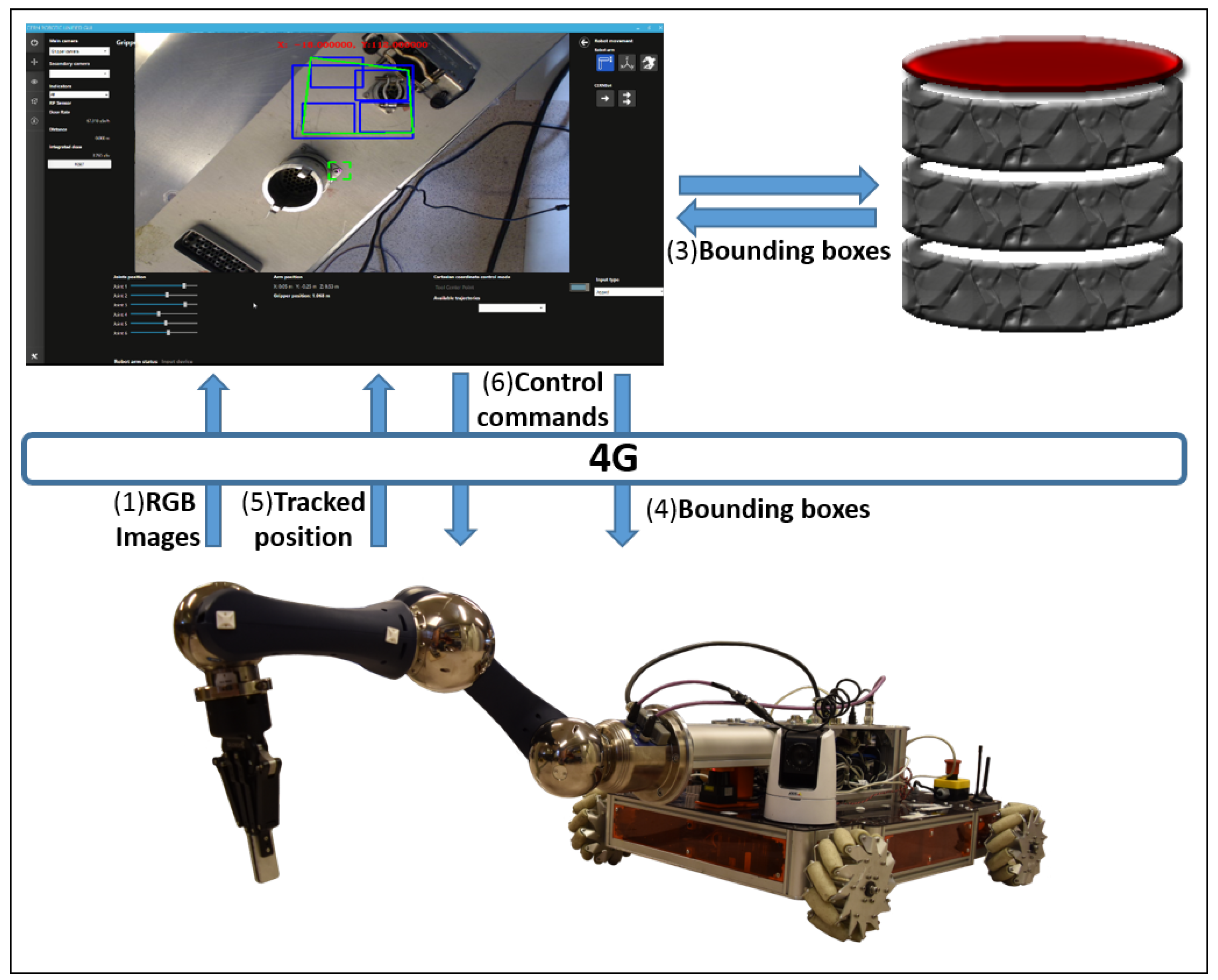
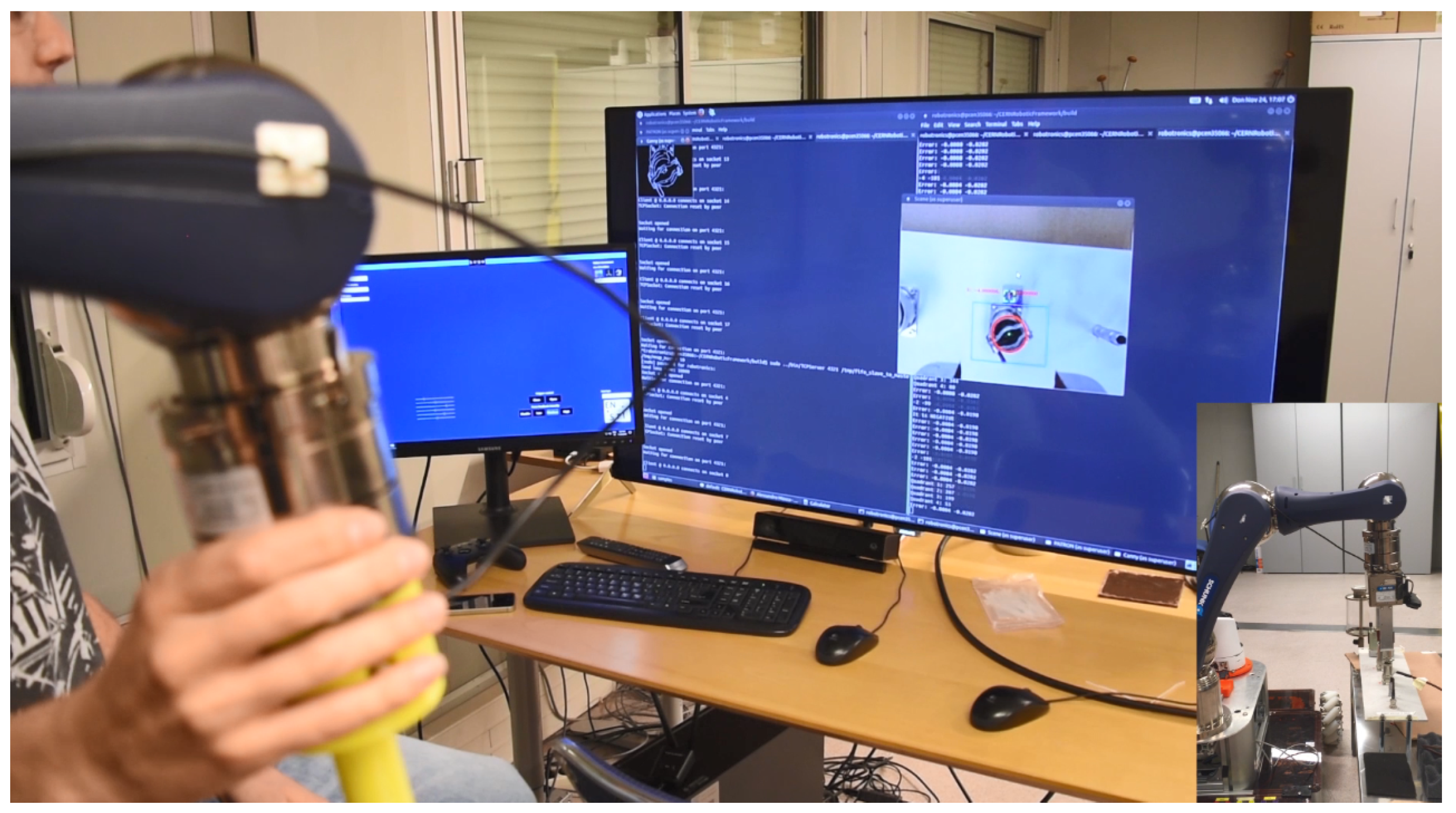
3. System Overview
4. Target Tracking, Surrounding and Approach
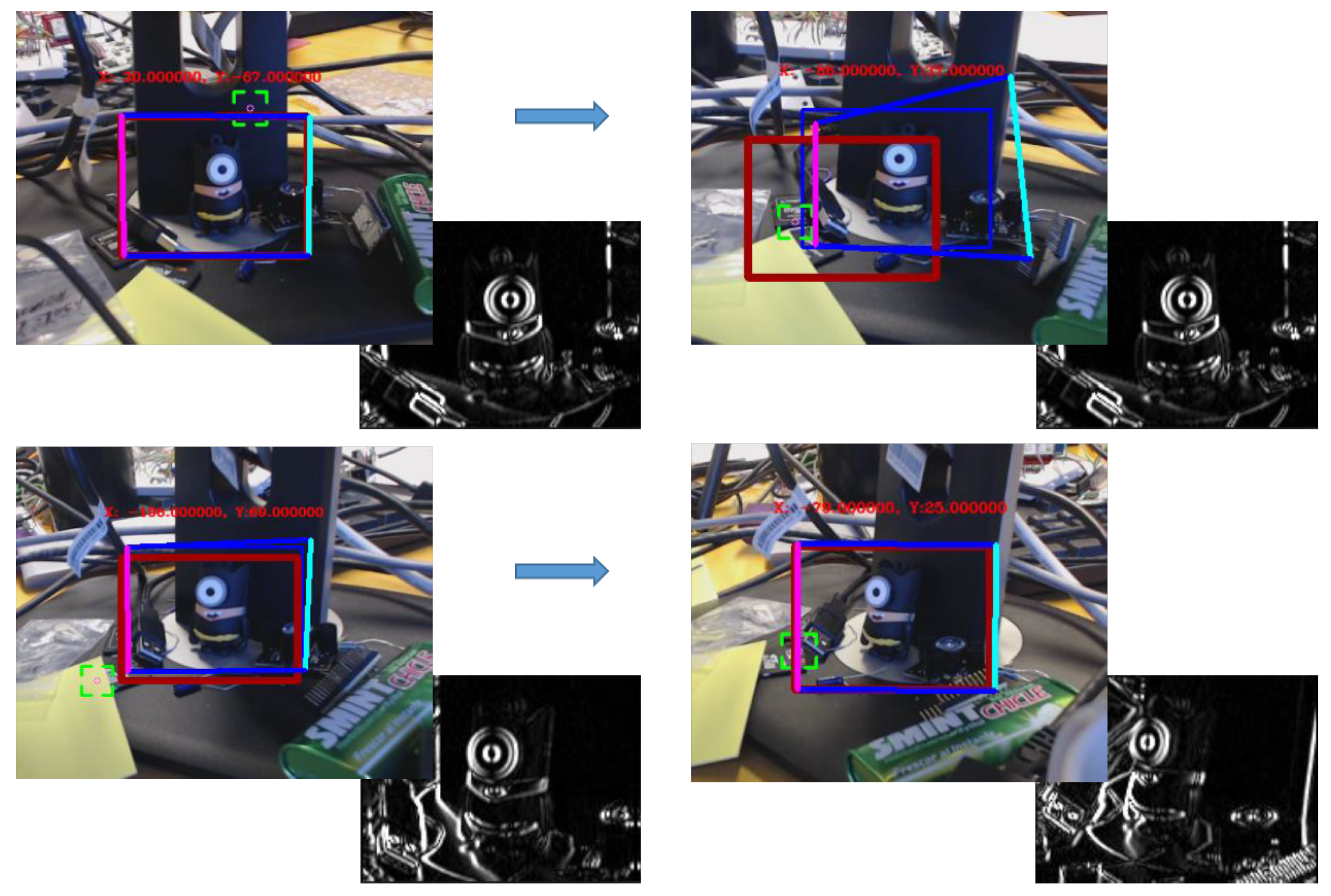
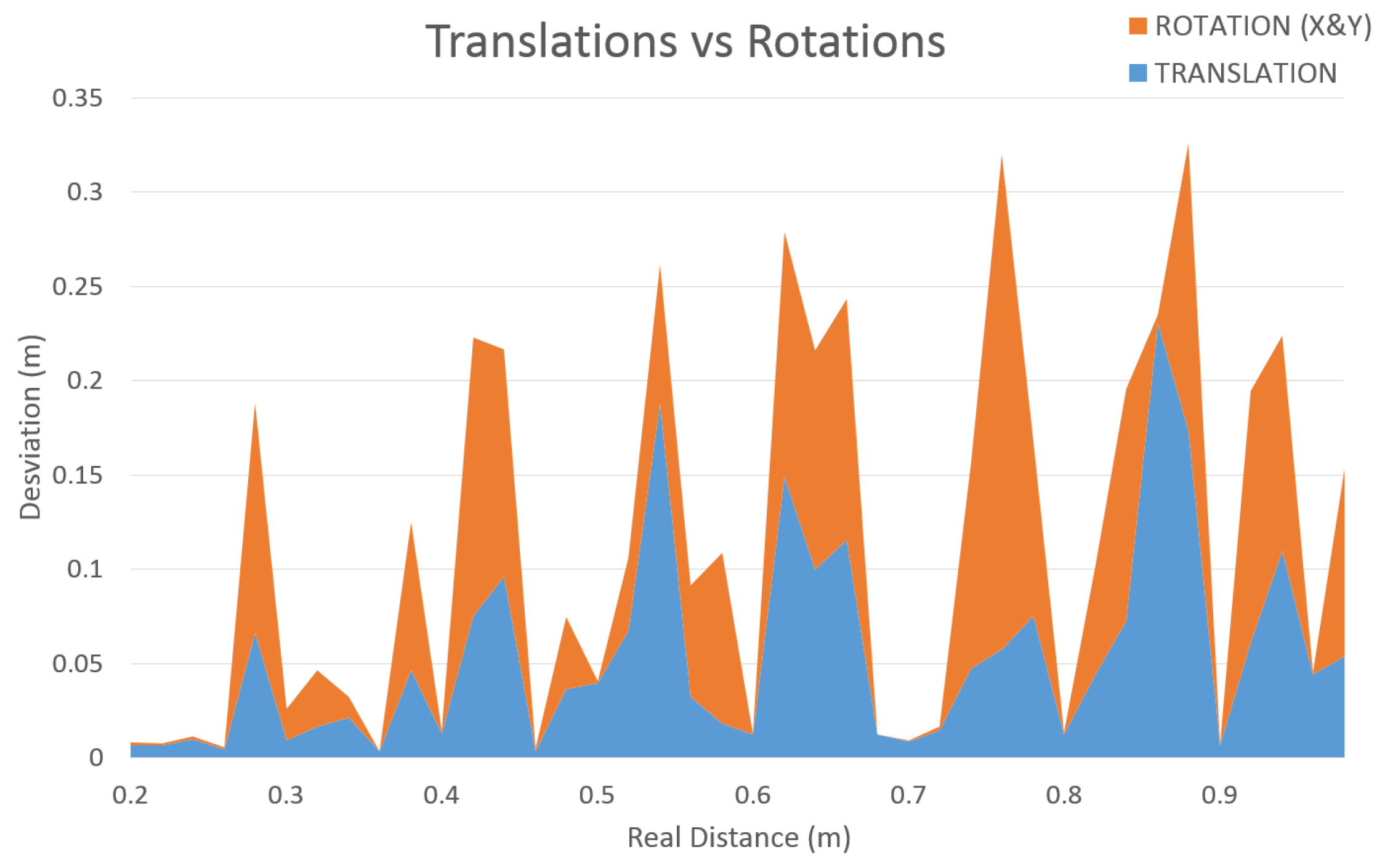
- Track the target: The tracking system must be performed in a reliable and close to real-time manner in order to avoid adding extra time, resulting in a delay, to the telerobotic task. Also, the ROI of the tracked object has to be well adjusted to the target contour in order to obtain better performance and accuracy. For this, it must be taken into account that the KCF algorithm is not invariant to scale. Therefore, when the camera approaches the lens, the ROI should be increased accordingly, avoiding losing the tracking that would otherwise occur. Likewise, when the camera is moving away from the target, the ROI has to be decreased, avoiding to track a wrong area, since the depth of the whole unstructured environment (where the robot is often used to perform the interventions) could generate errors. In summary, the tracking must be invariant to scale, orientation, translation, reflections due to metallic parts, lack of luminosity and partial occlusions.
- Surround the target: During intervention, according to the expert telerobotic human operators’ experience, it is very common to have to turn around the target once it is detected, due to the fact that the location of the components in an unstructured environment might need to dribble obstacles and study the best trajectory to reach the goal. Meanwhile, the tracking system has to be able to follow the ROI, helping to keep the target at the centre of the view.
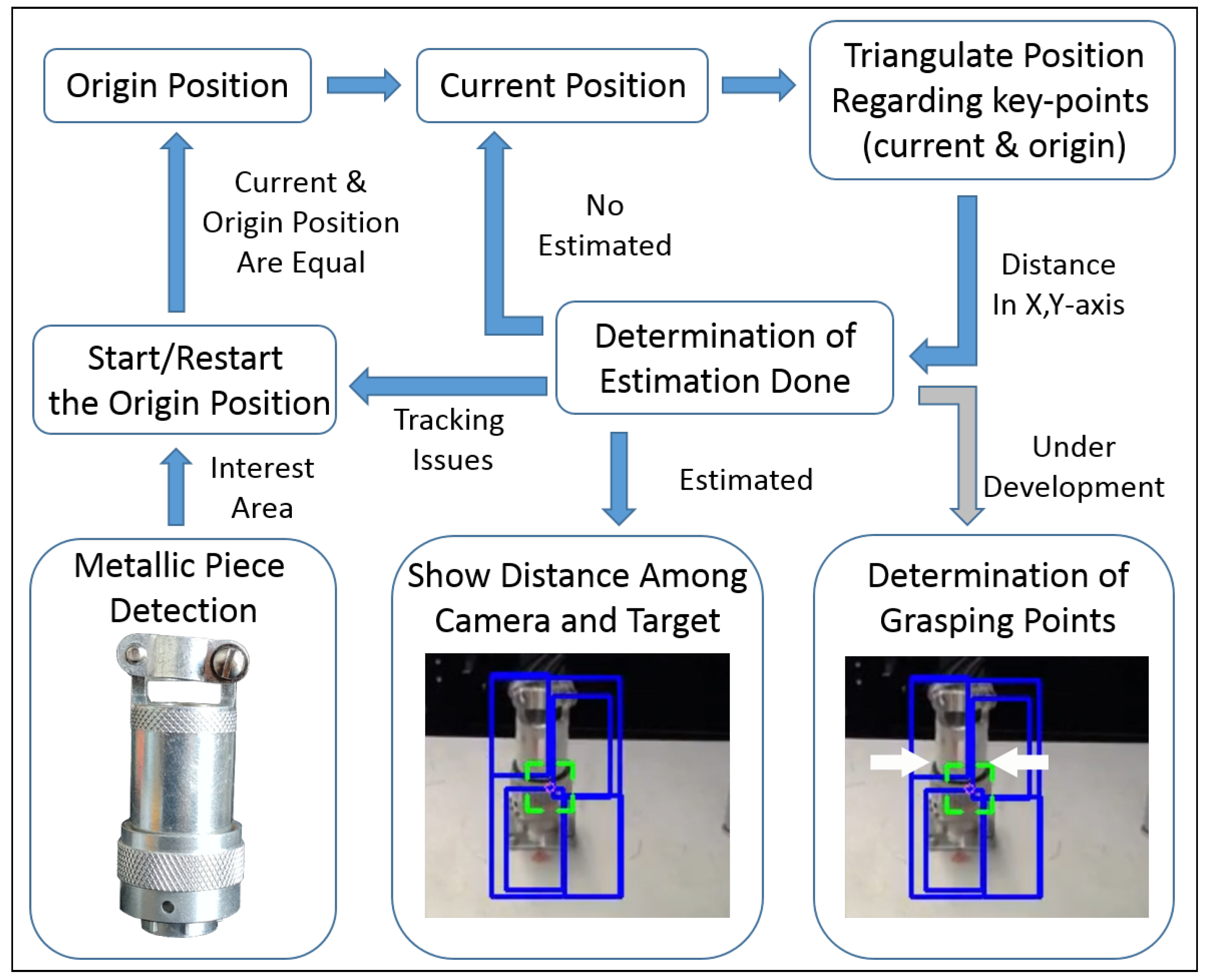
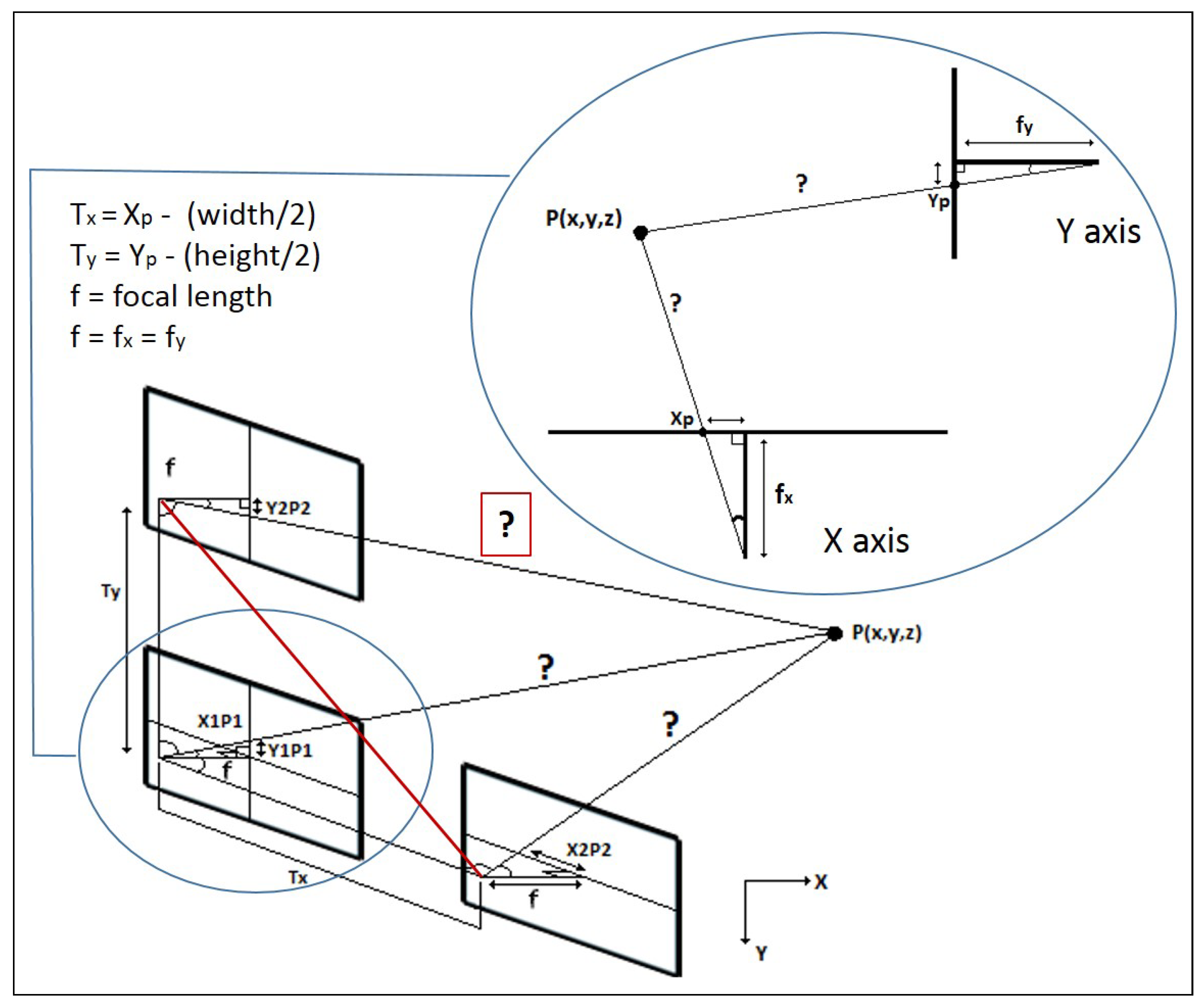
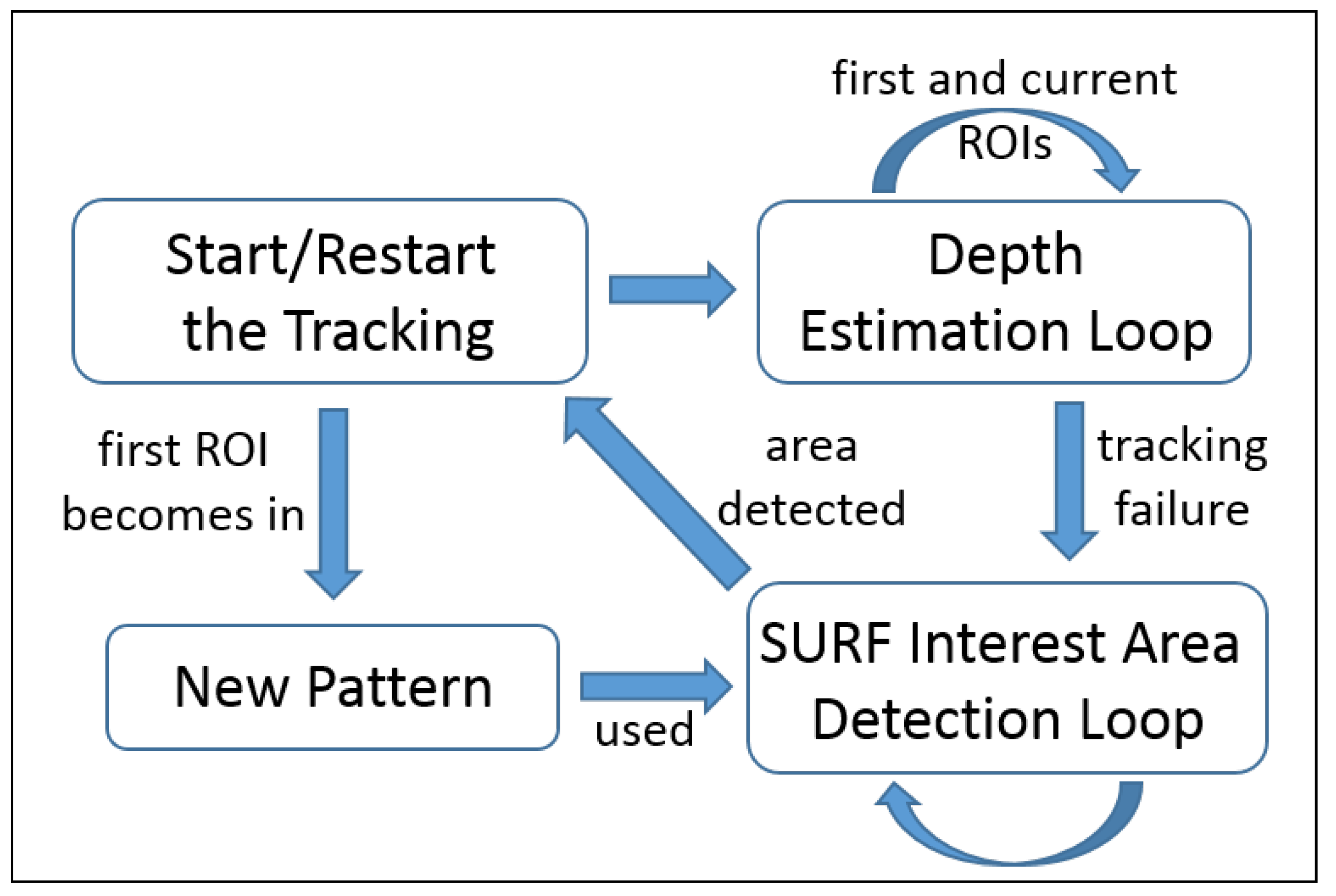
5. Tracking-Based Depth Estimation
| Algorithm 1 Depth estimation algorithm based on the tracking solution. |
| Require: OR function () for do if is not outlier then distance() distance() end if end for normalDistribution() if depth is estimated then Show the estimation and the error by AR and to adapt the arm velocity regarding to the depth end if end function function () if then ▹ Swapping pictures position end if end function |
5.1. Metallic Pieces Detection
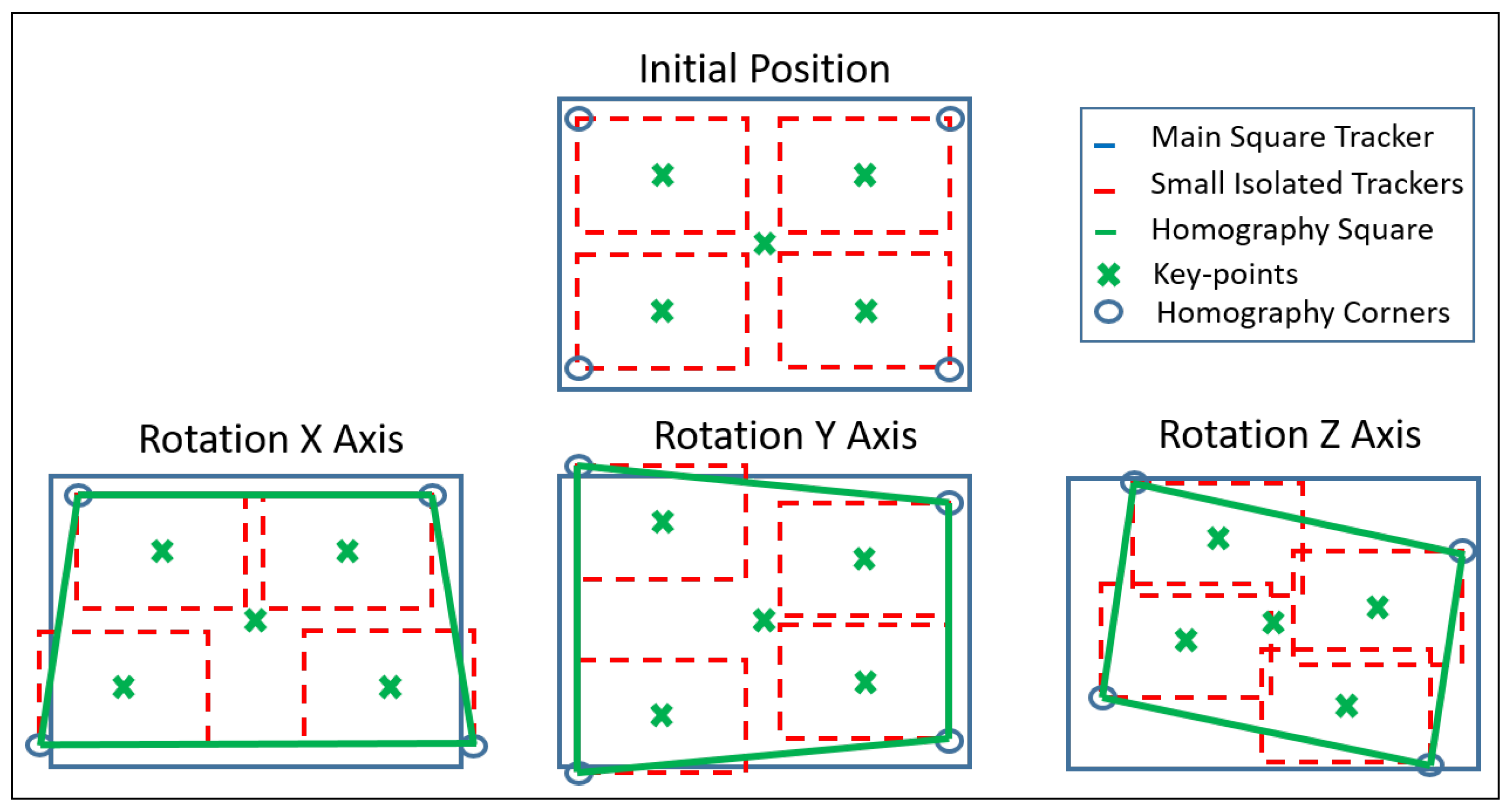
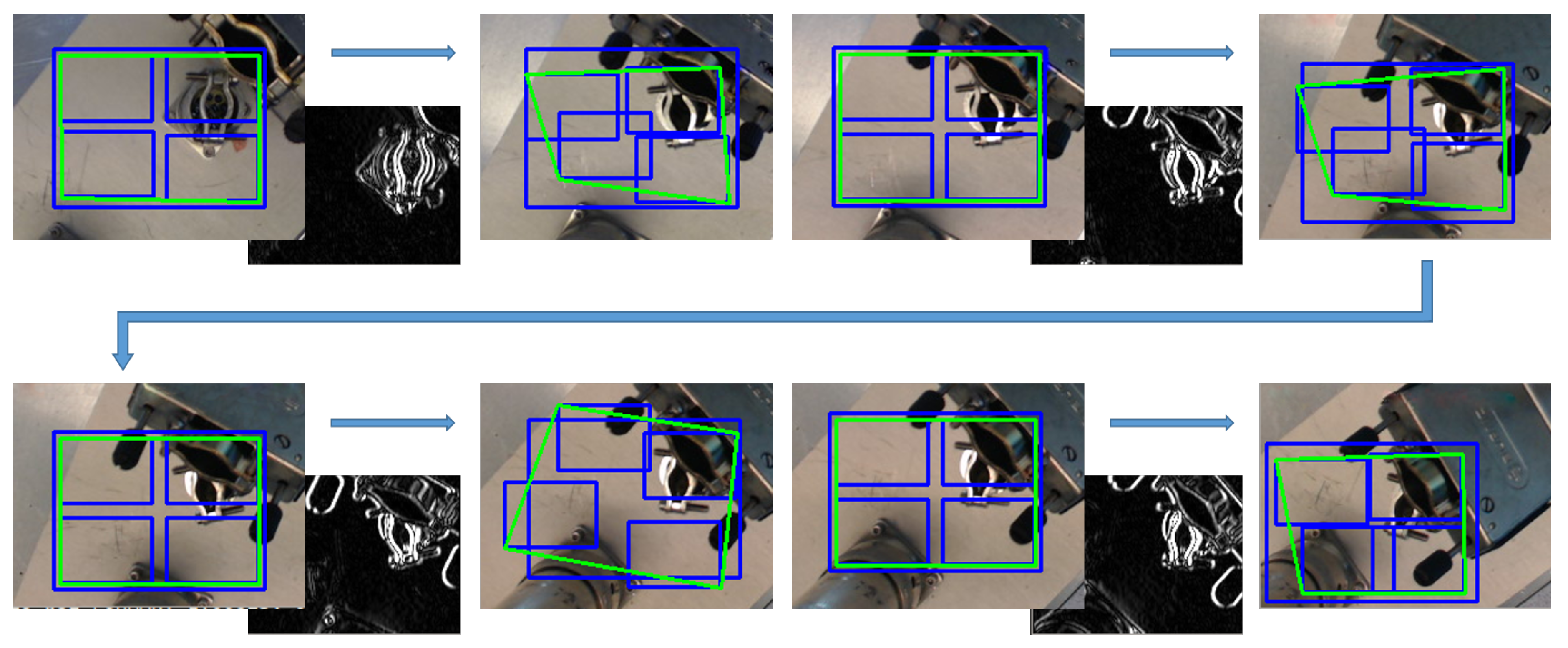
5.2. Features-Extractor-Based Key-Points Correlation
5.3. Tracking-Based Key-Points Correlation
| Algorithm 2 Euclidean-based threshold to avoid the wrong behaviour of the squares, where is the initial reference position of each ROI, and thresholdErr the threshold set by the user. |
| function () for do if is not outlier then ; ; distance_average += euclideanDistPoint[ROI]; end if end for for do error = (distance_average*(thresholdErr)/100) if then end if end for end function |
6. System Testing and Commissioning
6.1. Example of Vision-Based Autonomous Behaviour
- PTZ-Camera Visual Servoing Robot Control: A visual servoing system has been deployed to drive the robot (see Figure 10) to the target through an Axis PTZ-camera (see Figure 11), which is in charge of finding out the QPS, making use of the SURF algorithm, and a set of patterns previously loaded. Due to the fact that the camera’s framework uses the internet network protocols, a request and response communication-based Python controller has been embedded on the system (see Listing 1) to guide the platform and position it in front of the target in a proper distance, so that this can be reached.
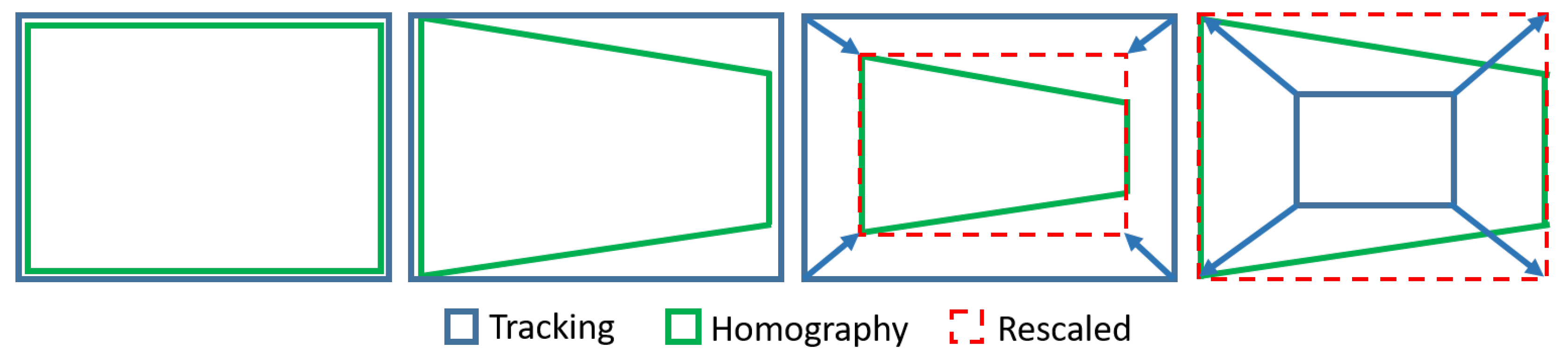
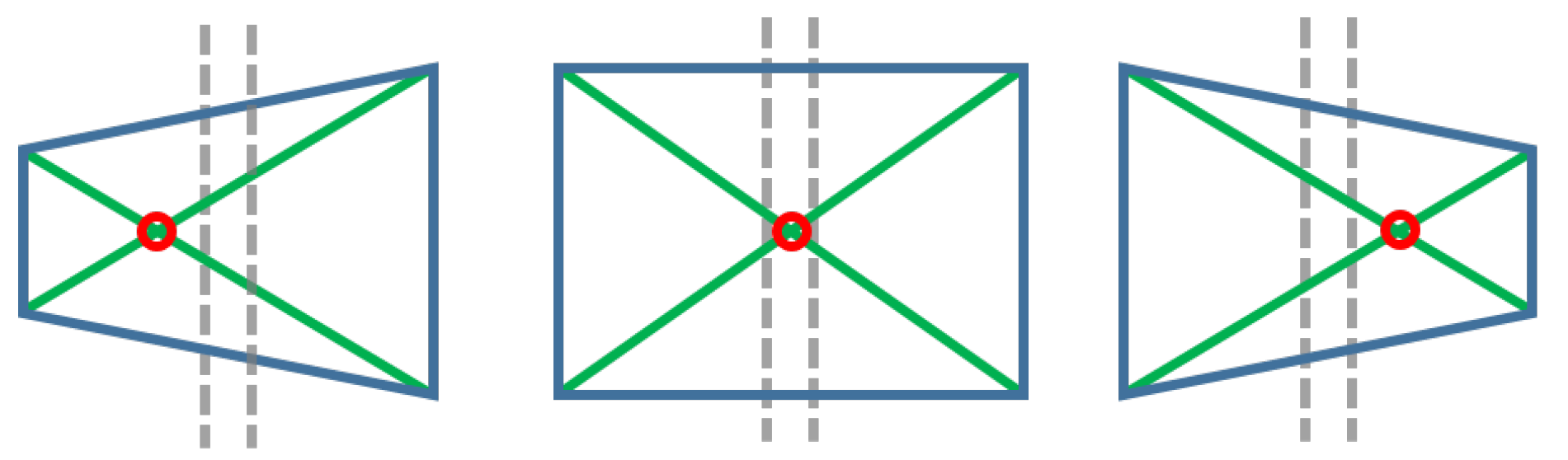
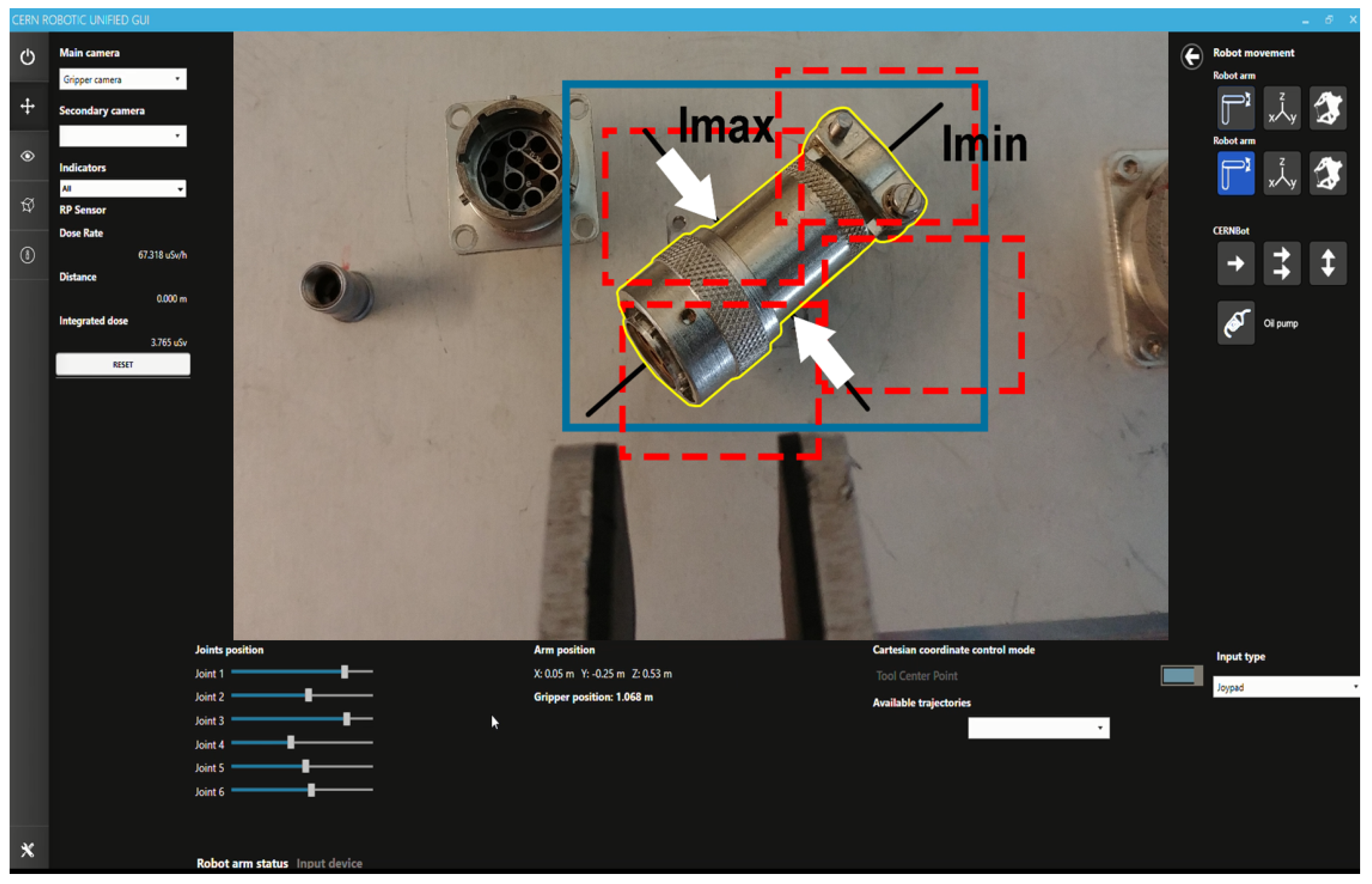
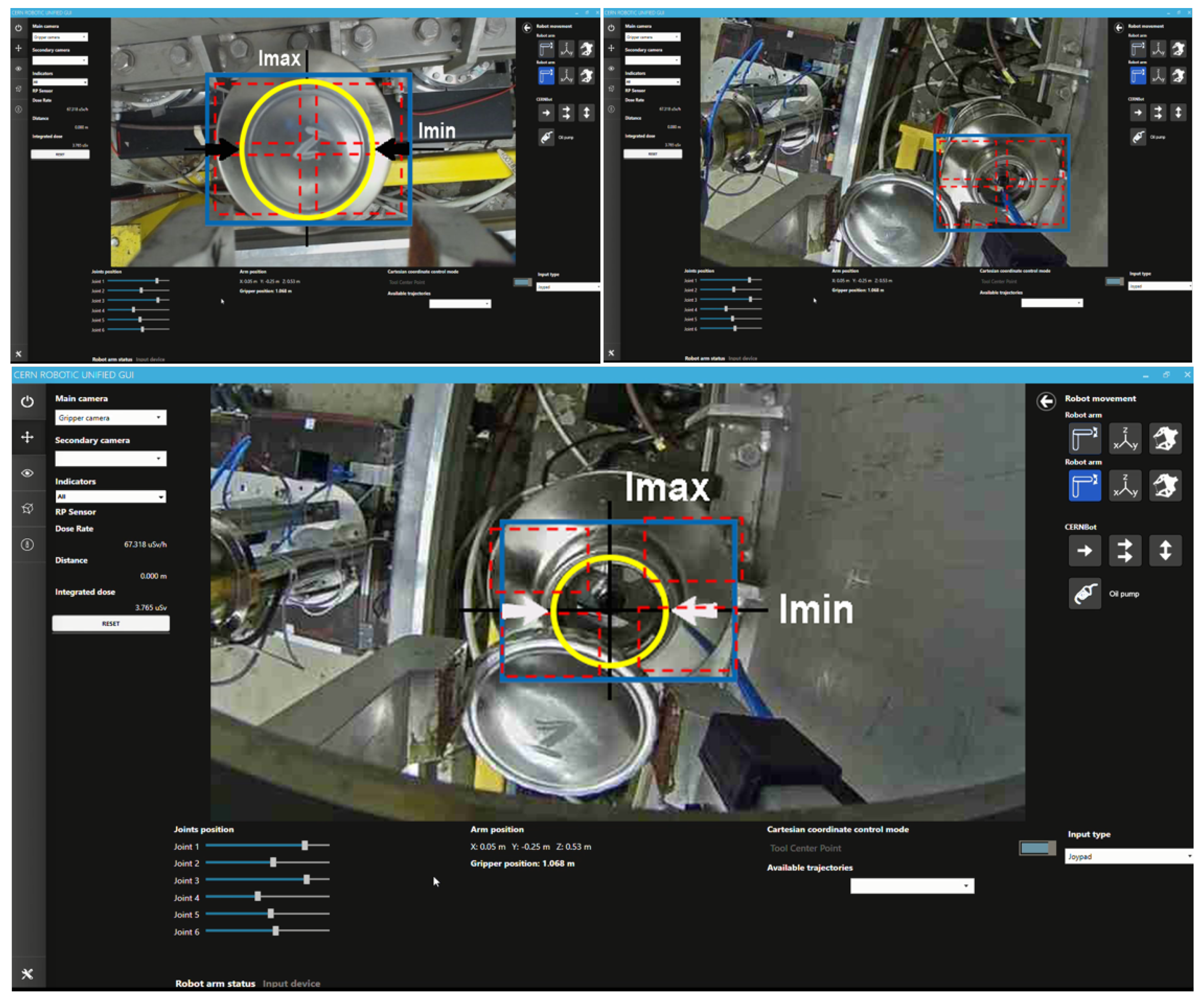
- Vision control for arm orientation: With the robot arm already approaching the target, the robotic arm is triggered to a specific position and the gripper camera is switched on, while the PTZ-camera remains disabled. Thus, the orientation of the robot with regards to the target device is calculated by the homography provided by SURF through the gripper camera. For that purpose, the intersection of the opposite corners of the square-homography gives the current orientation, as seen in Figure 12.
#include <python2.7/Python.h>
#include <curl/curl.h>
....
// It launches a request to the camera and returns its orientation
int queryPositionPTZCam(std::string &queryAxis) {
std::string readBuffer;
CURLcode res;
CURL *curl = curl_easy_init();
if (curl) {
curl_easy_setopt(curl, CURLOPT_URL, queryAxis.c_str());
curl_easy_setopt(curl, CURLOPT_WRITEFUNCTION, WriteCallback);
curl_easy_setopt(curl, CURLOPT_WRITEDATA, &readBuffer);
res = curl_easy_perform(curl);
curl_easy_cleanup(curl);
}
// Extracting the orientation figure from the response received
return std::stoi(readBuffer.substr(readBuffer.find("=") + 1,
readBuffer.find("\n") - readBuffer.find("=") - 1));
}
void movingCamera(const cv::Point centerScreenPoint, cv::Point ¢erError) {
// If target position is reached, stop PTZ-Camera
if (queryPositionPTZCam(queryAxis) == targetPosition) goto stopCamera;
Py_Initialize(); // Instantiate a Python’s interpreter
// Lambda function, it executes Python’s instructions within the
// scope of the interpreter
auto sendRequest = [&](std::string &URLRequestAxis) -> void {
PyRun_SimpleString("import requests");
PyRun_SimpleString(URLRequestAxis.c_str());
};
// If the target is not center in the scene
if ((abs(centerError.x) > 1 or abs(centerError.y) > 1)) {
sendRequest(movementURLPythonRequestAxis);
} else if ((abs(centerError.x) <= 1 and abs(centerError.y) <= 1)) {
stopCamera:
sendRequest(stopURLPythonRequestAxis);
}
Py_Finalize(); // Closing the interpreter
} - Depth Estimation: insofar as the switch detection is done (by using the split left side of the frame, since the switch location is perfectly known), the depth estimation presented in this document is launched, providing the distance to the camera and placing the gripper towards the switch.
- Fine-grained approach to the target: Apply (see Equation (7)) translation upon approaching direction by inverse kinematics to reach the switch, where is the distance from the camera to the end-effector, taken from the approach parameter on Equation (8) (wherefore and are the position of the camera and the end-effector respectively with regards to the TCP), and Depth is the measure done by Depth Estimation algorithm. The velocity is adapted to the distance estimated for a proper performance.
6.2. Example of Semi-Autonomous Vision Human-Supervised Task
6.3. Contingency Behaviours
7. Results
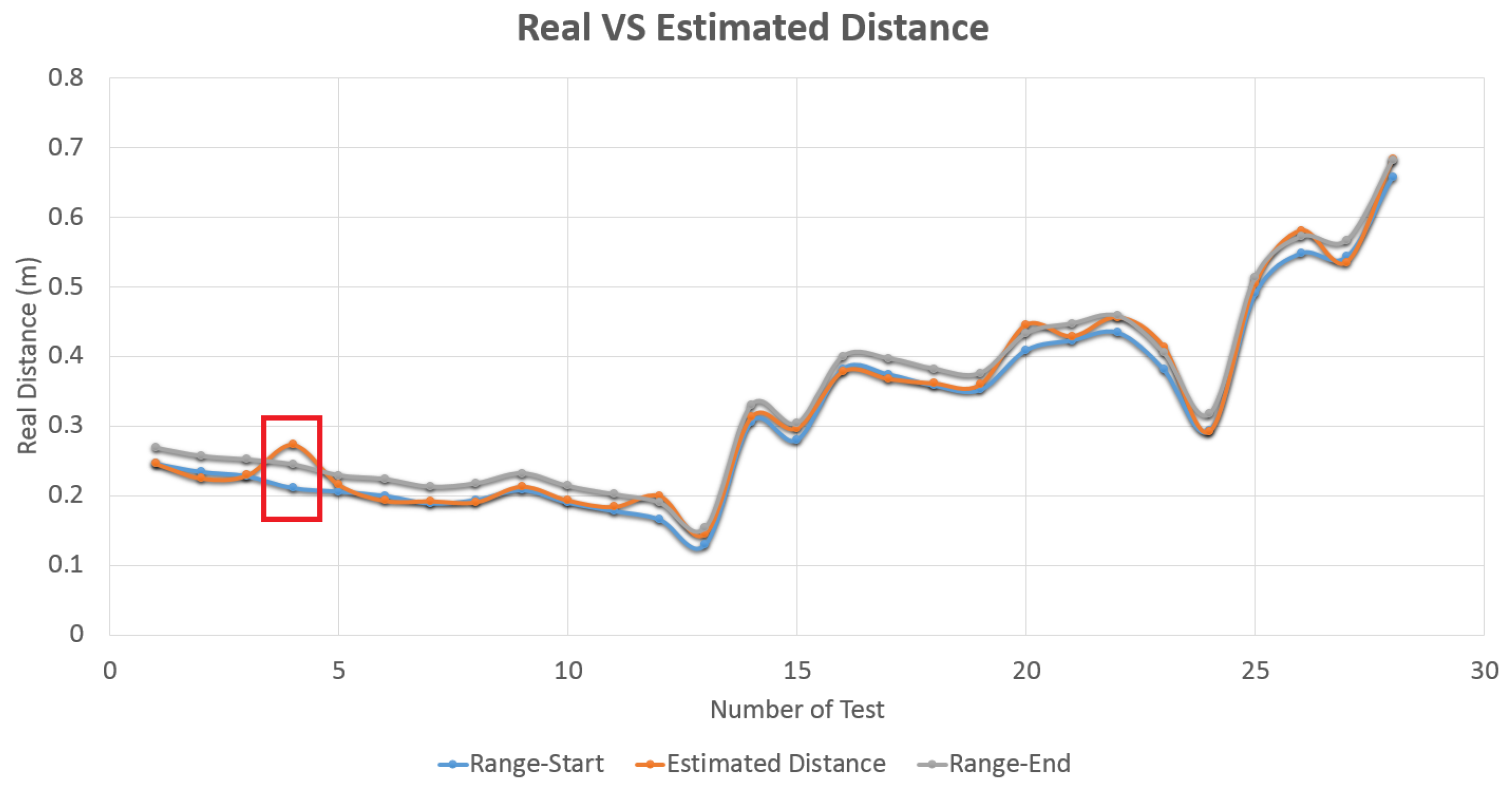
7.1. Accuracy Experiments
7.2. Metallic Targets Data-Set for Tracking and Object Recognition Benchmarking
7.3. Videos
- Contingency behaviour: this video shows a safety contingency procedure used in the tracking and depth estimation algorithm, to avoid the robot to move once the tracking has been lost, and also helping it to recover the track once the object is facing the camera. For this, once the tracked object is lost, the last tracked ROI is used by a tracking thread to explore the next camera frames, which allows the system to better recover the track according to the new reflections and luminosity target state. (https://cernbox.cern.ch/index.php/s/kEIIK6hdPwnUdDk)
- Depth Estimation: in this video a robotic arm with on-hand camera facing a pool of metallic connectors (i.e., targets) is presented. First of all, the video shows the selection of the ROI by the operator, which enables the tracking and depth estimation procedure. Also, in the second part of the video the connectors are recognized by the deep learning algorithm. Then, once the operator selects to object to track, the system calculates its depth. (https://cernbox.cern.ch/index.php/s/Qguw2RMNLr0SwuO)
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CERN | European Organization for Nuclear Research |
| LHC | Large Hadron Collider |
| BLM | Bean Loss Monitor |
| HRI | Human-Robot Interface |
| ToF | Time-of-Flight |
| RT | Real-Time |
| HD | High Definition |
| PTZ | Pan–Tilt–Zoom |
| MIL | Multiple Instance Learning |
| TLD | Tracking-Learning-Detection |
| KCF | Kernelized Correlation Filters |
| HOG | Histogram of Oriented Gradients |
| ROI | Region of Interest |
| RCNN | Regions with Convolutional Neural Network |
| TCP | Tool Center Point |
| SURF | Speeded-Up Robust Features |
| SIFT | Scale Invariant Feature Transform |
| DoF | Degrees of Freedom |
| QPS | Heater Discharge Power Supply |
| CRF | CERN Robotic Framework |
| GUI | Graphical User Interface |
References
- Di Castro, M.; Ferre, M.; Masi, A. CERNTAURO: A Modular Architecture for Robotic Inspection and Telemanipulation in Harsh and Semi-Structured Environments. IEEE Access 2018, 6, 37506–37522. [Google Scholar] [CrossRef]
- Kugler, E. The ISOLDE facility. Hyperfine Interact. 2000, 129, 23–42. [Google Scholar] [CrossRef]
- Di Castro, M.; Almagro, C.V.; Lunghi, G.; Marin, R.; Ferre, M.; Masi, A. Tracking-Based Depth Estimation of Metallic Pieces for Robotic Guidance. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5503–5508. [Google Scholar]
- Sheridan, T.B. Telerobotics, Automation, and Human Supervisory Control; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Di Castro, M.; Buonocore, L.R.; Ferre, M.; Gilardoni, S.; Losito, R.; Lunghi, G.; Masi, A. A Dual Arms Robotic Platform Control for Navigation, Inspection and Telemanipulation. In Proceedings of the 16th International Conference on Accelerator and Large Experimental Control Systems (ICALEPCS’17), Barcelona, Spain, 8–13 October 2017; JACOW: Geneva, Switzerland, 2018; pp. 709–713. [Google Scholar]
- Lunghi, G.; Prades, R.M.; Castro, M.D. An Advanced, Adaptive and Multimodal Graphical User Interface for Human-robot Teleoperation in Radioactive Scenarios. In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics, Lisbon, Portugal, 29–31 July 2016. [Google Scholar]
- Wu, Y.; Wang, M.; Mayer, N.M. A new type of eye-on-hand robotic arm system based on a low-cost recognition system. In Proceedings of the 2017 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 6–8 September 2017; pp. 110–114. [Google Scholar] [CrossRef]
- Van, M.; Wu, D.; Ge, S.S.; Ren, H. Fault diagnosis in image-based visual servoing with eye-in-hand configurations using kalman filter. IEEE Trans. Ind. Inf. 2016, 12, 1998–2007. [Google Scholar] [CrossRef]
- Peñalver, A.; Pérez, J.; Fernández, J.; Sales, J.; Sanz, P.; García, J.; Fornas, D.; Marín, R. Visually-guided manipulation techniques for robotic autonomous underwater panel interventions. Annu. Rev. Control. 2015, 40, 201–211. [Google Scholar] [CrossRef][Green Version]
- Emarose, S.; Ranganathan, M.; Siranjeevi, M.; Sugadev, M. Monocular vision based autonomous indoor mobile service robot. In Proceedings of the 2015 Online International Conference on Green Engineering and Technologies (IC-GET), Coimbatore, India, 27 November 2015; pp. 1–5. [Google Scholar]
- Yang, Y.; Cao, Q.X. Monocular vision based 6D object localization for service robot’s intelligent grasping. Comput. Math. Appl. 2012, 64, 1235–1241. [Google Scholar] [CrossRef]
- Joglekar, A.; Joshi, D.; Khemani, R.; Nair, S.; Sahare, S. Depth estimation using monocular camera. Int. J. Comput. Sci. Inf. Technol. 2011, 2, 1758–1763. [Google Scholar]
- McGuire, S.; Heckman, C.; Szafir, D.; Julier, S.; Ahmed, N. Extrinisic Calibration of a Camera-Arm System Through Rotation Identification. arXiv 2018, arXiv:1812.08280. [Google Scholar]
- Hajiloo, A.; Keshmiri, M.; Xie, W.F.; Wang, T.T. Robust online model predictive control for a constrained image-based visual servoing. IEEE Trans. Ind. Electron. 2016, 63, 2242–2250. [Google Scholar]
- Keshmiri, M.; Xie, W.F.; Mohebbi, A. Augmented image-based visual servoing of a manipulator using acceleration command. IEEE Trans. Ind. Electron. 2014, 61, 5444–5452. [Google Scholar] [CrossRef]
- León, B.; Felip, J.; Marti, H.; Morales, A. Simulation of robot dynamics for grasping and manipulation tasks. In Proceedings of the 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Osaka, Japan, 29 November –1 December 2012; pp. 291–296. [Google Scholar]
- Silva, V.; Soares, F.; Esteves, J.S.; Figueiredo, J.; Santos, C.; Pereira, A.P. Happiness and Sadness Recognition System—Preliminary Results with an Intel RealSense 3D Sensor. In CONTROLO 2016; Springer: Berlin, Germany, 2017; pp. 385–395. [Google Scholar]
- Kumar, S.; Gupta, D.; Yadav, S. Sensor fusion of laser and stereo vision camera for depth estimation and obstacle avoidance. Int. J. Comput. Appl. 2010, 1, 22–27. [Google Scholar] [CrossRef]
- Gascón, R.; Barraza, M. Six DoF Stereoscopic Eye-in-Hand Visual Servo System BIBOT. In Proceedings of the 2012 Brazilian Robotics Symposium and Latin American Robotics Symposium (SBR-LARS), Fortaleza, Brazil, 6–19 October 2012; pp. 284–289. [Google Scholar]
- Perez, J.; Sales, J.; Penalver, A.; Fornas, D.; Fernandez, J.J.; Garcia, J.C.; Sanz, P.J.; Marin, R.; Prats, M. Exploring 3-D Reconstruction Techniques: A Benchmarking Tool for Underwater Robotics. IEEE Robot. Autom. Mag. 2015, 22, 85–95. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C. A computer algorithm for reconstructing a scene from two projections. Nature 1981, 293, 133. [Google Scholar] [CrossRef]
- Pradeep, V.; Rhemann, C.; Izadi, S.; Zach, C.; Bleyer, M.; Bathiche, S. MonoFusion: Real-time 3D reconstruction of small scenes with a single web camera. In Proceedings of the 2013 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Adelaide, Australia, 1–4 October 2013; pp. 83–88. [Google Scholar]
- Tongloy, T.; Boonsang, S. An image-based visual servo control system based on an eye-in-hand monocular camera for autonomous robotic grasping. In Proceedings of the 2016 International Conference on Instrumentation, Control and Automation (ICA), Bandung, Indonesia, 29–31 August 2016; pp. 132–136. [Google Scholar]
- Shaw, J.; Cheng, K. Object identification and 3-D position calculation using eye-in-hand single camera for robot gripper. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1622–1625. [Google Scholar]
- Nobakht, H.; Liu, Y. A hybrid positioning method for eye-in-hand industrial robot by using 3D reconstruction and IBVS. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 2609–2614. [Google Scholar]
- May, S.; Droeschel, D.; Holz, D.; Fuchs, S.; Malis, E.; Nüchter, A.; Hertzberg, J. Three-dimensional mapping with time-of-flight cameras. J. Field Robot. 2009, 26, 934–965. [Google Scholar] [CrossRef]
- Dos Santos, V.R.N.; Porsani, J.L.; Hirata, N.S.T. Automatic classification of metallic targets using pattern recognition of GPR reflection: A study in the IAG-USP Test Site, Sao Paulo (Brazil). In Proceedings of the XIII Internarional Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Lunghi, G.; Prades, R.M.; Di Castro, M.; Masi, A.; Sanz, P.J. Multimodal Human-Robot Interface for Supervision and Programming of Cooperative Behaviours of Robotics Agents in Hazardous Environments: Validation in Radioactive and Underwater Scenarios for Objects Transport. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems Workshop (IROS Workshop), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.K.; Woodley, T.; Stenger, B.; Stenger, B.; Cipolla, R. Online multiple classifier boosting for object tracking. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), San Francisco, CA, USA, 13–18 June 2010; pp. 1–6. [Google Scholar]
- Babenko, B.; Yang, M.H.; Belongie, S. Robust object tracking with online multiple instance learning. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1619–1632. [Google Scholar] [CrossRef] [PubMed]
- Dietterich, T.G.; Lathrop, R.H.; Lozano-Pérez, T. Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell. 1997, 89, 31–71. [Google Scholar] [CrossRef]
- Kalal, Z.; Matas, J.; Mikolajczyk, K. Online learning of robust object detectors during unstable tracking. In Proceedings of the IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops), Kyoto, Japan, 27 September–4 October 2009; pp. 1417–1424. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef]
- Freeman, W.T.; Roth, M. Orientation histograms for hand gesture recognition. Int. Workshop Autom. Face Gesture Recognit. 1995, 12, 296–301. [Google Scholar]
- Dalal, N.; Triggs, B. Object detection using histograms of oriented gradients. In Proceedings of the Pascal VOC Workshop, European Conferenceon Computer Vision (ECCV), Graz, Austria, 7 May 2006. [Google Scholar]
- Hare, S.; Golodetz, S.; Saffari, A.; Vineet, V.; Cheng, M.M.; Hicks, S.L.; Torr, P.H. Struck: Structured output tracking with kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2096–2109. [Google Scholar] [CrossRef]
- Papageorgiou, C.P.; Oren, M.; Poggio, T. A general framework for object detection. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 555–562. [Google Scholar]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Messom, C.H.; Barczak, A.L. Stream processing for fast and efficient rotated Haar-like features using rotated integral images. Int. J. Intell. Syst. Technol. Appl. 2009, 7, 40–57. [Google Scholar] [CrossRef]
- OpenCV. Camera Calibration With OpenCV. Available online: https://docs.opencv.org/2.4/doc/tutorials/calib3d/camera_calibration/camera_calibration.html (accessed on 19 July 2019).
- Tsai, R.Y.; Lenz, R.K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- Visual Servoing Platform. Camera Extrinsic Calibration. Available online: https://visp-doc.inria.fr/doxygen/visp-daily/tutorial-calibration-extrinsic.html (accessed on 19 July 2019).
- Veiga Almagro, C.; García Sánchez, J.C.; Fornas García, D.; Marín Prades, R.; Sanz, P.J. Integration of an underwater pan–tilt camera for object detection and guidance of an underwater ROV. In Proceedings of the 39th Automatic Conference, Badajoz, Spain, 5–7 September 2018; Available online: http://dehesa.unex.es/handle/10662/8367 (accessed on 19 July 2019).
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale Invariant Feature Transform. Available online: http://www.csc.kth.se/~tony/Lin12-SIFT.pdf (accessed on 19 July 2019).
- Paul, R.P. Robot Manipulators: Mathematics, Programming, and Control: The Computer Control of Robot Manipulators; The MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Nguyen, C.C.; Pooran, F.J. Kinematic analysis and workspace determination of a 6 DOF CKCM robot end-effector. J. Mech. Work. Technol. 1989, 20, 283–294. [Google Scholar] [CrossRef]
- Hasan, A.T.; Hamouda, A.M.S.; Ismail, N.; Al-Assadi, H. An adaptive-learning algorithm to solve the inverse kinematics problem of a 6 DOF serial robot manipulator. Adv. Eng. Softw. 2006, 37, 432–438. [Google Scholar] [CrossRef]
- Weisstein, E.W. Euler Angles. Available online: http://mathworld.wolfram.com/EulerAngles.html (accessed on 19 July 2019).
- Di Castro, M.; Vera, J.C.; Ferre, M.; Masi, A. Object Detection and 6D Pose Estimation for Precise Robotic Manipulation in Unstructured Environments. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, Madrid, Spain, 26–28 July 2017; pp. 392–403. [Google Scholar]
- ModelZoo. Object Detection—Tensorflow Object Detection API. Available online: https://modelzoo.co/model/objectdetection (accessed on 19 July 2019).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Danielsson, P.E. Euclidean distance mapping. Comput. Graph. Image Process. 1980, 14, 227–248. [Google Scholar] [CrossRef]
- Doty, K.L.; Melchiorri, C.; Schwartz, E.M.; Bonivento, C. Robot manipulability. IEEE Trans. Robot. Autom. 1995, 11, 462–468. [Google Scholar] [CrossRef]
- Bayle, B.; Fourquet, J.Y.; Renaud, M. Manipulability analysis for mobile manipulators. In Proceedings of the 2001 ICRAIEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; Volume 2, pp. 1251–1256. [Google Scholar]
- Harish, A.; Babu, G.S. Manipulability Index of a Parallel Robot Manipulator. Int. J. 2015, 6, 9–17. [Google Scholar]
- Shamir, T. The singularities of redundant robot arms. Int. J. Robot. Res. 1990, 9, 113–121. [Google Scholar] [CrossRef]
- Chiaverini, S. Singularity-robust task-priority redundancy resolution for real-time kinematic control of robot manipulators. IEEE Trans. Robot. Autom. 1997, 13, 398–410. [Google Scholar] [CrossRef]
- Sanz, P.J.; Requena, A.; Inesta, J.M.; Del Pobil, A.P. Grasping the not-so-obvious: vision-based object handling for industrial applications. IEEE Robot. Autom. Mag. 2005, 12, 44–52. [Google Scholar] [CrossRef]
- Speth, J.; Morales, A.; Sanz, P.J. Vision-based grasp planning of 3D objects by extending 2D contour based algorithms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2240–2245. [Google Scholar] [CrossRef]






| Image | Model | Description |
|---|---|---|
 | Endoscope VOLTCRAFT BS-24 | HD 720p, 54°field of view, IP67-rated, diameter 8 mm., length 50 mm., 4 white LEDs light source, USB 2.0 connection |
 | iDS uEye XS | HDTV 720p, 8MP CMOS sensor, dimensions: 23 × 26.5 × 21.5 mm., 12 grams weight, USB 2.0 connection |
 | Axis F1005-E | Full HD 1080p, 113°field of view, IP66-rated, Ethernet connection |
 | iDS uEye-se | VGA to 10.5 MP, CMOS sensor, up to 93 fps in AOI mode, USB 2.0 connection |
 | Logitech C930e | Full HD 1080p, 90°field of view, Auto-focus, zoom to 4X in 1080p, USB 3.0 connection |
| Setup | Description |
|---|---|
 | Default CERNBot’s end-effector with 7 cm fingers length and eye-in-hand mono-camera attached to the Schunk GP15 gripper |
 | 2 monocular cameras TCP system: red box shows an eye-in-hand camera; green circle shows an end-effector endoscope camera on the pneumatic angular screwdriver key held by the Schunk GP15 gripper |
 | Axis monocular camera attached to a ROBOTIQ 2-Finger 140 mm Adaptive gripper |
 | Endoscope eye-in-hand camera on the Schunk GP15 gripper with extension fingers (22 cm. length) for fragile and hardly reachable radioactive source manipulation |
 | Webcam attached to the screwdriver head and carried by a Schunk GP15 gripper |
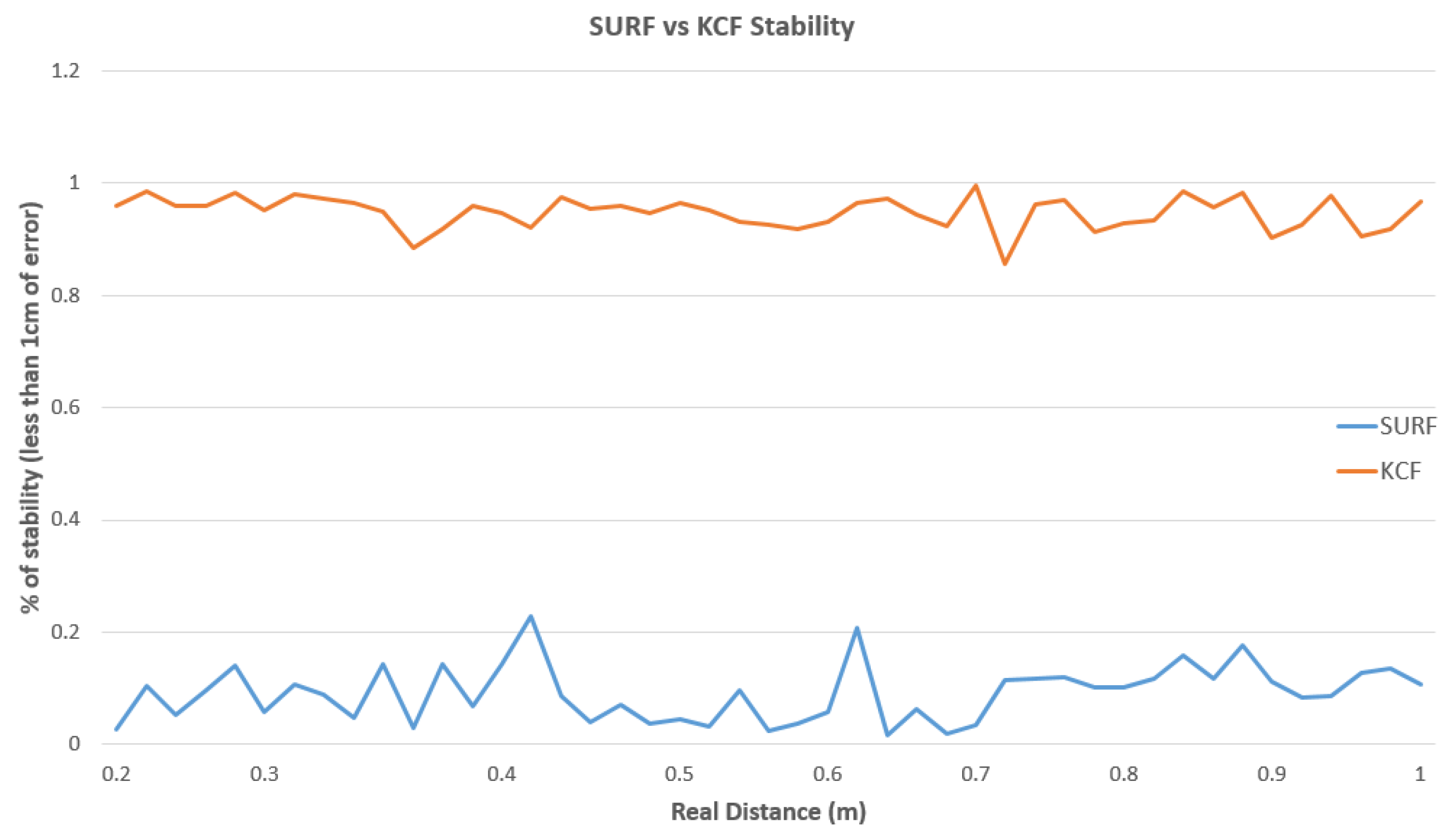
| Real Dist. | SURF-Error (m) | KCF-Error (m) | SURF-Stability (%) | KCF-Stability (%) |
|---|---|---|---|---|
| 0.20 m. | 0.0022346 | 0.0047224 | 0.083957663 | 0.970001464 |
| 0.30 m. | 0.0046036 | 0.0043484 | 0.088593119 | 0.963883933 |
| 0.40 m. | 0.0020228 | 0.0055516 | 0.12287338 | 0.92588872 |
| 0.50 m. | 0.0038266 | 0.0033858 | 0.055642677 | 0.959756087 |
| 0.60 m. | 0.0033424 | 0.0044288 | 0.049432454 | 0.932125796 |
| 0.70 m. | 0.003555 | 0.0051822 | 0.068023731 | 0.959685824 |
| 0.80 m. | 0.0041976 | 0.0060142 | 0.111163444 | 0.926650095 |
| 0.90 m. | 0.002221 | 0.0045714 | 0.1359251 | 0.952898557 |
| 1.00 m. | 0.0020276 | 0.0026512 | 0.108168958 | 0.939239064 |
| Average | 0.00311458 | 0.004539556 | 0.09153117 | 0.947792171 |
| Image | Metallic Object | Description |
|---|---|---|
 | Collimator | Device present in the LHC accelerator to filter particles that got not aligned in the beam |
 | Guide | Beacons for alignment used in different tasks according to the ending placed on top |
 | Socket | Electrical socket connection |
 | Separator | Device to separate the collimator from the beam |
 | Relay | Switch to turn off/on the machine functions |
 | Spikes | Guide designed to help the the separator installation |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veiga Almagro, C.; Di Castro, M.; Lunghi, G.; Marín Prades, R.; Sanz Valero, P.J.; Pérez, M.F.; Masi, A. Monocular Robust Depth Estimation Vision System for Robotic Tasks Interventions in Metallic Targets. Sensors 2019, 19, 3220. https://doi.org/10.3390/s19143220
Veiga Almagro C, Di Castro M, Lunghi G, Marín Prades R, Sanz Valero PJ, Pérez MF, Masi A. Monocular Robust Depth Estimation Vision System for Robotic Tasks Interventions in Metallic Targets. Sensors. 2019; 19(14):3220. https://doi.org/10.3390/s19143220
Chicago/Turabian StyleVeiga Almagro, Carlos, Mario Di Castro, Giacomo Lunghi, Raúl Marín Prades, Pedro José Sanz Valero, Manuel Ferre Pérez, and Alessandro Masi. 2019. "Monocular Robust Depth Estimation Vision System for Robotic Tasks Interventions in Metallic Targets" Sensors 19, no. 14: 3220. https://doi.org/10.3390/s19143220
APA StyleVeiga Almagro, C., Di Castro, M., Lunghi, G., Marín Prades, R., Sanz Valero, P. J., Pérez, M. F., & Masi, A. (2019). Monocular Robust Depth Estimation Vision System for Robotic Tasks Interventions in Metallic Targets. Sensors, 19(14), 3220. https://doi.org/10.3390/s19143220







