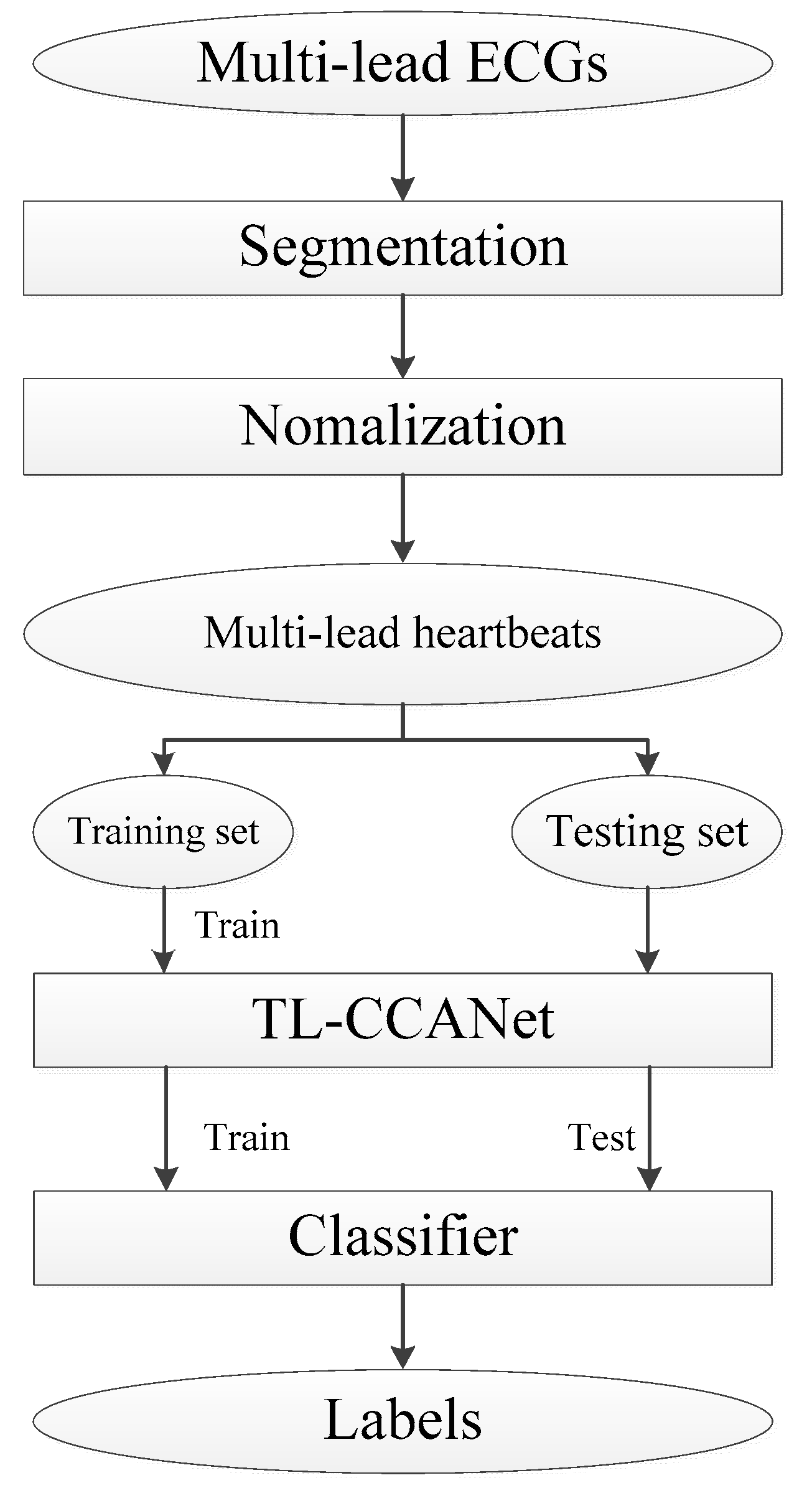
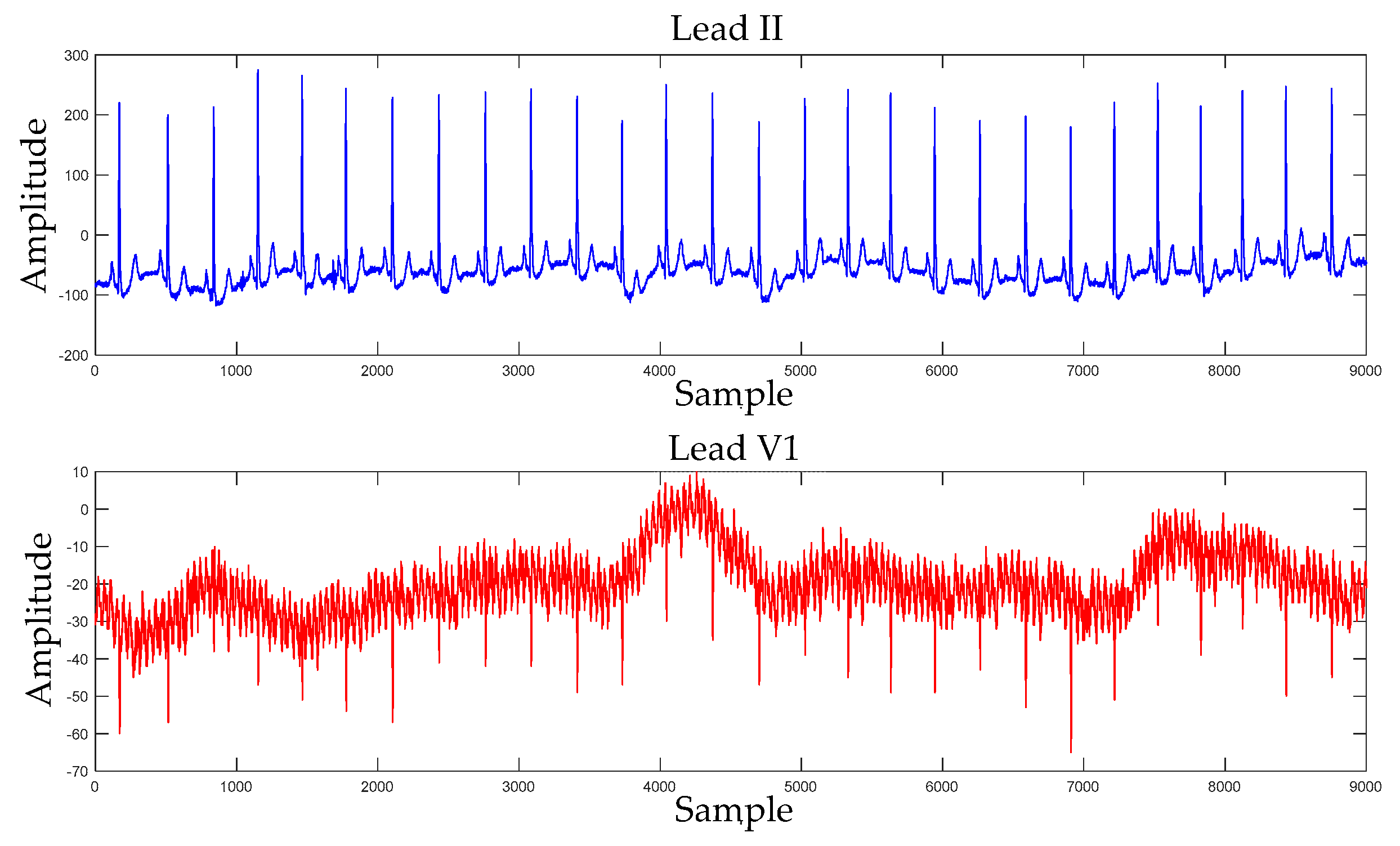
3.2.1. DL-CCANet
CCANet, designed for processing two-view images, was first proposed by Yang et al. in 2017 [
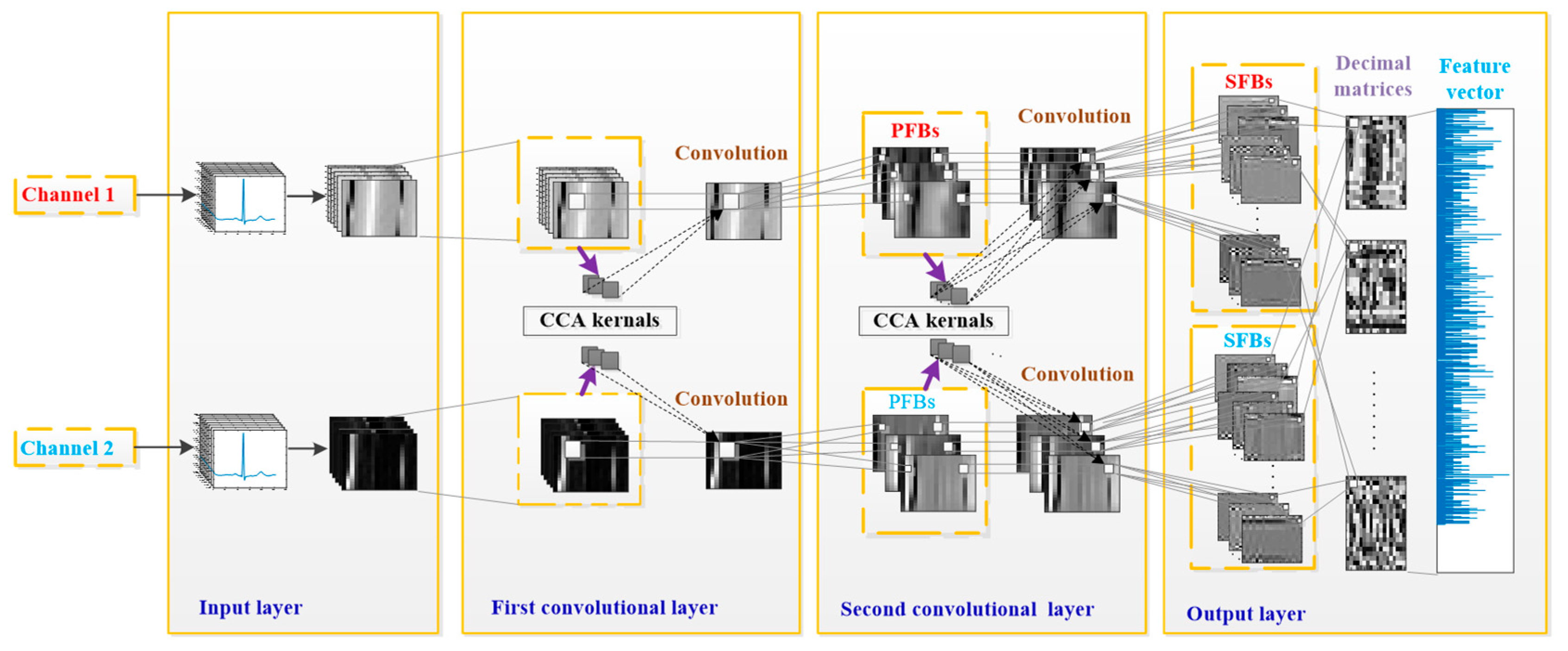
20]. Compared to one-view image-based PCANet and RandNet, CCANet yields superior performance in recognizing images. A standard CCANet consists of two cascaded convolutional layers and an output layer: (1) in the convolutional layers, the CCA technique is used to extract dua-lead filter banks; (2) in the output layer, the CCA features extracted from the second convolutional layer was mapped into the final feature vector. In this work, we adopted CCANet as the feature extraction method of dual-lead ECGs. Because the 2D convolutional process in CCANet can only handle 2D matrices, an input layer is introduced before the first convolutional layer, by which the complete dual-lead CCANet (DL-CCANet) is obtained. The structure of the DL-CCANet is shown in
Figure 2.
(1) Input layer
In this layer, each heartbeat containing m × n samples is reshaped into an ECG matrix with a size of m × n, which represents the i-th heartbeat in the h-th ECG lead.
(2) First convolutional layer
Initial stage: Given two-lead ECG matrices and , a t1 × t2 patch is adopted to extract a series of local feature blocks by centering on each pixel. We then carry out zero-center and vectorization operations on each local block, by which a set of pending vectors are obtained. Next, the pending vectors corresponding to all the heartbeats in the h-th lead are concatenated into and the pending matrix .
Filter extraction stage: Then, the CCA filters can be obtained by reshaping several canonical vectors. With the constraints
and
, the first canonical vector is calculated by the CCA model
where
, and the terms
a1 and
b1 are the first canonical vectors for two ECG leads, respectively. As per Equation (2), a Lagrange multiplier technique with multipliers λ and ν is adopted to solve the above CCA model:
To obtain the maximum value
, we need to solve Equation (3).
Then, Equation (3) is converted into the forms and , by which we obtain the canonical vectors a1 and b1. Next, the subsequent canonical vectors al, l > 1 and bl, l > 1 can be calculated by solving the CCA model with the combination of Lagrange multiplier technique and new constraints
As per Equation (4), all the 2
L1 canonical vectors (
al,
l = 1, 2, …,
L1 and
bl,
l = 1, 2, …,
L1) are mapped into matrices
and
, which are adopted as the CCA filters corresponding to two ECG leads, respectively:
V or
W?
where
reshapes the vectors
al and
bl into matrices
and
, and
L1 is the number of CCA filters.
Convolutional stage: The preliminary feature blocks (PFBs) can be obtained as per where is the convolutional symbol.
(3) Second convolutional layer
Initial stage: The PFBs are employed as the input of this layer, and an initial operation similar to the previous layer is carried out to obtain and
Filter extraction stage: Similarly, taking
Yh,
h = 1,2 as the object to be processed, we employ the Lagrange multiplier technique to solve the CCA model with
, by which the canonical vectors
c𝓁 and
d𝓁 can be obtained. Then, we calculate the CCA filters
and
as per Equation (5):
where the meanings of
and
L2 are the same as in Equation (4).
Convolutional stage: Similarly, the secondary feature blocks (SFBs) are calculated as per , where and are concatenated as a whole.
(4) Output layer
In this layer, each SFB is converted into several decimal matrices as per
where the function
H(
) maps the
onto binary images as per Equation (6):
Ultimately, the final feature vector is obtained as per fi = [Bhist(T1),Bhist(T2), …, Bhist(] , where Bhist() denotes the block segmentation (the size of the block is u1 × u2)fhg with a fixed overlap rate R and a histogram statistics approach, and B is the number of blocks collected from Ti,j. The laconic workflow of the DL-CCANet is illustrated in Algorithm 1.
| Algorithm 1. The algorithm of two convolutional stages of the DL-CCANet. |
| Input: | Raw Two-Lead Heartbeats |
| Output: | fi |
| 1: | Form ECG matrix |
| 2: | for the first convolutional stage do |
| 3: | Form the two-lead pending matrices Xh |
| 4: | Compute the covariance matrix sij of Xi and Xj |
| 5: | Solve the CCA model by the Lagrange multiplier technique to obtain the two-lead project directions a, b |
| 6: | Construct two-lead filter banks |
| 7: | Calculate the preliminary feature blocks of the first convolutional stage |
| 8: | end for |
| 9: | for the second convolutional stage do |
| 10: | Form the two-lead pending matrices |
| 11: | Compute the covariance matrix sij of Yi and Yj |
| 12: | Solve the CCA model to obtain the two-lead project directions c, d |
| 13: | Construct two-lead filter banks |
| 14: | Calculate the output of the second convolutional stage: |
| 15: | end for |
| 16: | Compute the binarized images |
| 17: | Compute the one decimal image |
| 18: | Construct the histogram vector fi |
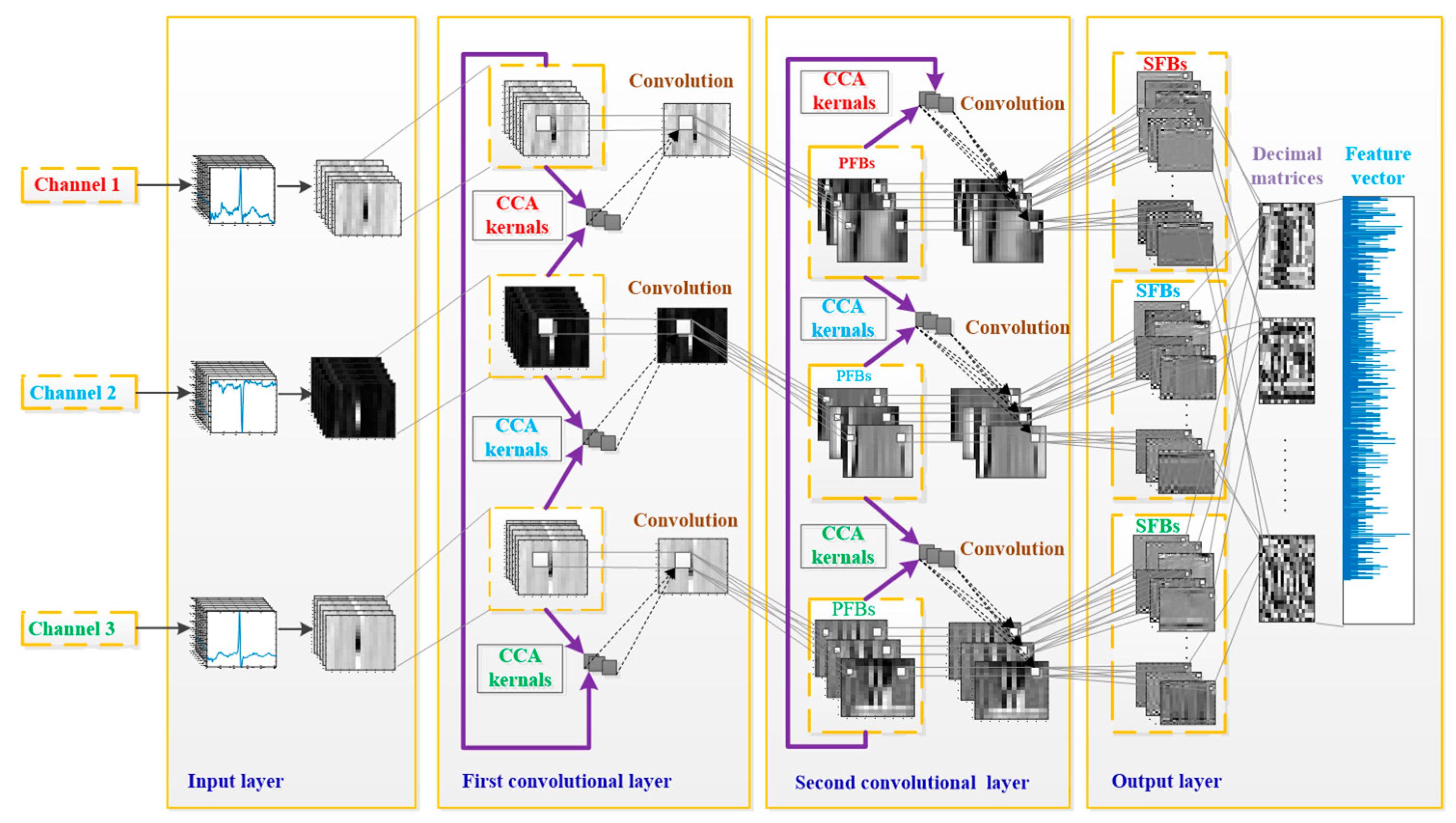
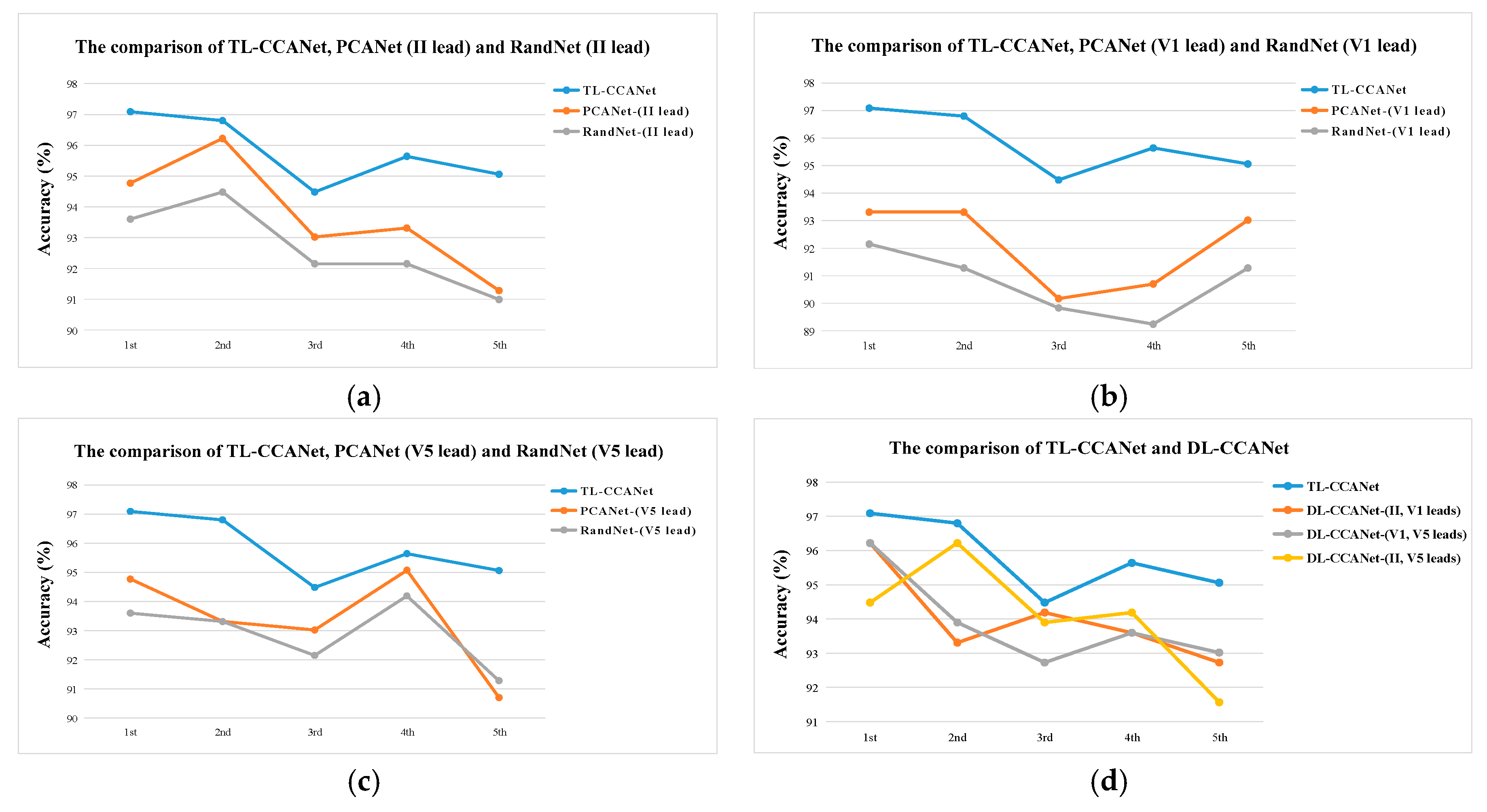
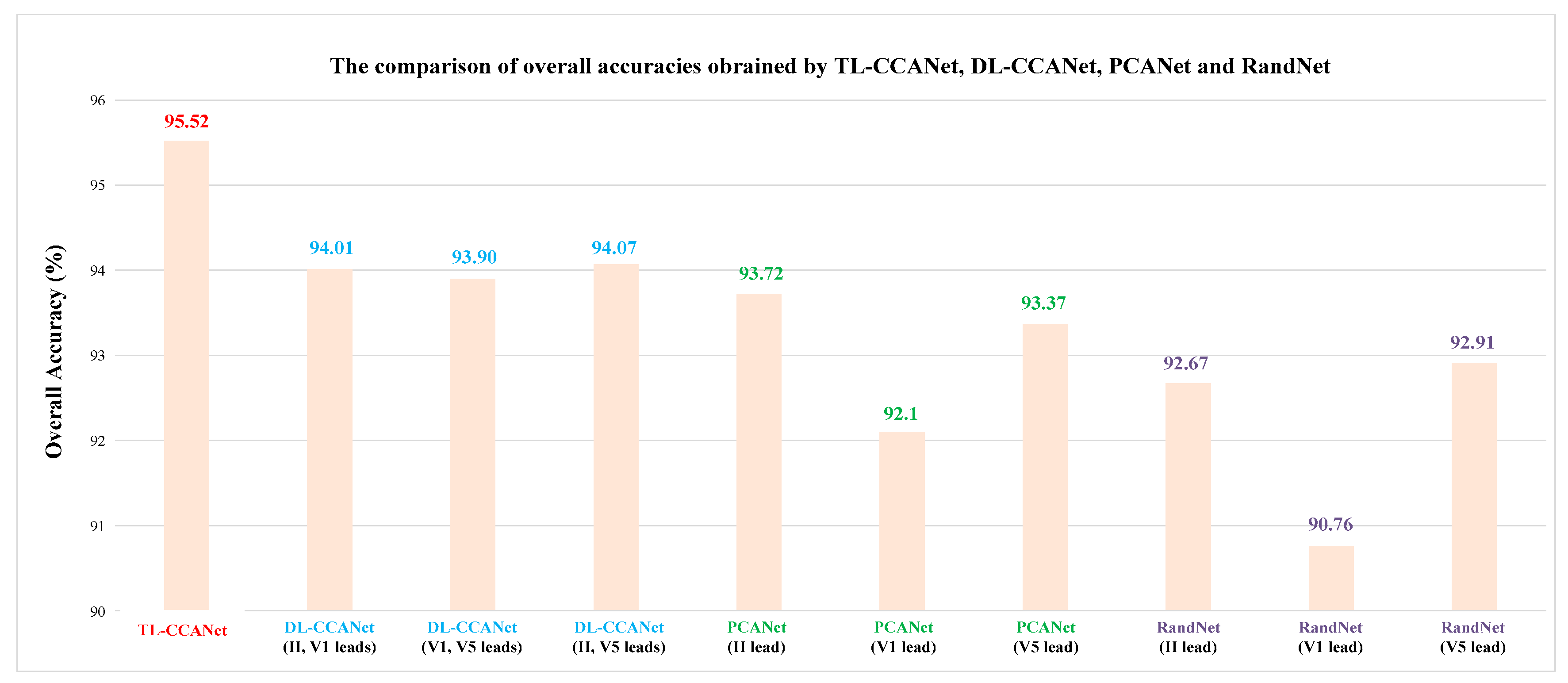
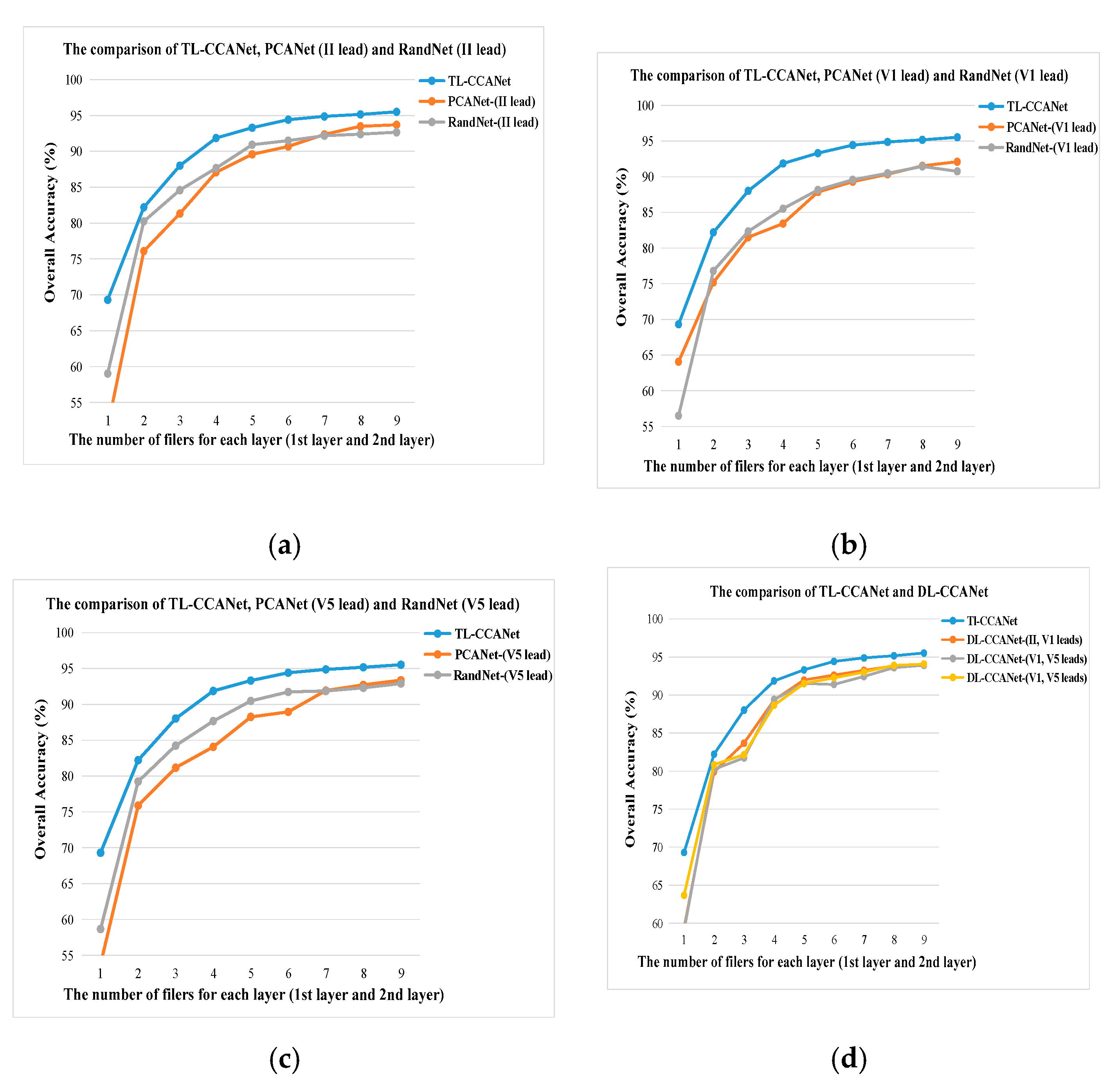
3.2.2. TL-CCANet
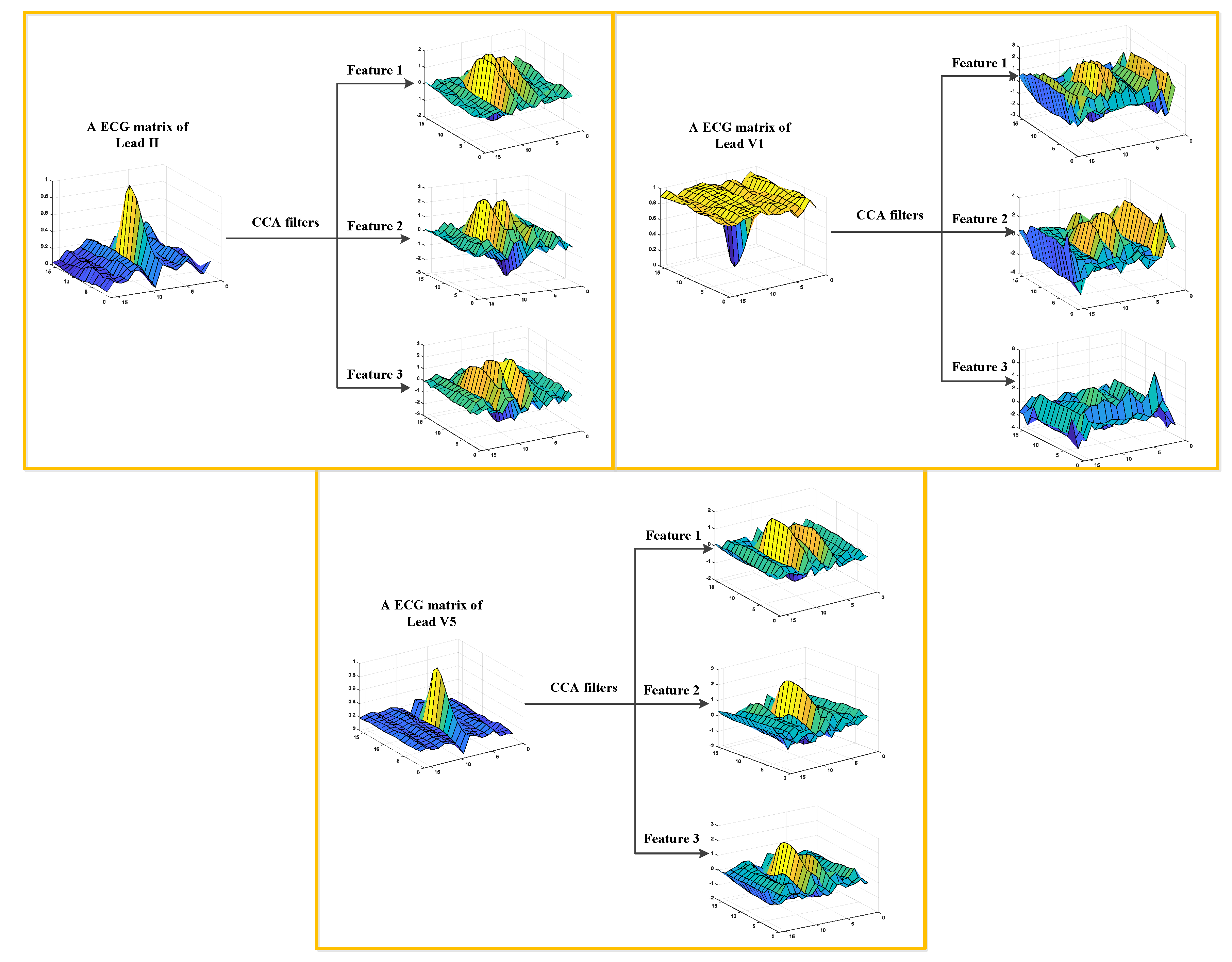
In this work, we developed a TL-CCANet to extract features from three-lead ECGs. TL-CCANet contains an input layer, two cascaded convolutional layers and an output layer. Different from DL-CCANet, there are three input channels for TL-CCANet, in which the CCA processing is alternately performed on the two-lead data in the two cascaded convolutional layers.
Figure 3 presents the specific structure of TL-CCANet.
(1) Input layer
In this layer, ECG matrices , h = 1, 2, 3, h with a size of m × n are obtained by reshaping all the heartbeats.
(2) First convolutional layer
Initial stage: The operation of this stage is the same as that in DL-CCANet, and the pending matrix corresponding to the h-th lead is then obtained.
Filter extraction stage: In this step, the CCA filters are obtained based on three combinations of
Xh, respectively. The specific allocation scheme is shown in
Table 3.
Taking the combination 1 as an example, we first calculate the canonical vectors
al and
bl by solving the CCA model between
X1 and
X2 using the Lagrange multiplier technique. Then, we reserve the
al corresponding to the
X1, and the CCA filters are obtained as per Equation (7).
where the function
is similar to that in DL-CCANet. After processing all the above three combinations, three sets of filters
, and
are obtained.
Convolutional stage: Based on three ECG leads, we calculate the preliminary feature blocks (PFBs) according to .
(3) Second convolutional layer
Initial stage: The is employed as the input of this layer, and an operation similar to the previous layer is used to obtain and .
Filter extraction stage: Taking the
and
of combination 1 in
Table 4 as an example, we handle the CCA model using Lagrange multiplier technique, by which the canonical vectors
and
are obtained. Next, the CCA filters of
are obtained as per Equation (8).
where the function
is similar to that in Equation (8). Finally, we obtain three filters
and
for
Y1,
Y2 and
Y3, respectively.
Convolutional stage: Similarly, the secondary feature blocks (SFBs) are calculated as per Equation (9):
(4) Output layer
Similar to that in DL-CCANet, the final feature vector fi of is obtained as per and fi = . The laconic workflow of the TL-CCANet is illustrated in Algorithm 2.
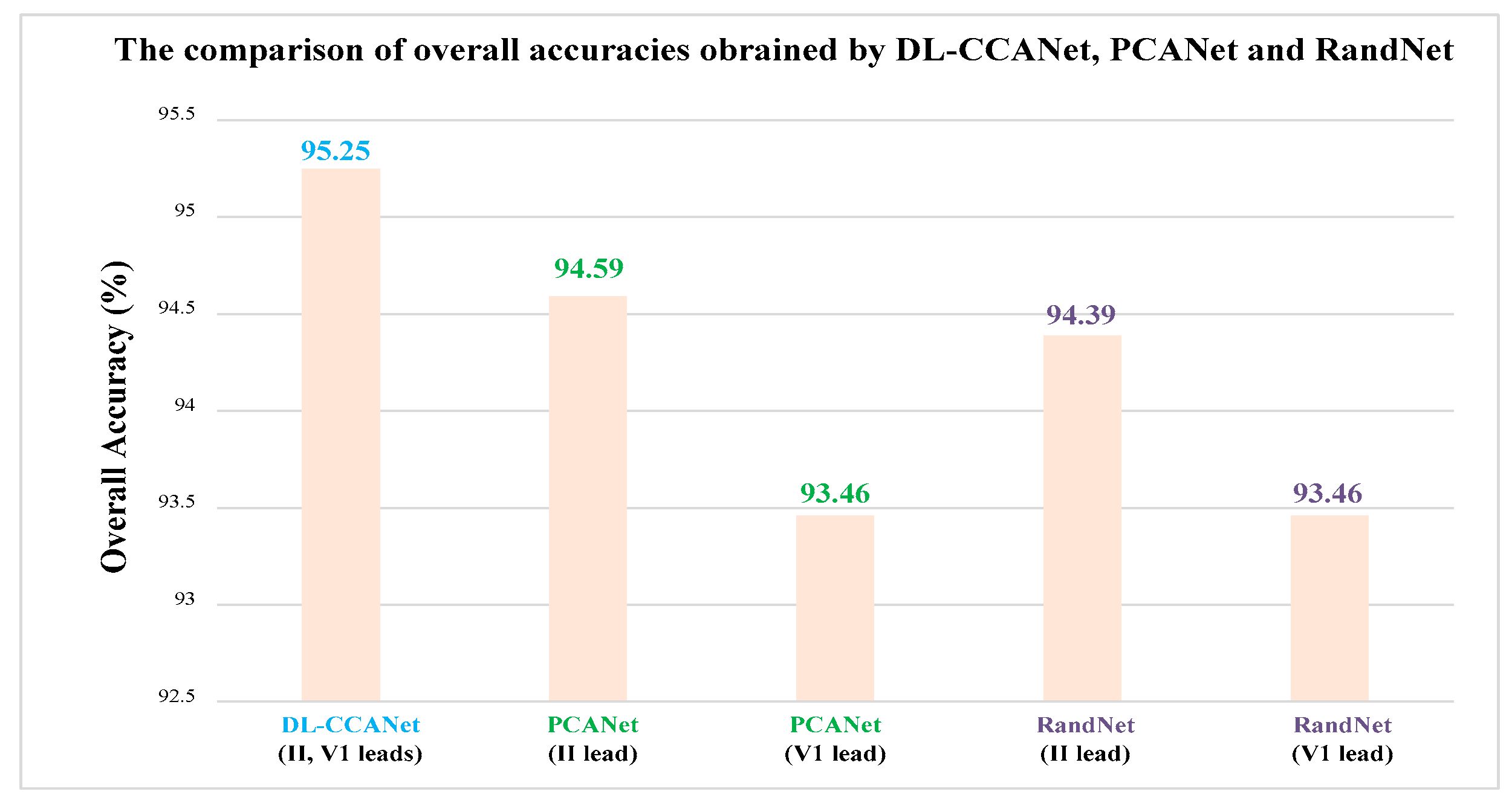
The DL-CCANet and TL-CCANet are achieved by using the PCANet [
24] and canoncorr function in MATLAB. Their parameters are shown in
Table 5.
| Algorithm 2. The algorithm of two convolutional stages of TL-CCANet. |
| Input: | Raw Three-Lead Heartbeats |
| Output: | |
| 1: | Form ECG matrix |
| 2: | for the first convolutional stage do |
| 3: | Form the three-lead pending matrices Xh |
| 4: | Compute the covariance matrix of and |
| 5: | Solve the CCA model by the Lagrange multiplier technique to obtain the three-lead project directions ah, h = 1, 2, 3 and bh, h = 1, 2, 3 |
| 6: | Construct three-lead filter banks , h = 1,2, l = 1, 2, …, L1 |
| 7: | Calculate the preliminary feature blocks of the first convolutional stage |
| 8: | end for |
| 9: | for the second convolutional stage do |
| 10: | Form the three-lead pending matrices |
| 11: | Compute the covariance matrix of and |
| 12: | Solve the CCA model to obtain the three-lead project directions ch, h = 1, 2, 3 and dh, h = 1, 2, 3 |
| 13: | Construct three-lead filter banks |
| 14: | Calculate the output of the second convolutional stage: |
| 15: | end for |
| 16: | Compute the binarized images , l = 1, 2, 3, …, L1 |
| 17: | Compute the one decimal image |
| 18: | Construct the histogram vector fi |