Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment
Abstract
1. Introduction
2. Materials and Methods
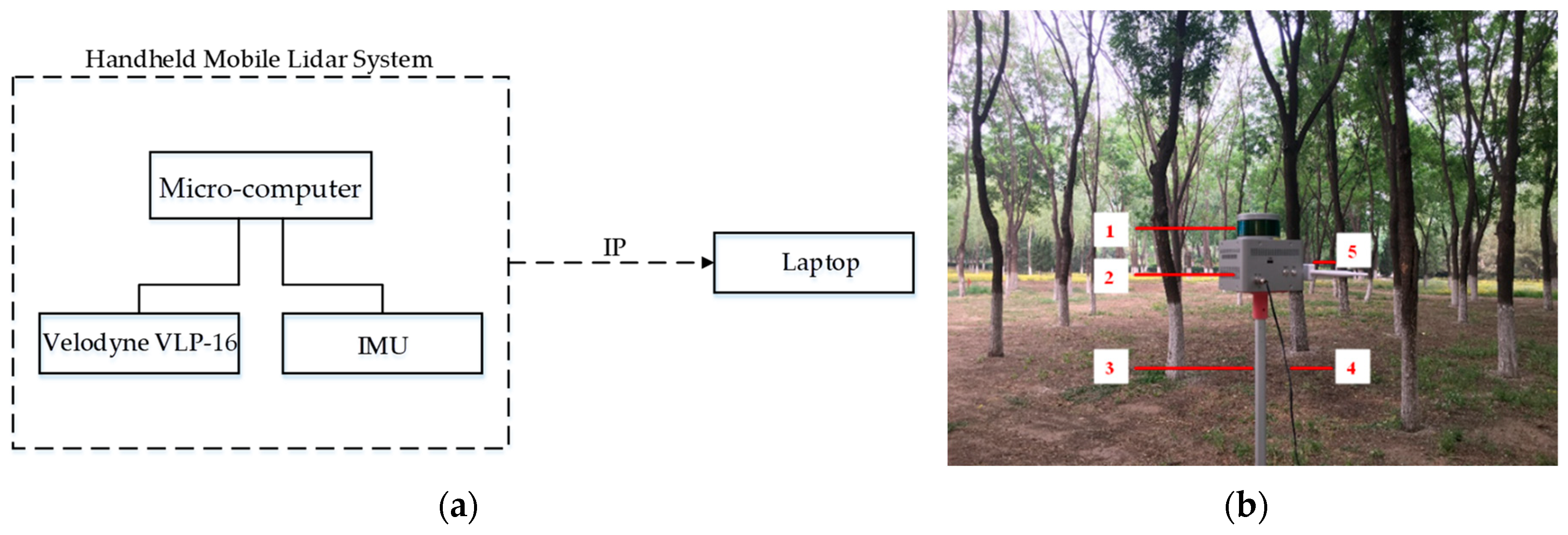
2.1. Hardware and Software Setup
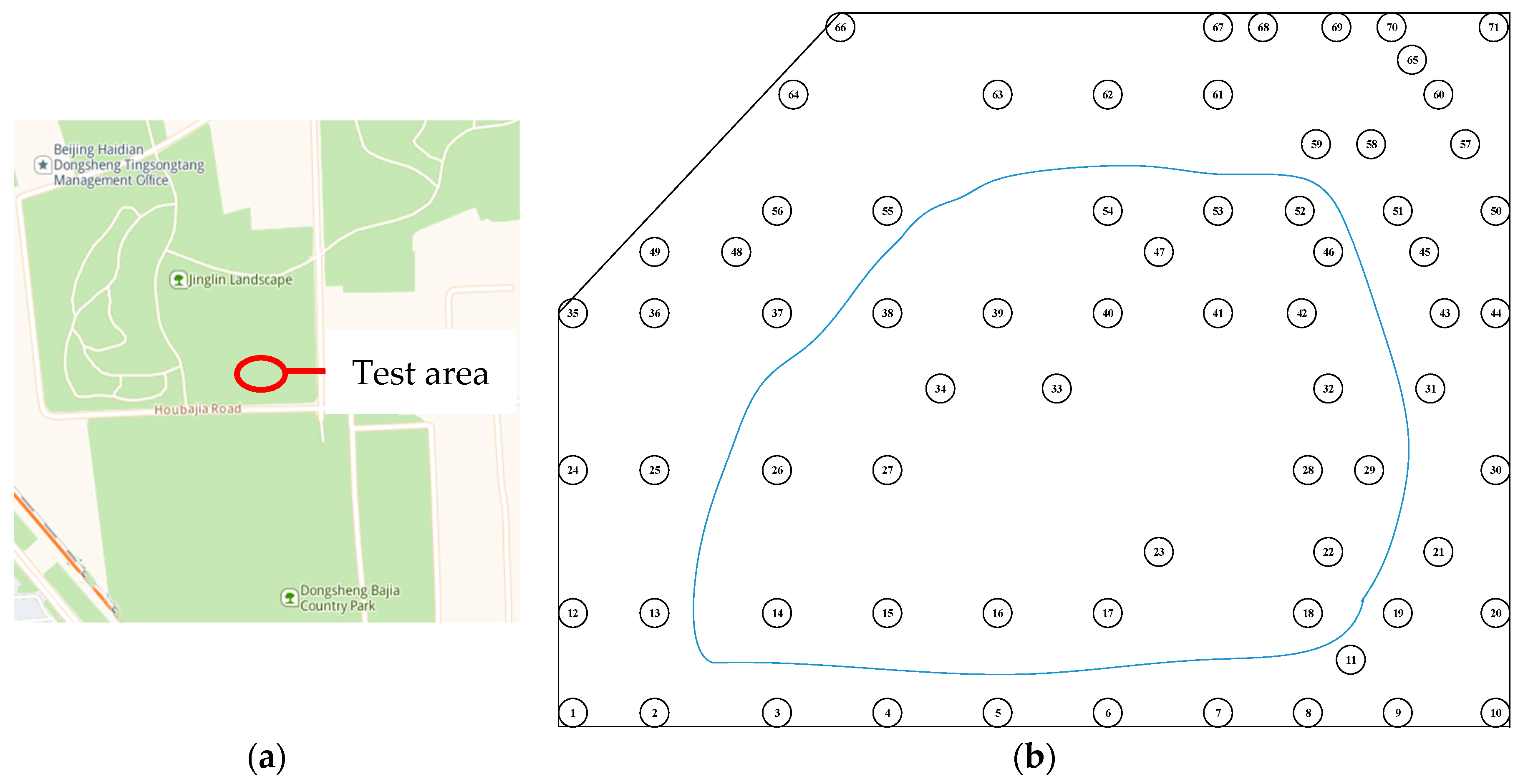
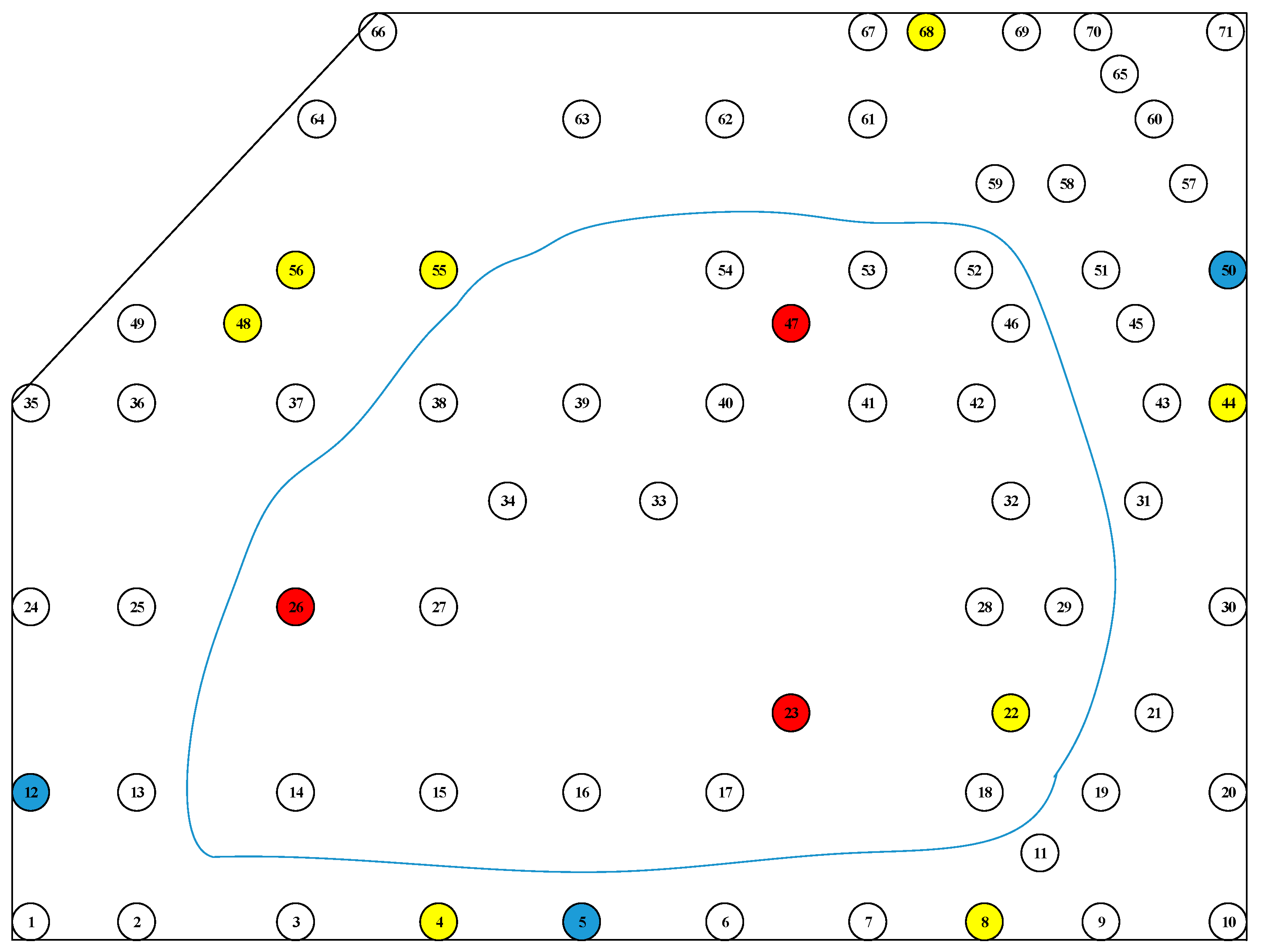
2.2. Experimental Area
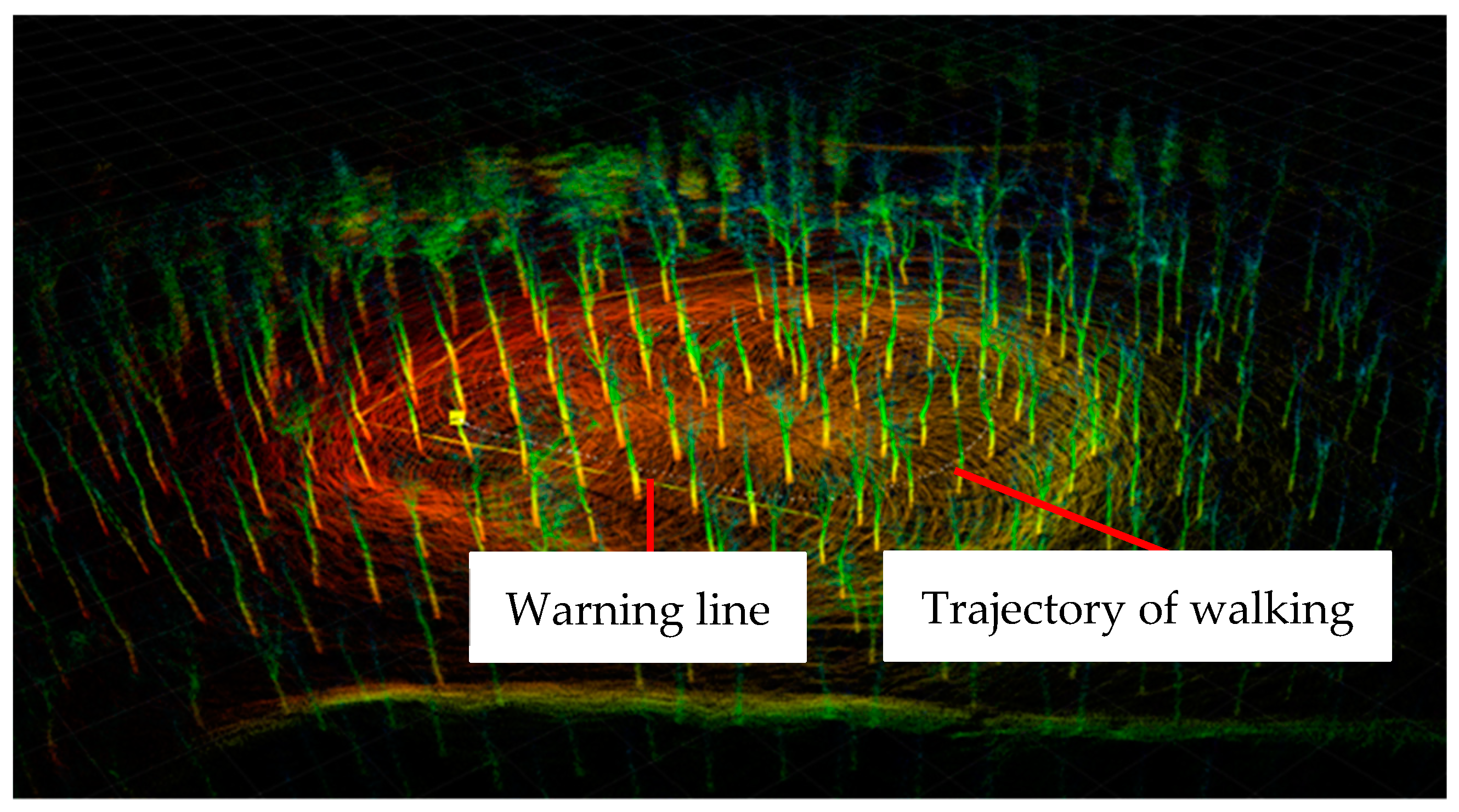
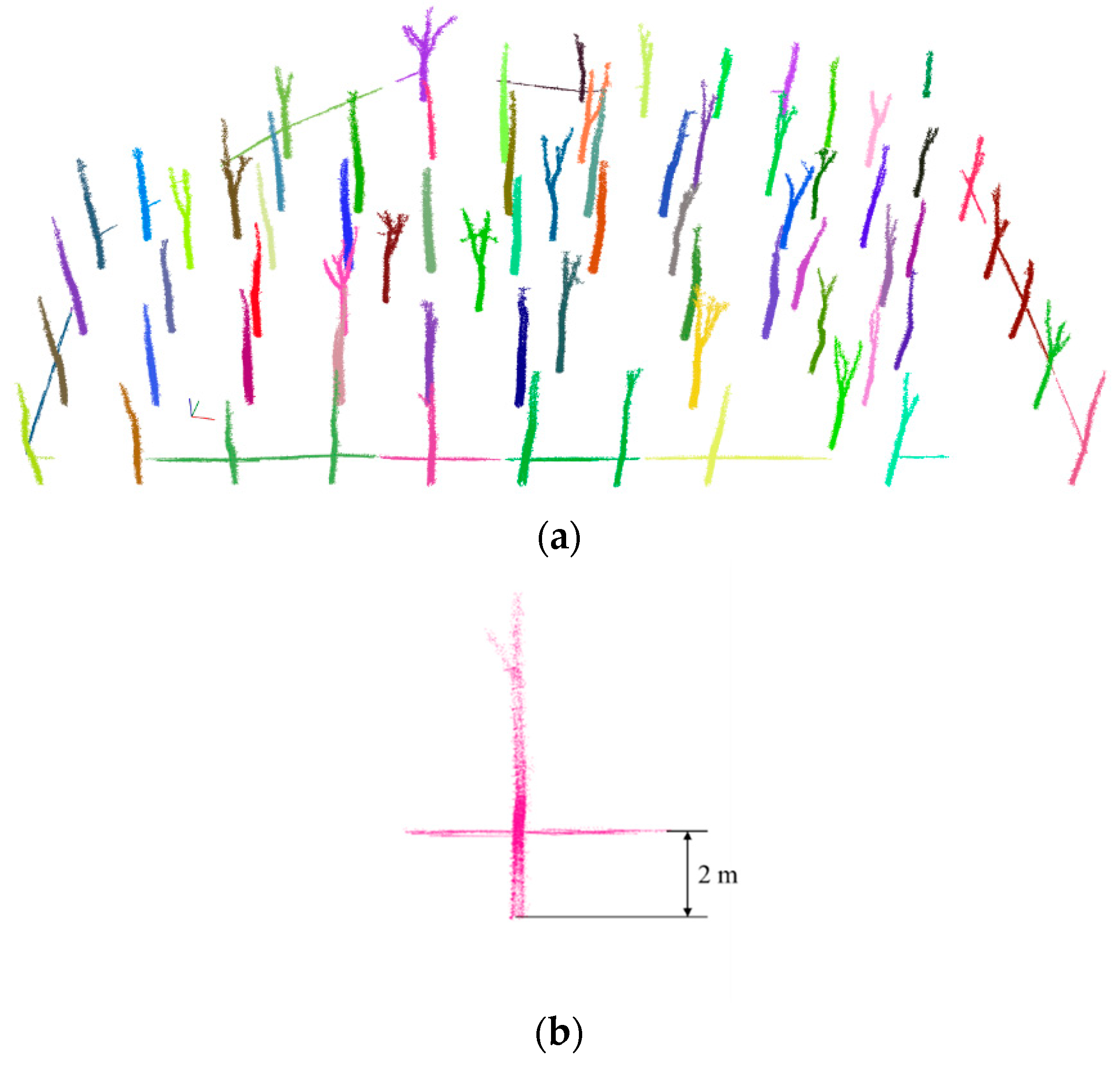
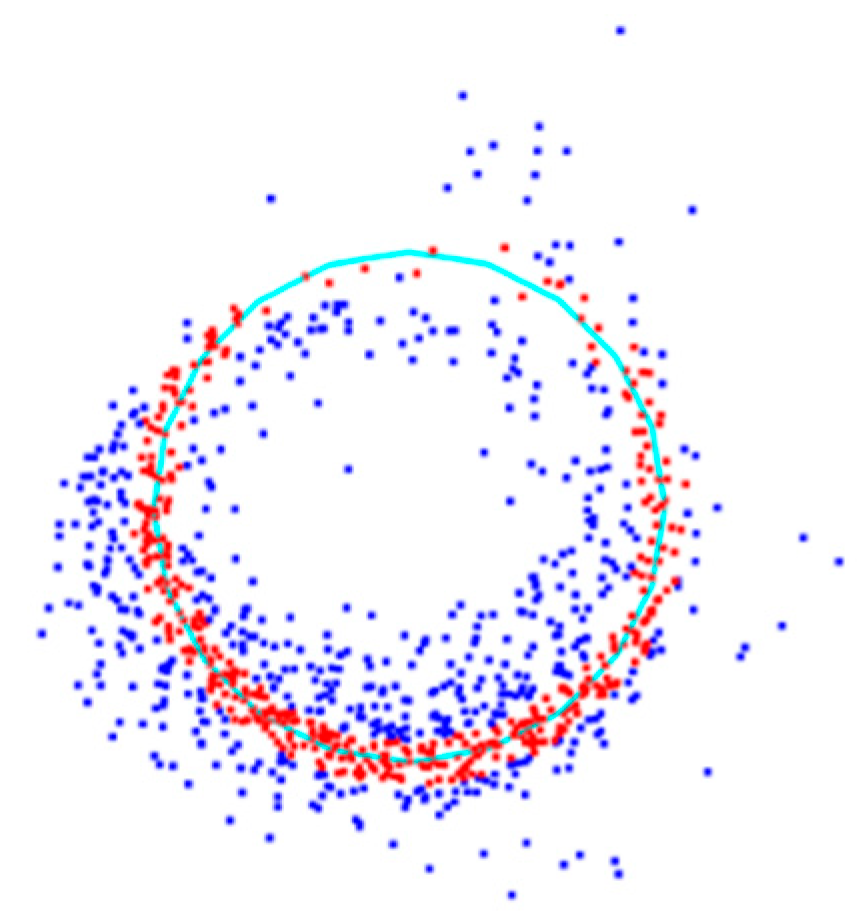
2.3. Extraction of DBH from the SLAM Map
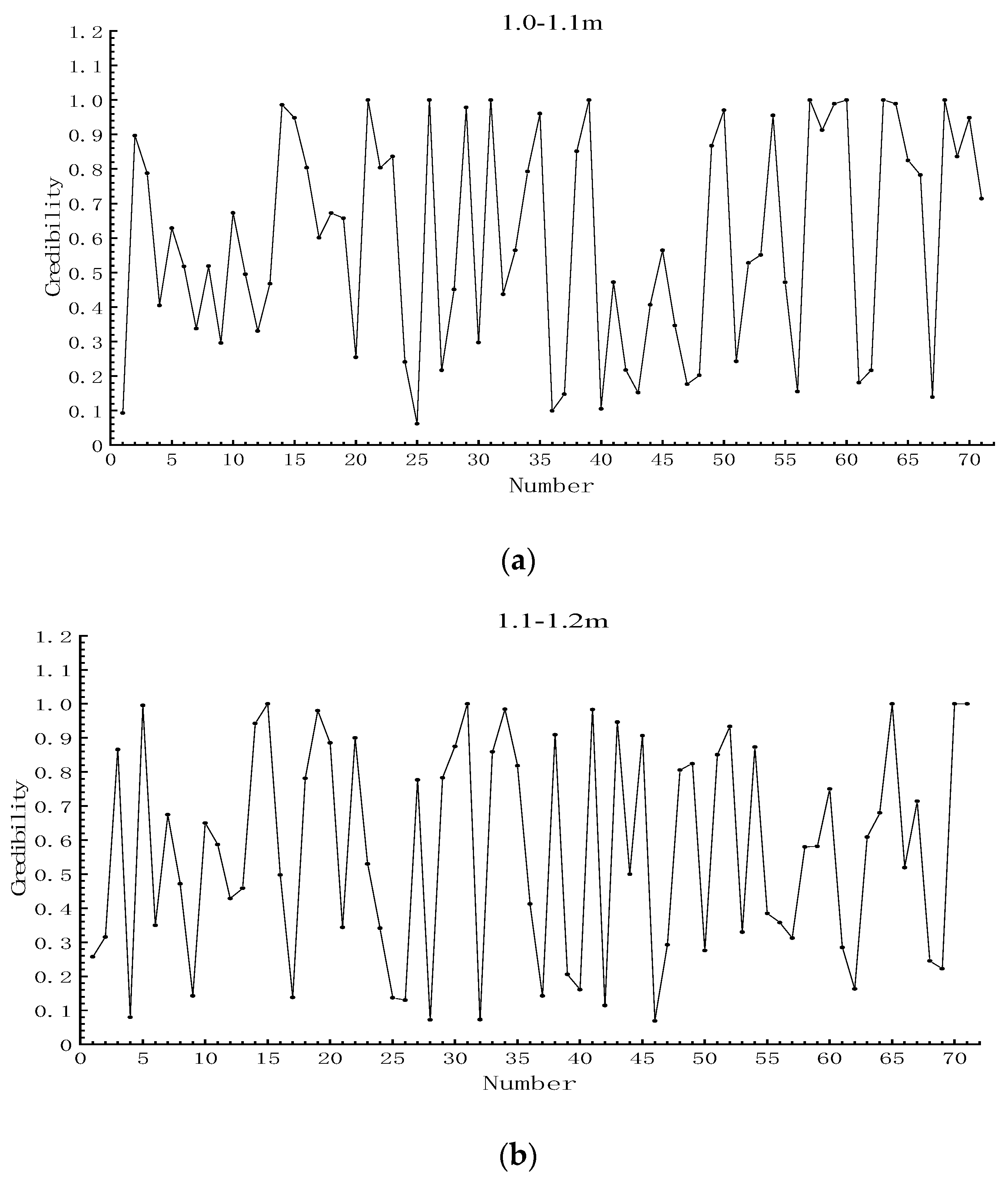
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Qiu, Y.; Duan, X.; Xu, K.; Yang, A.C. An Improved Robust Method for Pose Estimation of Cylindrical Parts with Interference Features. Sensors 2019, 19, 2234. [Google Scholar] [CrossRef] [PubMed]
- Burdziakowski, P.; Tysiac, P. Combined Close Range Photogrammetry and Terrestrial Laser Scanning for Ship Hull Modelling. Geosciences 2019, 9, 242. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Hyyppä, J. Outlook for the Next Generation’s Precision Forestry in Finland. Forests 2014, 5, 1682–1694. [Google Scholar] [CrossRef]
- Brolly, G.; Király, G. Algorithms for stem mapping by means of terrestrial laser scanning. Acta Silv. Lignaria Hung. 2009, 5, 119–130. [Google Scholar]
- Tang, J.; Chen, Y.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Khoramshahi, E.; Hakala, T.; Hyyppä, J.; Holopainen, M.; Hyyppä, H. SLAM-Aided Stem Mapping for Forest Inventory with Small-Footprint Mobile LiDAR. Forests 2015, 6, 4588–4606. [Google Scholar] [CrossRef]
- Holopainen, M.; Kankare, V.; Vastaranta, M.; Liang, X.; Lin, Y.; Vaaja, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; et al. Tree mapping using airborne, terrestrial and mobile laser scanning—A case study in a heterogeneous urban forest. Urban For. Urban Green. 2013, 12, 546–553. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Che, E.; Jung, J.; Olsen, M.J. Object Recognition, Segmentation, and Classification of Mobile Laser Scanning Point Clouds: A State of the Art Review. Sensors 2019, 19, 810. [Google Scholar] [CrossRef] [PubMed]
- Xinlian, L.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Xiaowei, Y. The Use of a Mobile Laser Scanning System for Mapping Large Forest Plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Herrero-Huerta, M.; Lindenbergh, R.; Rodriguez-Gonzalvez, P. Automatic tree parameter extraction by a Mobile LiDAR System in an urban context. PLoS ONE 2018, 13, e0196004. [Google Scholar] [CrossRef] [PubMed]
- Čerňava, J.; Mokroš, M.; Tuček, J.; Antal, M.; Slatkovská, Z. Processing Chain for Estimation of Tree Diameter from GNSS-IMU-Based Mobile Laser Scanning Data. Remote Sens. 2019, 11, 615. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Colaço, A.; Trevisan, R.; Molin, J.; Rosell-Polo, J.; Escolà, A. A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling. Remote Sens. 2017, 9, 763. [Google Scholar] [CrossRef]
- Underwood, J.P.; Hung, C.; Whelan, B.; Sukkarieh, S. Mapping almond orchard canopy volume, flowers, fruit and yield using lidar and vision sensors. Comput. Electron. Agric. 2016, 130, 83–96. [Google Scholar] [CrossRef]
- Escolà, A.; Martínez-Casasnovas, J.A.; Rufat, J.; Arnó, J.; Arbonés, A.; Sebé, F.; Pascual, M.; Gregorio, E.; Rosell-Polo, J.R. Mobile terrestrial laser scanner applications in precision fruticulture/horticulture and tools to extract information from canopy point clouds. Precis. Agric. 2016, 18, 111–132. [Google Scholar] [CrossRef]
- Scientia. Available online: https://www.scientia.global/dr-peter-krzystek-the-future-of-forest-mapping/ (accessed on 18 May 2018).
- Li, J.; Yang, B.; Cong, Y.; Cao, L.; Fu, X.; Dong, Z. 3D Forest Mapping Using A Low-Cost UAV Laser Scanning System: Investigation and Comparison. Remote Sens. 2019, 11, 717. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Li, J.; Wang, C.; Wang, R.; Chapman, M. Mobile Laser Scanned Point-Clouds for Road Object Detection and Extraction: A Review. Remote Sens. 2018, 10, 1531. [Google Scholar] [CrossRef]
- Gargoum, S.A.; Koch, J.C.; El-Basyouny, K. A Voxel-Based Method for Automated Detection and Mapping of Light Poles on Rural Highways using LiDAR Data. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 274–283. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Wang, C.; Wen, C. Bag of Contextual-Visual Words for Road Scene Object Detection From Mobile Laser Scanning Data. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3391–3406. [Google Scholar] [CrossRef]
- Shi, Z.; Kang, Z.; Lin, Y.; Liu, Y.; Chen, W. Automatic Recognition of Pole-Like Objects from Mobile Laser Scanning Point Clouds. Remote Sens. 2018, 10, 1891. [Google Scholar] [CrossRef]
- Griffiths, D.; Boehm, J. A Review on Deep Learning Techniques for 3D Sensed Data Classification. Remote Sens. 2019, 11, 1499. [Google Scholar] [CrossRef]
- Zou, X.; Cheng, M.; Wang, C.; Xia, Y.; Li, J. Tree Classification in Complex Forest Point Clouds Based on Deep Learning. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2360–2364. [Google Scholar] [CrossRef]
- Guan, H.; Yu, Y.; Ji, Z.; Li, J.; Zhang, Q. Deep learning-based tree classification using mobile LiDAR data. Remote Sens. Lett. 2015, 6, 864–873. [Google Scholar] [CrossRef]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Kukko, A.; Kaijaluoto, R.; Kaartinen, H.; Lehtola, V.V.; Jaakkola, A.; Hyyppä, J. Graph SLAM correction for single scanner MLS forest data under boreal forest canopy. ISPRS J. Photogramm. Remote Sens. 2017, 132, 199–209. [Google Scholar] [CrossRef]
- Holmgren, J.; Tulldahl, H.M.; Nordlöf, J.; Nyström, M.; Olofsson, K.; Rydell, J.; Willén, E. Estimation of Tree Position and Stem Diameter Using Simultaneous Localization and Mapping with Data from a Backpack-Mounted Laser Scanner. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2017, XLII-3/W3, 59–63. [Google Scholar] [CrossRef]
- Tsubouchi, T.; Asano, A.; Mochizuki, T.; Kondou, S.; Shiozawa, K.; Matsumoto, M.; Tomimura, S.; Nakanishi, S.; Mochizuki, A.; Chiba, Y.; et al. Forest 3D Mapping and Tree Sizes Measurement for Forest Management Based on Sensing Technology for Mobile Robots. In Field and Service Robotics: Results of the 8th International Conference; Yoshida, K., Tadokoro, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 357–368. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Nava, Y. Visual-LiDAR SLAM with Loop Closure. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2016, 41, 401–416. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, USA, 12–16 July 2014; p. 9. [Google Scholar]
- Trevor, A.J.; Gedikli, S.; Rusu, R.B.; Christensen, H.I. Efficient organized point cloud segmentation with connected components. In Proceedings of the Semantic Perception Mapping and Exploration (SPME), Karlsruhe, Germany, 5 May 2013. [Google Scholar]
- Miknis, M.; Davies, R.; Plassmann, P.; Ware, A. Near real-time point cloud processing using the PCL. In Proceedings of the 2015 International Conference on Systems, Signals and Image Processing (IWSSIP), London, UK, 10–12 September 2015; pp. 153–156. [Google Scholar]
- Kumar, G.A.; Patil, A.K.; Patil, R.; Park, S.S.; Chai, Y.H. A LiDAR and IMU Integrated Indoor Navigation System for UAVs and Its Application in Real-Time Pipeline Classification. Sensors 2017, 17, 1268. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Qian, X.; Ye, C. NCC-RANSAC: A fast plane extraction method for 3-D range data segmentation. IEEE Trans. Cybern. 2014, 44, 2771–2783. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An Improved RANSAC for 3D Point Cloud Plane Segmentation Based on Normal Distribution Transformation Cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Belton, D.; West, G. Robust segmentation in laser scanning 3D point cloud data. In Proceedings of the 2012 International Conference on Digital Image Computing Techniques and Applications (DICTA), Fremantle, Australia, 3–5 Decenber 2012; pp. 1–8. [Google Scholar]
- Golovinskiy, A.; Funkhouser, T. Min-cut based segmentation of point clouds. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 39–46. [Google Scholar]
- Ioannou, Y.; Taati, B.; Harrap, R.; Greenspan, M. Difference of normals as a multi-scale operator in unorganized point clouds. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 501–508. [Google Scholar]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. Voxel Cloud Connectivity Segmentation—Supervoxels for Point Clouds. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2027–2034. [Google Scholar] [CrossRef]
- Keqi, Z.; Shu-Ching, C.; Whitman, D.; Mei-Ling, S.; Jianhua, Y.; Chengcui, Z. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Sun, S.; Salvaggio, C. Aerial 3D Building Detection and Modeling From Airborne LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1440–1449. [Google Scholar] [CrossRef]
- Wiśniewski, Z.; Zienkiewicz, M.H. Shift-Msplit* Estimation in Deformation Analyses. J. Surv. Eng. 2016, 142, 04016015. [Google Scholar] [CrossRef]
- Nykiel, G.; Janowski, A. The circle object detection with the use of Msplit estimation. E3s Web Conf. 2018, 26, 00014. [Google Scholar] [CrossRef]
- Janowski, A.; Bobkowska, K.; Szulwic, J. 3D modelling of cylindrical-shaped objects from lidar data-an assessment based on theoretical modelling and experimental data. Metrol. Meas. Syst. 2018, 25. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Gr. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]



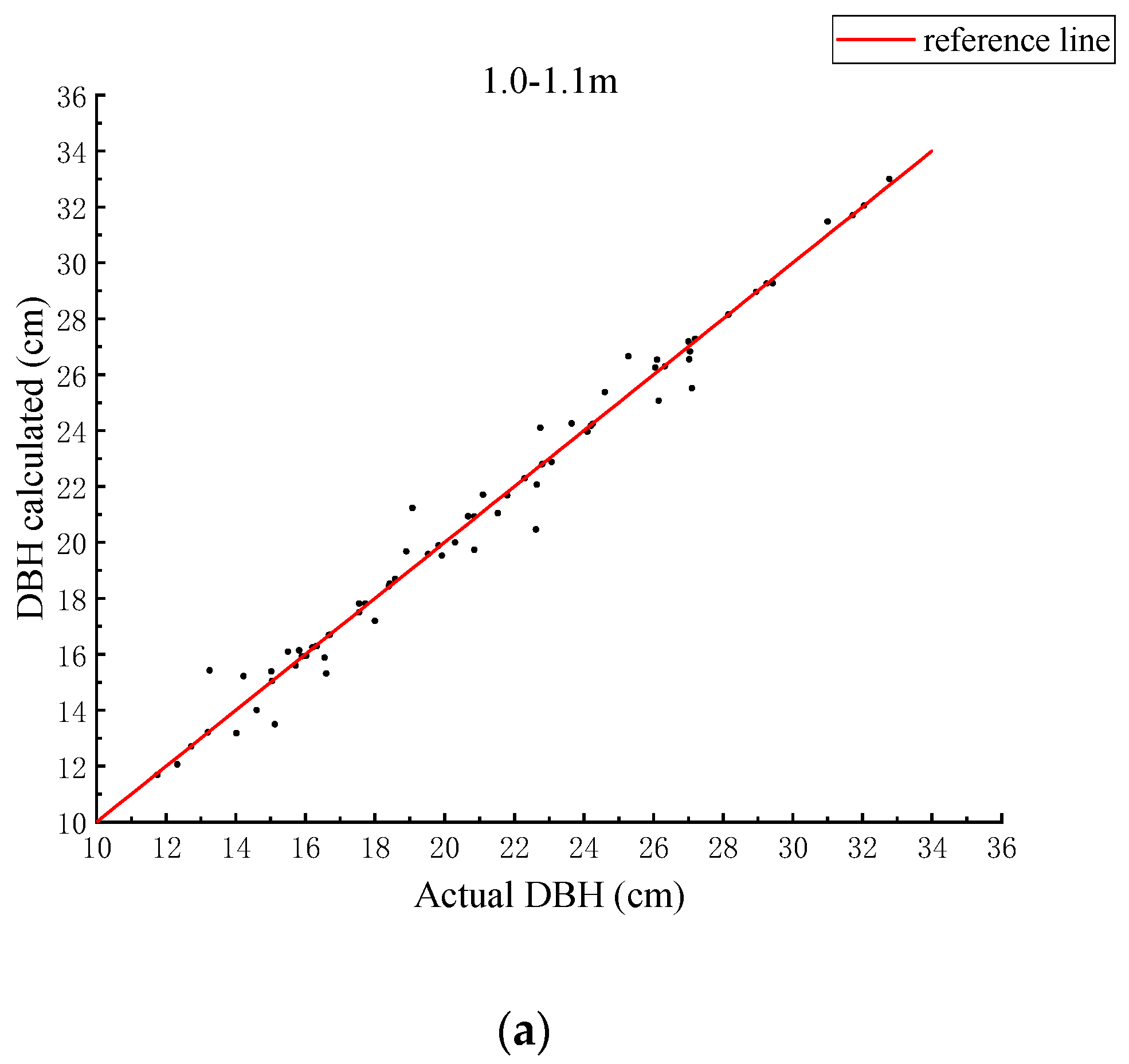
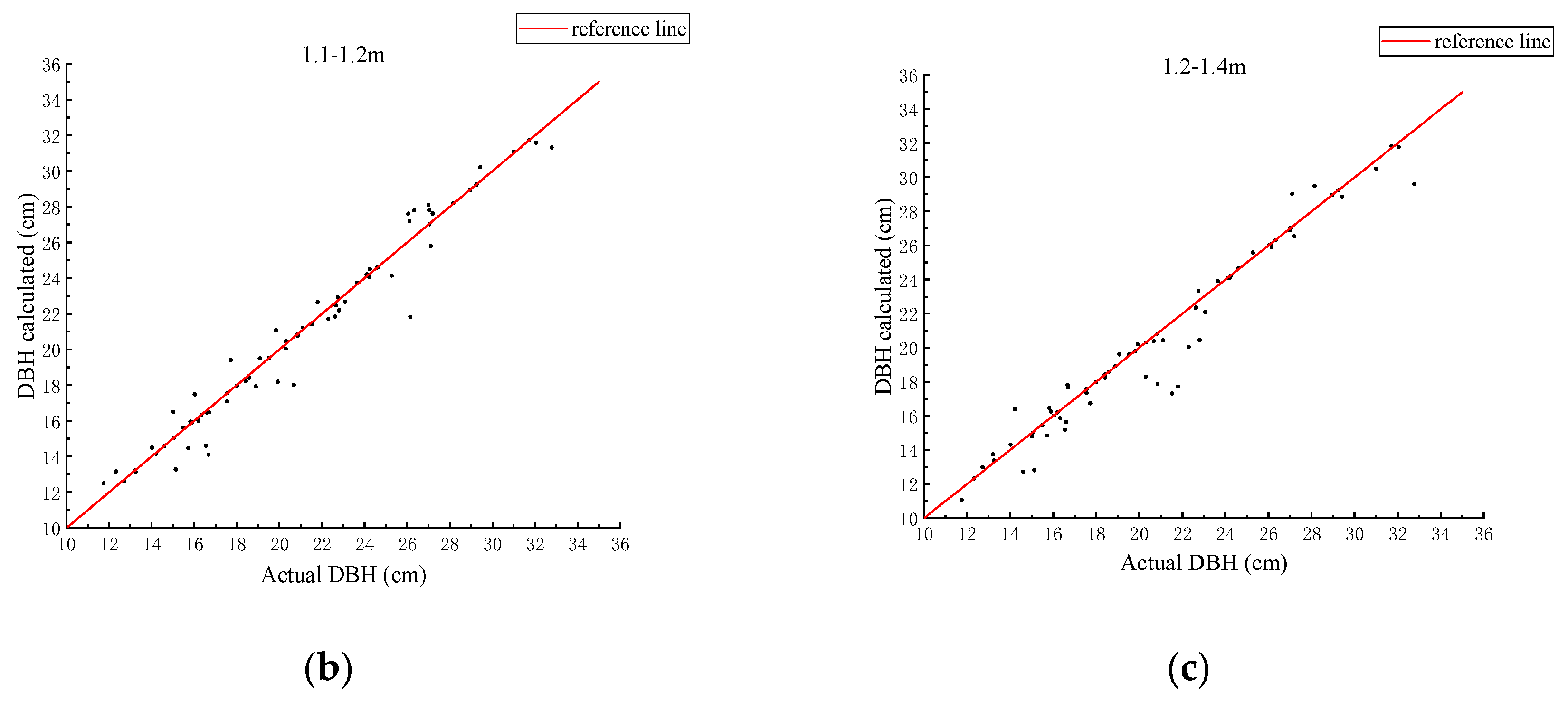
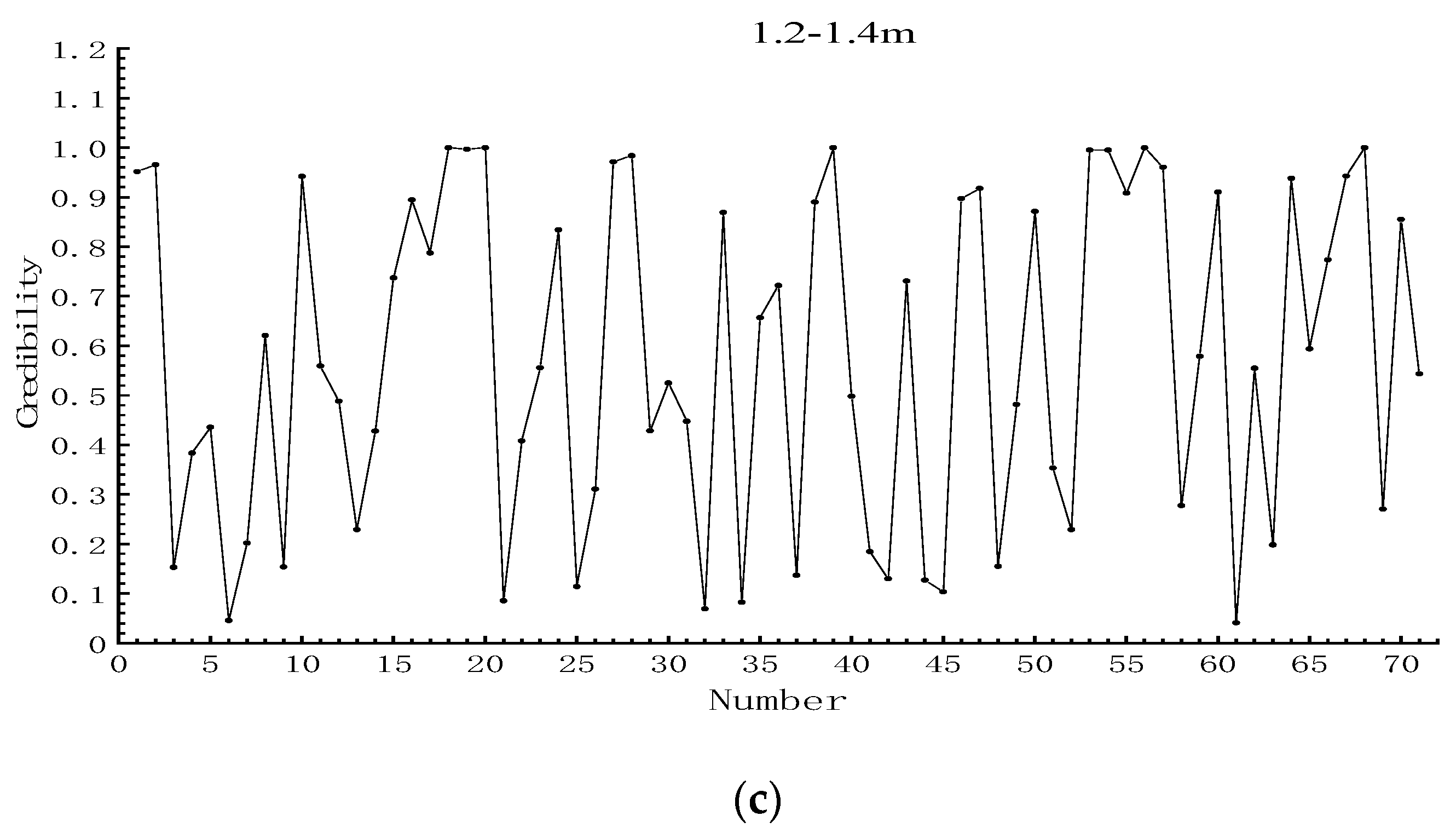
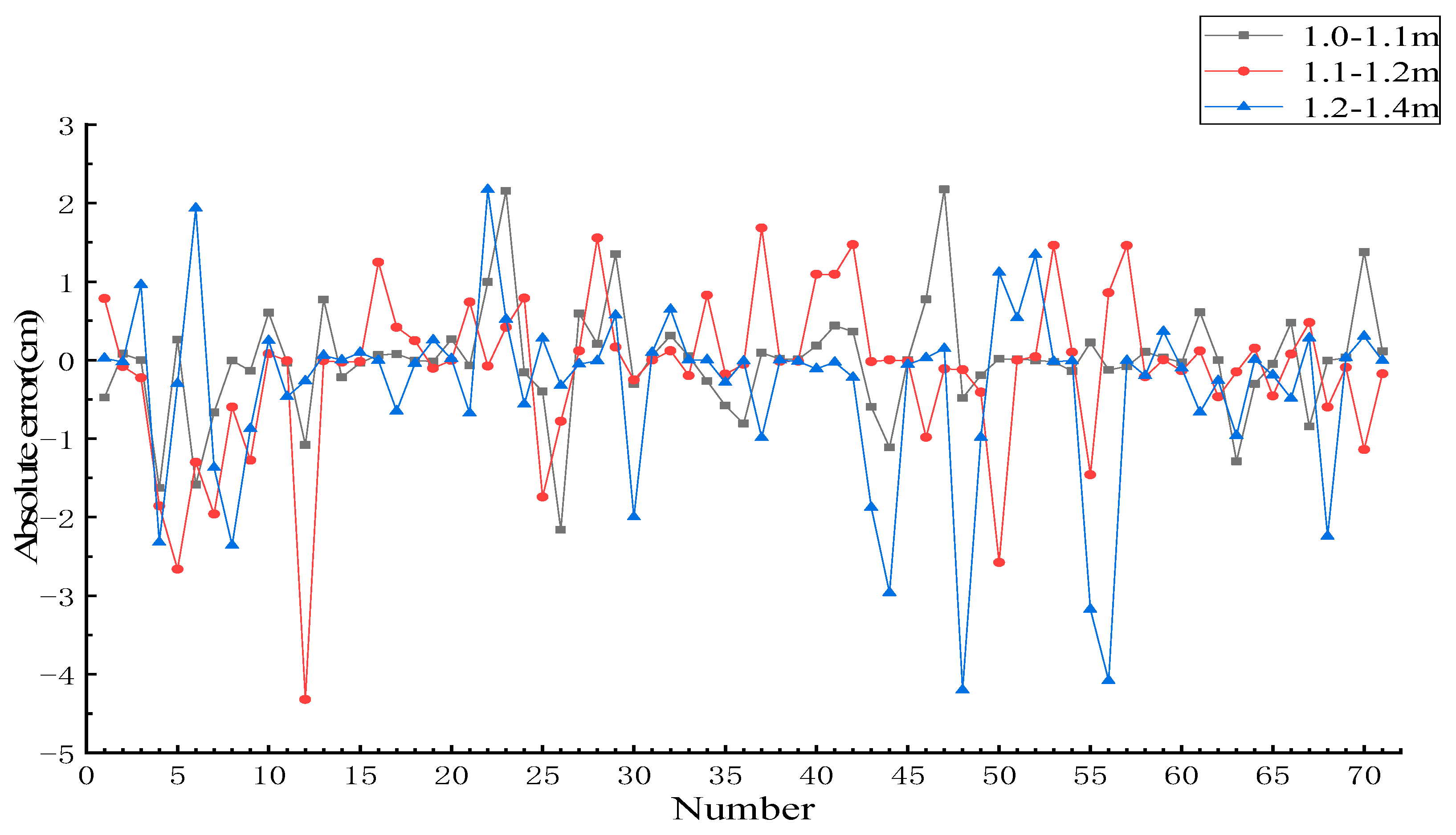
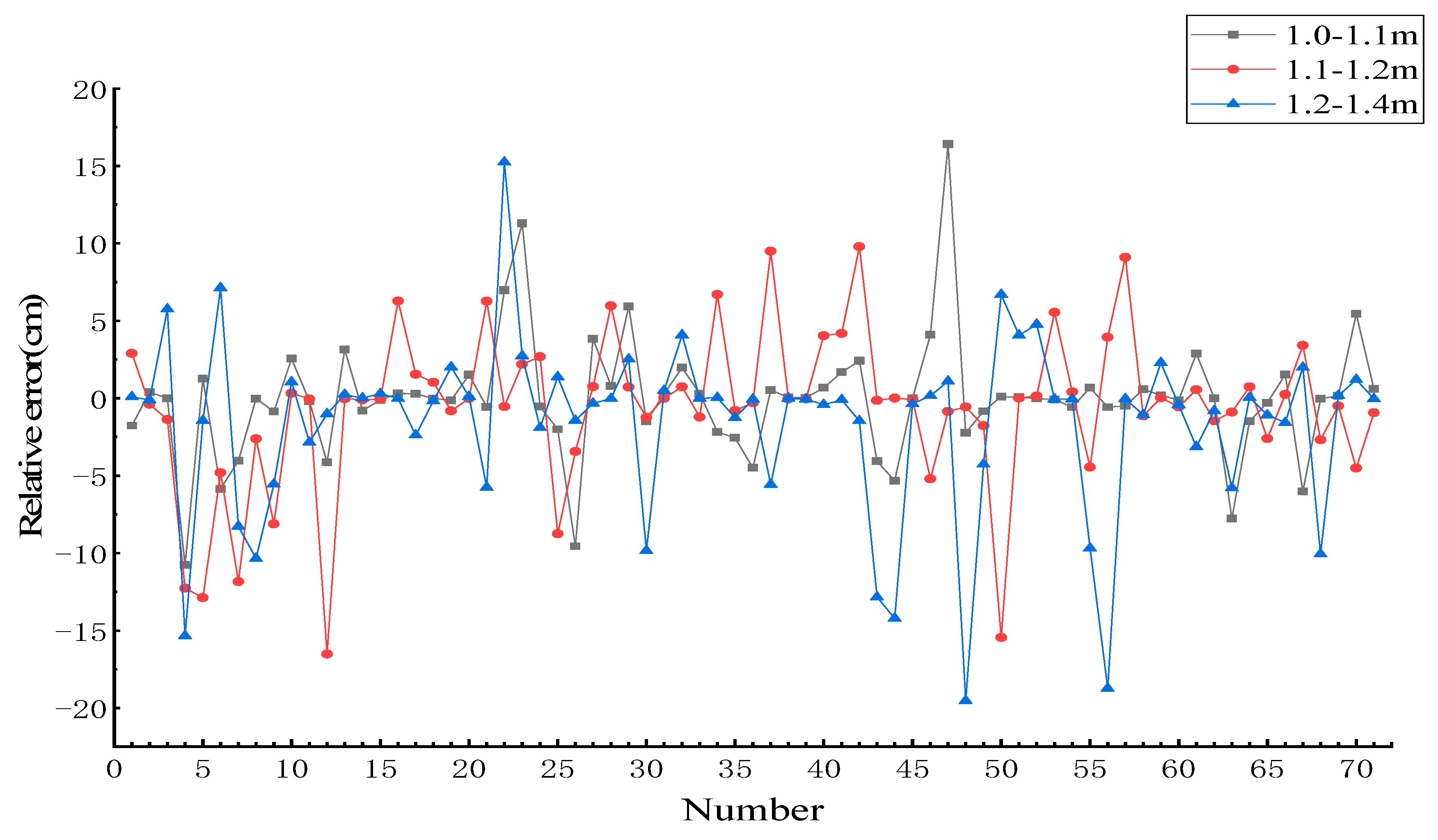
| Interval | 1.0–1.1 m | 1.1–1.2 m | 1.2–1.4 m |
|---|---|---|---|
| Variance | 0.50 | 1.02 | 1.30 |
| Mean of absolute error | 0.43 cm | 0.63 cm | 0.68 cm |
| Interval | 1.0–1.1 m | 1.1–1.2 m | 1.2–1.4 m |
|---|---|---|---|
| Variance | 15.09 | 25.31 | 32.26 |
| Mean of relative error | 2.27% | 3.12% | 3.45% |
| Interval | 1.0–1.1 m | 1.1–1.2 m | 1.2–1.4 m |
|---|---|---|---|
| Correlation coefficient | 0.05 | −0.03 | −0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Kang, F.; Li, W.; Kan, J.; Zheng, Y.; He, G. Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment. Sensors 2019, 19, 3212. https://doi.org/10.3390/s19143212
Zhou S, Kang F, Li W, Kan J, Zheng Y, He G. Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment. Sensors. 2019; 19(14):3212. https://doi.org/10.3390/s19143212
Chicago/Turabian StyleZhou, Sanzhang, Feng Kang, Wenbin Li, Jiangming Kan, Yongjun Zheng, and Guojian He. 2019. "Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment" Sensors 19, no. 14: 3212. https://doi.org/10.3390/s19143212
APA StyleZhou, S., Kang, F., Li, W., Kan, J., Zheng, Y., & He, G. (2019). Extracting Diameter at Breast Height with a Handheld Mobile LiDAR System in an Outdoor Environment. Sensors, 19(14), 3212. https://doi.org/10.3390/s19143212





