1. Introduction
Nowadays, communication networks are widely used to cope with signal estimation problems in engineering, economy, health or security, among others, since they generally provide more robust and precise estimators of the target signal than a single sensor. Conventional centralized and distributed fusion estimation architectures have been widely studied under a state-space approach (see e.g., [
1,
2,
3,
4] and references therein). In addition, assuming that the evolution model of the signal is not fully known and only covariance information is available, centralized and distributed fusion estimation algorithms have been proposed for sensor networks affected by different network-induced random uncertainties (see e.g., [
5,
6,
7]). A comprehensive survey of recent developments in estimation and fusion for networked systems with randomly occurring phenomena can be found in [
8]. The key theories and methodologies of distributed multisensor data fusion are comprehensively reviewed in [
9] and a survey of distributed fusion estimation algorithms with applications in networked systems, including an interesting analysis of some network-induced uncertainties, is provided in [
10].
These conventional centralized and distributed fusion architectures require connecting all sensor nodes to a central processor, which sometimes can involve a serious communication burden, especially when the number of sensors is large. Additionally, in the distributed fusion estimation architecture, equipping each single sensor with a local estimator may be sometimes unaffordable. To overcome these shortcomings, a usual practice in engineering consists of arranging the sensors in clusters and selecting one node per cluster (called cluster-head node) acting as a local processor. Each cluster head first collects measurements from the regular sensor nodes of its cluster to generate a local estimator and then all local estimators are collected in the central processor, where the distributed fusion estimator is generated. This structure, called hierarchical cluster-based estimation structure, provides an efficient way to analyze big data in a great variety of application fields [
11]. Clustering is also widely used, for example, in underwater sensor networks established for military purposes, such as anti-submarine warfare, communications, positioning and guidance [
12]. An essential issue when dealing with complex networked systems consisting of multiple clusters or individual subsystems is coordination control and the design of appropriate consensus protocols; relevant results concerning these problems in different kinds of networked systems are found in [
13,
14,
15,
16]. A state-of-the-art and comprehensive survey on clustering approaches can be found in [
17] and a detailed outline of some modern energy-efficient clustering approaches to improve the lifetime of wireless sensor networks can be seen in [
18]. Recently, a comprehensive review with comparisons and classifications of different optimized clustering approaches according to different metrics has been carried out in [
19].
A remarkable disadvantage of using sensor networks for signal estimation is that their reliability can be compromised by possible cyber-attacks from adversaries. For this reason, cyber-security of networked systems is drawing considerable research attention. The most typical kinds of attacks are the denial-of-service attacks and the deception attacks [
20]. While the first ones strike at data availability by obstructing the flow of information through the network, the second ones violate data integrity by injecting false information that modifies the real data packets. Such false information can include a wrong sensor measurement or control input, an incorrect time-stamp or a wrong identity of the sending device. The fusion estimation problem for stochastic signals from measured data coming from a sensor network subject to deception attacks is currently an important focus of research (see e.g., [
20,
21,
22,
23,
24,
25,
26] and references therein). In [
20], new insecurity conditions for the state estimation problem under false data injection attacks are proposed. In [
21], the variance-constrained distributed filtering problem is studied for time-varying systems subject to multiplicative deception attacks with bounded attack noises. A distributed recursive filtering algorithm is designed in [
22] for a class of discrete time-delayed systems subject to both uniform quantization and intermittent deception attacks. In [
23], the security-guaranteed filtering problem is addressed for a class of nonlinear discrete time-delayed systems with both stochastic sensor saturations and deception attacks. The centralized security-guaranteed filtering problem for linear discrete time-invariant stochastic systems with multi-rate sensor nodes is addressed in [
24], when deception attacks are launched during the transmission of information from the sensors to the centralized filter. In [
25], the cluster-based covariance intersection fusion estimation problem under stochastic deception attacks is investigated. An integrated analysis of event-triggered fault detection and fault estimation is proposed in [
26] for a class of discrete-time stochastic systems subject to unknown disturbances and stochastic deception attacks.
Research motivation. In this paper, distributed fusion filtering and fixed-point smoothing algorithms are designed for clustered sensor networks subject to stochastic linear deception attacks. This study is motivated by the following challenges:
(i) To find out fusion estimation structures for multi-sensor networked systems that reduce transmission burdens (with respect to both centralized and distributed fusion) and the cost of embedding a local processor in each sensor (with respect to distributed fusion).
(ii) To design recursive and easily implementable estimation algorithms with high estimation accuracy, fusing unreliable multi-sensor data, corrupted by possible deception attacks, under general assumptions on the target signal that do not require the full knowledge of the system state-space model.
Paper contributions. In light of our motivations, the main contributions of this paper are highlighted as follows:
(i) The fusion estimation problem in multi-sensor networked systems when the sensors are grouped into clusters is investigated assuming, on the one hand, that the measurements are subject to stochastic deception attacks and, on the other, that the signal evolution model is not necessarily known, but only information about its first and second order statistical properties (covariance information) is available. This covariance-based estimation approach is more general than the conventional one based on the full knowledge of the state-space model of the system since, in that case, the mean and autocovariance function of the signal process can be calculated. Hence, this estimation approach provides a comprehensive framework to deal with a great variety of stochastic signals.
(ii) A two-stage fusion estimation algorithm is designed for both filtering and fixed-point smoothing problems. In the first stage, each local processor collects measurements (subject to random deception attacks) from its cluster to generate local least-squares linear estimators; in this stage, the innovation approach is used to design the local estimation algorithms, which are recursive and computationally simple. In the second stage, in order to improve the estimation performance, all these local estimators are transmitted to the fusion center, where fusion estimators are obtained by matrix-weighted linear combinations of the local estimators; the weight matrices are computed by minimizing the mean squared estimation error, for which the cross-correlation matrices between any two local estimators need to be previously calculated.
In contrast with previous papers concerning the fusion estimation problem under a covariance-based approach, this is the first time that a cluster structure of the sensor network is used and stochastic deception attacks are considered. In comparison with the existing literature about the estimation problem in clustered sensor networks, either subject to random deception attacks or not, the main difference is the kind of information required for the derivation of the algorithms: full knowledge of the state-space model in the existing literature and only covariance information (which covers the conventional formulation based on state-space model and also more general situations) in the current paper.
Paper structure. The measurement model framework is presented in
Section 2, where the equations of the clustering sensor measurements and the stochastic deception attacks, together with the hypotheses under which the distributed estimation problem will be addressed, are specified. In
Section 3 and
Section 4 the first and second stages of the proposed cluster-based fusion estimation structure are developed. The local least-squares linear filtering and fixed-point smoothing estimators, as well as formulas for the error covariance matrices, are obtained by recursive algorithms in
Section 3. The proposed distributed fusion estimators are proposed in
Section 4 by a matrix-weighted linear combination of the local estimators using the mean squared error as optimality criterion; also, to measure the estimation accuracy, recursive formulas for the error covariance matrices are derived. The performance of the proposed estimation algorithms is analyzed in a numerical simulation study, carried out in
Section 5. Finally, some concluding remarks are provided in
Section 6.
Notation. Unless otherwise stated, the notation used in the paper is fairly standard. denotes the n-dimensional Euclidean space and the set of all real matrices. When the dimensions of vectors or matrices are not specified, they are assumed to be compatible with algebraic operations. denotes the n-dimensional column vector with all ones, while the identity and zero matrices are denoted by I and 0, respectively. For any function , depending on h and k, and , depending on r and s, we will write and , respectively, for simplicity. The Kronecker product of the matrices and , which is a matrix in , is denoted by . The Hadamard product of the matrices , which is also a matrix in , is denoted by and it is defined by . is the Kronecker delta function, i.e., when and zero otherwise. The autocovariance function of a second-order process is defined as where stands for the mathematical expectation operator.
2. Estimation Problem Formulation and Measurement Model
In this paper, we consider the distributed fusion estimation problem of a discrete-time stochastic signal from a set of measurements provided by multiple sensors. A cluster-based estimation structure will be adopted: the sensors are grouped into different clusters, each of them connected with a local processor which, in turn, is connected with a global fusion center (FC). The distributed fusion estimation process operates in two stages. In the first one, the measured outputs provided by the sensors of each cluster are sent to the corresponding local processor, where local least-squares (LS) linear estimators are obtained; it is assumed that, during the transmission to the local processors, the clustering sensor measurements are subject to stochastic linear deception attacks. In the second stage, the local estimators received from all the local processors are gathered and fused in the FC, where the proposed distributed signal estimators are generated by a matrix-weighted linear combination of the local estimators using the mean squared error as optimality criterion.
The aforementioned estimation problem will be addressed without requiring full knowledge of the evolution model generating the signal process. Instead, it will be assumed that the signal mean function is zero and its covariance function is factorizable (
covariance-based estimation approach). More precisely, the following assumption is required ([
7]):
- (A1)
The -dimensional signal is a zero-mean second-order process and its autocovariance function is expressed in a separable form; namely, where are known matrices.
The signal process of the most common signal evolution models (e.g., the signal of linear systems, or that of uncertain systems with a sum of multiple multiplicative noise terms) meets this assumption (A1) and, hence, the covariance-based estimation approach provides a comprehensive framework to cope with different signal evolution models, thus overcoming the necessity of deriving specific algorithms for each situation.
2.1. Clustering Sensor Measurements and Stochastic Deception Attacks
Consider a sensor network and assume that the sensor nodes are grouped into
L clusters to measure the stochastic signal of interest. Specifically, assume that each cluster
is made up of
sensors that provide measurements of the signal according to the following model:
where
are known matrices and
is the signal measured output from the
i-th sensor of the
r-th cluster at time
k, which is transmitted to the
r-th local processor to obtain the local LS linear signal estimators. The following assumption is required on the measurement noises,
,
:
- (A2)
The measurement noises of different clusters are independent and, for each , the noises , , are zero-mean second-order white processes with known covariance matrices
For each cluster
, the transmissions of the measured outputs
to the
r-th local processor are affected by random linear deception attacks and the deceptive signal injected by the attackers,
, is described by:
This signal involves two parts: the first one neutralizes the true information and the second one is the blurred information (noise) added by the attackers. These noises, , , are assumed to satisfy the following requirement:
- (A3)
The attack noises of different clusters are independent and, for each , the noises , , are zero-mean second-order white processes with known covariance matrices
2.2. Measurements Received by the Local Processors
Usually, in practice, the attacks may randomly succeed or not. So, taking into account this random nature of the attacks, for every
, the measurements received by the
r-th local processor are modelled by introducing different sequences of Bernoulli random variables,
,
. For each
, and
, the value
models a successful attack into the
i-th communication channel from the
r-th cluster, meaning that only noise
arrives to the
r-th local processor; conversely, the value
models a failed attack, which means that the real measured output
is received by the
r-th local processor. Taking these considerations into account, the following model for
, the measurements received by the
r-th local processor, is considered:
or, equivalently, by substituting (
1) and (
2) into (
3), we have:
The following assumption is imposed on the Bernoulli random variables describing the success or failure of attacks:
- (A4)
, , , are independent sequences of independent Bernoulli random variables with known probabilities .
From this assumption, if we denote
, for
, then the correlation matrices
and
are known and their entries are easily calculated taking into account that
Finally, the following independence hypothesis is also assumed:
- (A5)
For and , the signal process and the processes , and are mutually independent.
4. Second Stage: Distributed Signal Estimators
As we have already mentioned, once the local LS linear estimators, , , have been obtained, they are sent to the FC and our goal is to fuse these local estimators to obtain distributed estimators, , , as matrix-weighted linear combinations that minimize the mean squared estimation error.
Defining the stacked vectors by comprising all the local estimators,
, and applying the LS criterion, the proposed distributed fusion estimators are given by:
where
and, from the Orthogonal Projection Lemma (OPL),
. Hence, the derivation of the distributed estimators in (
16) requires to obtain the cross-covariance matrices between the local ones
. Since the initial condition of the recursive Formula (
15) for the local smoothing estimators is the local filter, the cross-covariance matrices,
between the local smoothers will be recursively obtained by starting from the cross-covariance matrices,
, between the local filters.
4.1. Cross-Covariance Matrices between Local Filtering Estimators
From expression (
12) for the filter
, denoting
it is clear that the cross-covariance matrices between any two local filtering estimators
and
satisfy:
Using (
13) for
and denoting
, for
, we get that
is recursively obtained by:
Using again (
13) and denoting
, the following expression for
is immediately obtained:
Next, we derive an expression for
. Using (
14) for
, with (
6) for
, and taking into account that, from the OPL,
, we obtain:
Finally, an expression for the innovation cross-covariance matrices,
, is derived. First we write
Next, for
we use (
6) for
and (
14) for
; then, using again that, from the OPL,
, the following expression is clear:
where the matrices
are given in (
7).
4.2. Cross-Covariance Matrices between Local Smoothing Estimators
From expression (
15), denoting
, it is clear that the cross-covariance matrices between any two local smoothing estimators
and
satisfy:
To obtain the expectations
, we use (
14) for
and denote
; then, we have:
Using now (
6) for
and the independence of
with
,
and
, we have
Next, we use that, from the OPL, the estimator is orthogonal to the estimation error, to write
. So, since
, the following expression for
is immediately derived:
Finally, the expectations
are calculated. Using (
15) for
and (
13) for
, the following expression for
is clear:
4.3. Distributed Filtering and Fixed-Point Smoothing Estimators
The distributed estimators,
, are calculated from (
16), while a formula for the error covariance matrices,
, is easily derived from assumption
(A1) and (
16). More specifically, we can state the following results:
Let be the vectors constituted by the local estimators calculated from the recursive algorithms in Section 3.2; then, the distributed filtering and smoothing estimators are given bywith and where , are obtained by (18)) for , with initial condition given in (17). The error covariance matrices of the distributed estimators are computed by 5. Numerical Simulation Study
A numerical simulation example is presented to illustrate the application of the algorithms designed in the current paper to estimate a two-dimensional signal. Specifically, such algorithms have been implemented by using MATLAB software and both local and distributed filtering and fixed-point smoothing error variances of the signal components have been calculated, for 100 iterations, in order to examine the estimation accuracy. The effect of the stochastic deception attacks on the estimation performance has also been analyzed.
Consider a two-dimensional signal,
, whose evolution is described by the following model:
where
The multiplicative noise,
, and the additive noise,
, are standard white gaussian scalar noises. The initial signal
is a gaussian two-dimensional random vector with zero mean and covariance matrix
. The noise sequences and initial signal vector are assumed to be mutually independent; then, it is easy to see that the signal covariance function is given by
so assumption
(A1) is satisfied taking
and
where
is recursively obtained by:
This example shows that assumption (A1) on the signal autocovariance function is fulfilled by uncertain systems with state-dependent multiplicative noise.
Suppose that a sensor network, comprising 12 sensors, is deployed to measure the stochastic signal
. These sensors are grouped into three clusters and the number of sensors in each cluster is
,
and
, respectively. Scalar measurements are provided by the 12 sensors, according to model (
1), with the following time-invariant observation matrices:
The additive measurement noises are defined as , for all , where , , , and , are independent zero-mean Gaussian white process with variance 10; so the measurement noises in each cluster are correlated with
Assume that the transmissions to the local processors are subject to linear deception attacks and the data injected by the attackers are described by (
2), where the attack noises are defined as
, for all
, with
,
,
, and
,
independent standard Gaussian white processes. Clearly, in each cluster
the attack noises are correlated with
According to the theoretical study, for
, the measurements received at the
r-th local processor are modelled by (
3); that is, the attacks are considered to take place randomly and the statuses of the attacks are described by independent sequences of independent Bernoulli random variables with known probabilities
.
First, considering
, for
, and
, the performance of the local filtering estimators has been compared with that of the local fixed-point smoothing estimators; for
, these local estimators are computed in each
r-th processor using only the measurements received from the sensors of the corresponding
r-th cluster. For the first signal component,
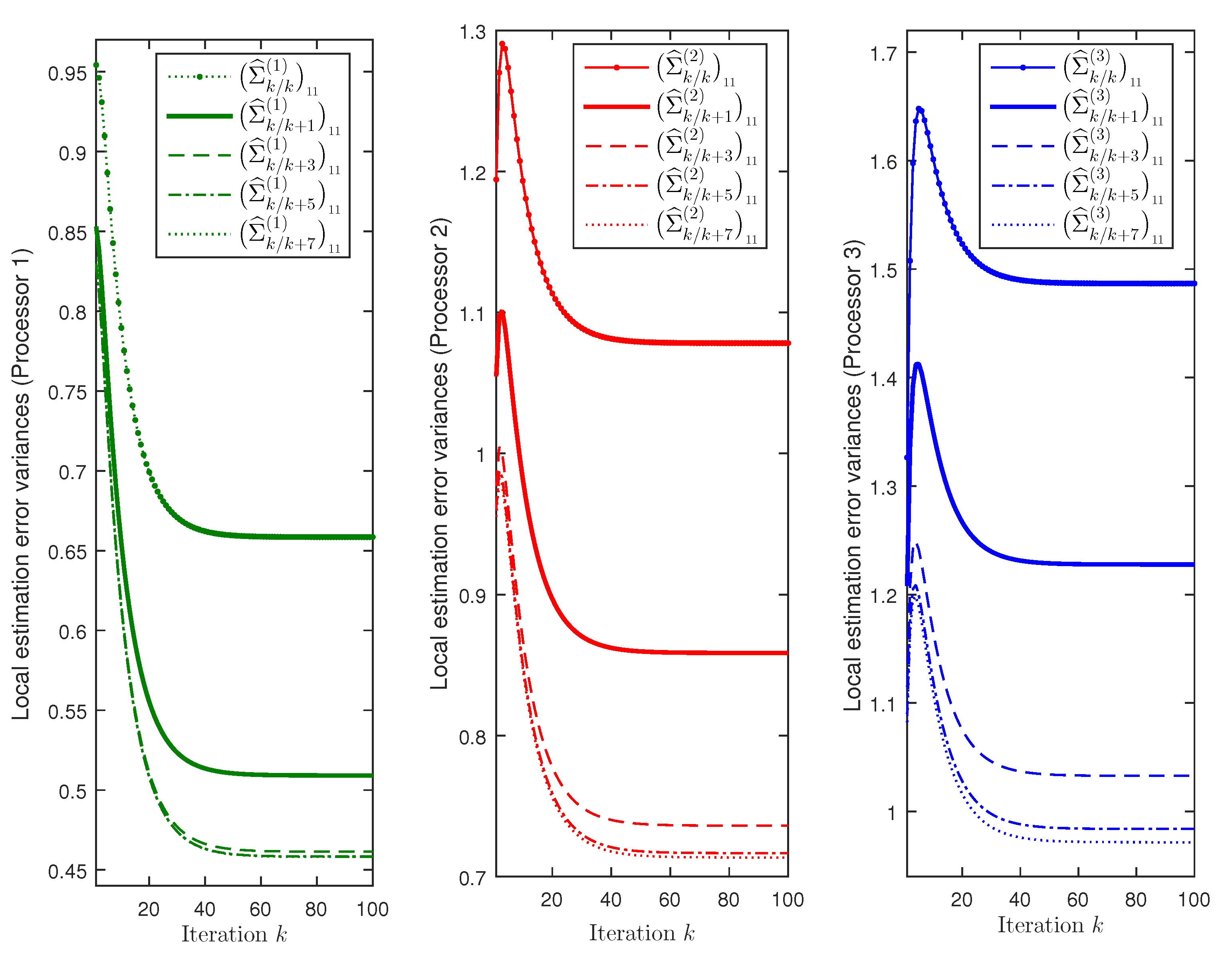
Figure 1 displays the error variances of the local filtering estimators,
, and the local fixed-point smoothing estimators
, for
, are displayed. For the three processors,
Figure 1 shows that, as expected, the error variances corresponding to the local smoothers are less than those of the local filters. It is also observed that the accuracy of the smoothers at each fixed-point,
k, becomes better as the number of available observations,
, increases, although this improvement is practically imperceptible for
in processor 1,
in processor 2 and
in processor 3. Note that the best estimation accuracy is obtained in processor 1 and the worst one in processor 3; therefore, we can conclude that, when the filtering performance is better, the improvement of the smoothers is less significant and, actually, it becomes practically negligible for lower values of
N. Similar results and conclusions are obtained for the second signal component.
Next, considering again
, for
, and
, the performance of the distributed filtering and fixed-point smoothing estimators have been compared with that of the local filtering estimators of the three processors.
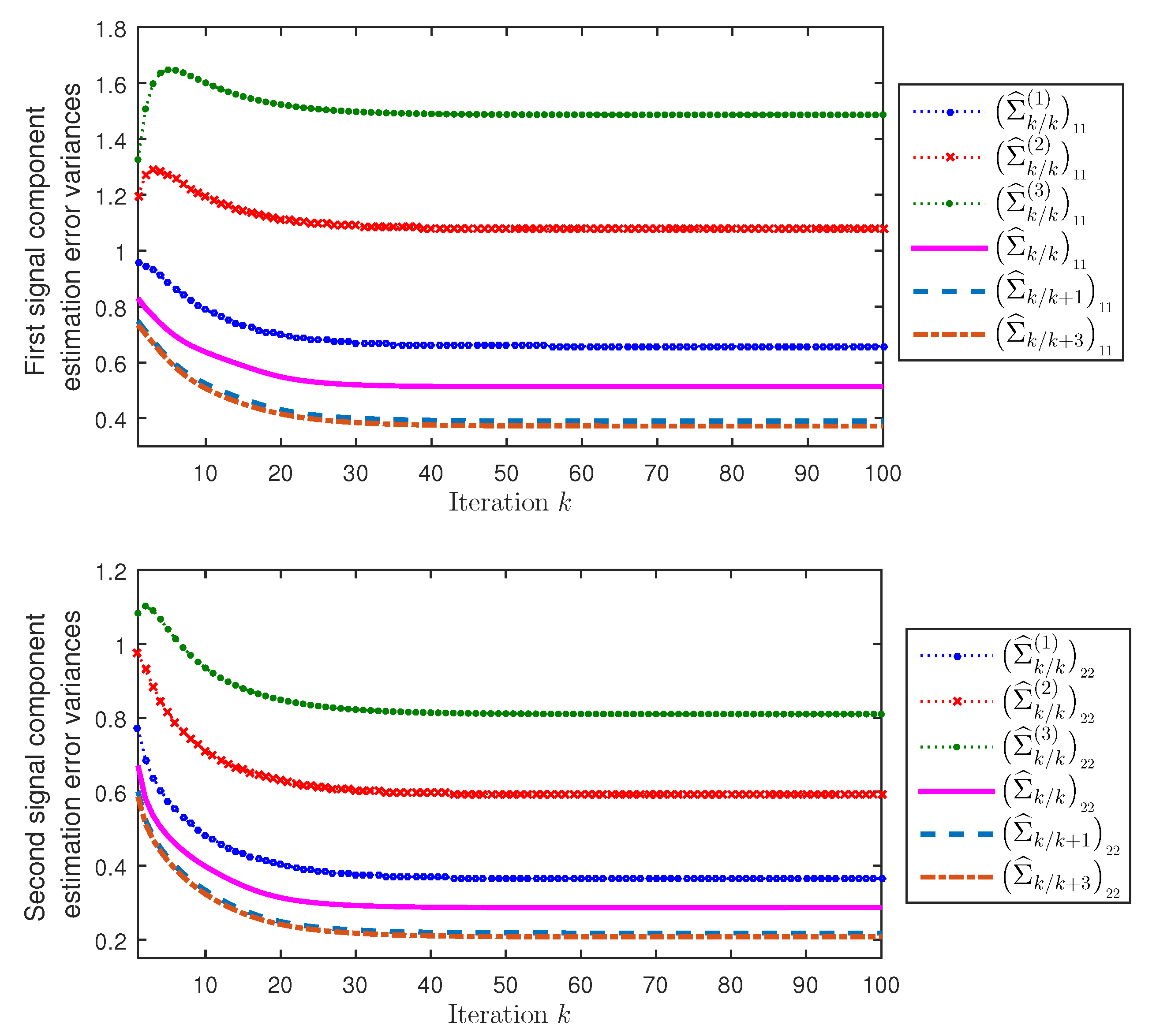
Figure 2 displays, for both first and second signal components (
), the error variances of the local filtering estimators
,
, and the distributed filtering and smoothing estimators
,
. On the one hand, this figure shows that the error variances of the distributed fusion filtering estimators are smaller than those of every local filter; consequently, the distributed fusion filtering estimators outperform all the local ones, agreeing with what theoretically is expected, since all the information of the three clusters is available to the distributed filters, while the local ones are based on the information of a single cluster. On the other hand, agreeing with the comments made about
Figure 1, from
Figure 2 it is also concluded that the error variances of the distributed fusion smoothers are less than those of the filters and, at each fixed-point,
k, the performance of the smoothers is better as the number of available observations,
, increases (note that, in this case, the improvement is practically imperceptible for
).
Finally, assuming the same success probability of attack during the transmissions of the measured outputs of all the sensors in the three clusters,
,
,
, we analyze how this probability affects the error variances of the distributed filtering estimators. Taking into account that these variances stabilize after a sufficiently large number of iterations, only the results of the last iteration (
) are shown in
Table 1. Specifically, the distributed filtering error variances of the first and second signal components,
,
, together with the corresponding percent variation rates are shown in
Table 1, when
varies from 0.1 to 0.9. From this table, we conclude that, for both signal components, as
increases, the distributed filtering error variances become higher, meaning that, as expected, the lower the probability of successful attacks is, the better estimators are obtained. In addition, for both signal components, it is observed that the deterioration of the estimators is more significant (the percent variation rate of the error variance is larger) for high attack probabilities (
).