Adaptive Consensus-Based Unscented Information Filter for Tracking Target with Maneuver and Colored Noise
Abstract
1. Introduction
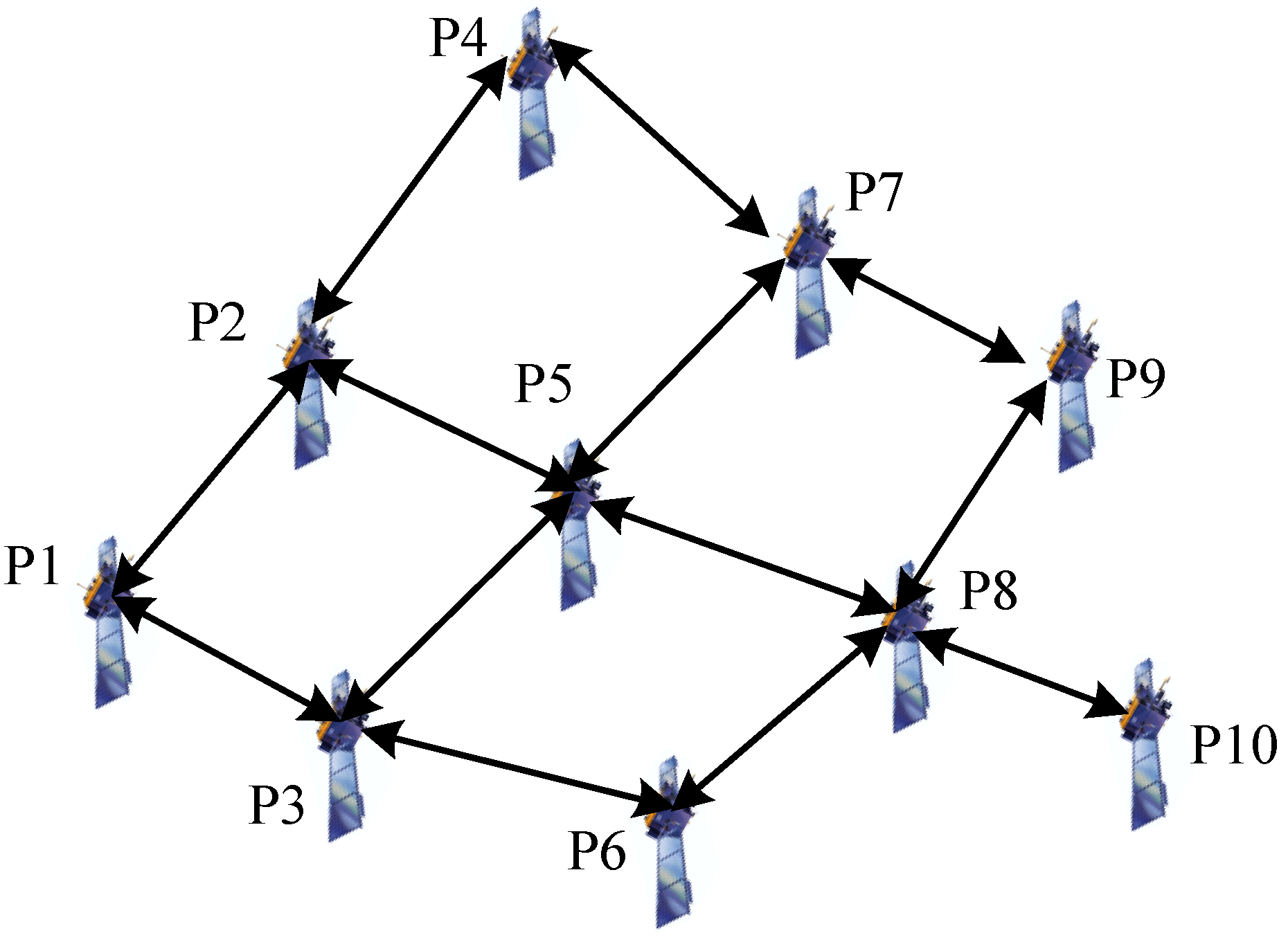
2. Space Target Tracking System Model
2.1. The Orbital Dynamical Model
2.2. The Measurement Model
3. Fundamentals of the Proposed Filter
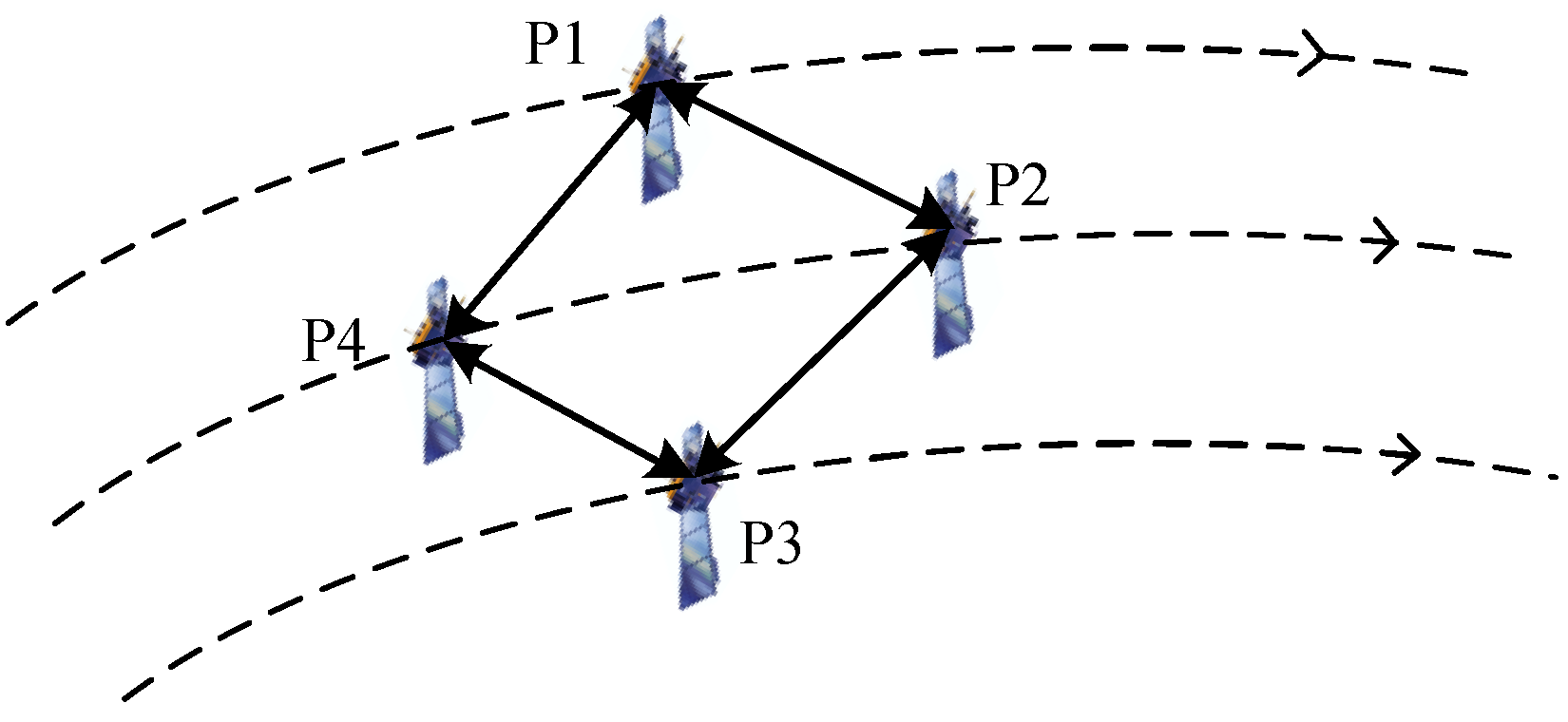
3.1. Brief Review of Consensus-Based State Estimation Algorithm
| Algorithm 1 Consensus-based unscented information filter (CUIF) |
| Step 1. Compute consensus proposals of local filter: |
| Step 2. Perform consensus on and |
| for l = 1 to L |
| I. Send and to all neighbors; |
| II. Receive and from all neighbors; |
| III. Update consensus terms: |
| end for |
| Step 3. Compute the posterior at kth time step: |
| Step 4. Prediction for the next time step: |
| The predicted system state and its covariance matrix are obtained by: |
3.2. Method for Handling Colored Measurement Noise
3.2.1. State Augmentation
3.2.2. Measurement Differencing
3.3. Method for Handling Dynamical Model Error
4. Adaptive Consensus-Based Unscented Information Filter
| Algorithm 2 Adaptive CUIF based on state augmentation (ACUIF-SA) | |
| Step 1. Compute consensus proposals of the original state for local filter: | |
| The fading factor is calculated according to (42)–(44), then and are calculated by | |
| where and are obtained by: | |
| and | |
| in which, is given by (32). | |
| Step 2. Perform consensus on and via (13) and (14). | |
| Step 3. Compute the posterior at kth time step: | |
| (1) Compute the posterior of the original state at kth time step according to (15) and (16), and can be obtained; | |
| (2) Compute the posterior of the augmented state and the associated covariance matrix by: | |
| and | |
| (3) Reset the local filter: | |
| where , and n is the dimension of the original state. | |
| Step 4. Prediction for the next time step: | |
| The predicted augmented state and its covariance matrix can be calculate in a similar way shown in (18) and (19). | |
| Algorithm 3 Adaptive CUIF based on measurement differencing (ACUIF-MD) | |||
| Step 1. Compute consensus proposals of local filter: | |||
| The fading factor is calculated according to (42)–(44), then and are calculated by: | |||
| where and are obtained by: | |||
| and | |||
| in which, and are given by (37) and (41). | |||
| Step 2. Perform consensus on and via (13) and (14). | |||
| Step 3. Compute the posterior at kth time step according to (15) and (16). | |||
| Step 4. Prediction for the next time step: | |||
| Compute the predicted system state and covariance matrix by (18) and (19). | |||
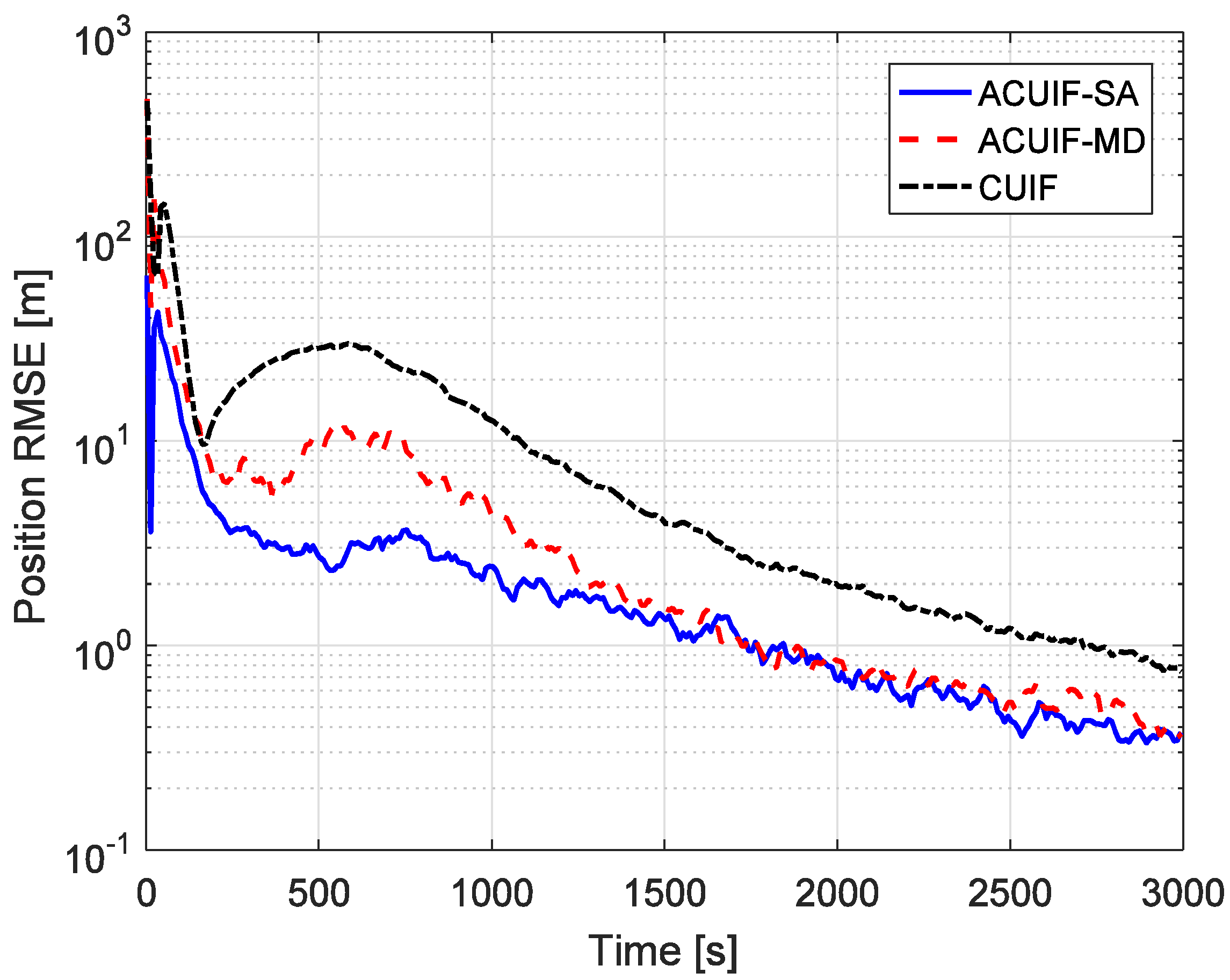
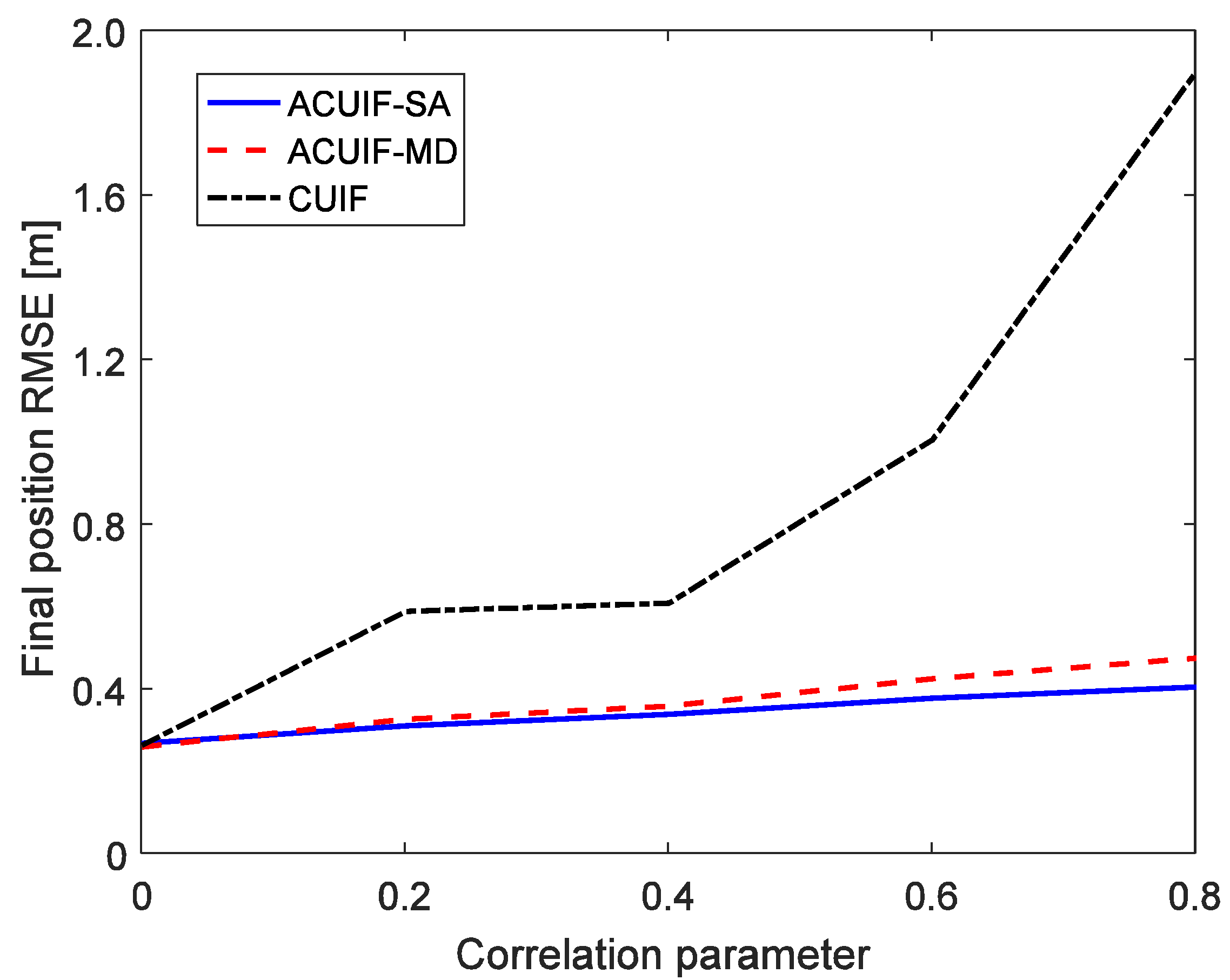
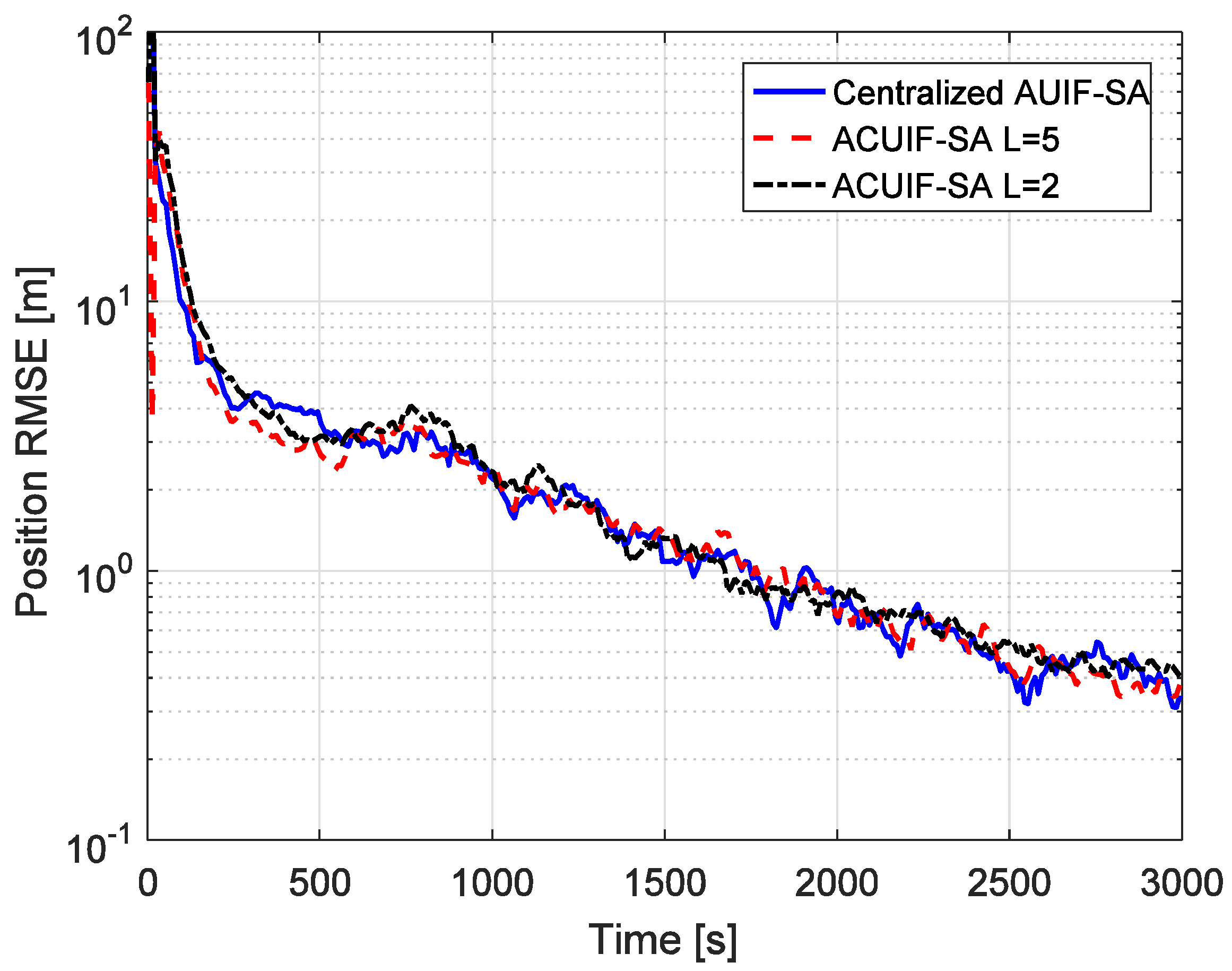
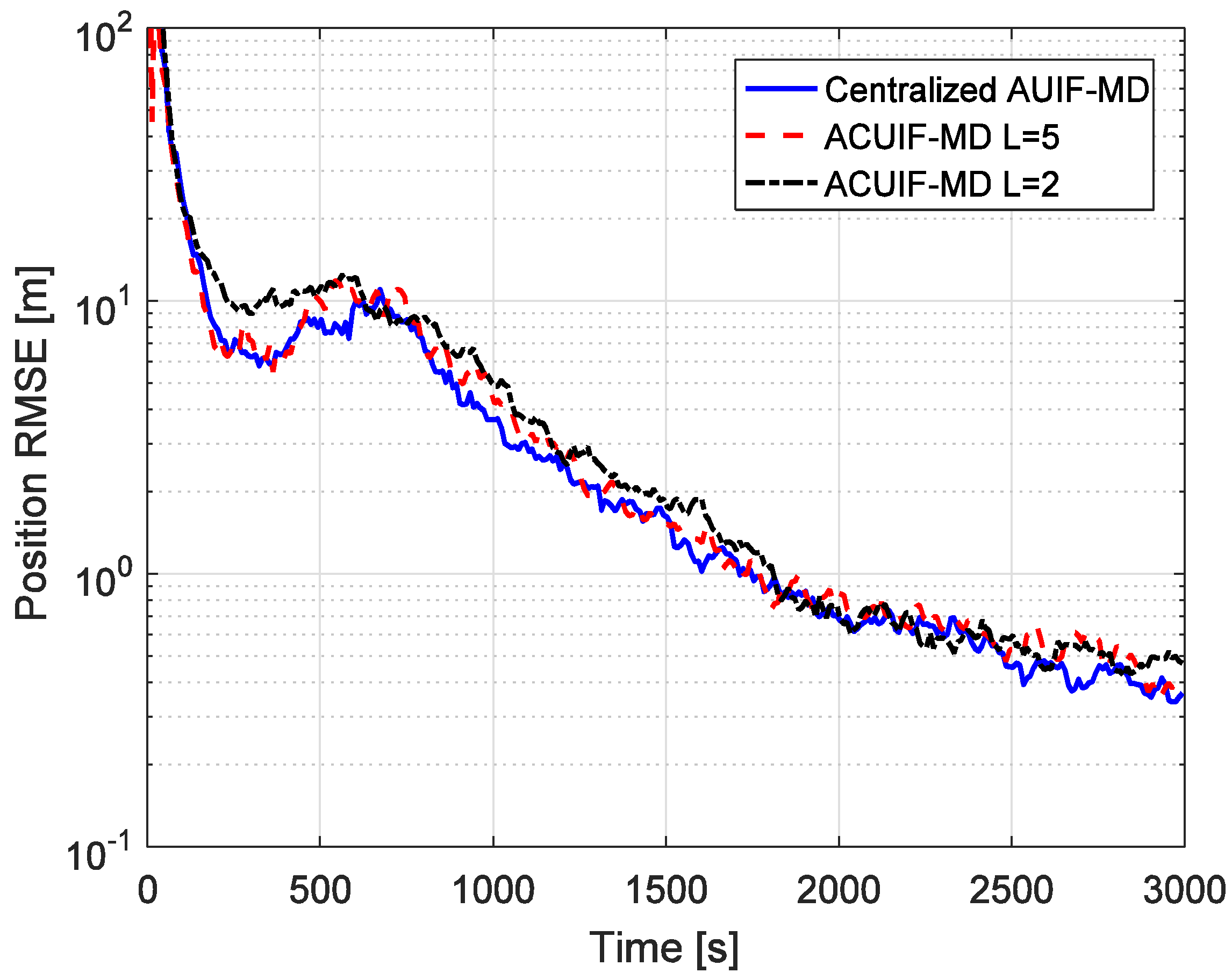
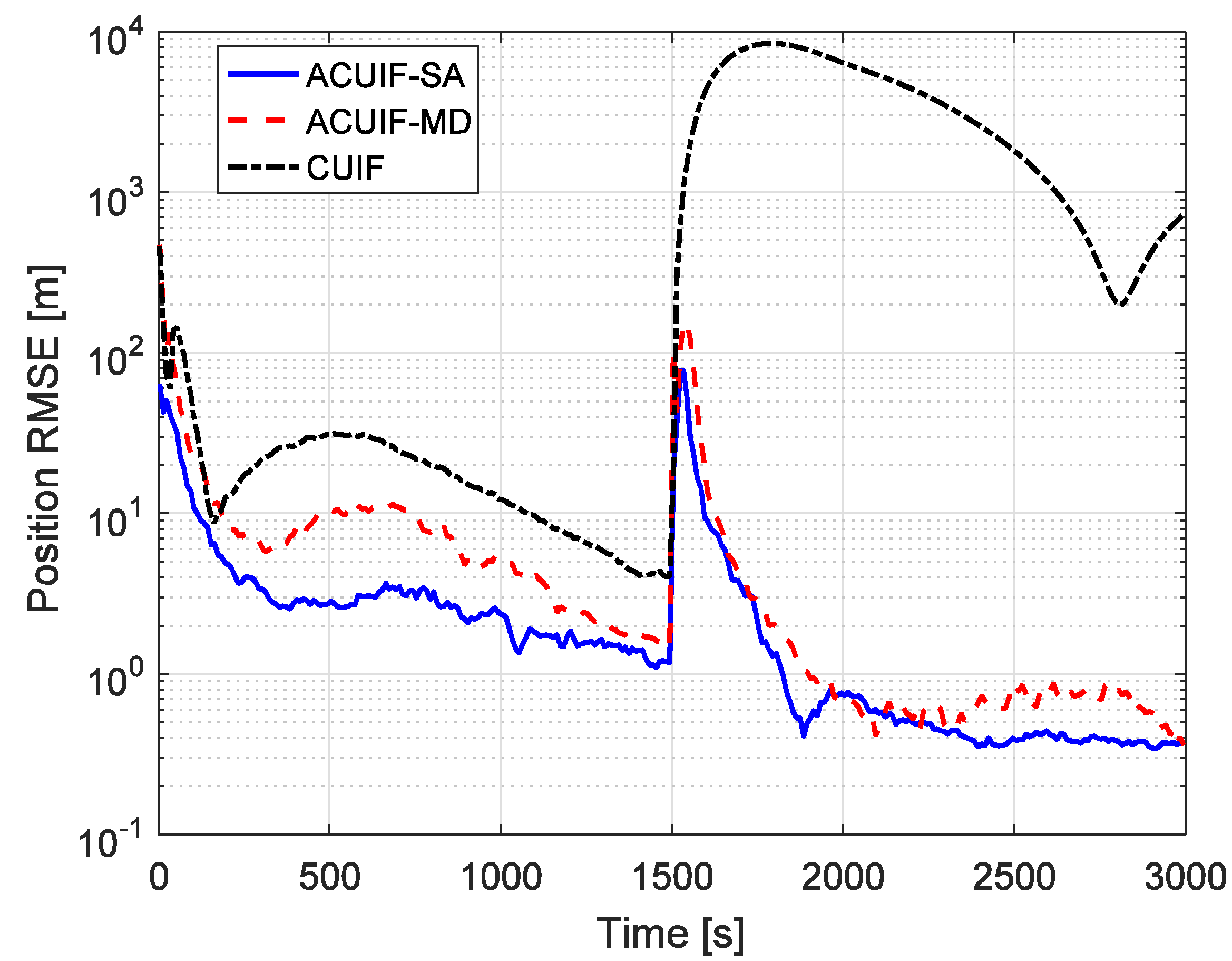
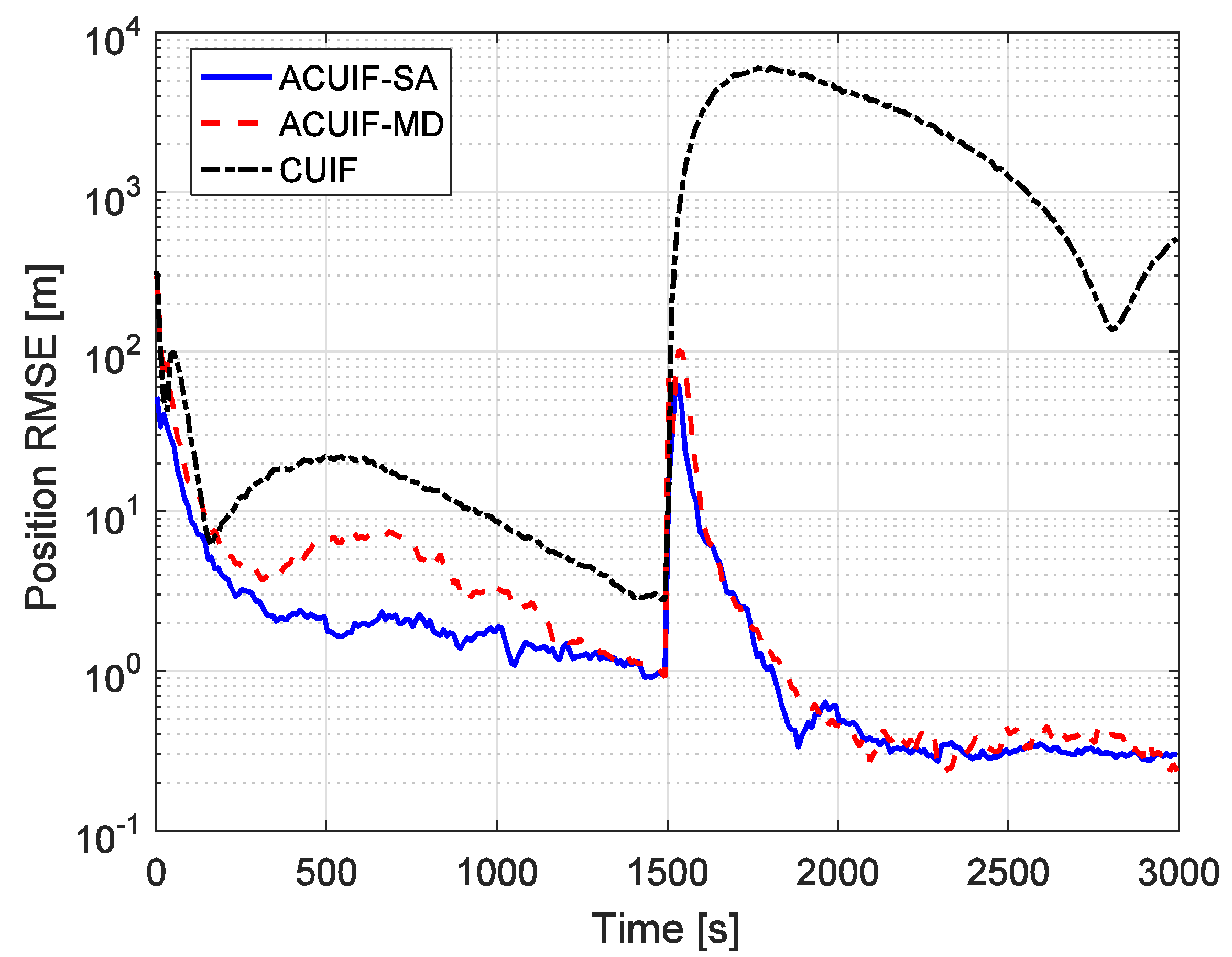
5. Simulation Results Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Feng, H.; Cai, Z. Target tracking based on improved square root cubature particle filter via underwater wireless sensor networks. IET Commun. 2019, 13, 1008–1015. [Google Scholar] [CrossRef]
- Wang, L.; Yan, J.; Han, T.; Deng, D. On Connectivity and Energy Efficiency for Sleeping-Schedule-Based Wireless Sensor Networks. Sensors 2019, 19, 2126. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Su, S.; Yin, H.; Guo, X.; Zuo, Z.; Wei, J.; Zhang, L. Optimized Non-Cooperative Spectrum Sensing Algorithm in Cognitive Wireless Sensor Networks. Sensors 2019, 19, 2174. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yang, W.; Ding, D.; Liao, Y.; Clark, D. Simplex cubature Kalman-consensus filter for distributed space target tracking. Wirel. Commun. Mob. Comput. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Felicetti, L.; Emami, R. A multi-spacecraft formation approach to space debris surveillance. Acta Astronaut. 2016, 127, 491–504. [Google Scholar] [CrossRef]
- Song, T.L.; Kim, H.W.; Musicki, D. Distributed target tracking in clutter. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 654–668. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Dong, K.; Ding, Z.; He, Y. A Novel Distributed State Estimation Algorithm with Consensus Strategy. Sensors 2019, 19, 2134. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L. Kullback–Leibler average, consensus on probability densities, and distributed state estimation with guaranteed stability. Automatica 2014, 50, 707–718. [Google Scholar] [CrossRef]
- Keshavarz-Mohammadiyan, A.; Khaloozadeh, H. Consensus-based distributed unscented target tracking in wireless sensor networks with state-dependent noise. Signal Process. 2018, 144, 283–295. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica 2016, 68, 169–178. [Google Scholar] [CrossRef]
- He, X.; Xue, W.; Fang, H. Consistent distributed state estimation with global observability over sensor network. Automatica 2018, 92, 162–172. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Kalman-Consensus Filter: Optimality, stability, and performance. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control, Shanghai, China, 15–18 December 2009; pp. 7036–7042. [Google Scholar]
- Olfati-Saber, R.; Shamma, J.S. Consensus Filters for Sensor Networks and Distributed Sensor Fusion. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 6698–6703. [Google Scholar]
- Li, W.; Wei, G.; Han, F.; Liu, Y. Weighted average consensus-based unscented Kalman filtering. IEEE Trans. Cybern. 2016, 46, 558–567. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Jia, Y. Consensus-based distributed information filter for a class of jump Markov systems. IET Control Theory Appl. 2011, 5, 1214–1222. [Google Scholar] [CrossRef]
- Kamal, A.T.; Farrell, J.A.; Roy-Chowdhury, A.K. Information weighted consensus. In Proceedings of the IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 2732–2737. [Google Scholar]
- Jia, B.; Pham, K.D.; Blasch, E.; Shen, D.; Wang, Z.; Chen, G. Cooperative space object tracking using space-based optical sensors via consensus-based filters. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1908–1936. [Google Scholar] [CrossRef]
- Liu, G.; Tian, G. Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation. Sensors 2017, 17, 800. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. Robust information filter based on maximum correntropy criterion. J. Guid. Contr. Dyn. 2016, 39, 1124–1129. [Google Scholar] [CrossRef]
- Wu, W.R.; Chang, D.C. Maneuvering target tracking with colored noise. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1311–1320. [Google Scholar]
- Sun, J.; Xu, X.; Liu, Y.; Zhang, T.; Li, Y. FOG Random Drift Signal Denoising Based on the Improved AR Model and Modified Sage-Husa Adaptive Kalman Filter. Sensors 2016, 16, 1073. [Google Scholar] [CrossRef]
- Wang, J.; Dong, P.; Jing, Z.; Cheng, J. Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise. Sensors 2018, 18, 3678. [Google Scholar] [CrossRef]
- Bryson, A.; Johansen, D. Linear filtering for time-varying systems using measurements containing colored noise. IEEE Trans. Autom. Control 1965, 10, 4–10. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. X-ray pulsar-based navigation using time-differenced measurement. Aerosp. Sci. Technol. 2014, 36, 27–35. [Google Scholar] [CrossRef]
- Bryson, A., Jr.; Henrikson, L. Estimation using sampled data containing sequentially correlated noise. J. Spacecr. Rocket. 1968, 5, 662–665. [Google Scholar] [CrossRef]
- Lee, B.J.; Park, J.B.; Lee, H.J.; Joo, Y.H. Fuzzy-logic-based IMM algorithm for tracking a manoeuvring target. IEE Proc. Radar Sonar Navig. 2005, 152, 16–22. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-radial cubature Kalman filter for maneuvering target tracking. Sensors 2017, 17, 1374. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Liu, Y.; Liu, J.; Yu, K.; You, Y.; Jing, P.; He, Y. Adaptive Interacting Multiple Model Algorithm Based on Information-Weighted Consensus for Maneuvering Target Tracking. Sensors 2018, 18, 2012. [Google Scholar] [CrossRef]
- Deng, Z.; Yin, L.; Huo, B.; Xia, Y. Adaptive Robust Unscented Kalman Filter via Fading Factor and Maximum Correntropy Criterion. Sensors 2018, 18, 2406. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S.-B.; Zhang, Q.-Z. Adaptive Estimation of Multiple Fading Factors for GPS/INS Integrated Navigation Systems. Sensors 2017, 17, 1254. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Li, L. Adaptively robust unscented Kalman filter for tracking a maneuvering vehicle. J. Guid. Contr. Dyn. 2014, 37, 1696–1701. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamical and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Mahmoudi, A.; Karimi, M.; Amindavar, H. Parameter estimation of autoregressive signals in presence of colored AR(1) noise as a quadratic eigenvalue problem. Signal Process. 2012, 92, 1151–1156. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K.; Zhang, L. Square-Root Unscented Information Filter and Its Application in SINS/DVL Integrated Navigation. Sensors 2018, 18, 2069. [Google Scholar] [CrossRef]
- Joseph, B. Preliminary circular orbit from a single station of range-only Data. AIAA J. 1967, 12, 2264–2265. [Google Scholar]
| Terms | Values |
|---|---|
| Initial state error | |
| Initial covariance matrix | |
| Process noise matrix | |
| Simulation duration | 3000 s |
| Sampling step | 1 s |
| 1 m | |
| L | 5 |
| 0.25 |
| x (km) | y (km) | z (km) | vx (km/s) | vy (km/s) | vz (km/s) | |
|---|---|---|---|---|---|---|
| Target | −251.66 | 2591.94 | −6796.42 | 3.83 | −5.87 | −2.38 |
| Observation platform 1 | −117.92 | 2389.05 | −6873.86 | 3.83 | −5.96 | −2.14 |
| Observation platform 2 | −368.43 | 2104.52 | −6957.49 | 3.75 | −6.05 | −2.03 |
| Observation platform 3 | −496.83 | 2310.90 | −6883.62 | 3.73 | −5.97 | −2.27 |
| Observation platform 4 | −434.62 | 2207.66 | −6921.61 | 3.75 | −6.01 | −2.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, Y.; Zheng, W. Adaptive Consensus-Based Unscented Information Filter for Tracking Target with Maneuver and Colored Noise. Sensors 2019, 19, 3069. https://doi.org/10.3390/s19143069
Li Z, Wang Y, Zheng W. Adaptive Consensus-Based Unscented Information Filter for Tracking Target with Maneuver and Colored Noise. Sensors. 2019; 19(14):3069. https://doi.org/10.3390/s19143069
Chicago/Turabian StyleLi, Zhao, Yidi Wang, and Wei Zheng. 2019. "Adaptive Consensus-Based Unscented Information Filter for Tracking Target with Maneuver and Colored Noise" Sensors 19, no. 14: 3069. https://doi.org/10.3390/s19143069
APA StyleLi, Z., Wang, Y., & Zheng, W. (2019). Adaptive Consensus-Based Unscented Information Filter for Tracking Target with Maneuver and Colored Noise. Sensors, 19(14), 3069. https://doi.org/10.3390/s19143069




