Discovering Speed Changes of Vehicles from Audio Data
Abstract
1. Introduction
2. Use of Audio Data in Automotive Research
2.1. Parametrization and Classification of Audio Data
- time domain parameters: Zero Crossing Rate (the rate of sign-changes of the signal in a particular frame), or Zero Crossing Rising (the number of times when the audio signal rises to 0 and becomes positive);
- Energy;
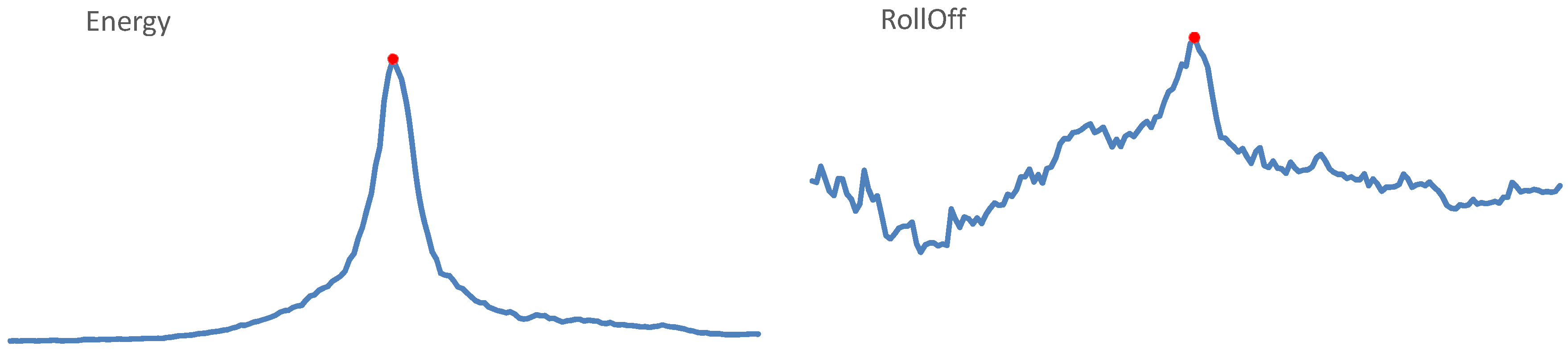
- spectral features: Spectral Centroid (the gravity center of the spectrum), Spectral Spread (the second central moment of the spectrum), RollOff (the frequency below which 85–90% of the spectrum is concentrated; the threshold value depends on implementation), Spectral Flux (the squared difference between the normalized magnitudes of the spectra of two successive frames);
- Mel Frequency Cepstral Coefficients (MFCC), a cepstral representation where the frequency bands are distributed according to the mel-scale;
- features designed to describe music: Pitch, Chroma Vector (12-element vector, with elements representing the spectral energy of the 12 pitch classes in equal temperament); Harmonic Spectral Centroid and Harmonic Spectral Flux.
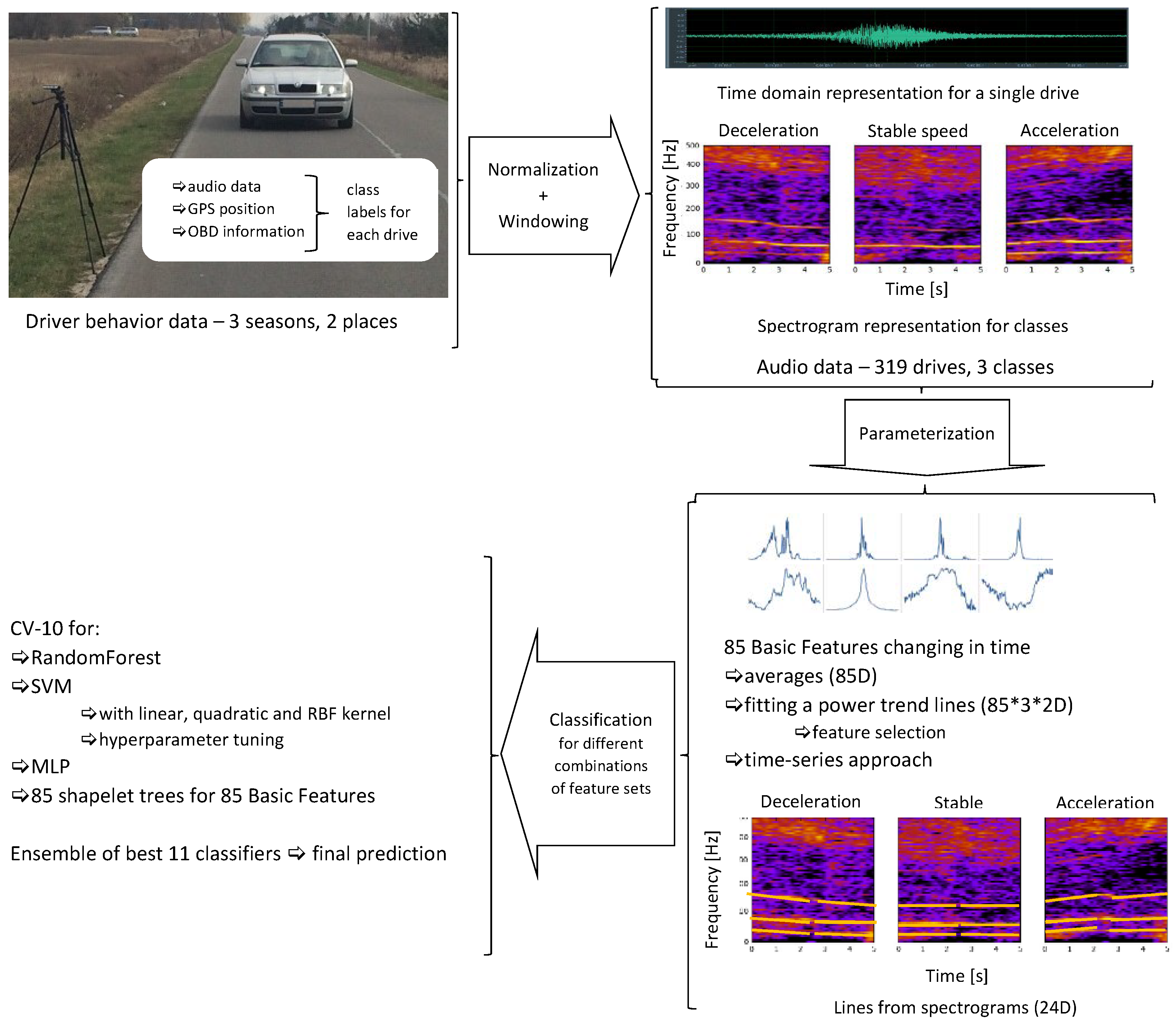
3. Materials and Methods
3.1. Audio Data
- in the summer, on August 2nd 2016, in Ciecierzyn, Lublin voivodship, Poland,
- in the winter, on January 16th 2017, in Lubartów, Lublin voivodship, Poland,
- in the spring, on March 31st 2017 and on April 5th 2017, in Lubartów, Lublin voivodship, Poland.
3.1.1. Summer Recordings
3.1.2. Winter Recordings
3.1.3. Spring Recordings
- 77 drives for acceleration, from 50 to 70 km/h, and from 50 to 80 km/h for Skoda Octavia;
- 58 drives for stable speed, at 60, 70, and 80 km/h; the speed limit in this area is 90 km/h;
- 80 drives for deceleration, with the following speed ranges: 80–40 km/h, 80–50 km/h, and 70–40 km/h; deceleration included applying brakes in these recordings, as we wanted to obtain data corresponding to more intensive deceleration.
3.2. Data Parametrization
- feature vector, consisting of 85 features calculated for consecutive frames (with 2/3 frame overlap) of the entire parameterized audio segment and then averaged;
- parametric description of the evolution of 85 basic features in time, observed within the analyzed audio segment on frame-by-frame basis; these trends were also approximated separately for the time segments before and after passing the microphone;
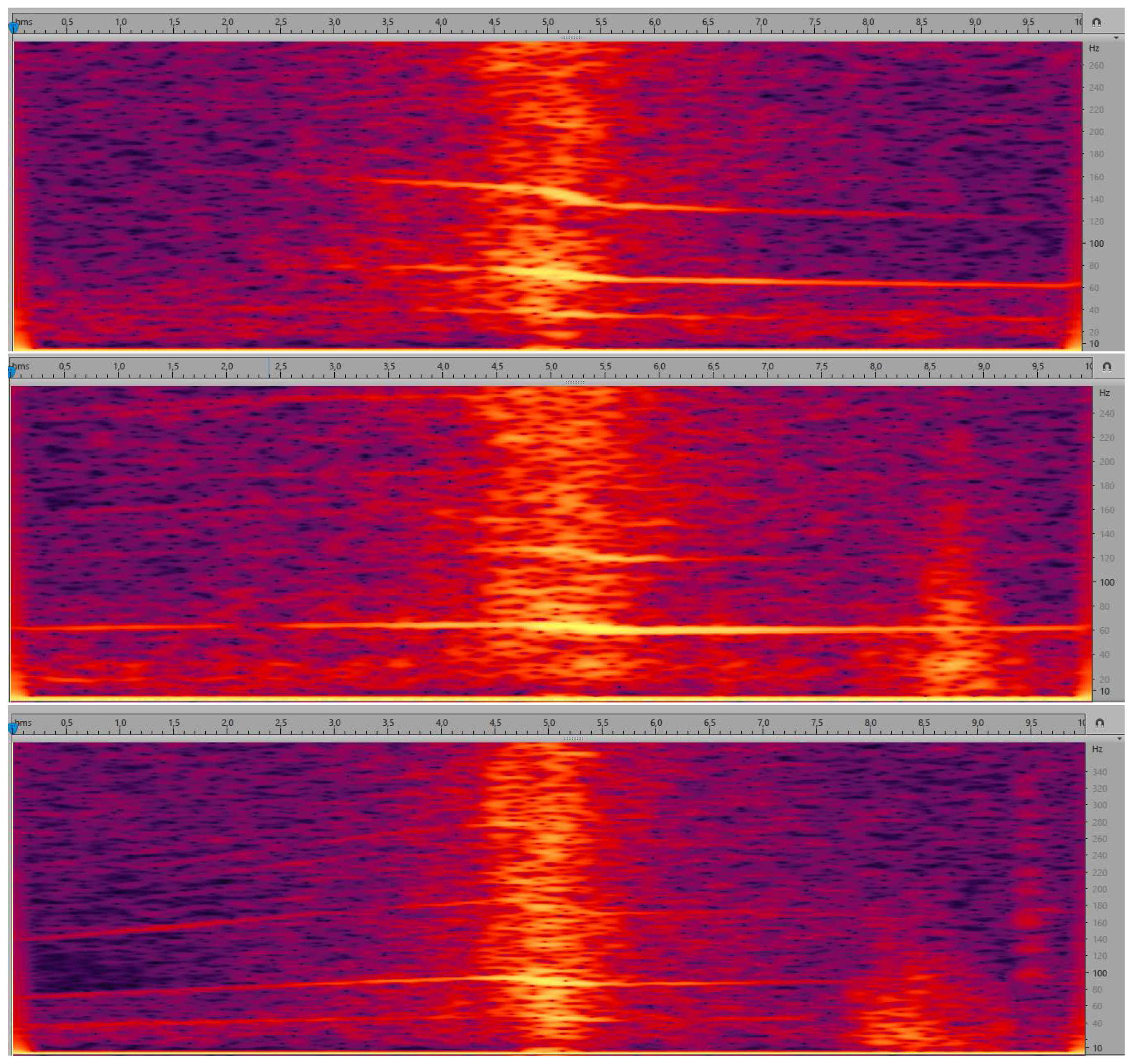
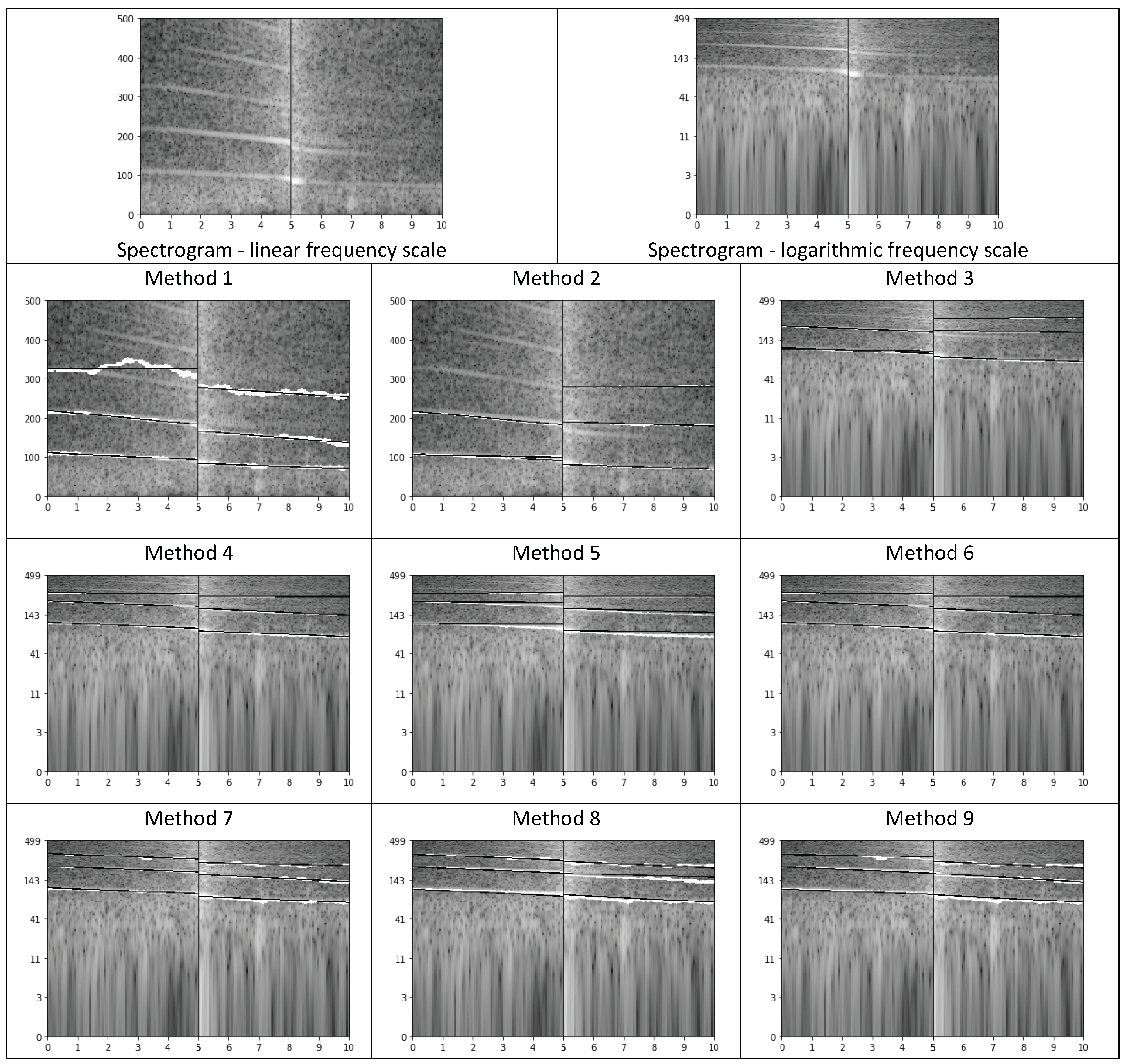
- parametric description of curves (lines) in the spectrogram, calculated separately for the time segment before approaching the microphone and for the time segment after passing the microphone. Spectrogram shows the evolution of spectrum over time, i.e., horizontal axis represents time, vertical axis represents frequency, and spectral coefficients are encoded using a selected color scale. Exemplary spectrograms for our audio data are shown in Figure 5. As we can see, lines can be observed in these spectrograms, but very few of them are pronounced.
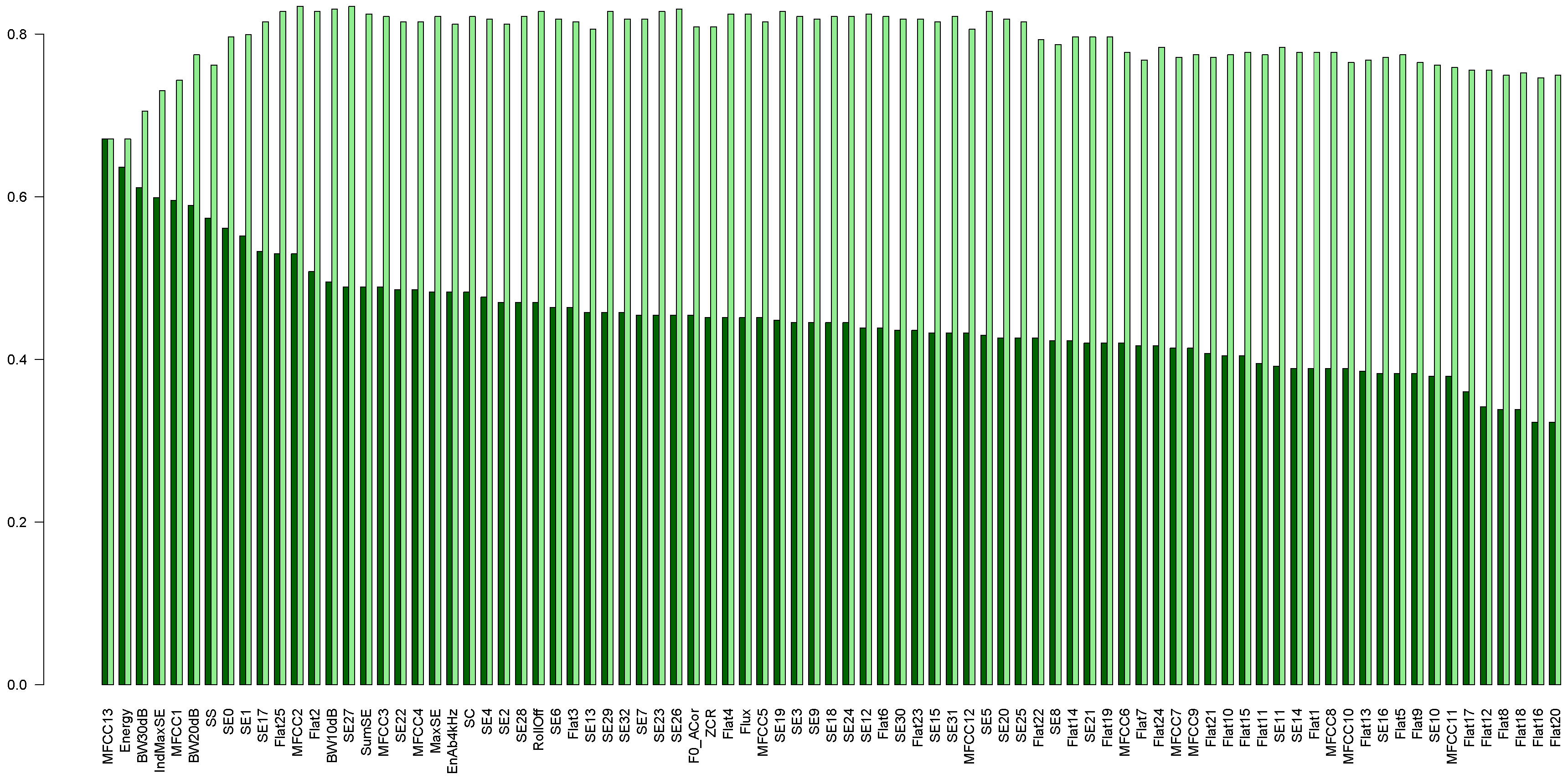
3.2.1. 85 Basic Features
- Zero Crossings Rising (ZCR);
- Audio Spectrum Envelope (SE) calculated as sums of the power spectrum coefficients within logarithmically spaced frequency bands [53];
- SumSE—sum of the spectrum envelope values;
- MaxSE, IndMaxSE—value and index of the SE maximum;
- Audio Spectrum Flatness, Flat1, …, —a vector describing the flatness property of the power spectrum [53], i.e., the deviation of the signal’s power spectrum from a flat shape; flat spectrum corresponds to noises, otherwise the spectrum has tonal components;
- MFCC—13 coefficients. The cepstrum is calculated as the logarithm of the mel-scaled magnitudes of the spectral coefficients, submitted to DCT (discrete cosine transform); the mel scale reflects the properties of the human perception of frequency; 24 mel filters were applied, and we took the first 12 coefficients. The thirteenth coefficient is the 0-order coefficient of MFCC, corresponding to the logarithm of the energy;
- F0_ACor—fundamental frequency, calculated from the autocorrelation function; this frequency changes with the speed change;
- Energy—energy of the entire spectrum;
- EnAb4kHz—proportion of the spectral energy above 4 kHz to Energy;
- Audio Spectrum Centroid (SC) [53];
- Audio Spectrum Spread (SS); [53];
- RollOff—the frequency below which 85% of the accumulated magnitudes of the spectrum is concentrated,
- BW10dB, BW20dB, BW30dB—bandwidth of the frequency band comprising the power spectrum maximum and the level drop by 10, 20 and 30 dB, respectively, towards both lower and upper frequencies;
- Flux—the comparison of the power spectrum for a given frame and the previous one, calculated as the sum of squared differences between the magnitudes of the DFT points in the given frame and their corresponding values in the preceding frame.
3.2.2. Trends
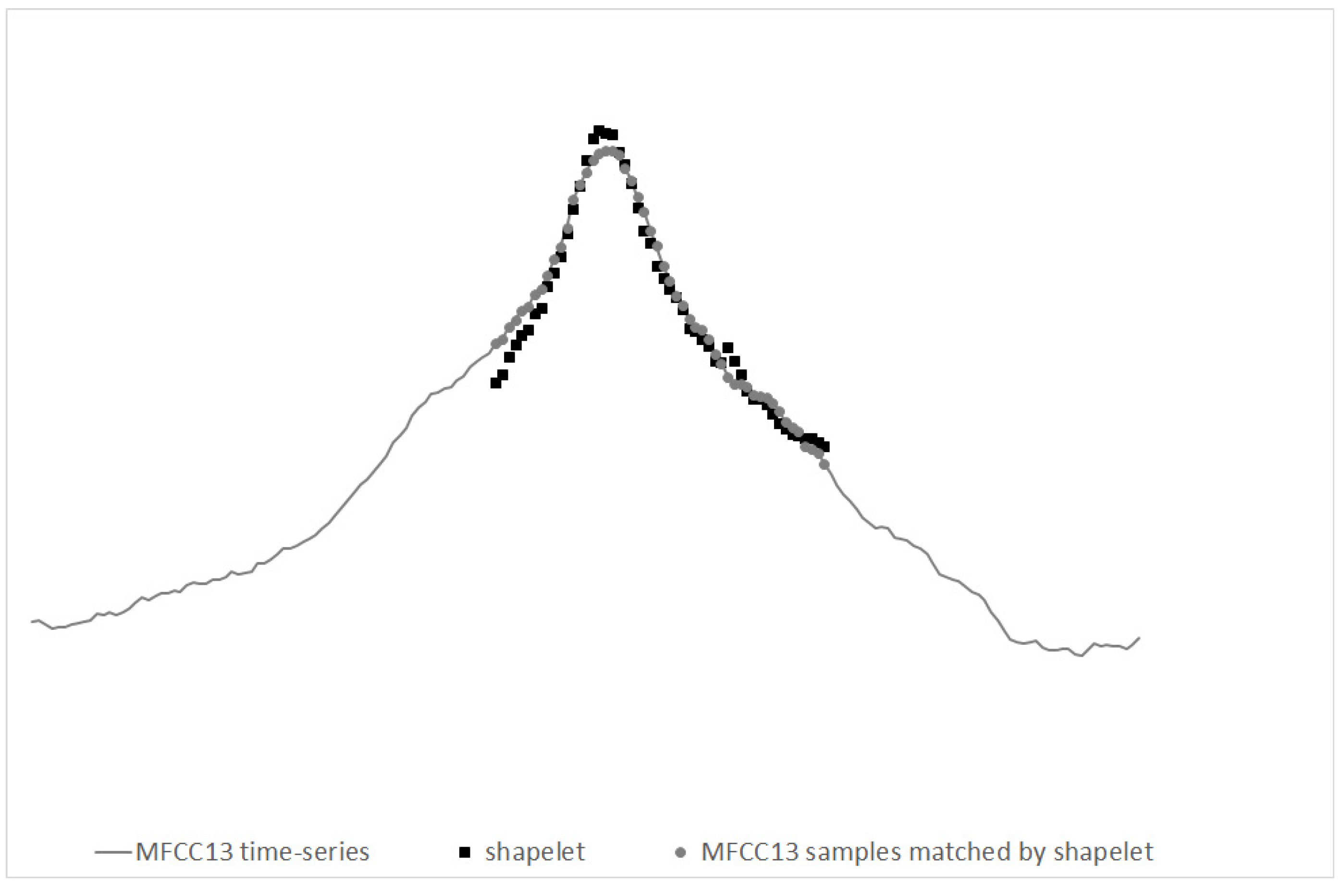
3.2.3. Time Series-Based Approach
3.2.4. Lines
- Method 1
- In the 5 s when the vehicle is approaching the microphone, we look for the three lines of the highest energy, spanning slantwise in the spectrogram (based on 8192-element spectrum), as follows [58]:
- For each frame, we look for three candidates for the lines. We analyze the following ranges: 50–100 Hz, 100–200 Hz, 200–300 Hz, 300–400 Hz, and 400–500 Hz. Frequencies most often indicated as local maxima in these ranges are returned as candidates to start lines. For the selected three candidates, three continuous paths in the spectrogram are traced starting from the moment of passing the microphone (towards the decrease of energy). We traced the paths through following local maxima, i.e., in the next frame we considered the average of the last three frequencies (if available) already added to the line and its two neighbors. Next, for each path we find a line, which best approximates this path, by means of linear approximation.
- Similarly, we look for three lines in the 5 s segment after passing the microphone.
This solution has several drawbacks, namely we can lose the path, or the algorithm may follow the path even if the line is no longer visible in the spectrogram, and each point influences the line with the same weight. - Method 2
- In this method we decided to down-sample audio data to 1 kHz sampling rate; low-pass filter was applied here (averaging). We aimed at high-resolution spectrogram, so we decided to perform zero-padding of our 170 ms long frames to 1024 samples, thus achieving spectral bins of 1 Hz. The procedure of calculating lines remained the same.
- Method 3
- In this case we calculated the logarithm of the energy (base 10), and frequency was also expressed in logarithmic scale (base 2). On a logarithmic scale lines are parallel on the spectrogram.
- Method 4
- Since we expected harmonic lines (i.e., for frequencies representing multiples of the lowest, fundamental frequency) and the obtained lines were often situated very close to each other, we decided to simplify the procedure of searching for candidates. The candidate from 50–150 Hz was considered to represent the first line, with maximal value of energy in the center of our 10 s segment. Additionally, we corrected octave errors, i.e., erroneous indication of the double of the fundamental frequency.
- Method 5
- Weighted linear regression. The linear regression was weighted with , where is the normalized energy of each point, on a logarithmic scale.
- Method 6
- Modification of method no. 4 by changing the starting moment of tracing lines. Namely, the tracing starts from the time moment when the energy is 10 dB less than in the loudest moment (center, passing the microphone), to avoid the part most affected by the Doppler effect. As we can see in Figure 5, the central part of the spectrogram shows curves, corresponding to frequency changes. Extracting line parameters is difficult in such case.
- Method 7
- Higher tolerance of local declinations. In this method, the range of possible declination of each line was increased, from 2 nearest neighbors of the average of the last 3 points, to the range of a musical tone, i.e., a semitone below and a semitone above. As a result, lines for higher frequencies were properly tracked.
- Method 8
- Modification of determining the gradient of each line, through searching for the most frequent gradient. In this method, when line tracking was completed, the mode of gradient values for ten-point segments was indicated as the new gradient.
- Method 9
- Variation of the method above: three most frequent values were found (i.e., the mode and the next two most frequent values), and their average was used as the new gradient value.
3.3. Classification
3.3.1. Forest of Shapelets
4. Results and Discussion
- RF: 90.5%,
- SVM: SVML 85.4%, SVMQ 87.1%, SVMR 90.9%,
- MLP: 88.6%.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Elvik, R.; Vaa, T. The Handbook of Road Safety Measures; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Finch, D.J.; Kompfner, P.; Lockwood, C.R.; Maycock, G. Speed, Speed Limits and Accidents; (Project report 58, TRL 59); Transport Research Laboratory: Crowthorne, UK, 1994. [Google Scholar]
- Huvarinen, Y.; Svatkova, E.; Oleshchenko, E.; Pushchina, S. Road Safety Audit. Transp. Res. Procedia 2017, 20, 236–241. [Google Scholar] [CrossRef]
- ITF. Road Safety Annual Report 2017; OECD Publishing: Paris, France, 2017. [Google Scholar]
- Krystek, R.; Sitarz, M.; Żurek, J.; Gucma, S. Integrated system of transport safety. J. KONBiN 2008, 1, 421–436. [Google Scholar] [CrossRef][Green Version]
- National Council BRD. The National Road Safety Programme 2013–2020; National Road Safety Council: Warsaw, Poland, 2013. [Google Scholar]
- POBR Polish Road Safety Observatory. Road Safety Problems in Poland. 2013. Available online: http://www.obserwatoriumbrd.pl/en/road_safety_analyses/road_safety_problems/ (accessed on 8 July 2019).
- Żukowska, J.; Mikusova, M.; Michalski, L. Integrated safety systems—The approach toward sustainable transport. Arch. Transp. Syst. Telemat. 2017, 10, 44–48. [Google Scholar]
- Żukowska, J.; Krystek, R. The role of observatories in the integrated transport safety systems. Sci. J. 2012, 32, 191–195. [Google Scholar]
- Elvik, R.; Christensen, P.; Amundsen, A. Speed and Road Accidents. An Evaluation of the Power Model; Rep. No. 740/2004; The Institute of Transport Economics (TOI): Oslo, Norway, 2004. [Google Scholar]
- World Health Organization. Road Traffic Injuries. 2018. Available online: https://www.who.int/en/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 8 July 2019).
- Winter, K. Research Links Speed Increases With Increased Accidents and Accident Severity, Though Lower Speed Increases Only Effect Crashes Marginally; VDOT Research Library: Charlottesville, VA, USA, 2008. [Google Scholar]
- Evans, L. Traffic Safety. 2004. Available online: http://www.scienceservingsociety.com/traffic-safety.htm (accessed on 8 July 2019).
- Krol, M. Road Accidents in Poland in the Years 2006–2015. World Sci. News 2016, 48, 222–232. [Google Scholar]
- TNS Pentor. Przekraczanie prȩdkości [Speeding]. 2011. Available online: www.krbrd.gov.pl/files/file_add/download/26_file_add-2.pdf (accessed on 8 July 2019).
- TranBC Ministry of Transportation and Infrastructure Online British Columbia. Keep Right, Let Others Pass Law is Now Official on BC Highways. 2015. Available online: https://www.tranbc.ca/2015/06/15/keep-right-let-others-pass-law-is-now-official-on-bc-highways/ (accessed on 8 July 2019).
- TRIMIS Transport Research and Innovation Monitoring and Information System. PROJECT The Speed of Vehicles in Poland in 2015. 2015. Available online: https://trimis.ec.europa.eu/project/speed-vehicles-poland-2015#tab-docs (accessed on 8 July 2019). (In Polish).
- Fridman, L. Deep Learning for Understanding Driver Behavior in 275,000 Miles of Semi-Autonomous Driving Data; Seminar, Human-Computer Interaction Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2017. [Google Scholar]
- Kilicarslan, M.; Zheng, J.Y. Visualizing driving video in temporal profile. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 1263–1269. [Google Scholar]
- Grengs, J.; Wang, X.; Kostyniuk, L. Using GPS Data to Understand Driving Behavior. J. Urban Technol. 2008, 15, 33–53. [Google Scholar] [CrossRef]
- Fugiglando, U.; Massaro, E.; Santi, P.; Milardo, S.; Abida, K.; Stahlmann, R.; Netter, F.; Ratt, C. Driving Behavior Analysis through CAN Bus Data in an Uncontrolled Environment. arXiv 2017, arXiv:1710.04133v1. [Google Scholar] [CrossRef]
- Liu, H.; Taniguchi, T.; Tanaka, Y.; Takenaka, K.; Bando, T. Visualization of Driving Behavior Based on Hidden Feature Extraction by Using Deep Learning. IEEE Trans. Intell. Transp. Syst. 2011, 18, 2477–2489. [Google Scholar] [CrossRef]
- Eboli, L.; Mazzulla, G.; Pungillo, G. Combining speed and acceleration to define car users’ safe or unsafe driving behaviour. Transp. Res. Part C Emerg. Technol. 2016, 68, 113–125. [Google Scholar] [CrossRef]
- López, J.R.; González, L.C.; Wahlström, J.; Montes y Gómez, M.; Trujillo, L.; Ramírez-Alonso, G. A Genetic Programming Approach for Driving Score Calculation in the Context of Intelligent Transportation Systems. IEEE Sens. J. 2018, 18, 7183–7192. [Google Scholar] [CrossRef]
- Arhin, S.A.; Eskandarian, A. Driver behaviour models for a driving simulator-based intelligent speed adaptation system. WIT Trans. Built Environ. 2009, 107, 185–198. [Google Scholar]
- Neptis, S.A. Yanosik.pl. 2019. Available online: https://yanosik.pl/ (accessed on 8 July 2019).
- Agora, S.A. Moto.pl. Fotoradary zmniejszaja̧ bezpieczeństwo na drogach [Traffic Enforcement Cameras Decrease Road Safety]. 2010. Available online: http://moto.pl/Porady/1,115890,8169018,Fotoradary_zmniejszaja_bezpieczenstwo_na_drogach.html (accessed on 8 July 2019).
- Høye, A. Speed cameras, section control, and kangaroo jumps—A meta-analysis. Accid. Anal. Prev. 2014, 73, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Marciano, H.; Setter, P.; Norman, J. Overt vs. covert speed cameras in combination with delayed vs. immediate feedback to the offender. Accid. Anal. Prev. 2015, 79, 231–240. [Google Scholar] [CrossRef]
- TomTom International BV. TomTom Traffic Index. 2019. Available online: www.tomtom.com/en_gb/trafficindex/ (accessed on 8 July 2019).
- Ginzburg, C.; Raphael, A.; Weinshall, D. A Cheap System for Vehicle Speed Detection. arXiv 2015, arXiv:1501.06751v1. [Google Scholar]
- US Department of Transportation, Federal Highway Administration. Traffic Detector Handbook: Third Edition—Volume I. 2006. Available online: https://www.fhwa.dot.gov/publications/research/operations/its/06108/06108.pdf (accessed on 8 July 2019).
- US Department of Transportation, Federal Highway Administration. Traffic Detector Handbook: Third Edition—Volume II. 2006. Available online: https://www.fhwa.dot.gov/publications/research/operations/its/06139/06139.pdf (accessed on 8 July 2019).
- Pretorius, J.F.W.; Steyn, B.M. The use of pattern recognition algorithms in an Automatic Vehicle Identification system. In Computers in Railways; WIT Press: Chilworth, UK, 2004; pp. 371–379. [Google Scholar]
- Borkar, P.; Malik, L.G. Acoustic Signal based Traffic Density State Estimation using Adaptive Neuro-Fuzzy Classifier. Paper presented at IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Hyderabad, India, 7–10 July 2013. [Google Scholar]
- Koops, H.V.; Franchetti, F. An Ensemble Technique for Estimating Vehicle Speed and Gear Position from Acoustic Data. Paper presented at IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 422–426. [Google Scholar]
- Almaadeed, N.; Asim, M.; Al-Maadeed, S.; Bouridane, A.; Beghdadi, A. Automatic Detection and Classification of Audio Events for Road Surveillance Applications. 2018, 18, 1858. [Google Scholar] [CrossRef]
- Kubera, E.; Wieczorkowska, A.; Słowik, T.; Kuranc, A.; Skrzypiec, K. Audio-Based Speed Change Classification for Vehicles. In New Frontiers in Mining Complex Patterns NFMCP 2016; LNCS 10312; Springer: Cham, Switzerland, 2017; pp. 54–68. [Google Scholar]
- Tyagi, V.; Kalyanaraman, S.; Krishnapuram, R. Vehicular Traffic Density State Estimation Based on Cumulative Road Acoustics. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1156–1166. [Google Scholar] [CrossRef]
- Dandare, S.N.; Dudul, S.V. Multiple Fault Detection in typical Automobile Engines: A Soft computing approach. WSEAS Trans. Signal Process. 2014, 10, 254–262. [Google Scholar]
- Kabiri, P.; Ghaderi, H. Automobile Independent Fault Detection based on Acoustic Emission Using Wavelet. Paper presented at Singapore International NDT Conference & Exhibition, Singapore, 3–4 November 2011. [Google Scholar]
- Siegel, J.; Kumar, S.; Ehrenberg, I.; Sarma, S. Engine Misfire Detection with Pervasive Mobile Audio. In ECML PKDD 2016, Part III; LNAI 9853; Springer: Cham, Switzerland, 2016; pp. 26–241. [Google Scholar]
- Ahn, I.S.; Bae, S.G.; Bae, M.J. A Study on Fault Diagnosis of Vehicles using the Sound Signal in Audio Signal Processing. J. Eng. Technol. 2015, 3, 89–95. [Google Scholar]
- Navea, R.F.; Sybingco, E. Design and Implementation of an Acoustic Based Car Engine Fault Diagnostic System in the Android Platform. Paper presented at International Research Conference in Higher Education, Manila, Philippines, 3–4 October 2013. [Google Scholar]
- Alexandre, E.; Cuadra, L.; Salcedo-Sanz, S.; Pastor-Sánchez, A.; Casanova-Mateo, C. Hybridizing extreme learning machines and genetic algorithms to select acoustic features in vehicle classification applications. Neurocomputing 2015, 152, 58–68. [Google Scholar] [CrossRef]
- Erb, S. Classification of Vehicles Based on Acoustic Features. Unpublished Master’s Thesis, Institute for Technical Informatics, Graz University of Technology, Graz, Austria, 2007. [Google Scholar]
- George, J.; Cyril, A.; Koshy, B.I.; Mary, L. Exploring sound signature for vehicle detection and classification using ANN. Int. J. Soft Comput. 2013, 4, 29–36. [Google Scholar] [CrossRef]
- Mayvan, A.D.; Beheshti, S.A.; Masoom, M.H. Classification of vehicles based on audio signals using quadratic discriminant analysis and high energy feature vectors. Int. J. Soft Comput. 2015, 6, 53–64. [Google Scholar]
- Wieczorkowska, A.; Kubera, E.; Słowik, T.; Skrzypiec, K. Spectral features for audio based vehicle and engine classification. J. Intell. Inf. Syst. 2018, 50, 265–290. [Google Scholar] [CrossRef]
- Evans, N. Automated Vehicle Detection and Classification using Acoustic and Seismic Signals. Ph.D. Thesis, Department of Electronics, University of York, York, UK, 2010. [Google Scholar]
- Giannakopoulos, T. pyAudioAnalysis: An Open-Source Python Library for Audio Signal Analysis. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- McEnnis, D.; McKay, C.; Fujinaga, I. jAudio: Additions and Improve ments. Paper presented at 7th International Conference on Music Information Retrieval ISMIR, Victoria, BC, Canada, 8–12 October 2006. [Google Scholar]
- Moving Picture Experts Group. MPEG-7. 2001. Available online: http://mpeg.chiariglione.org/standards/mpeg-7 (accessed on 8 July 2019).
- Tzanetakis, G.; Cook, P. MARSYAS: A framework for audio analysis. Organised Sound 2000, 4, 169–175. [Google Scholar] [CrossRef]
- Choi, K.; Fazekas, G.; Sandler, M. Automatic tagging using deep convolutional neural networks. Paper presented at 17th International Society for Music Information Retrieval Conference, New York, NY, USA, 7–11 August 2016. [Google Scholar]
- McLoughlin, I.; Zhang, H.; Xie, Z.; Song, Y.; Xiao, W.; Phan, H. Continuous robust sound event classification using time-frequency features and deep learning. PLoS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Oramas, S.; Nieto, O.; Barbieri, F.; Serra, X. Multi-label Music Genre Classification from audio, text, and images using Deep Features. Paper presented at 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October2017. [Google Scholar]
- Wieczorkowska, A.; Kubera, E.; Koržinek, D.; Słowik, T.; Kuranc, A. Time-Frequency Representations for Speed Change Classification: A Pilot Study. Foundations of Intelligent Systems; ISMIS 2017, LNCS 10352; Springer: Cham, Switzerland, 2017; pp. 404–413. [Google Scholar]
- Pons, J.; Lidy, T.; Serra, X. Experimenting with musically motivated convolutional neural networks in Content-Based Multimedia Indexing. Paper presented at 2016 14th International Workshop on Content-Based Multimedia Indexing (CBMI), Bucharest, Romania, 15–17 June 2016. [Google Scholar]
- Heittola, T. (2003). Automatic Classification of Music Signals. Master’s Thesis, Tampere University of Technology, Tampere, Finland, 2003. [Google Scholar]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-Series Classification with COTE: The Collective of Transformation-Based Ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Keogh, E. Fast-Shapelets: A Scalable Algorithm for Discovering Time Series Shapelets. In Proceedings of the SIAM International Conference on Data Mining SDM13, Austin, TX, USA, 2–4 May 2013. [Google Scholar]
- Adobe. Adobe Audition. 2019. Available online: https://www.adobe.com/products/audition.html (accessed on 8 July 2019).
- R Development Core Team. R: A language and environment for statistical computing. In R Foundation for Statistical Computing; R Development Core Team: Vienna, Austria, 2008. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]


| Method | RF | SVML | SVMQ | SVMR |
|---|---|---|---|---|
| Method1 | 84.9% | 72.9% | 74.1% | 74.5% |
| Method2 | 80.4% | 74.1% | 75.9% | 77.6% |
| Method3 | 80.7% | 75.3% | 75.6% | 77.8% |
| Method4 | 89.8% | 89.4% | 89.3% | 89.0% |
| Method5 | 81.3% | 75.0% | 76.6% | 78.5% |
| Method6 | 81.7% | 74.6% | 76.1% | 80.3% |
| Method7 | 87.3% | 82.6% | 84.2% | 88.3% |
| Method8 | 83.1% | 76.5% | 77.8% | 81.2% |
| Method9 | 90.3% | 85.6% | 87.4% | 88.3% |
| Method | RF | SVML | SVMQ | SVMR | MLP |
|---|---|---|---|---|---|
| Basic 85 + Method4 | 92.6% | 89.7% | 89.8% | 91.8% | 92.6% |
| Basic 85 + Method9 | 91.8% | 86.2% | 86.5% | 91.5% | 89.7% |
| Method | Features | RF | SVML | SVMQ | SVMR |
|---|---|---|---|---|---|
| NS, no selection | 595 | 85.6% | 87.5% | 88.2% | 90.2% |
| SM3, no selection | 595 | 85.7% | 87.1% | 87.8% | 88.9% |
| SM5, no selection | 595 | 85.9% | 86.1% | 87.1% | 89.9% |
| SM7, no selection | 595 | 86.3% | 86.4% | 87.3% | 90.1% |
| No smoothing, SEL1 | 217 | 88.4% | 84.7% | 86.7% | 88.6% |
| SM3, SEL1 | 283 | 88.5% | 85.3% | 86.8% | 89.7% |
| SM5, SEL1 | 340 | 87.8% | 82.7% | 85.1% | 89.2% |
| SM7, SEL1 | 364 | 87.4% | 85.3% | 87.0% | 89.6% |
| No smoothing, SEL2 | 91 | 90.8% | 85.7% | 88.3% | 90.7% |
| SM3, SEL2 | 97 | 90.8% | 85.1% | 88.2% | 91.0% |
| SM5, SEL2 | 100 | 90.6% | 84.5% | 87.1% | 90.6% |
| SM7, SEL2 | 106 | 90.6% | 84.5% | 86.9% | 90.5% |
| SEL3 | 345 | 86.4% | 88.2% | 89.2% | 91.3% |
| Classified as: | Acceleration | Deceleration | Stable Speed |
|---|---|---|---|
| Acceleration | 216 | 0 | 6 |
| Deceleration | 0 | 216 | 12 |
| Stable speed | 5 | 11 | 172 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubera, E.; Wieczorkowska, A.; Kuranc, A.; Słowik, T. Discovering Speed Changes of Vehicles from Audio Data. Sensors 2019, 19, 3067. https://doi.org/10.3390/s19143067
Kubera E, Wieczorkowska A, Kuranc A, Słowik T. Discovering Speed Changes of Vehicles from Audio Data. Sensors. 2019; 19(14):3067. https://doi.org/10.3390/s19143067
Chicago/Turabian StyleKubera, Elżbieta, Alicja Wieczorkowska, Andrzej Kuranc, and Tomasz Słowik. 2019. "Discovering Speed Changes of Vehicles from Audio Data" Sensors 19, no. 14: 3067. https://doi.org/10.3390/s19143067
APA StyleKubera, E., Wieczorkowska, A., Kuranc, A., & Słowik, T. (2019). Discovering Speed Changes of Vehicles from Audio Data. Sensors, 19(14), 3067. https://doi.org/10.3390/s19143067






