A Generalized SDP Multi-Objective Optimization Method for EM-Based Microwave Device Design
Abstract
1. Introduction
2. GSDP Algorithm
2.1. Problem Formulation
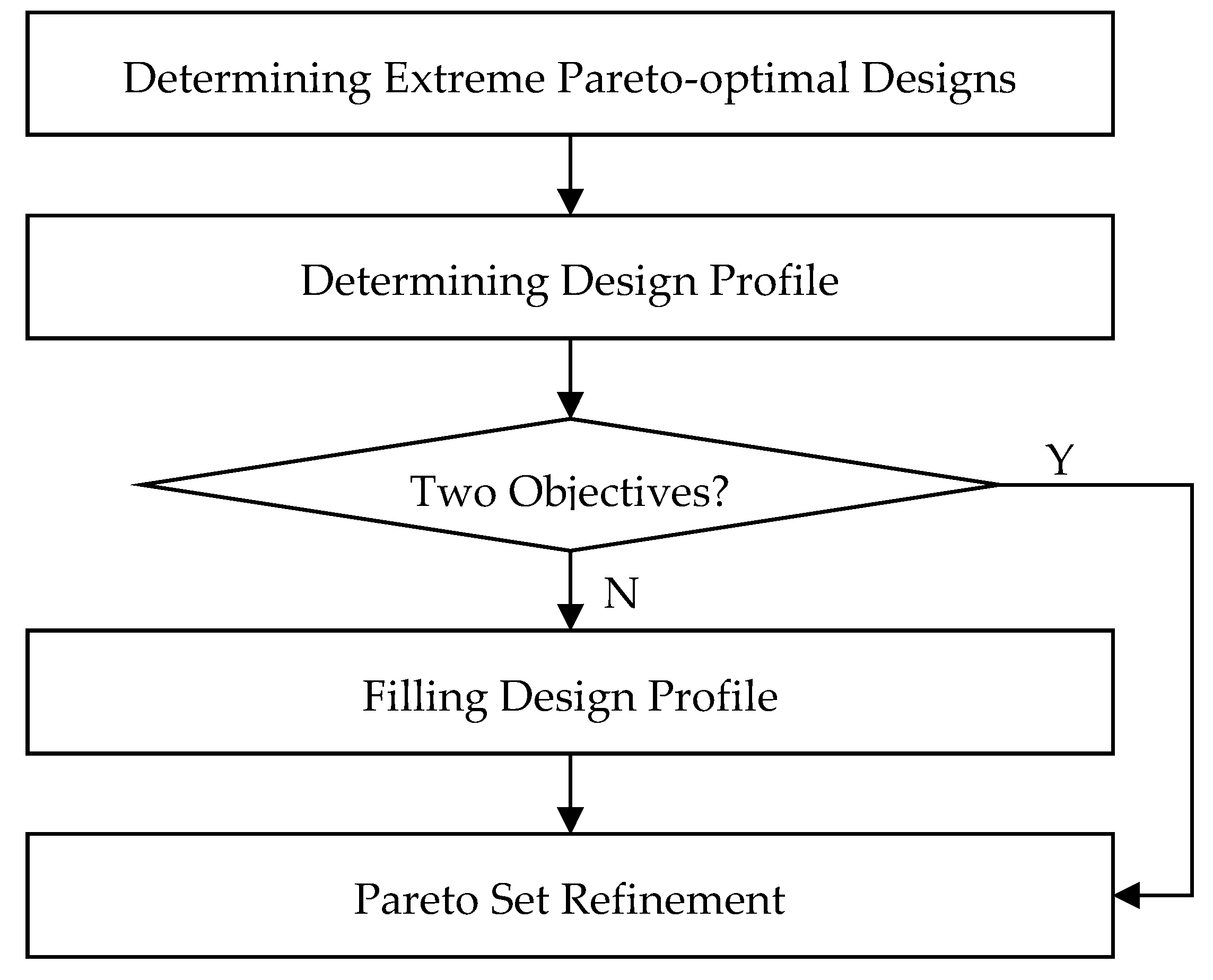
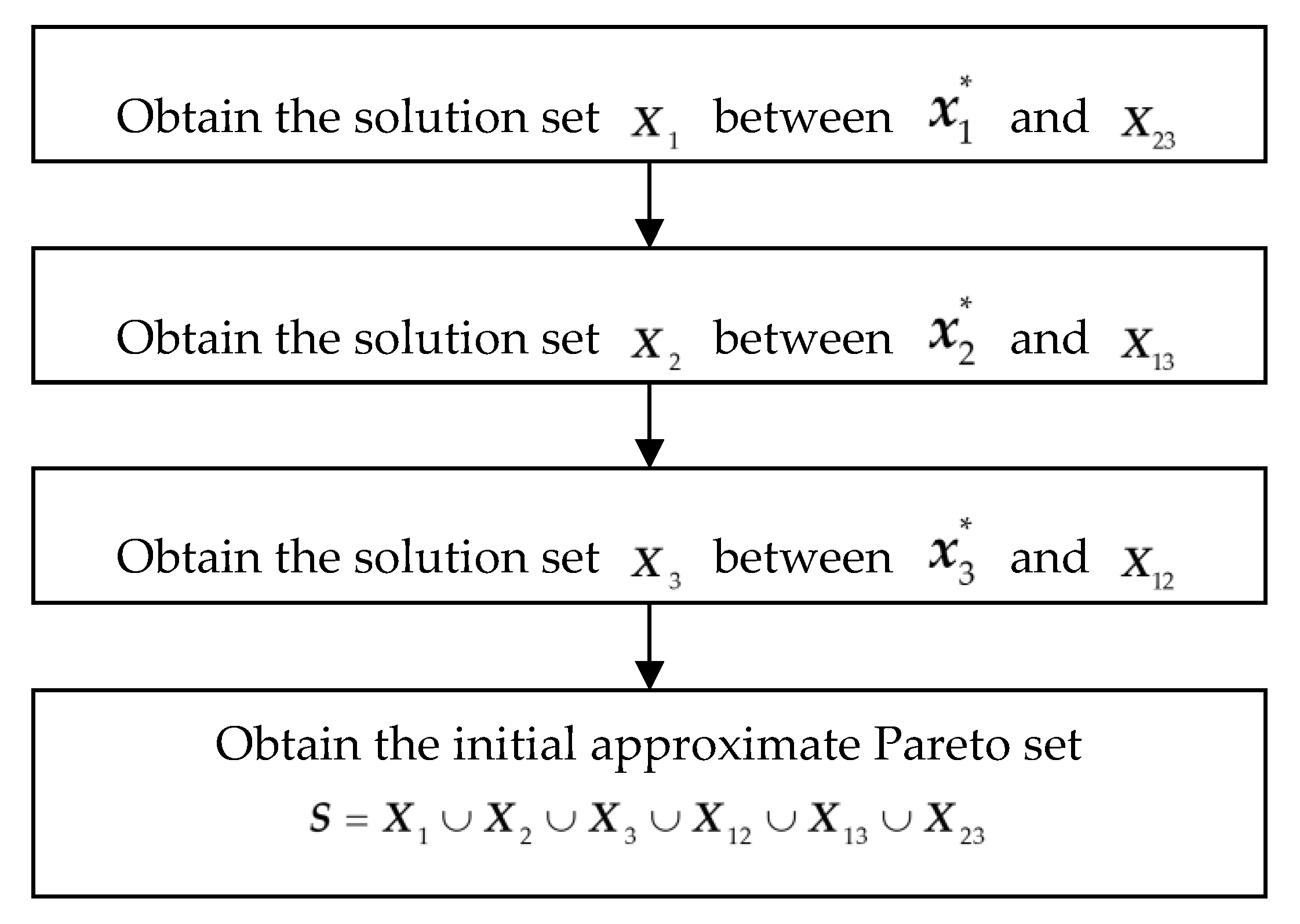
2.2. Framework of GSDP Algorithm
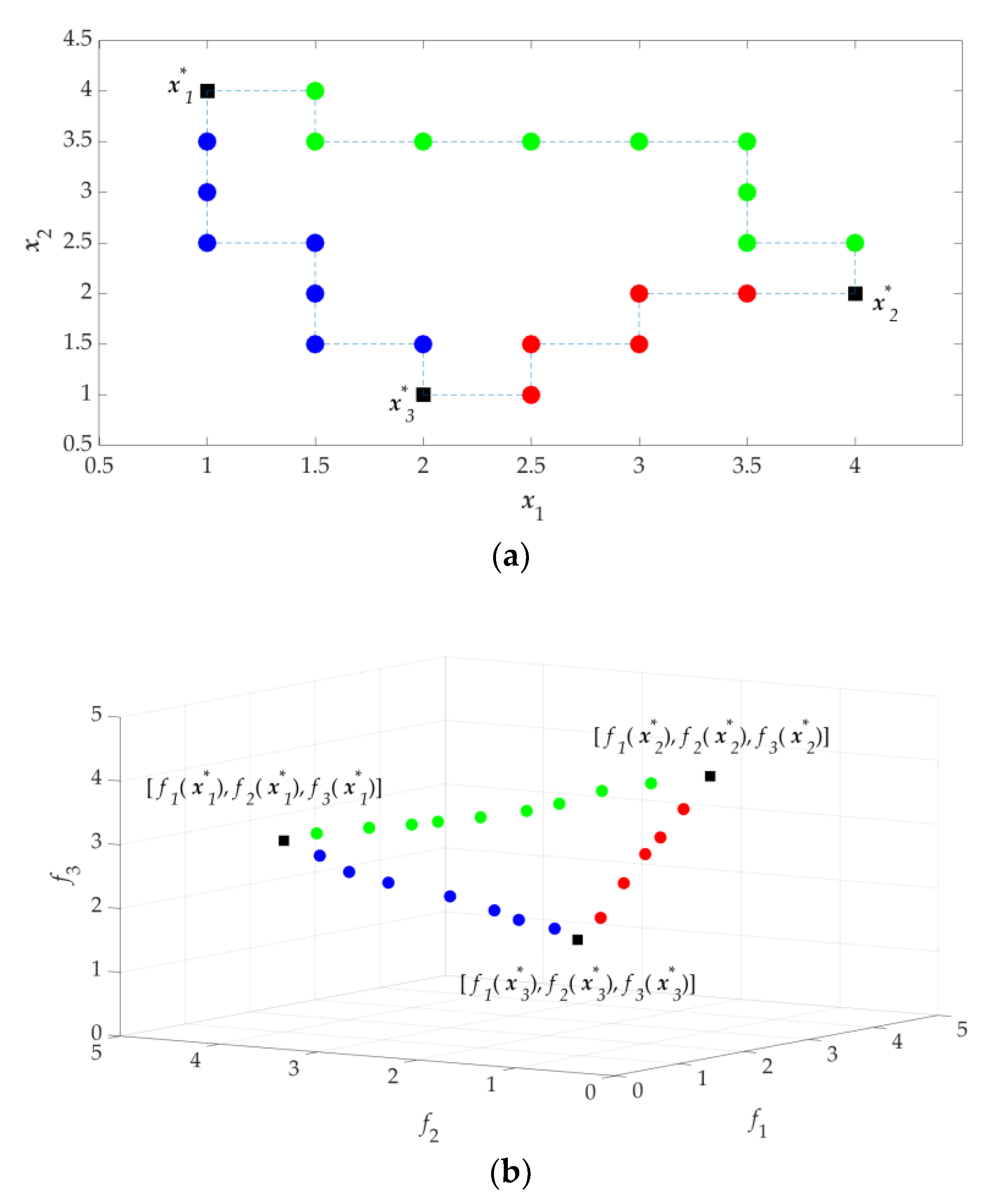
2.3. Determining Extreme Pareto-Optimal Designs
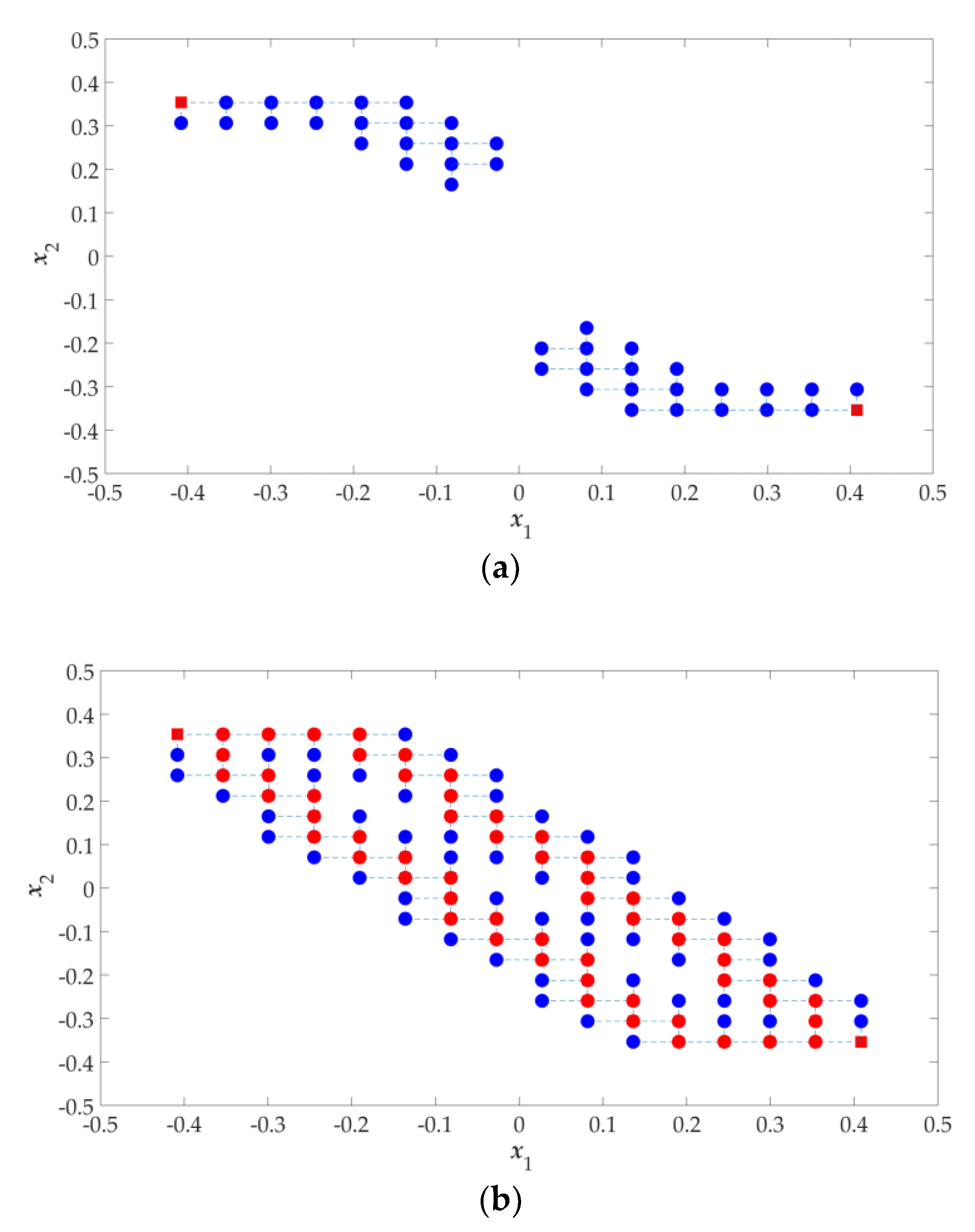
2.4. Determining Design Profile
- Determine the design space; the lower bound vector lb and upper bound vector ub can be defined as follows:where and are the jth variables of vectors lb and ub respectively; and are the jth variables of vectors and respectively.
- Set the perturbation size vector d = [d1, …, dn]T.
- Let the current points and .
- Evaluate n perturbations (k = 1, …, n) around (towards only) and select the one that leads to the largest improvement with regard to the second objective F2 as the current point .
- Evaluate n perturbations (k = 1, …, n) around (towards only) and select the one that leads to the largest improvement with regard to the first objective F1 as the current point .
- If or exceeds the design space, the process is stopped. If both and are in the design space, return to step 4.
2.5. Filling Design Profile
- Let be the ith solution in , .
- If i > N, the process stops, where N is the number of solutions in .
- Determine the design subspace, the lower bound vector lb and upper bound vector ub can be defined as follows:where and are the jth variables of vectors lb and ub, respectively, and and are the jth variables of vectors and , respectively, where is the ith solution in .
- Set the perturbation size vector d = [d1, …, dn]T, ; K is up to the user.
- Let the current points and .
- Evaluate n perturbations (k = 1, …, n) around (towards only) and select the one that leads to the largest improvement with regard to as the current point .
- Evaluate n perturbations (k = 1, …, n) around (towards only) and select the one that leads to the largest improvement with regard to as the current point .
- If and exceeds the design subspace, , return to step 2. If both and are still in the design space, return to step 6.
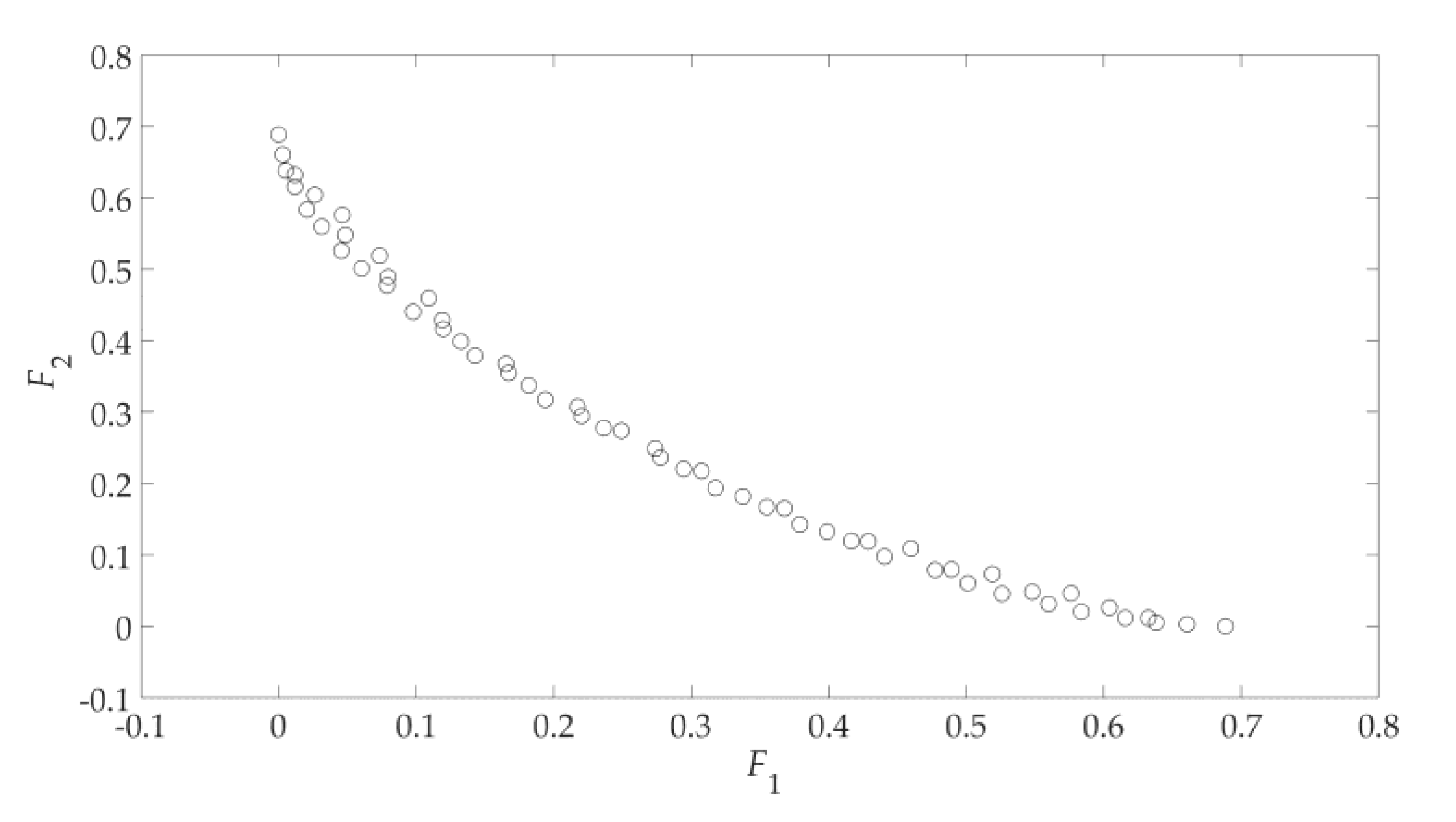
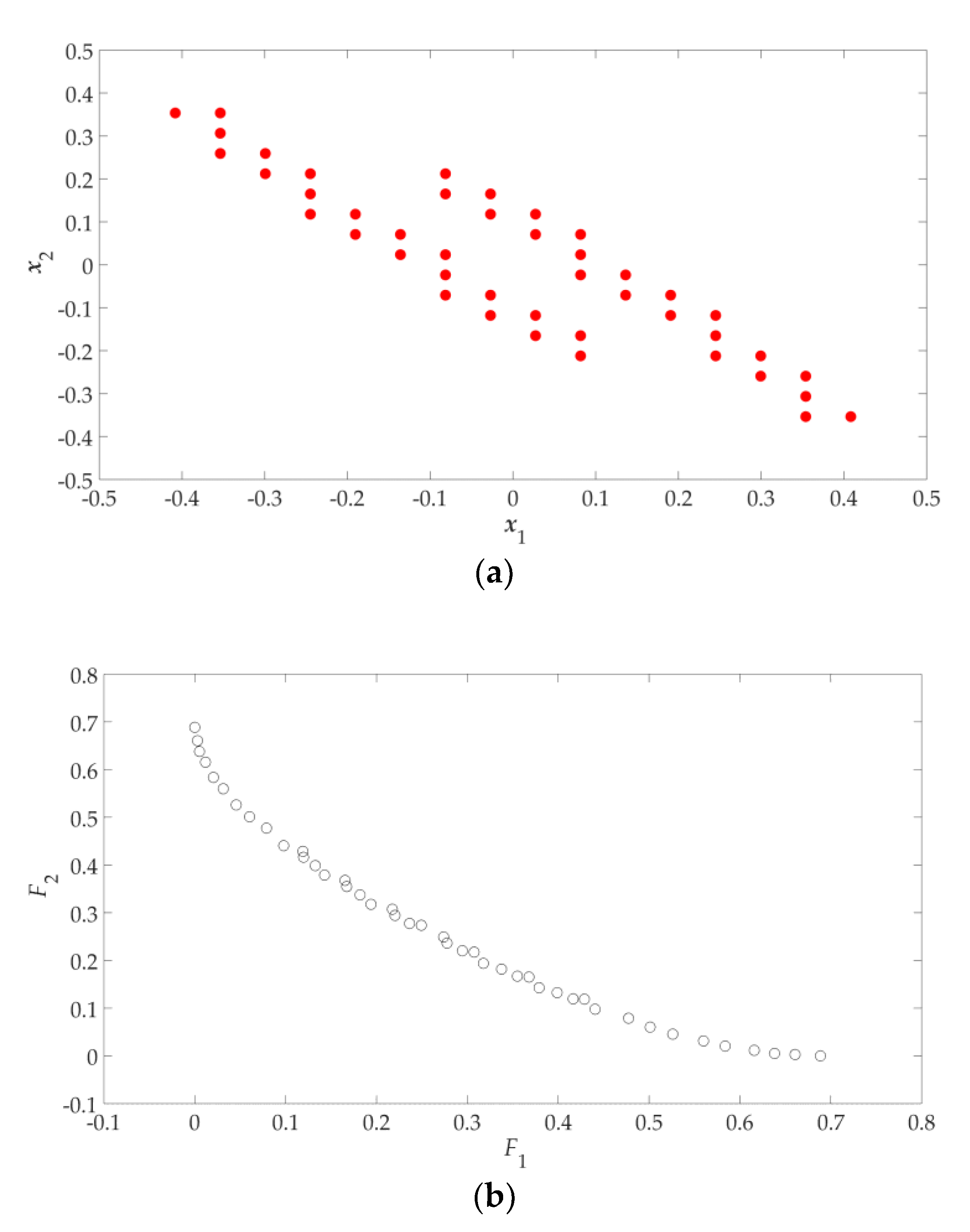
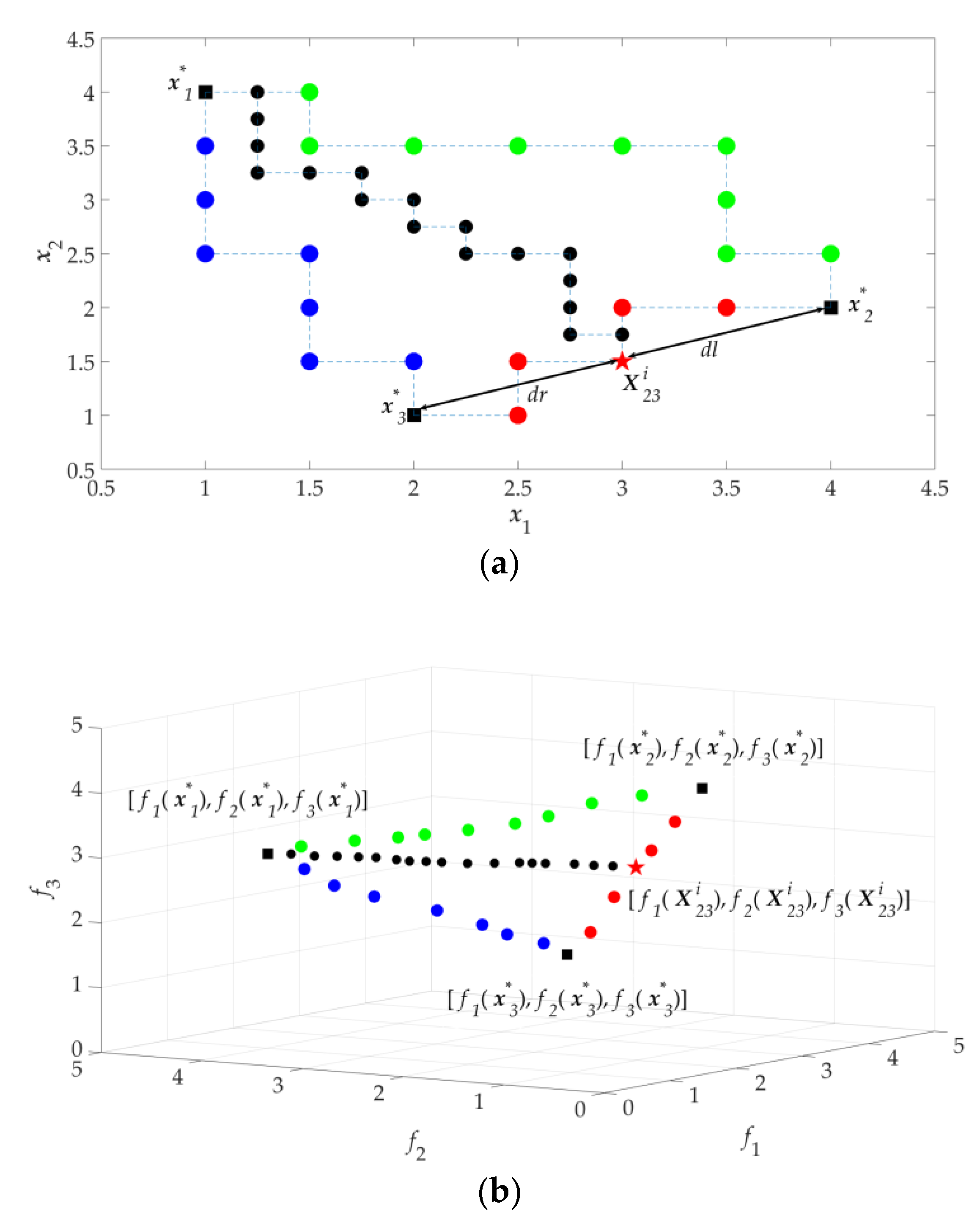
2.6. Pareto Set Refinement
2.7. Evaluation
3. Illustration and Verification Examples
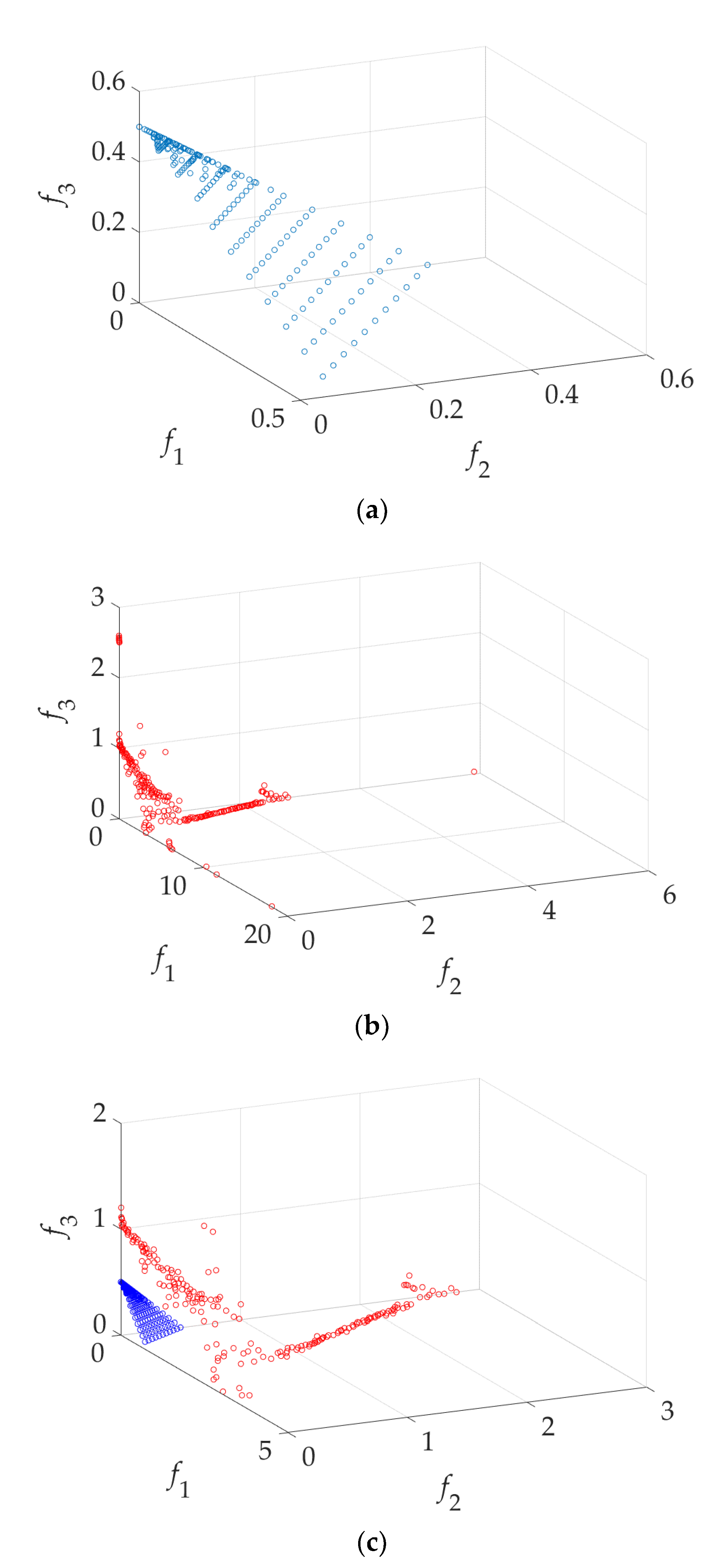
3.1. Design Case 1: DTLZ1
3.2. Design Case 2: DTLZ2
3.3. Design Case Validation Summary
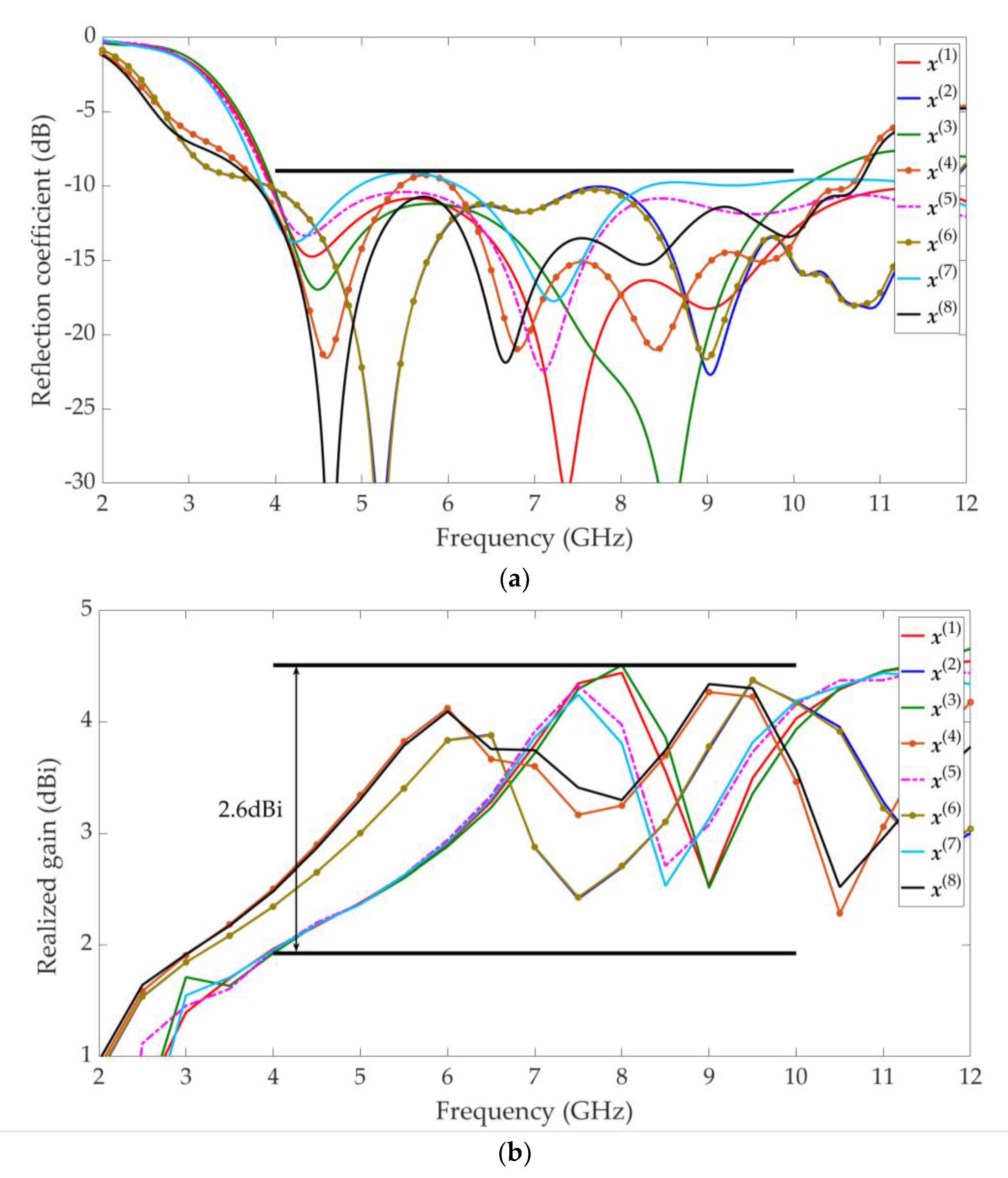
4. UWB Antenna Multi-Objective Design Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chadebec, O.; Coulomb, J.L.; Janet, F. A review of magnetostatic moment method. IEEE Trans. Magn. 2006, 42, 515–520. [Google Scholar] [CrossRef]
- Wu, Y.; Wassell, I. Introduction to the Segmented Finite-Difference Time-Domain Method. IEEE Trans. Magn. 2009, 45, 1364–1367. [Google Scholar]
- Dennis, J.E. Quasi-Newton Methods, Motivation and Theory. Siam Rev. 1977, 19, 46–89. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A.; Zieniutycz, W. Expedited EM-Driven Multiobjective Antenna Design in Highly Dimensional Parameter Spaces, Motivation and Theory. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 631–634. [Google Scholar] [CrossRef]
- Hsieh, L.H.; Chang, K. Compact, low insertion-loss, sharp-rejection, and wide-band microstrip bandpass filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 1241–1246. [Google Scholar] [CrossRef]
- Koziel, S.; Ogurtsov, S. Multi-Objective Design of Antennas Using Variable-Fidelity Simulations and Surrogate Models. IEEE Trans. Antennas Propag. 2013, 61, 5931–5939. [Google Scholar] [CrossRef]
- Coello, C.A.C. Evolutionary Multi-Objective Optimization a Historical View of the Field. IEEE Comput. Int. Mag. 2006, 1, 28–36. [Google Scholar] [CrossRef]
- Rütschlin, M.; Wittig, T. State of the Art Antenna Simulation with CST STUDIO SUITE. In Proceedings of the 2015 9th European Conference on Antennas and Propagation, Lisbon, Portugal, 7–12 April 2015. [Google Scholar]
- Dar, S.H.; Ahmed, Z.; Ihsan, M.B. Characterization of Waveguide Slots Using Full Wave EM Analysis Software HFSS. In Proceedings of the 2008 IEEE International Multitopic Conference, Karachi, Pakistan, 23–24 December 2008. [Google Scholar]
- Torczon, V. On the Convergence of Pattern Search Algorithms. SIAM J. Optim. 1997, 7, 1–25. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Sha, D.; Lin, H.-H. A multi-objective PSO for job-shop scheduling problems. Expert Syst. Appl. 2010, 37, 1065–1070. [Google Scholar] [CrossRef]
- Leal-Romo, F.; Moreyra-González, R.; Rayas-Sánchez, J.E. HFSS Automated Driver Based on Non-GUI Scripting for EM-Based Design of High-Frequency Circuits. In Proceedings of the 2012 IEEE 3rd Latin American Symposium on Circuits and Systems (LASCAS), Playa del Carmen, Mexico, 29 February–2 March 2012. [Google Scholar]
- Bandler, J.W.; Cheng, Q.S.; Gebre-Mariam, D.H.; Madsen, K.; Pedersen, F.; Sondergaard, J. EM-Based Surrogate Modeling and Design Exploiting Implicit, Frequency and Output Space Mappings. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Philadelphia, PA, USA, 10–15 July 2003. [Google Scholar]
- Rayas-Sánchez, J.E.; Estrada-Arámbula, E. EM-Based Design Optimization of Microstrip Lines Traversing a Rectangular Gap in the Reference Plane. In Proceedings of the 2012 International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Seville, Spain, 19–21 September 2012. [Google Scholar]
- Koziel, S.; Sigurasson, A.T. Multi-Objective Design of Antennas Using Variable-Fidelity EM Models and Constrained Surrogates. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar]
- Koziel, S.; Ogurtsov, S.; Zieniutycz, W.; Bekasiewicz, A. Design of a Planar UWB Dipole Antenna with an Integrated Balun Using Surrogate-Based Optimization. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 366–369. [Google Scholar] [CrossRef]
- Akinsolu, M.O.; Liu, B.; Grout, V.; Lazaridis, P.I.; Mognaschi, M.E.; Di Barba, P. A Parallel Surrogate Model Assisted Evolutionary Algorithm for Electromagnetic Design Optimization. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 93–105. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, C.; Na, W.; Zhang, J.; Zhang, W.; Zhang, Q.J. Adaptive Feature Zero Assisted Surrogate-Based EM Optimization for Microwave Filter Design. IEEE Microw. Wirel. Components Lett. 2019, 29, 2–4. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Multi-Objective Antenna Design by Means of Sequential Domain Patching. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1089–1092. [Google Scholar] [CrossRef]
- Lee, L.H.; Chew, E.P.; Teng, S.; Goldsman, D. Finding the non-dominated Pareto set for multi-objective simulation models. IIE Trans. 2010, 42, 656–674. [Google Scholar] [CrossRef]
- Kim, I.; De Weck, O. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Optim. 2004, 29, 149–158. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Multi-objective design optimization of antenna structures using sequential domain patching with automated patch size determination. Eng. Optim. 2017, 50, 218–234. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Diversity Comparison of Pareto Front Approximations in Many-Objective Optimization. IEEE Trans. Cybern. 2014, 44, 2568–2584. [Google Scholar] [PubMed]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Multi-Objective Optimization Test Problems. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Koziel, S.; Bekasiewicz, A.; Szczepanski, S. Multi-objective design optimization of antennas for reflection, size, and gain variability using kriging surrogates and generalized domain segmentation. Int. J. RF Microw. Comput. Eng. 2018, 28, e21253. [Google Scholar] [CrossRef]
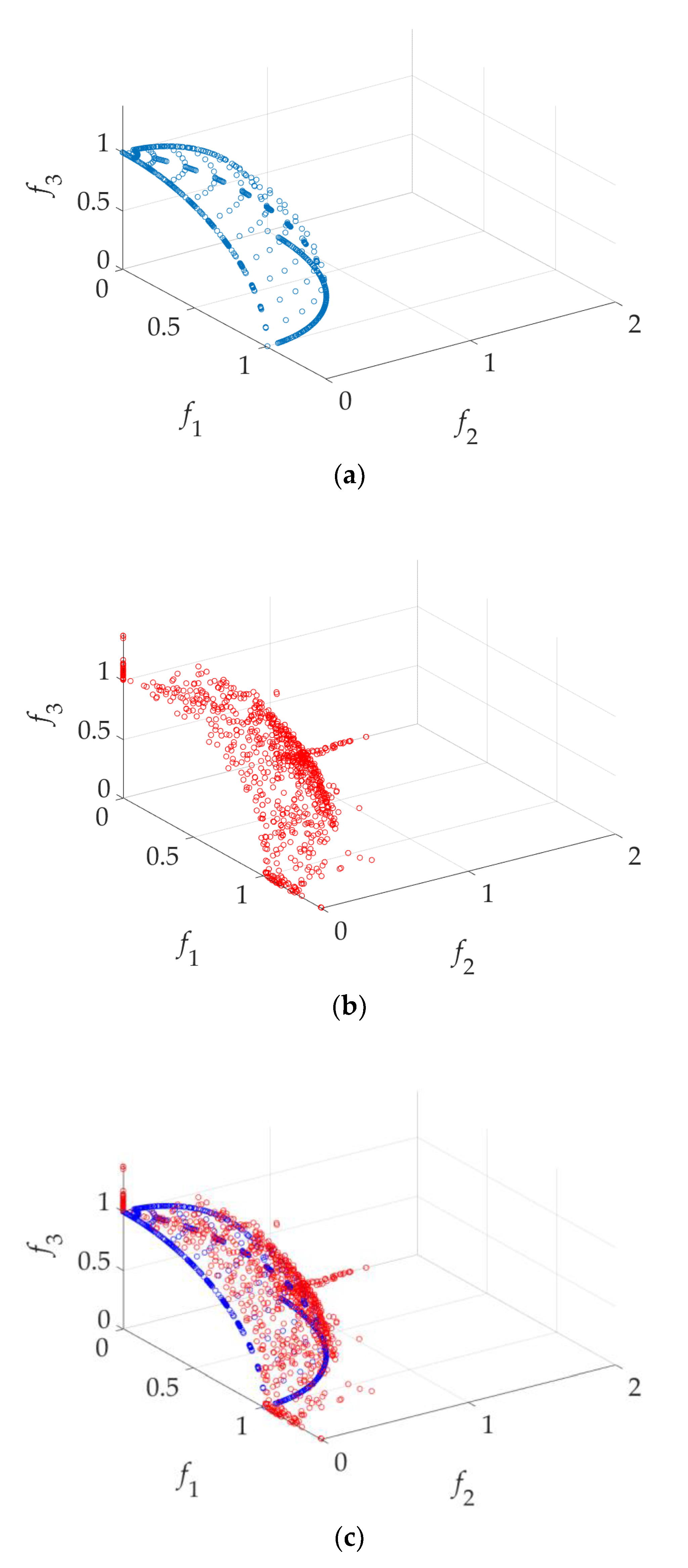
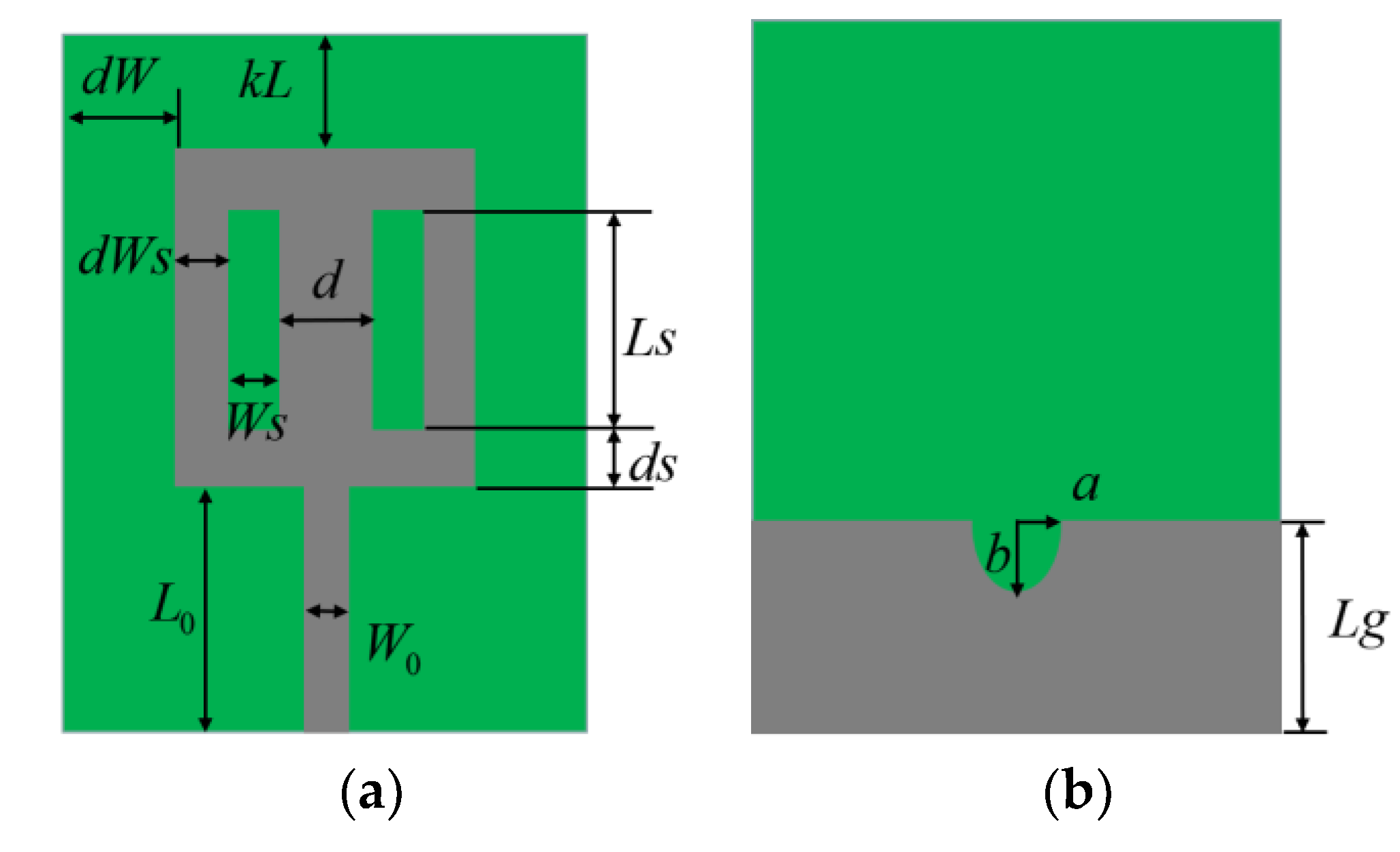
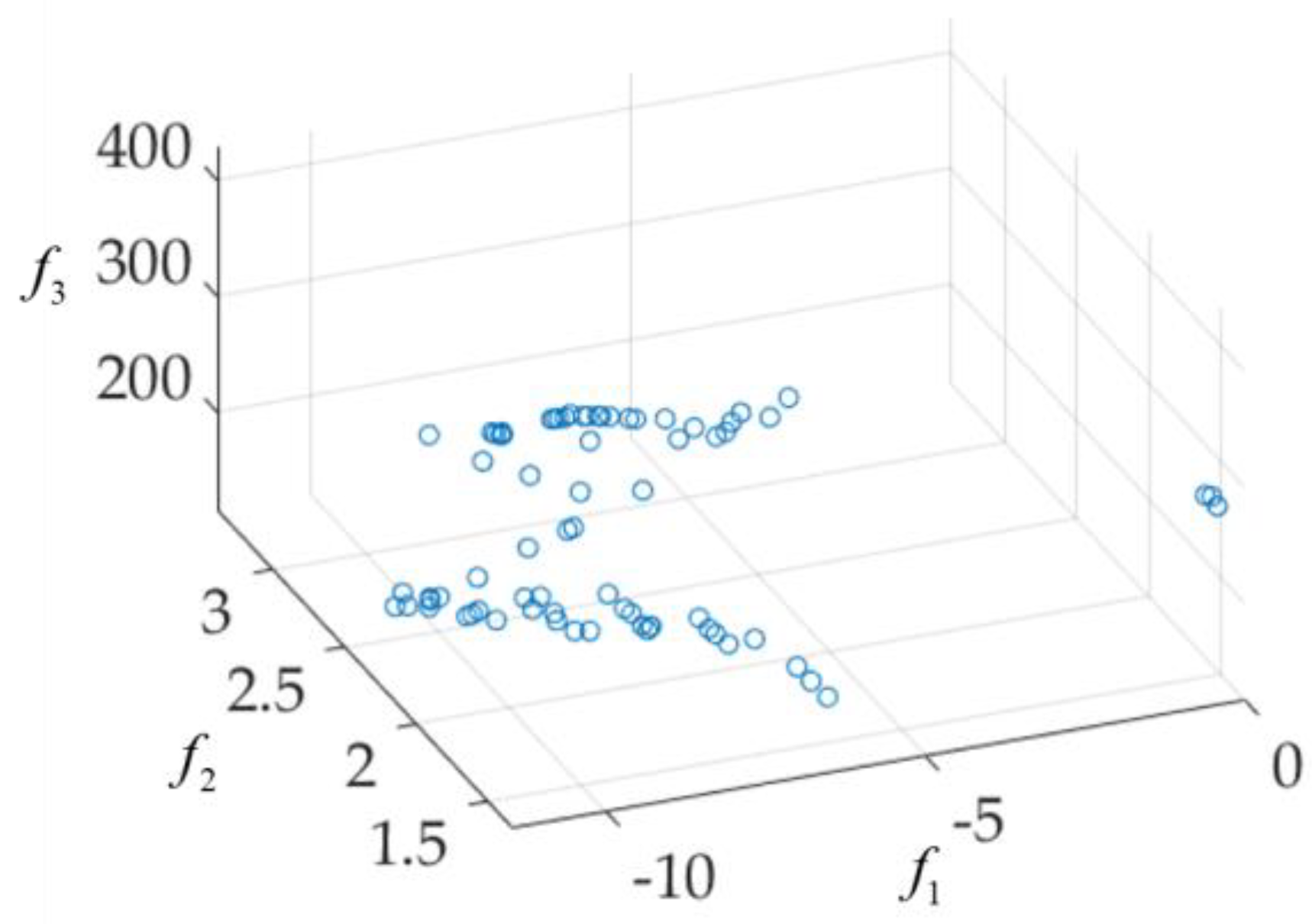
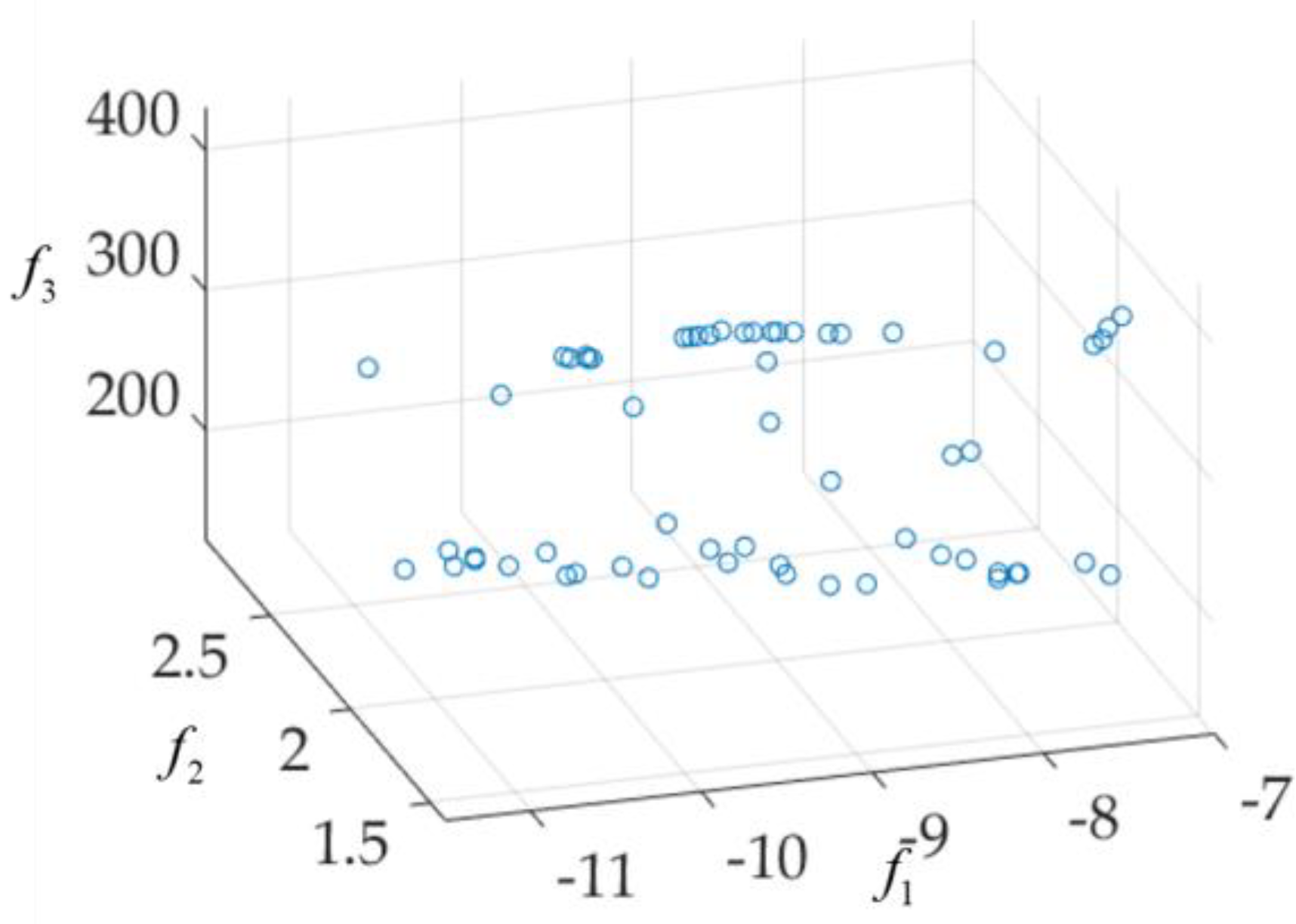
| Functions (Dimension of Design Parameter) | Number of Solutions in P1 or P2 | Function Evaluation Times Using GSDP (P1) | Function Evaluation Times Using NSGA-II (P2) | Time Saving | DCI (P1) | DCI (P2) |
|---|---|---|---|---|---|---|
| DTLZ1 (6) | 233 | 15,915 | 317,205 | 95% | 0.7667 | 0.2333 |
| DTLZ2 (9) | 833 | 21,806 | 806,820 | 97% | 0.4840 | 0.5426 |
| DTLZ1 (5) | 470 | 13,299 | 232,650 | 94% | 0.9424 | 0.0576 |
| DTLZ2 (11) | 348 | 10,043 | 124,236 | 92% | 0.4737 | 0.5533 |
| DTLZ3 (12) | 1921 | 58,338 | 1,192,941 | 95% | 0.9602 | 0.0398 |
| DTLZ4 (7) | 530 | 24,358 | 179,670 | 86% | 0.4148 | 0.6049 |
| −10.7307 | −10.0570 | −10.3724 | −9.2783 | −10.4177 | −10.2159 | −9.1132 | −10.7473 | |
| 2.4739 | 2.0232 | 2.5810 | 1.7619 | 2.369881 | 2.0293 | 2.2915 | 1.8562 | |
| 145.9946 | 347.8369 | 140.0131 | 369.7517 | 164.1404 | 350.5260 | 162.1286 | 353.8818 | |
| a | 1.1813 | 0.5991 | 1.1813 | 1.1149 | 1.1813 | 0.5991 | 1.1813 | 1.1149 |
| b | 0.3480 | 0.4793 | 0.3480 | 0.5310 | 0.3480 | 0.4793 | 0.3480 | 0.5310 |
| d | 3.0089 | 4.9893 | 2.3139 | 4.3989 | 2.3139 | 3.2057 | 2.3139 | 4.3989 |
| kL | 3.6562 | 6.4903 | 4.5111 | 6.2208 | 3.6562 | 6.4903 | 3.6562 | 6.2208 |
| ds | 0.9149 | 1.7809 | 0.6466 | 1.4515 | 0.6466 | 1.7809 | 0.6466 | 1.4515 |
| dW | 1.1315 | 2.0737 | 1.1315 | 2.3120 | 1.9185 | 2.0737 | 1.8398 | 1.9185 |
| dWs | 1.1168 | 1.1168 | 1.1168 | 1.3032 | 1.1789 | 2.0558 | 1.1168 | 1.3032 |
| L0 | 7.3929 | 9.5941 | 7.0745 | 11.9876 | 7.9143 | 9.5941 | 8.2712 | 12.5860 |
| Lg | 3.6096 | 6.2921 | 3.6096 | 8.6279 | 3.6096 | 6.2921 | 3.6096 | 8.6279 |
| Ls | 5.3438 | 8.8158 | 6.2574 | 8.0845 | 5.3438 | 8.8158 | 5.3438 | 8.0845 |
| Ws | 0.2531 | 0.4254 | 0.2531 | 0.5176 | 0.2531 | 0.4254 | 0.2531 | 0.5176 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Cheng, Q.S.; Koziel, S. A Generalized SDP Multi-Objective Optimization Method for EM-Based Microwave Device Design. Sensors 2019, 19, 3065. https://doi.org/10.3390/s19143065
Liu Y, Cheng QS, Koziel S. A Generalized SDP Multi-Objective Optimization Method for EM-Based Microwave Device Design. Sensors. 2019; 19(14):3065. https://doi.org/10.3390/s19143065
Chicago/Turabian StyleLiu, Ying, Qingsha S. Cheng, and Slawomir Koziel. 2019. "A Generalized SDP Multi-Objective Optimization Method for EM-Based Microwave Device Design" Sensors 19, no. 14: 3065. https://doi.org/10.3390/s19143065
APA StyleLiu, Y., Cheng, Q. S., & Koziel, S. (2019). A Generalized SDP Multi-Objective Optimization Method for EM-Based Microwave Device Design. Sensors, 19(14), 3065. https://doi.org/10.3390/s19143065






