Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment
Abstract
1. Introduction
2. Related Work
2.1. Point-Based Scan Matching
2.2. Feature-Based Scan Matching
2.3. Scan Matching Based on Mathematical Characteristics
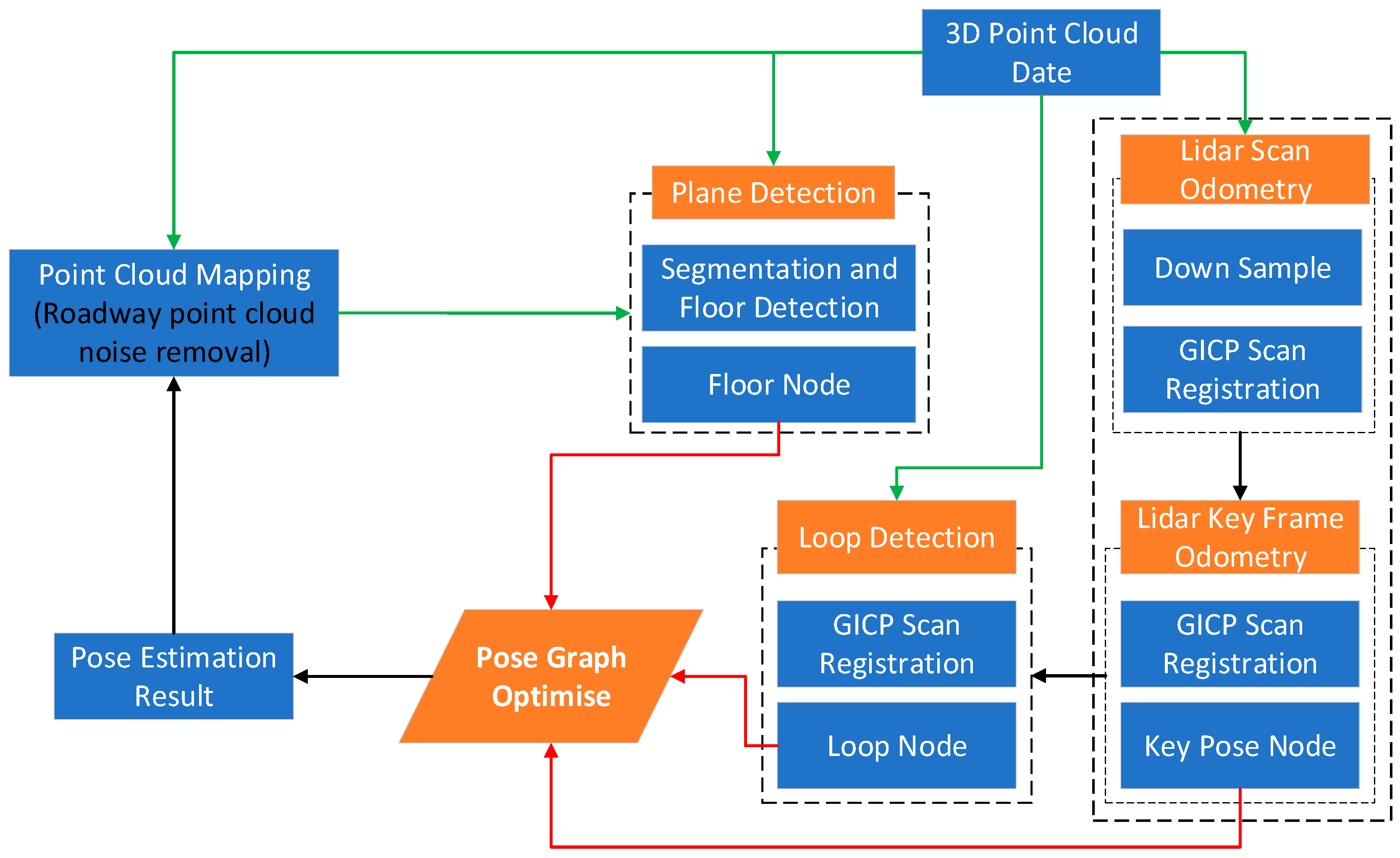
3. Simultaneous Localization and Mapping Framework
3.1. Overview
3.2. GICP Method Description
3.3. Laser Odometer
3.3.1. Laser Odometer between Consecutive Frames
3.3.2. Laser Odometer between Consecutive Key Frames
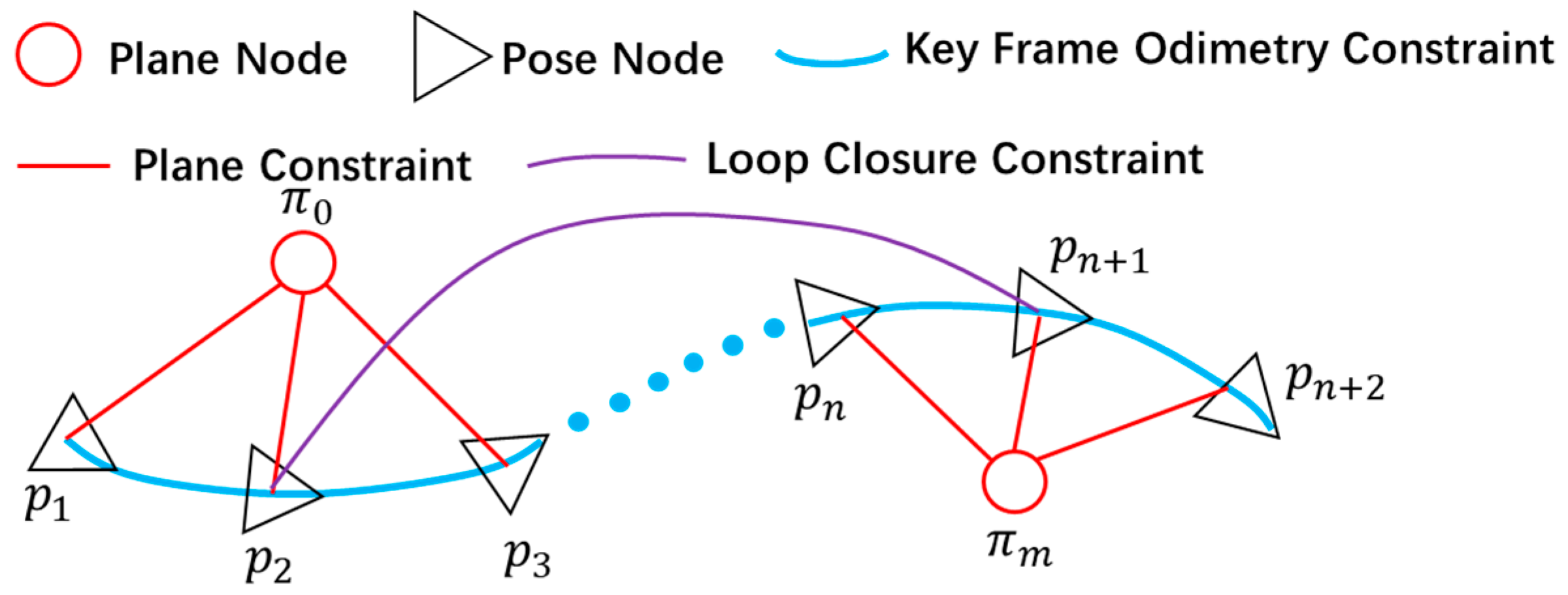
3.4. Graph SLAM Optimization
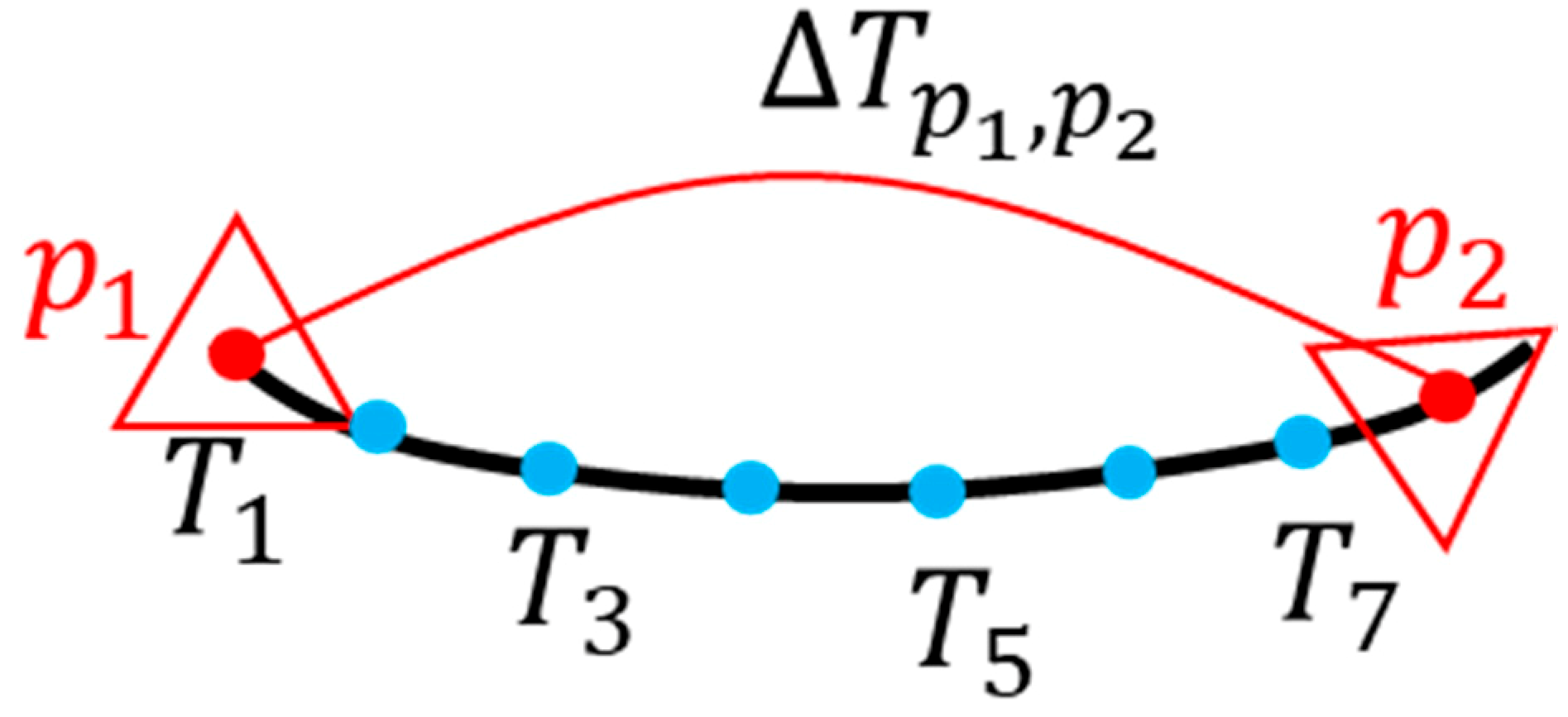
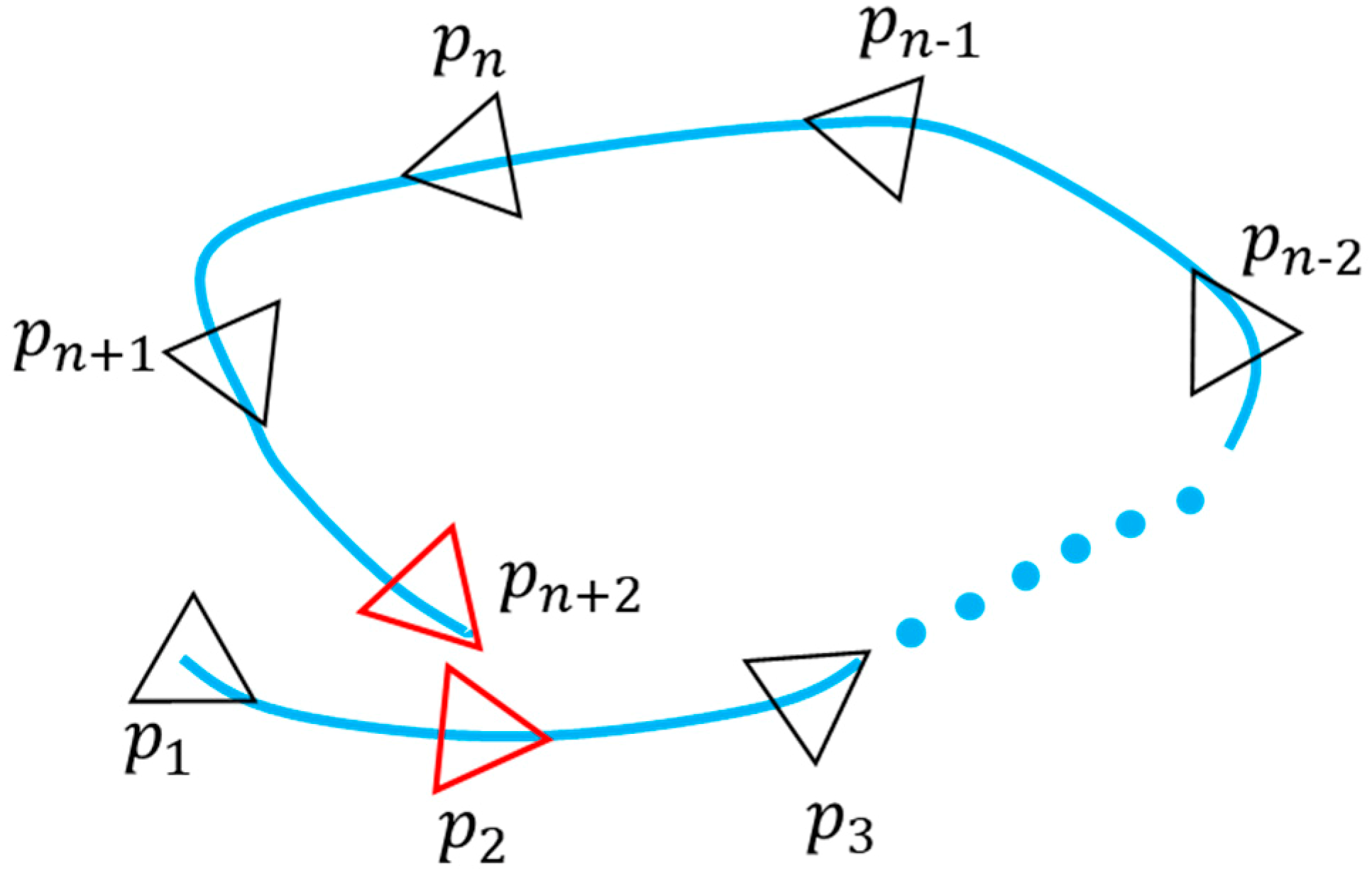
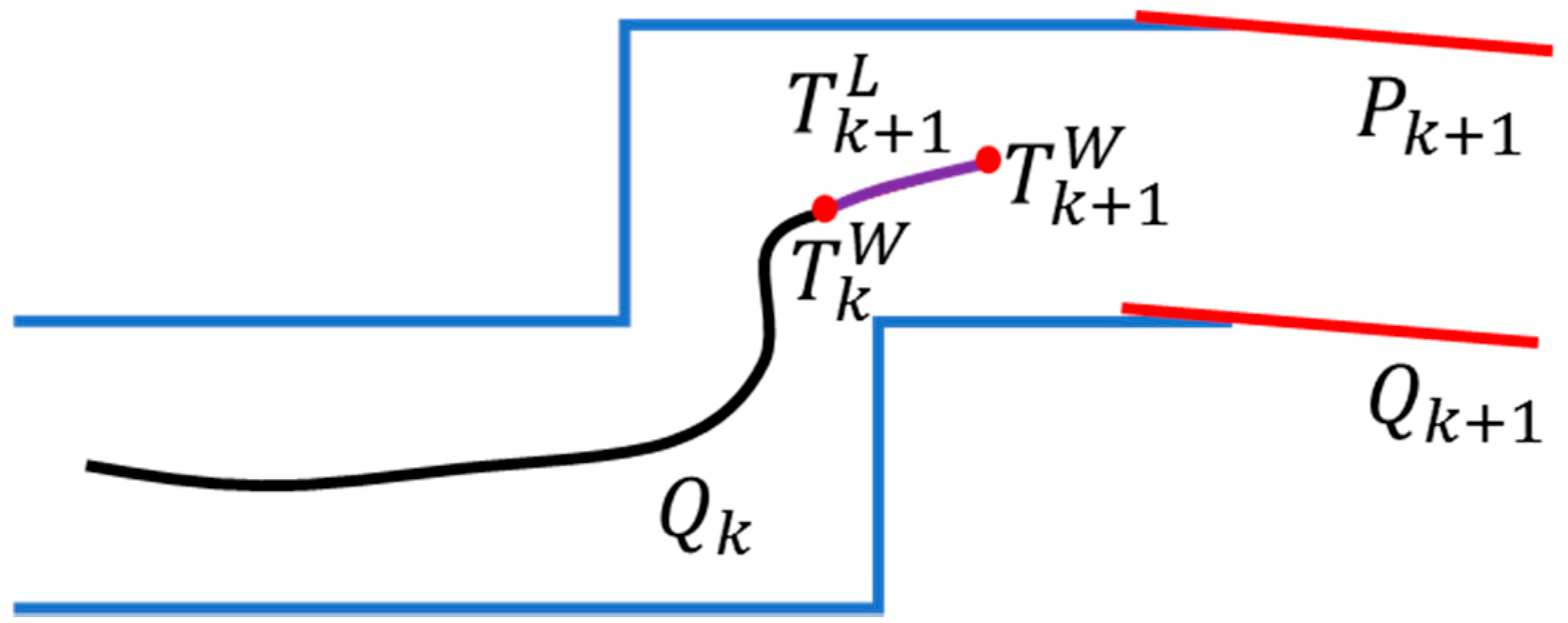
3.4.1. Loop Detection
- The index of the current key frame is larger than the index of the historical key frame;
- The difference between the trajectory distances of the current key frame and the historical key frame is greater than a set threshold;
- The relative translation distance between the current key frame and the historical key frame is less than a set threshold.
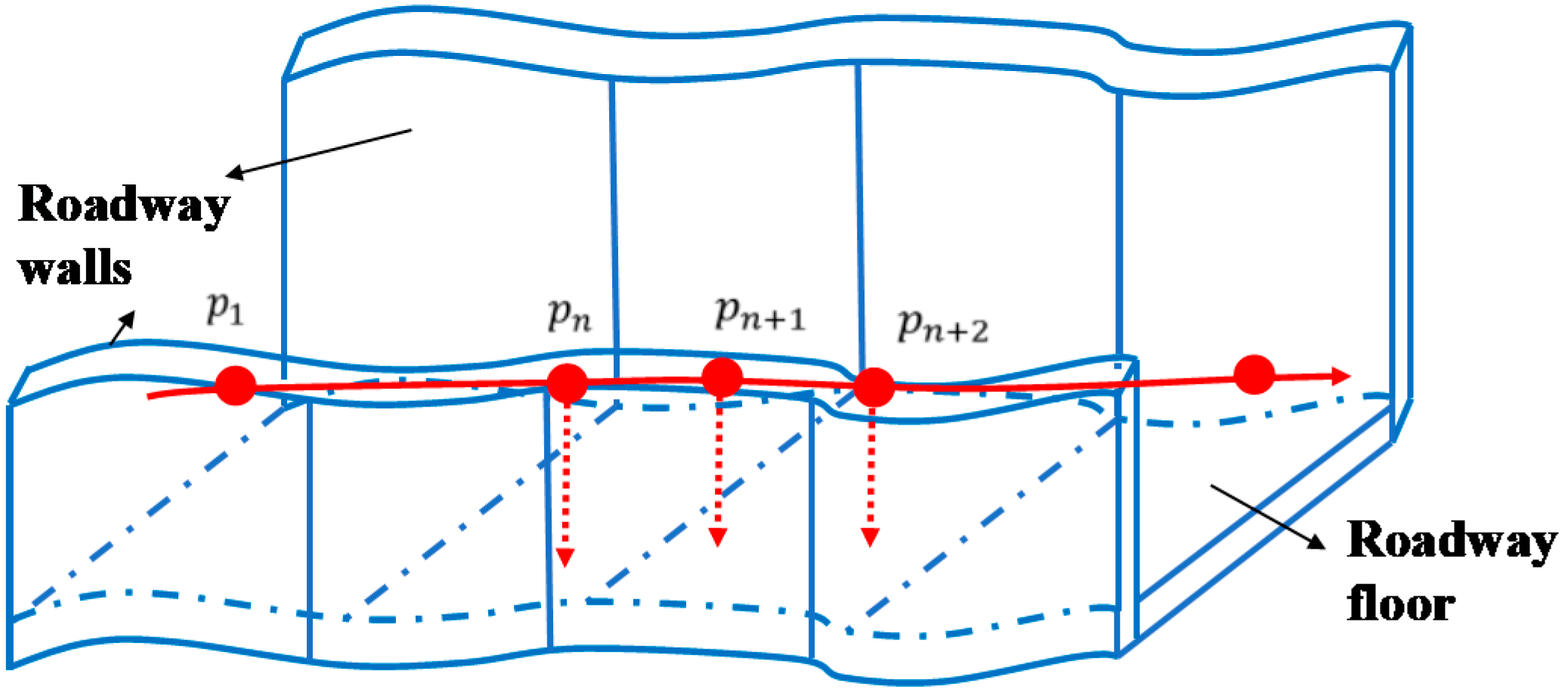
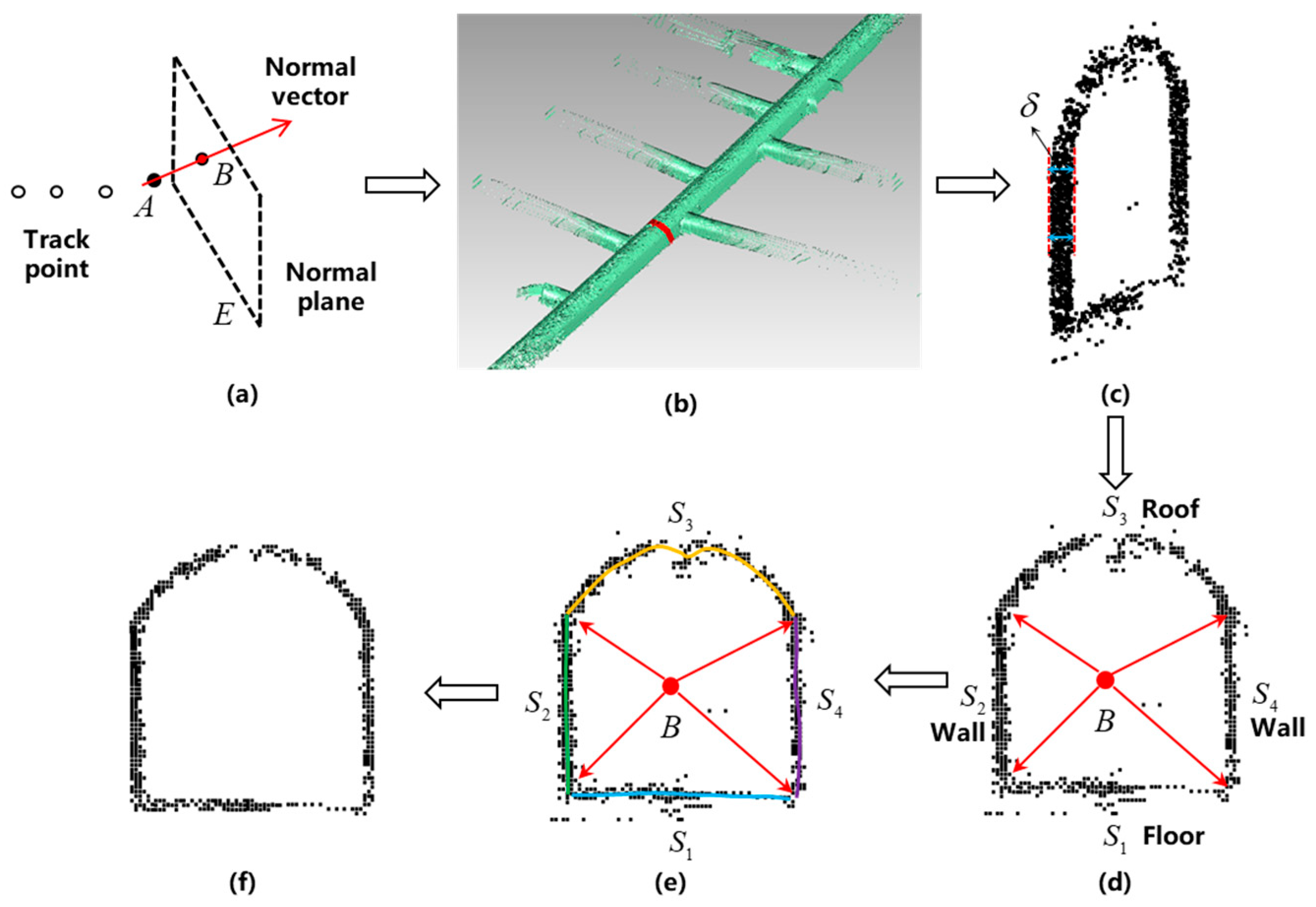
3.4.2. Roadways Plane Detection
3.4.3. Graph Optimization Construction
3.5. Point Cloud Map Construction
- Calculate the curvature of the point, and exclude the calculation as a normal vector in the case of large fluctuations in curvature;
- Calculating the distance between the track point and the previous point. When the distance is greater than a certain threshold, the point is excluded from the normal vector calculation;
- Calculate the angle between the line connecting the track point and the previous point and the X axis, and compare the relationship between the angle and the heading angle of the point. When it is greater than a certain threshold, the point is excluded from the normal vector calculation.
4. Experiment
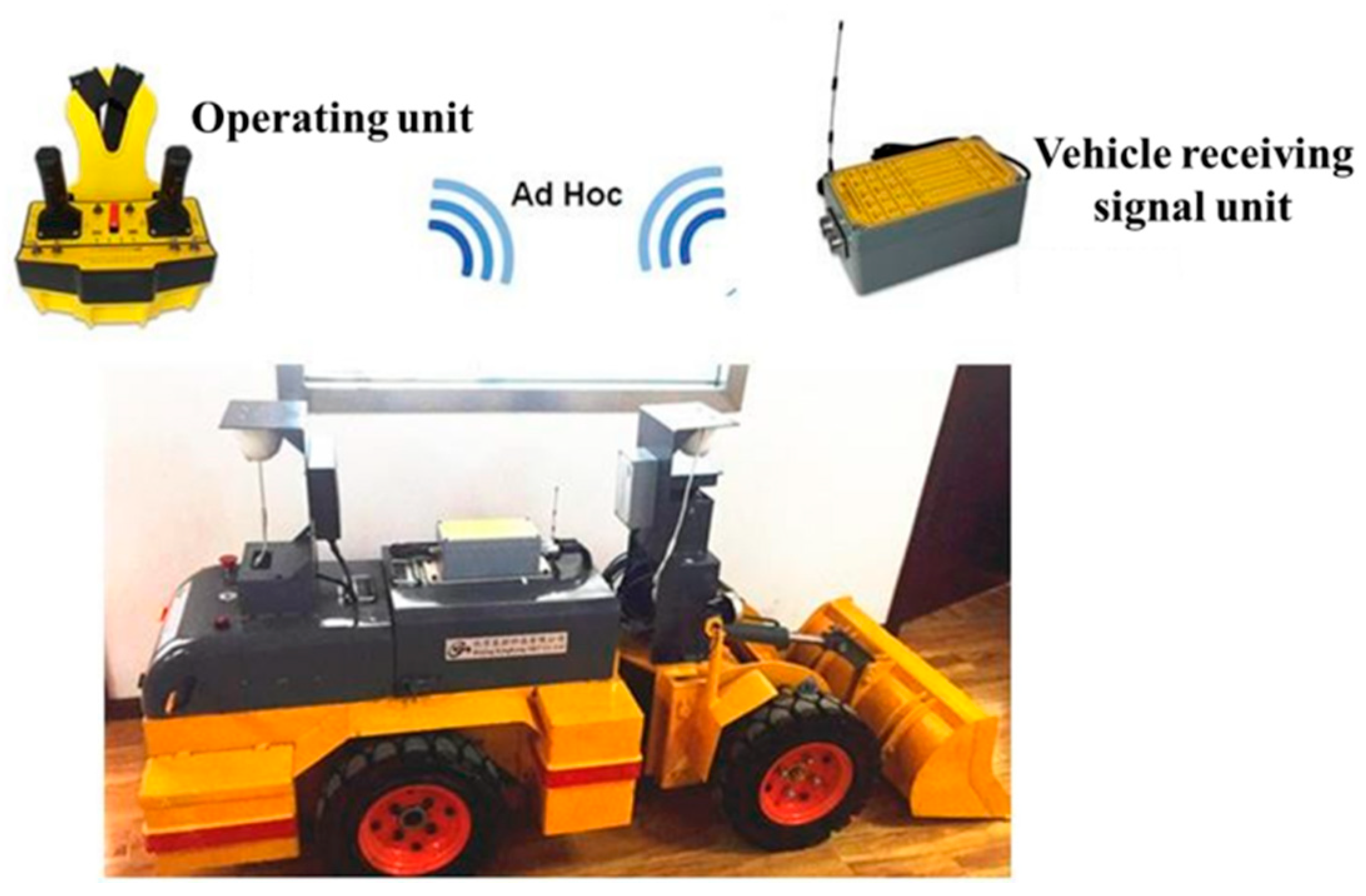
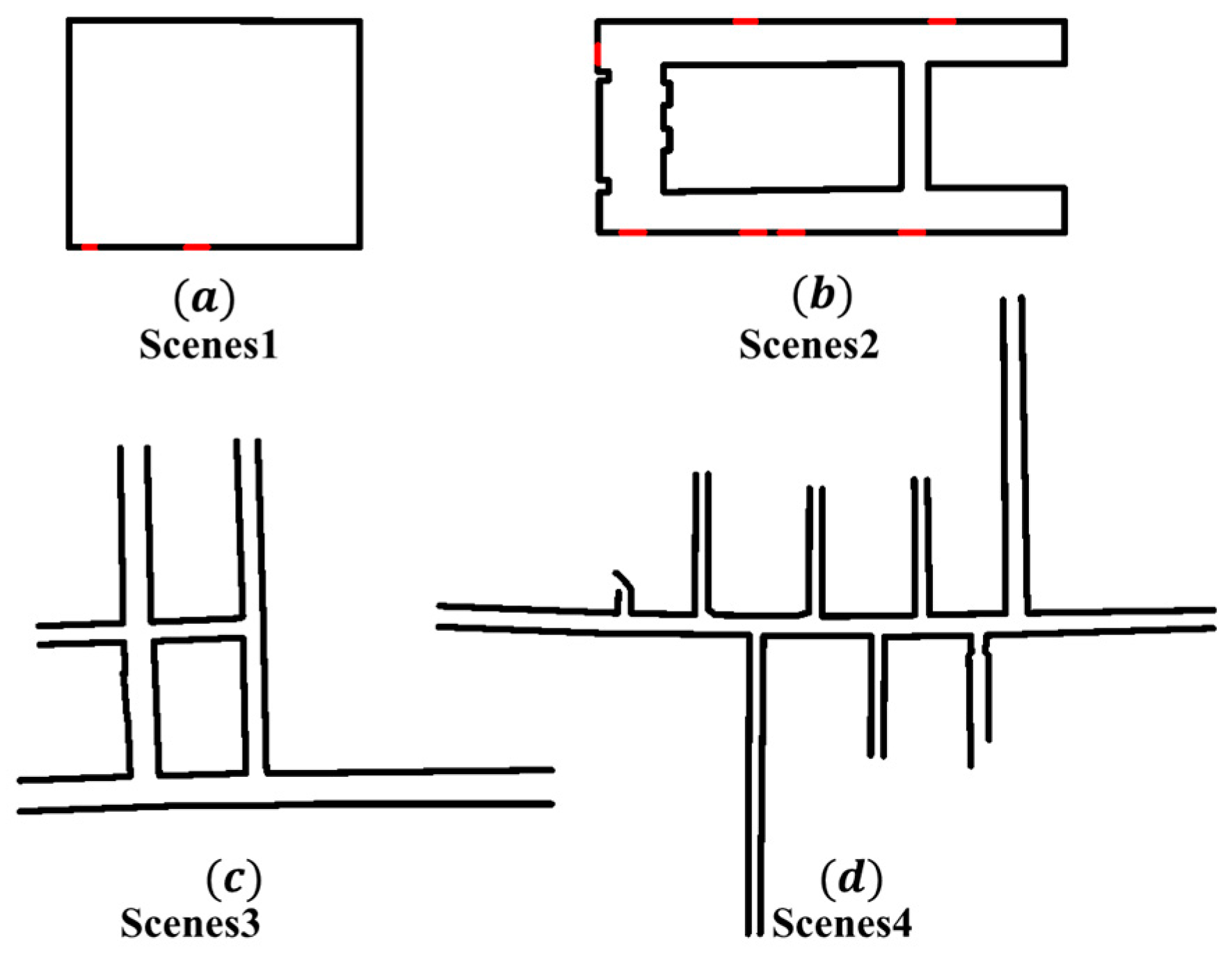
4.1. Introduction to the Experimental Platform
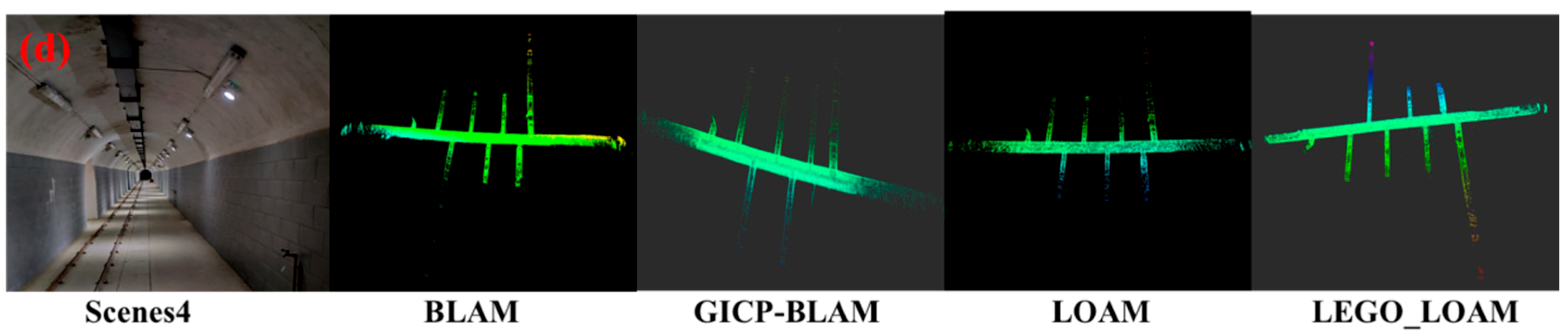
4.2. Results
4.3. Discussion of Results
4.3.1. Impact of Point Cloud Registration
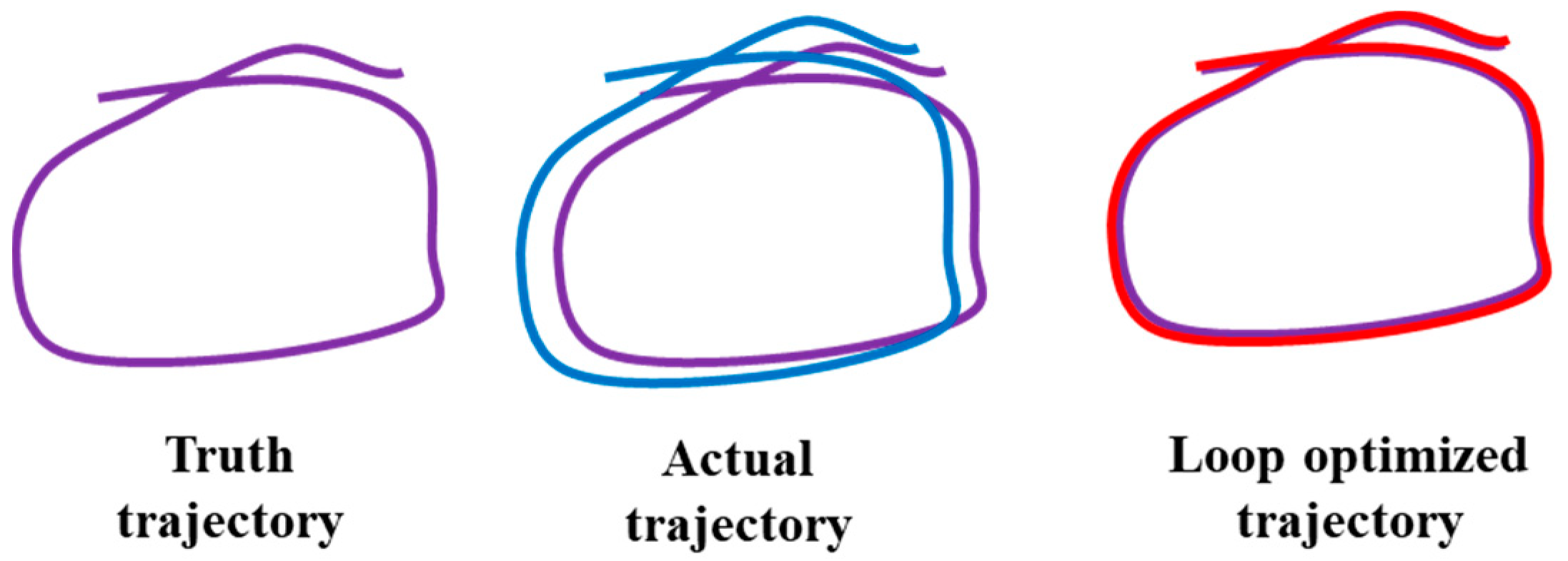
4.3.2. Impact of Loop Constraints
4.3.3. Influence of Plane Constraints
4.3.4. Run Time Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Feng, X.; Li, Y.; Sheng, Y. Studies on temporal and spatial variation of microseismic activities in a deep metal mine. Int. J. Rock Mech. Min. Sci. 2013, 60, 171–179. [Google Scholar] [CrossRef]
- El Assaf, A.; Zaidi, S.; Affes, S.; Kandil, N. Accurate sensors localization in underground mines or tunnels. In Proceedings of the 2015 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Montreal, QC, Canada, 4–7 October 2015; pp. 1–6. [Google Scholar]
- Kumar, S.S.; Jabannavar, S.S.; Shashank, K.R.; Nagaraj, M.; Shreenivas, B. Localization and tracking of unmanned vehicles for underground mines. In Proceedings of the 2017 Second International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 22–24 February 2017; pp. 1–4. [Google Scholar]
- Zlot, R.; Bosse, M. Efficient large-scale three-dimensional mobile mapping for underground mines. J. Field Robot. 2014, 31, 758–779. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, W.; You, K.; Li, W.; Kim, Y. Vehicle autonomous localization in local area of coal mine tunnel based on vision sensors and ultrasonic sensors. PLoS ONE 2017, 12, e0171012. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.; Self, M.; Cheeseman, P. Estimating uncertain spatial relationships in robotics. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1990; pp. 167–193. [Google Scholar]
- Huber, D.F.; Vandapel, N. Automatic three-dimensional underground mine mapping. Int. J. Robot. Res. 2006, 25, 7–17. [Google Scholar] [CrossRef]
- López, E.; García, S.; Barea, R.; Bergasa, L.; Molinos, E.; Arroyo, R.; Romera, E.; Pardo, S. A multi-sensorial simultaneous localization and mapping (SLAM) system for low-cost micro aerial vehicles in GPS-denied environments. Sensors 2017, 17, 802. [Google Scholar] [CrossRef] [PubMed]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a spring-mounted 3-d range sensor with application to mobile mapping. IEEE Trans. Robot. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Leingartner, M.; Maurer, J.; Ferrein, A.; Steinbauer, G. Evaluation of sensors and mapping approaches for disasters in tunnels. J. Field Robot. 2016, 33, 1037–1057. [Google Scholar] [CrossRef]
- Moosmann, F.; Stiller, C. Velodyne SLAM. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 393–398. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Sens. Fusion IV: Control Paradig. Data Struct. 1992, 1611, 586–607. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. In Proceedings of the Robotics: Science and Systems, Zurich, Switzerland, 25–28 June 2009; p. 435. [Google Scholar]
- Serafin, J.; Grisetti, G. Using augmented measurements to improve the convergence of ICP. In Proceedings of the International Conference on Simulation, Modeling, and Programming for Autonomous Robots, Bergamo, Italy, 20–23 October 2014; pp. 566–577. [Google Scholar]
- Serafin, J.; Grisetti, G. NICP: Dense normal based point cloud registration. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 742–749. [Google Scholar]
- Censi, A.; Iocchi, L.; Grisetti, G. Scan matching in the Hough domain. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2739–2744. [Google Scholar]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Grisetti, G.; Kummerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Proceedings of the International workshop on vision algorithms, Corfu, Greece, 20–25 September 1999; pp. 298–372. [Google Scholar]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time for pose graph SLAM. Int. J. Robot. Res. 2013, 32, 1611–1626. [Google Scholar] [CrossRef]
- Magnusson, M.; Andreasson, H.; Nuchter, A.; Lilienthal, A.J. Appearance-based loop detection from 3D laser data using the normal distributions transform. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 23–28. [Google Scholar]
- Sivic, J.; Zisserman, A. Efficient visual search of videos cast as text retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 591–606. [Google Scholar] [CrossRef] [PubMed]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Ulrich, I.; Nourbakhsh, I. Appearance-based place recognition for topological localization. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 1023–1029. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Ma, L.; Kerl, C.; Stückler, J.; Cremers, D. CPA-SLAM: Consistent plane-model alignment for direct RGB-D SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1285–1291. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. g2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robots 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Erik-Nilson. Blam—Berkeley Localization and Mapping. Available online: https://github.com/erik-nelson/blam (accessed on 26 June 2019).

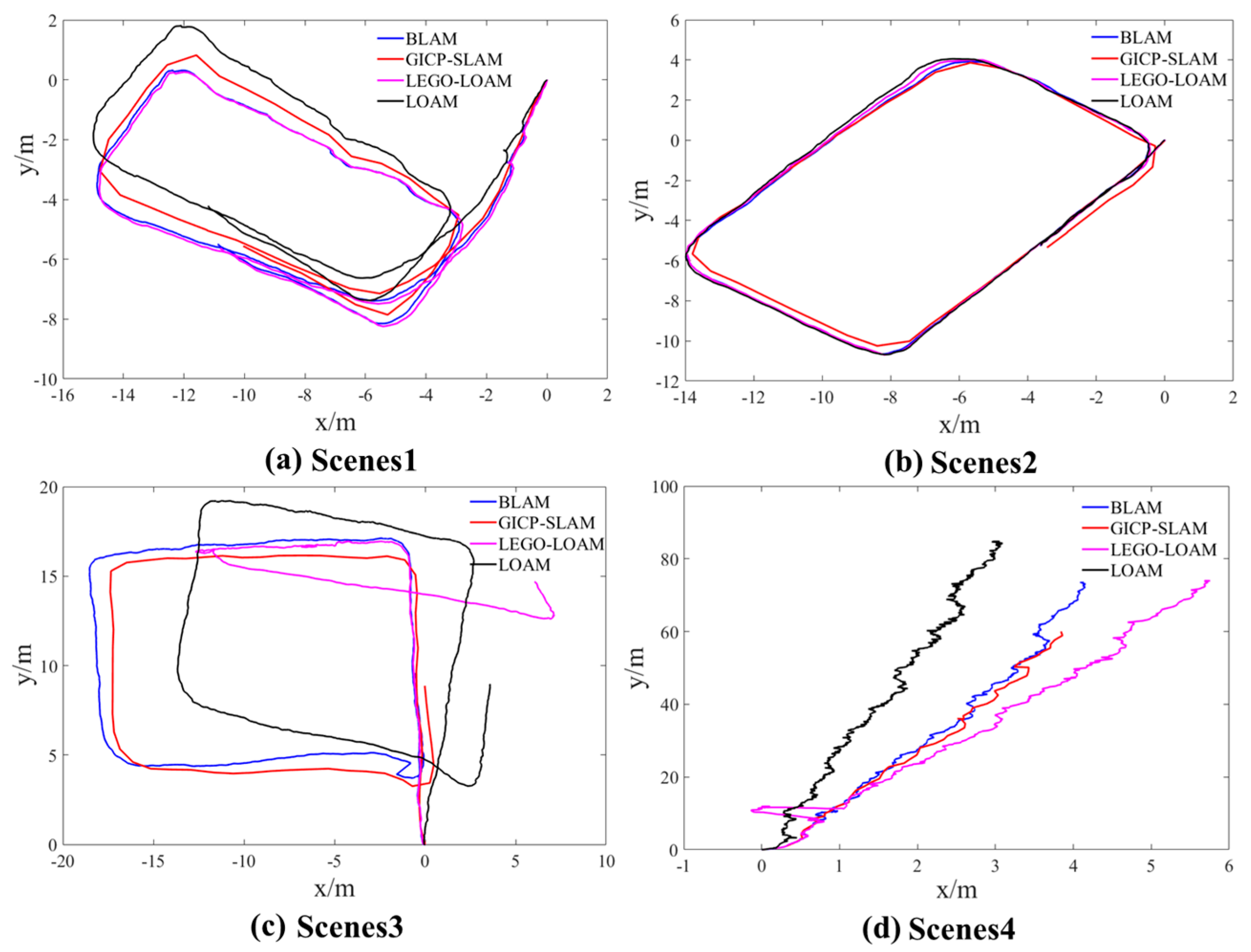



| Scenes | Method | Trans.1 X | Trans. Y | Trans. Z | Total Trans. (m) | Roll | Pitch | Yaw | Total Rotat. 2 (rad) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Blam | −10.88 | −5.50 | 0.19 | 12.19 | −0.02 | 0.05 | −1.42 | 1.42 |
| Gicp_Slam | −10.04 | −5.56 | 1.46 | 11.57 | −0.01 | 0.03 | −1.42 | 1.42 | |
| Lego_Loam | −10.78 | −5.64 | 0.14 | 12.17 | −0.16 | −1.41 | −0.17 | 1.43 | |
| Loam | −11.20 | −4.23 | 0.21 | 11.97 | −0.49 | −1.51 | −0.50 | 1.67 | |
| 2 | Blam | −3.64 | −5.25 | −0.12 | 6.38 | 0.00 | 0.00 | 0.02 | 0.02 |
| Gicp_Slam | −3.44 | −5.35 | 1.45 | 6.52 | 0.00 | 0.02 | −0.09 | 0.09 | |
| Lego_Loam | −3.61 | −5.22 | −0.01 | 6.35 | −0.04 | 0.02 | −0.04 | 0.06 | |
| Loam | −3.61 | −5.23 | −0.09 | 6.35 | 0.00 | 0.02 | 0.00 | 0.02 | |
| 3 | Blam | −0.57 | 9.57 | 0.40 | 9.59 | 0.01 | 0.03 | 0.46 | 0.46 |
| Gicp_Slam | −0.01 | 8.88 | 1.22 | 8.96 | −0.03 | −0.02 | 0.37 | 0.37 | |
| Lego_Loam | 6.05 | 14.71 | −3.51 | 16.28 | −0.61 | 0.04 | 1.14 | 1.29 | |
| Loam | 3.57 | 8.94 | −3.13 | 10.13 | 0.31 | 0.24 | −0.04 | 0.39 | |
| 4 | Blam | 4.09 | 73.50 | 3.77 | 73.71 | 0.05 | −0.02 | 0.19 | 0.20 |
| Gicp_Slam | 3.84 | 60.04 | 1.28 | 60.18 | 0.01 | −0.03 | 0.07 | 0.07 | |
| Lego_Loam | 5.70 | 73.96 | 2.96 | 74.24 | −0.06 | 0.15 | 0.03 | 0.17 | |
| Loam | 2.99 | 84.75 | 3.85 | 84.89 | −0.01 | 0.19 | 0.05 | 0.20 |
| Model | Max (ms) | Min (ms) | Mean (ms) |
|---|---|---|---|
| Planar Detection | 10.13 | 10.04 | 10.09 |
| LiDAR Odometry | 111.00 | 10.09 | 51.22 |
| Loop Detection | 252.13 | 80.59 | 114.67 |
| Graph Optimization | 50.41 | 10.05 | 14.39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Wang, L.; Bi, L. Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment. Sensors 2019, 19, 2915. https://doi.org/10.3390/s19132915
Ren Z, Wang L, Bi L. Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment. Sensors. 2019; 19(13):2915. https://doi.org/10.3390/s19132915
Chicago/Turabian StyleRen, Zhuli, Liguan Wang, and Lin Bi. 2019. "Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment" Sensors 19, no. 13: 2915. https://doi.org/10.3390/s19132915
APA StyleRen, Z., Wang, L., & Bi, L. (2019). Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment. Sensors, 19(13), 2915. https://doi.org/10.3390/s19132915






