Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Preprocessing
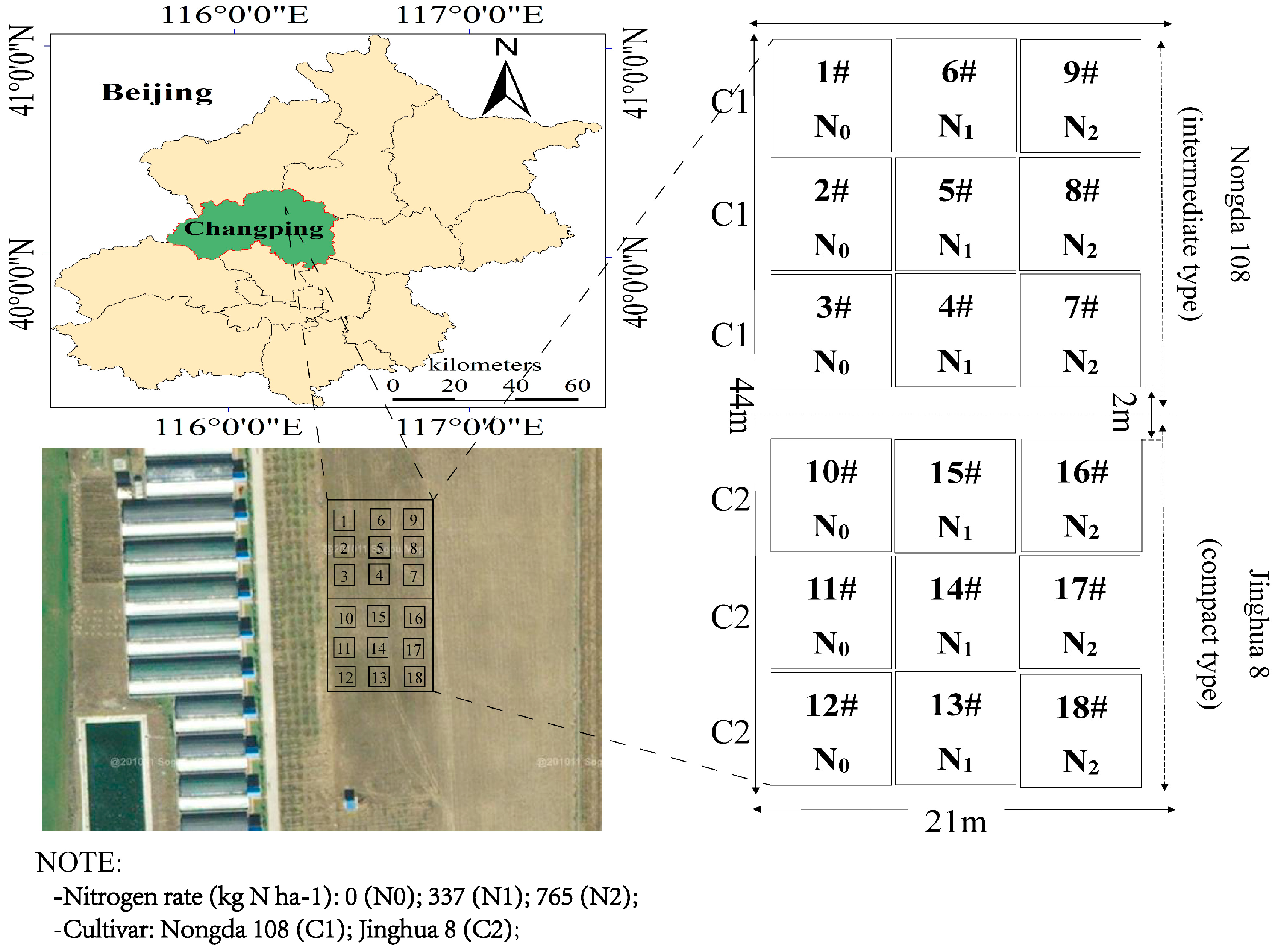
2.1.1. Study Area
2.1.2. Spectrum Acquisition
2.1.3. Plant Sample and LNC Acquirement
2.2. Principles and Methods
2.2.1. Preprocessing of Hyperspectral Data
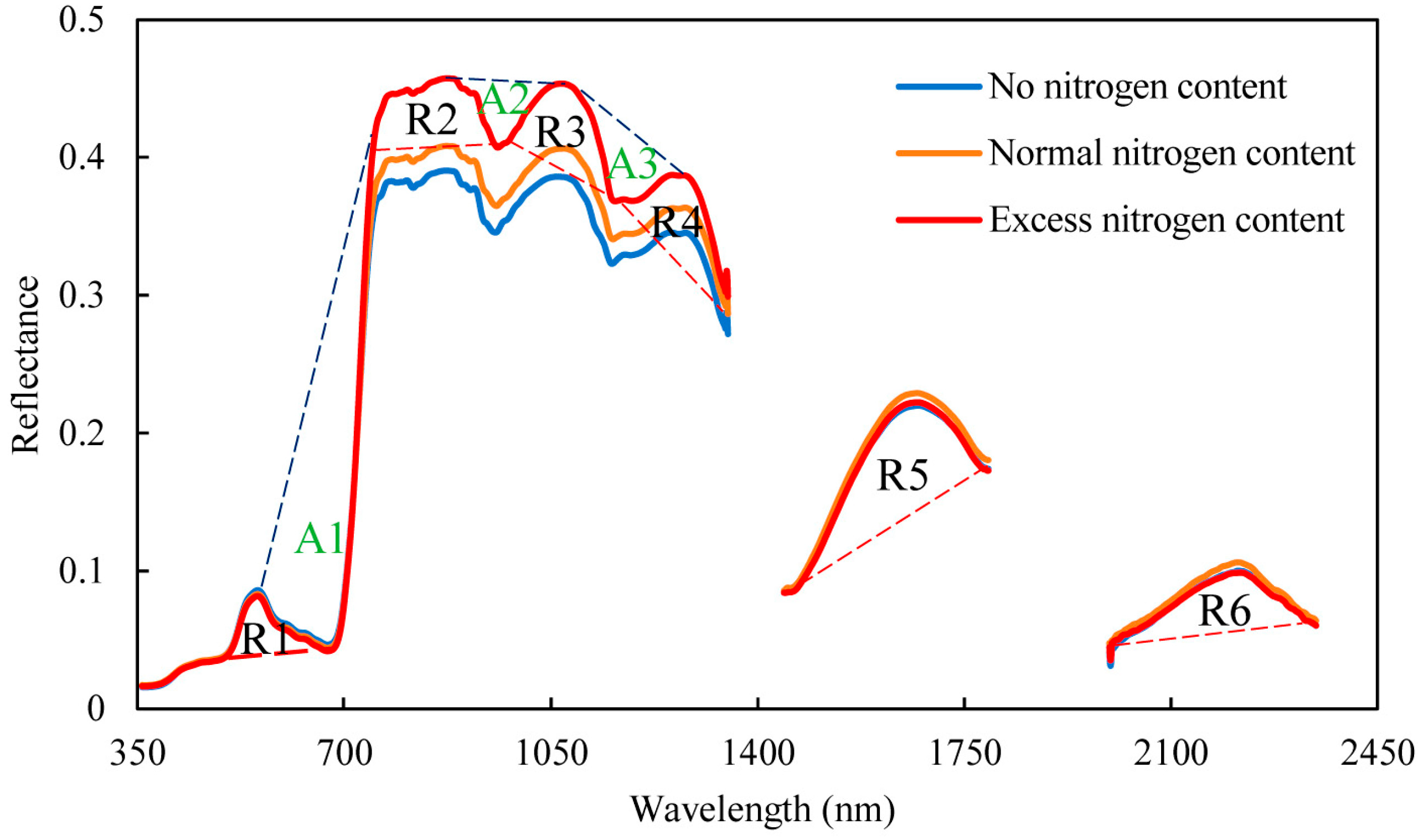
2.2.2. Spectral Position Features
2.2.3. Vegetation Indices
2.3. Screening and Modeling Methods
2.3.1. Successive Projections Algorithm
2.3.2. Partial Least Squares Regression
2.3.3. Random Forest
2.3.4. Statistical Analysis Method
3. Results
3.1. Optimal Spectral Characteristics
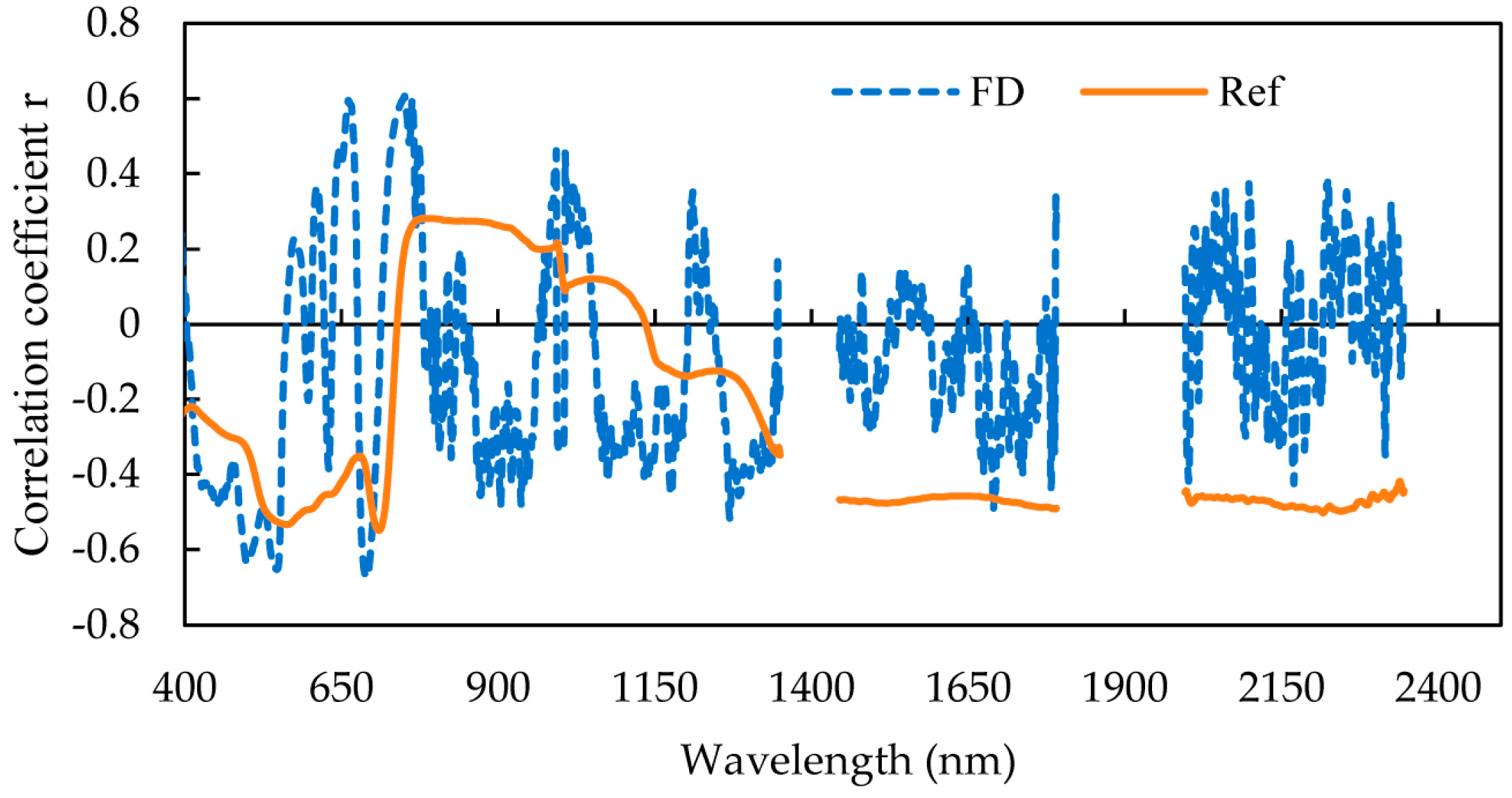
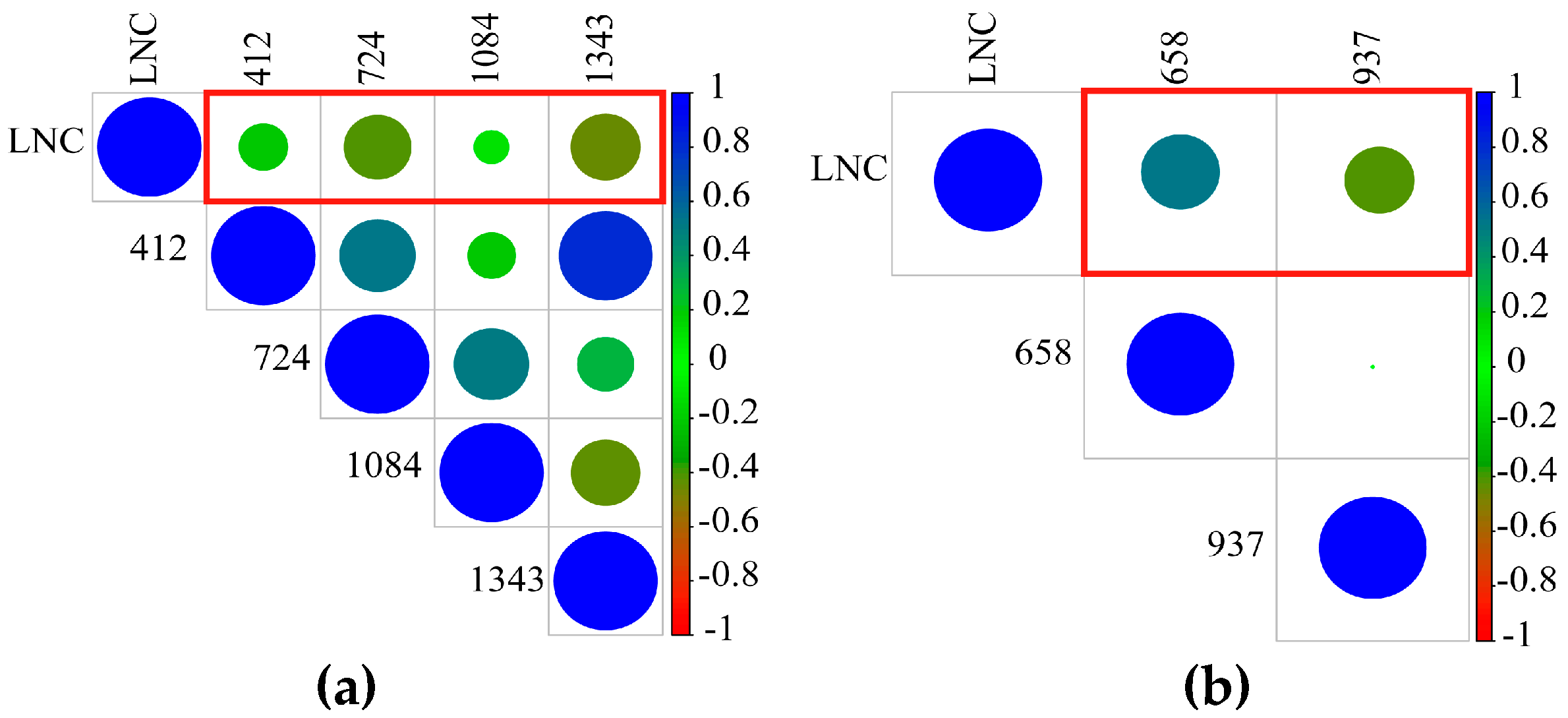
3.1.1. Sensitive Reflectance Feature Data Set
3.1.2. Position Feature Data Set
3.1.3. Vegetation Indices Data Set
3.2. Composite Spectral Features
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S.; Van der Meer, B. Accuracy assessments of hyperspectral waveband performance for vegetation analysis applications. Remote Sens. Environ. 2004, 91, 354–376. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Chang, Q.; Zeng, F.; Cao, J.; Lu, G. Increasing accuracy of hyper·spectral remote sensing for total nitrogen of winter wheat canopy by use of SPA and PLS methods. J. Plant. Nutr. Fertil. 2018, 24, 52–58. [Google Scholar]
- Peng, H.; Xingang, X.; Baolei, Z.; Zhenhai, L.; Haikuan, F.; Guijun, Y.; Yongfeng, Z. Estimation of leaf chlorophyll content in winter wheat using variable importance for projection (VIP) with hyperspectral data. Remote Sens. Agric. Ecosyst. Hydrol. XVII 2015, 12. [Google Scholar] [CrossRef]
- Strachan, I.; Pattey, E.; Boisvert, J. Impact of nitrogen and environmental conditions on corn as detected by hyperspectral reflectance. Remote Sens. Environ. 2002, 80, 213–224. [Google Scholar] [CrossRef]
- Dandan, W.; Xiaobing, L.; Hong, W.; Han, W.; Wanyu, W. Comparative study on estimation of nitrogen content in the heterogenious typical steppe using various red edge position extraction techniques. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar] [CrossRef]
- Cho, M.; Skidmore, A. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Chen, P.F.; Haboudane, D.N.T.; Wang, J.H.; Vigneault, P.; Li, B.G. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Shu, M.; Gu, X.; Sun, L.; Zhu, J.; Yang, G.; Wang, Y.; Zhang, L. High spectral inversion of winter wheat LAI based on new vegetation index. Sci. Agric. Sin. 2018, 51, 57–67. [Google Scholar]
- Tan, C.; Huang, Y.; Huang, W.; Wang, J.; Zhao, C.; Liu, L. Study on colony leaf area index of summer maize by remote sensing vegetation indexes method. J. Anh. Agric. Univ. 2004, 31. [Google Scholar] [CrossRef]
- Li, S.; Ren, Z. Quantitative analysis of near infrared spectroscopy based on wavelet coefficients and partial least-squares regression. J. Changchun Univ. 2018, 28, 5. [Google Scholar]
- Zhang, L.; Chen, S. Measurements and analysis of marginal effect of water use efficiency by scientific and technological innovation based on PLS-PATH method. Adv. Sci. Technol. Water Res. 2018, 38, 8. [Google Scholar]
- Qi, B.; Zhang, N.; Zhao, T.; Xing, G.; Zhao, J.; Gai, J. Using canopy hyperspectral reflectance to predict growth traits and seed yield of soybeans from middle and lower yangtze valleys through partial least squares regression. Soybean Sci. 2015, 34, 7. [Google Scholar]
- Zhang, L.; Wang, L.; Zhang, X.; Liu, S.; Sun, P.; Wang, T. The basic principle of random forest and its applications in ecology: A case study of Pinus yunnanensis. Acta Ecol. Sin. 2014, 34, 3. [Google Scholar] [CrossRef]
- Lu, N.; Han, P.; Wang, J. Prediction on firmness of strawberry based on hyperspectral imaging. Softw. Guide 2018, 17, 3. [Google Scholar]
- Sun, J.; Cong, S.; Mao, H.; Wu, X.; Zhang, X.; Wang, P. CARS-ABC-SVR model for predicting leaf moisture of leaf-used lettuce based on hyperspectral. Trans. Chin. Soc. Agric. Eng. 2017, 33, 178–184. [Google Scholar]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. 1984, 89, 6329. [Google Scholar] [CrossRef]
- Mutanga, O.; KSkidmore, A. Hyperspectral band depth analysis for a better estimation of grass biomass (Cenchrus ciliaris) measured under controlled laboratory conditions. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 87–96. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Wang, L. Study on Nutrition Diagnosis of Nitrogen Content in Maize Leaves of Cold Region Based on Hyperspectral Imaging. Master’s Thesis, Northeast Agricultural University, Harbin, China, June 2017. (In Chinese). [Google Scholar]
- Xie, W. Estimation of chlorophyll content in maize leaves based on hyperspectral under the action of microorganism. West. Dev. Land Dev. Eng. Res. 2018, 3, 31–37. [Google Scholar]
- He, T. Hyperspectral remote sensing estimation models for nitrogen nutrition monitoring of maize. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, June 2016. (In Chinese). [Google Scholar]
- Li, X.C.; Zhang, Y.J.; Bao, Y.S.; Luo, J.H.; Jin, X.L.; Xu, X.G.; Song, X.Y.; Yang, G.J. Exploring the best hyperspectral features for LAI estimation using partial least squares regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, W.; Chu, X.; Xi, M.J. Selection of characteristic wavelengths using SPA and qualitative discrimination of mildew degree of corn kernels based on SVM. Spectrosc. Spect. Anal. 2016, 36, 226–230. [Google Scholar] [CrossRef]
- Wu, D.; Ning, J.; Liu, X.; Liang, M.; Yang, S.; Zhang, Z. Determination of anthocyanin content in grape skins using hyperspectral imaging technique and successive projections algorithm. Food Sci. 2014, 35, 5. [Google Scholar]
- Reyniers, M.; Walvoort, D.; De Baardemaaker, J. A linear model to predict with a multi-spectral radiometer the amount of nitrogen in winter wheat. Int. J. Remote Sens. 2006, 27, 21. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Tian, Y.C.; Liu, X.J.; Cao, W.X. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Xue, L.H.; Cao, W.X.; Luo, W.H.; Dai, T.B.; Zhu, Y. Monitoring leaf nitrogen status in rice with canopy spectral reflectance. Agron. J. 2004, 96, 135–142. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E.; Smith, A.M.S. Using in-situ mea-surements to evaluate the new RapidEye™ satellite series for prediction of wheat nitrogen status. Int. J. Remote Sens. 2007, 28, 4183–4190. [Google Scholar] [CrossRef]
- Adams, M.L.; Philpot, W.D.; Norvell, W.A. Yellowness index: An application of spectral second derivatives to estimate chlorosis of leaves in stressed vegetation. Int. J. Remote Sens. 1999, 20, 3663–3675. [Google Scholar] [CrossRef]
- Serrano, L.; Penuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in mediterranean vegetation from AVIRIS data: Decomposing biochemical from structural signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Fitzgerald, G.J.; Rodriguez, D.; Christensen, L.K.; Belford, R.; Sadras, V.O.; Clarke, T.R. Spectral and thermal sensing for nitrogen and water status in rainfed and irrigated wheat environments. Precis Agric. 2006, 7, 233–248. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Liu, H.Q.; Huete, A. Feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Geosci. Remote Sens. Soc. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. Nasa Spec. Publ. 1974, 351, 309. [Google Scholar]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and Fpar: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Q.; Wang, J.; Zhou, Y.; Zhao, F. Theoretical bases and application of three gradient difference vegetation index. Sci. China Ser. D 2003, 33, 9. (In Chinese) [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves. spectral features and relation to chlorophyll estimation. J. Plant Phys. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. Banner 2003, 30, 1248. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Serrano, L.; Savé, R. Cell wall elasticity and water index (R970 nm/R900 nm) in wheat under different nitrogen availabilities. Int. J. Remote Sens. 1996, 17, 373–382. [Google Scholar] [CrossRef]
- Gao, B.C.; Goetzt, A.F. Retrieval of equivalent water thickness and information related to biochemical components of vegetation canopies from AVIRIS data. Remote Sens. Environ. 1995, 52, 155–162. [Google Scholar] [CrossRef]
- Hardisky, M.; Klemas, V.; Smart, R.M. The influences of soil salinity, growth form, and leaf moisture on the spectral reflectance of spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 48, 77–84. [Google Scholar]
- Apan, A.; Held, A.; Phinn, S.; Markley, J. Detecting sugarcane ‘orange rust’ disease using EO-1 Hyperion hyperspectral imagery. Int. J. Remote Sens. 2004, 25, 489–498. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Hereijgers, S.; Verstraeten, W.W.; Keulemans, W.; Coppin, P. A near-infrared narrow-waveband ratio to determine Leaf Area Index in orchards. Remote Sens. Environ. 2008, 112, 3672–3772. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, W.J. Comparison of different methods for variable selection. Anal. Chim. Acta 2001, 446, 477–483. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, H.; Wold, H.; Dunn, W.J. The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; EImasry, G.; Sun, D.W.; Allen, P. Prediction of some quality attributes of lamb meat using near-infrared hyperspectral imaging and multivariate analysis. Anal. Chim. Acta 2012, 714, 57–67. [Google Scholar] [CrossRef]
- Lü, J.; Hao, N.; Cui, X. Inversion model for copper content in farmland of tailing area based on visible-near infrared reflectance spectroscopy. Trans. Chin. Soc. Agric. Eng. 2015, 6, 265–270. [Google Scholar]
- Han, Z.; Zhu, X.; Fang, X.; Wang, Z.; Wang, L.; Zhao, G.; Jiang, Y. Hyperspectral estimation of apple tree canopy LAI based on SVM and RF regression. Spectrosc. Spect. Anal. 2016, 36, 6. [Google Scholar]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf area index derivation from hyperspectral vegetation indicesand the red edge position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Yue, J.B.; Feng, H.K.; Yang, G.J.; Li, Z.H. A Comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Xu, X. Remote Sensing Physics; Peking University Press: Beijing, China, 2006. [Google Scholar]
- Wang, K.R.; Pan, W.C.; Li, S.K.; Chen, B.; Xiao, H.; Wang, F.Y.; Chen, J.L. Monitoring models of the plant nitrogen content based on cotton canopy hyperspectral reflectance. Spectrosc. Spect. Anal. 2011, 31, 1868–1872. [Google Scholar] [CrossRef]
- Liang, J.; Hu, K.; Tian, M.; Wei, D.; Li, H.; Bai, Y.; Jun-zhen, Z. Diagnosis of nitrogen content in upper and lower corn leaves based on hyperspectral data. Spectrosc. Spect. Anal. 2013, 33, 1032–1037. [Google Scholar]
- Luo, P.; Guo, J.; Li, Q. Modeling construction based on partial least-squares regression. J. Tianjin Univ. 2002, 35, 783–786. [Google Scholar]
- Wang, H.B.; Zhao, Z.Q.; Lin, Y.; Feng, R.; Li, L.G.; Zhao, X.L.; Wen, R.H.; Wei, N.; Yao, X.; Zhang, Y.S. Leaf area index estimation of spring maize with canopy hyperspectral data based on linear regression algorithm. Spectrosc. Spect. Anal. 2017, 37, 1489–1496. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, C.; Wang, J.; Li, C.; Yang, X. Associating new spectral features from visible and near infrared regions with optimal combination principle to monitor leaf nitrogen concentration in barley. Int. J. Infrared Millimeter Waves 2013, 32, 9. [Google Scholar] [CrossRef]
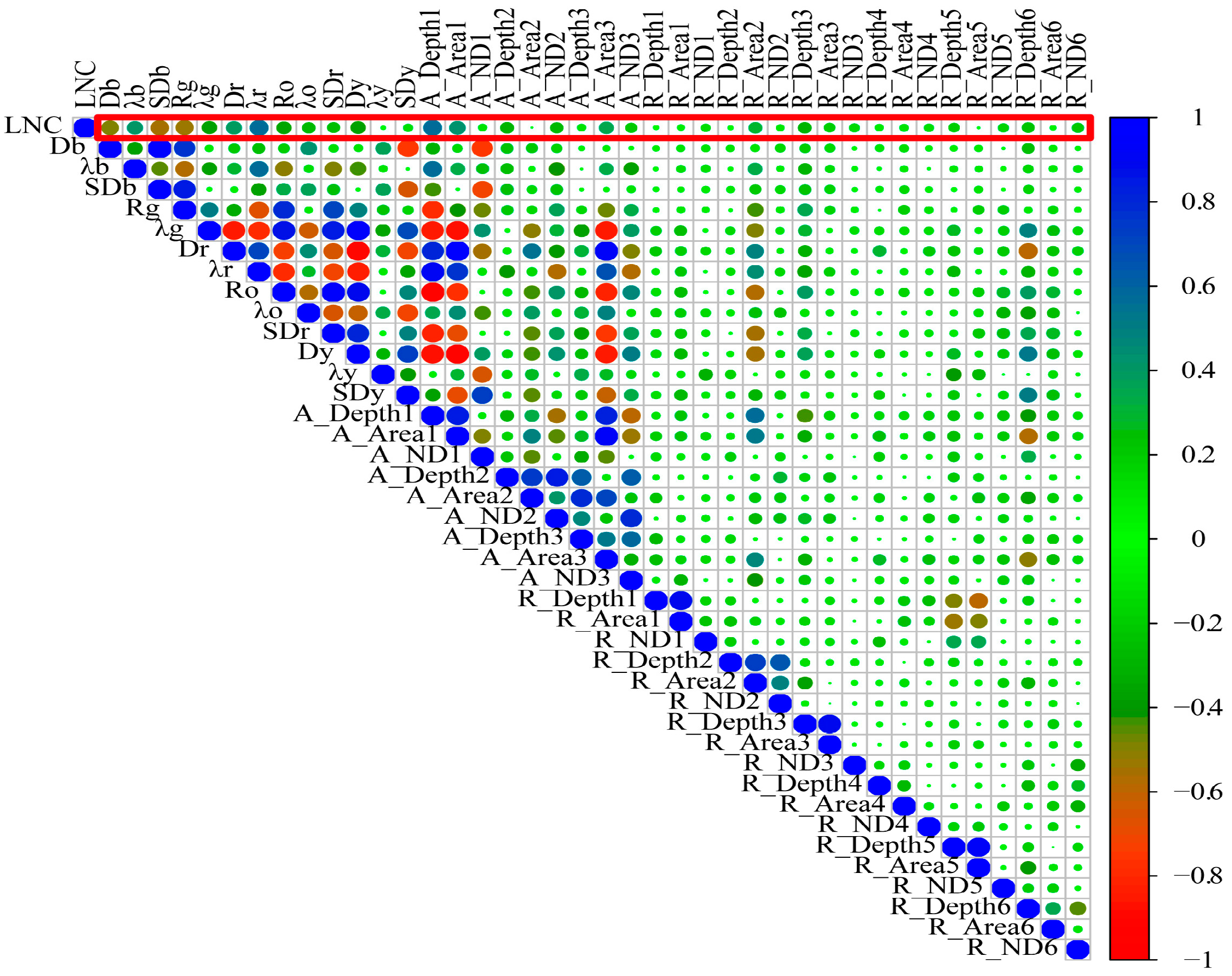
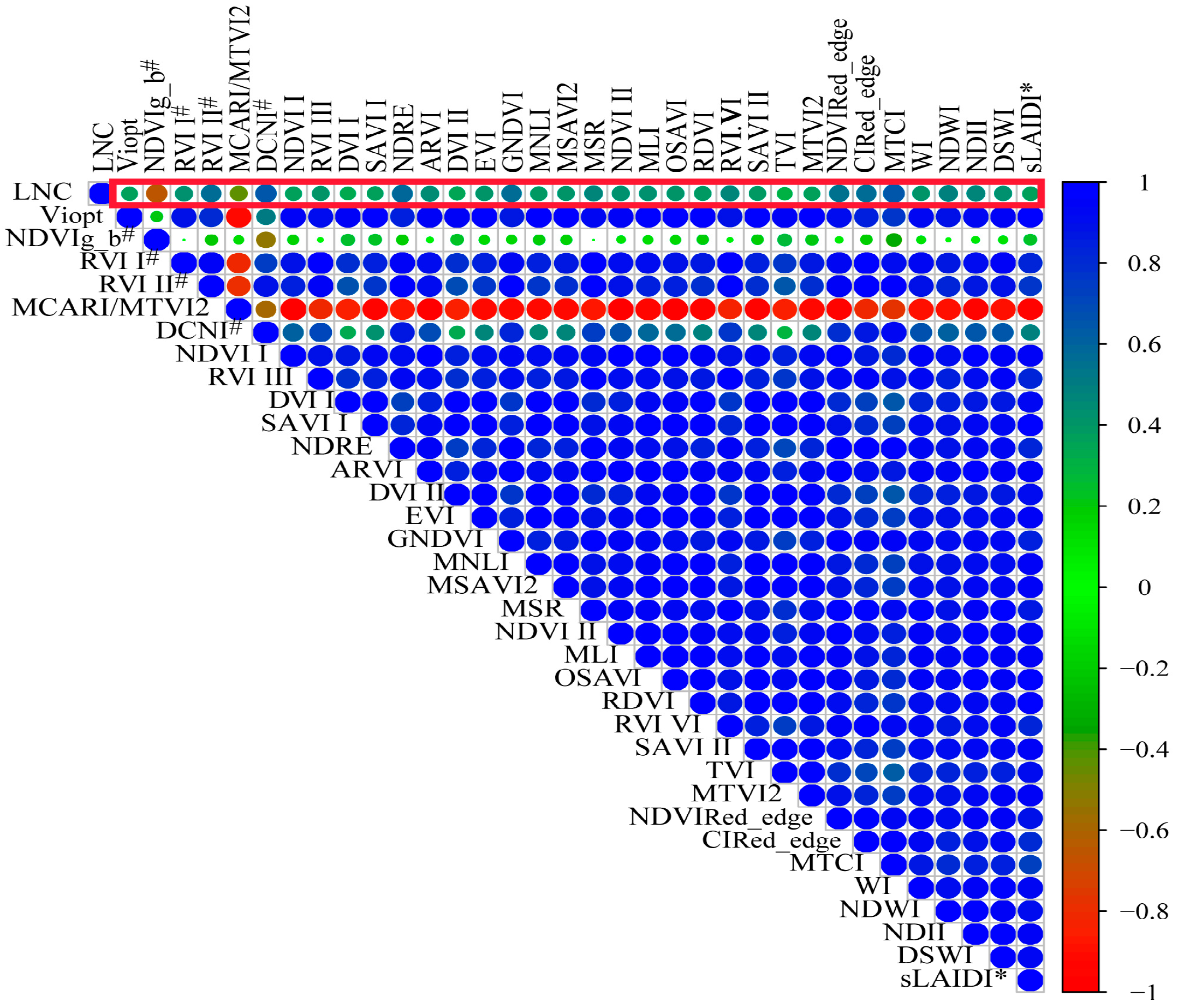
| Dataset | Year | Samples | Max | Min | Mean | SD | Coefficient of Variation |
|---|---|---|---|---|---|---|---|
| Calibration dataset | 2012 | 48 | 2.83 | 0.92 | 1.91 | 0.59 | 0.31 |
| Validation dataset | 2012 | 24 | 2.68 | 0.82 | 1.81 | 0.65 | 0.36 |
| Variables | Definition and Description |
|---|---|
| Db | Maximum value of the 1st derivative with a blue edge (490–530 nm) |
| λb | Wavelength at Db |
| Dy | Maximum value of the 1st derivative with a yellow edge (560–640 nm) |
| λy | Wavelength at Dy |
| Dr | Maximum value of the 1st derivative with a red edge (680–760 nm) |
| λr | Wavelength at Dr |
| Rg | Maximum reflectance with a green peak (510–560 nm) |
| λg | Wavelength at Rg |
| Ro | Lowest reflectance with a red well (650–690 nm) |
| λo | Wavelength at Ro |
| SDb | Sum of the 1st derivative values within the blue edge |
| SDy | Sum of the 1st derivative values within the yellow edge |
| SDr | Sum of the 1st derivative values within the red well |
| Index | Name | Formula | Reference |
|---|---|---|---|
| Viopt | Optimal vegetation index | (1 + 0.45) ((R800)2 + 1)/(R670 + 0.45) | [25] |
| NDVIg-b# | Normalized difference vegetation index# | (R573 − R440)/(R573 + R440) | [26] |
| RVI I# | Ratio vegetation index I# | R810/R660 | [27] |
| RVI II# | Ratio vegetation index II# | R810/R560 | [28] |
| MCARI/MTVI2 | Combined index | MCARI/MTVI2 MCARI:(R700 − R670 − 0.2(R700 − R550)) (R700/R670) MTVI2: | [29] |
| DCNI# | Double-peak canopy nitrogen index I# | (R720 − R700)/(R700 − R670)/(R720 − R670 + 0.03) | [7] |
| NDVI I | Normalized difference vegetation index I | (R800 − R670)/(R800 + R670) | [30] |
| RVI III | Ratio vegetation index III | R800/R670 | [31] |
| DVI I | Difference vegetation index I | R800-R670 | [32] |
| SAVI I | Soil-adjusted vegetation index I | 1.5(R800 − R670)/(R800 + R670 + 0.5) | [33] |
| NDRE | Normalized difference red edge | (R790 − R720)/(R790 + R720) | [34] |
| ARVI | Atmospherically-resistant vegetation index | ARVI = (RNIR − RB)/(RNIR + RB) RB = R-γ(B-R), γ = 1 | [35] |
| DVI II | Difference vegetation index II | DVI = RNIR − RR | [36] |
| EVI | Enhanced vegetation index | EVI = 2.5(RNIR − RR)/(RNIR + 6RR − 7.5RB + 1) | [37] |
| GNDVI | Green normalized difference vegetation index | GNDVI = (RNIR − RR)/(RNIR + RR) | [38] |
| MNLI | Modified nonlinear vegetation index | MNLI = 1.5(RNIR2 − RR)/(RNIR2 + RR + 0.5) | [39] |
| MSAVI2 | The second modified SAVI | MSAVI2 = | [40] |
| MSR | Modified simple ratio | MSR = (RNIR/RR − 1) / (RNIR/RR + 1) | [41] |
| NDVI II | Normalized difference vegetation index II | NDVI = (RNIR − RR) / (RNIR + RR) | [42] |
| NLI | Nonlinear vegetation index | NLI = (RNIR2 − RR)/(RNIR2 + RR) | [43] |
| OSAVI | Optimization of soil-adjusted vegetation index | OSAVI = (1 + 0.16) (RNIR − RR)/(RNIR + RR + 0.16) | [44] |
| RDVI | Renormalization difference vegetation index | RDVI = | [45] |
| RVI IV | Ratio vegetation index | RVI = RNIR/RR | [33] |
| SAVI II | Soil-adjusted vegetation index II | SAVI = 1.5(RNIR − RR)/ (RNIR + RR + 0.5) | [46] |
| TVI | Triangular vegetation index | TVI = 60(RNIR − RG) − 100(RR − RG) | [47] |
| MTVI2 | Modified triangular vegetation index | MTVI2 = 1.5(1.2(RNIR − RG) − 2.5(RR − RG))/(sqrt ((2RNIR + 1)2 − (6RNIR − 5sqrt (RR) − 0.5)) | [48] |
| NDVIRed-edge | Red-edge NDVI | NDVIRed-edge = (RNIR − RRed-edge)/(RNIR − RRed-edge) | [49] |
| CIRed-edge | Red-edge Chlorophyll Index | CIRed-edge = (RNIR/RRed-edge) − 1 | [50] |
| MTCI | MERIS Terrestrial Chlorophyll Index | MTCI = (RNIR − RRed-edge)/(RRed-edge − RNIR) | [51] |
| WI | Water Index | WI = R900/R970 | [52] |
| NDWI | Normalized difference water index | NDWI = (R860 − R1240)/(R860 + R1240) | [53] |
| NDII | Normalized difference infrared index | NDII = (R819 − R1600)/(R819 + R1600) | [54] |
| DSWI | Disease water stress index | DSWI = (R803 − R549)/(R1659 + R681) | [55] |
| sLAIDI * | Standardized LAI-determining index | sLAIDI * = s(R1050 − R1250)/(R1050 + R1250)R1555, s = 1 | [56] |
| Algorithm | Feature Types | Calibration Set (n = 48) | Validation Set (n = 24) | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | R2 | RMSE | NRMSE | ||
| Partial Least Squares (PLS) | Ref | 0.59 | 0.38 | 19.8% | 0.82 | 0.28 | 15.2% |
| FD | 0.54 | 0.40 | 20.8% | 0.64 | 0.38 | 21.0% | |
| Random Forest (RF) | Ref | 0.61 | 0.42 | 22.1% | 0.60 | 0.48 | 26.4% |
| FD | 0.59 | 0.38 | 19.9% | 0.58 | 0.43 | 23.6% | |
| Algorithm | Feature Types | Calibration set (n = 48) | Validation set (n = 24) | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | R2 | RMSE | NRMSE | ||
| Partial Least Squares (PLS) | Positions | 0.50 | 0.41 | 21.6% | 0.62 | 0.41 | 22.9% |
| Random Forest (RF) | Positions | 0.57 | 0.40 | 20.9% | 0.52 | 0.47 | 26.1% |
| Algorithm | Feature Types | Calibration Set (n = 48) | Validation Set (n = 24) | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | R2 | RMSE | NRMSE | ||
| Partial Least Squares (PLS) | VIs | 0.68 | 0.33 | 17.4% | 0.80 | 0.31 | 16.9% |
| Random Forest (RF) | VIs | 0.64 | 0.36 | 18.6% | 0.60 | 0.42 | 23.1% |
| Algorithm | Feature Types | Calibration Set (n = 48) | Validation Set (n = 24) | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | R2 | RMSE | NRMSE | ||
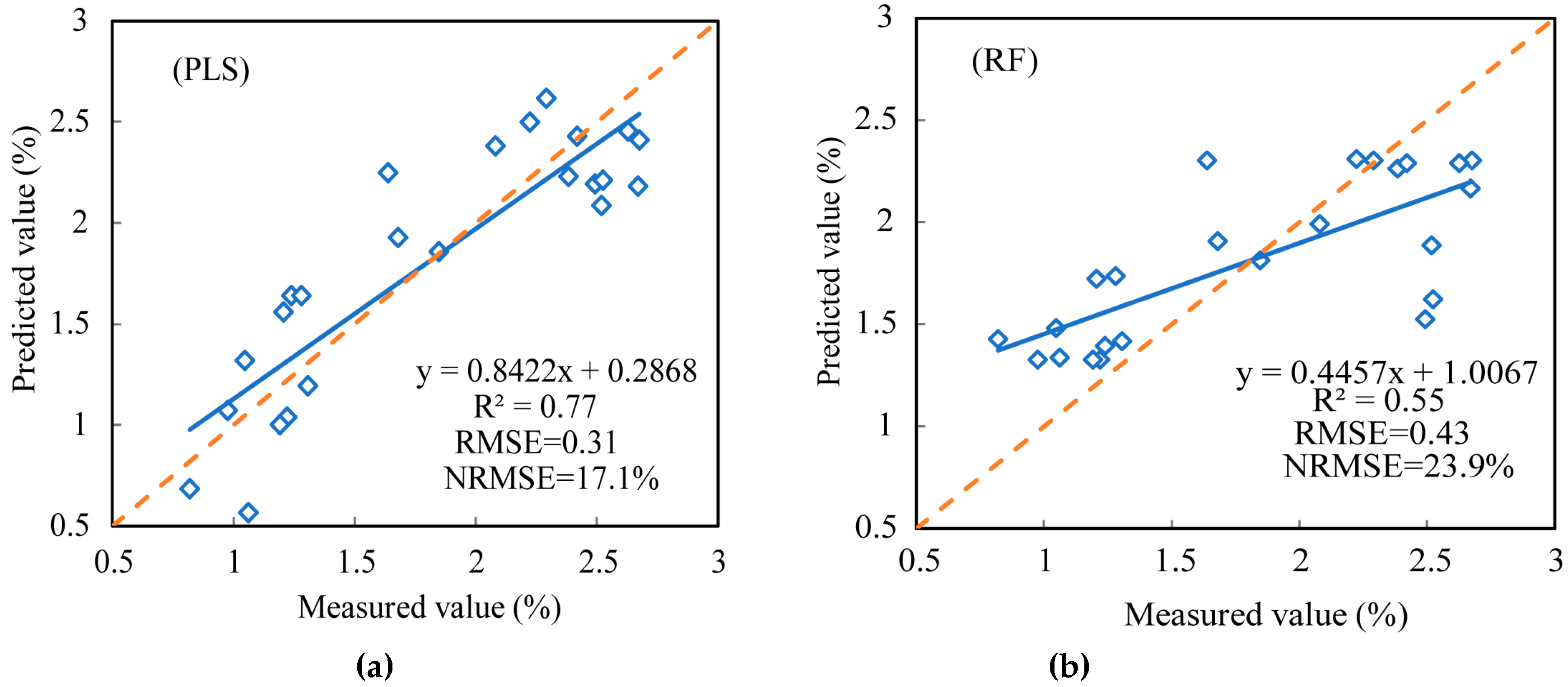
| Partial Least Squares (PLS) | Integrated data | 0.71 | 0.32 | 16.7% | 0.77 | 0.31 | 17.1% |
| Random Forest (RF) | Integrated data | 0.57 | 0.39 | 20.4% | 0.55 | 0.43 | 23.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Zhao, J.; Xu, X.; Liang, D.; Yang, G.; Feng, H.; Yang, H.; Wang, Y.; Chen, G.; Wei, P. Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables. Sensors 2019, 19, 2898. https://doi.org/10.3390/s19132898
Fan L, Zhao J, Xu X, Liang D, Yang G, Feng H, Yang H, Wang Y, Chen G, Wei P. Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables. Sensors. 2019; 19(13):2898. https://doi.org/10.3390/s19132898
Chicago/Turabian StyleFan, Lingling, Jinling Zhao, Xingang Xu, Dong Liang, Guijun Yang, Haikuan Feng, Hao Yang, Yulong Wang, Guo Chen, and Pengfei Wei. 2019. "Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables" Sensors 19, no. 13: 2898. https://doi.org/10.3390/s19132898
APA StyleFan, L., Zhao, J., Xu, X., Liang, D., Yang, G., Feng, H., Yang, H., Wang, Y., Chen, G., & Wei, P. (2019). Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables. Sensors, 19(13), 2898. https://doi.org/10.3390/s19132898







