Refined PHD Filter for Multi-Target Tracking under Low Detection Probability
Abstract
1. Introduction
2. Background
2.1. PHD Filter
2.2. SMC-PHD Filter
3. Refined PHD Filter
3.1. Survival Probability Dependent on Target State
3.2. Labeling Target and Particle
- The label of one target is determined by the label with the largest number of particles belonging to this target.
- If the label of one target is zero, a new positive number will be assigned to it as its label.
- When there are multiple targets with the same label at time , the optimal successor will be selected and keep its label unchanged while others will be assigned a new positive number sequentially.
- 4.
- The label of appearing particles is initialized as zero.
- 5.
- Particles remain their labels unchanged when surviving.
- 6.
- The resampling technique doesn’t change the labels of particles.
- 7.
- If the label of one target is zero, the corresponding particles with label zero will be also assigned a new label corresponding to the target’s new label.
- 8.
- When there are multiple targets with the same label at time , the label of the particles representing optimal successor will remain unchanged, while others will be changed with their targets.
| Algorithm 1 Labelling Particles and Targets |
| Initialization: the initialization particles are labelled with zeros, and maximum label is set to . |
| Prediction: labels of the prediction particles are , where and . |
| Correction: labels of the posterior particles are , and the resampling technique doesn’t change the labels of particles. |
| Trajectory extraction: targets are extracted from the posterior PHD. The label of target can be determined by , where represents the cardinality of set . |
| For each target , if its label is zero, then , set its label to , and set to . |
| If there are multiple targets with the same label , the optimal successor can be selected by Equation (10), and for other target similar operation will be performed like the scene that the label of target is zero. |
3.3. Revision of Posterior Weights
| Algorithm 2 Revision of Posterior Weights |
| For each target at previous time |
| If the survival probability of is above the threshold: , then |
| Find the prediction weights and posterior weights corresponding to target : |
| , where is the set of the index representing target . |
| If , do |
| End |
| End |
| End |
3.4. Target Confirmation Based on Sequential Probability Ratio Test
3.5. Refined PHD Filter
| Algorithm 3 Refined PHD Filter |
| Initialization: suppose prior PHD at time 0 is Equation (3), , and . |
| Prediction: the predicted PHD at time is Equation (5), and labels of the prediction particles are and . |
| Correction: the posterior particle weights at time are calculated by Equation (7), and . |
| Revision of Posterior Weights: execute revision of posterior weights introduced in Section 3.3, the revised weights are still represented as , and the posterior PHD at time is Equation (6). |
| State estimation: , resample with no change of particle labels, and targets are extracted by k-means clustering: . |
| Trajectory extraction: determine the label of target and corresponding particles according to Section 3.2. |
| Survival Probability Calculation: calculate survival probability of individual target according to Section 3.1. |
| Target Confirmation: calculate test statistic , and for individual target, add it to the confirmation set, discard it, or make no decision according to Section 3.4. |
4. Simulation
4.1. Simulation Scenery
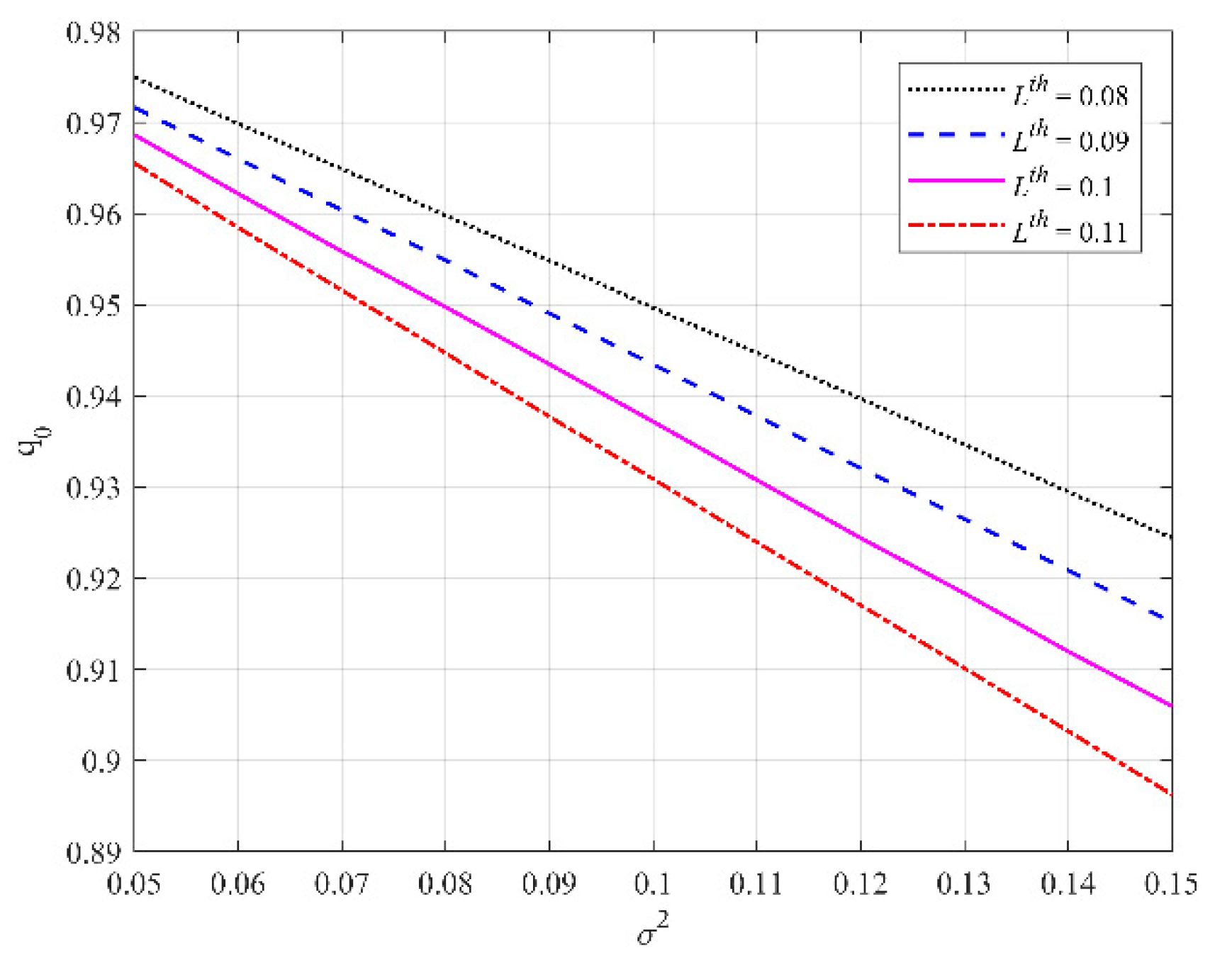
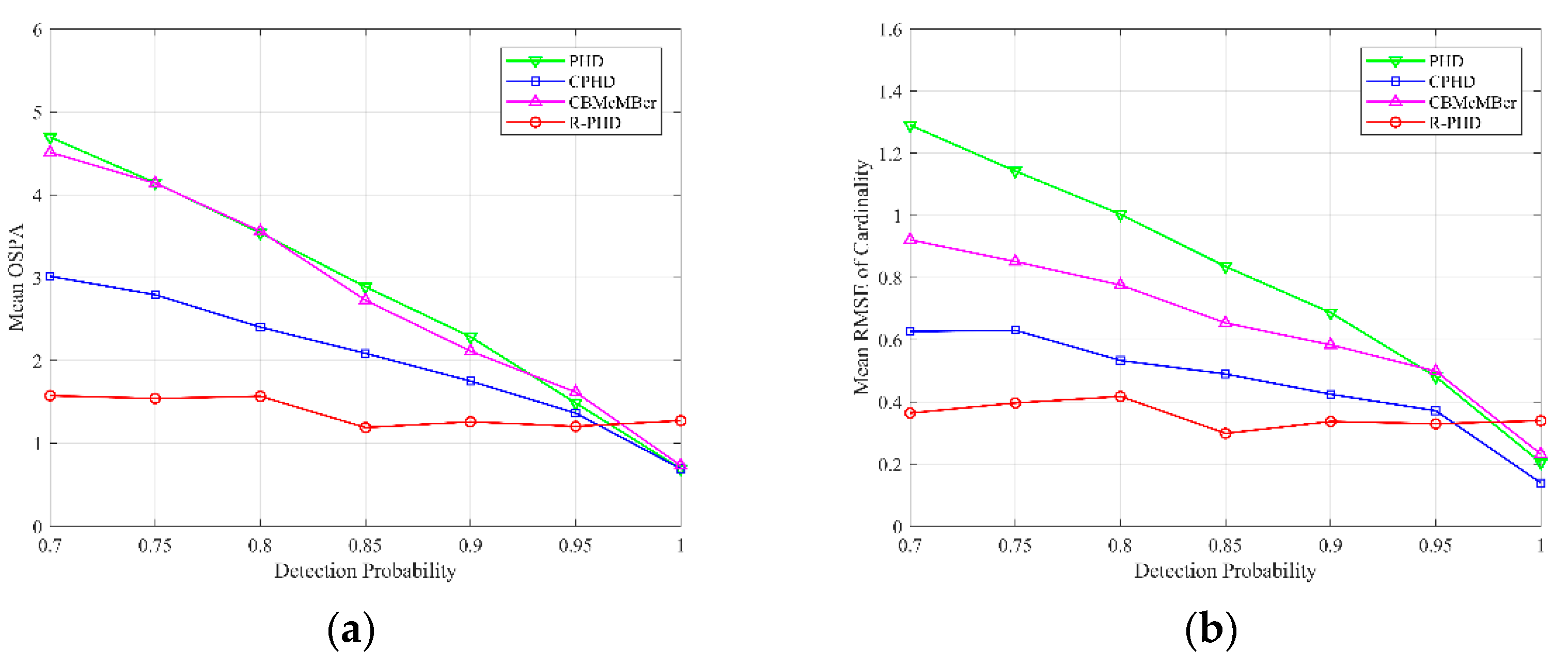
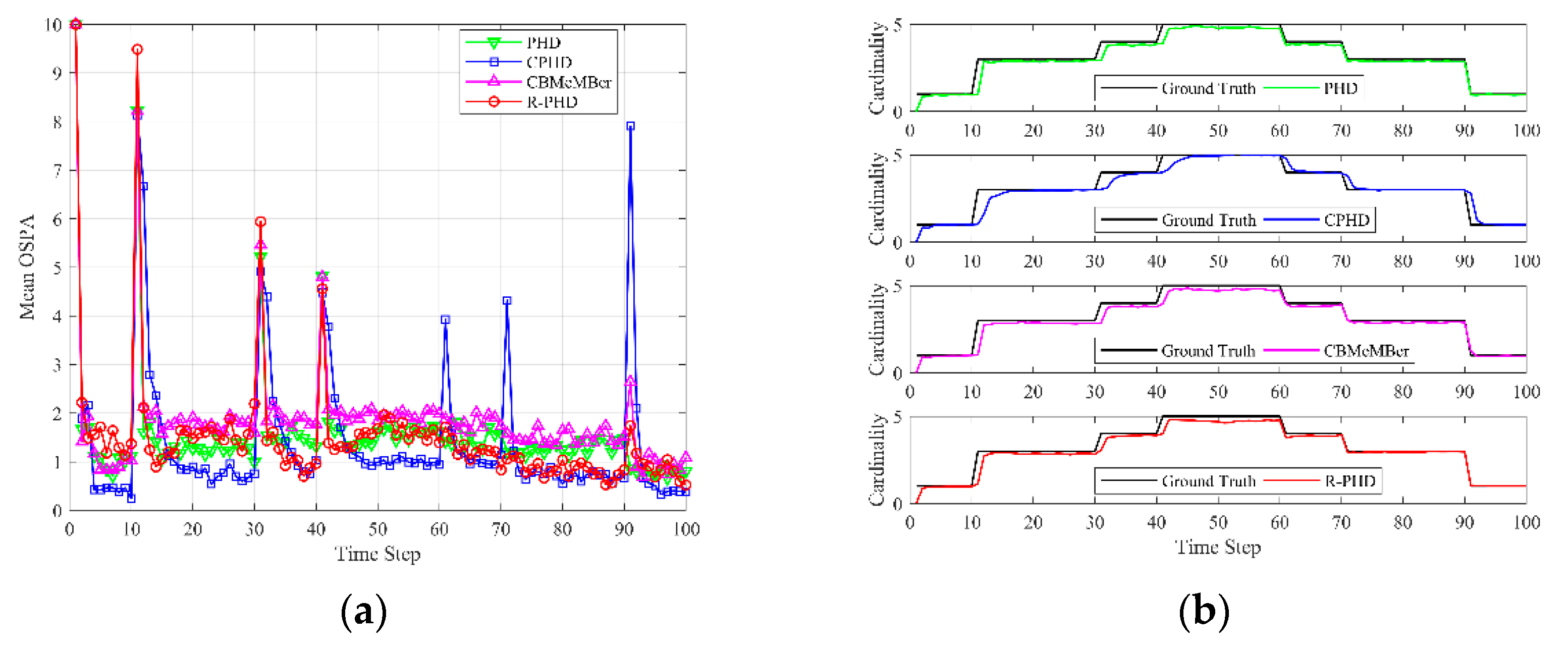
4.2. Evaluation of Different Detection Probabilities
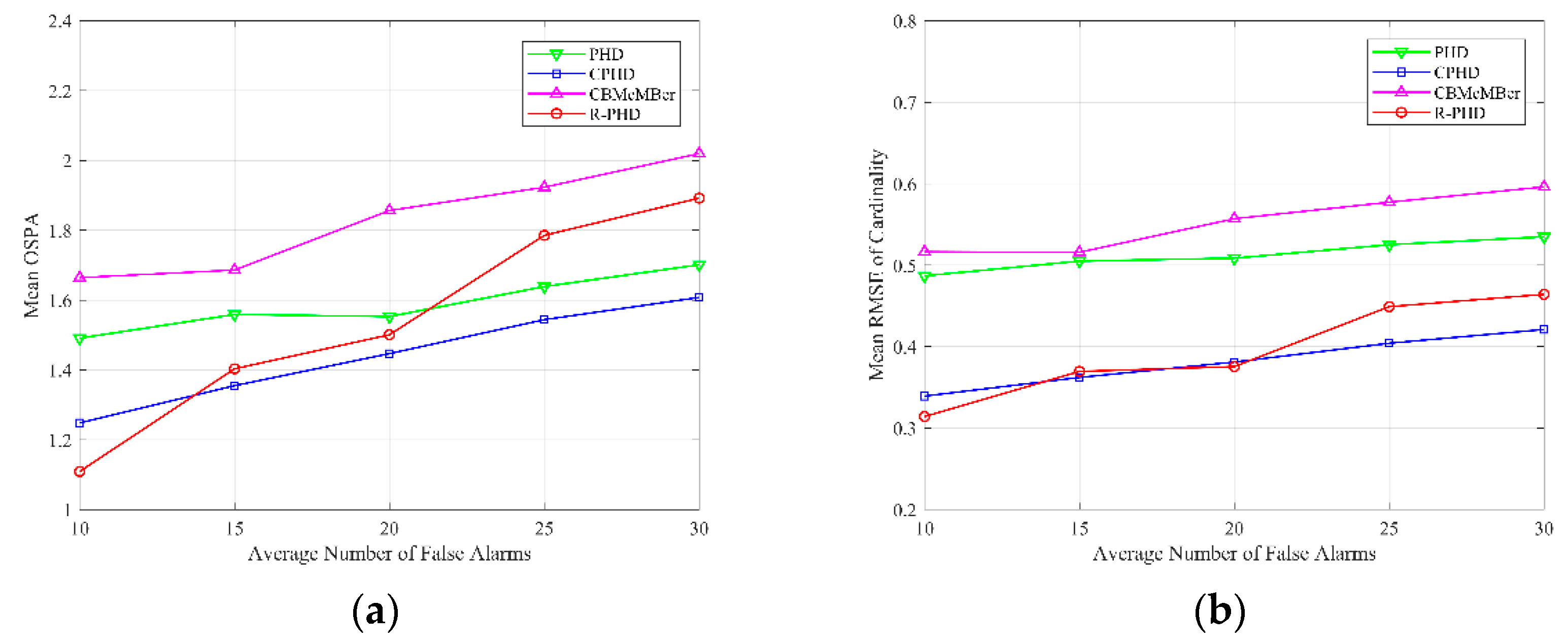
4.3. Evaluation of Different Average Numbers of False Alarms
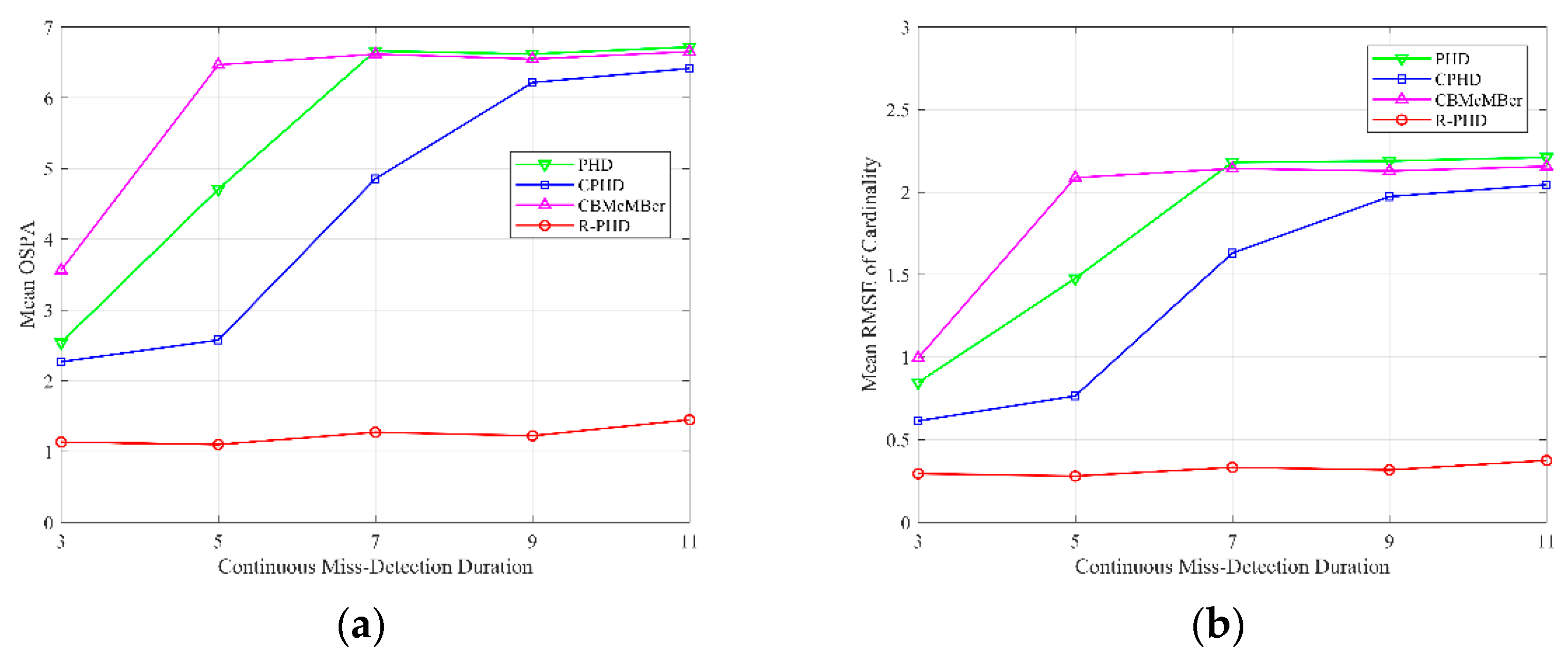
4.4. Evaluation of Different Continuous Miss detection Durations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, D.; Liu, M.; Gao, Y.; Gao, Y.; Fu, W.; Han, Y. Time-matching random finite set-based filter for radar multi-target tracking. Sensors 2018, 18, 4416. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Xie, Y.; Song, T.L. Distributed multi-target tracking in clutter for passive linear array sonar systems. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar]
- Scheidegger, S.; Benjaminsson, J.; Rosenberg, E.; Krishnan, A.; Granström, K. Mono-camera 3D multi-object tracking using deep learning detections and PMBM filtering. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 433–440. [Google Scholar]
- Bar-Shalom, Y. Extension of the probabilistic data association filter in multi-target tracking. In Proceedings of the 5th Symposium on Nonlinear Estimation, San Diego, CA, USA, 23–25 September 1974; pp. 16–21. [Google Scholar]
- Reid, D.B. An algorithm for tracking multiple targets. In Proceedings of the 1978 IEEE Conference on Decision and Control including the 17th Symposium on Adaptive Processes, San Diego, CA, USA, 10–12 January 1979; pp. 1202–1211. [Google Scholar]
- Mahler, R.P. Random-set approach to data fusion. In Proceedings of the Automatic Object Recognition IV, Orlando, FL, USA, 6–7 April 1994; pp. 287–296. [Google Scholar]
- Goodman, I.R.; Mahler, R.P.; Nguyen, H.T. Mathematics of Data Fusion; Springer Science & Business Media: Heidelberg, Germany, 2013; Volume 37. [Google Scholar]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multi-target filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Vo, B.; Ma, W. The gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. Analytic implementations of the cardinalized probability hypothesis density filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Statistical Multisource-Multitarget Information Fusion; Artech House: London, UK, 2007. [Google Scholar]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. The cardinality balanced multi-target multi-bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar] [CrossRef]
- Papi, F.; Vo, B.N.; Vo, B.T.; Fantacci, C.; Beard, M. Generalized labeled multi-bernoulli approximation of multi-object densities. IEEE Trans. Signal Process. 2015, 63, 5487–5497. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.N.; Vo, B.T.; Dietmayer, K. The labeled multi-bernoulli filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Phung, D. Labeled random finite sets and the bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. Multi-scan generalized labeled multi-bernoulli filter. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 195–202. [Google Scholar]
- Vo, B.T.; Vo, B.N. A multi-scan labeled random finite set model for multi-object state estimation. arXiv 2018, arXiv:1805.10038. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Hoang, H.G. An efficient implementation of the generalized labeled multi-bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. A solution for large-scale multi-object tracking. arXiv 2018, arXiv:1804.06622. [Google Scholar]
- Punchihewa, Y.G.; Vo, B.T.; Vo, B.N.; Kim, D.Y. Multiple object tracking in unknown backgrounds with labeled random finite sets. IEEE Trans. Signal Process. 2018, 66, 3040–3055. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Z.; Lu, R.; Hong, S.; Shen, X. An efficient data-driven particle PHD filter for multitarget tracking. IEEE Trans. Ind. Inform. 2013, 9, 2318–2326. [Google Scholar] [CrossRef]
- Macagnano, D.; Abreu, G.T.F.D. Adaptive gating for multitarget tracking with gaussian mixture filters. IEEE Trans. Signal Process. 2012, 60, 1533–1538. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y.J.C.G. A local search approximation algorithm for k-means clustering. Comput. Geom. 2004, 28, 89–112. [Google Scholar] [CrossRef]
- Everitt, B.S.; Dunn, G. Applied Multivariate Data Analysis; Arnold Wiley: London, UK, 2001; Volume 2. [Google Scholar]
- Zhao, L.; Ma, P.; Su, X.; Zhang, H. A new multi-target state estimation algorithm for PHD particle filter. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–8. [Google Scholar]
- Li, T.; Corchado, J.M.; Sun, S.; Fan, H.J.C.J.O.A. Multi-EAP: Extended EAP for multi-estimate extraction for SMC-PHD filter. Chin. J. Aeronaut. 2016, 30, 368–379. [Google Scholar] [CrossRef]
- Schikora, M.; Koch, W.; Streit, R.; Cremers, D. A Sequential Monte Carlo Method for Multi-target Tracking with the Intensity Filter; Springer: Berlin, Germany, 2012. [Google Scholar]
- Li, T.; Sun, S.; Bolić, M.; Corchado, J.M. Algorithm design for parallel implementation of the SMC-PHD filter. Signal Process. 2016, 119, 115–127. [Google Scholar] [CrossRef]
- Li, T.; Prieto, J.; Fan, H.; Corchado, J.M. A robust multi-sensor PHD filter based on multi-sensor measurement clustering. IEEE Commun. Lett. 2018, 22, 2064–2067. [Google Scholar] [CrossRef]
- Liu, L.; Ji, H.; Zhang, W.; Liao, G. Multi-sensor multi-target tracking using probability hypothesis density filter. IEEE Access 2019, 7, 67745–67760. [Google Scholar] [CrossRef]
- Li, T.; Elvira, V.; Fan, H.; Corchado, J.M. Local-diffusion-based distributed SMC-PHD filtering using sensors with limited sensing range. IEEE Sens. J. 2019, 19, 1580–1589. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, J.; Lei, P.; Sun, Z.; Xiang, H. Maneuvering multi-target tracking based on PHD filter for phased array radar. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Li, C.; Wang, W.; Kirubarajan, T.; Sun, J.; Lei, P. PHD and CPHD filtering with unknown detection probability. IEEE Trans. Signal Process. 2018, 66, 3784–3798. [Google Scholar] [CrossRef]
- Chen, X.; Tharmarasa, R.; Pelletier, M.; Kirubarajan, T. Integrated clutter estimation and target tracking using poisson point processes. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1210–1235. [Google Scholar] [CrossRef]
- Han, Y.; Han, C. Two measurement set partitioning algorithms for the extended target probability hypothesis density filter. Sensors 2019, 19, 2665. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Song, Z.; Fan, H.; Fu, Q. RFS-based extended target multipath tracking algorithm. IET Radar Sonar Navig. 2017, 11, 1031–1040. [Google Scholar] [CrossRef]
- Yazdian-Dehkordi, M.; Azimifar, Z. Refined GM-PHD tracker for tracking targets in possible subsequent missed detections. Signal Process. 2015, 116, 112–126. [Google Scholar] [CrossRef]
- Gao, L.; Liu, H.; Liu, H. Probability hypothesis density filter with imperfect detection probability for multi-target tracking. Optik 2016, 127, 10428–10436. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Y.; Li, X.R. Tracking-aided classification of targets using multihypothesis sequential probability ratio test. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 233–245. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
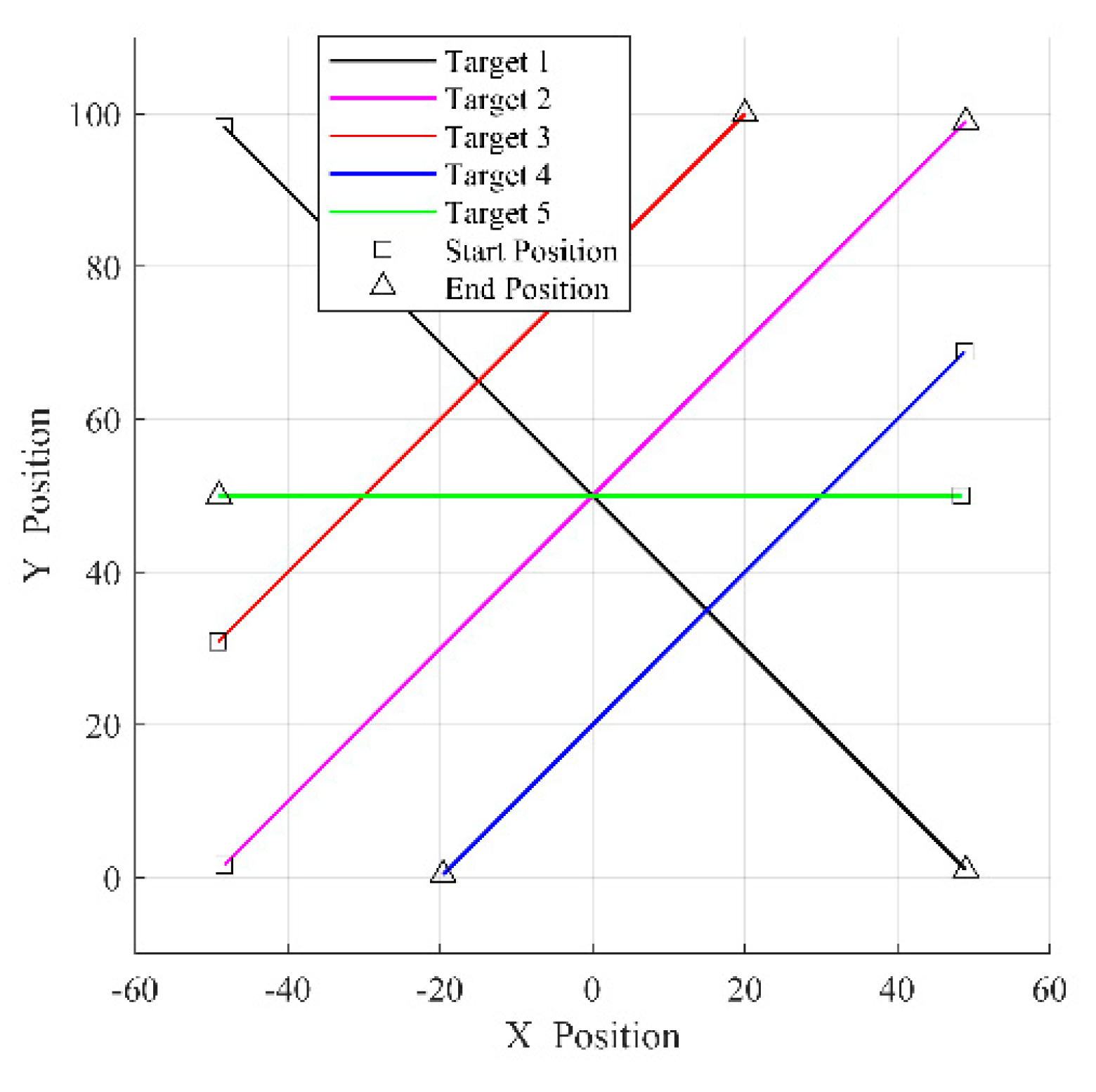


| Target | Initial State | Birth Time | Death Time |
|---|---|---|---|
| 1 | 1 | 60 | |
| 2 | 11 | 70 | |
| 3 | 11 | 90 | |
| 4 | 31 | 90 | |
| 5 | 41 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Bao, Q.; Chen, Z. Refined PHD Filter for Multi-Target Tracking under Low Detection Probability. Sensors 2019, 19, 2842. https://doi.org/10.3390/s19132842
Wang S, Bao Q, Chen Z. Refined PHD Filter for Multi-Target Tracking under Low Detection Probability. Sensors. 2019; 19(13):2842. https://doi.org/10.3390/s19132842
Chicago/Turabian StyleWang, Sen, Qinglong Bao, and Zengping Chen. 2019. "Refined PHD Filter for Multi-Target Tracking under Low Detection Probability" Sensors 19, no. 13: 2842. https://doi.org/10.3390/s19132842
APA StyleWang, S., Bao, Q., & Chen, Z. (2019). Refined PHD Filter for Multi-Target Tracking under Low Detection Probability. Sensors, 19(13), 2842. https://doi.org/10.3390/s19132842




