Mooring test-fly data and real flight data were used to verify the effectiveness of the proposed method.
3.1. Mooring Test-Fly Experiment
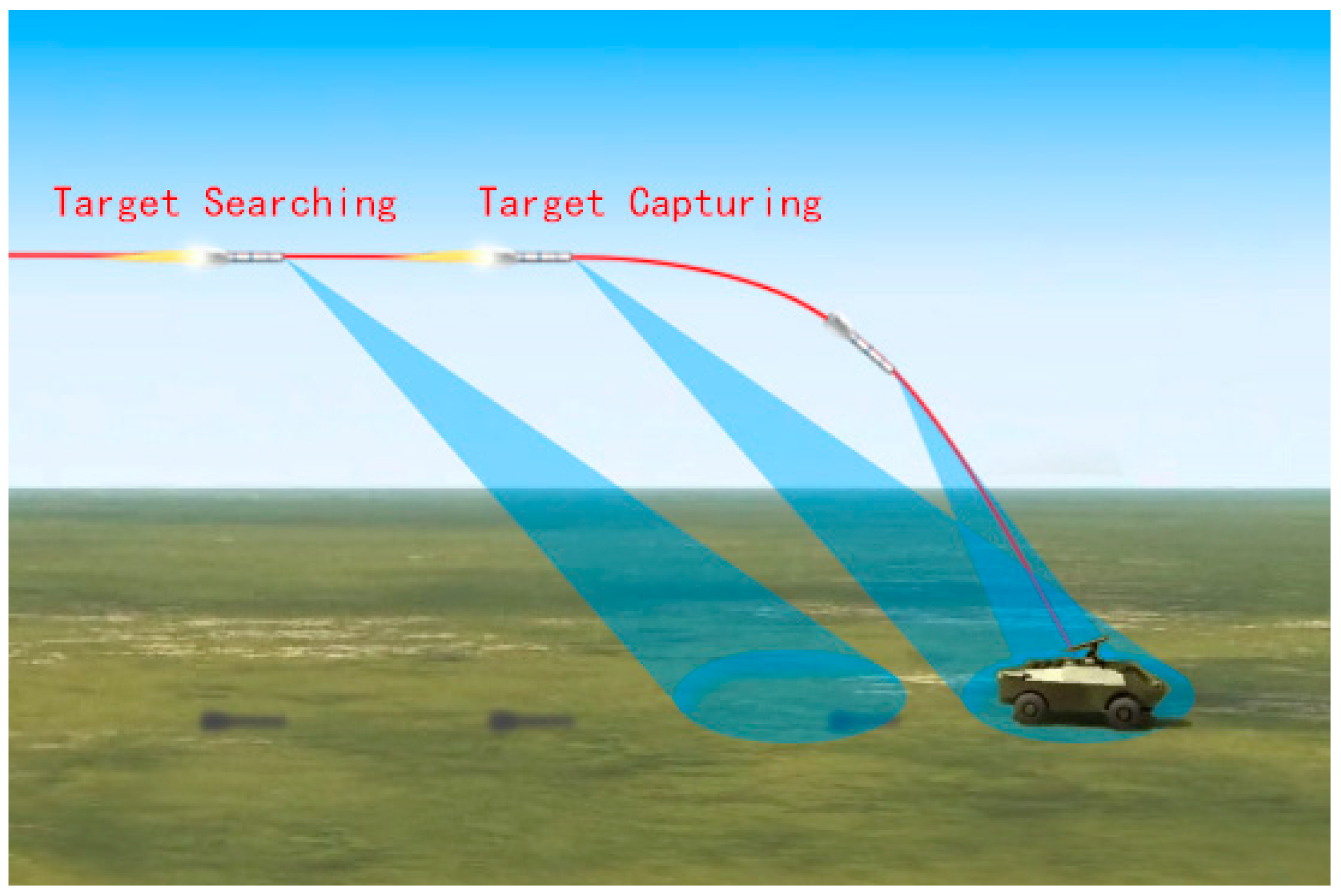
Firstly, we tested the proposed method on a mooring test-fly experiment. Here, we will give an explanation of the mooring test-fly experiment. As is known, a seeker is very expensive, especially for the MMW seeker. As a result, before a seeker is mounted on the missile for launching, we have to evaluate its performance carefully. To fulfill the task, we usually conduct the mooring test-fly experiment. In the mooring test-fly experiment, we mounted the seeker on a platform, such as a helicopter with pilots or an unmanned aerial vehicle (UAV) with remote control on the ground. The platform with the seeker mounted on will move according to the missile trajectory. When the distance from the seeker to the target is within the effective range of the seeker, the seeker will start to illuminate an electromagnetic wave, and implement all the processing just as the real missile fight case. The track will continue until the platform approaches the target, i.e., the distance from the seeker to the target is zero. Then, the platform will fly high and far from the target, getting ready for the next round trip for seeker data collection and performance evaluation. Since the seeker still exists, we can conduct similar processes again and again to search satisfying parameters. For the MMW seeker that we focus on, the platform with the MMW seeker mounted on flies a simulated trajectory. The thresholds for correlation matching are set to be 15 m for range, and 2° for angles, respectively.
The seeker starts to work when reaching the effective working range. Two round scanning of the seeker was conducted subsequently. A total of 11 targets were detected in the first round scanning. The corresponding target information is tabulated in
Table 1, target 1-
denotes the
th detected target. We can know that target 1-3 is the accurate target by the prior information calculation from target location and seeker position obtained by the high-precision global position system (GPS) mounted on the target and the INS mounted on the seeker [
15,
16].
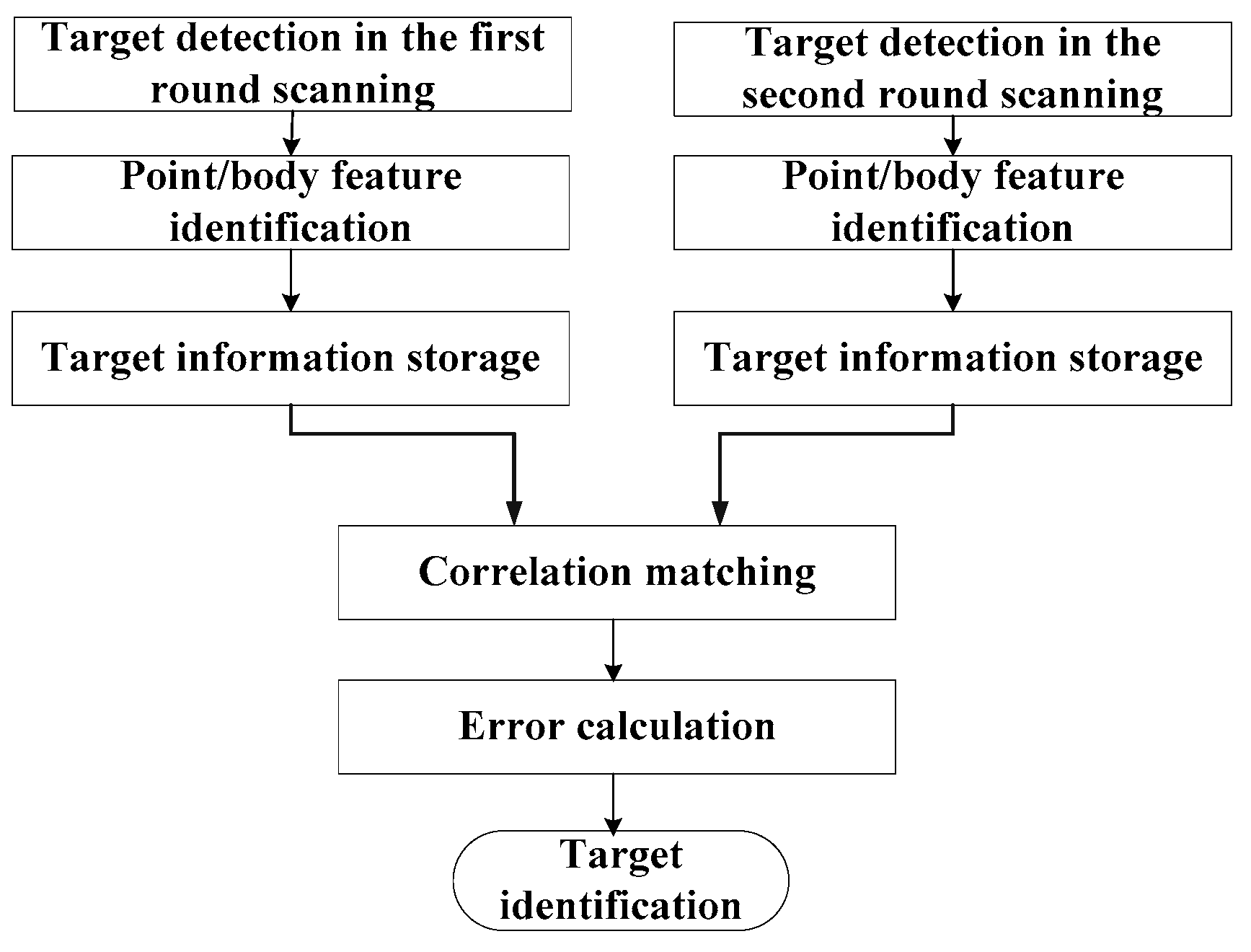
As previously discussed, point/body feature of the target can be determined by using the HRRP [
7,
8,
9]. The HRRP of the MMW echo is given in
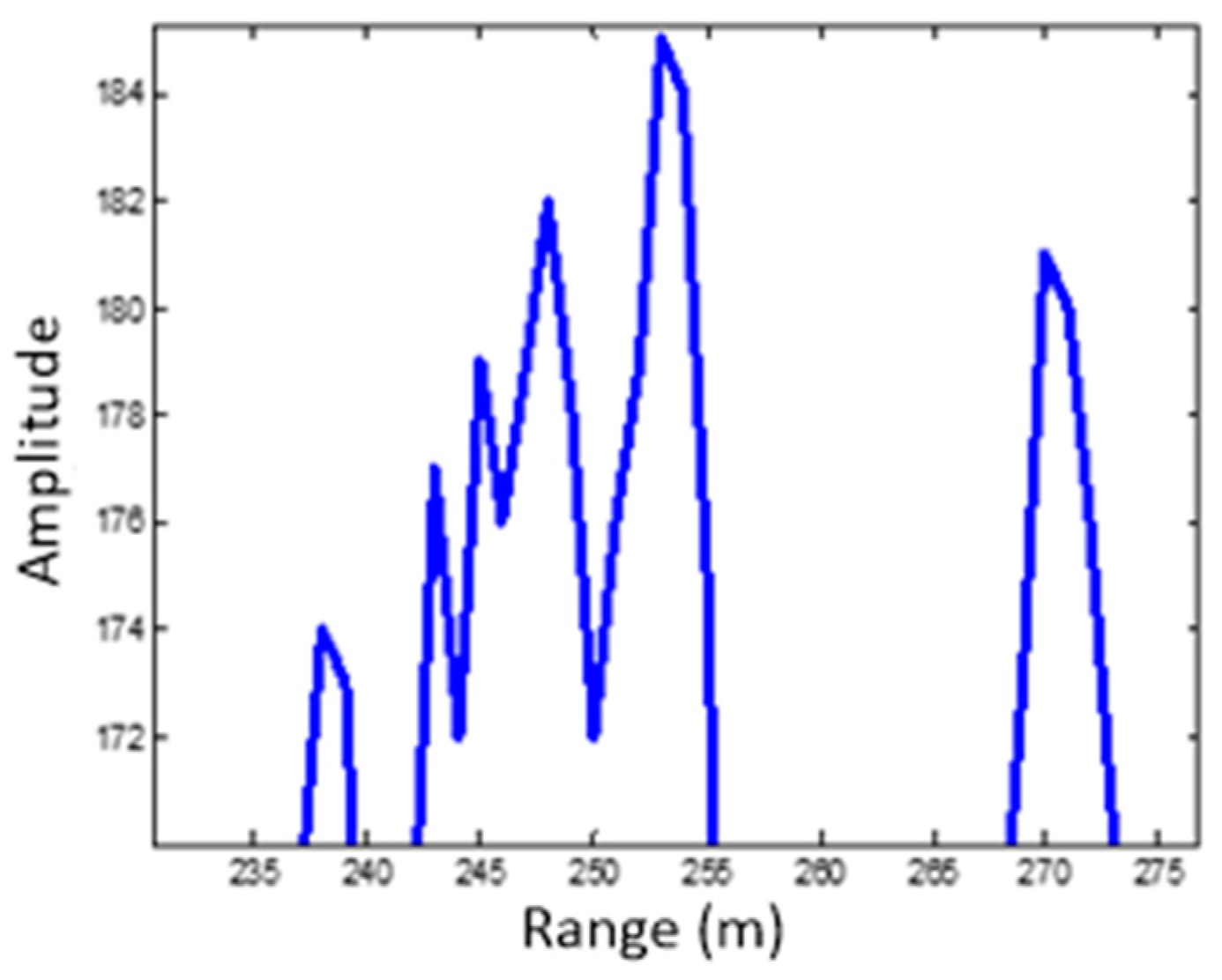
Figure 3. Additionally, the profile after target detection is shown in
Figure 4. As can be seen, there are two objects that exceed the threshold. One appears as a body target, which coincides with the size of a tank, and the other one appears as a point target.
As can be seen in
Table 1, targets that appear as point features will be discarded (targets 1-5 and 1-7 in
Table 1), and the five strongest reflection targets with body features will be chosen for correlation matching, i.e., targets 1-1, 1-2, 1-3, 1-4, and 1-6.
Then, the seeker implemented the second round scanning, and 10 targets were detected in this round scanning. The corresponding target information is shown in
Table 2. Similar to
Table 1, 2-
denotes the
th target in the second round scanning.
Likewise, discarding the targets appearing as point features (targets 2-7, 2-8, and 2-10 in
Table 2), and choosing the five strongest reflection targets with body features, we can get targets 2-1, 2-2, 2-3, 2-4 and 2-5 for correlation matching.
From
Table 3, we can see that only target 2-1 can realize satisfying matching with target 1-1. The range difference is only 6 m, and the value is the smallest of all the candidate targets. We can tell that the range difference may be viewed as the top choice for correlation matching. In addition, the second effective factor is the pitching angle difference. The azimuth angle can provide further assistance.
From
Table 4, we can see that only target 2-2 realizes satisfying matching with target 1-2, and we can further find that the range difference of target 2-4 is also quite small, which is 24 m. Although the range difference is the top choice, we have to set the threshold appropriately to avoid misjudging. Combining the pitching and azimuth angles provides great discriminating power.
From
Table 5, we can see that target 2-3 realizes satisfying matching with target 1-3. In addition, from
Table 6, we can see that there is no target that matches target 1-4. All the targets selected in the second round scanning cannot match target 1-4. In other words, target 1-4 will not arrive at the final stage of target identification. From
Table 7, we can see that target 1-6 realizes satisfying correlation with target 2-4.
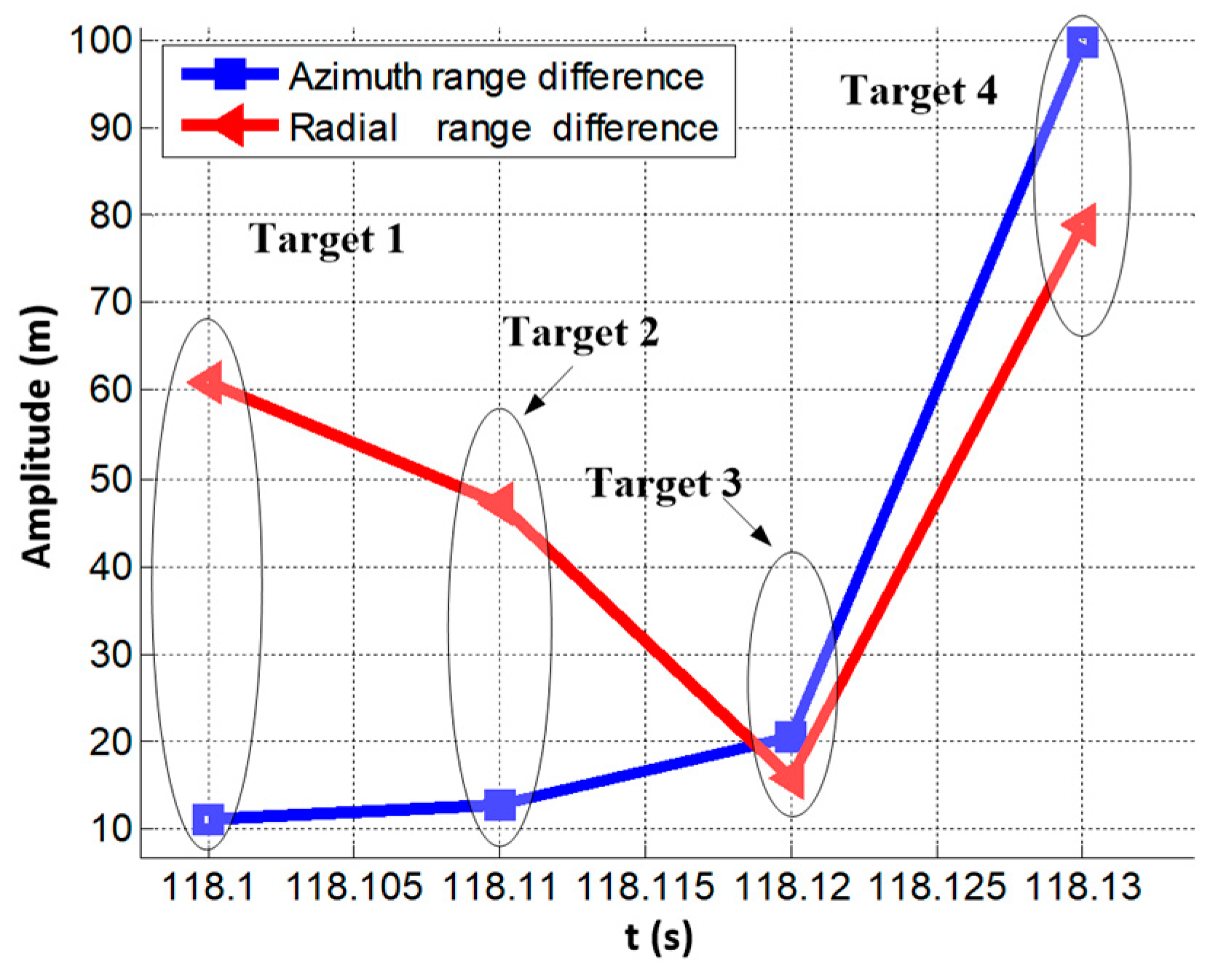
To summarize, after two round target correlation matching, the following target pairs realize satisfying matching: targets 1-1 and 2-1, targets 1-2 and 2-2, targets 1-3 and 2-3, targets 1-6 and 2-4. Here, we label the successfully matched targets as target 1, target 2, target 3, and target 4, respectively. The radial range and azimuth range errors with respect to the beam pointing center are given in
Figure 5. In
Figure 5, the blue line and the red line represent the distance differences in radial and azimuth directions with respect to the origin, i.e., the beam pointing center, respectively.
Then, we calculated error distances associated with the error distribution zone. Just as the determination of the thresholds set for correlation matching, the calculation of the error distribution zone is even more complex. The determination of the parameters along the range and azimuth directions involves plenty of error terms, such as target orientation error by the fire control system, floating error of the INS, and angle determination error of the seeker, etc. Here, we set the parameters empirically through massive data exploration again. The error distribution rectangular zone is formed by 35 and 50 m in the radial and azimuth directions, respectively. Said another way, for a given seeker, the determination of these parameters is achieved by excessive times of mooring test-fly experiments to support the real missile flight.
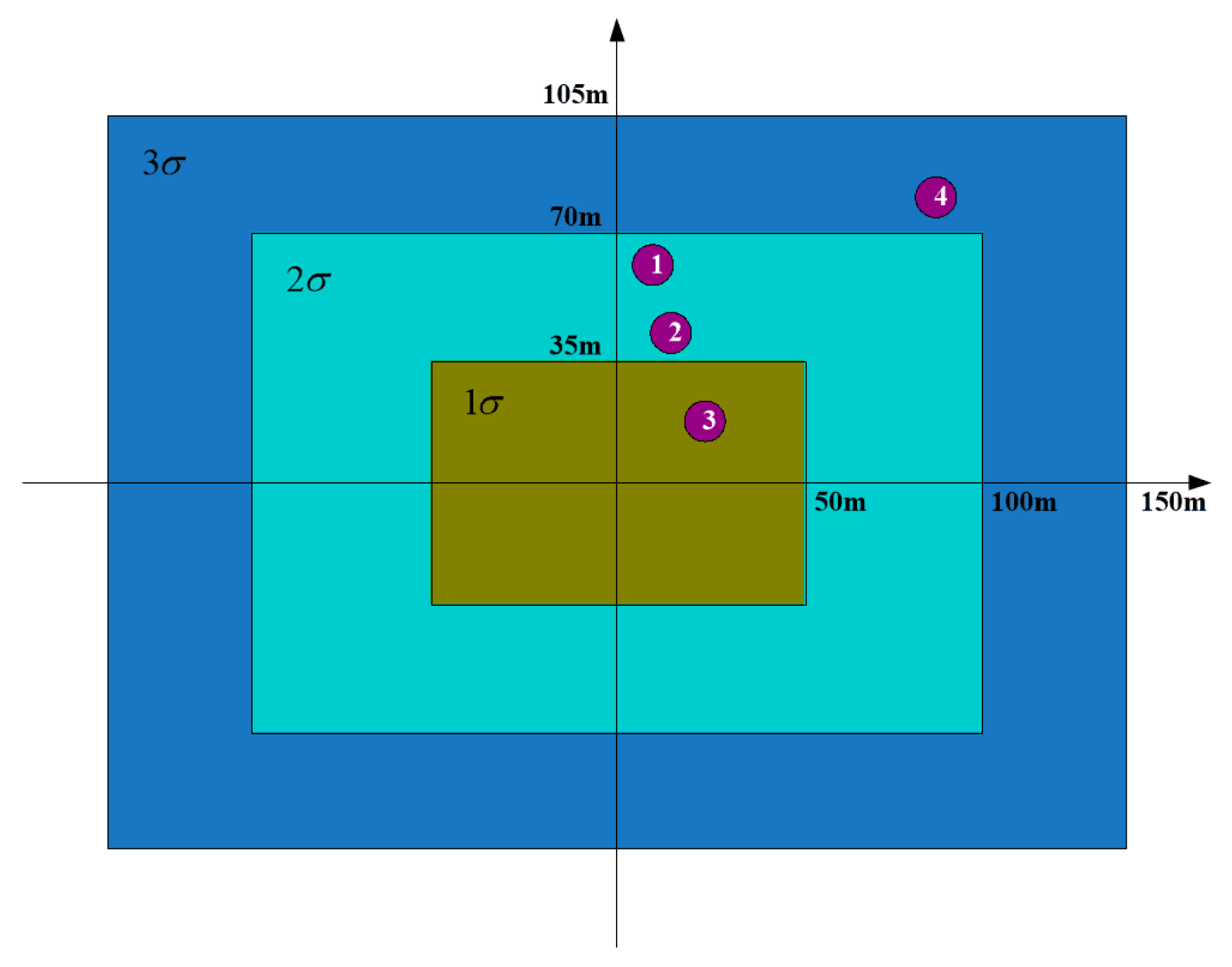
According to the geometry between the interested targets and the beam pointing center, the error distribution zone with the four successfully matched targets are shown in
Figure 6. The abscissa denotes the azimuth range error, and the ordinate denotes the radial range error. From
Figure 6, we can see that target 1 and target 2 lie in the
error zone of the beam pointing center. Target 4 lies in the
error zone of the beam pointing center. Only target 3 lies in the
error zone of the beam pointing center. From
Figure 6, we can see that target 3 lies in the closest error distribution zone of the beam pointing of the seeker. Target 3 will be viewed as the interested target for the seeker. We can see that target identification can be obtained, and the proposed method is capable of providing powerful assistance and support for precise attack of the missile.
Here, we will give more explanations of the parameters, which will affect the final identification result. Although satisfying results can be obtained by using the proposed method, parameter setting is of great importance, and appropriate parameter setting is the precondition of accurate identification. When the parameters are not well-selected, wrong target identification will emerge. In this part, we will display examples in situations with inappropriate parameter setting. Firstly, we take the azimuth angle difference threshold as an example. From
Table 3, we can see that if we set the azimuth angle difference threshold to be less than 1.48°, the correlation matching for the interested target 3 will fail. In other words, target 3 will not be selected for further processing. Wrong identification will inevitably occur.
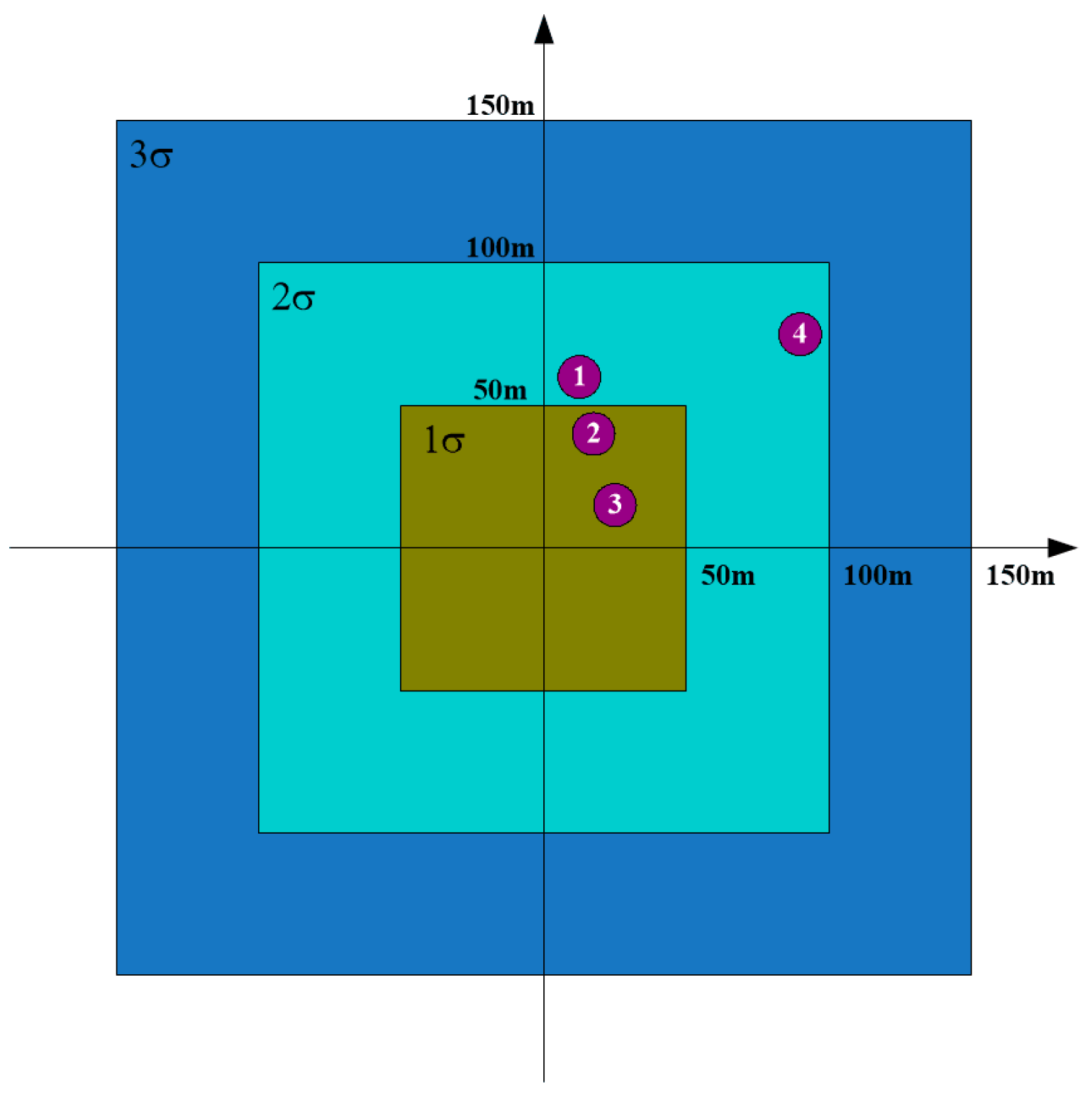
In the following, we take the error distribution zone threshold as another example of inappropriate parameter setting for illustration. In the experiment, the 1
error distribution zone is given by the inside rectangular with radial range threshold of 35 m and azimuth range threshold of 50 m, as shown in
Figure 6. If we set the radial range threshold to be 50 m, the error distribution zone for the targets will change, as shown in
Figure 7. Comparing
Figure 6 with
Figure 7, we can see that for the four interested targets, although target 1 and target 3 still lie in the same error distribution zone with different radial range thresholds, target 2 and target 4 change their error distribution zones. Target 2 lies in the 2
error distribution zone in
Figure 6, whereas it lies in the 1
error distribution zone in
Figure 7. As for target 4, it lies in the 3
error distribution zone in
Figure 6, but it approaches to the 2
error distribution zone in
Figure 7.
As can be seen, both target 2 and target 3 lie in the 1
error distribution zone in
Figure 7. We will choose the target with larger amplitude to be the final identification result, when more than one target lies in the same error distribution zone. That is to say, wrong target identification will emerge in this situation. Target 2 corresponds to target 1-2 in the first round and target 2-2 in the second round, whereas target 3 corresponds to target 1-3 in the first round and target 2-3 in the second round. From
Table 1, we can see that the amplitude of target 1-2 is 120, and the amplitude of target 1-3 is 100. From
Table 2, we can see that the amplitude of target 2-2 is 120, whereas the amplitude of target 2-3 is 111. As can be seen, the amplitude of target 2 is larger than that of target 3 in both rounds. In other words, target 2 will be viewed to be more threatening than target 3. This is definitely what we would like to avoid.
Above all, appropriate parameter setting is of great importance to target identification by using the proposed method. Inappropriate parameter setting will lead to undesirable failure. That is to say, one has to adjust the parameters according to the real seeker system in practice.