Heuristics for Two Depot Heterogeneous Unmanned Vehicle Path Planning to Minimize Maximum Travel Cost
Abstract
1. Introduction
2. Problem Statement
| a set of UVs | |
| a set of depots | |
| a set of targets | |
| a set of vertices for | |
| a set of edges that connect all vertices in | |
| a set of travel costs of all edges in | |
| the subset of the edges of that have one end in S and the other end in | |
| the subset of the edges such that and |
| the decision variable that represents whether edge is used for the tour of | |
| the decision variable that represents partition of targets in T | |
| t | the maximum travel cost |
| the final tour cost of within a given partition of the targets | |
| the final tour of within a given partition of the targets | |
| a set of edges in the forest corresponding to | |
| a set of connected components in | |
| the dual variable of a set C in , which keeps track of |
| the dual variable of a set C where , which keeps track of | |
| the dual variable of a set C in , which keeps track of | |
| the activeness of set . only if C is active. | |
| the subsets of set in |
3. TDHTSP with Symmetric Travel Costs
3.1. Problem Formulation
3.2. A Heuristic for the TDHTSP
| Algorithm 1 A heuristic for min-max TDHTSP | |
| 1: | ; |
| 2: | Determine a heterogeneous spanning forest using the proposed primal-dual heuristic. |
| 3: | fordo |
| 4: | Let the connected targets reachable from the depot be a partition and label it as . |
| 5: | end for |
| 6: | For , derive and for within (using an existing routing algorithm). |
| 7: | |
| 8: | ifthen |
| 9: | while do |
| 10: | |
| 11: | Redetermine a target assignment using the proposed primal-dual heuristic and obtain the partitions . |
| 12: | for do |
| 13: | Derive and within . |
| 14: | end for |
| 15: | if is infeasible then |
| 16: | break, {comment: for some } |
| 17: | else |
| 18: | |
| 19: | if then |
| 20: | |
| 21: | for do |
| 22: | |
| 23: | end for |
| 24: | end if |
| 25: | end if |
| 26: | end while |
| 27: | else |
| 28: | while do |
| 29: | |
| 30: | Redetermine a target assignment using the proposed primal-dual heuristic and obtain the partitions . |
| 31: | for do |
| 32: | Derive and within . |
| 33: | end for |
| 34: | |
| 35: | if then |
| 36: | |
| 37: | for do |
| 38: | |
| 39: | end for |
| 40: | end if |
| 41: | end while |
| 42: | end if |
| 43: | return |
| Algorithm 2 Primal-dual heuristic for finding an HSF | |
| 1: | Initialization |
| 2: | , for |
| 3: | All vertices are unmarked. |
| 4: | All dual variables are set to zero. |
| 5: | , , for |
| 6: | , for |
| 7: | Main loop |
| 8: | while there exists any active component in do |
| 9: | for do |
| 10: | Find an edge with where that minimizes . |
| 11: | end for |
| 12: | Let . |
| 13: | Find that minimizes |
| 14: | |
| 15: | for do |
| 16: | for do |
| 17: | |
| 18: | |
| 19: | if then |
| 20: | |
| 21: | end if |
| 22: | end for |
| 23: | end for |
| 24: | if for or 2 then |
| 25: | |
| 26: | |
| 27: | |
| 28: | if then |
| 29: | |
| 30: | end if |
| 31: | if then |
| 32: | |
| 33: | if then |
| 34: | |
| 35: | end if |
| 36: | else |
| 37: | |
| 38: | end if |
| 39: | else |
| 40: | |
| 41: | Mark all of the vertices of with the label . |
| 42: | end if |
| 43: | end while |
| 44: | Pruning |
| 45: | |
| 46: | |
| 47: | Let be the minimum spanning tree of . |
| 48: | Let be the sum of edge costs present in |
| 49: | while is not empty do |
| 50: | Find the shortest edge that connects a vertex in and a vertex in for each k. |
| 51: | if then |
| 52: | Add to , remove the corresponding vertex from , and add it to . |
| 53: | else |
| 54: | Add to , remove the corresponding vertex from and add it to . |
| 55: | end if |
| 56: | end while |
4. TDHTSP with Asymmetric Travel Costs
4.1. Problem Formulation
4.2. A Heuristic for the TDHATSP
| Algorithm 3 Primal-dual heuristic for finding an HDSF | |
| 1: | Initialization |
| 2: | , for |
| 3: | All the vertices are unmarked. |
| 4: | All the dual variables are set to zero. |
| 5: | , , for |
| 6: | , for |
| 7: | Main loop |
| 8: | while there exists any active component in do |
| 9: | for k = 1, 2 do |
| 10: | Find an edge with , where that minimizes |
| 11: | end for |
| 12: | Let the corresponding be , while satisfies and are active. |
| 13: | |
| 14: | Increase the dual variables of by . |
| 15: | if forms a new strongly connected component and the component is not reachable from then |
| 16: | Let the strongly connected component be an active component. |
| 17: | else if makes any vertex reachable from then |
| 18: | Let the depot and all vertices that are reachable from the depot be an inactive component. |
| 19: | if then |
| 20: | Deactivate all subsets of this component in . |
| 21: | else |
| 22: | Mark all vertices in the supersets of this component in . Deactivate it if the corresponding component consists of all marked vertices. |
| 23: | end if |
| 24: | else |
| 25: | Deactivate . |
| 26: | end if |
| 27: | if there exists no that can be chosen that satisfies the given conditions and there exists any inactive set without an incoming edge that is not connected to the depot then |
| 28: | Pick an inactive component for each k that consists of marked vertices that have incoming or outgoing edges. Combine those connected components until the new component does not have any incoming edges. |
| 29: | end if |
| 30: | end while |
| 31: | Pruning |
| 32: | |
| 33: | |
| 34: | Let be the minimum directed spanning tree of . |
| 35: | Let be the sum of the edge costs present in . |
| 36: | while is not empty do |
| 37: | Find the shortest edge that makes a vertex in reachable from the vertices in for each k. |
| 38: | if then |
| 39: | Add to , remove the corresponding vertex from , and add it to . |
| 40: | else |
| 41: | Add to , remove the corresponding vertex from , and add it to . |
| 42: | end if |
| 43: | end while |
5. Implementation
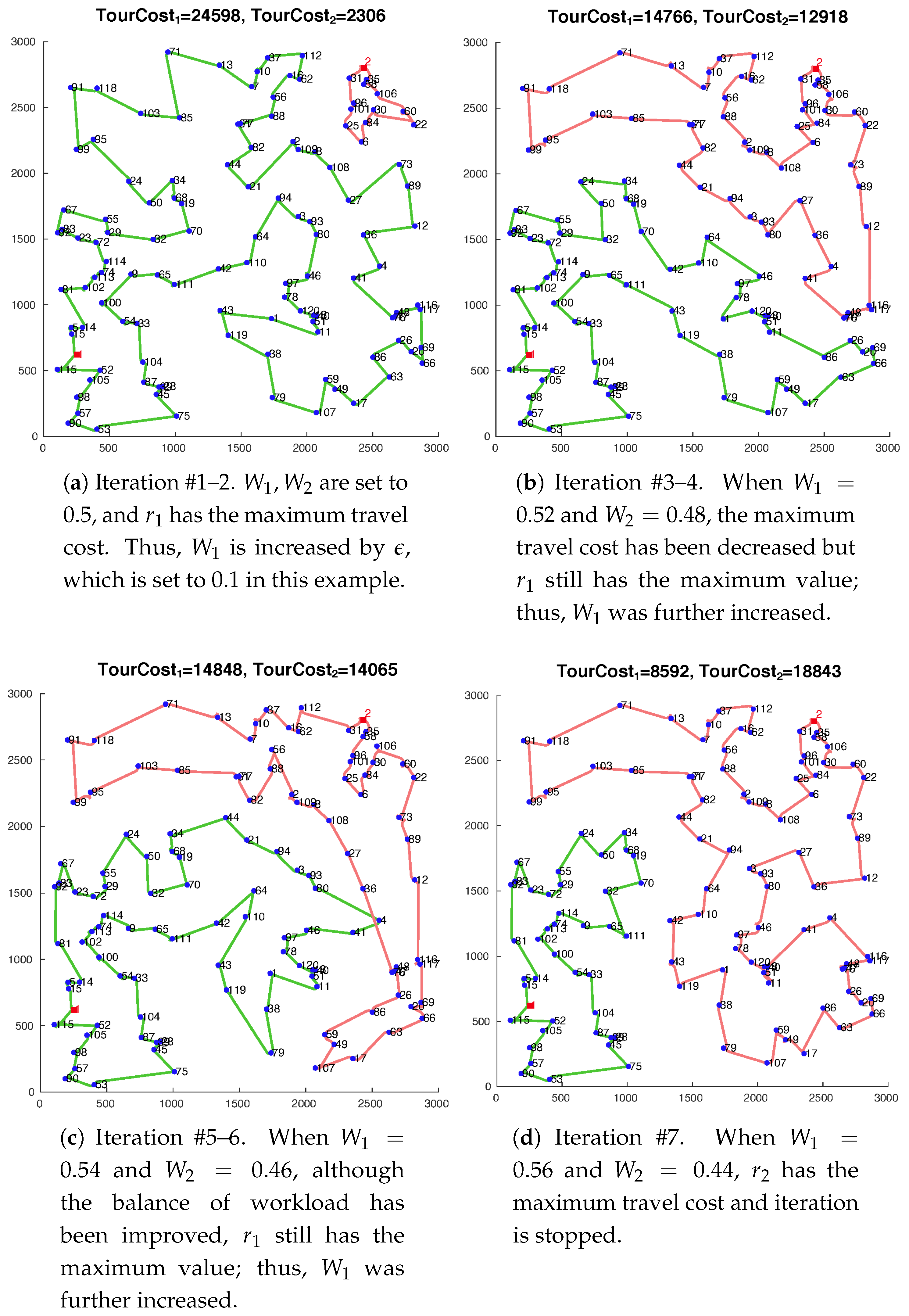
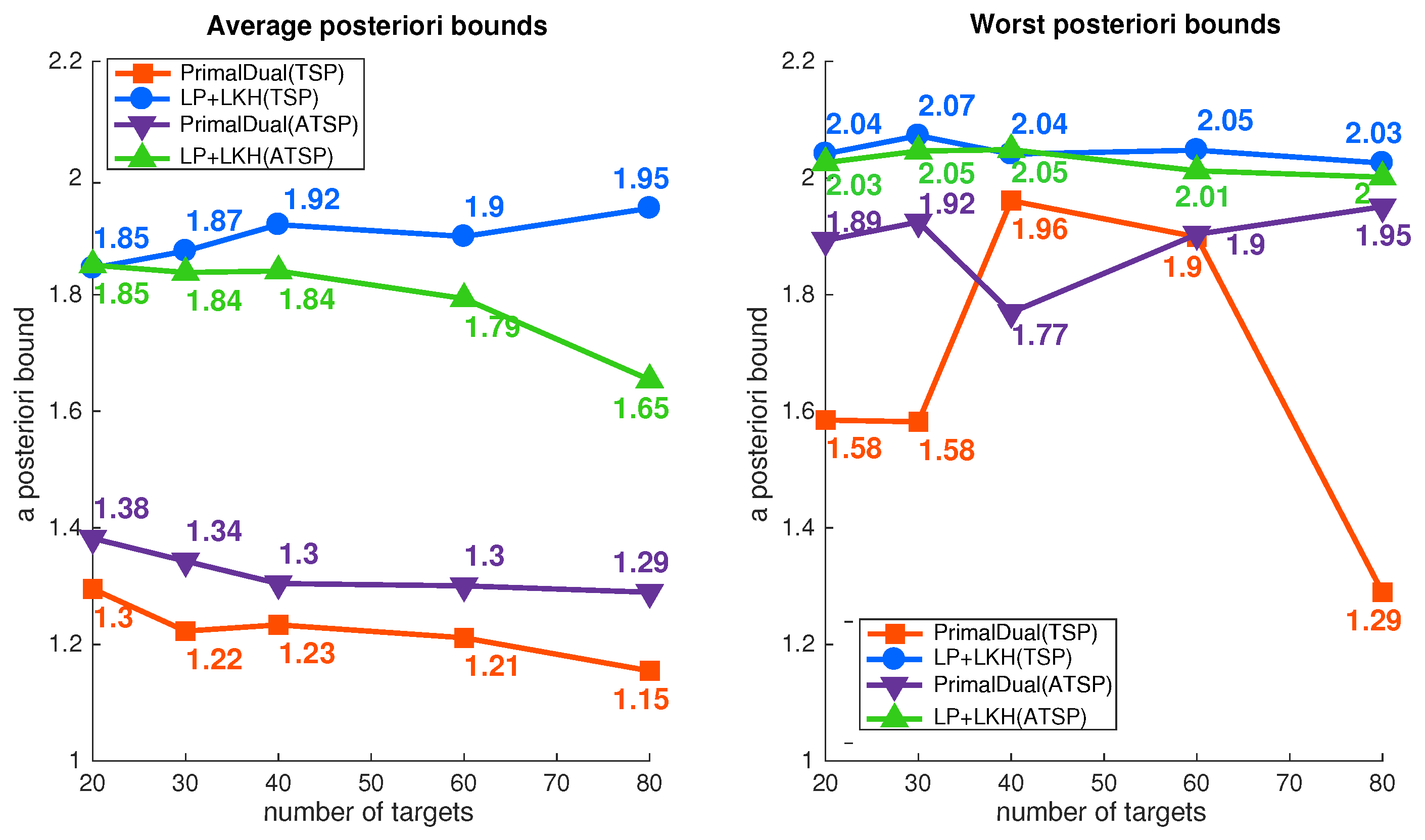
Discussion of Implementation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reinecke, M.; Prinsloo, T. The influence of drone monitoring on crop health and harvest size. In Proceedings of the 2017 1st International Conference on Next Generation Computing Applications (NextComp), Moka, Mauritius, 19–21 July 2017; pp. 5–10. [Google Scholar] [CrossRef]
- Malveaux, C.; Hall, S.G.; Price, R. Using Drones in Agriculture: Unmanned Aerial Systems for Agricultural Remote Sensing Applications. Am. Soc. Agric. Biol. Eng. 2014, 1. [Google Scholar] [CrossRef]
- Kanistras, K.; Martins, G.; Rutherford, M.J.; Valavanis, K.P. A survey of unmanned aerial vehicles (UAVs) for traffic monitoring. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 221–234. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, Y.; Liu, Z. A survey on technologies for automatic forest fire monitoring, detection, and fighting using unmanned aerial vehicles and remote sensing techniques. Can. J. For. Res. 2015, 45, 783–792. [Google Scholar] [CrossRef]
- Casbeer, D.W.; Kingston, D.B.; Beard, R.W.; McLain, T.W. Cooperative forest fire surveillance using a team of small unmanned air vehicles. Int. J. Syst. Sci. 2006, 37, 351–360. [Google Scholar] [CrossRef]
- Mendonça, R.; Marques, M.M.; Marques, F.; Lourenço, A.; Pinto, E.; Santana, P.; Coito, F.; Lobo, V.; Barata, J. A cooperative multi-robot team for the surveillance of shipwreck survivors at sea. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Ai, X.; Xu, X.; Yang, D. Cooperative multiple task assignment problem with stochastic velocities and time windows for heterogeneous unmanned aerial vehicles using a genetic algorithm. Aerosp. Sci. Technol. 2018, 76, 112–125. [Google Scholar] [CrossRef]
- Calhoun, G.; Ruff, H.; Behymer, K.; Frost, E. Human-autonomy teaming interface design considerations for multi-unmanned vehicle control. Theor. Issues Ergon. Sci. 2018, 19, 321–352. [Google Scholar] [CrossRef]
- Murphy, R.R.; Kravitz, J.; Stover, S.L.; Shoureshi, R. Mobile robots in mine rescue and recovery. IEEE Robot. Autom. Mag. 2009, 16, 91–103. [Google Scholar] [CrossRef]
- Middleton, W.; Miller, G.; Pollman, A. Architecture models for coordination of unmanned air and ground vehicles conducting humanitarian assistance and disaster relief. In Proceedings of the Conference on Systems Engineering Research, Charlottesville, VA, USA, 8–9 May 2018. [Google Scholar]
- Kulich, M.; Kubalik, J.; Přeučil, L. An Integrated Approach to Goal Selection in Mobile Robot Exploration. Sensors 2019, 19, 1400. [Google Scholar] [CrossRef] [PubMed]
- Jungyun Bae, W.C. A Heuristic for Path Planning of Multiple Heterogeneous Automated Guided Vehicles. Int. J. Precis. Eng. Manuf. 2018, 19, 1765–1771. [Google Scholar]
- Vazirani, V.V. Approximation Algorithms; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- De Oliveira, G.C.R.; de Carvalho, K.B.; Brandão, A.S. A Hybrid Path-Planning Strategy for Mobile Robots with Limited Sensor Capabilities. Sensors 2019, 19, 1049. [Google Scholar] [CrossRef]
- Tang, J.; Yang, W.; Zhu, L.; Wang, D.; Feng, X. An Adaptive Clustering Approach Based on Minimum Travel Route Planning for Wireless Sensor Networks with a Mobile Sink. Sensors 2017, 17, 964. [Google Scholar] [CrossRef]
- Dahan, F.; El Hindi, K.; Mathkour, H.; AlSalman, H. Dynamic Flying Ant Colony Optimization (DFACO) for Solving the Traveling Salesman Problem. Sensors 2019, 19, 1837. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Sundar, K.; Rathinam, S. A Two-Stage Approach for Routing Multiple Unmanned Aerial Vehicles with Stochastic Fuel Consumption. Sensors 2018, 18, 3756. [Google Scholar] [CrossRef]
- Bae, J.; Rathinam, S. A primal-dual approximation algorithm for a two depot heterogeneous traveling salesman problem. Optim. Lett. 2016, 10, 1269–1285. [Google Scholar] [CrossRef]
- Franceschelli, M.; Rosa, D.; Seatzu, C.; Bullo, F. Gossip algorithms for heterogeneous multi-vehicle routing problems. Nonlinear Anal. Hybrid Syst. 2013, 10, 156–174. [Google Scholar] [CrossRef]
- Prasad, A.; Sundaram, S.; Choi, H. Min-Max Tours for Task Allocation to Heterogeneous Agents. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 1706–1711. [Google Scholar] [CrossRef]
- Stodola, P. Using Metaheuristics on the Multi-Depot Vehicle Routing Problem with Modified Optimization Criterion. Algorithms 2018, 11, 74. [Google Scholar] [CrossRef]
- Wang, X.; Golden, B.; Wasil, E. The min-max multi-depot vehicle routing problem: Heuristics and computational results. J. Oper. Res. Soc. 2015, 66, 1430–1441. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for Heterogeneous, Multiple Depot, Multiple Unmanned Vehicle Path Planning Problems. J. Intell. Robot. Syst. 2017, 88, 513–526. [Google Scholar] [CrossRef]
- Cho, D.H.; Jang, D.S.; Choi, H.L. Sampling-Based Tour Generation of Arbitrarily Oriented Dubins Sensor Platforms. J. Aerosp. Inf. Syst. 2019, 16, 168–186. [Google Scholar] [CrossRef]
- Azadeh, A.; Farrokhi-Asl, H. The close–open mixed multi depot vehicle routing problem considering internal and external fleet of vehicles. Transp. Lett. 2019, 11, 78–92. [Google Scholar] [CrossRef]
- Goemans, M.X.; Williamson, D.P. The Primal-dual Method for Approximation Algorithms and Its Application to Network Design Problems. In Approximation Algorithms for NP-Hard Problems; Hochbaum, D.S., Ed.; PWS Publishing Co.: Boston, MA, USA, 1997; pp. 144–191. [Google Scholar]
- Helsgaun, K. An effective implementation of the Lin-Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Reeds, J.; Shepp, L. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Sussmann, H.J.; Tang, G. Shortest Paths for the Reeds-Shepp Car: A Worked out Example of the Use of Geometric Techniques in Nonlinear Optimal Control; Rutgers Univ., Tech. Rep.; SYNCON: Piscataway, NJ, USA, 1991. [Google Scholar]
- IBM ILOG CPLEX Optimization Studio. 2017. Available online: https://www.ibm.com/us-en/marketplace/ibm-ilog-cplex (accessed on 8 April 2019).
- LKH-2.0.9. 2009. Available online: http://www.akira.ruc.dk/~keld/research/LKH/ (accessed on 8 April 2019).
- Bae, J. Algorithms for Multiple Vehicle Routing Problems. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2014. [Google Scholar]


| Depots | Heterogeneity(s) | Heterogeneity(f) | Objective | Methodology | Cost | |
|---|---|---|---|---|---|---|
| This Paper | Two | Yes | No | Min-Max | Primal-Dual | Symmetric and Asymmetric |
| [18] | two | Yes | No | min-sum | primal-dual | symmetric |
| [19] | multiple | Yes | No | min-max | gossip algorithm | symmetric |
| [20] | single | No | Yes | min-max | 5-approx algo. | symmetric |
| [21] | multiple | No | No | min-max | ant colony opt. | symmetric |
| [22] | multiple | No | No | min-max | LP based heuristic | symmetric |
| [23] | multiple | Yes | Yes | min-sum | branch and cut | asymmetric |
| [24] | multiple | Yes | No | min-sum | transformation | asymmetric |
| [25] | multiple | No | Yes | min-sum | hybrid GA | symmetric |
| Average | Worst | |||
|---|---|---|---|---|
| No. of Jobs | LP Rounding | Primal-Dual | LP Rounding | Primal-Dual |
| 20 | 2.11 | 0.81 | 2.91 | 1.61 |
| 30 | 31.13 | 1.79 | 41.23 | 2.35 |
| 40 | 429.61 | 3.30 | 867.66 | 5.26 |
| 60 | 5623.48 | 8.62 | 8470.95 | 11.72 |
| 80 | 39,891.46 | 19.65 | 63,239.30 | 31.02 |
| Average | Worst | |||
|---|---|---|---|---|
| No. of Jobs | LP Rounding | Primal-Dual | LP Rounding | Primal-Dual |
| 20 | 1.59 | 1.23 | 2.38 | 3.28 |
| 30 | 17.70 | 4.80 | 22.11 | 12.31 |
| 40 | 237.06 | 4.86 | 345.81 | 12.79 |
| 60 | 3634.76 | 16.00 | 10006.30 | 46.08 |
| 80 | 30,329.19 | 36.21 | 41,330.20 | 99.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J.; Chung, W. Heuristics for Two Depot Heterogeneous Unmanned Vehicle Path Planning to Minimize Maximum Travel Cost. Sensors 2019, 19, 2461. https://doi.org/10.3390/s19112461
Bae J, Chung W. Heuristics for Two Depot Heterogeneous Unmanned Vehicle Path Planning to Minimize Maximum Travel Cost. Sensors. 2019; 19(11):2461. https://doi.org/10.3390/s19112461
Chicago/Turabian StyleBae, Jungyun, and Woojin Chung. 2019. "Heuristics for Two Depot Heterogeneous Unmanned Vehicle Path Planning to Minimize Maximum Travel Cost" Sensors 19, no. 11: 2461. https://doi.org/10.3390/s19112461
APA StyleBae, J., & Chung, W. (2019). Heuristics for Two Depot Heterogeneous Unmanned Vehicle Path Planning to Minimize Maximum Travel Cost. Sensors, 19(11), 2461. https://doi.org/10.3390/s19112461





