Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals and Seawater Samples
2.2. Electrochemical Measurements
2.3. Library and Sample Preparation
2.4. Data Preprocessing
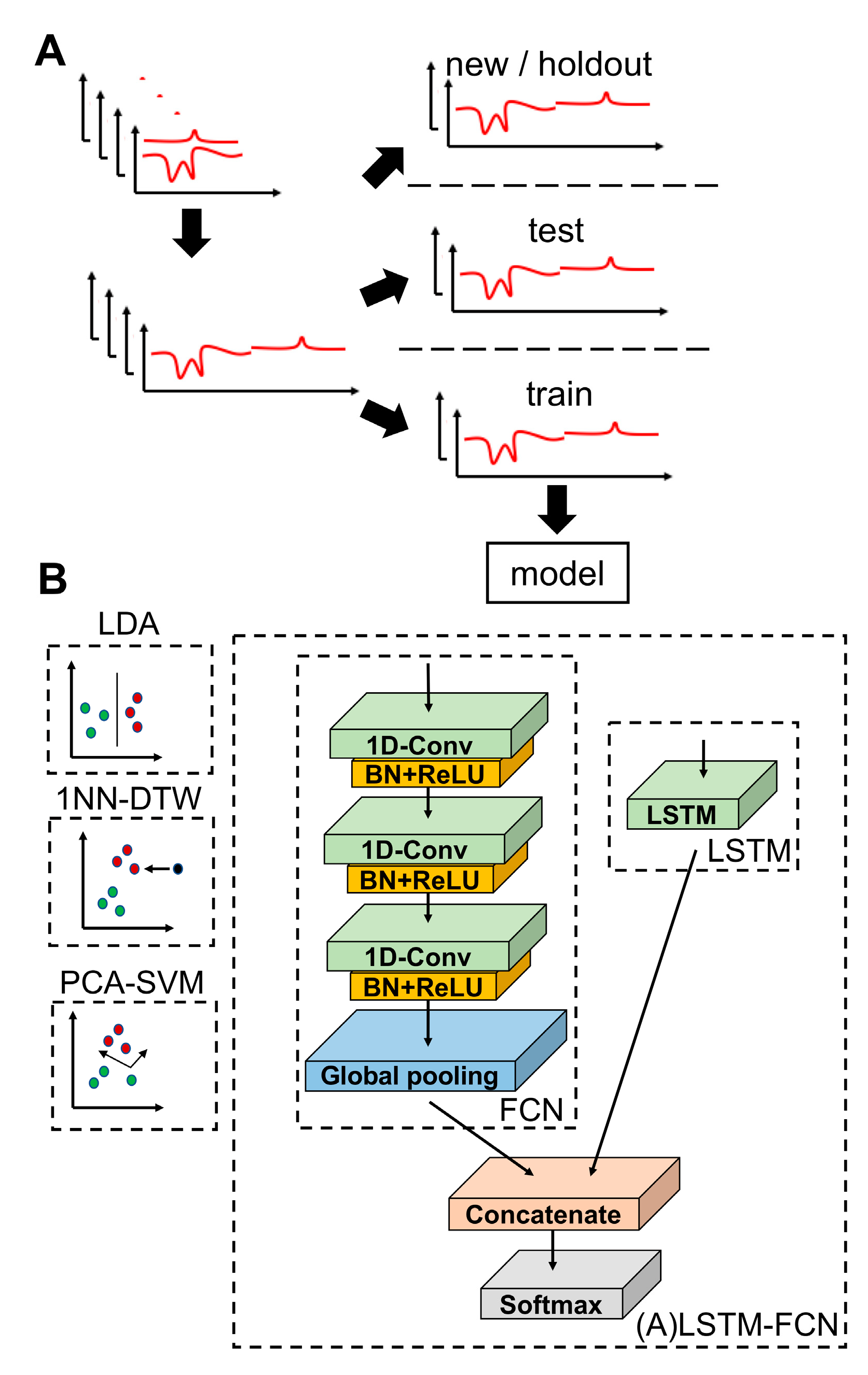
2.5. Model Training
2.6. Model Analysis and Refinement
3. Results
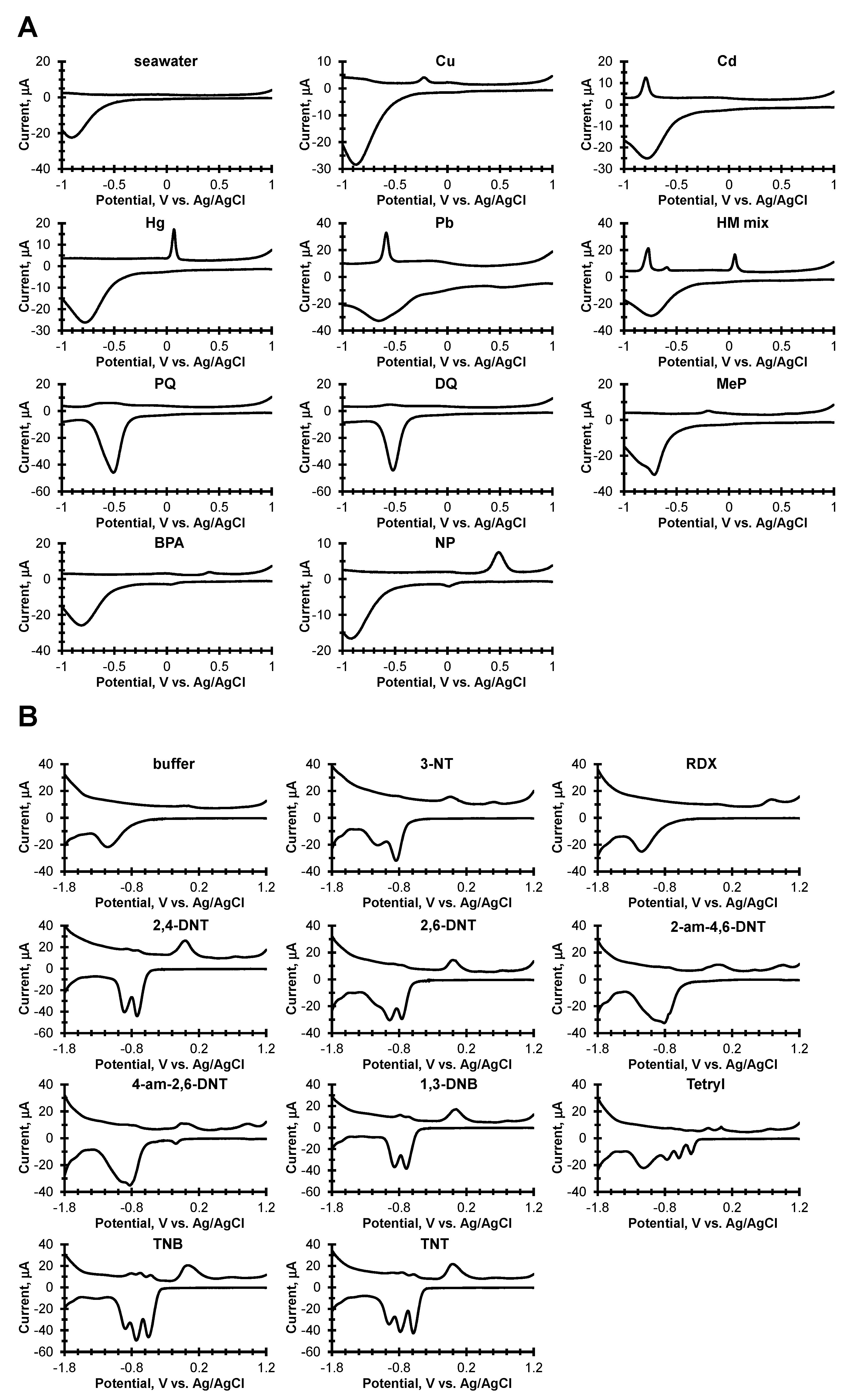
3.1. Cyclic Square Wave Voltammograms, Model Schematics and Data Processing
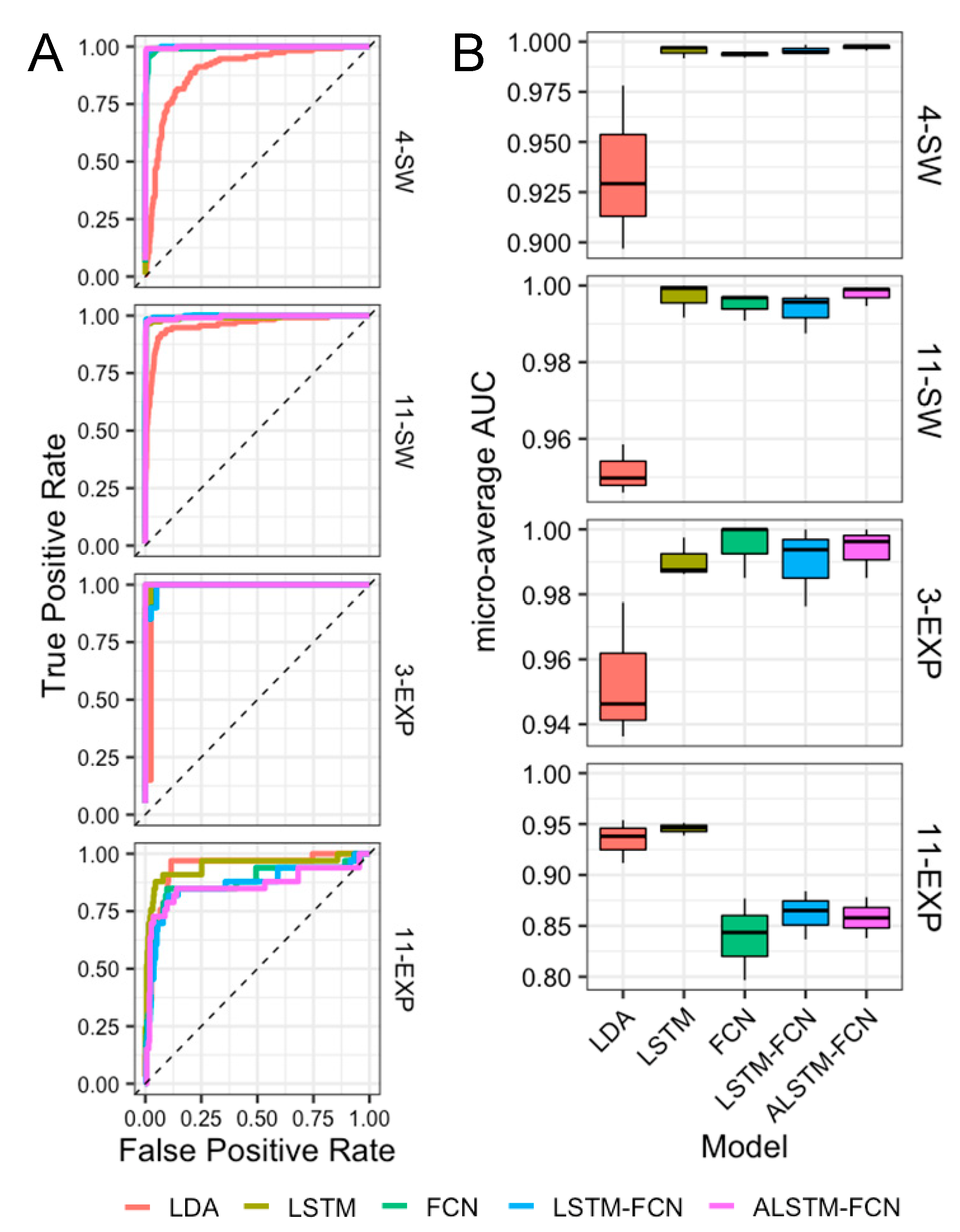
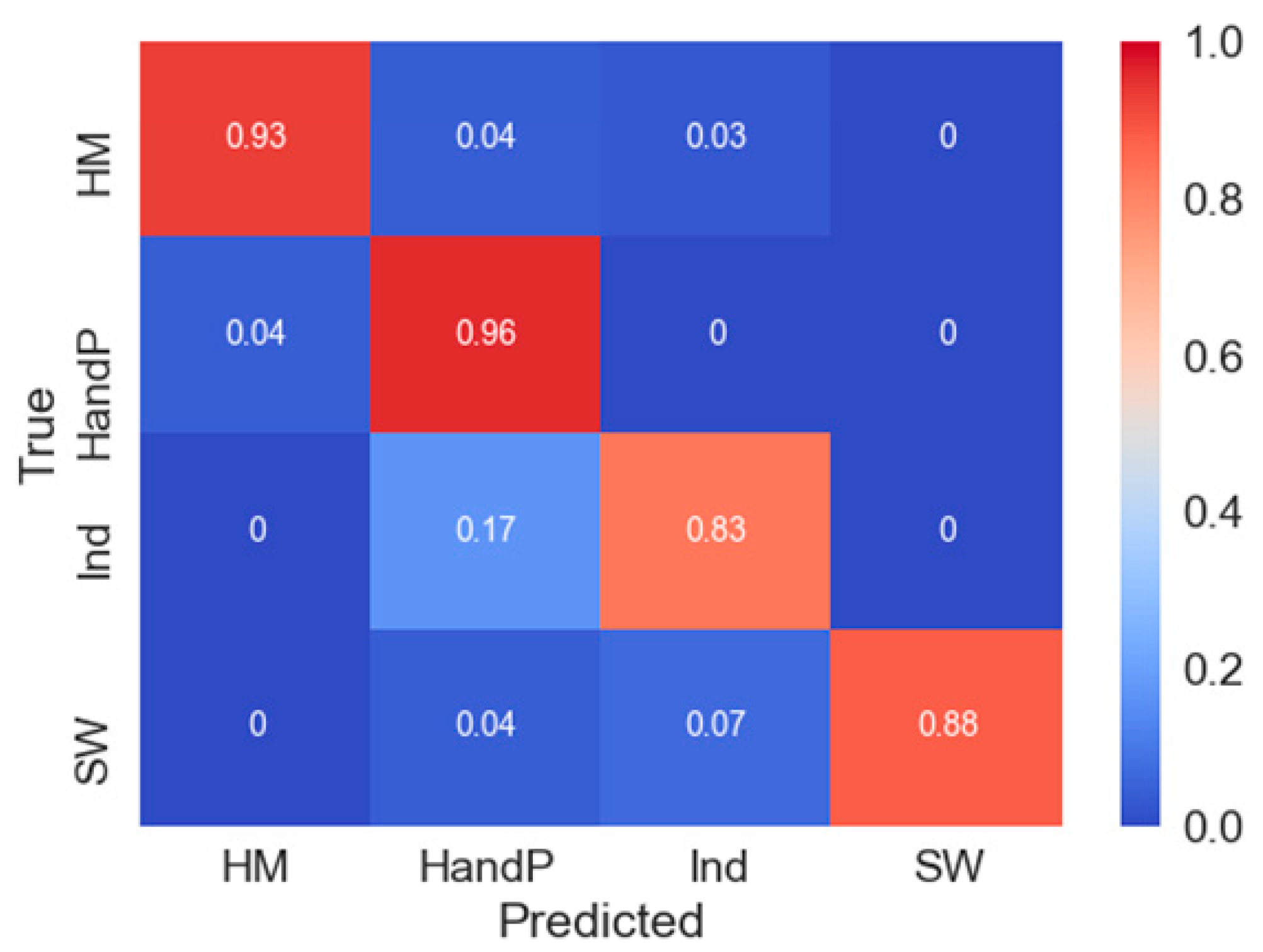
3.2. Comparison of the Classifiers
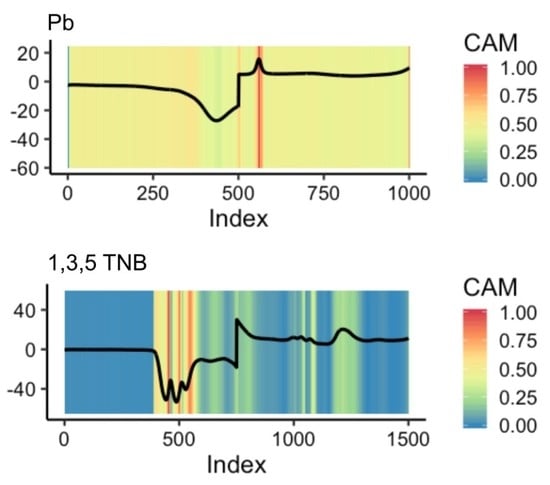
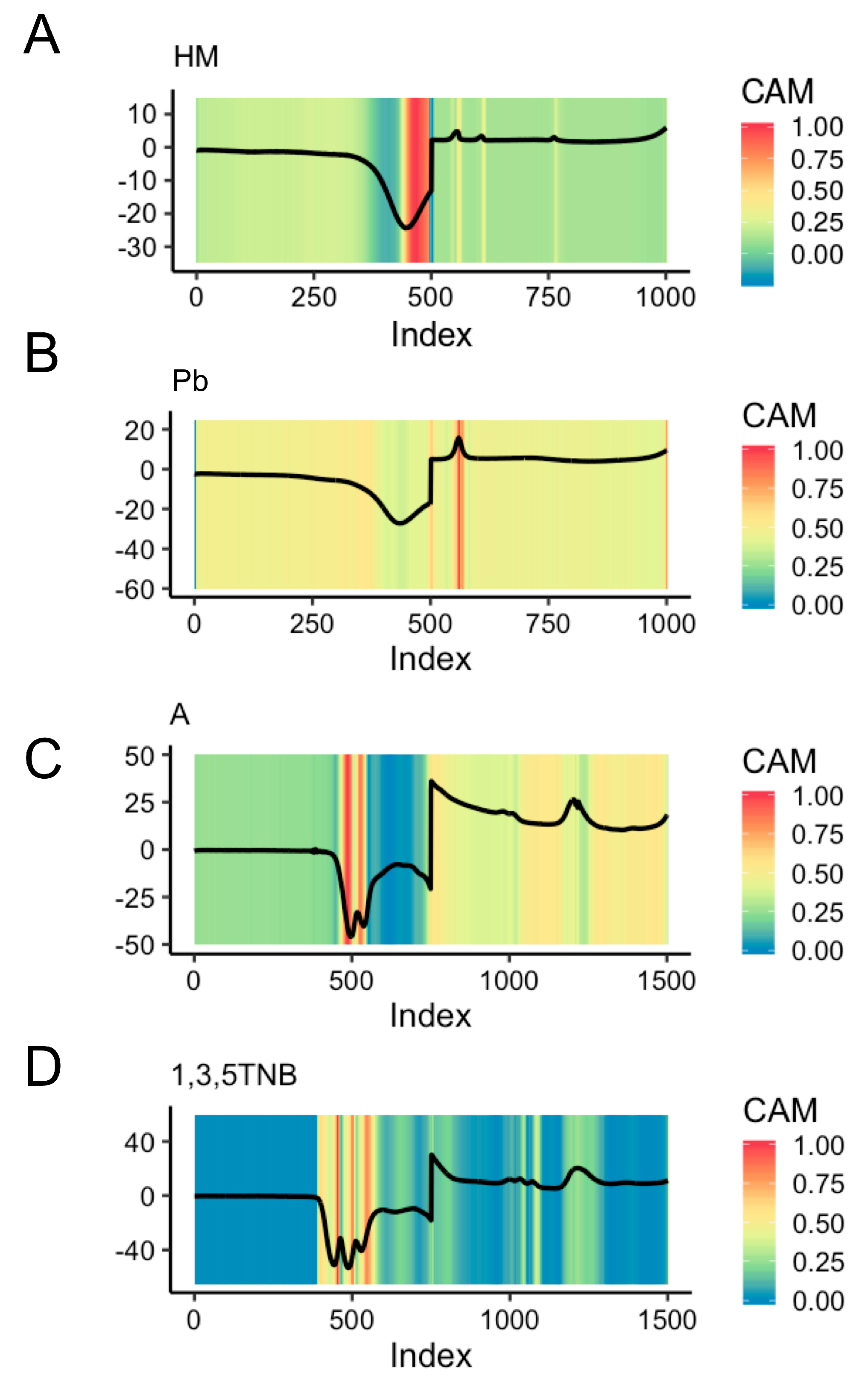
3.3. Class Activation Mapping
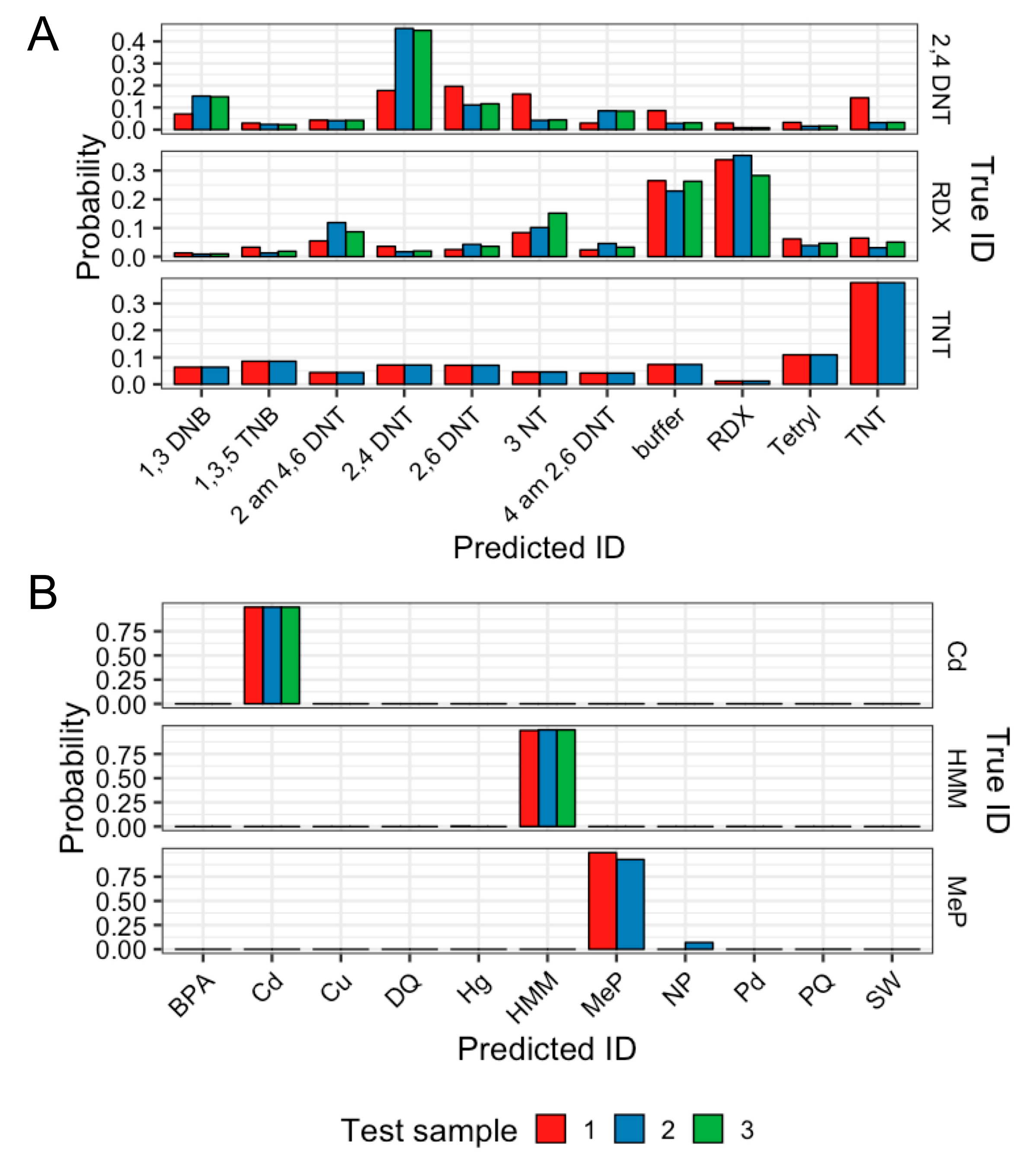
3.4. Evaluation of Best Classifier on New Datasets
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Grieshaber, D.; MacKenzie, R.; Voros, J.; Reimhult, E. Electrochemical biosensors—Sensor principles and architectures. Sensors 2008, 8, 1400–1458. [Google Scholar] [CrossRef] [PubMed]
- Helfrick, J.C.; Bottomley, L.A. Cyclic square wave voltammetry of single and consecutive reversible electron transfer reactions. Anal. Chem. 2009, 81, 9041–9047. [Google Scholar] [CrossRef] [PubMed]
- Mirceski, V.; Gulaboski, R.; Lovric, M.; Bogeski, I.; Kappl, R.; Hoth, M. Square-wave voltammetry: A review on the recent progress. Electroanalysis 2013, 25, 2411–2422. [Google Scholar] [CrossRef]
- Novak, I.; Šeruga, M.; Komorsky-Lovrić, Š. Characterisation of catechins in green and black teas using square-wave voltammetry and RP-HPLC-ECD. Food Chem. 2010, 122, 1283–1289. [Google Scholar] [CrossRef]
- Rodriguez-Mendez, M.L.; Apetrei, C.; de Saja, J.A. Evaluation of the polyphenolic content of extra virgin olive oils using an array of voltammetric sensors. Electrochim Acta 2008, 53, 5867–5872. [Google Scholar] [CrossRef]
- Liu, N.A.; Liang, Y.Z.; Bin, J.; Zhang, Z.M.; Huang, J.H.; Shu, R.X.; Yang, K. Classification of green and black teas by pca and svm analysis of cyclic voltammetric signals from metallic oxide-modified electrode. Food Anal. Method 2014, 7, 472–480. [Google Scholar] [CrossRef]
- Ceto, X.; O’ Mahony, A.M.; Wang, J.; Del Valle, M. Simultaneous identification and quantification of nitro-containing explosives by advanced chemometric data treatment of cyclic voltammetry at screen-printed electrodes. Talanta 2013, 107, 270–276. [Google Scholar] [CrossRef] [PubMed]
- Erickson, J.S.; Shriver-Lake, L.C.; Zabetakis, D.; Stenger, D.A.; Trammell, S.A. A simple and inexpensive electrochemical assay for the identification of nitrogen containing explosives in the field. Sensors 2017, 17, 1769. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Keogh, E.; Shelton, C.; Wei, L.; Ratanamahatana, C. Fast time series classification using numerosity reduction. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 1033–1040. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Gurbani, S.S.; Schreibmann, E.; Maudsley, A.A.; Cordova, J.S.; Soher, B.J.; Poptani, H.; Verma, G.; Barker, P.B.; Shim, H.; Cooper, L.A.D. A convolutional neural network to filter artifacts in spectroscopic MRI. Magn. Reson. Med. 2018, 80, 1765–1775. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhou, B.; Peck, D.; Hsieh, S.; Dialani, V.; Mackey, L.; Patterson, G. Deepminer: Discovering interpretable representations for mammogram classification and explanation. arXiv 2018, arXiv:1805.12323. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- King, G.; Zeng, L. Logistic regression in rare events data. Political Anal. 2001, 9, 137–163. [Google Scholar] [CrossRef]
- Chollet, F. Keras. Available online: https://keras.io (accessed on 31 March 2019).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Vol. 26. [Google Scholar]
- Wickham, H. Tidy data. Journal of Statistical Software 2014, 59, 1–23. [Google Scholar] [CrossRef]
- Kate, R.J. Using dynamic time warping distances as features for improved time series classification. Data Min. Knowl. Disc. 2016, 30, 283–312. [Google Scholar] [CrossRef]
- Kumar, N.; Bansal, A.; Sarma, G.S.; Rawal, R.K. Chemometrics tools used in analytical chemistry: An overview. Talanta 2014, 123, 186–199. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
| Model | 11-EXP | 3-EXP | 11-SW | 4-SW | ||||
|---|---|---|---|---|---|---|---|---|
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | |
| PCA-SVM | 0.335 | 0.069 | 0.587 | 0.093 | 0.190 | 0.051 | 0.233 | 0.025 |
| 1NN-DTW | 0.712 | 0.226 | 0.923 | 0.043 | 0.680 | 0.058 | 0.735 | 0.015 |
| LDA | 0.775 | 0.090 | 0.923 | 0.167 | 0.842 | 0.010 | 0.803 | 0.105 |
| LSTM | 0.763 | 0.074 | 0.960 | 0.040 | 0.965 | 0.012 | 0.962 | 0.027 |
| FCN | 0.679 | 0.016 | 1.000 | 0.040 | 0.961 | 0.010 | 0.962 | 0.018 |
| LSTM-FCN | 0.687 | 0.060 | 1.000 | 0.040 | 0.975 | 0.012 | 0.953 | 0.030 |
| ALSTM-FCN | 0.697 | 0.061 | 1.000 | 0.040 | 0.985 | 0.006 | 0.960 | 0.033 |
| Model | 11-EXP | 3-EXP | 11-SW | 4-SW | ||||
|---|---|---|---|---|---|---|---|---|
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | |
| LDA | 0.938 | 0.021 | 0.946 | 0.021 | 0.950 | 0.006 | 0.929 | 0.041 |
| LSTM | 0.946 | 0.006 | 0.988 | 0.006 | 0.999 | 0.004 | 0.997 | 0.003 |
| FCN | 0.843 | 0.040 | 1.000 | 0.008 | 0.997 | 0.003 | 0.994 | 0.001 |
| LSTM-FCN | 0.865 | 0.024 | 0.994 | 0.012 | 0.996 | 0.005 | 0.995 | 0.002 |
| ALSTM-FCN | 0.858 | 0.020 | 0.996 | 0.008 | 0.999 | 0.002 | 0.998 | 0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dean, S.N.; Shriver-Lake, L.C.; Stenger, D.A.; Erickson, J.S.; Golden, J.P.; Trammell, S.A. Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry. Sensors 2019, 19, 2392. https://doi.org/10.3390/s19102392
Dean SN, Shriver-Lake LC, Stenger DA, Erickson JS, Golden JP, Trammell SA. Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry. Sensors. 2019; 19(10):2392. https://doi.org/10.3390/s19102392
Chicago/Turabian StyleDean, Scott N., Lisa C. Shriver-Lake, David A. Stenger, Jeffrey S. Erickson, Joel P. Golden, and Scott A. Trammell. 2019. "Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry" Sensors 19, no. 10: 2392. https://doi.org/10.3390/s19102392
APA StyleDean, S. N., Shriver-Lake, L. C., Stenger, D. A., Erickson, J. S., Golden, J. P., & Trammell, S. A. (2019). Machine Learning Techniques for Chemical Identification Using Cyclic Square Wave Voltammetry. Sensors, 19(10), 2392. https://doi.org/10.3390/s19102392