Energy-Efficient Spatial Query-Centric Geographic Routing Protocol in Wireless Sensor Networks
Abstract
1. Introduction
2. Related Work
2.1. Energy Efficiency and Load Balancing
2.2. Spatial Query Efficiency
3. QTGrid Routing Protocol
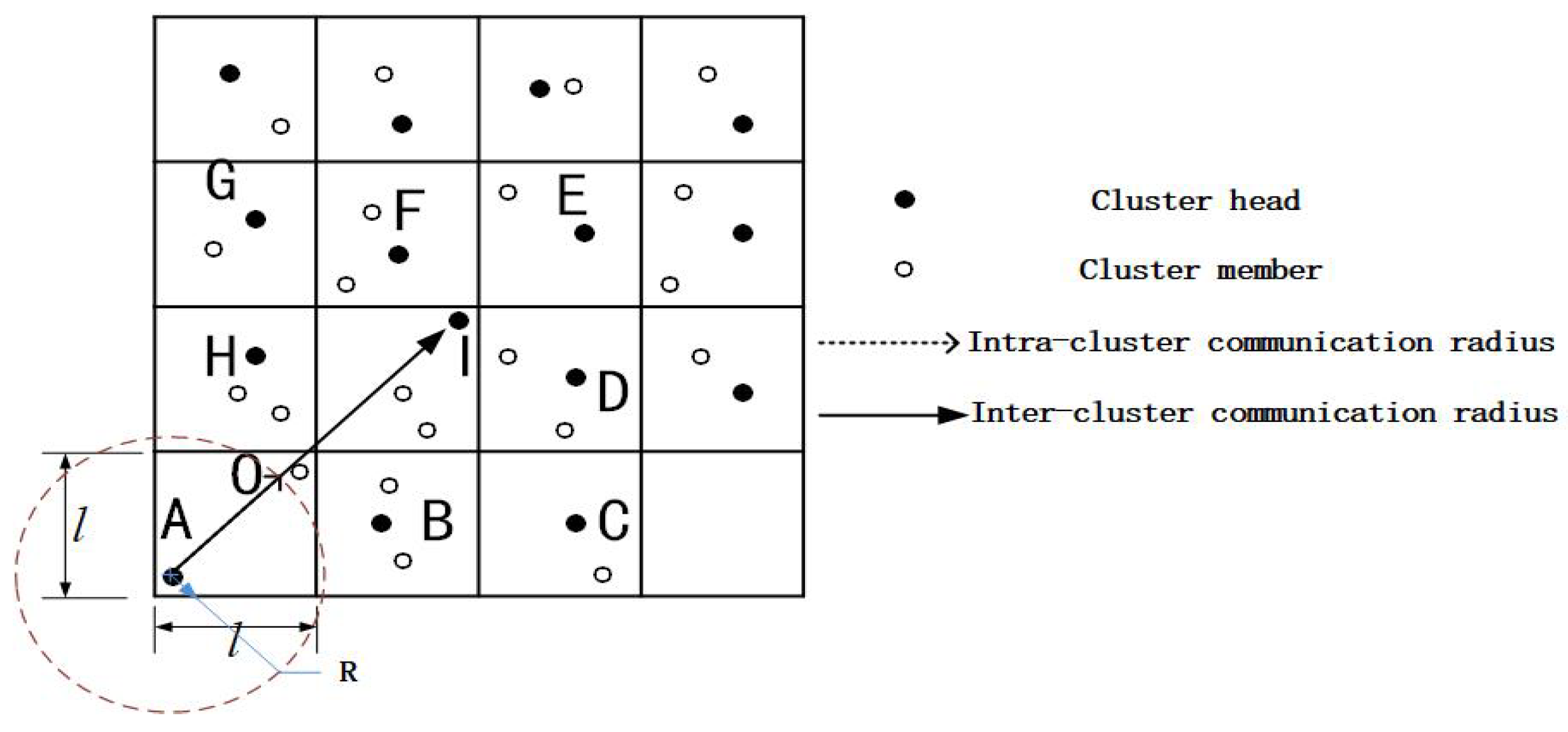
3.1. Cluster Setup
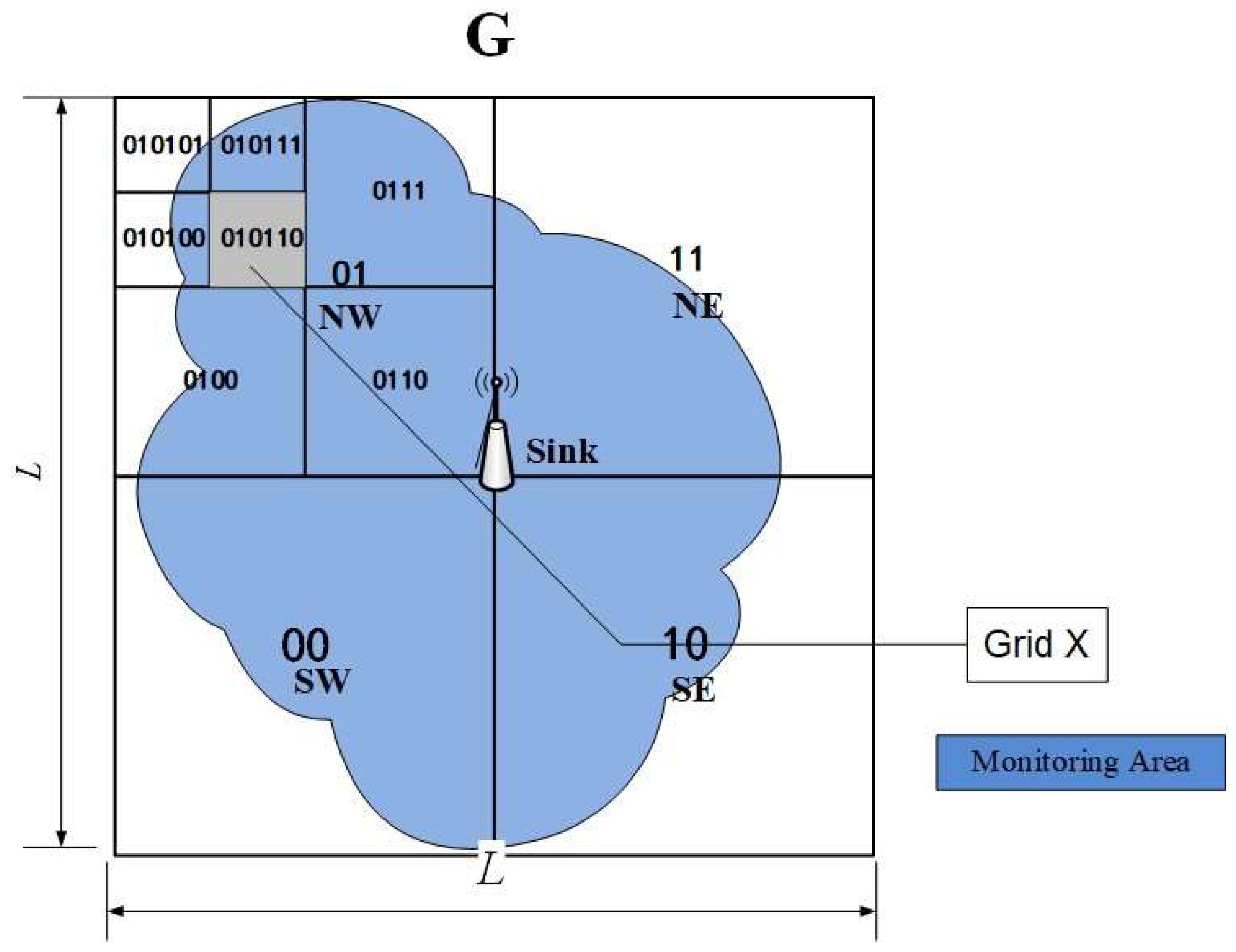
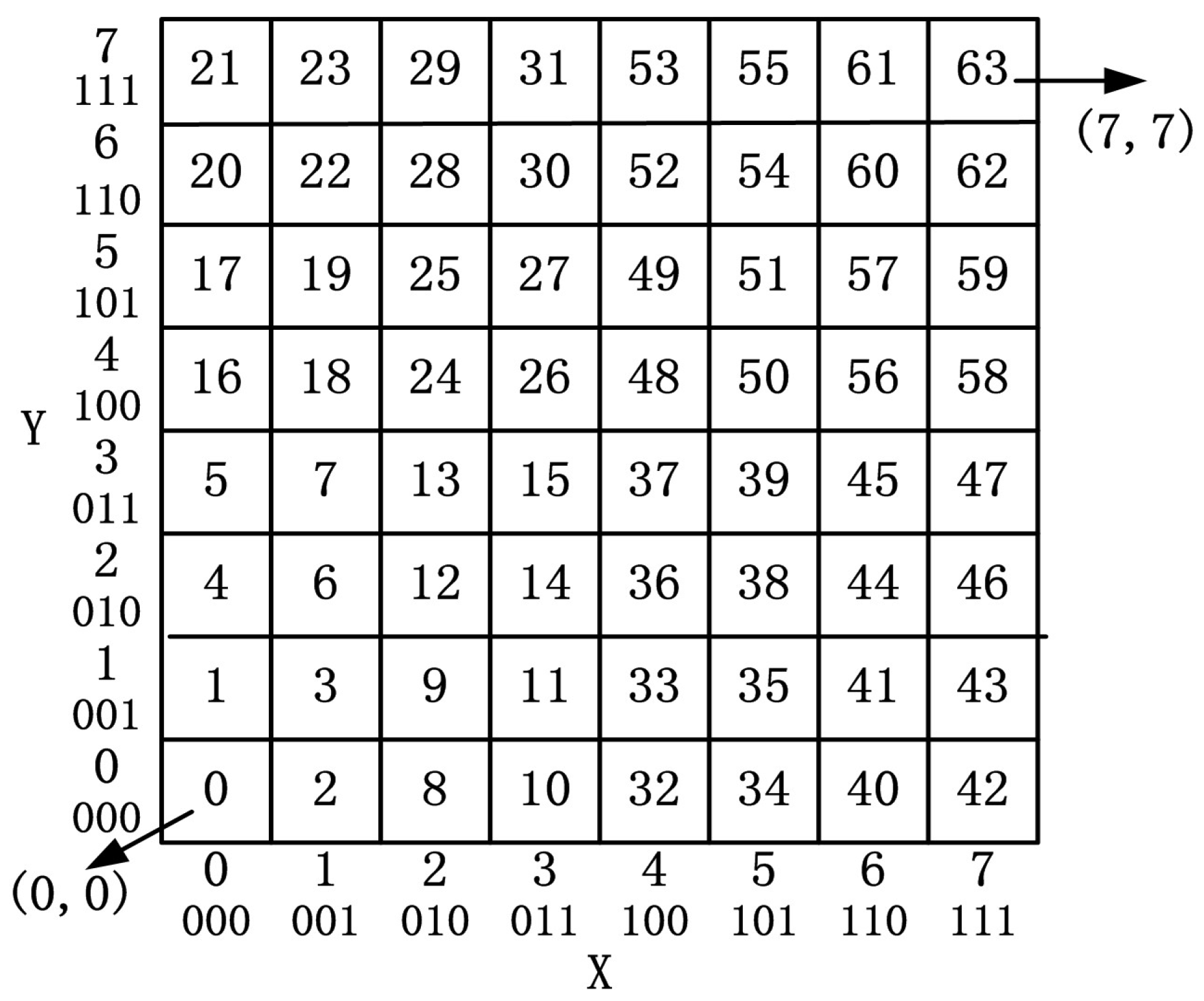
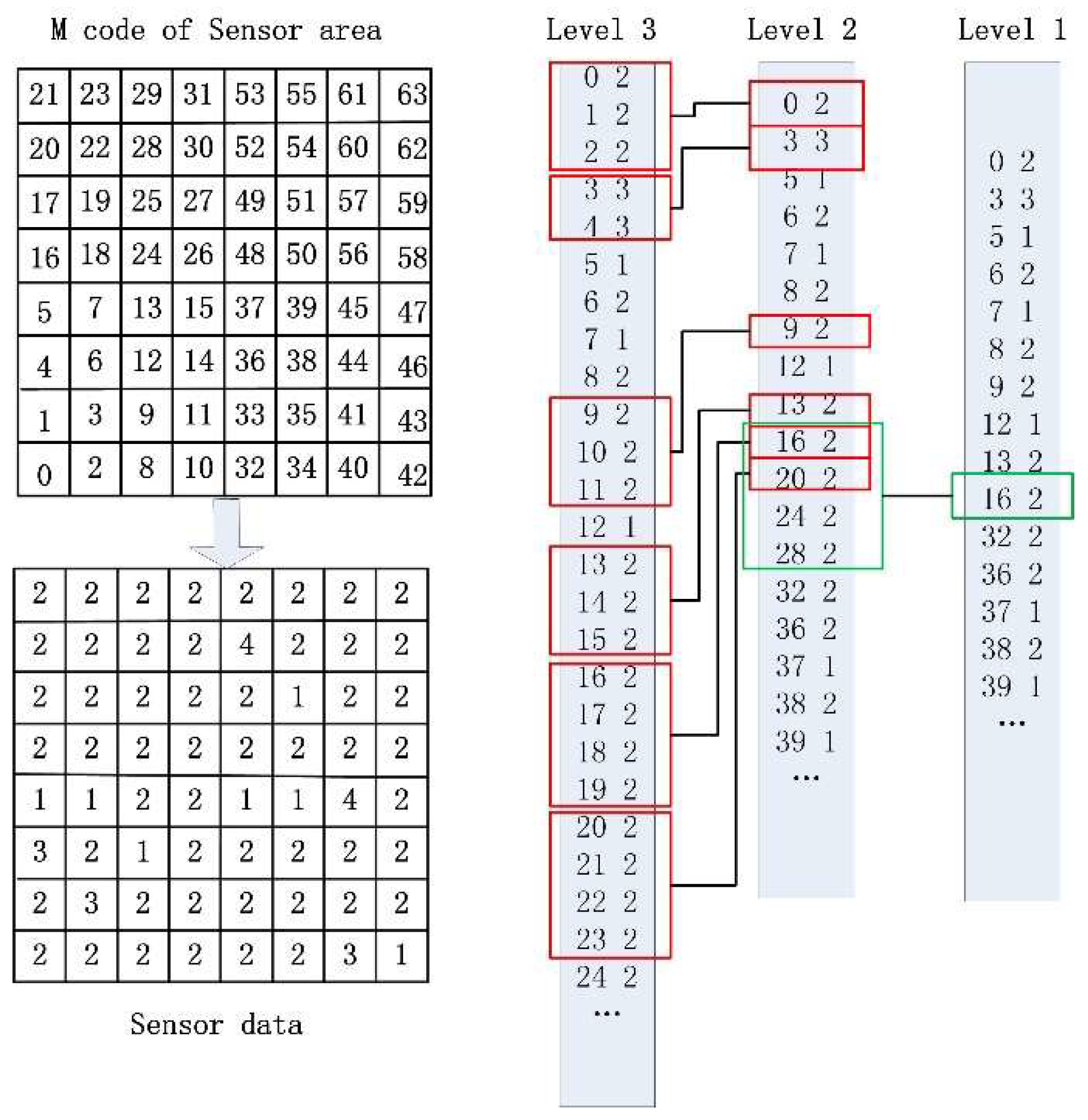
3.1.1. Grid Position Encoding
3.1.2. Communication Radius
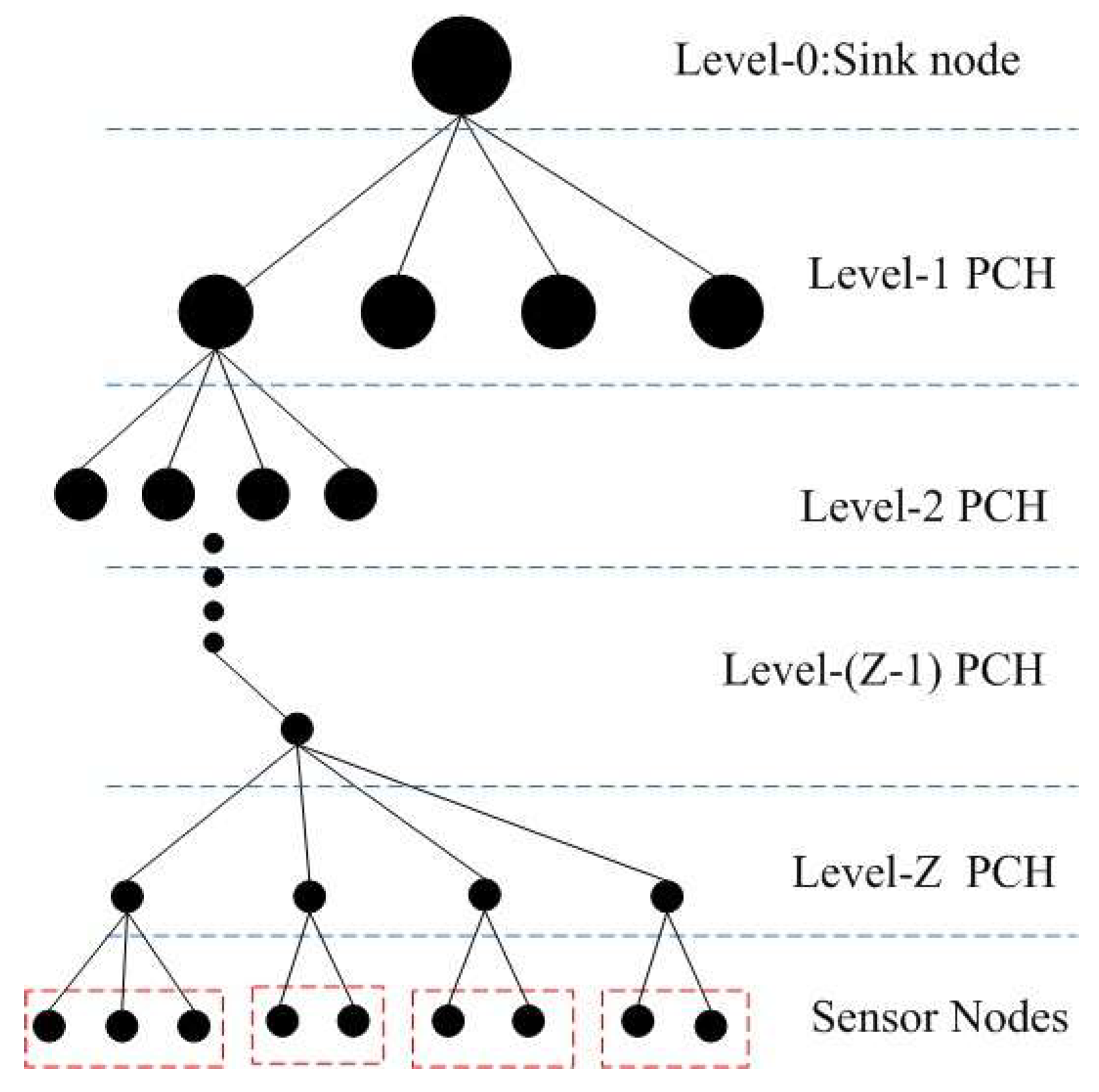
3.2. CH and PCH Election
3.2.1. CH Election
3.2.2. PCH Election
| Algorithm 1 PCH Election |
| ← the M code of the CH |
| Level i ← the level of the PCH |
| d ← the depth of the quadtree |
| sink ← the location of Sink node |
| Get PCH (, level i, d, sink) |
| { |
| begin |
| [CHs] = [NW, NE, SW, SE]// Get the 4 CHs of the i-th level whose M code are |
| [Xc,Yc] = (M,i)// Get the center coordinate of the area where the M code is |
| [Xs,Ys] = sink //Get the coordinates of the sink node |
| If(Xs>Xc)&(Ys>Yc) |
| PCH =SE |
| Else if(Xs<Xc)&(Ys>Yc) |
| PCH = SW |
| Else if(Xs<Xc)&(Ys>Yc) |
| PCH = NW |
| Else (Xs>Xc)&(Ys<Yc) |
| PCH = NE |
| end |
| end |
| Return PCH// Return the calculated PCH node |
| } |
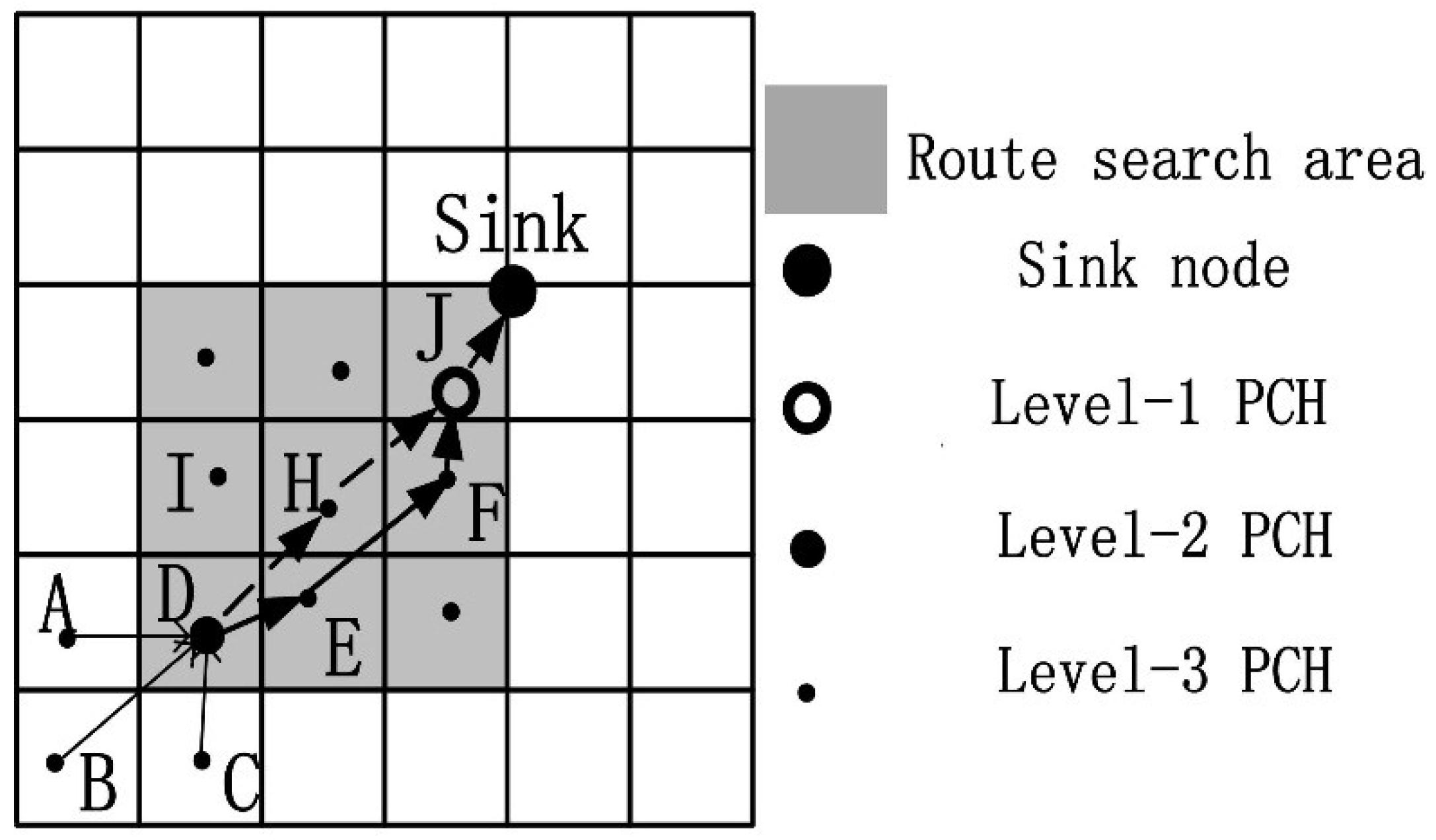
3.3. Routing Strategy
- Step 1.
- The sink node sent the data collection request to the event area, and the nodes in the routing area added their own energy information to the data package.
- Step 2.
- After receiving the package, the sensor nodes in the event area sent the data to the CH. Then, CHs A, B, and C sent the data to PCH D.
- Step 3.
- D aggregated the data and calculated the values of the candidate next-hop routing nodes (E, H, I) using Equation (5).
- Step 4.
- D sent the data to the node with the smallest value. Here, we assumed that the value of E was the smallest. Then, E continued to aggregate and forward the data to its next-hop routing node with the smallest value until J received the data and forwarded them to the sink. Finally, data routing was completed.
3.4. Data Aggregation
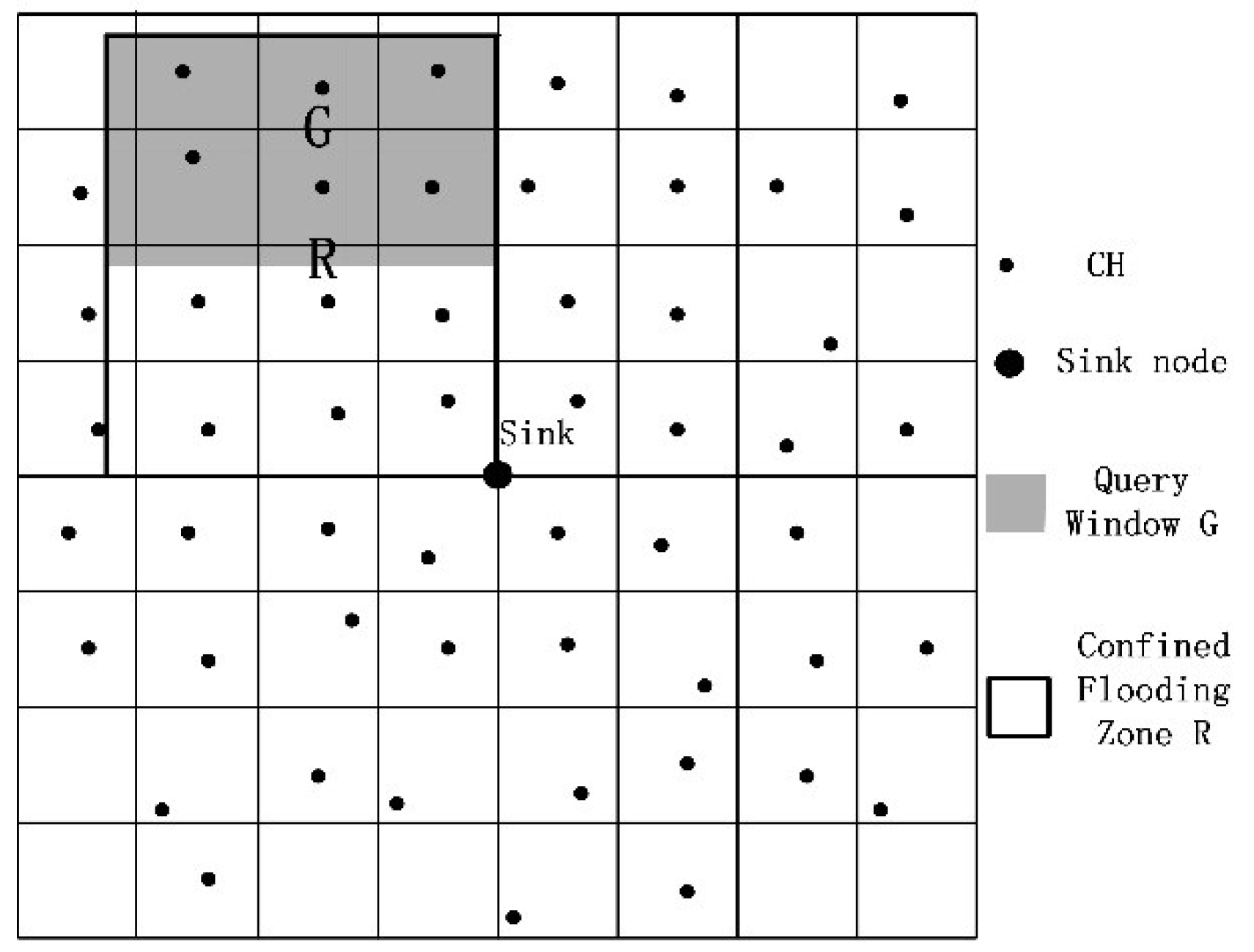
3.5. Spatial Query
| Algorithm 2 Spatial Query Request Sent |
| G ←the minimum rectangle covers the query window |
| R ←the minimum rectangle that totally covers the sink node and query window G |
| id ← the identification of the data packet |
| X ← the sensor node that receives the packets |
| ReceiveQueryRequestPackage (G, R, id){ |
| Begin |
| if (X is within the zone R) |
| then begin |
| if (X is a CH) |
| then begin |
| //Judge that whether X has ever received the |
| //current request packet before |
| if (package ID==id) |
| then begin |
| Step1. X directly discards the packet; |
| end |
| else begin |
| Step2. X sends the packet to its next routing hop CH; |
| end |
| else begin |
| Step3. X sends the packet to its CH |
| end |
| end |
| else if (X is within the query window G) |
| then begin |
| if (X is a CH) |
| then begin |
| //Judge that whether X has ever received the |
| //current request packet before |
| if (package ID==id) |
| then begin |
| Step1. X directly discards the packet; |
| end |
| else begin |
| Step4. X sends the packet to its CMs; |
| end |
| end |
| else begin |
| Step2. X sends the packet to its CH |
| end |
| else begin |
| Step1. X directly discards the packet; |
| end |
| } |
| Algorithm 3 Sensor Data Feedback |
| X ← a sensor node in the query window |
| queryWindow ← the query window |
| L ← the hierarchical level of X’s PCH in the query window input by the user |
| Depth ← the depth of the quadtree structure |
| GetDataOfRegion(queryWindow, L, Depth){ |
| Begin |
| if (X is a CH) |
| if (0<Level<Depth-1) |
then begin
|
| end |
| if (Level =Depth-1) |
then begin
|
| end |
| end |
| else begin |
|
| end |
| end |
| } |
4. Simulations and Analyses
4.1. Simulation Setup
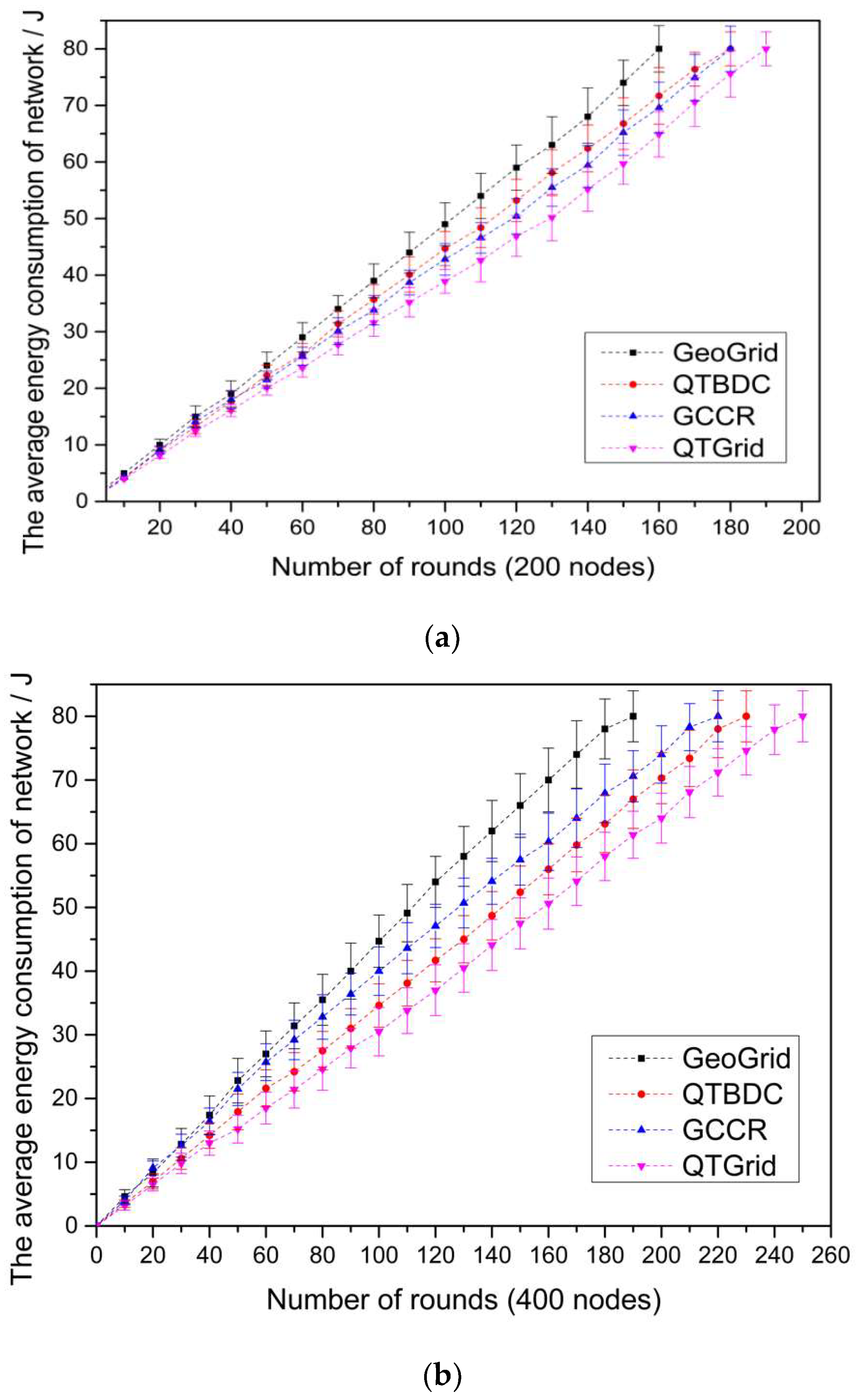
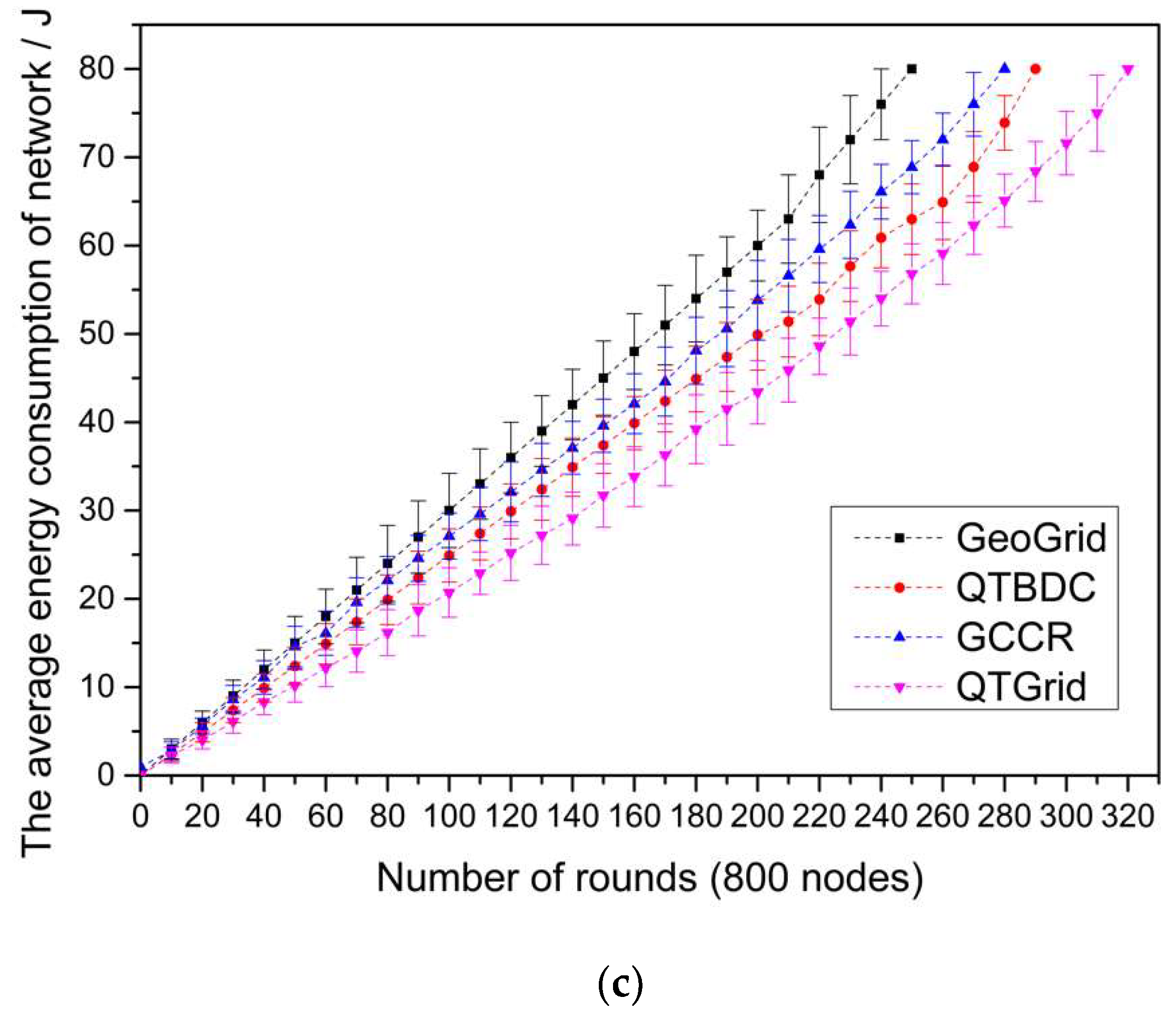
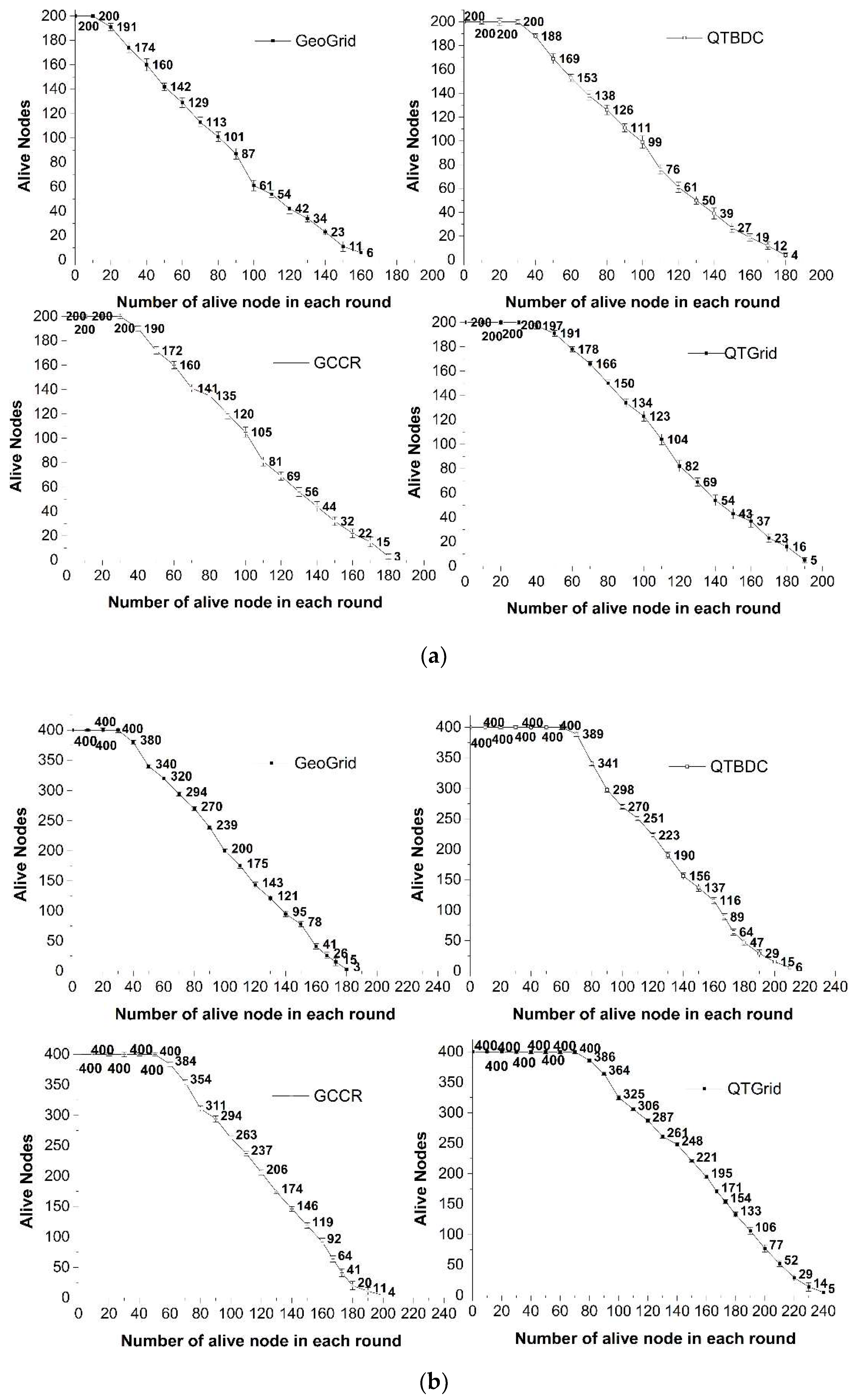
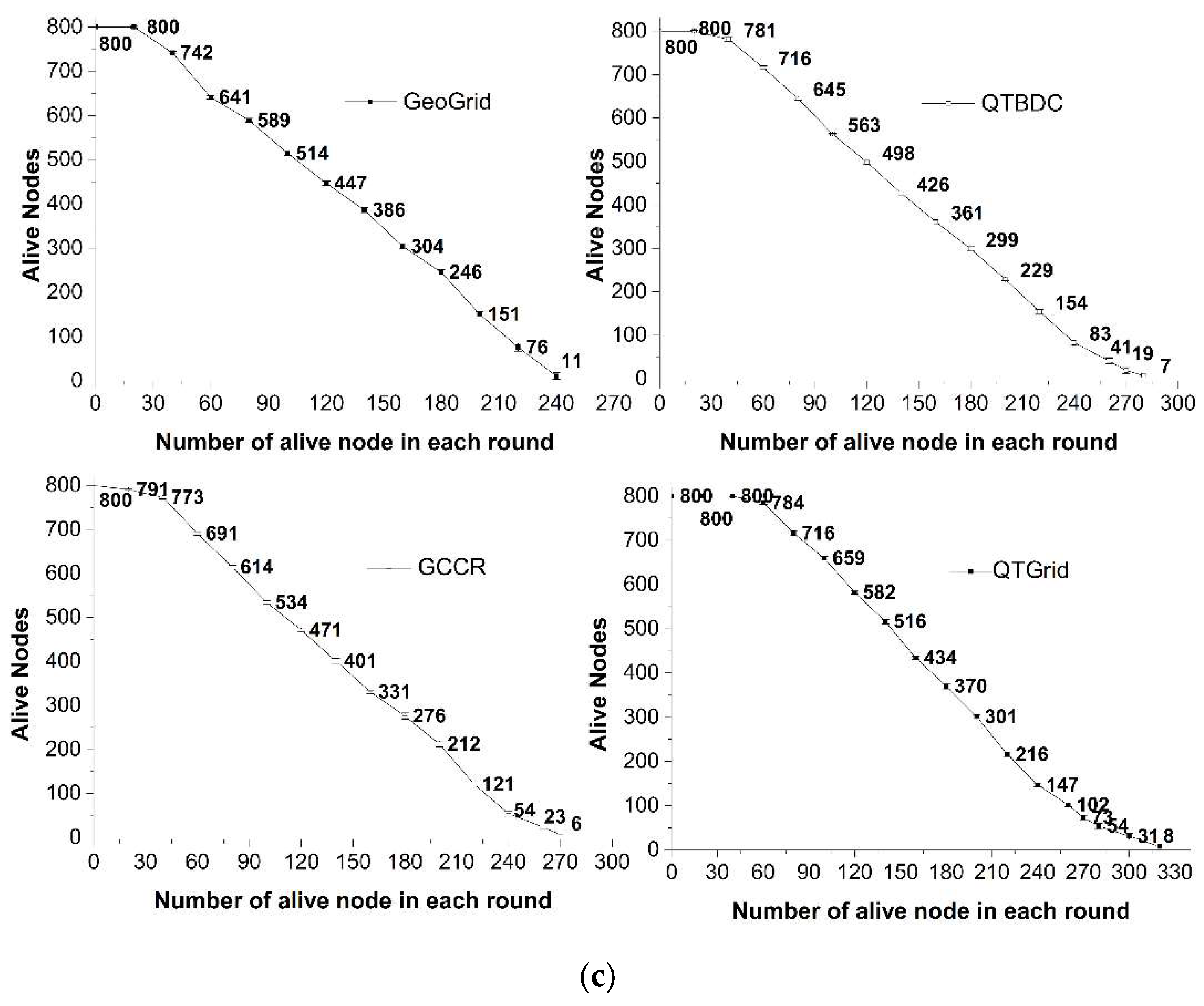
4.2. Network Lifetime
- (1)
- Among the four routing protocols, QTGrid had the lowest average energy consumption, whereas GeoGrid had the highest one. Specifically, the average energy consumption of QTGrid was about 0.043 (200 nodes), 0.051 (400 nodes), and 0.075 J/round (800 nodes) lower than GeoGrid; about 0.032 (200 nodes), 0.043 (400 nodes), and 0.058 J/round (800 nodes) lower than GCCR; about 0.038 (200 nodes), 0.036 (400 nodes), and 0.049 J/round (800 nodes) lower than QTBDC.
- (2)
- When the number of nodes was 200, the average energy consumption of GCCR was about 0.006 J/round lower than that of QTBDC, but when the number of nodes was 400 and 800, the average energy consumption of GCCR was about 0.007 and 0.009 J/round higher than that of QTBDC, respectively. Compared with GCCR, QTDBC reduced the maximum length of data transmission and increased the number of forwarding hops to reduce the transmission duration. In the case of a network with few nodes (200 nodes), candidates for the next hop routing nodes tended to be few and resulted in routing paths that were not the shortest, which consumed much node energy to some extent. The above problem changed when many nodes were available in the network (400 and 800 nodes).
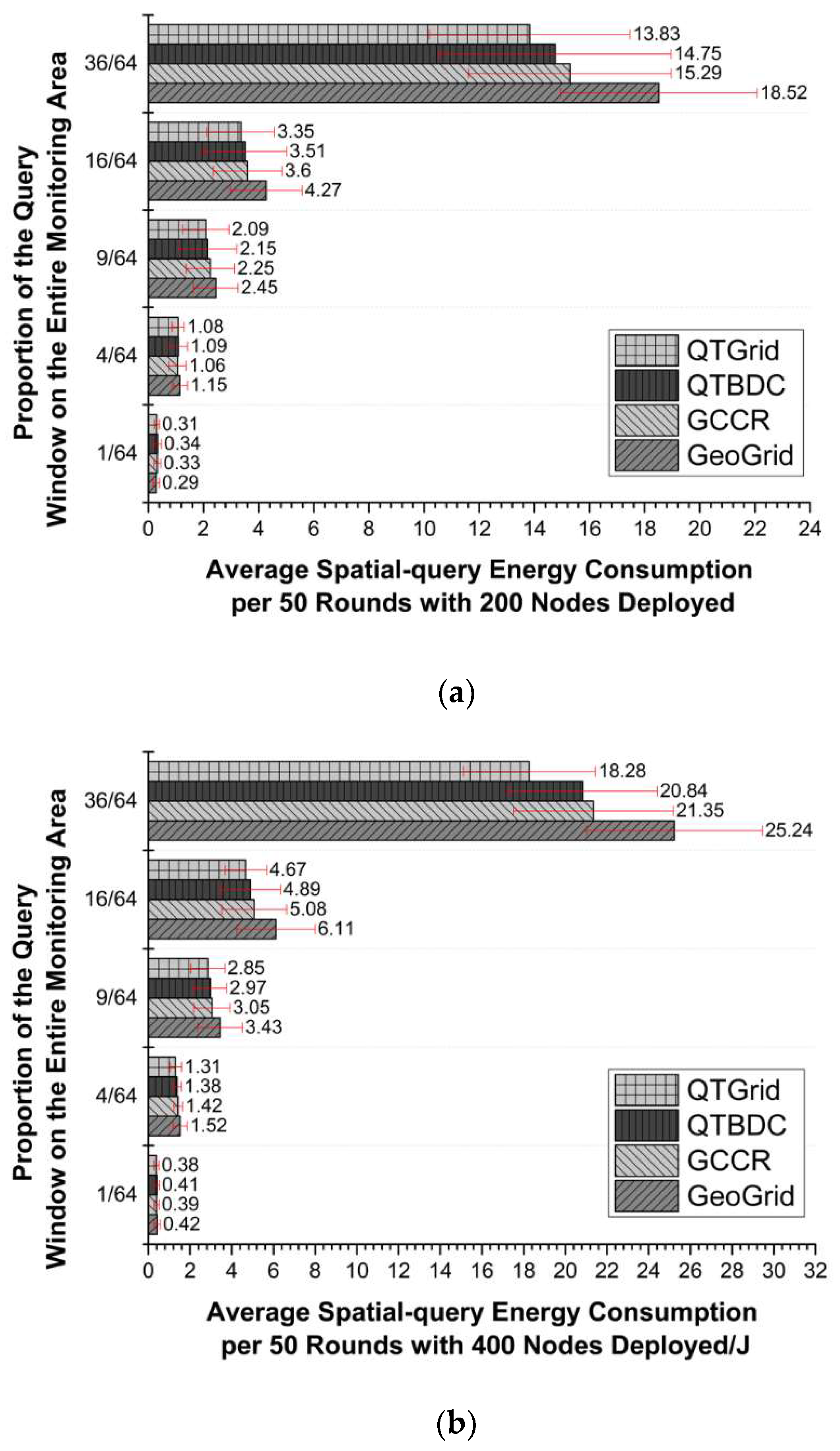
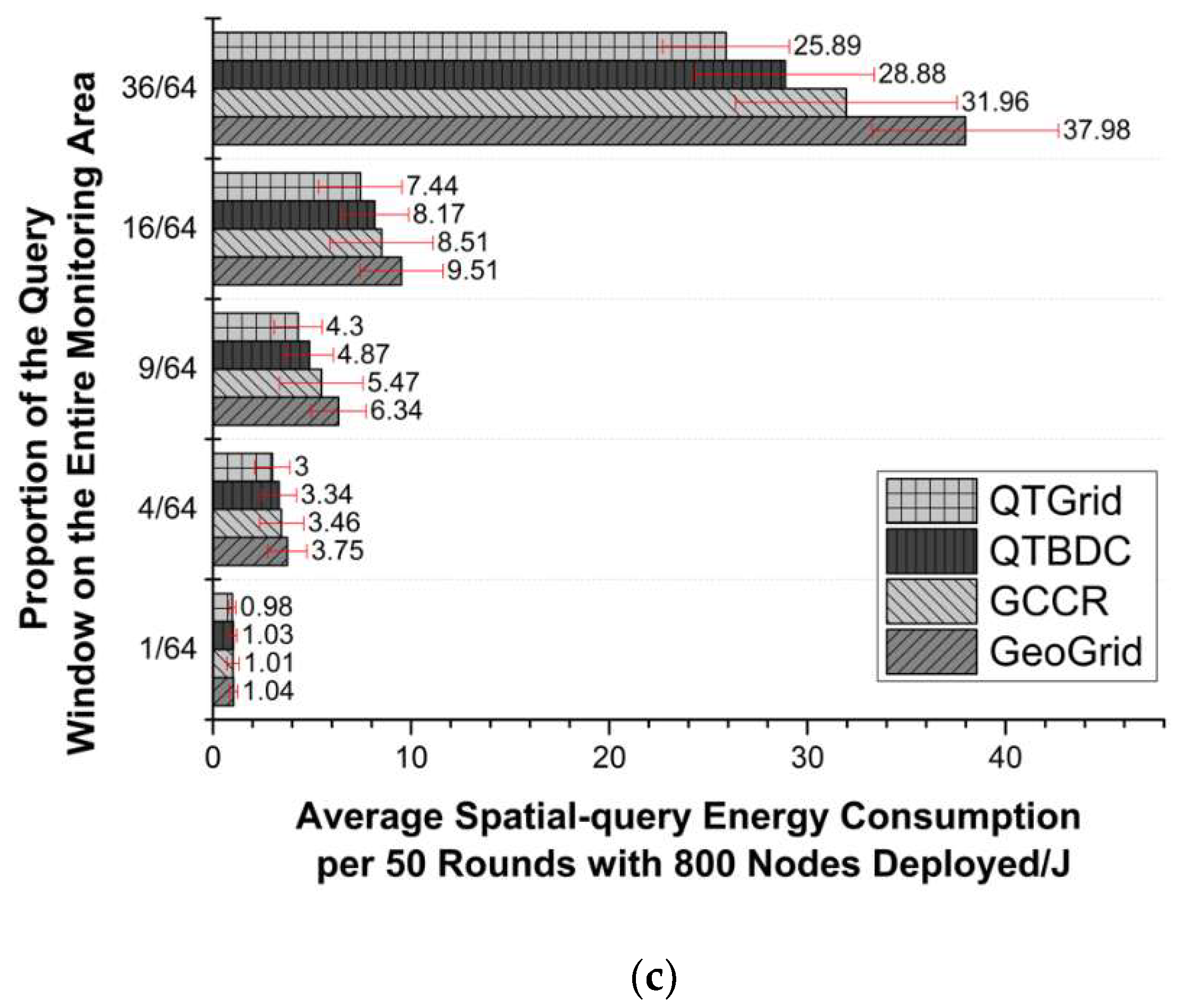
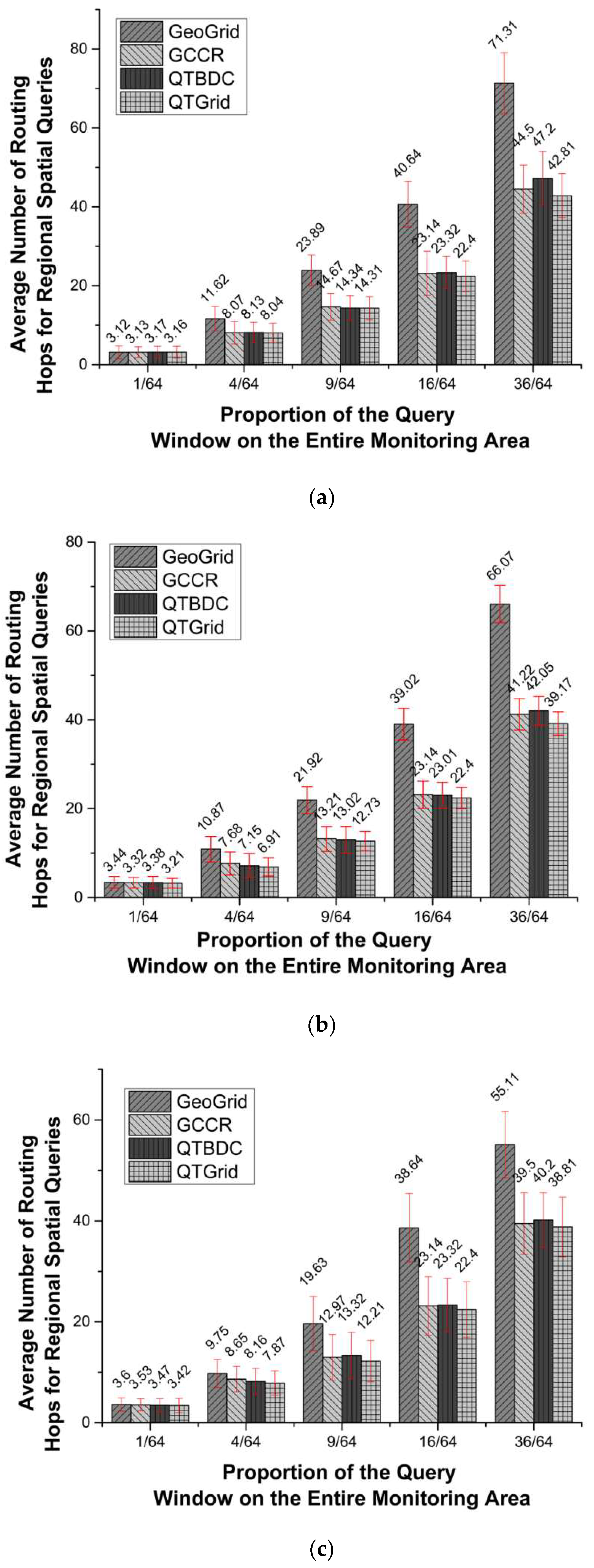
4.3. Spatial Query
- (1)
- The three protocols improved to varying degrees compared with GeoGrid, except for the network with 200 nodes where only one grid was covered. The reason was that compared with GeoGrid, the three other algorithms needed to consume more energy in CH election and replacement to obtain more energy-saving routes. In the above network, few candidate nodes were available for updating CHs, and the next-hop routing node and routing lines were not much different. However, excessive CH replacement increased the communication energy cost.
- (2)
- The value of QTGrid was the lowest among those of the protocols, and the difference became more obvious with the increase in the number of nodes in the network. The value of QTGrid was lower than that of GeoGrid and GCCR because of the use of data fusion technology, which can largely decrease the achieved redundant sensor data and the corresponding energy consumption of redundant data transmission. The value of QTGrid was lower than that of QTBDC because the use of the new CH selection mechanism and new next-hop selection procedure made the nodes’ load more balanced.
- (3)
- When query windows had the same size, more nodes were available, and the superiority of QTGrid over the three other protocols in energy saving became more obvious because redundant data increased as the number of nodes increased. QTGrid fused sensing data, which played a crucial role in energy conservation. Although QTBDC and QTGrid used a similar data fusion strategy, QTGrid employed a more energy-efficient next-hop routing node selection method, which made the energy distribution of intra-cluster and inter-cluster communication balanced and energy conservation obvious for large-scale networks.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar]
- Curry, R.M.; Smith, J.C. A Survey of Optimization Algorithms for Wireless Sensor Network Lifetime Maximization. Comput. Ind. Eng. 2016, 101, 145–166. [Google Scholar] [CrossRef]
- Manolopoulos, Y. Spatial Databases: Technologies, Techniques and Trends; IGI Publishing: Hershey, PA, USA, 2005. [Google Scholar]
- Adnan, A.I.; Hanapi, Z.M.; Othman, M.; Zukarnain, Z.A. A Secure Region-Based Geographic Routing Protocol (SRBGR) for Wireless Sensor Networks. PLoS ONE 2017, 12, e0170273. [Google Scholar] [CrossRef] [PubMed]
- Can, Z.; Demirbas, M. A survey on in-network querying and tracking services for wireless sensor networks. Ad Hoc Netw. 2013, 11, 596–610. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.P.; Zhou, S.-W.; Lin, Y.-P.; Li, G. A Survey on Position-Based Routing Algorithms in Wireless Sensor Networks. Algorithms 2009, 2, 158–182. [Google Scholar]
- Da Silva, R.I.; Macedo, D.F.; Nogueira, J.M. Spatial query processing in wireless sensor networks–A survey. Inf. Fusion 2014, 15, 32–43. [Google Scholar] [CrossRef]
- Karp, B.; Kung, HT. GPSR: Greedy Perimeter Stateless Routing for Wireless Networks. In Proceedings of the 6th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MobiCom 2000), Boston, MA, USA, 6–11 August 2000. [Google Scholar]
- Yu, Y.; Govindan, R.; Estrin, D. Geographical and Energy Aware Routing: A Recursive Data Dissemination Protocol for Wireless Sensor Networks; Technical Report; UCLA Computer Science Department: Los Angeles, CA, USA, 2001. [Google Scholar]
- Newsome, J.; Song, D. GEM: Graph EMbedding for Routing and Data-Centric storage in Sensor Networks without Geographic Information. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; ACM Press: New York, NY, USA, 2003; pp. 76–88. [Google Scholar]
- Demirbas, M.; Lu, X. Distributed Quadtree for Spatial Querying in Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Communications, Glasgow, Scotland, 24–28 June 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Demirbas, M.; Lu, X.; Singla, P. An In-Network Querying Framework for Wireless Sensor Networks. IEEE Transact. Parall. Distrib. Syst. 2009, 20, 1202–1215. [Google Scholar] [CrossRef]
- Lyu, C.; Gu, D.; Zhang, X.; Sun, S.; Zhang, Y.; Pande, A. SGOR: Secure and scalable geographic opportunistic routing with received signal strength in WSNs. Comput. Commun. 2015, 59, 37–51. [Google Scholar] [CrossRef]
- Schulzrinne, H.; Casner, S.; Frederick, R.; Jacobson, V. RTP: A Transport Protocol for Real-Time Applications. RFC 1995, 2, 459–482. [Google Scholar]
- Heinzelman, W. Adaptive Protocols for Information Dissemination in Wireless Sensor Networks. In Proceedings of the International Conference on Mobile Computing & Networking, Seattle, WA, USA, 15–20 August 1999. [Google Scholar]
- Kuila, P.; Jana, P.K. An Energy Balanced DISTRIBUTED clustering and Routing Algorithm for Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Parallel Distributed & Grid Computing, Taipei, Taiwan, 16–18 December 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Shen, H.; Chen, Z. A grid-based reliable multi-hop routing protocol for energy-efficient wireless sensor networks. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Hosen, A.; Cho, G.H. An Energy Centric Cluster-Based Routing Protocol for Wireless Sensor Networks. Sensors 2018, 18, 1520. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, N.A.; Nikolidakis, S.A.; Vergados, D.D. Energy-Efficient Routing Protocols in Wireless Sensor Networks: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 551–591. [Google Scholar] [CrossRef]
- Lalitha, K.; Thangarajan, R.; Udgata, S.K.; Poongodi, C.; Sahu, A. PGCCR: An Efficient Grid Based Clustering and Combinational Routing in Wireless Sensor Networks. Wirel. Pers. Commun. 2017, 4, 1–21. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; IEEE: Piscataway, NJ, USA, 2000; p. 8020. [Google Scholar]
- Younis, O.; Fahmy, S. HEED: A Hybrid, Energy-Efficient, Distributed Clustering Approach for Ad Hoc Sensor Networks. IEEE Transact. Mobile Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: Power-Efficient Gathering in Sensor Information Systems. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 8–15 March 2002; IEEE: Piscataway, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Xu, Y.; Heidemann, J.; Estrin, D. Geography-informed Energy Conservation for Ad Hoc Routing. In Proceedings of the Seventh Annual ACM/IEEE International Conference on Mobile Computing and Networking (ACM Mobico), Rome, Italy, 16–21 July 2001; Volume 3, pp. 70–84. [Google Scholar]
- Liao, W.H.; Sheu, J.P.; Tseng, Y.C. GRID: A Fully Location-Aware Routing Protocol for Mobile Ad Hoc Networks. Telecommun. Syst. 2001, 18, 37–60. [Google Scholar] [CrossRef]
- Liao, W.H.; Tseng, Y.C.; Lo, K.L.; Sheu, J.P. GeoGRID: A Geocasting Protocol for Mobile Ad Hoc Networks Based on GRID. J. Internet Technol. 2000, 1, 23–32. [Google Scholar]
- Shu, L.; Mukherjee, M.; Hu, L.; Bergmann, N.; Zhu, C. Geographic Routing in Duty-Cycled Industrial Wireless Sensor Networks with Radio Irregularity. IEEE Access 2016, 4, 9043–9052. [Google Scholar] [CrossRef]
- Lu, T.; Chang, S.; Li, W. Fog computing enabling geographic routing for urban area vehicular network. Peer-to-Peer Netw. Appl. 2017, 11, 749–755. [Google Scholar] [CrossRef]
- Biagi, M.; Greco, S.; Lampe, L. Geo-Routing Algorithms and Protocols for Power Line Communications in Smart Grids. IEEE Trans. Smart Grid 2018, 9, 1472–1481. [Google Scholar] [CrossRef]
- Ren, P.; Zhang, J.Y.; Feng, X.L. Energy efficient cross-layer routing for wireless sensor network in coal mine roadway. J. China Coal Soc. 2016, 41, 522–530. [Google Scholar] [CrossRef]
- Park, K. A hierarchical binary quadtree index for spatial queries. Wireless Netw. 2018, 4, 1–17. [Google Scholar] [CrossRef]
- Ticona-Zegarra, E.; Schouery, R.C.; Villas, L.A.; Miyazawa, F.K. Improved continuous enhancement routing solution for energy-aware data aggregation in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Thomas, S.; Mathew, T. Lossless address data compression using quadtree clustering of the sensors in a grid based WSN. Ad Hoc Netw. 2016, 56, 84–95. [Google Scholar] [CrossRef]
- Mohite, P. Adaptive Data Fusion for Energy Efficient Routing in Wireless Sensor Network. Int. J. Energy Optim. Eng. 2015, 4, 1–17. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, Y.; Xidao, L.; Zhang, X. Multi-Source Heterogeneous Data Fusion. In Proceedings of the International Conference on Artificial Intelligence & Big Data, Guangzhou, China, 21–23 June 2008; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Singh, V.K.; Kumar, M. A Compressed Sensing Approach to Resolve the Energy Hole Problem in Large Scale WSNs. Wirel. Personal. Commun. 2018, 99, 185–201. [Google Scholar] [CrossRef]
- Jannu, S.; Jana, P.K. A grid based clustering and routing algorithm for solving hot spot problem in wireless sensor networks. Wirel. Netw. 2015, 22, 1901–1916. [Google Scholar] [CrossRef]
- Yan, B.; Zhou, X.; Wang, H.; Li, B.A. Grid-Based Clustering Method for Large-Scale Wireless Sensor Networks. In Proceedings of the International Conference on Communications, Glasgow, Scotland, 24–28 June 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Logambigai, R.; Ganapathy, S.; Kannan, A. Energy–efficient grid–based routing algorithm using intelligent fuzzy rules for wireless sensor networks. Comput. Electr. Eng. 2018, 68, 62–75. [Google Scholar] [CrossRef]
- Khelifi, M.; Bourouais, S.; Lounis, O.; Moussaoui, S. GRCS: A cluster-based geographic routing protocol for WSNs. In Proceedings of the Ninth International Conference on Ubiquitous & Future Networks, Milan, Italy, 4–7 July 2007. [Google Scholar]
- Arafeh, B.; Day, K.; Touzene, A.; Alzeidi, N. GEGR: A grid-based enabled geographic routing in Wireless Sensor Networks. In Proceedings of the IEEE Malaysia International Conference on Communications, Kuala Lumpur, Malaysia, 3–5 November 2014. [Google Scholar]
- Ahmed, G.; Zou, J.; Zhao, X.; Sadiq Fareed, M. Markov Chain Model-Based Optimal Cluster Heads Selection for Wireless Sensor Networks. Sensors 2017, 17, 440. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yu, H.B.; Zeng, P. Energy-efficient algorithm for network status information collecting in wireless sensor networks. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2009. [Google Scholar]
- Mir, Z.H.; Ko, Y.B. A Quadtree-Based Data Dissemination Protocol for Wireless Sensor Networks with Mobile Sinks. In Proceedings of the International Conference on Personal Wireless Communications, Albacete, Spain, 20–22 September 2006; Springer: Heidelberg, Germany, 2006; pp. 447–458. [Google Scholar]
- Avin, C.; Dvory, Y.; Giladi, R. Geographical quadtree routing. In Proceedings of the IEEE Symposium on Computers and Communications, IEEE Computer Society, Corfu, Greece, 28 June–1 July 2011; pp. 302–308. [Google Scholar]
- Sheng, Y.; Tang, H.; Du, P. Fast Dynamic Encoding of Linear Quadtree and Its Realization. J. Wuhan Technol. Univ. Surv. Mapp. 2000, 4, 324–328. [Google Scholar]
- Qian, Z.H.; Wang, Y.J. Internet of things-oriented wireless sensor networks review. J. Electron. Inf. Technol. 2013, 35, 215–227. [Google Scholar] [CrossRef]
- Siddiqui, S.; Khan, A.A.; Ghani, S. A survey on data aggregation mechanisms in wireless sensor networks. In Proceedings of the International Conference on Information & Communication Technologies, Bali, Indonesia, 27–29 May 2015. [Google Scholar]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Lung, C.H.; Zhou, C. Using Hierarchical Agglomerative Clustering in Wireless Sensor Networks: An Energy-Efficient and Flexible Approach. Ad Hoc Netw. 2010, 8, 328–344. [Google Scholar] [CrossRef]
| Protocols | Energy Saving | Load Balancing | Spatial Query Efficiency | Large-Scale WSN |
|---|---|---|---|---|
| GeoGrid [26] | High | Low | Middle | Yes |
| GFTCRA [37] | Middle | Yes | Low | Yes |
| CEBCRA [16] | Middle | Yes | Middle | Yes |
| GCP [38] | Middle | Low | Low | Yes |
| EEGBR [39] | Middle | Low | Middle | No |
| GRCS [40] | Middle | Low | High | No |
| GEGR [41] | Middle | Low | Middle | No |
| MOCHs [42] | High | Middle | Middle | Yes |
| QTBDC [43] | High | Low | High | Yes |
| GCCR [20] | High | High | Middle | Yes |
| Parameters | Values |
|---|---|
| Network size (m × m) | 160 × 160 |
| Location of the Sink Node | Network center |
| Nodes’ initial energy (J) | 10 |
| Cluster heads’ energy threshold (J) | 4 |
| Eelec (nJ/bit) | 50 |
| εamp (pJ/bit/m2) | 10 |
| Computation cost of Data aggregation Eda (nJ/bit/signal) | 3 |
| Computation cost of routing Er (nJ/bit/signal) | 5 |
| Number of network layers/Number of nodes | 5 |
| Radius of the intra-cluster communication (m) | 28.28 |
| Radius of the inter-cluster communication (m) | 56.56 |
| Size of the data packet (bits) | 500 |
| Size of the packet header (bits) | 200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, X.; Wang, M.; Nie, Y.; Bian, Y. Energy-Efficient Spatial Query-Centric Geographic Routing Protocol in Wireless Sensor Networks. Sensors 2019, 19, 2363. https://doi.org/10.3390/s19102363
Wang X, Liu X, Wang M, Nie Y, Bian Y. Energy-Efficient Spatial Query-Centric Geographic Routing Protocol in Wireless Sensor Networks. Sensors. 2019; 19(10):2363. https://doi.org/10.3390/s19102363
Chicago/Turabian StyleWang, Xing, Xuejun Liu, Meizhen Wang, Yunfeng Nie, and Yuxia Bian. 2019. "Energy-Efficient Spatial Query-Centric Geographic Routing Protocol in Wireless Sensor Networks" Sensors 19, no. 10: 2363. https://doi.org/10.3390/s19102363
APA StyleWang, X., Liu, X., Wang, M., Nie, Y., & Bian, Y. (2019). Energy-Efficient Spatial Query-Centric Geographic Routing Protocol in Wireless Sensor Networks. Sensors, 19(10), 2363. https://doi.org/10.3390/s19102363







