Decoupling of Airborne Dynamic Bending Deformation Angle and Its Application in the High-Accuracy Transfer Alignment Process
Abstract
1. Introduction
2. Coupled Error Angle Model of Dynamic Bending Deformation
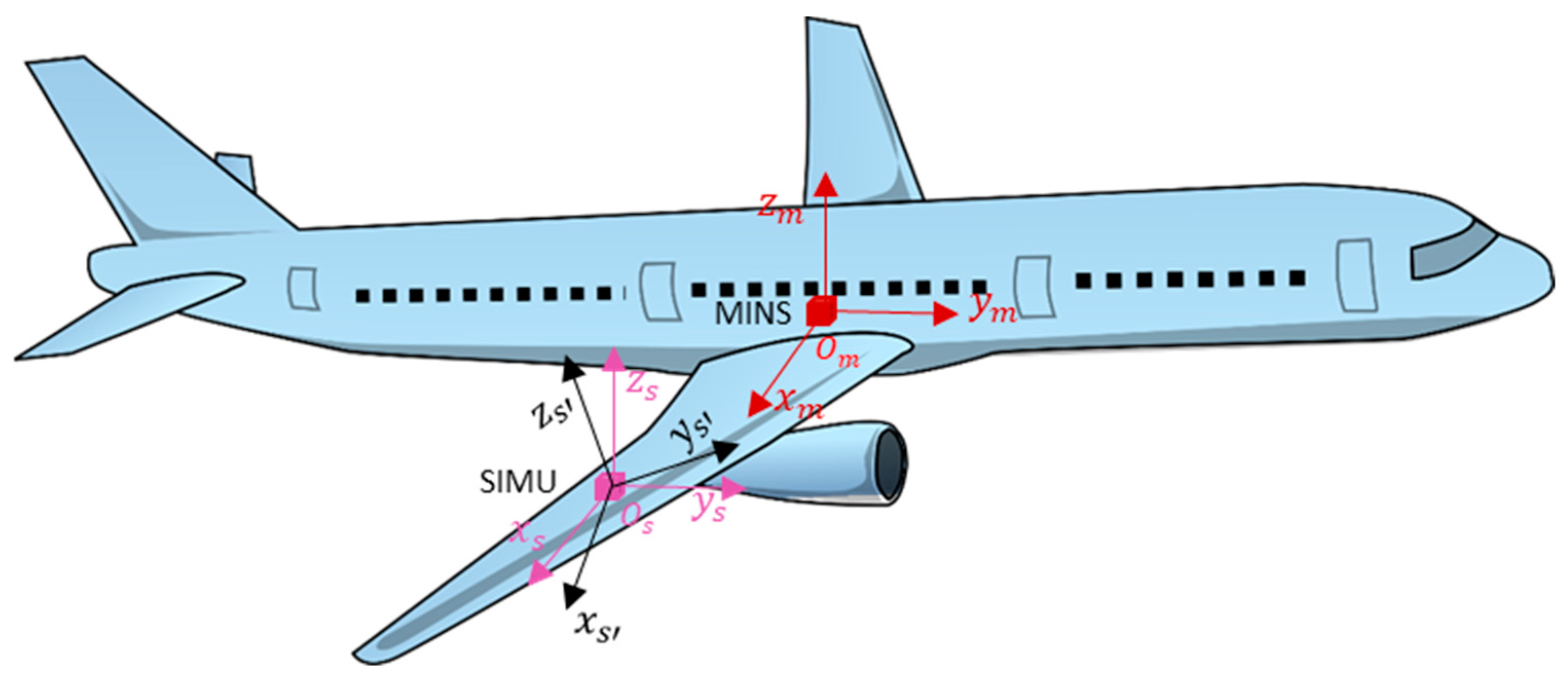
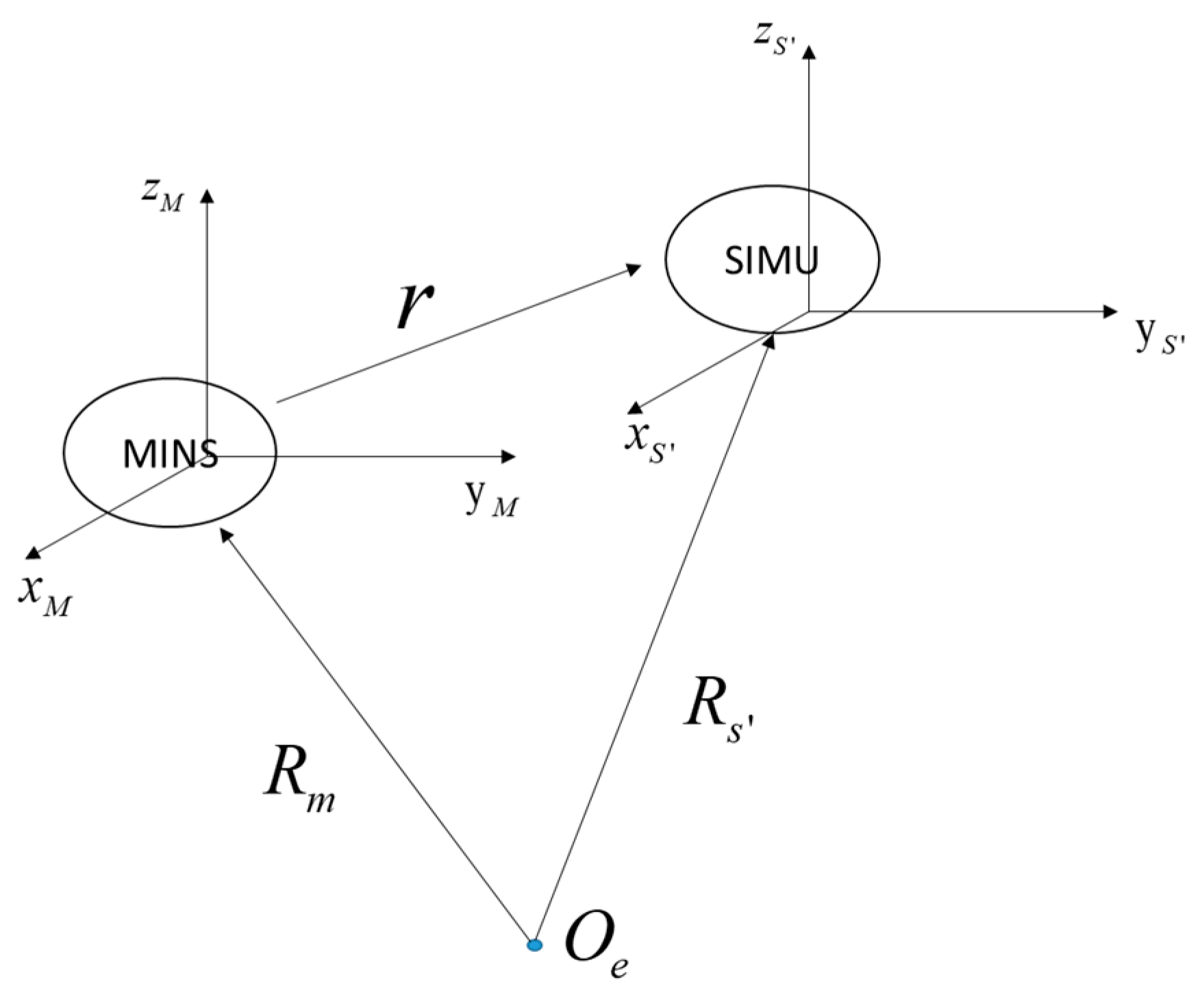
2.1. Coordinate System Description
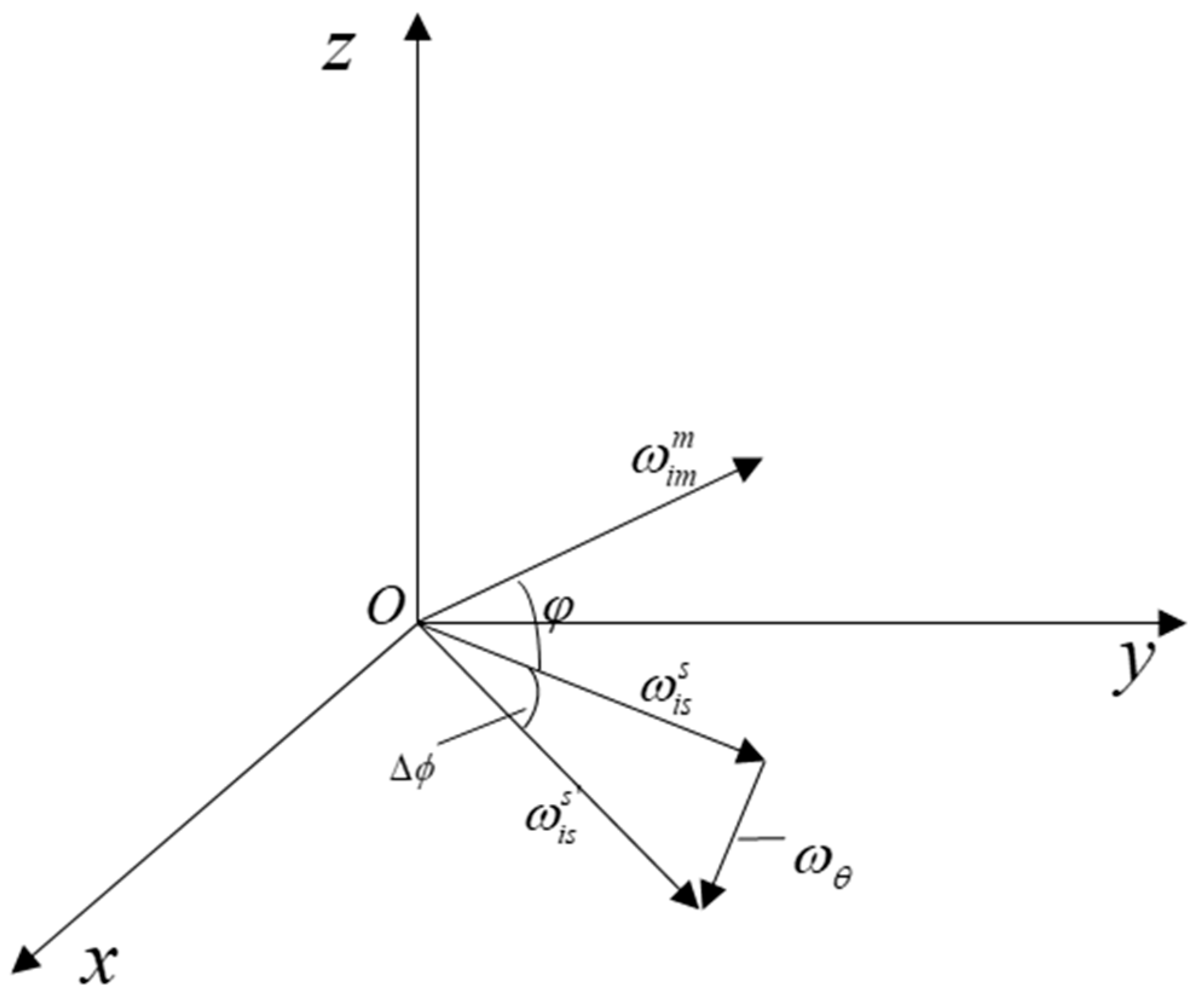
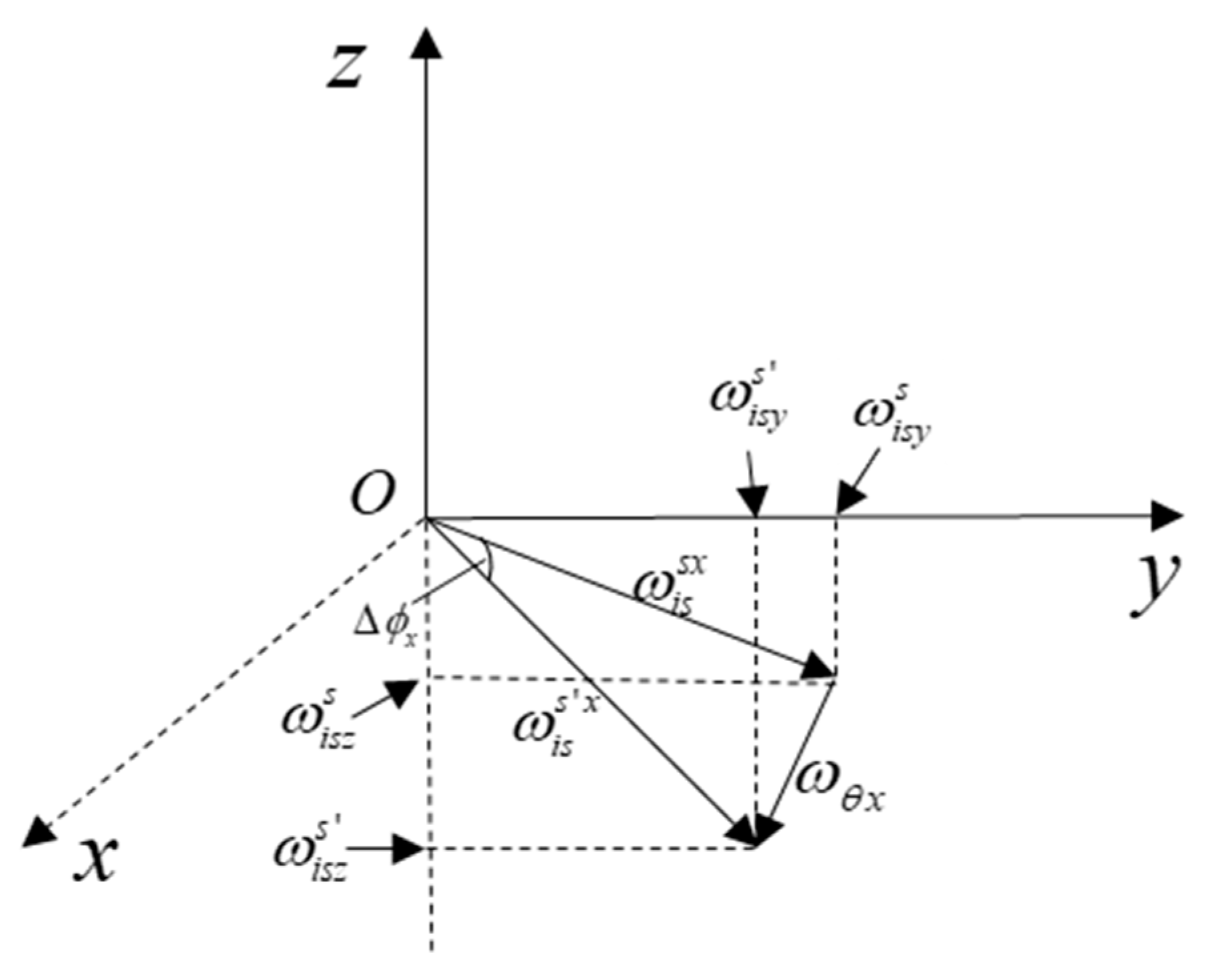
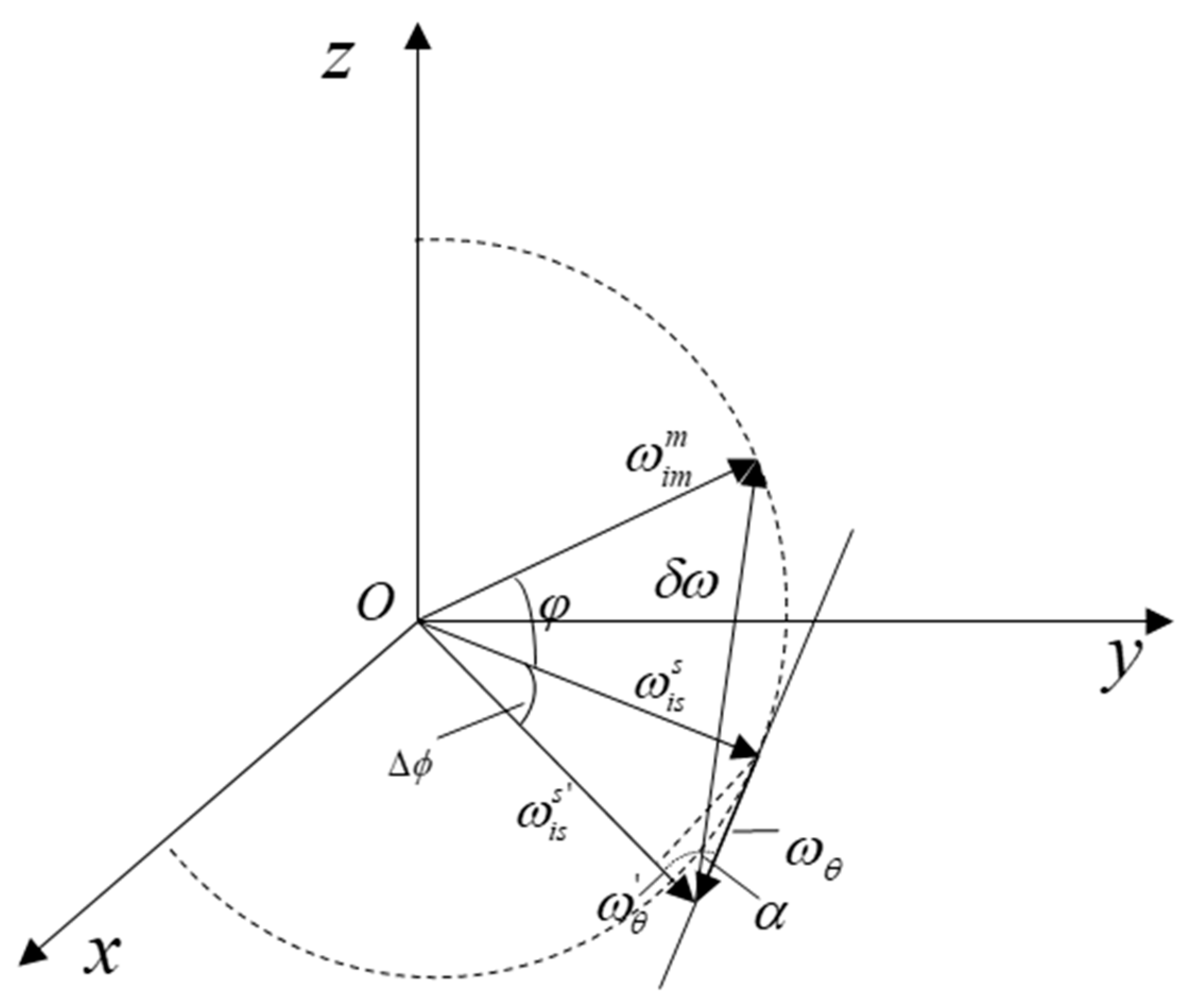
2.2. Model of Coupling Angle
- is the errorless angular velocity of the slave IMU,
- is the static or invariant component of angular velocity, which is generated under rigid body motion,
- is the dynamic component of angular velocity, which is generated under elastic body motion,
- is the component of due to flexure motion,
- is the component of vibration motion, which is assumed to be white noise.
3. Transfer Alignment Model
3.1. Model of Angular Velocity Error and Compensation
3.2. Model of Velocity Error and Compensation
3.3. State Equation
3.4. Measurement Equation
3.5. Filter Selection
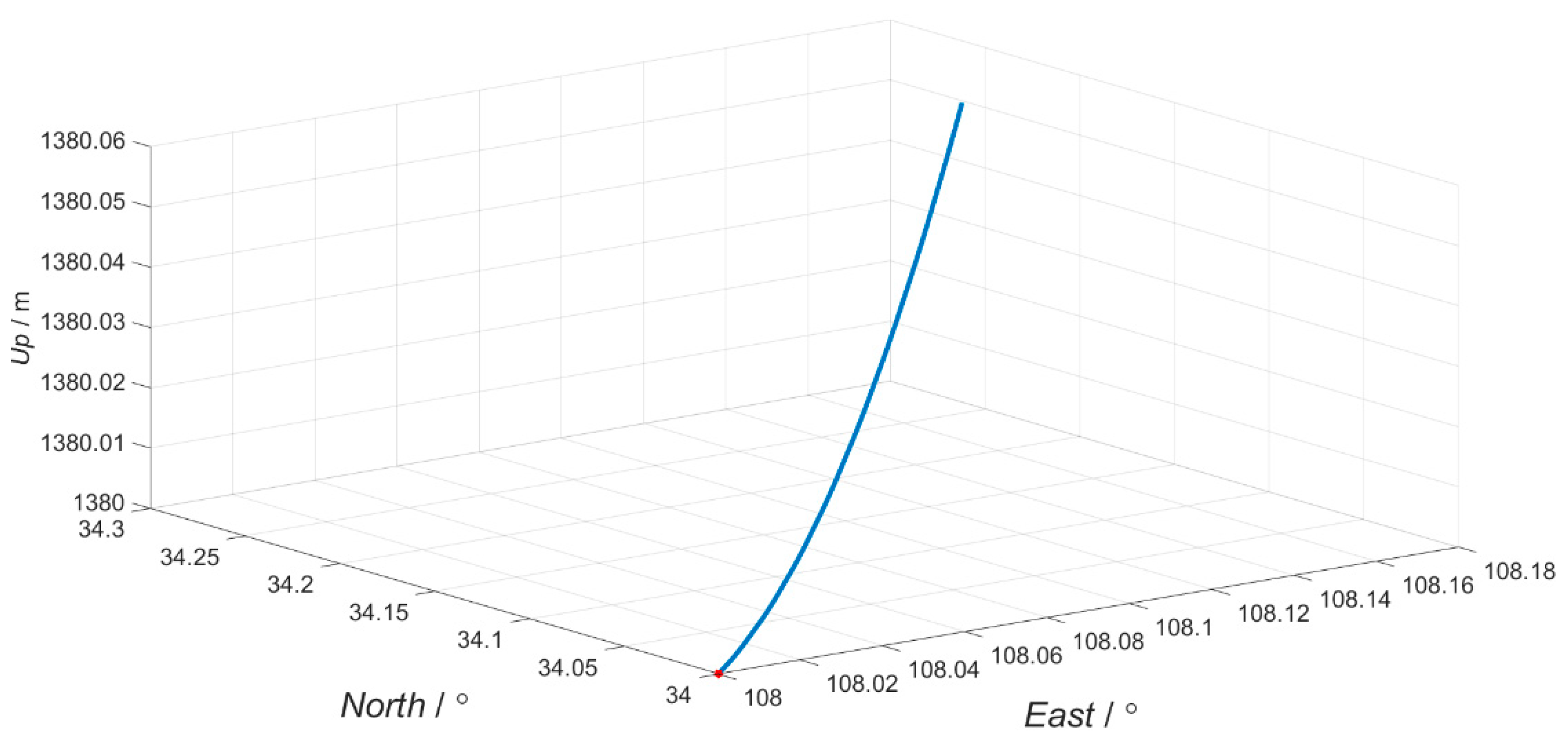
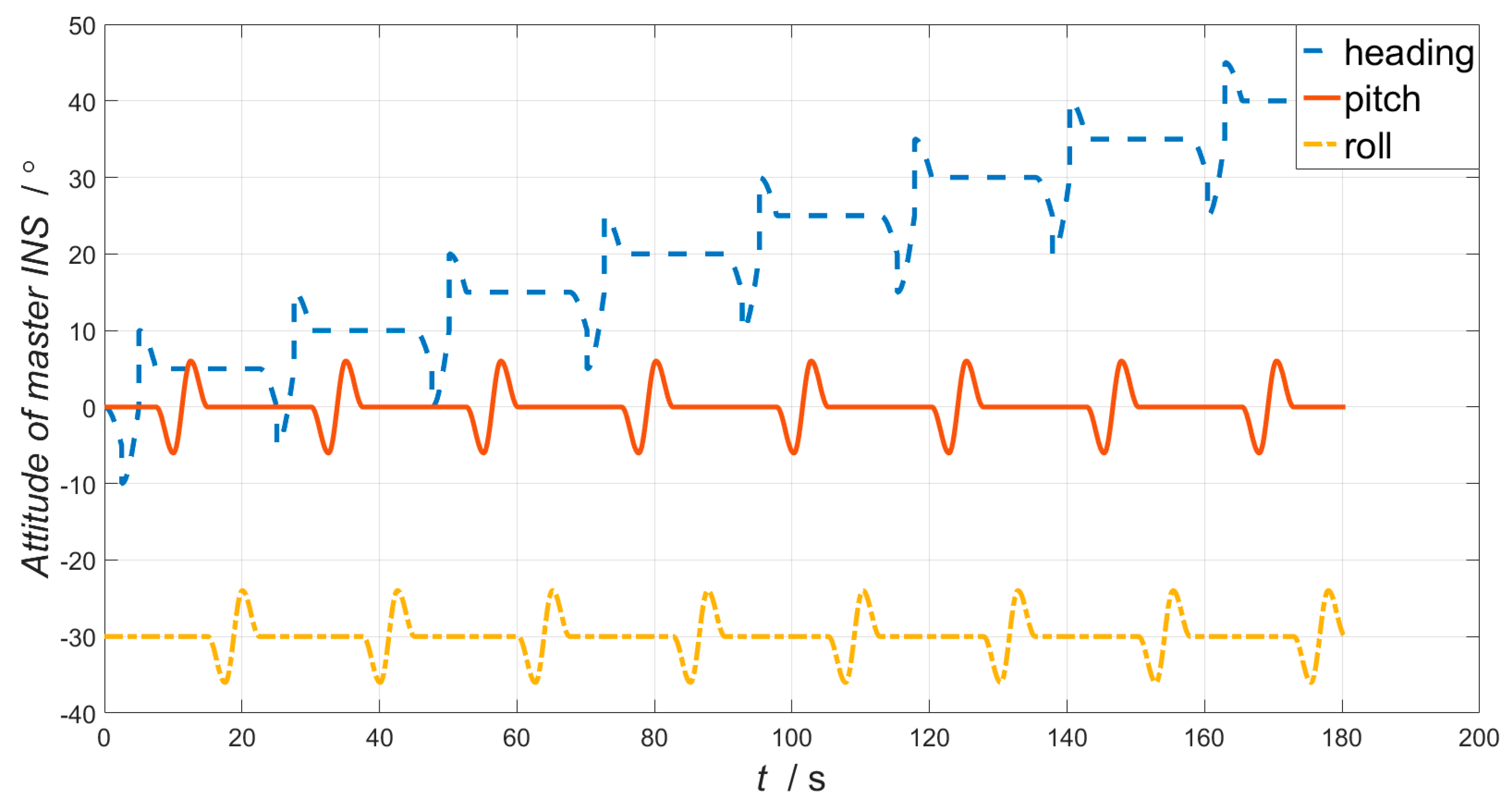
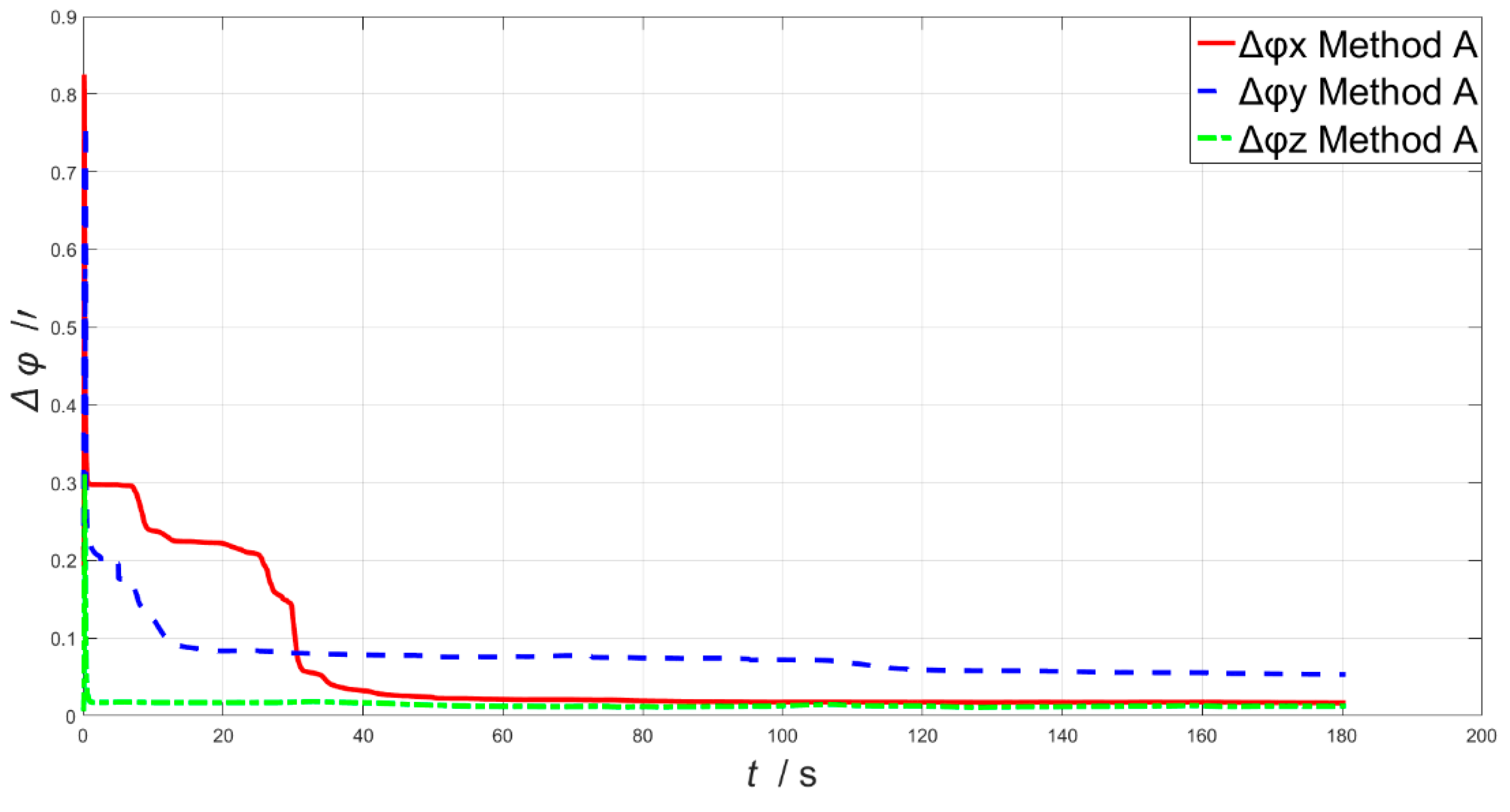
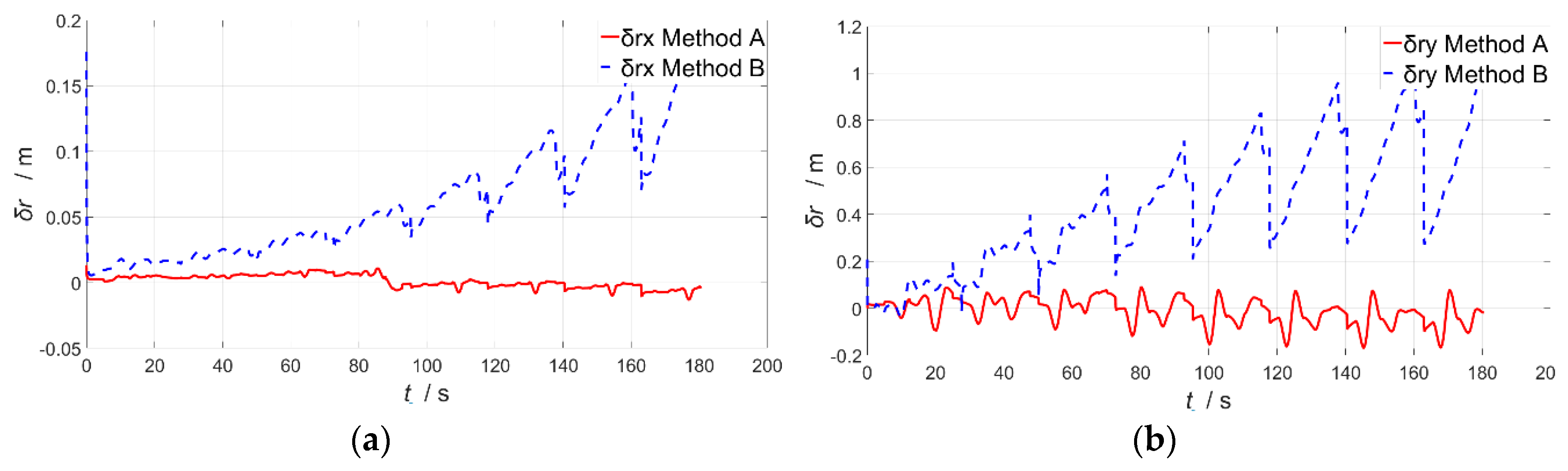
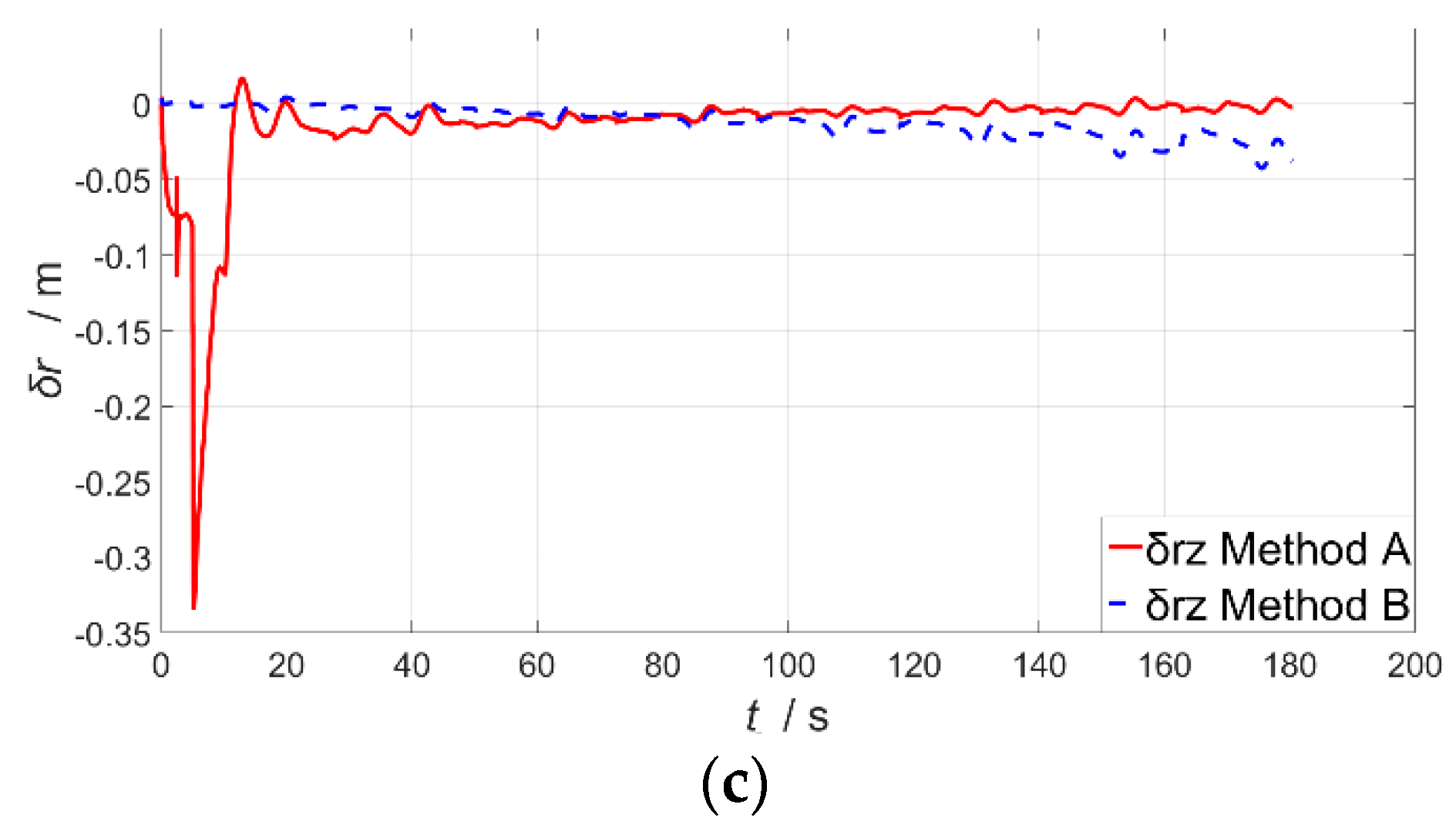
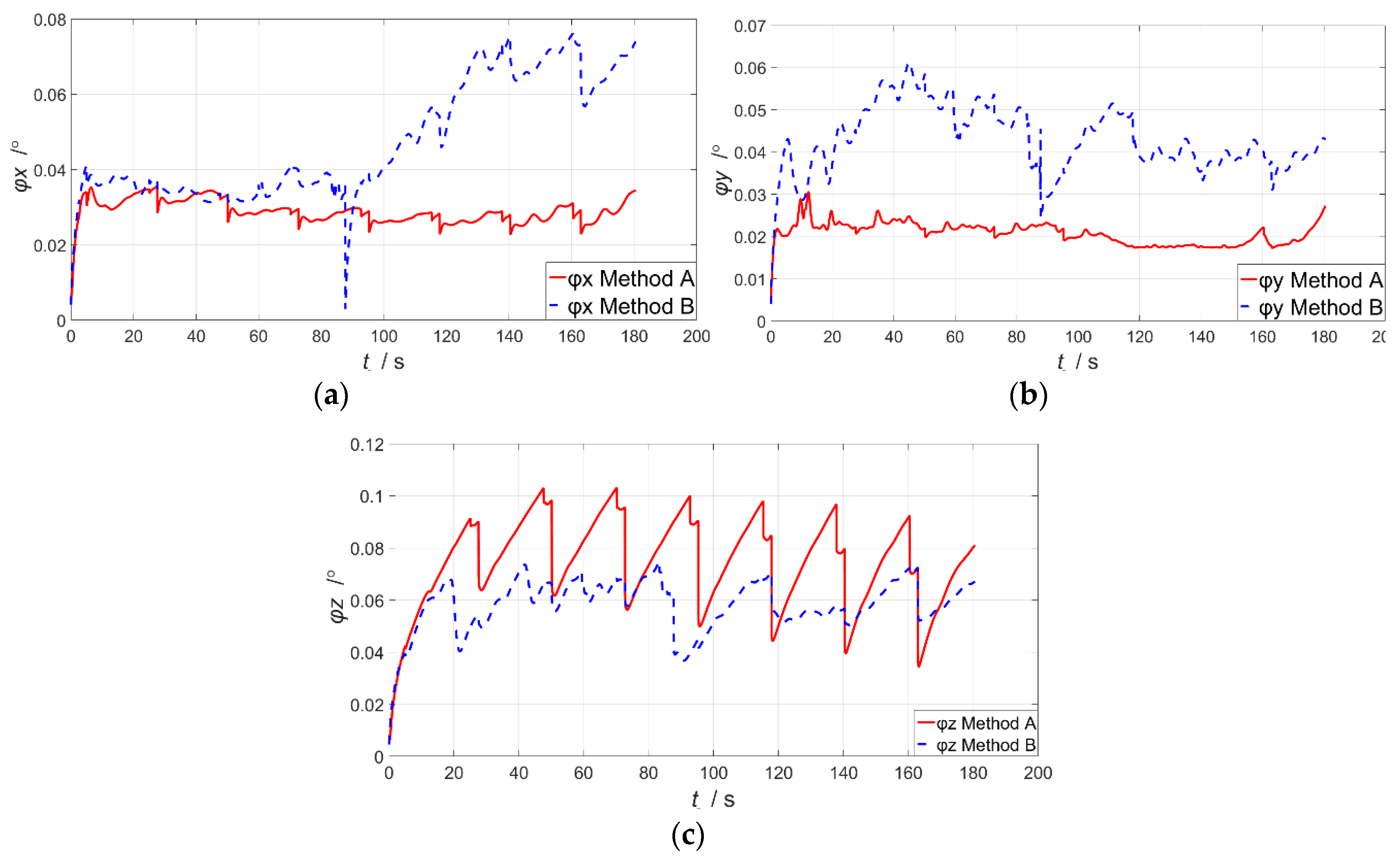
4. Simulation and Results
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Fang, J.C.; Chen, L.; Yao, J.F. An accurate gravity compensation method for high-precision airborne POS. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4564–4573. [Google Scholar] [CrossRef]
- Allerton, D.J.; Jia, H. Distributed data fusion algorithms for inertial network systems. IET Radar Sonar Navig. 2008, 2, 51–62. [Google Scholar] [CrossRef]
- Chen, X.Y.; Wang, W. Extracting and compensating for FOG vibration error based on improved empirical mode decomposition with masking signal. Appl. Opt. 2017, 56, 3848–3856. [Google Scholar]
- Gao, L.; Zeng, Y.H.; Wang, L.D. Design of array for airborne forward looking SAR based on compressed sensing. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing, Guilin, China, 5–8 August 2014; pp. 473–476. [Google Scholar]
- Wang, W.; Chen, X.Y. Application of Improved 5th-Cubature Kalman Filter in Initial Strapdown Inertial Navigation System Alignment for Large Misalignment Angles. Sensors 2018, 18, 659. [Google Scholar] [CrossRef] [PubMed]
- Fatoyinbo, T.; Rincon, R.F.; Sun, G.Q.; Ranson, J.K. Ecosar: A P-band digital beamforming polarimetric interferometric SAR INSTRUMENT to measure ecosystem structure and biomass. In Proceedings of the International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1524–1527. [Google Scholar]
- Kain, J.E.; Cloutier, J.R. Rapid transfer alignment for tactical weapon applications. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Boston, MA, USA, 14–16 August 1989; pp. 1290–1300. [Google Scholar]
- Chen, X.Y.; Shen, C.; Zhang, W.-B.; Tomizuka, M.; Xu, Y.; Chiu, K. Novel hybrid of strong tracking Kalman filter and wavelet neural network for GPS/INS during GPS outages. Measurement 2013, 46, 3847–3854. [Google Scholar] [CrossRef]
- Gu, F.F.; Zhang, Q.; Chi, L.; Chen, Y.A.; Li, S. A novel motion compensating method for MIMO-SAR imaging based on compressed sensing. IEEE Sens. J. 2015, 15, 2157–2165. [Google Scholar] [CrossRef]
- Wu, W.; Chen, S.; Qin, S. Online estimation of ship dynamic flexure model parameters for transfer alignment. IEEE Trans. Control Syst. Technol. 2013, 21, 1666–1678. [Google Scholar] [CrossRef]
- Yoldemir, A.N.; Sezgin, M. A least squares approach to buried object detection using ground penetrating radar. IEEE Sens. J. 2011, 11, 1337–1341. [Google Scholar] [CrossRef]
- Rhee, I.; Abdel-Hafez, M.F.; Speyer, J.L. Observability of an integrated GPS/INS during maneuvers. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 526–535. [Google Scholar] [CrossRef]
- Xu, J.S.; Wang, Y.J. Rapid transfer alignment for SINS of carrier craft. J. Syst. Eng. Electron. 2013, 24, 303–308. [Google Scholar] [CrossRef]
- Pehlivanoglu, A.G.; Ercan, Y. Investigation of flexure effect on transfer alignment performance. J. Navig. 2013, 66, 1–15. [Google Scholar] [CrossRef]
- Gong, X.; Liu, H.; Fang, J.; Liu, G. Multi-node Transfer Alignment based on Mechanics Modeling for Airborne DPOS. IEEE Sens. J. 2017, 18, 669–679. [Google Scholar] [CrossRef]
- Gong, X.; Liu, H.; Yan, X.G. Deformation Measuring Methods Based on Inertial Sensors for Airborne Distributed POS. Int. J. Aerosp. Eng. 2017, 2017, 9343215. [Google Scholar] [CrossRef]
- Browne, B.H.; Lackowski, D.H. Estimation of dynamic alignment errors in shipboard firecontrol systems. In Proceedings of the IEEE Conference on Decision and Control Including the 15th Symposium on Adaptive Processes, Clearwather, FL, USA, 1–3 December 1976; pp. 48–57. [Google Scholar]
- Mochalov, A.V.; Kazantasev, A.V. Use of the ring laser units for measurement of the moving object deformation. In Proceedings of the SPIE 4680, Petersburg, Russia, 5 February 2002; pp. 85–92. [Google Scholar]
- Wu, W.; Qin, S.; Chen, S. Coupling influence of ship dynamic flexure on high accuracy transfer alignment. Int. J. Model. Identif. Control 2013, 19, 224–234. [Google Scholar] [CrossRef]
- Wang, B.; Deng, Y.; Liu, C.; Xia, Y.; Fu, M. Estimation of information sharing error by dynamic deformation between inertial navigation systems. IEEE Trans. Ind. Electron. 2014, 61, 2015–2023. [Google Scholar] [CrossRef]
- Lawrence, C.B. Master reference system for rapid at sea alignment of aircraft inertial navigation systems. In Proceedings of the AIAA/JACC Conference Guidance and Control, Seattle, WA, USA, 15–17 August 1966; pp. 15–17. [Google Scholar]
- Majeed, S.; Fang, J. Comparison of INS based angular rate matching methods for measuring dynamic deformation. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009; pp. 332–336. [Google Scholar]
| Master INS | Slave IMU | ||
|---|---|---|---|
| gyroscope | random drift | ||
| white noise | |||
| accelerometer | random drift | ||
| white noise |
| Estimation Error | Method A | Method B |
|---|---|---|
| (m) | 0.004998 | 0.074664 |
| (m) | 0.056484 | 0.499977 |
| (m) | 0.037366 | 0.015182 |
| Estimation Error | Method A | Method B |
|---|---|---|
| (°) | 0.021147 | 0.043164 |
| (°) | 0.019393 | 0.061425 |
| (°) | 0.078595 | 0.045374 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Chen, X.; Wang, J. Decoupling of Airborne Dynamic Bending Deformation Angle and Its Application in the High-Accuracy Transfer Alignment Process. Sensors 2019, 19, 214. https://doi.org/10.3390/s19010214
Yang P, Chen X, Wang J. Decoupling of Airborne Dynamic Bending Deformation Angle and Its Application in the High-Accuracy Transfer Alignment Process. Sensors. 2019; 19(1):214. https://doi.org/10.3390/s19010214
Chicago/Turabian StyleYang, Ping, Xiyuan Chen, and Junwei Wang. 2019. "Decoupling of Airborne Dynamic Bending Deformation Angle and Its Application in the High-Accuracy Transfer Alignment Process" Sensors 19, no. 1: 214. https://doi.org/10.3390/s19010214
APA StyleYang, P., Chen, X., & Wang, J. (2019). Decoupling of Airborne Dynamic Bending Deformation Angle and Its Application in the High-Accuracy Transfer Alignment Process. Sensors, 19(1), 214. https://doi.org/10.3390/s19010214





