Extended Multiple Aperture Mapdrift-Based Doppler Parameter Estimation and Compensation for Very-High-Squint Airborne SAR Imaging
Abstract
1. Introduction
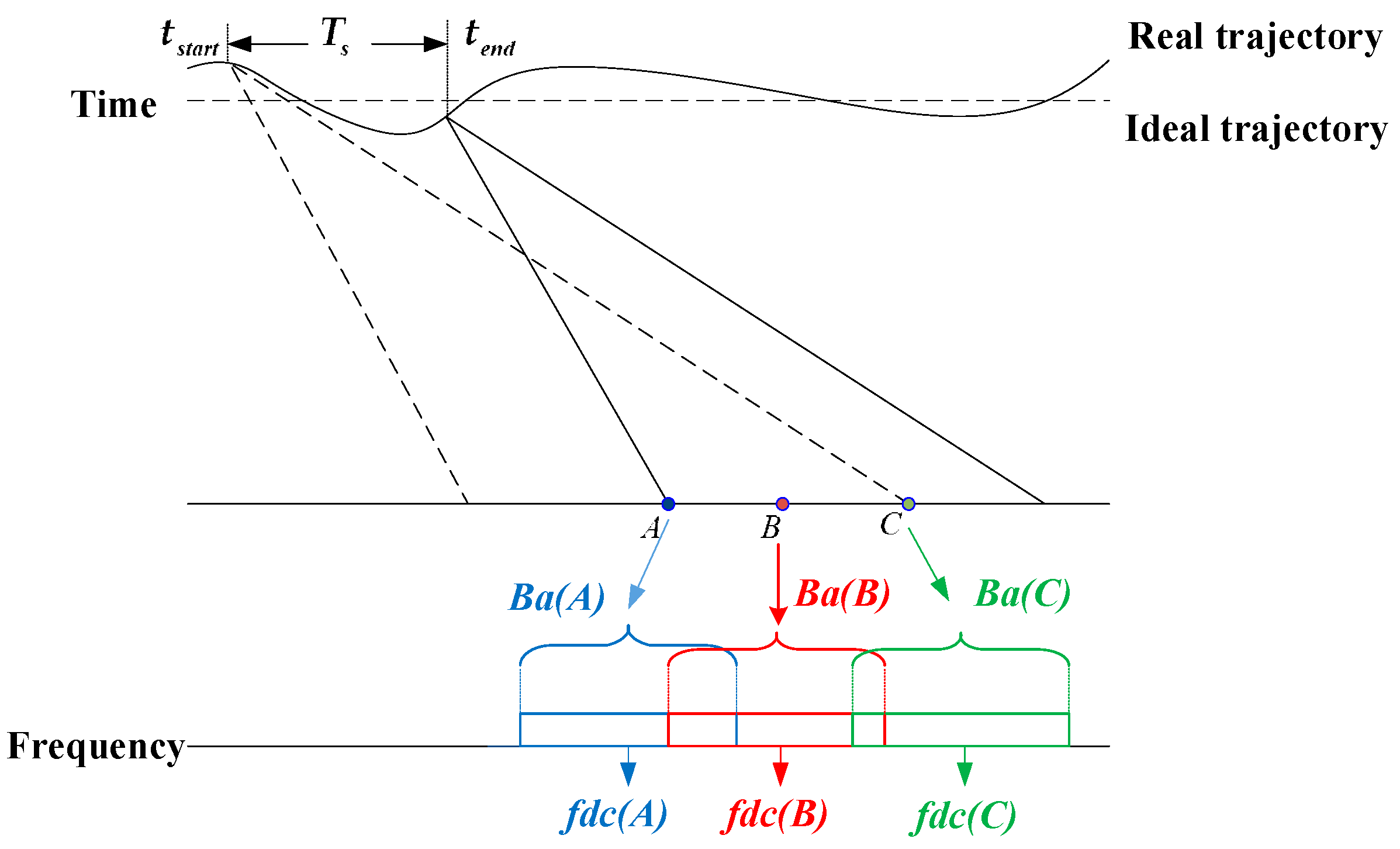
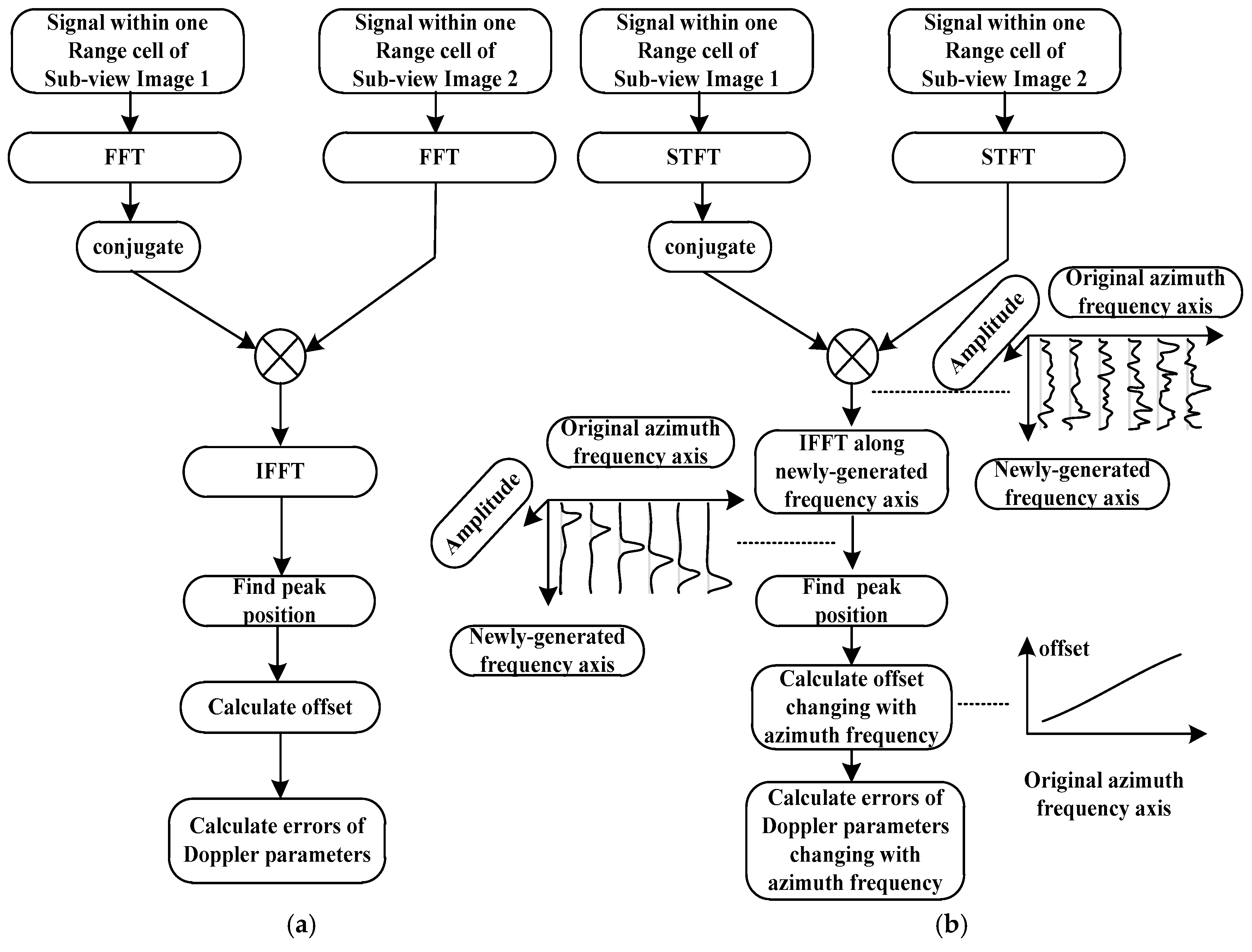
2. Basic Multiple Aperture Mapdrift Method
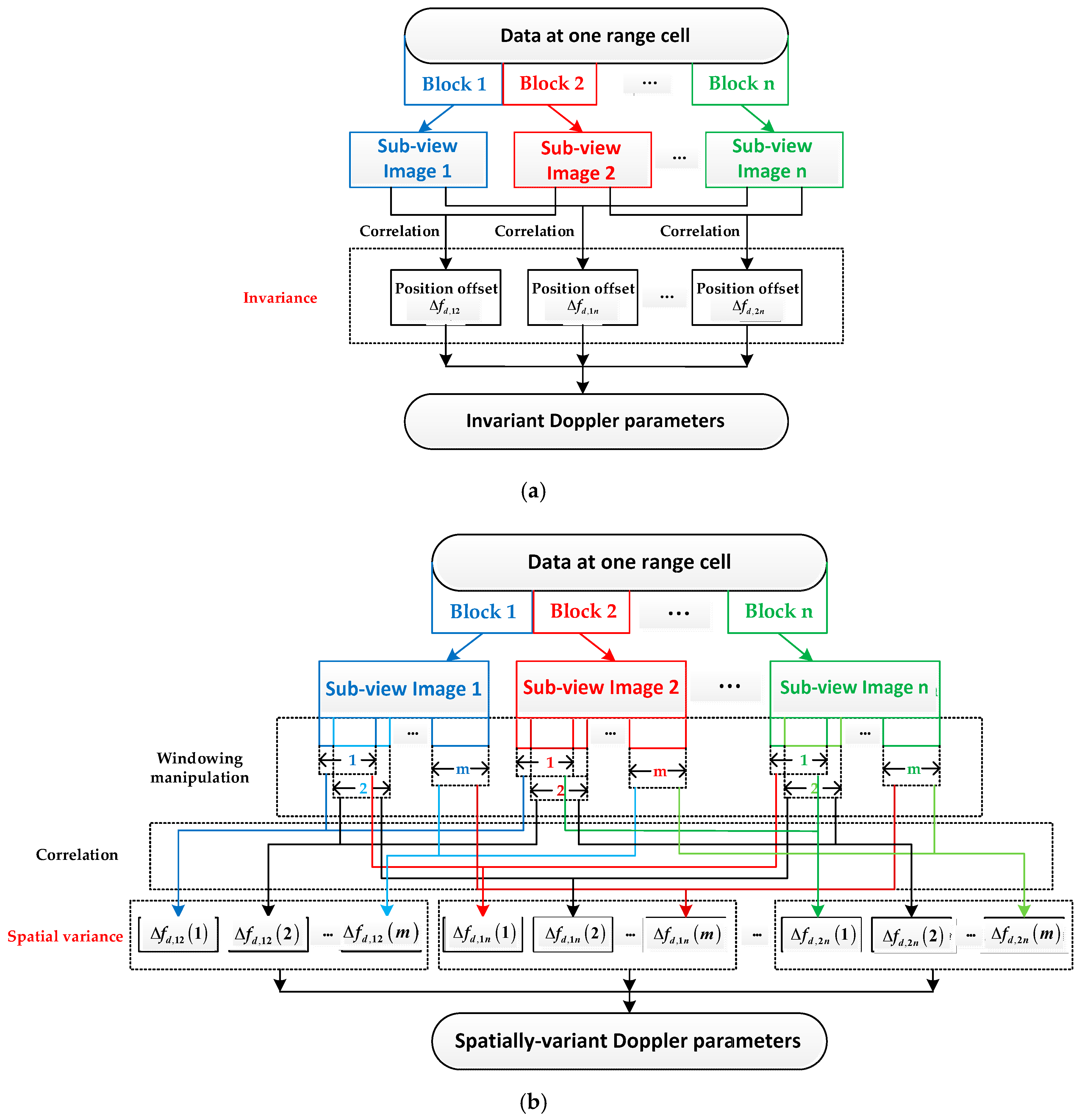
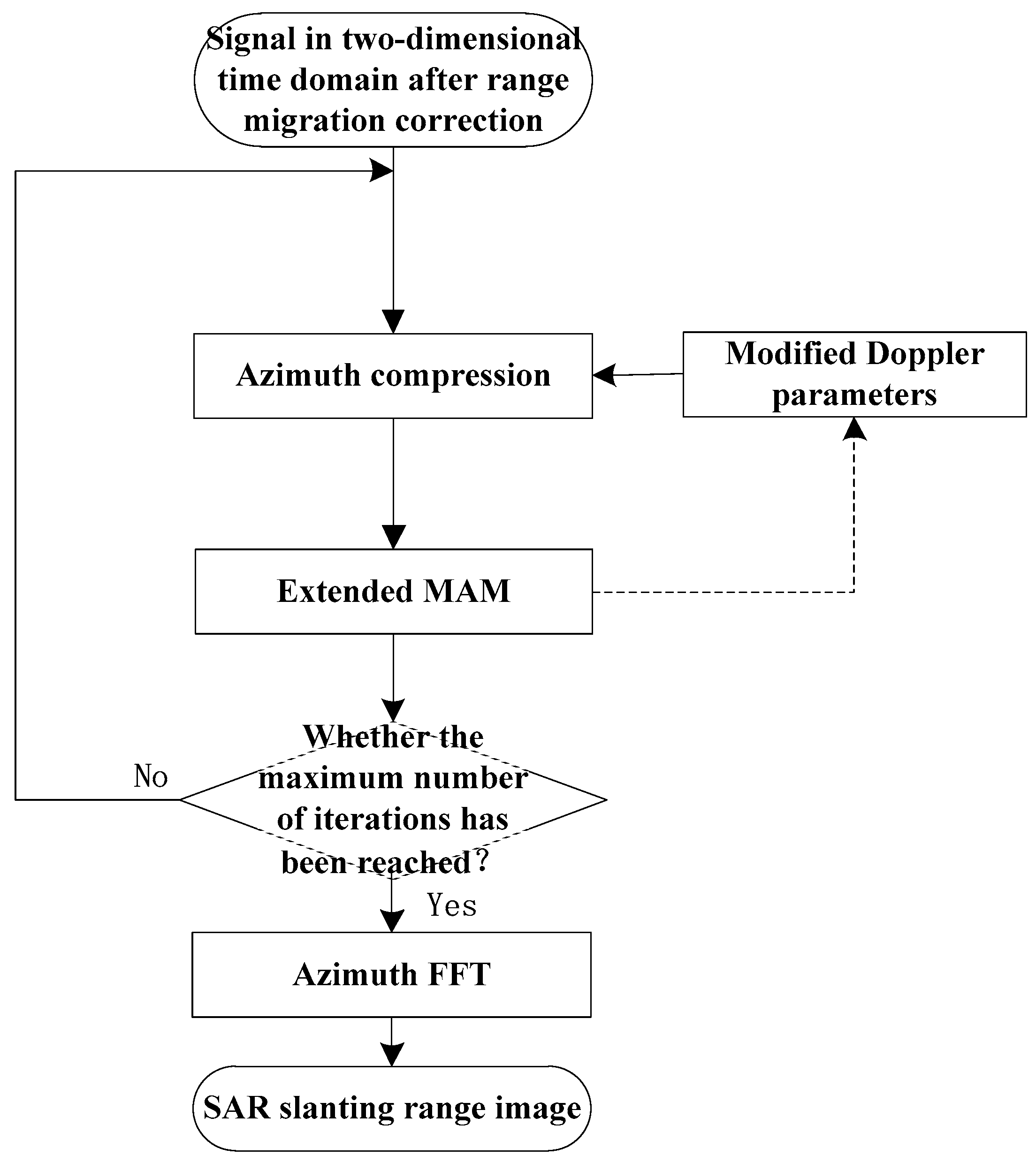
3. Extended Multiple Aperture Mapdrift Method
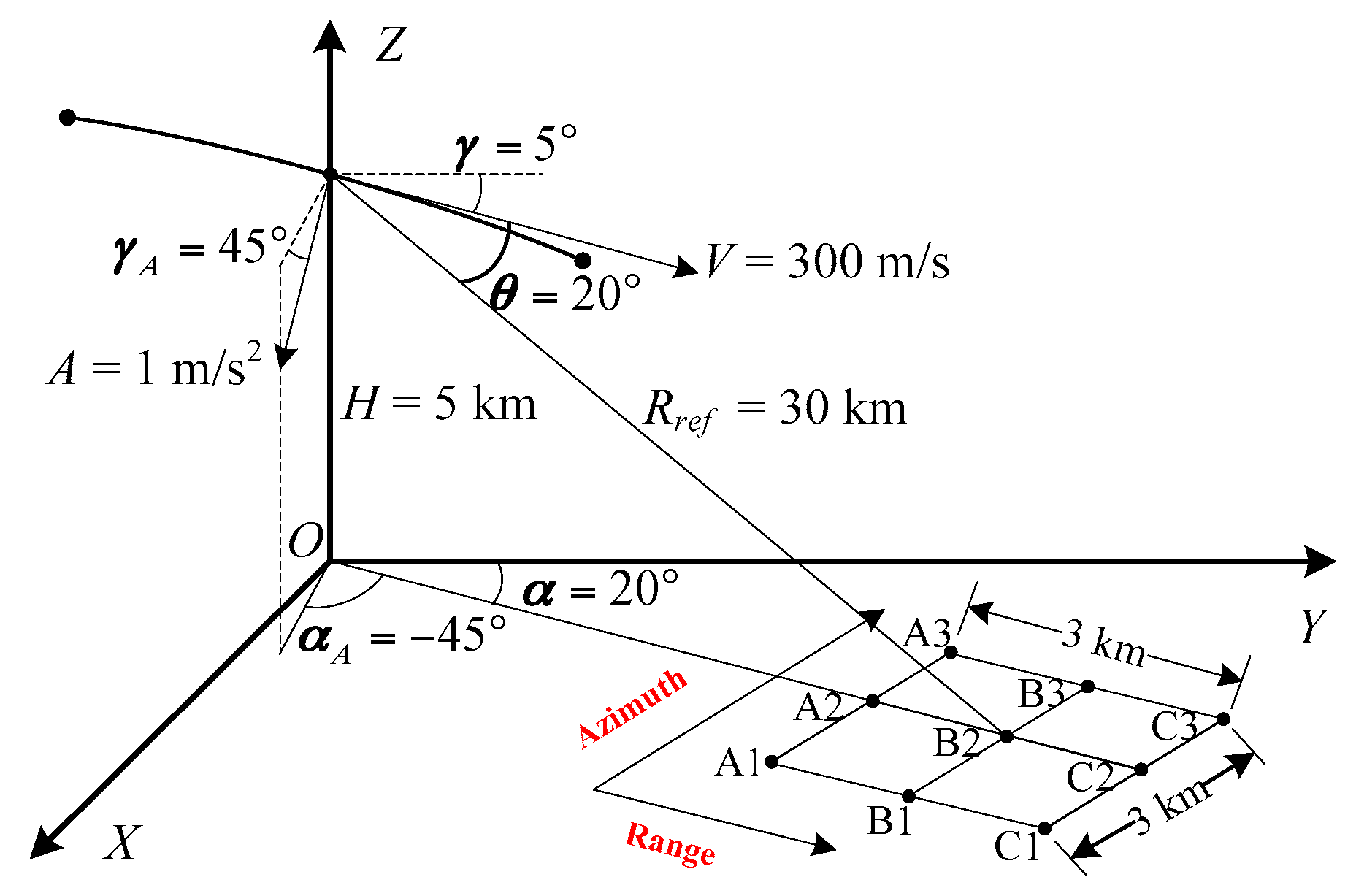
4. Performance Analysis
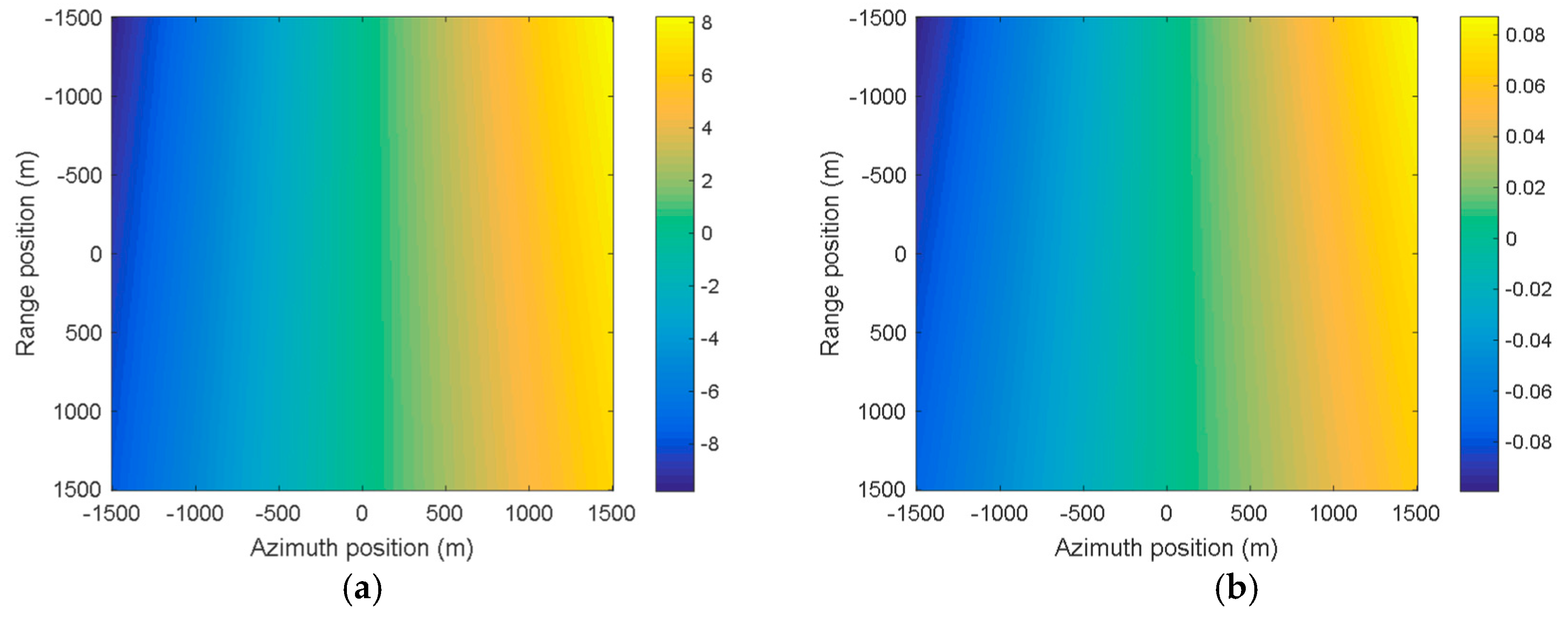
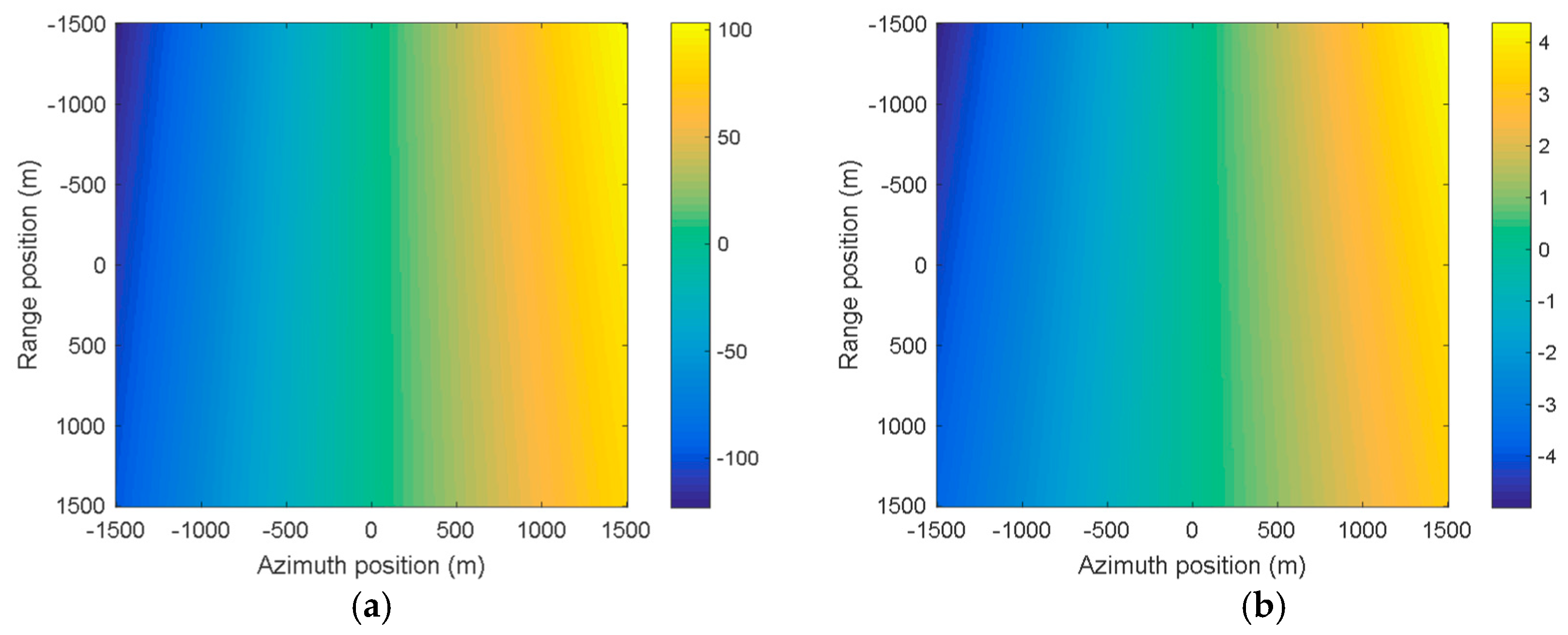
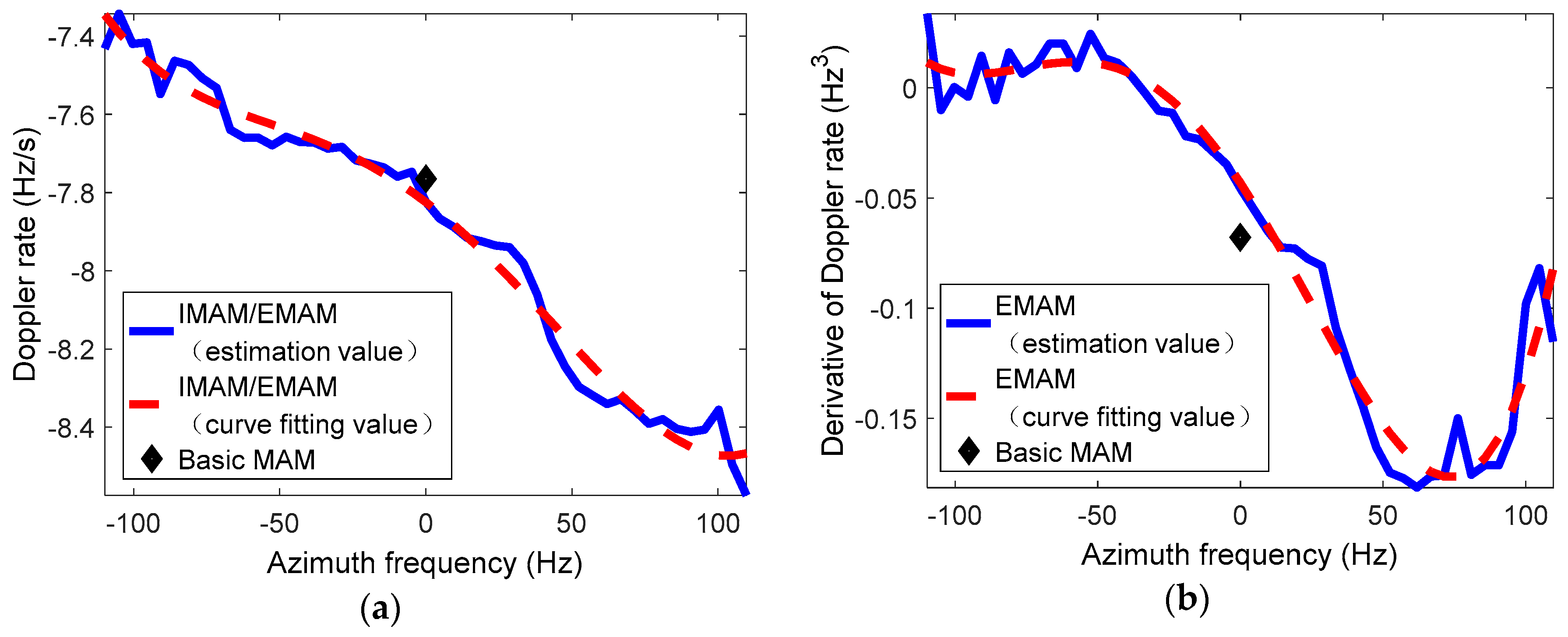
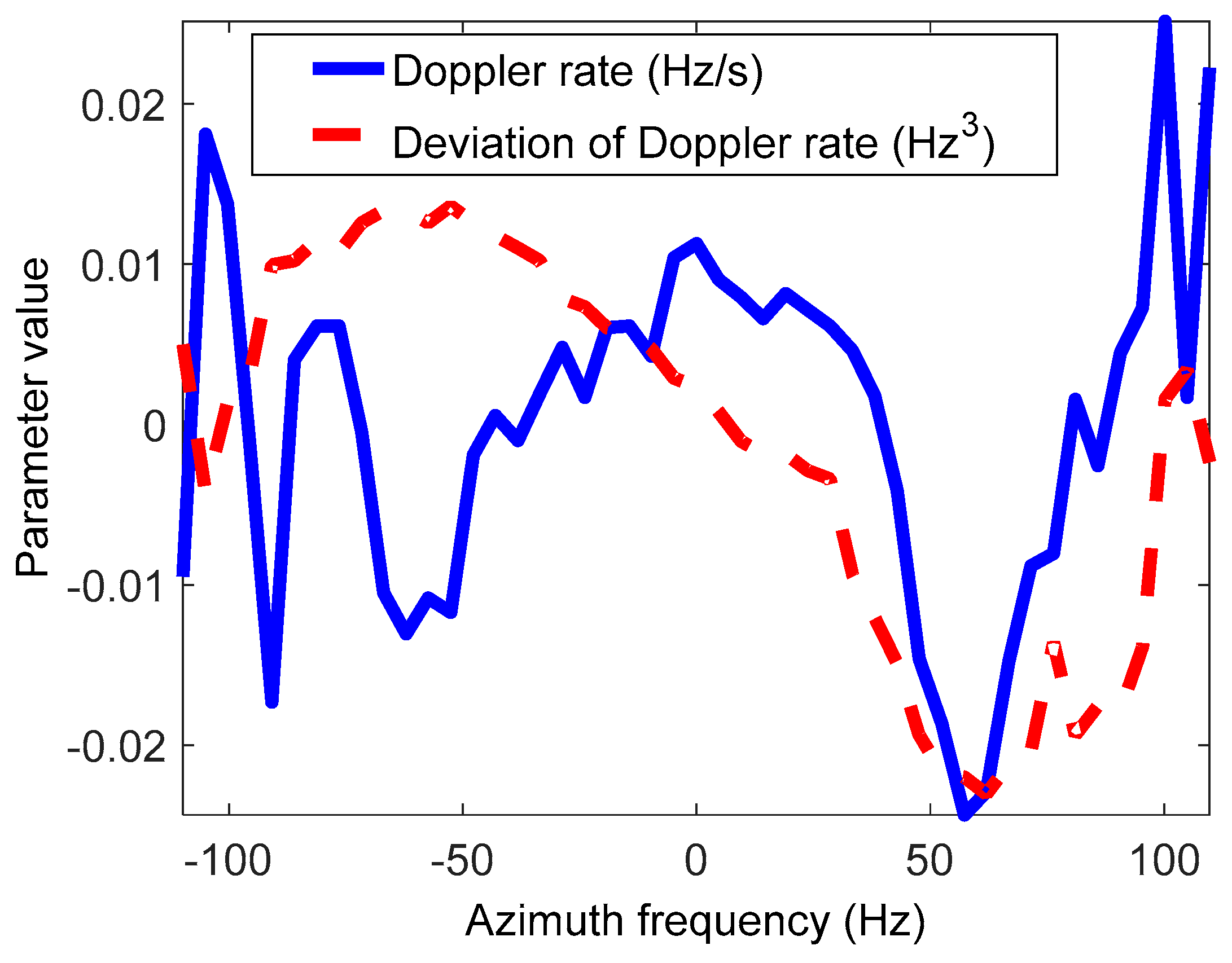
4.1. Spatial Variance of Doppler Parameters
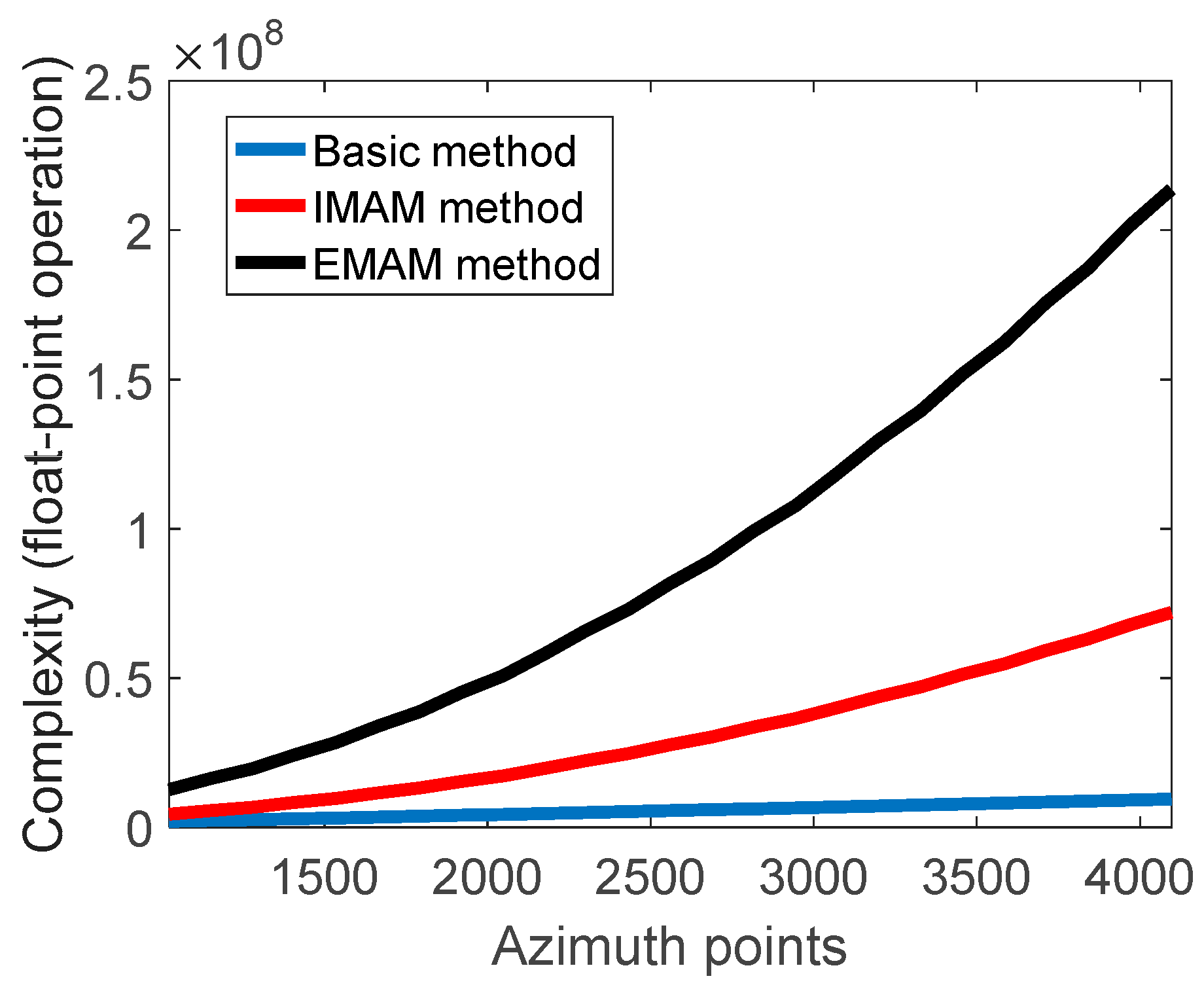
4.2. Complexity
5. Results
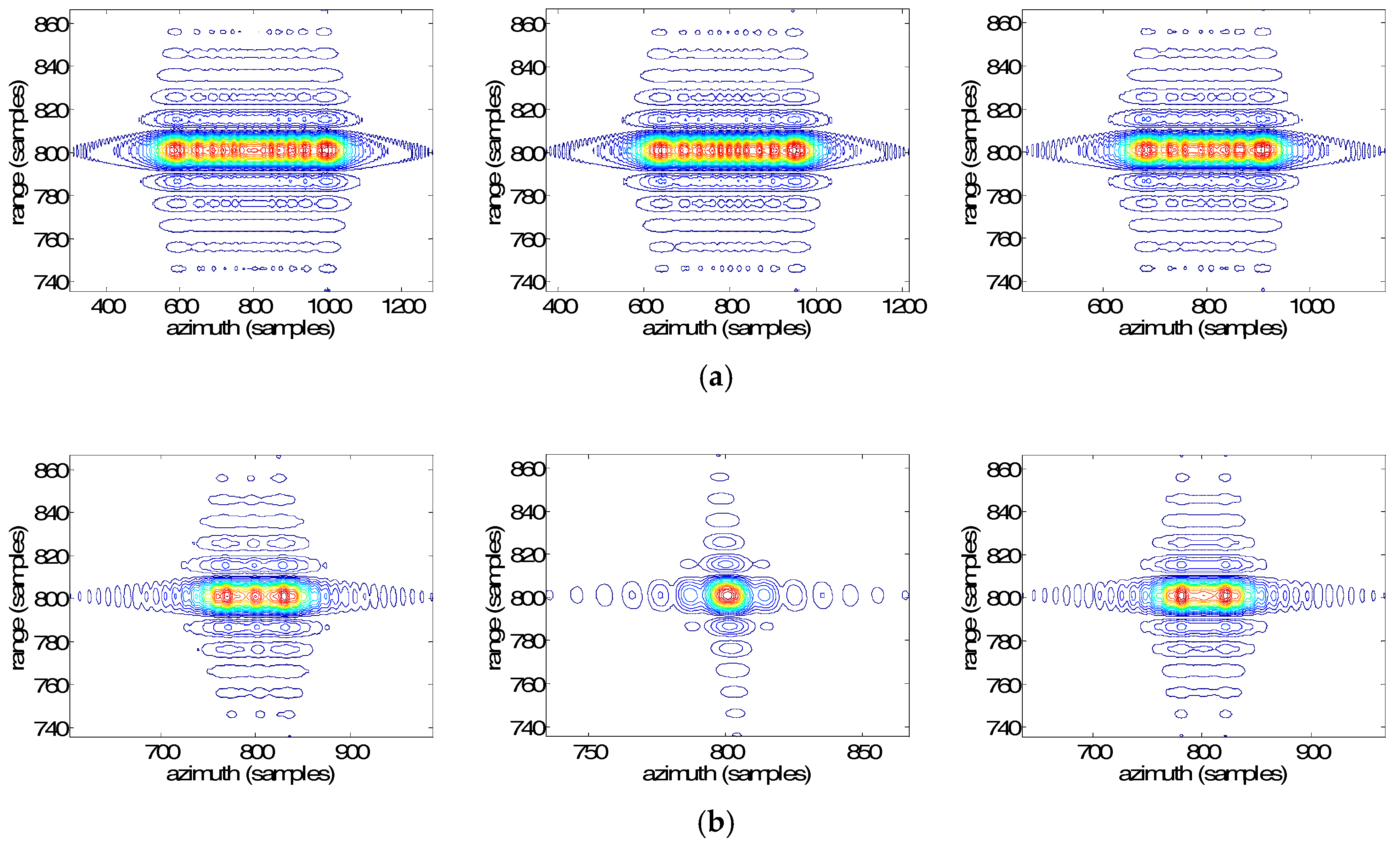
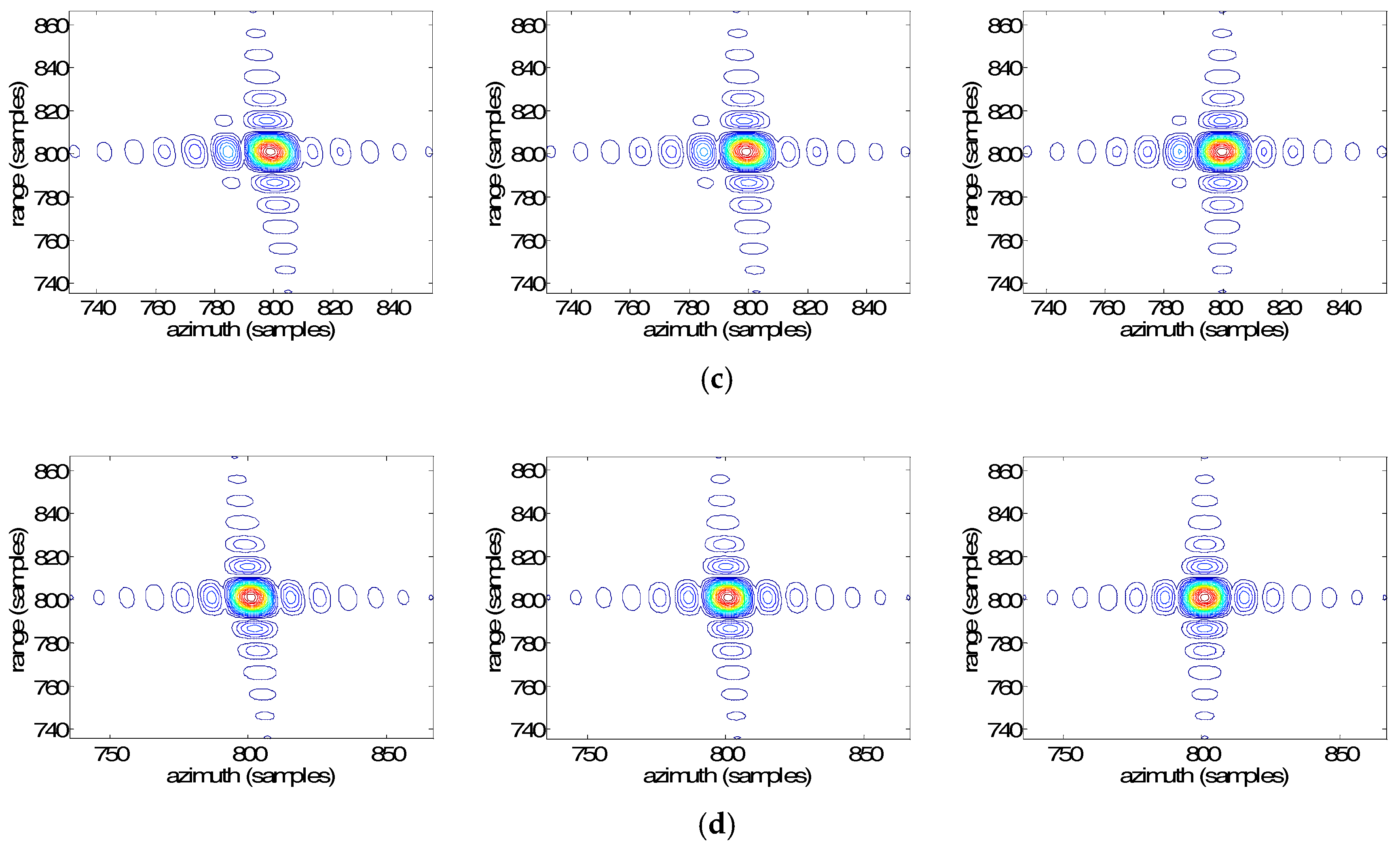
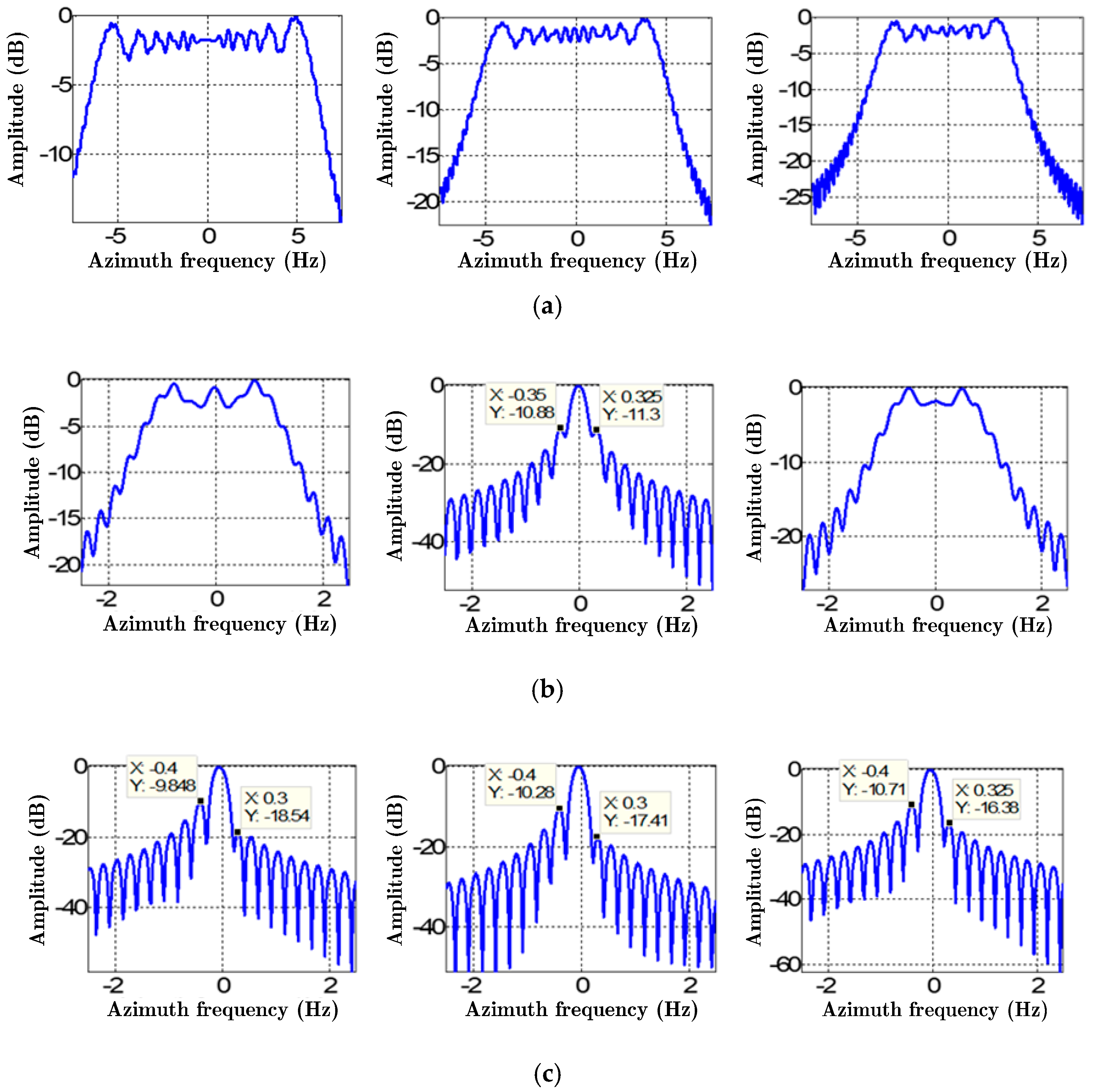
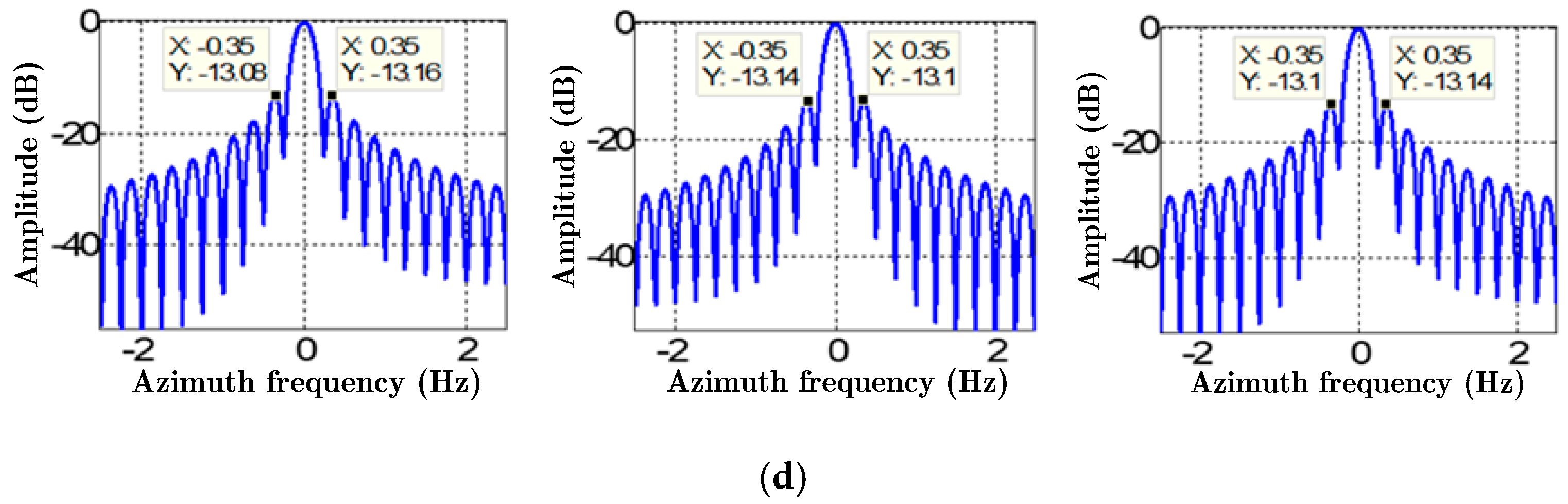
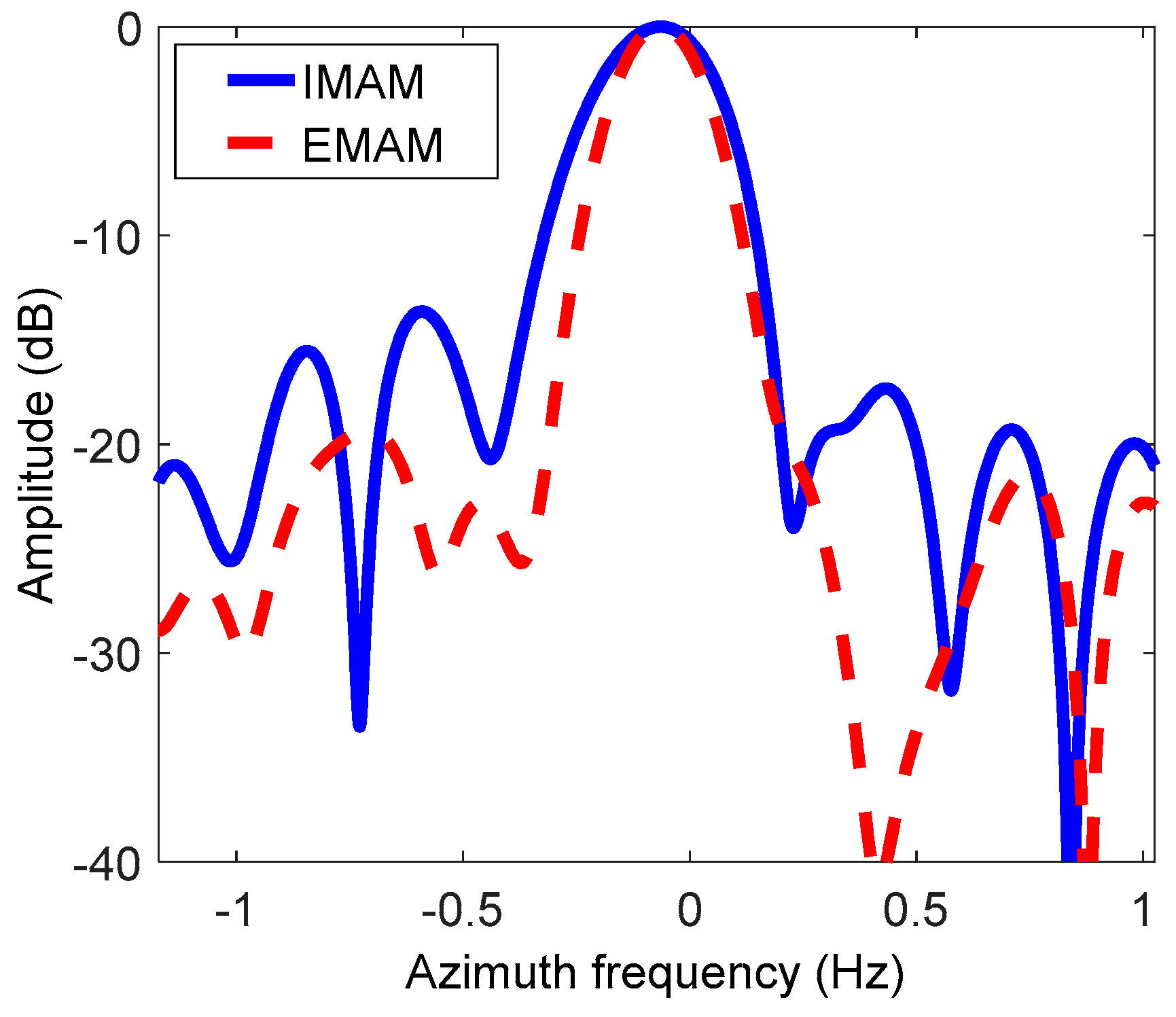
5.1. Simulation
5.2. Real Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Cantalloube, H.; Dubois-Fernandez, P. Airborne X-band SAR imaging with 10 cm resolution: Technical challenge and preliminary results. IET Radar Sonar Navig. 2006, 153, 163–176. [Google Scholar] [CrossRef]
- Ballester-Berman, J.; Lopez-Sanchez, J.; Fortuny-Guash, J. Retrieval of biophysical parameters of agricultural crops using polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 683–694. [Google Scholar] [CrossRef]
- Curlander, J.; McDonough, R. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Zeng, T.; Li, Y.; Ding, Z.; Long, T.; Yao, D.; Sun, Y. Subaperture Approach Based on Azimuth-Dependent Range Cell Migration Correction and Azimuth Focusing Parameter Equalization for Maneuvering High-Squint-Mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6718–6734. [Google Scholar] [CrossRef]
- Steele-Dunne, S.; Mcnairn, H.; Monsivais-Huertero, A.; Judge, J.; Liu, P.; Papathanassiou, K. Radar Remote Sensing of Agricultural Canopies: A Review. IEEE J. Sel. Top. Appl. Earth Obs. 2017, 10, 2249–2273. [Google Scholar] [CrossRef]
- Guo, H.; Li, X. Technical characteristics and potential application of the new generation SAR for Earth observation. Chin. Sci. Bull. 2011, 56, 1155–1168. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.; Dong, X.; Wang, R.; Cui, C. Optimal 3D deformation measuring in inclined geosynchronous orbit SAR differential interferometry. Sci. China (Inf. Sci.) 2017, 60, 060303. [Google Scholar] [CrossRef]
- Yin, W.; Ding, Z.; Lu, X.; Zhu, Y. Beam scan mode analysis and design for geosynchronous SAR. Sci. China (Inf. Sci.) 2017, 60, 060306. [Google Scholar] [CrossRef]
- Kennedy, T. Strapdown inertial measurement units for motion compensation for synthetic aperture radars. IEEE Trans. Aerosp. Electron. Syst. Mag. 1988, 3, 32–35. [Google Scholar] [CrossRef]
- Bamler, R. Doppler frequency estimation and the Cramer-Rao bound. IEEE Trans. Geosci. Remote Sens. 1991, 29, 385–390. [Google Scholar] [CrossRef]
- Madsen, S. Estimating the Doppler centroid of SAR data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 134–140. [Google Scholar] [CrossRef]
- Cantalloube, H.; Nahum, C. Multiscale Local Map-Drift-Driven Multilateration SAR Autofocus Using Fast Polar Format Image Synthesis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3730–3736. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Li, F.; Held, D.; Curlander, J.; Wu, C.; Curlander, J. Doppler Parameter Estimation for Spaceborne Synthetic-Aperture Radars. IEEE Trans. Geosci. Remote Sens. 1985, 1, 47–56. [Google Scholar] [CrossRef]
- Long, T.; Lu, Z.; Ding, Z.; Liu, L. A DBS Doppler Centroid Estimation Algorithm Based on Entropy Minimization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3703–3712. [Google Scholar] [CrossRef]
- Zeng, T.; Wang, R.; Li, F. SAR Image Autofocus Utilizing Minimum-Entropy Criterion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1552–1556. [Google Scholar] [CrossRef]
- Samczynski, P.; Kulpa, K. Coherent mapdrift technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1505–1517. [Google Scholar] [CrossRef]
- Morrison, R.; Do, M.; Munson, D. SAR image autofocus by sharpness optimization: A theoretical study. IEEE Trans. Image Process. 2007, 16, 2309–2321. [Google Scholar] [CrossRef] [PubMed]
- Berizzi, F.; Corsini, G. Autofocusing of inverse synthetic aperture radar images using contrast optimization. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1185–1191. [Google Scholar] [CrossRef]
- Carrara, W.; Goodman, R.; Majewski, R. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Xing, M.; Jiang, X.; Wu, R.; Zhou, F.; Bao, Z. Motion Compensation for UAV SAR Based on Raw Radar Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2870–2883. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, B.; Xing, M.; Bao, Z.; Guo, L. The Space-Variant Phase-Error Matching Map-Drift Algorithm for Highly Squinted SAR. IEEE Geosci. Remote Sens. Lett. 2013, 10, 845–849. [Google Scholar] [CrossRef]
- Pu, W.; Li, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. An Azimuth-Variant Autofocus Scheme of Bistatic Forward-Looking Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 689–693. [Google Scholar]
- Wang, Y.; Li, J.; Chen, J.; Xu, H. A Parameter-Adjusting Polar Format Algorithm for Extremely High Squint SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 640–650. [Google Scholar] [CrossRef]


| Main Step | Operation | Complexity |
|---|---|---|
| : Achieving three sub-view images | FFT | |
| : Estimating and ( operations of sliding windowing manipulation, window width: ) | STFT | |
| Complex conjugate multiplication | ||
| IFFT | ||
| Modulus | ||
| : Estimating the fitting coefficients of and | Curve fitting | |
| : Total | ||
| Main Step | Operation | Complexity |
|---|---|---|
| : Achieving three sub-view images | FFT | |
| : Estimating and | FFT | |
| Complex conjugate multiplication | ||
| IFFT | ||
| Modulus | ||
| : Total | ||
| Main Step | Operation | Complexity |
|---|---|---|
| : Achieving two sub-view images | FFT | |
| : Estimating ( operations of sliding windowing manipulation, window width: ) | STFT | |
| Complex conjugate multiplication | ||
| IFFT | ||
| Modulus | ||
| : Estimating the fitting coefficients of | Curve fitting | |
| : Total | ||
| Method | Index | Point Target C1 | Point Target C2 | Point Target C3 |
|---|---|---|---|---|
| Basic MAM | PSLR (dB) | −4.72 | −10.88 | −6.12 |
| ISLR (dB) | −8.25 | −7.87 | −8.72 | |
| Azimuth resolution (m) | 5.67 | 0.59 | 4.35 | |
| IMAM | PSLR (dB) | −9.85 | −10.28 | −10.71 |
| ISLR (dB) | −8.69 | −8.95 | −9.18 | |
| Azimuth resolution (m) | 0.59 | 0.58 | 0.58 | |
| EMAM | PSLR (dB) | −13.08 | −13.10 | −13.10 |
| ISLR (dB) | −9.63 | −9.64 | −9.63 | |
| Azimuth resolution (m) | 0.57 | 0.57 | 0.57 |
| Error Coefficient | Real Value | Basic MAM | IMAM | EMAM |
|---|---|---|---|---|
| −2.6426 | −2.7048 | −2.6485 | −2.6464 | |
| 0.0012 | - | 0.0012 | 0.0012 | |
| 1.2575 × 10−7 | - | 1.4614 × 10−7 | 1.5608 × 10−7 | |
| −0.0360 | −0.0396 | - | −0.0390 | |
| 1.2540 × 10−5 | - | - | 1.2630 × 10−5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Li, Y.; Wang, Y.; Li, L.; Zeng, T. Extended Multiple Aperture Mapdrift-Based Doppler Parameter Estimation and Compensation for Very-High-Squint Airborne SAR Imaging. Sensors 2019, 19, 213. https://doi.org/10.3390/s19010213
Zhou Z, Li Y, Wang Y, Li L, Zeng T. Extended Multiple Aperture Mapdrift-Based Doppler Parameter Estimation and Compensation for Very-High-Squint Airborne SAR Imaging. Sensors. 2019; 19(1):213. https://doi.org/10.3390/s19010213
Chicago/Turabian StyleZhou, Zhichao, Yinghe Li, Yan Wang, Linghao Li, and Tao Zeng. 2019. "Extended Multiple Aperture Mapdrift-Based Doppler Parameter Estimation and Compensation for Very-High-Squint Airborne SAR Imaging" Sensors 19, no. 1: 213. https://doi.org/10.3390/s19010213
APA StyleZhou, Z., Li, Y., Wang, Y., Li, L., & Zeng, T. (2019). Extended Multiple Aperture Mapdrift-Based Doppler Parameter Estimation and Compensation for Very-High-Squint Airborne SAR Imaging. Sensors, 19(1), 213. https://doi.org/10.3390/s19010213




