BeiDou Augmented Navigation from Low Earth Orbit Satellites
Abstract
1. Introduction
2. Advantages of Navigation with LEO Constellation
2.1. Positioning Error
2.2. Integer Ambiguity Resolution
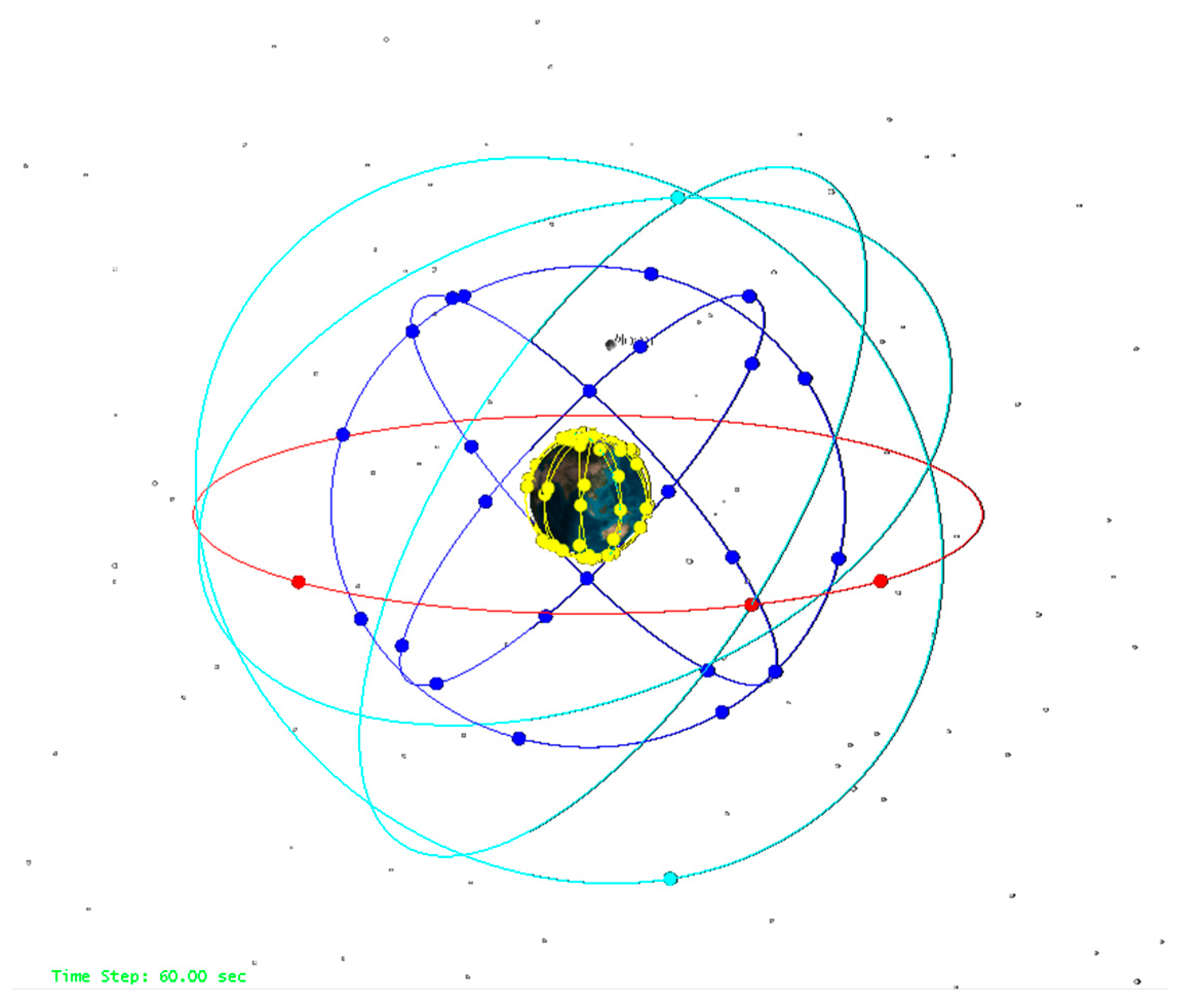
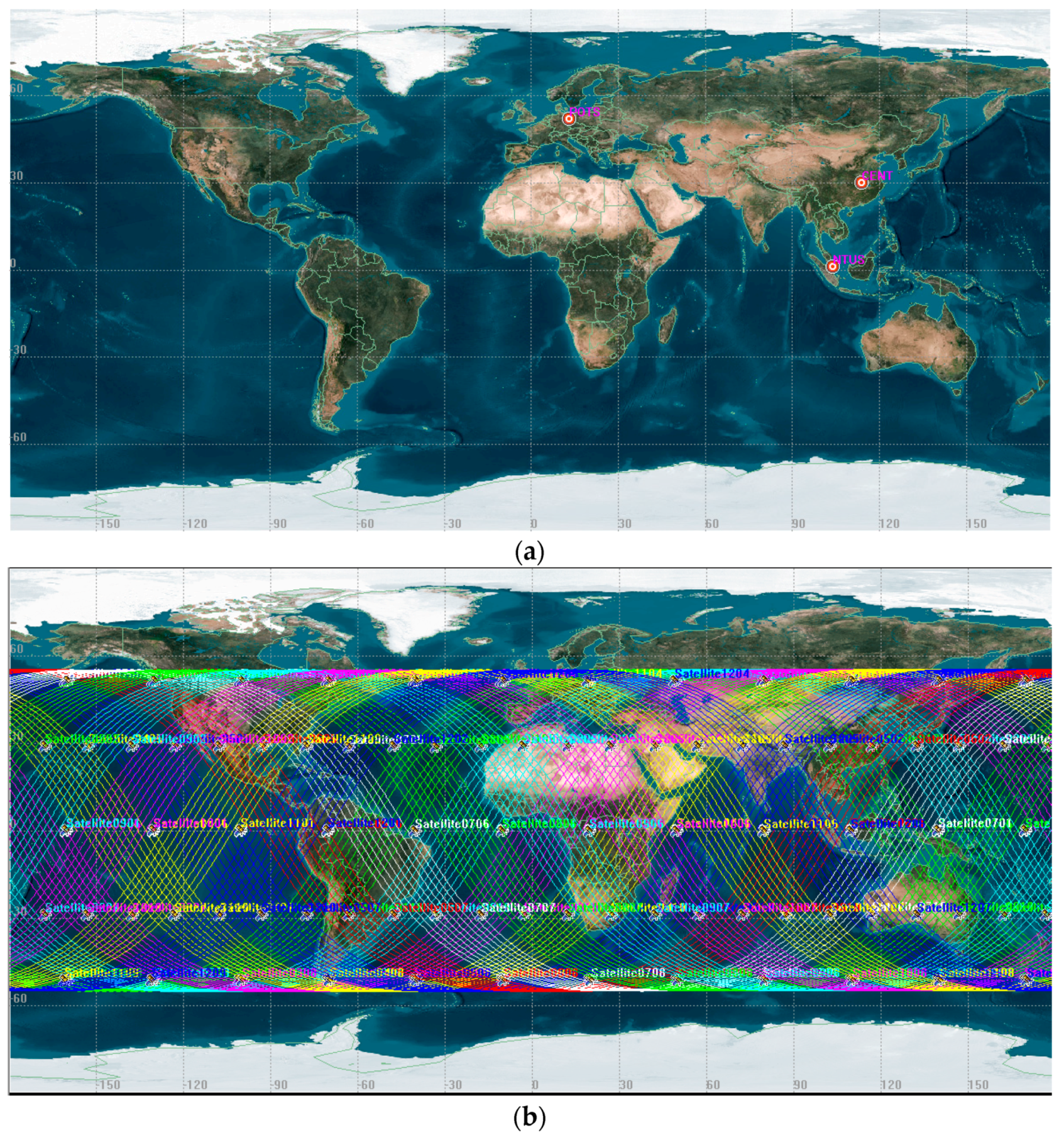
3. Strategy for Data Simulation and Procession
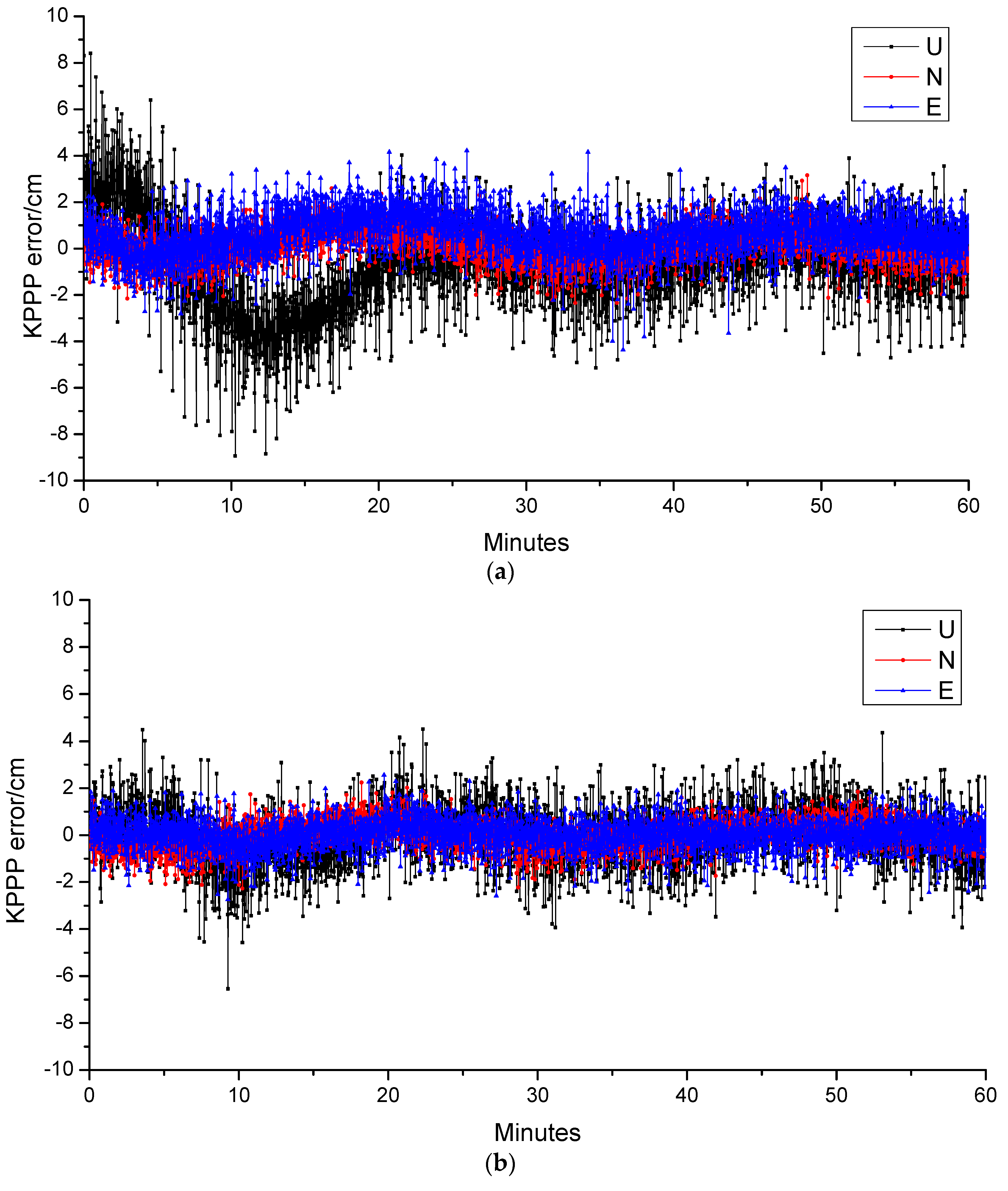
4. Results and Discussion
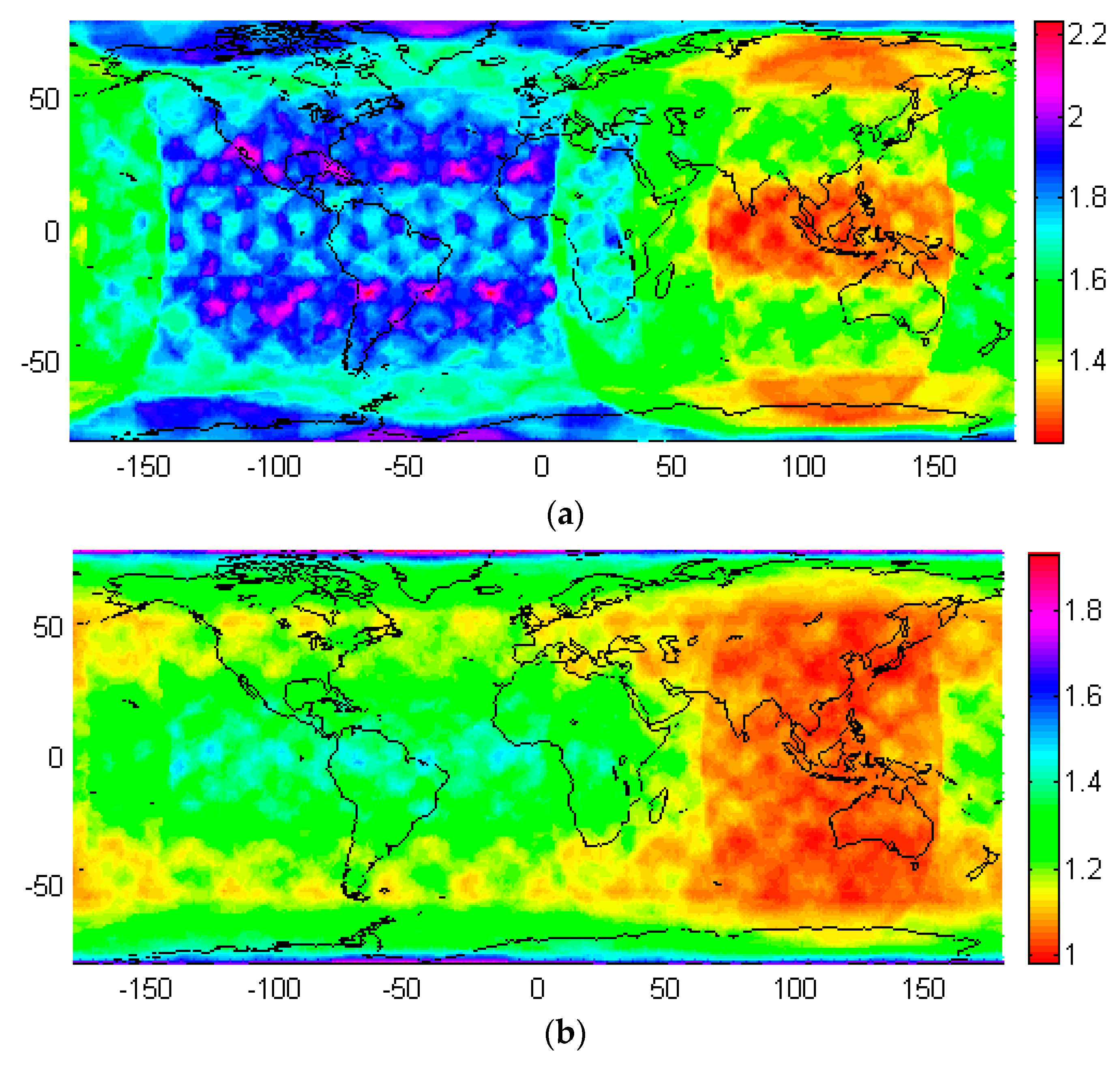
4.1. Satellite Visibility
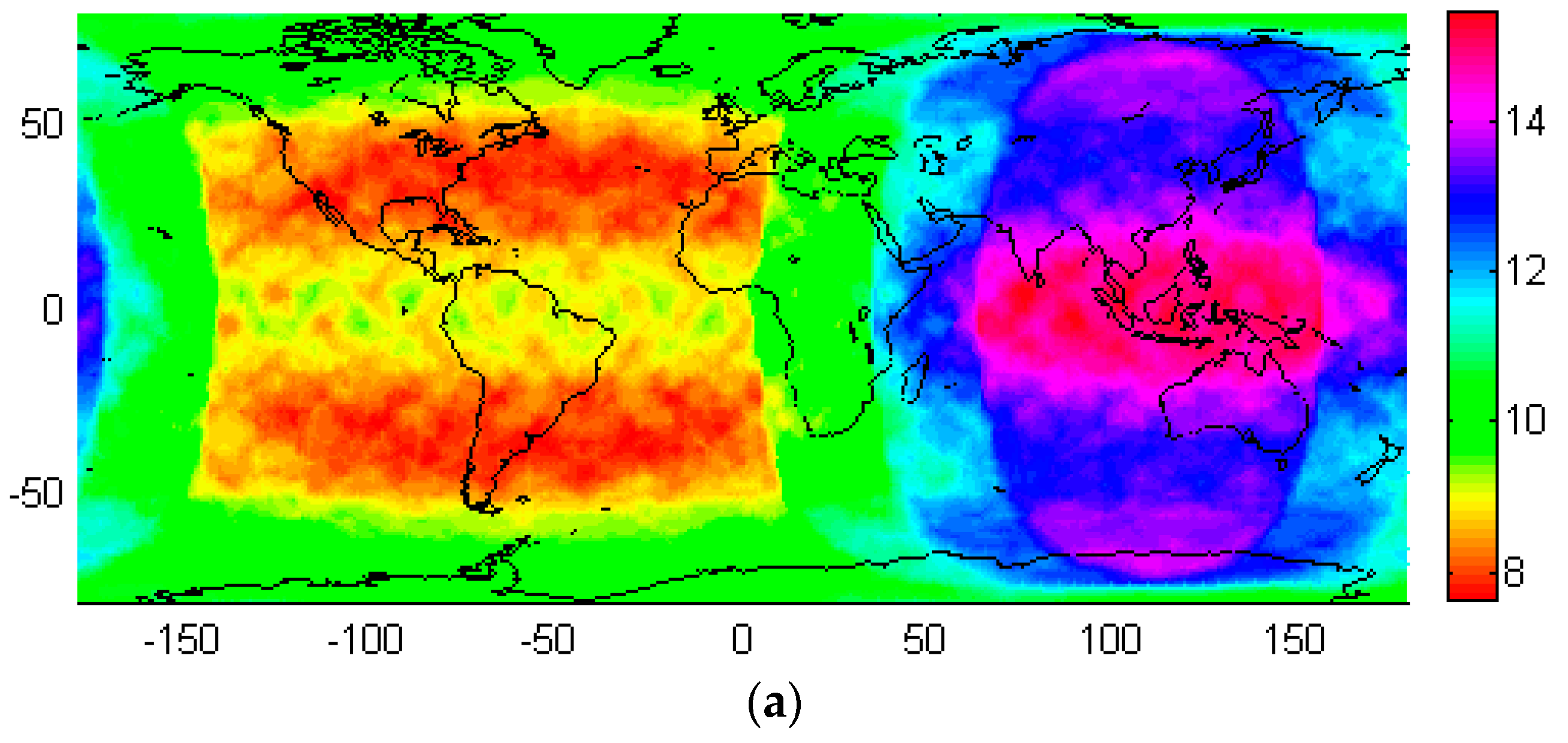
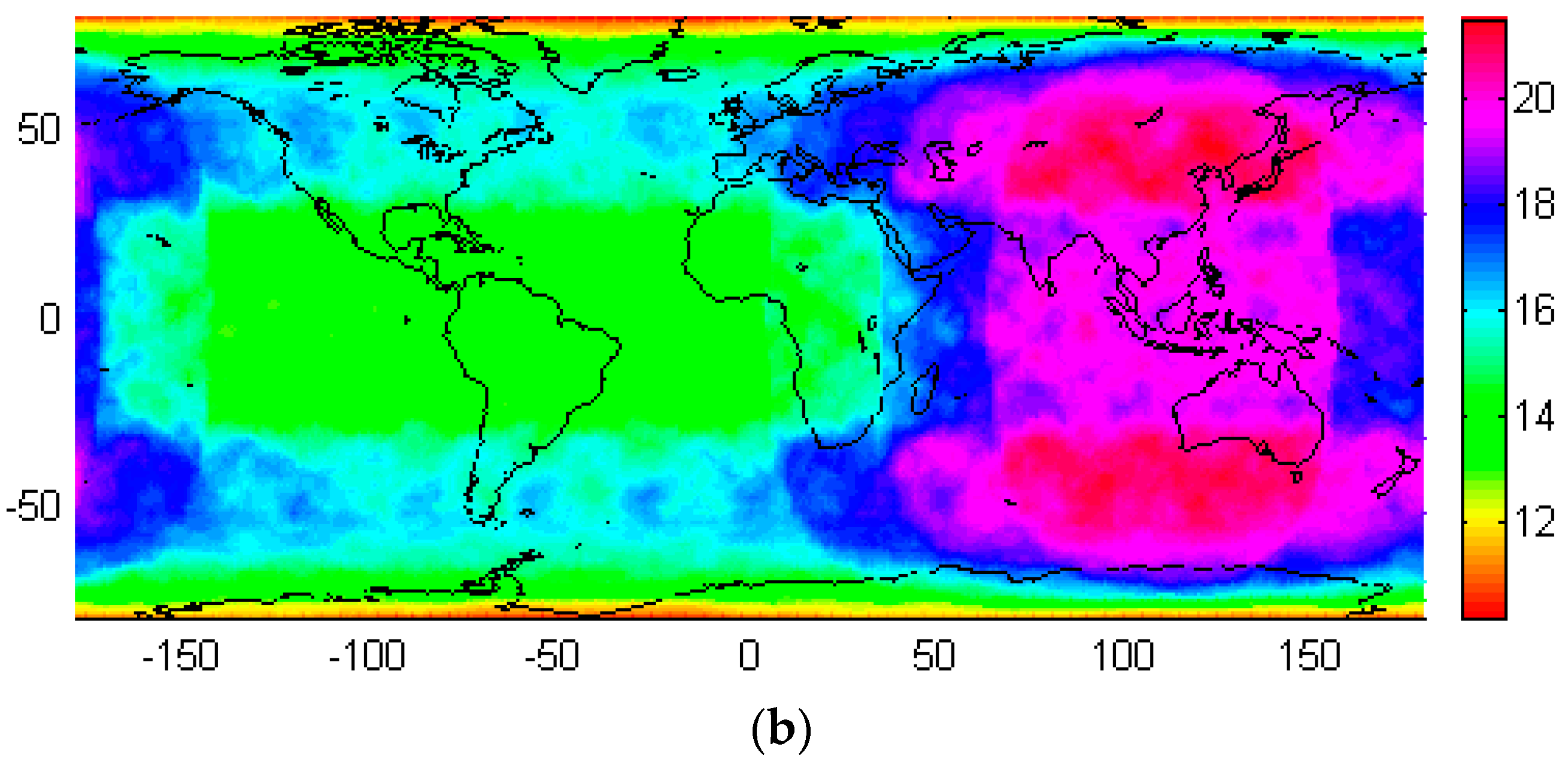
4.2. PDOP
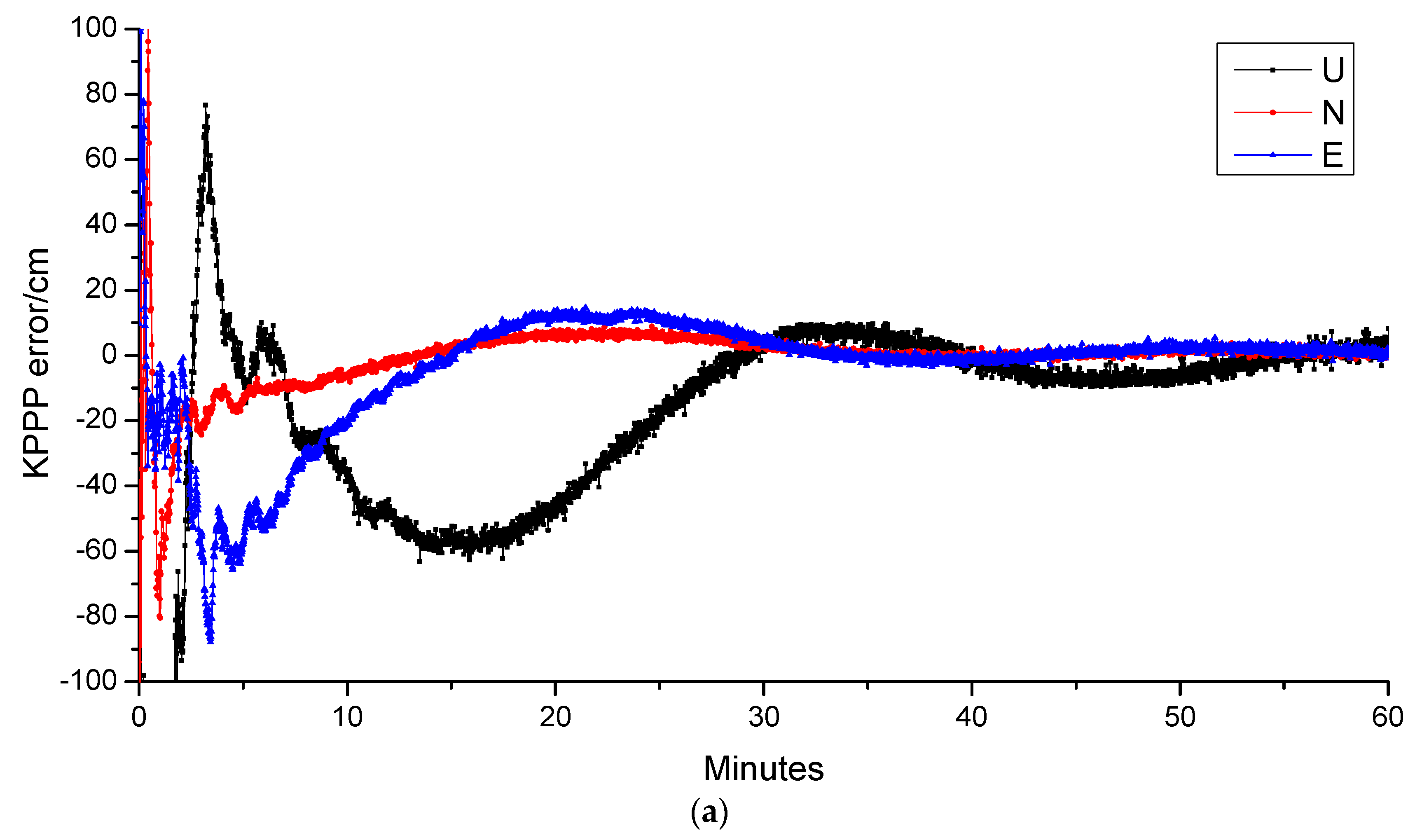
4.3. SPP
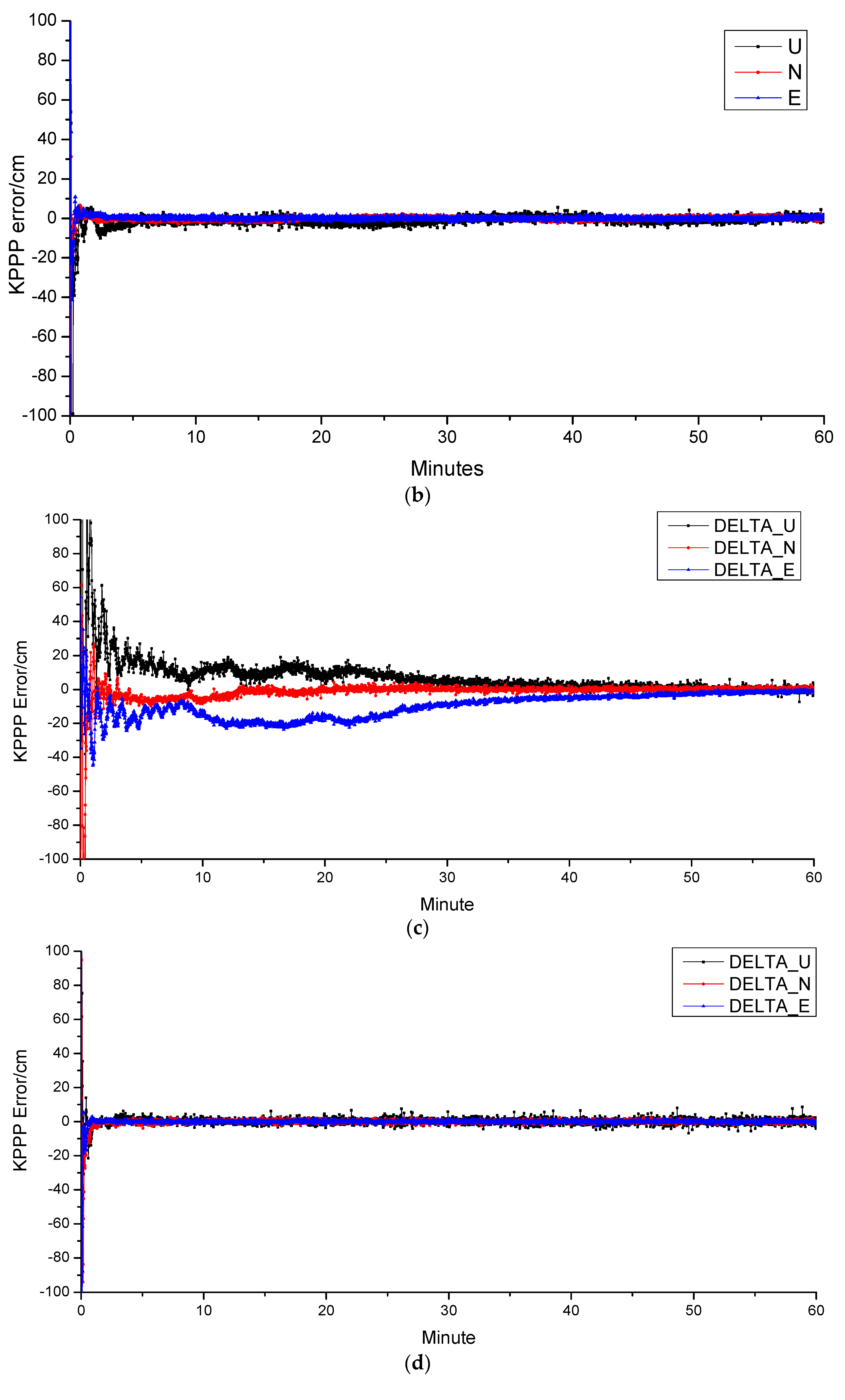
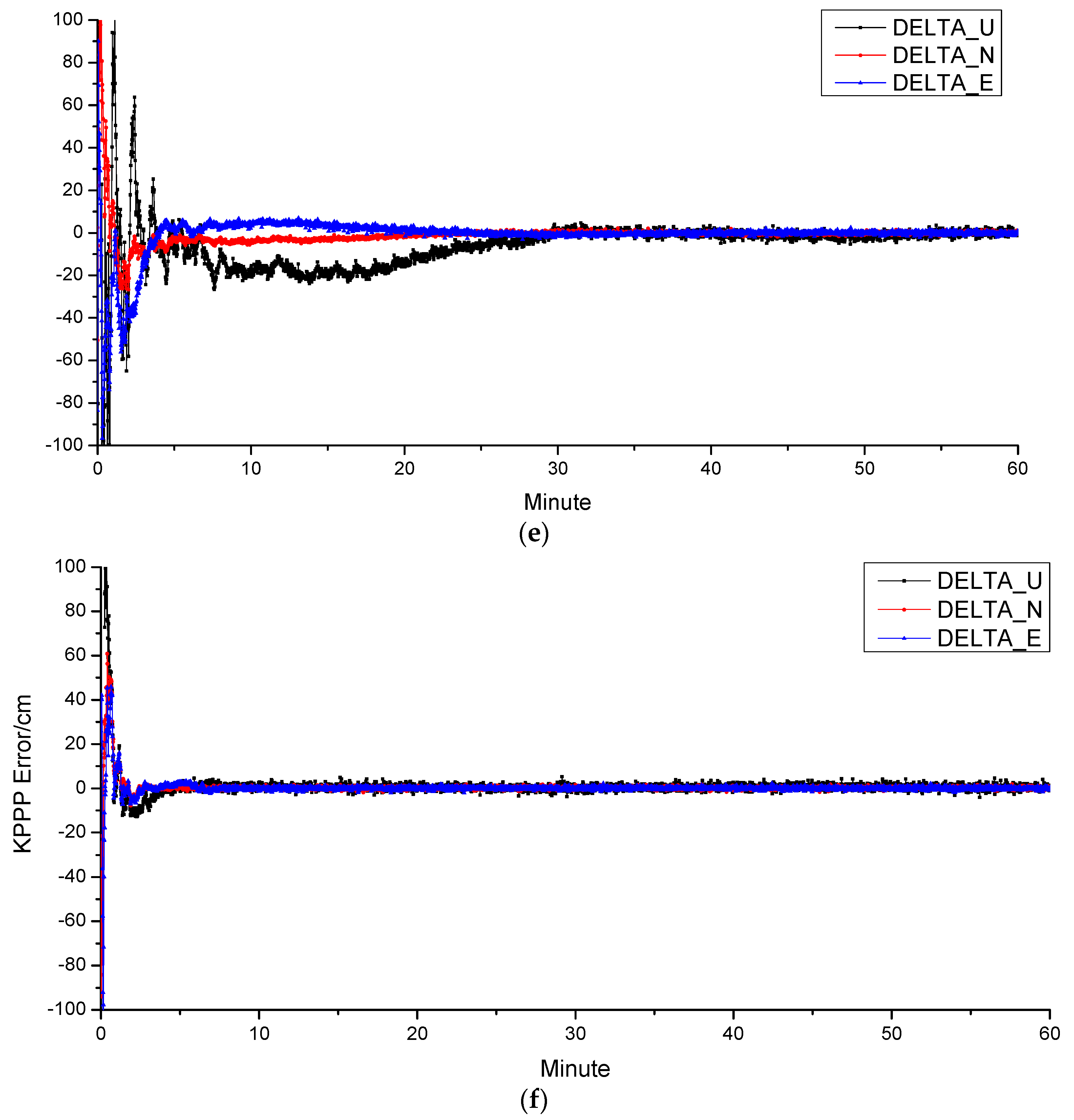
4.4. PPP
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing Switzerland: Basel, Switzerland, 2017. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Reid, T.G.; Neish, A.M.; Walter, T.F.; Enge, P.K. Leveraging Commercial broadband LEO constellation for navigation. In Proceedings of the ION GNSS+ 2016, Portland, OR, USA, 12–16 September 2016; pp. 2300–2314. [Google Scholar]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2018, 1–16. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Tong, K.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015. [Google Scholar]
- Lawrence, D.; Cobb, H.S.; Gutt, G.; Connor, M.O.; Reid, T.G.; Walter, T.; Whelan, D. Ionnovation: Navigation from LEO; GPS World: Cleveland, OH, USA, 2017. [Google Scholar]
- Fossa, C.E.; Raines, R.A.; Gunsch, G.H.; Temple, M.A. An overview of the IRIDIUM (R) low Earth orbit (LEO) satellite system. In Proceedings of the IEEE 1998 National Aerospace and Electronics Conference (NAECON 1998), Dayton, OH, USA, 17 July 1998; pp. 152–159. [Google Scholar] [CrossRef]
- De Selding, P.B. LeoSat Corporate Broadband Constellation Sees GEO Satellite Operators as Partners. Space News. 14 June 2016. Available online: https://spacenews.com/leosat-corporate-broadband-constellation-sees-geo-satellite-operators-as-partners/ (accessed on 17 October 2018).
- De Selding, P.B. Telesat: LEO Gives More User Bandwidth than GEO HTS. Space Intel Report. 2017. Available online: https://www.spaceintelreport.com/telesat-leo-gives-more-user-bandwidth-than-geo-hts/ (accessed on 17 October 2018).
- De Selding, P.B. Virgin, Qualcomm Invest in OneWeb Satellite Internet Venture. Space News. 15 January 2015. Available online: http://spacenews.com/virgin-qualcomm-invest-in-global-satellite-internet-plan/sthash.XtMF5rpE.dpuf (accessed on 12 February 2017).
- De Selding, P.B. SpaceX To Build 4000 Broadband Satellites in Seattle. Space News. 19 January 2015. Available online: http://spacenews.com/spacexopening-seattle-plant-to-build-4000-broadband-satellites/ (accessed on 12 February 2017).
- Via Satellite. SpaceX Receives FCC Approval to Launch 7518 Starlink Satellites. 16 November 2018. Available online: https://www.satellitetoday.com/broadband/2018/11/16/spacex-receives-fcc-approval-to-deploy-7518-satellites/ (accessed on 14 December 2018).
- Via Satellite. Samsung Exec Envisions LEO Constellation for Satellite Internet Connectivity. 18 August 2015. Available online: https://www.satellitetoday.com/telecom/2015/08/18/samsung-exec-envisions-leo-constellation-for-satellite-internet-connectivity/ (accessed on 10 October 2018).
- De Selding, P.B. Boeing Proposes Big Satellite Constellations in V- and Cbands. Space News. 23 June 2016. Available online: http://spacenews.com/boeingproposes-big-satellite-constellations-in-v-and-c-bands/ (accessed on 17 October 2018).
- CNAGA (China National Administration of GNSS and Applications). CASIC Plans to Launch 156 Small Satellites for the Hongyun Program. 2017. Available online: http://en.chinabeidou.gov.cn/c/393.html (accessed on 3 March 2018).
- Jones, A. China to Build 300-Satellite Hongyan Communications Constellation in Low-Earth Orbit. GBtimes. 2018. Available online: https://gbtimes.com/china-to-build-300-satellite-hongyan-communications-constellation-in-low-earth-orbit (accessed on 17 October 2018).
- Lawrence, D.; Cobb, H.S.; Gutt, G.; Tremblay, F.; Laplante, P.; O’Connor, M. Test Results from a LEO-Satellite-Based Assured Time and Location Solution. In Proceedings of the 2016 International Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 25–28 January 2016. [Google Scholar]
- Cobb, S.; Lawrence, D.; Gutt, G.; O’Conner, M. Differential and Rubidium Disciplined Test Results from an Iridium-Based Secure Timing Solution. In Proceedings of the 2017 International Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017. [Google Scholar]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2011. [Google Scholar]
- Montenbruck, O.; Steigenber, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 12, 321–333. [Google Scholar] [CrossRef]
- Reid, T.G. Orbital Diversity for Global Navigation Satellite Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2017. [Google Scholar]
- Su, H. Precise orbit determination of Global Navigation Satellite System of Second Generation (GNSS-2). Ph.D. Thesis, University FAF Munich, Neubiberg, Germany, 2000. [Google Scholar]
- China Satellite Navigation Office (CSNO). BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal (Version 2.1); China Satellite Navigation Office: Beijing, China, 2016. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010) (IERS Technical Note; 36); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; p. 179. ISBN 3-89888-989-6. [Google Scholar]
- Desai, S.D. Observing the pole tide with satellite altimetry. J. Geophys. Res. 2002, 107, 3186. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for Troposphere and Stratosphere in Radio Ranging of Satellites. Geophysical Monograph; American Geophysical Union: Washington, DC, USA, 1972; pp. 247–252. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Ge, M.; Nie, L.; Shen, Y.; Schuh, H. LEO enhanced Global Navigation Satellite System (LeGNSS) for real-time precise positioning services. Life Sci. Space Res. 2019, 63, 73–93. [Google Scholar] [CrossRef]
| Constellation | No. Sats | Altitude [km] | Inclination [°] | Year | Country |
|---|---|---|---|---|---|
| Iridium | 66 | 781 | 86.4 | 1998 | USA |
| Globalstar | 48 | 1400 | 52 | 2000 | USA |
| LeoSat | 108 | 1400 | Not defined, yet | 2019/2020 | USA |
| Telesat | 117 | 1000~1245 | 99.5 | 2021 | Canada |
| Hongyun | 156 | 1000 | Not defined, yet | 2022 | China |
| Hongyan | 324 | 1100 | Not defined, yet | 2023 | China |
| OneWeb | 648 | 1200 | 88 | 2019 | USA/UK |
| Boeing | 2956 | 1200 | 45, 55, 88 | Not defined, yet | USA |
| SpaceX Starlink | 7518 | 1110~1325 | 53, 53.8, 74, 81, 70 | 2020 | USA |
| Astrome Technology | 150 | 1400 | Not defined, yet | 2020 | India |
| Samsung | 4600 | <1500 | Not defined, yet | Not defined | Korea |
| Altitude | Convergence Time for Ambiguity of Float Solution | Time for Integer Ambiguity Resolution |
|---|---|---|
| 1000 km | 1 min | 10 min |
| 10,000 km | 7 min | 1 h |
| 20,000 km | 20 min | 4 h |
| IGSO 36,000 km | 2 h | 25 h |
| GEO 36,000 km | +∞ | +∞ |
| Geophysical Models | Description | |
|---|---|---|
| BeiDou-3 | LEO | |
| Static | EGM2008 up to degree and order 12 | Static part of EIGEN-6C up to degree and order 150 |
| Temporal | None | Temporal part of EIGEN-6C up to degree and order 50 |
| Secular rates for low degree coefficients | IERS Conventions 2010 [25] | IERS Conventions 2010 [25] |
| n-body | Moon, Sun, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto JPL DE405 | Moon, Sun, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto JPL DE405 |
| Solid Earth Tides | IERS Conventions 2010 [25] | IERS Conventions 2010 [25] |
| Ocean Tides | None | FES2004 |
| Ocean pole tides | None | Desai [26] |
| Relativistic effects | IERS Conventions 2010 [25] | IERS Conventions 2010 [25] |
| Satellite surface models and Attitude | ||
| Atmospheric drag | None | DTM94 with Box-wing model |
| Solar Radiation Pressure | 5-parameter ECOM model | Box-wing |
| Attitude | Nominal yaw-steering model | consistent with local orbital reference frame |
| Reference frame | ||
| Inertial frame | J2000.0 | J2000.0 |
| Earth tide and Ocean loading | IERS Conventions 2010 [25] | IERS Conventions 2010 [25] |
| Precession/Nutation | IAU 2000A | IAU 2000A |
| EOP | IERS EOP 08 C04 (IAU2000A) | IERS EOP 08 C04 (IAU2000A) |
| Constellation | BeiDou-3 | LEO |
|---|---|---|
| Cone angle | GEO/IGSO: 10 | 65 |
| MEO: 15 | ||
| PCO | (600, 0, 11,000) mm | (0, 0, 0) |
| PCV | 0 | 0 |
| Satellite clock | Clock file | Clock file |
| Mask elevation | 5 | 5 |
| PCO | 0 | 0 |
| PCV | 0 | 0 |
| Receiver clock | 0 | 0 |
| Solid/Ocean/Pole tide | IERS Conventions 2010 | IERS Conventions 2010 |
| Troposphere delay | Saastamonion for dray and wet delay | Saastamonion for dray and wet delay |
| GMF | GMF | |
| Ionosphere delay | No | No |
| Phase wide-up | Yes | Yes |
| Relativity | Yes | Yes |
| Code noise | 1 m | 1 m |
| Phase noise | 2 mm | 2 mm |
| Ambiguity | 0 | 0 |
| Constellation | Max. # of Tracked Satellites | Min. # of Tracked Satellites | Avg. # of Tracked Satellites |
|---|---|---|---|
| 3GEO + 3IGSO + 24MEO | 15.5 | 7.6 | 10.7 |
| 3GEO + 3IGSO + 24MEO + 120LEO | 21.6 | 10.1 | 16.3 |
| Constellation | Max. PDOP | Min. PDOP | Avg. of PDOP |
|---|---|---|---|
| 3GEO + 3IGSO + 24MEO | 2.24 | 1.19 | 1.63 |
| 3GEO + 3IGSO + 24MEO + 120LEO | 1.93 | 1.01 | 1.22 |
| Station | BDS | BDS + LEO | ||||
|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | |
| CENT | 99.1 | 105.3 | 293.7 | 93.2 | 100.7 | 261.3 |
| POTS | 152.7 | 131.8 | 290.7 | 121.3 | 87.4 | 229.9 |
| NTUS | 91.6 | 114.9 | 217.2 | 84.5 | 101.5 | 199.2 |
| Station | BDS | BDS + LEO | ||||
|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | |
| CENT | 0.74 | 1.12 | 2.05 | 0.59 | 0.65 | 1.23 |
| POTS | 0.93 | 0.99 | 1.96 | 0.50 | 0.72 | 1.44 |
| NTUS | 0.54 | 0.68 | 1.33 | 0.63 | 0.49 | 1.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, M.; Su, X.; Zhao, Q.; Liu, J. BeiDou Augmented Navigation from Low Earth Orbit Satellites. Sensors 2019, 19, 198. https://doi.org/10.3390/s19010198
Su M, Su X, Zhao Q, Liu J. BeiDou Augmented Navigation from Low Earth Orbit Satellites. Sensors. 2019; 19(1):198. https://doi.org/10.3390/s19010198
Chicago/Turabian StyleSu, Mudan, Xing Su, Qile Zhao, and Jingnan Liu. 2019. "BeiDou Augmented Navigation from Low Earth Orbit Satellites" Sensors 19, no. 1: 198. https://doi.org/10.3390/s19010198
APA StyleSu, M., Su, X., Zhao, Q., & Liu, J. (2019). BeiDou Augmented Navigation from Low Earth Orbit Satellites. Sensors, 19(1), 198. https://doi.org/10.3390/s19010198






