Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports
Abstract
1. Introduction
- We have developed and simulated a virtual port environment to account for the lack or real existing data. With it, we can perform further experiments that validate our system generalization. We have run a full set of common autonomous transportation situations with several vehicles such as approaching intersections, joining/leaving platoons, overtaking maneuvers, etc.
- We can run our system employing different sensor configurations on the platform, demonstrating that our system can easily be introduced in different existing AGV models and therefore its hardware generalization capabilities.
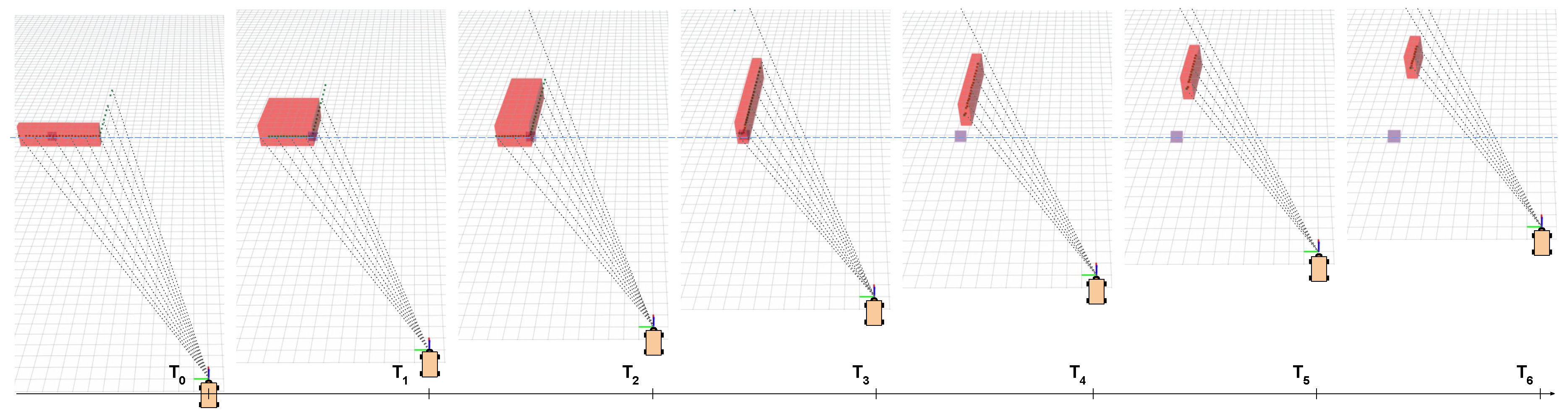
- We have increased the detector accuracy. A dynamic threshold according to the detected distance is introduced on the matching step. Moreover, due to the new complete sets of simulations performed, we are now capable of detecting more robustly different moving objects in ports, such as straddle carriers, loaded/empty AGVs, automated trucks, cars, etc. We have also improved our method for propagating the reference point of detected objects through time, gaining robustness against changes of perspective and occlusions. These changes will be detailed in Section 3.
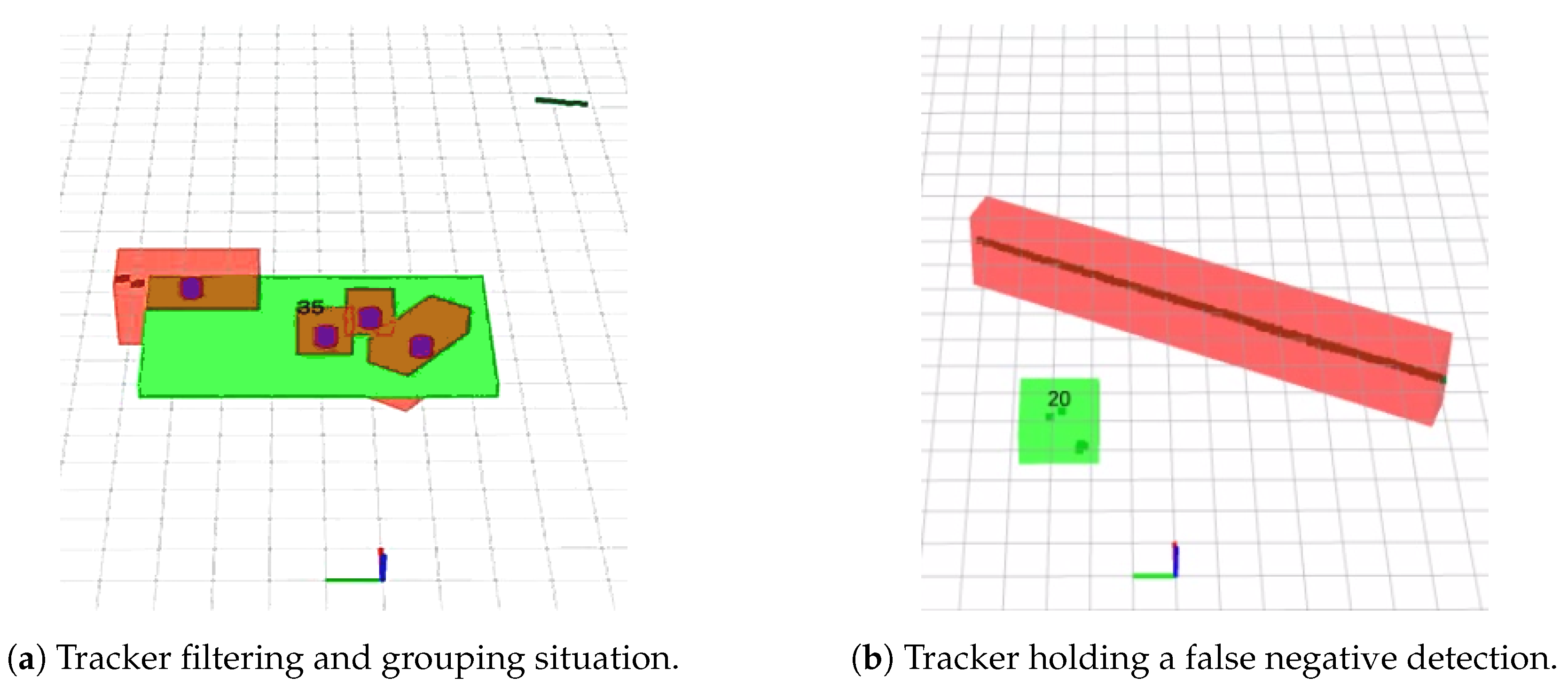
- We have boosted the general performance of our Multi-Hypothesis Tracker (MHT). Our local coordinates tracking has been improved obtaining better observations and velocity estimations from the AGV point of view, which helps in further filtering static objects as well as eliminating false positive detections. Being able to observe much more different situations in the new virtual environment, we obtain better insights to adjust our parameters. We are now able to hold tracks for a longer time when objects get occluded or are temporally not detected. We have also improved our target grouping strategy by merging the previously generated targets according to track similarity both in terms of velocity and distance. These changes will be detailed in Section 3.2.
- We perform a comparison of the new DATMO system over the real dataset with respect to [12], analyzing the contributions of the different improvements performed.
2. State of the Art
2D Laser-Based Detection
Tracking by Detection
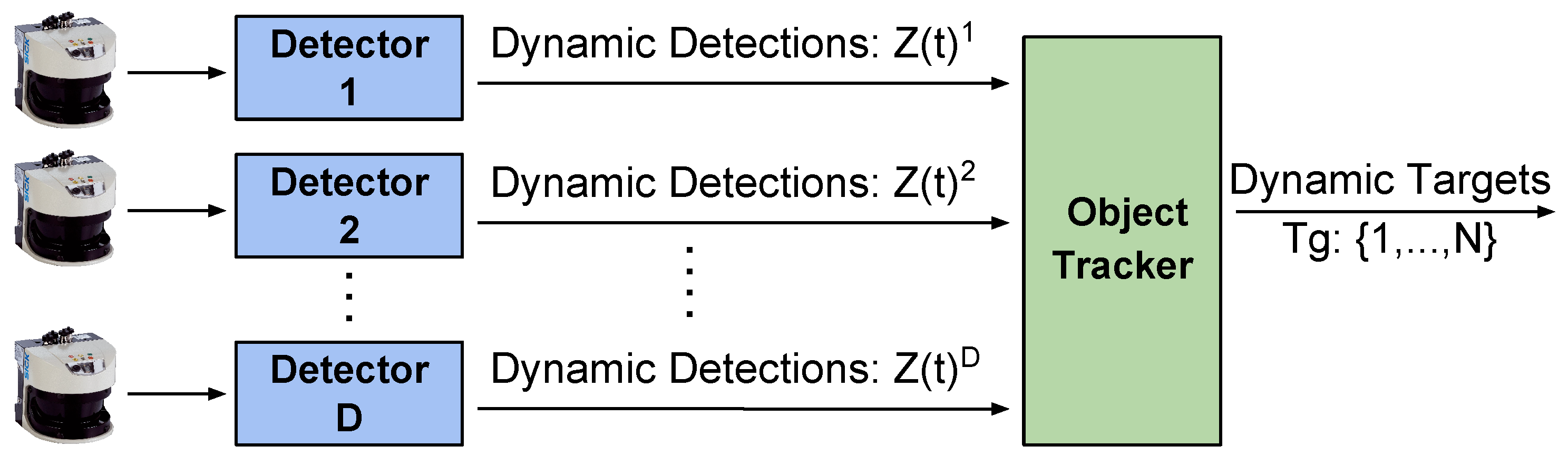
3. DATMO in Port Environments
3.1. Detecting Moving Objects with Single-Layer Laser Scanners
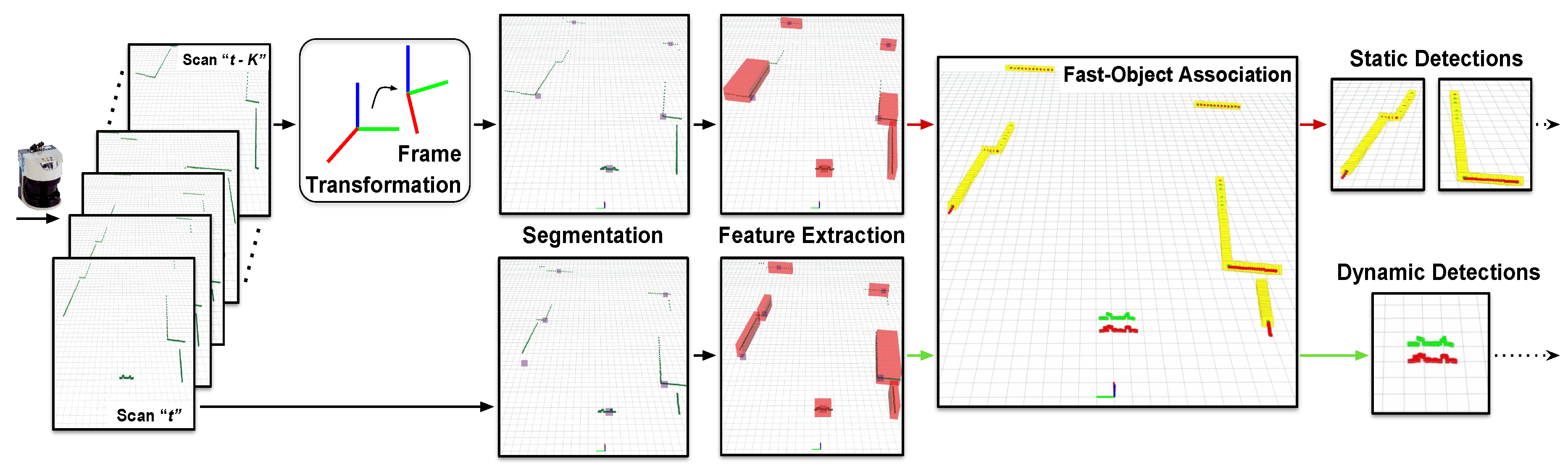
3.1.1. Input Data Pre-Processing
3.1.2. Scans Segmentation
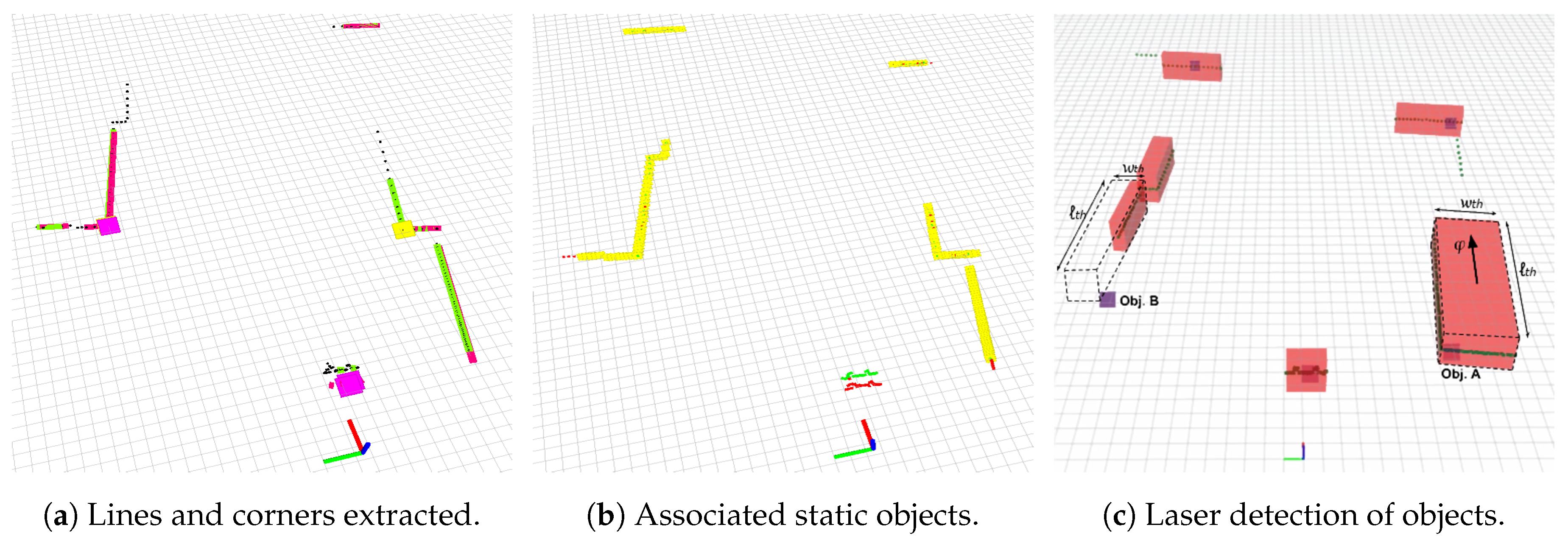
3.1.3. Geometric Primitive Extraction
3.1.4. Fast Object Matching and Reference Propagation
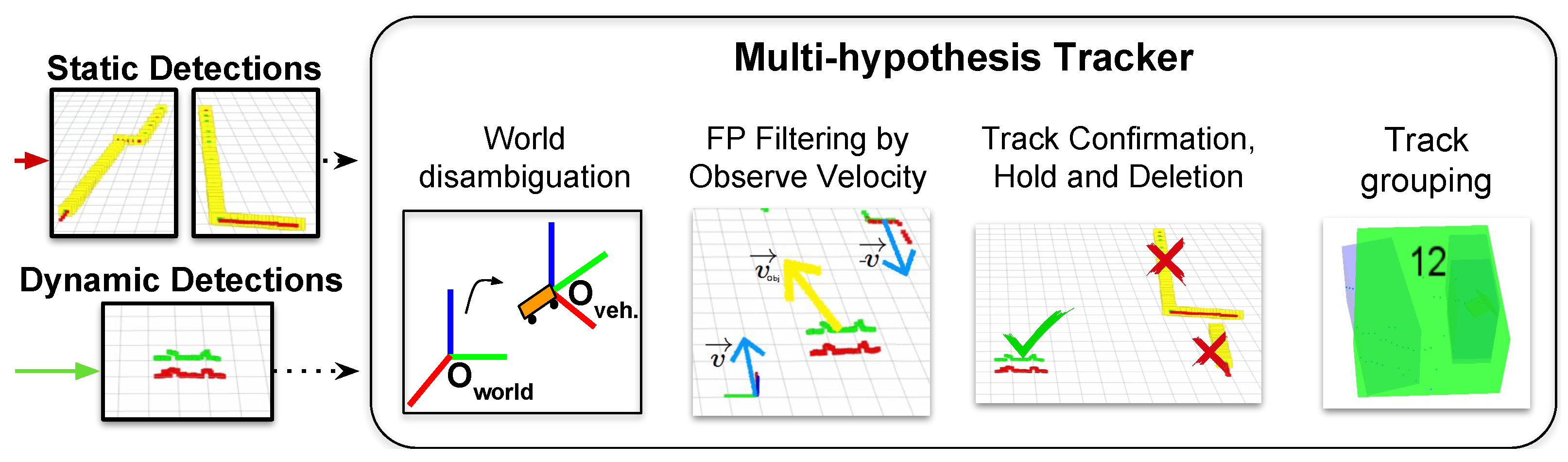
3.2. Tracking Dynamic Objects in Port Environments
3.2.1. Multiple-Hypothesis Tracking
3.2.2. Filtering Static Objects by Velocity
3.2.3. Confirmation, Hold and Deletion of Moving Object Tracks
3.2.4. Track Grouping
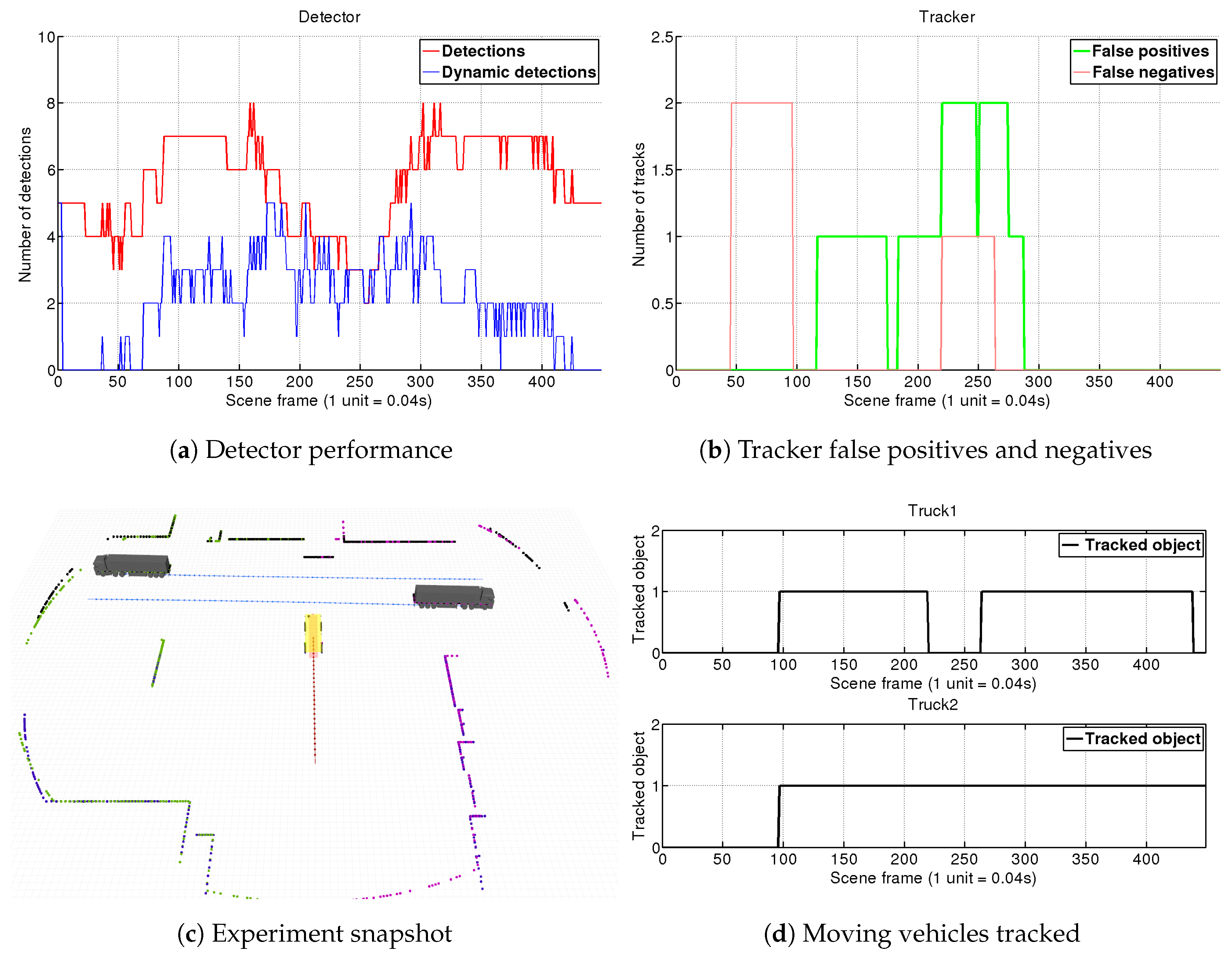
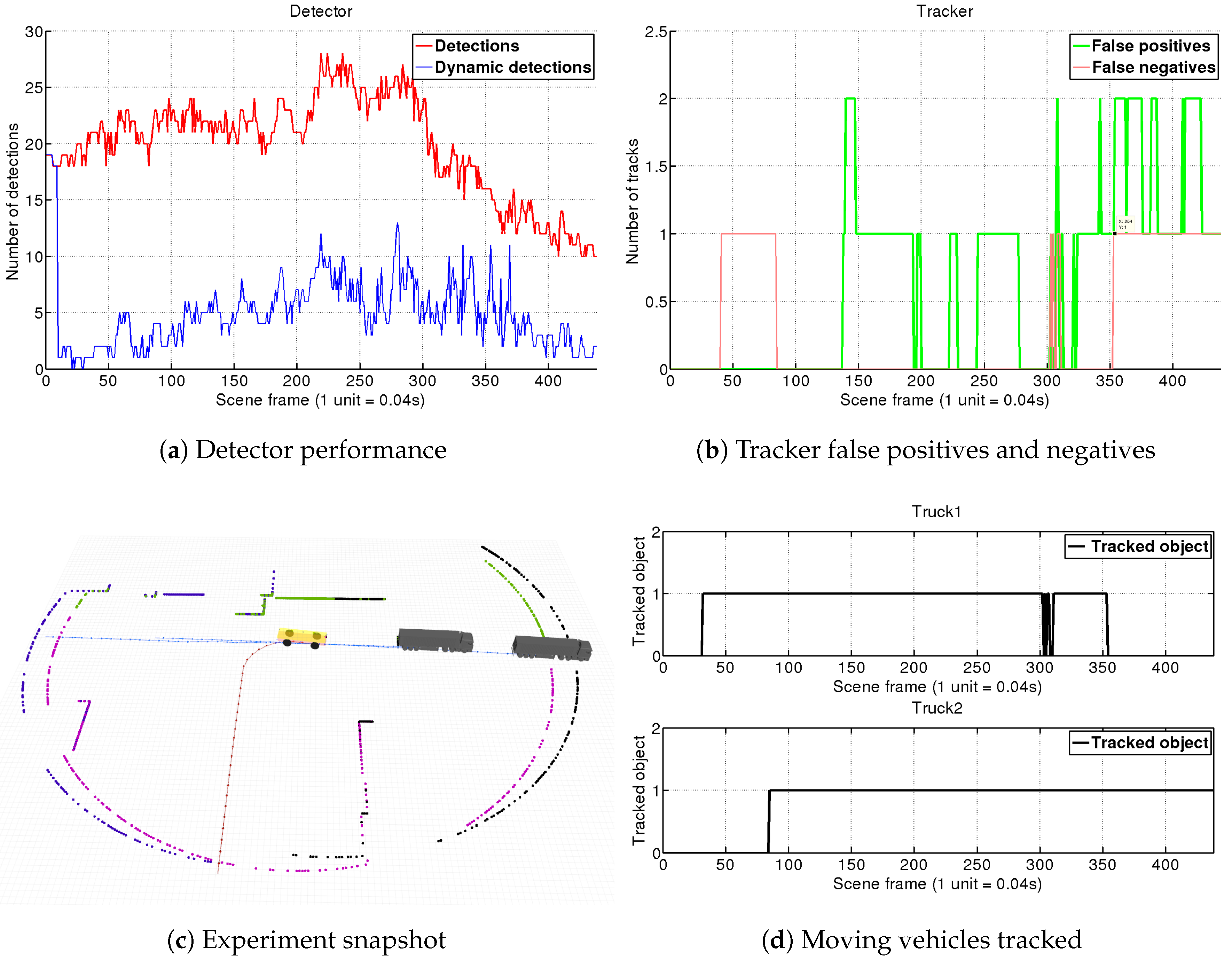
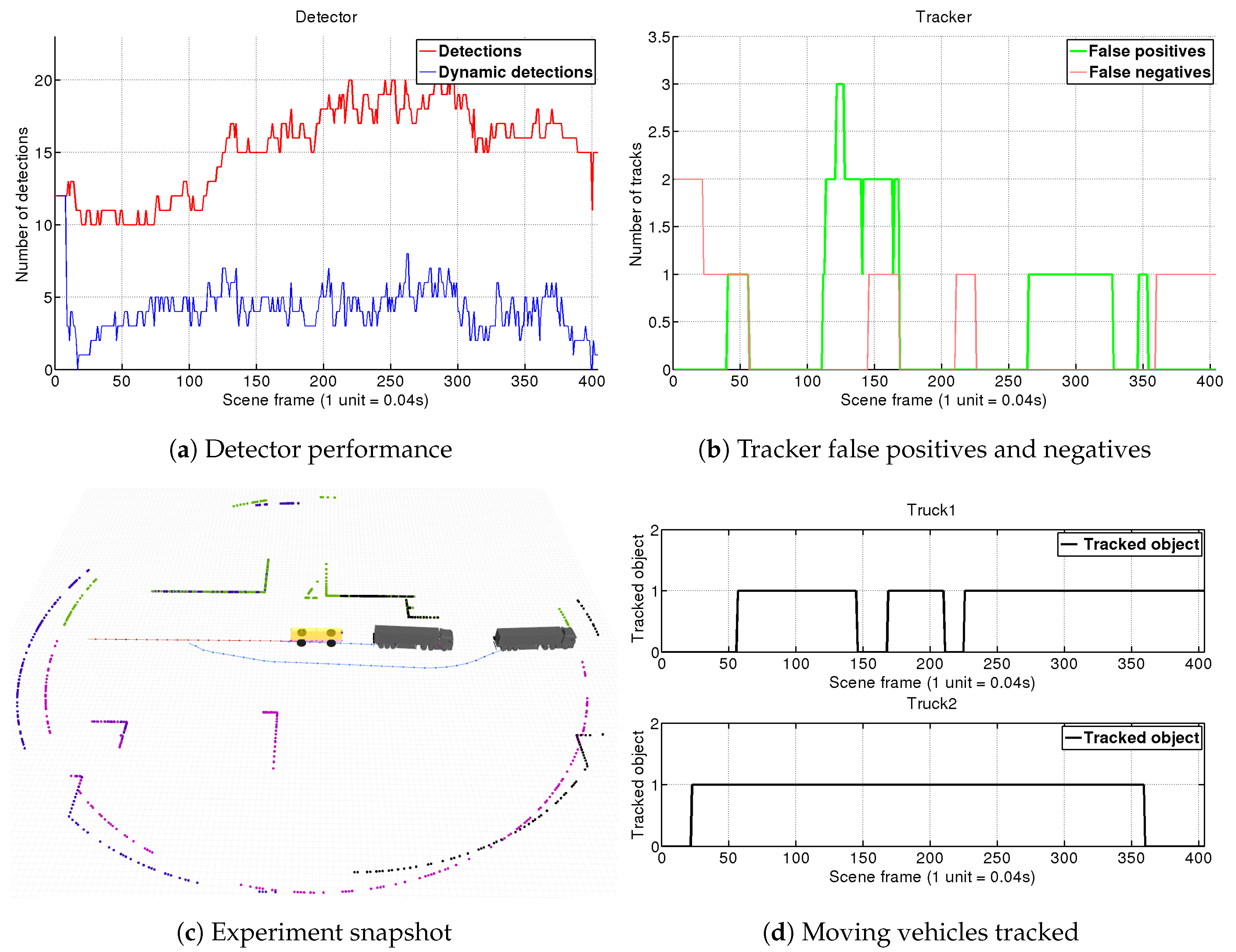
4. Simulations and Experiments
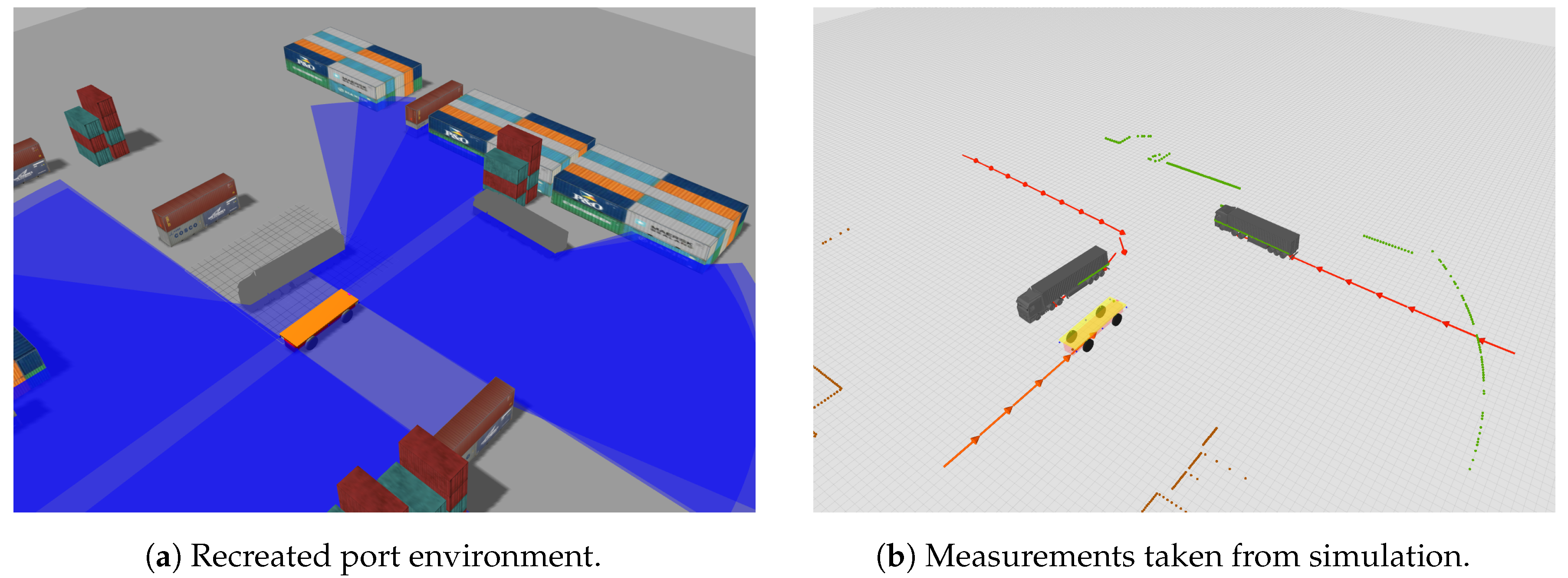
4.1. Simulated Environment
4.1.1. Scene 1: Two Trucks Crossing
4.1.2. Scene 2: AGV Turning Left at Intersection
4.1.3. Scene 3: AGV Turns Right at Intersection to Join Trucks Platoon
4.1.4. Scene 4: AGV Witnesses a Truck Overtaking Another Truck
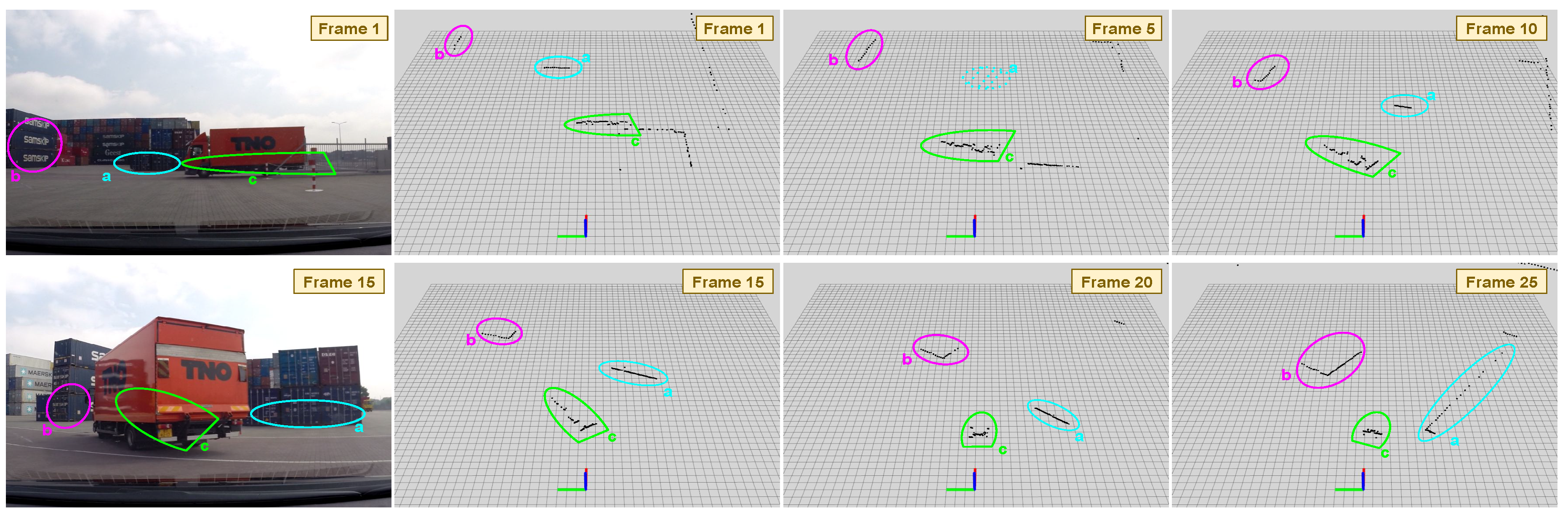
4.2. Real Environment Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| DATMO | Detecting and Tracking of Moving Objects |
| LRF | Laser RangeFinder |
| AGV | Autonomous Guided Vehicle |
| MHT | Multiple-Hypotheses Tracking |
| ACT | Automated Container Terminal |
| FLIRT | Fast Laser Interest Region Transform |
| SIFT | Scale-invariant feature transform |
| SURF | Speeded-Up Robust Features |
| MDP | Markov Decision Process |
| KF | Kalman Filter |
| JPDAF | Joint Probabilistic Data Association Filtering |
| MH-KF | Multiple-Hypothesis Tracking based on Kalman Filters |
| PDBS | Point-Distance-Based Segmentation |
| PCA | Principal Component Analysis |
| FOV | Field of View |
| Variables | |
| Laser Scan in time t | |
| Range measurement | |
| Bearing angle | |
| Set of point on a scan | |
| k | Number of scans buffered |
| Frame referred to the vehicle | |
| Absolute/Euclidean Distance | |
| Threshold | |
| Observed Object | |
| Set of segmented objects | |
| Current reference frame of an object | |
| Object’s width/length | |
| Object’s orientation regarding the longitudinal axis | |
| Number of laser points in an object | |
| Set of extracted lines in an object | |
| Laser Point in Euclidean coordinates | |
| Regression error of the line | |
| Director vector for the line | |
| Number of laser points of and object | |
| Set of extracted corners in an object | |
| Corner’s orientation | |
| Corner’s aperture | |
| Perimeter | |
| Area | |
| Tracked Dynamic Target | |
| Dynamic observations | |
| Set of dynamic detections at time t | |
| Tracked Targets | |
| Set of Targets tracked at time t | |
| Measurement matrix | |
| Propagation of the target state | |
| Covariance matrix of the propagated target | |
| Covariance matrix of the detection | |
| Target association threshold | |
| Probability of the actual hypothesis | |
| Poisson probability distribution for false alarms | |
| Poisson probability distribution for new targets | |
| Number of detections associated with false alarms | |
| Number of detections associated with new targets | |
| Probability of detection | |
| Number of detections associated with existing targets | |
| Number of the existing targets | |
| Gaussian probability distribution of the detections for the detector | |
| Probability distribution for the not confirmed targets | |
| Number of times that the target has a detection associated with it | |
| Probability distribution to hold a dynamic target | |
| Number of targets without dynamic detection associated | |
| Object velocity | |
| Ego vehicle linear/angular velocity | |
| Distance between ego vehicle and tracked object | |
| Weight controlling the rise of confirmation probability |
References
- Carlo, H.J.; Vis, I.F.; Roodbergen, K.J. Transport operations in container terminals: Literature overview, trends, research directions and classification scheme. Eur. J. Oper. Res. 2014, 236, 1–13. [Google Scholar] [CrossRef]
- UNCTAD. Review of Maritime Transport 2017; United Nations: New York, NY, USA, 2017; ISBN 978-92-1-112922-9. [Google Scholar]
- Vis, I.F.A. Survey of research in the design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 170, 677–709. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Saidi-Mehrabad, M. Methodologies to optimize automated guided vehicle scheduling and routing problems: A review study. J. Intell. Robot. Syst. 2015, 77, 525–545. [Google Scholar] [CrossRef]
- Wender, S.; Dietmayer, K. 3D vehicle detection using a laser scanner and a video camera. Intell. Transp. Syst. 2008, 2, 105–112. [Google Scholar] [CrossRef]
- Vivet, D.; Checchin, P.; Chapuis, R.; Faure, P.; Rouveure, R.; Monod, M.O. A mobile ground-based radar sensor for detection and tracking of moving objects. Eurasip J. Adv. Signal Process. 2012, 1–13. [Google Scholar] [CrossRef]
- Chavez-Garcia, R.O.; Aycard, O. Multiple Sensor Fusion and Classification for Moving Object Detection and Tracking. IEEE Trans. Intell. Trans. Syst. 2016, 17, 525–534. [Google Scholar] [CrossRef]
- Vaquero, V.; del Pino, I.; Moreno-Noguer, F.; Solà, J.; Sanfeliu, A.; Andrade-Cetto, J. Deconvolutional networks for point-cloud vehicle detection and tracking in driving scenarios. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017. [Google Scholar]
- Li, B. 3d fully convolutional network for vehicle detection in point cloud. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1513–1518. [Google Scholar]
- Vaquero, V.; Sanfeliu, A.; Moreno-Noguer, F. Deep Lidar CNN to Understand the Dynamics of Moving Vehicles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Luo, W.; Yang, B.; Urtasun, R. Fast and Furious: Real Time End-to-End 3D Detection, Tracking and Motion Forecasting with a Single Convolutional Net. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3569–3577. [Google Scholar]
- Vaquero, V.; Repiso, E.; Sanfeliu, A.; Vissers, J.; Kwakkernaat, M. Low Cost, Robust and Real Time System for Detecting and Tracking Moving Objects to Automate Cargo Handling in Port Terminals. In Robot 2015: Second Iberian Robotics Conference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 491–502. [Google Scholar]
- Mendes, A.; Bento, L.C.; Nunes, U. Multi-target detection and tracking with a laser scanner. In Proceedings of the 2004 IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 796–801. [Google Scholar]
- Mertz, C.; Navarro-Serment, L.E.; MacLachlan, R.; Rybski, P.; Steinfeld, A.; Suppe, A.; Urmson, C.; Vandapel, N.; Hebert, M.; Thorpe, C.; et al. Moving object detection with laser scanners. J. Field Robot. 2013, 30, 17–43. [Google Scholar] [CrossRef]
- Wang, D.Z.; Posner, I.; Newman, P. Model-free detection and tracking of dynamic objects with 2D lidar. Int. J. Robot. Res. 2015, 7, 1039–1063. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Dellaert, F.; Thorpe, C.E. Robust car tracking using Kalman filtering and Bayesian templates. In Proceedings of the Intelligent Transportation Systems Conference, Boston, MA, USA, 9–12 November 1997. [Google Scholar]
- Ess, A.; Leibe, B.; Schindler, K.; van Gool, L. Moving obstacle detection in highly dynamic scenes. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 56–63. [Google Scholar] [CrossRef]
- Zhao, H.; Shao, X.; Katabira, K.; Shibasaki, R. Joint tracking and classification of moving objects at intersection using a single-row laser range scanner. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 287–294. [Google Scholar]
- Nguyen, V.; Martinelli, A.; Tomatis, N.; Siegwart, R. A comparison of line extraction algorithms using 2D laser rangefinder for indoor mobile robotics. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 1929–1934. [Google Scholar]
- Diosi, A.; Kleeman, L. Fast laser scan matching using polar coordinates. Int. J. Robot. Res. 2007, 26, 1125–1153. [Google Scholar] [CrossRef]
- Premebida, C.; Nunes, U. Segmentation and geometric primitives extraction from 2d laser range data for mobile robot applications. Robotica 2005, 2005, 17–25. [Google Scholar]
- Tipaldi, G.D.; Braun, M.; Arras, K.O. FLIRT: Interest regions for 2D range data with applications to robot navigation. Exp. Robot. 2014, 79, 695–710. [Google Scholar]
- Arras, K.O.; Mozos, Ó.M.; Burgard, W. Using boosted features for the detection of people in 2d range data. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3402–3407. [Google Scholar]
- Arras, K.O.; Grzonka, S.; Luber, M.; Burgard, W. Efficient people tracking in laser range data using a multi-hypothesis leg-tracker with adaptive occlusion probabilities. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008. [Google Scholar] [CrossRef]
- Petrovskaya, A.; Thrun, S. Model based vehicle detection and tracking for autonomous urban driving. Auton. Robots 2009, 26, 123–139. [Google Scholar] [CrossRef]
- Rangesh, A.; Trivedi, M.M. No blind spots: Full-surround multi-object tracking for autonomous vehicles using cameras & LiDARs. arXiv, 2018; arXiv:1802.08755. [Google Scholar]
- Yilmaz, A.; Javed, O.; Shah, M. Object tracking: A survey. ACM Comput. Surv. 2006, 38, 13. [Google Scholar] [CrossRef]
- Kitagawa, G. Non-Gaussian state—Space modeling of nonstationary time series. J. Am. Stat. Assoc. 1987, 82, 1032–1041. [Google Scholar]
- Reid, D.B. An algorithm for tracking multiple targets. Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Cox, I.J. A review of statistical data association techniques for motion correspondence. Int. J. Comput. Vis. 1993, 10, 53–66. [Google Scholar] [CrossRef]
- Castanedo, F. A review of data fusion techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef]
- Kim, D.; Jo, K.; Lee, M.; Sunwoo, M. L-Shape Model Switching-Based Precise Motion Tracking of Moving Vehicles Using Laser Scanners. Trans. Intell. Trans. Syst. 2018, 19, 598–612. [Google Scholar] [CrossRef]
- Ferrer, G.; Sanfeliu, A. Bayesian human motion intentionality prediction in urban environments. Pattern Recognit. Lett. 2014, 44, 134–140. [Google Scholar] [CrossRef]
- Corominas-Murtra, A.; Pagés, J.; Pfeiffer, S. Multi-Target & Multi-Detector People Tracker for Mobile Robots. In Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, 2–4 September 2015. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaquero, V.; Repiso, E.; Sanfeliu, A. Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports. Sensors 2019, 19, 107. https://doi.org/10.3390/s19010107
Vaquero V, Repiso E, Sanfeliu A. Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports. Sensors. 2019; 19(1):107. https://doi.org/10.3390/s19010107
Chicago/Turabian StyleVaquero, Victor, Ely Repiso, and Alberto Sanfeliu. 2019. "Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports" Sensors 19, no. 1: 107. https://doi.org/10.3390/s19010107
APA StyleVaquero, V., Repiso, E., & Sanfeliu, A. (2019). Robust and Real-Time Detection and Tracking of Moving Objects with Minimum 2D LiDAR Information to Advance Autonomous Cargo Handling in Ports. Sensors, 19(1), 107. https://doi.org/10.3390/s19010107




