Average Accumulative Based Time Variant Model for Early Diagnosis and Prognosis of Slowly Varying Faults
Abstract
1. Introduction
2. Review of PCA and DCA
2.1. PCA
2.2. DCA
3. AA Based Early Diagnosis of Slowly Varying Small Faults
3.1. AA Based Time Variant PCA for Early Abnormal Detection
3.2. AA Based Time Variant DCA for Early Fault Diagnosis
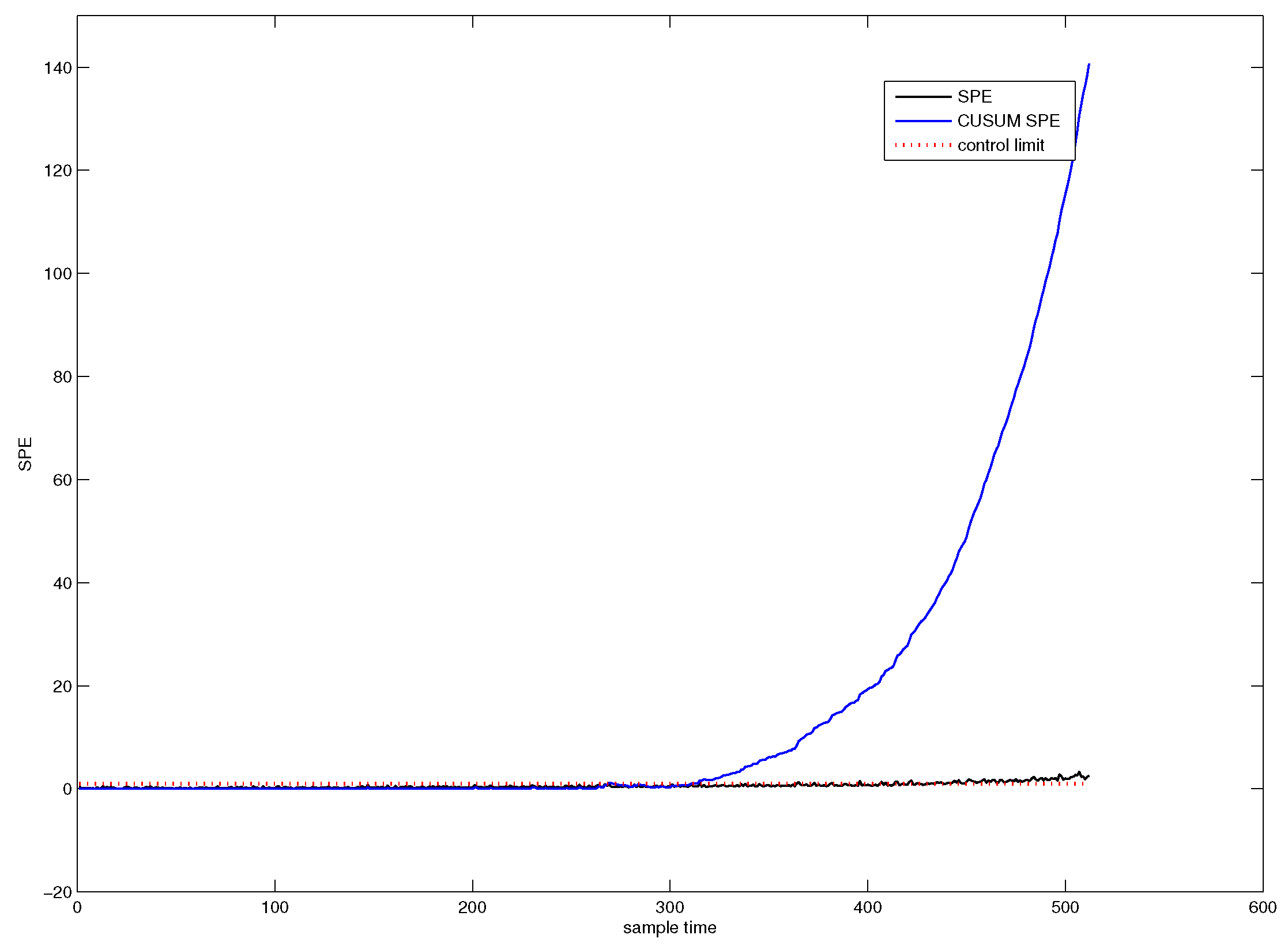
3.3. CUSUM-AA Based Early Diagnosis of Slowly Varying Small Faults
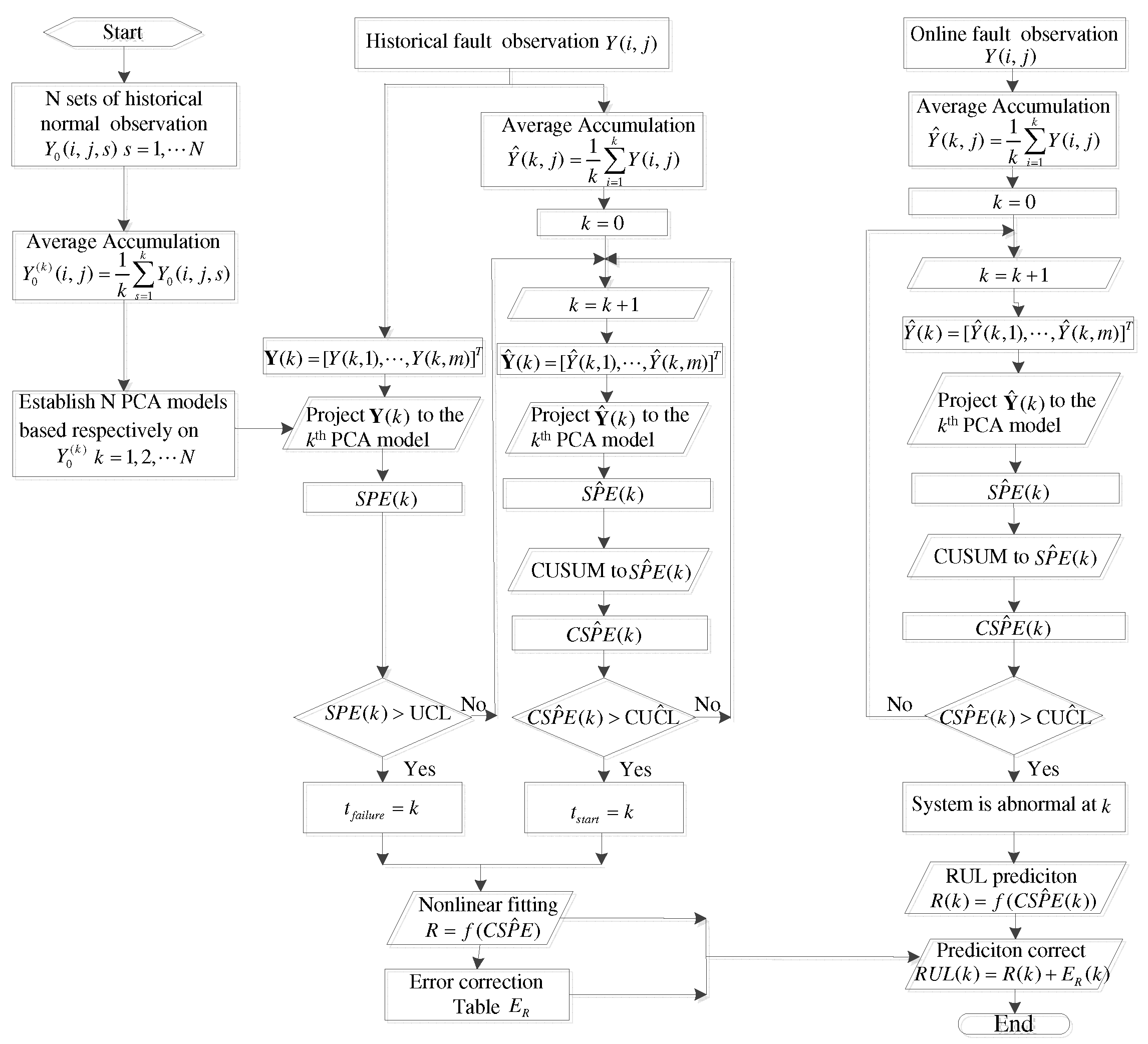
4. RUL Prediction
4.1. Damage Precursor and RUL Prediction Model Based on Historical Fault Data
4.1.1. CUSUM-AA-PCA Based System RUL Prediction Model
- (1)
- It can directly predict the RUL without extra recursive regression, thus it can insure ’real-time’ prediction of the RUL.
- (2)
- The model established has the error correction term, so it can come to an accurate prediction.
4.1.2. Online RUL Prediction
- (1)
- If there is a such that , then
- (2)
- If there is no such that , then
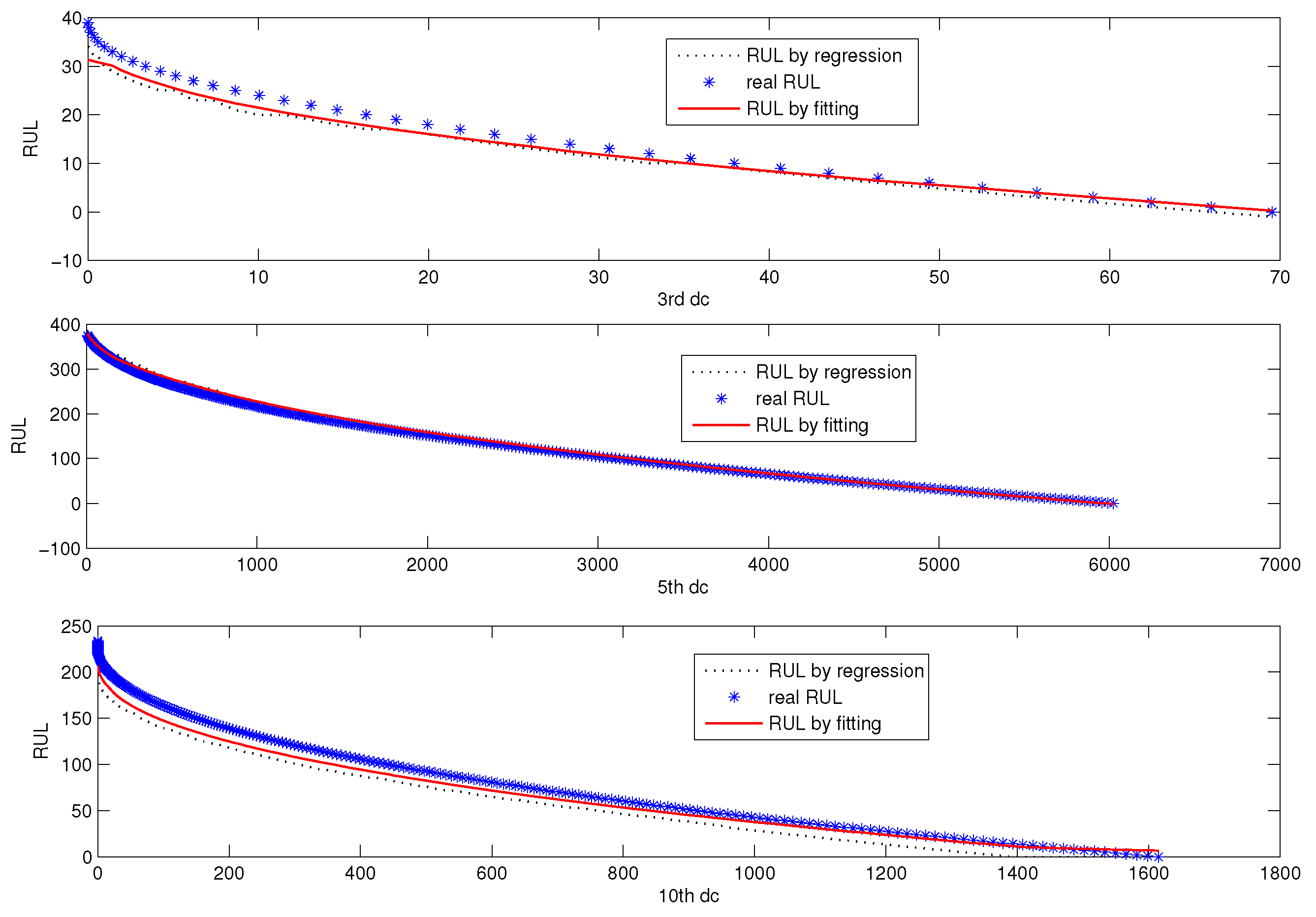
4.2. DCA Based RUL Prediction of Each DC
5. Simulation
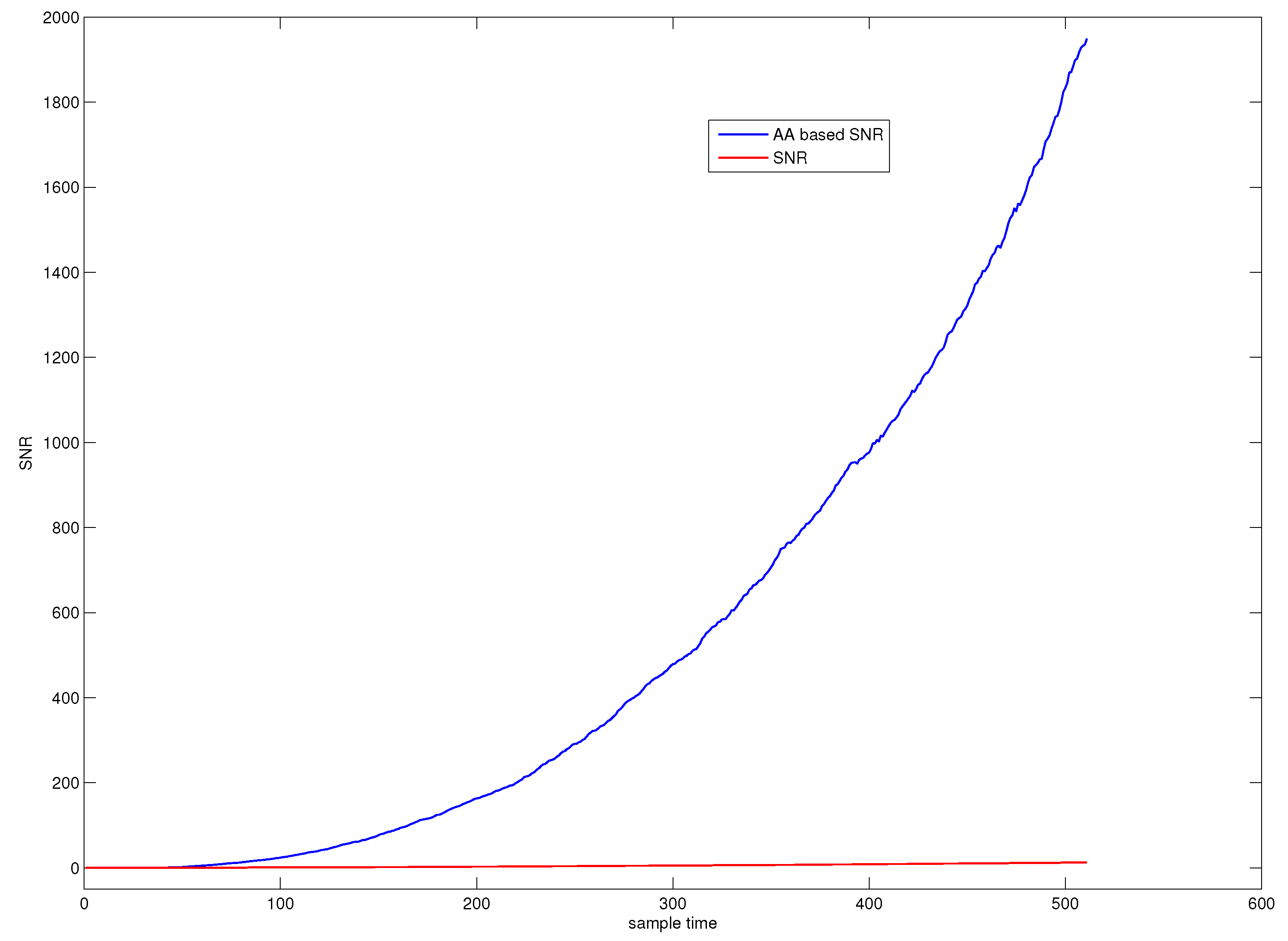
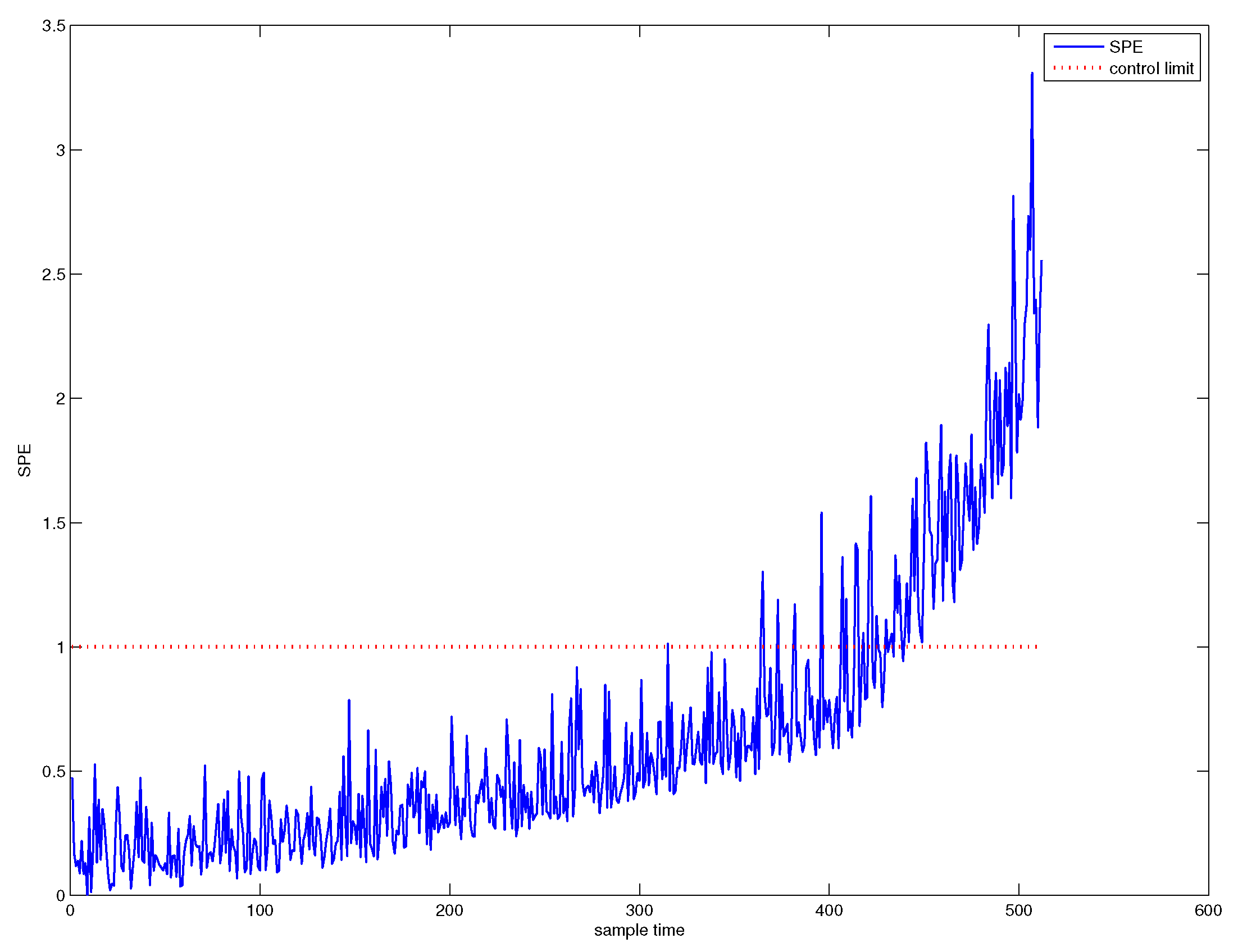
5.1. AA-Based Time Variant Early Detection of Slowly Varying Small Faults
5.1.1. AA-PCA Early Detection
5.1.2. AA-DCA Based Early Diagnosis
5.2. Fault Prognosis
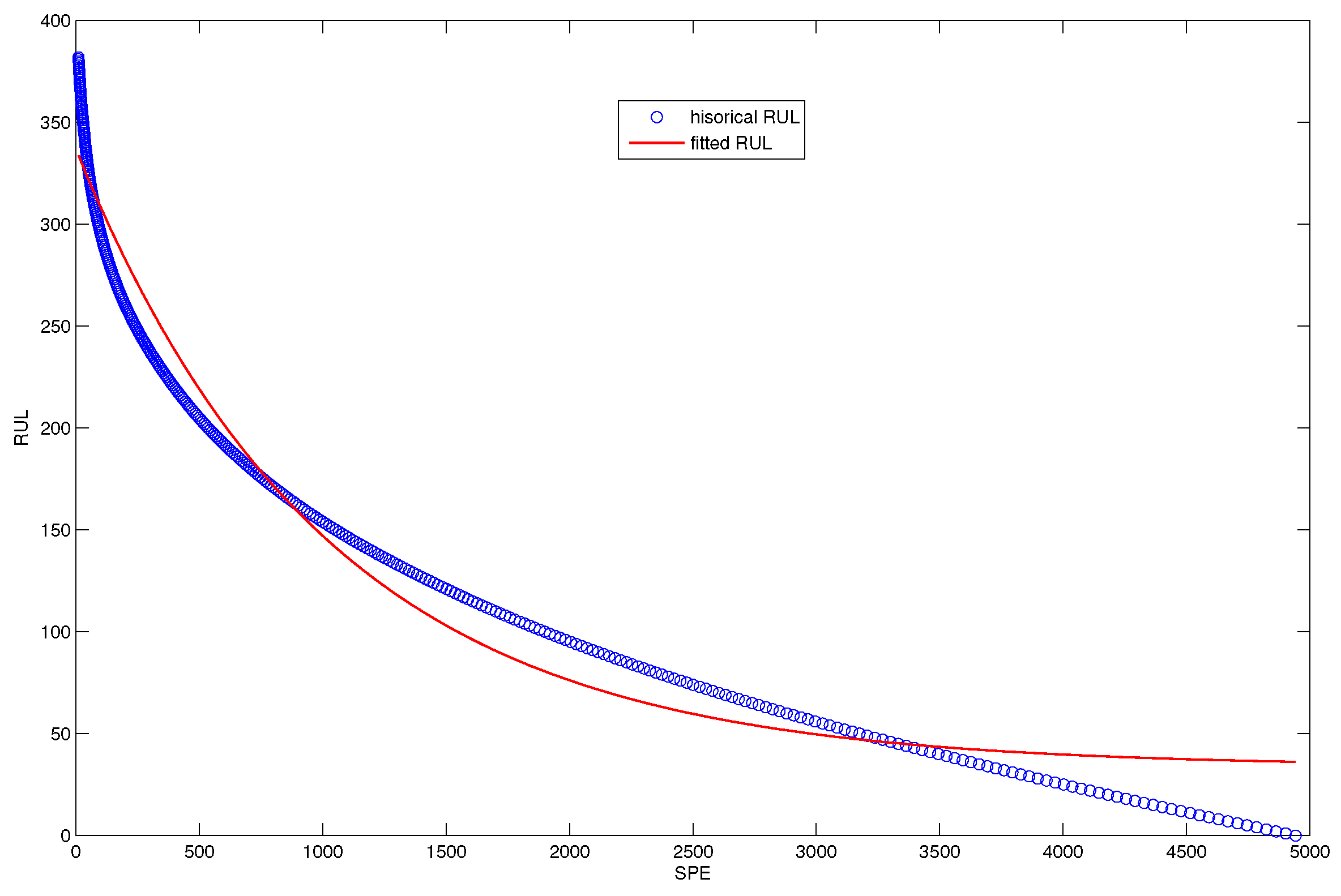
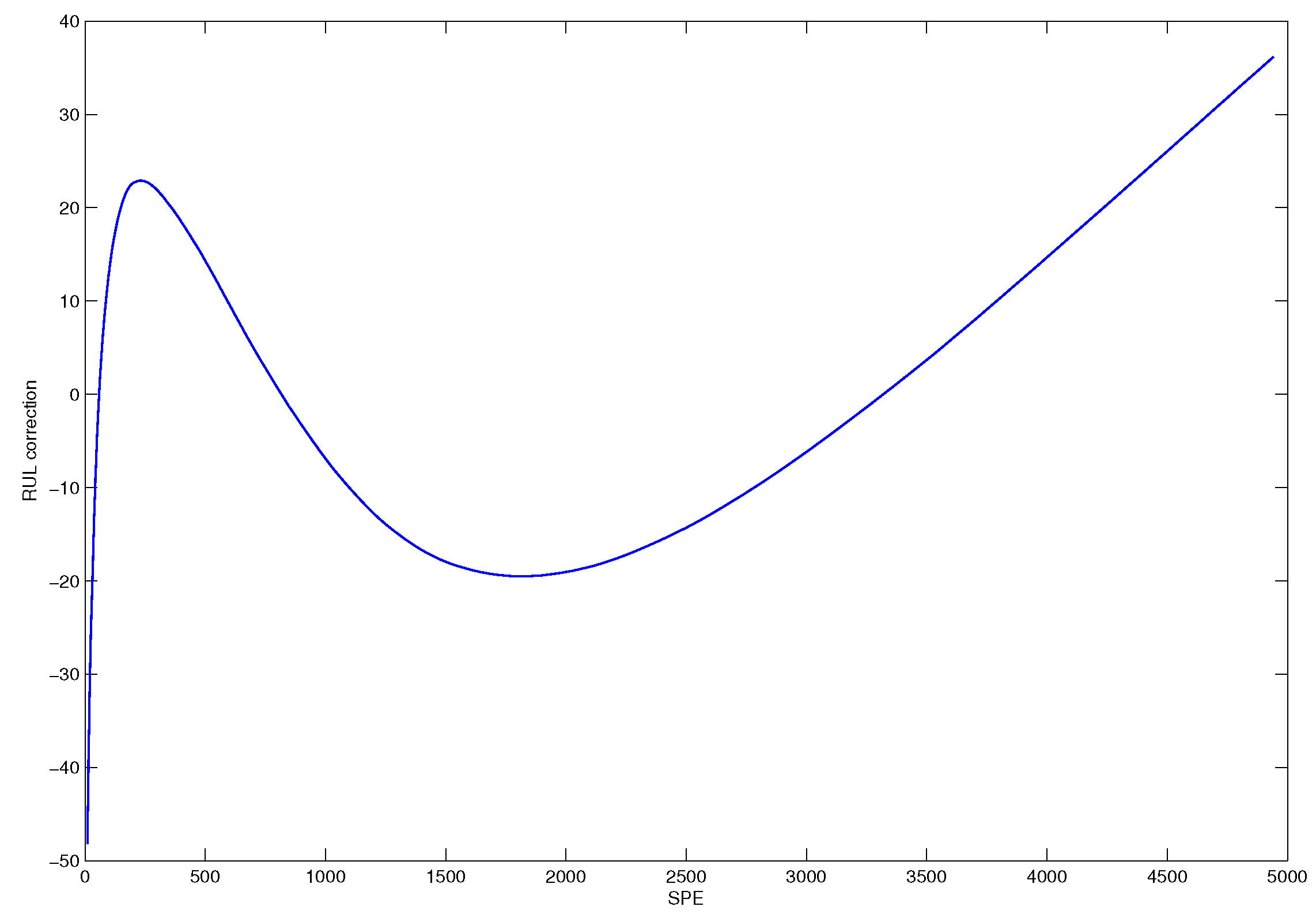
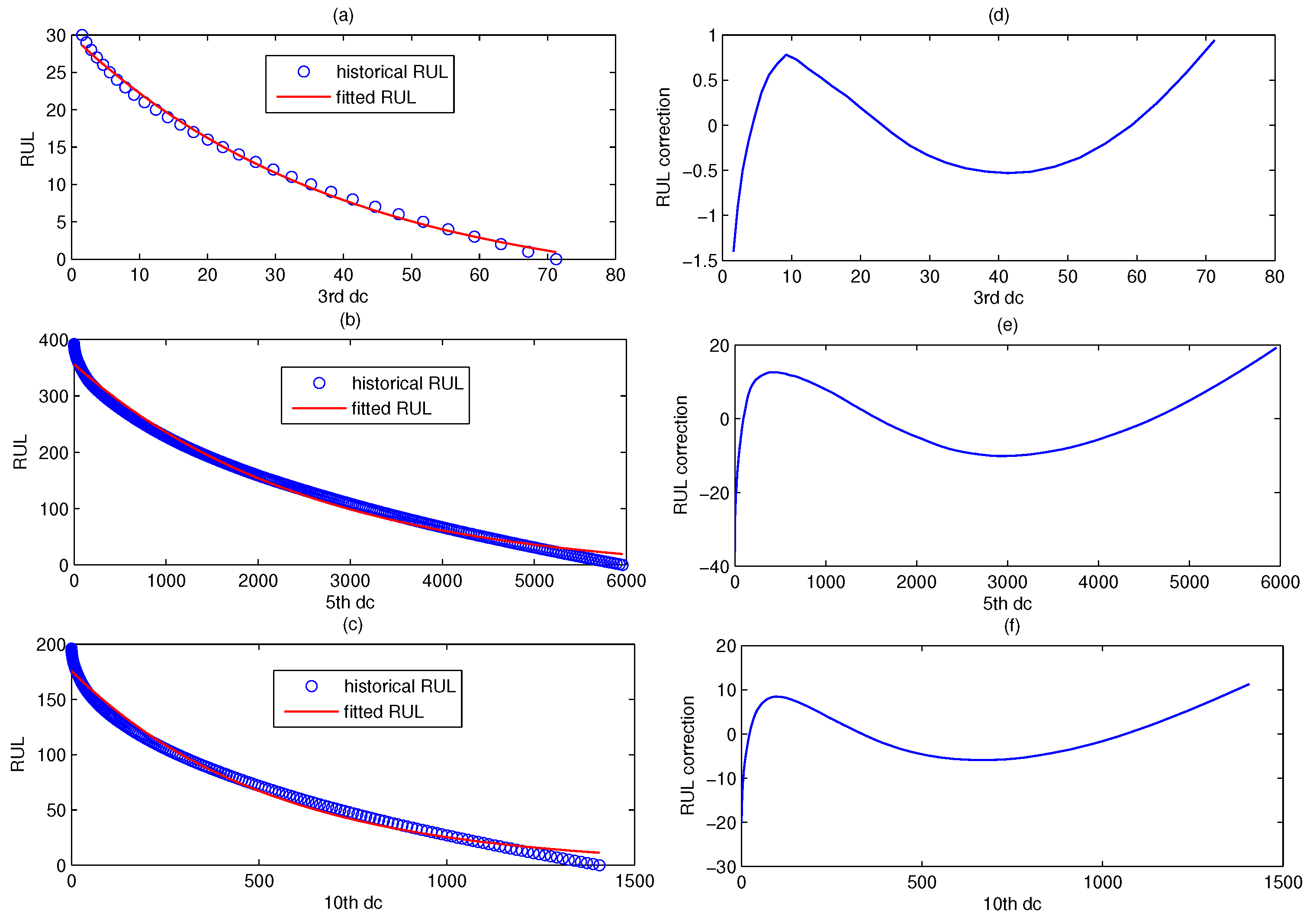
5.2.1. RUL Prediction Model Based on Historical Faulty Observation
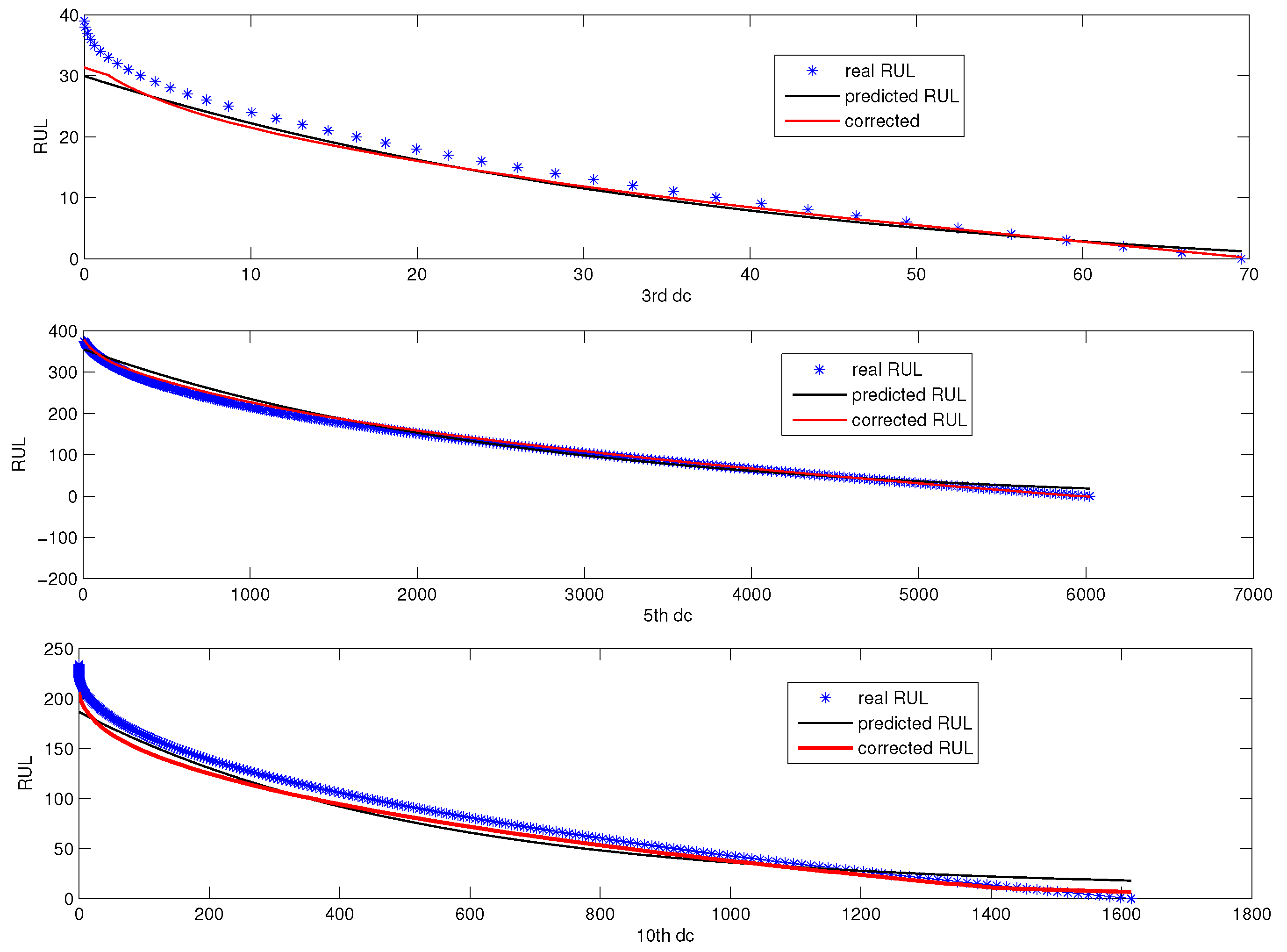
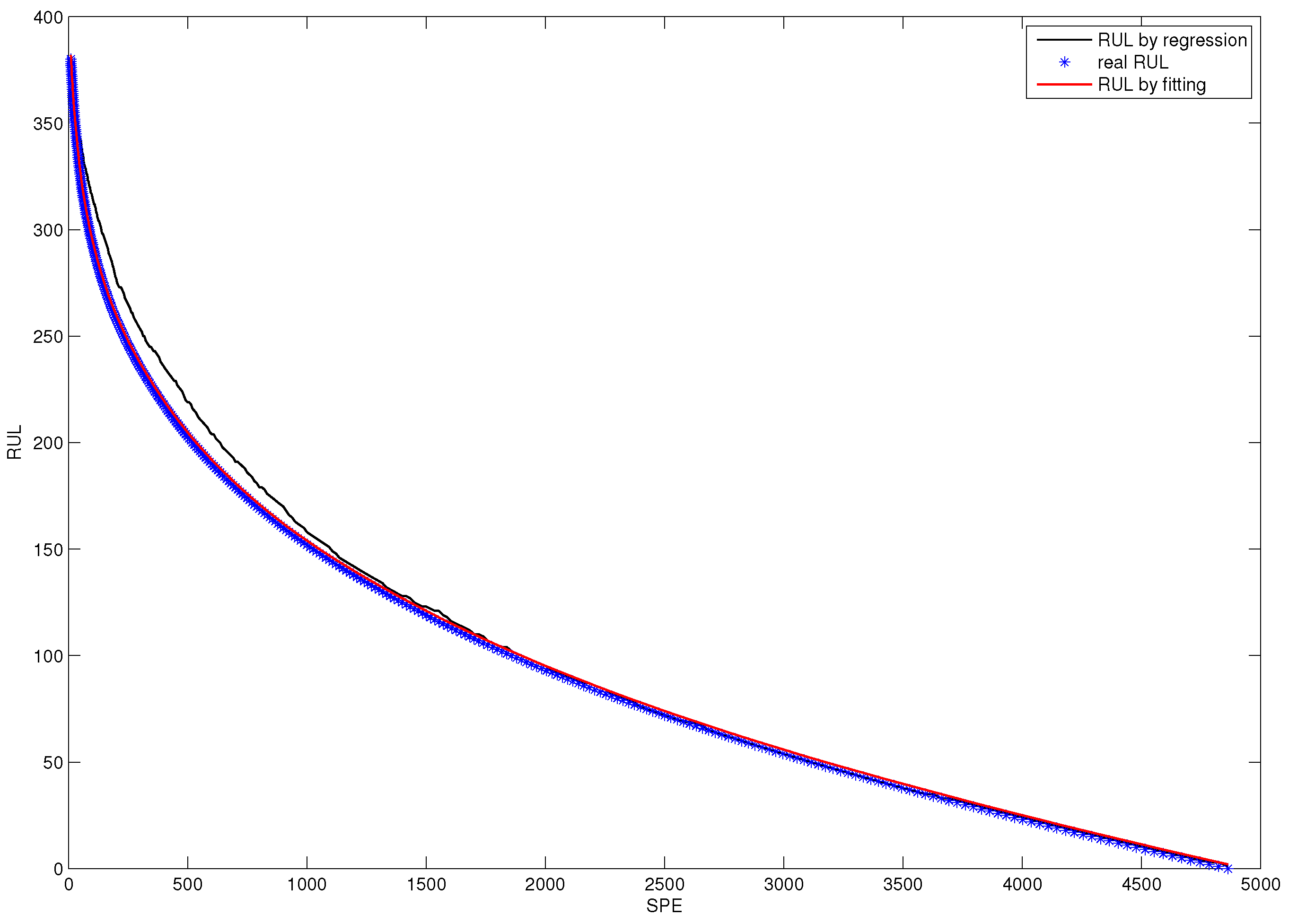
5.3. Online RUL Prediction
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cai, J.; Ferdowsi, H.; Sarangapani, J. Model-based fault detection, estimation, and prediction for a class of linear distributed parameter systems. Automatica 2016, 66, 122–131. [Google Scholar] [CrossRef]
- Li, Y.G.; Nilkitsaranont, P. Gas turbine performance prognostic for condition-based maintenance. Appl. Energy 2009, 86, 2152–2161. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive Bayes Bearing Fault Diagnosis Based on Enhanced Independence of Data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Li, X.; Gao, H.; Kaynak, O. Data-based techniques focused on modern industry: An overview. IEEE Trans. Ind. Electr. 2015, 62, 657–667. [Google Scholar] [CrossRef]
- Zhang, R.; Peng, Z.; Wu, L.; Yao, B.; Guan, Y. Fault Diagnosis from Raw Sensor Data Using Deep Neural Networks Considering Temporal Coherence. Sensors 2017, 17, 549. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Li, Z.; Li, G.; Zhou, Z. State Estimation Using Dependent Evidence Fusion: Application to Acoustic Resonance-Based Liquid Level Measurement. Sensors 2017, 17, 924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, T.; Tang, T.; Benbouzid, M.; Diallo, D. An imbalance fault detection method based on data normalization and EMD for marine current turbines. ISA Trans. 2017, 68, 302–312. [Google Scholar] [CrossRef] [PubMed]
- Du, D.; Jiang, B. Actuator fault estimation and accommodation for switched systems with time delay: Discrete-time case. ISA Trans. 2016, 62, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Youssef, T.; Chadli, M.; Karimi, H.R.; Wang, R. Actuator and sensor faults estimation based on proportional integral observer for TS fuzzy model. J. Frankl. Inst. 2017, 354, 2524–2542. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Allouani, F.; Filali, S. A new approach for fuzzy predictive adaptive controller design using particle swarm optimization algorithm. Int. J. Innov. Comput. Inf. Control 2013, 9, 3741–3758. [Google Scholar]
- Hu, C.; Jing, H.; Wang, R.; Yan, F.; Chadli, M. Robust H∞ output-feedback control for path following of autonomous ground vehicles. Mech. Syst. Signal Process. 2016, 70–71, 414–427. [Google Scholar] [CrossRef]
- Hajjaji, E.A.; Chadli, M.; Oudghiri, M.; Pages, O. Observer-based robust fuzzy control for vehicle lateral dynamics. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Hu, Z.; Chen, Z.; Gui, W.; Jiang, B. Adaptive PCA based fault diagnosis scheme in imperial smelting process. ISA Trans. 2014, 53, 1446–1455. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Wen, C.; Li, P.; Yuan, T. Direct projection to latent variable space for fault detection. J. Frankl. Inst. 2014, 351, 1226–1250. [Google Scholar] [CrossRef]
- Wang, T.; Qi, J.; Xu, H.; Wang, Y.; Liu, L.; Gao, D. Fault diagnosis method based on FFT-RPCA-SVM for Cascaded-Multilevel Inverter. ISA Trans. 2016, 60, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Wu, H.; Ni, M.; Zhang, M.; Dong, J. An adaptive confidence limit for periodic non-steady conditions fault detection. Mech. Syst. Signal Process. 2016, 72–73, 328–345. [Google Scholar] [CrossRef]
- Ge, Z.; Chen, T.; Song, Z. Quality prediction for polypropylene production process based on CLGPR model. Control Eng. Pract. 2011, 19, 423–432. [Google Scholar] [CrossRef]
- Ge, Z.; Gao, F.; Song, Z. Mixture probabilistic PCR model for soft sensing of multimode processes. Chemom. Intell. Lab. Syst. 2011, 105, 91–105. [Google Scholar] [CrossRef]
- Li, G.; Qin, S.J.; Ji, Y.; Zhou, D. Reconstruction based fault prognosis for continuous processes. Control Eng. Pract. 2010, 18, 1211–1219. [Google Scholar] [CrossRef]
- Li, G.; Qin, S.J.; Zhou, D. Geometric properties of partial least squares for process monitoring. Automatica 2010, 46, 204–210. [Google Scholar] [CrossRef]
- Ji, H.; He, X.; Zhou, D. On the use of reconstruction-based contribution for fault diagnosis. J. Process Control 2016, 40, 24–34. [Google Scholar] [CrossRef]
- Funa, Z.; Tianhao, T. DCA based multi-level small fault diagnosis. In Proceedings of the 11th IEEE International Conference on Communication Technology, Hangzhou, China, 10–12 November 2008; pp. 486–489. [Google Scholar]
- Enturk, S.S.; Erginel, N.; Kaya, I.; Kahraman, C. Fuzzy exponentially weighted moving average control chart for univariate data with a real case application. Appl. Soft Comput. 2014, 22, 1–10. [Google Scholar] [CrossRef]
- Bodnar, O.; Schmid, W. CUSUM charts for monitoring the mean of a multivariate Gaussian process. J. Stat. Plan. Inference 2011, 141, 2055–2070. [Google Scholar] [CrossRef]
- Shams, M.A.B.; Budman, H.M.; Duever, T.A. Fault detection, identification and diagnosis using CUSUM based PCA. Chem. Eng. Sci. 2011, 66, 4488–4498. [Google Scholar] [CrossRef]
- Asuhaimi, A.; Zin, M.; Saini, M.; Mustafa, M.W.; Sultan, A.R. New algorithm for detection and fault classification on parallel transmission line using DWT and BPNN based on Clarkes transformation. Neurocomputing 2015, 168, 983–993. [Google Scholar] [CrossRef]
- Zhou, F.; Wen, C.; Tang, T. DCA based multiple faults diagnosis method. Acta Autom. Sin. 2009, 35, 971–982. (In Chinese) [Google Scholar] [CrossRef]
- Camelio, J.; Hu, S.J.; Zhong, W. Diagnosis of multiple fixture faults in machining processes using designated component analysis. J. Manuf. Syst. 2004, 23, 309–315. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Wang, K. Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network. J. Intell. Manuf. 2013, 24, 1213–1227. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, F. Online fault prognosis with relative deviation analysis and vector autoregressive modeling. Chem. Eng. Sci. 2015, 138, 531–543. [Google Scholar] [CrossRef]
- Li, F.; Wang, J.X.; Tang, B.Q. Weak fault diagnosis of rotating machinery based on feature reduction with supervised orthogonal local fisher discriminant analysis. Neurocomputing 2015, 168, 505–519. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B. Singular value decomposition packet and its application to extraction of weak fault feature. Mech. Syst. Signal Process. 2016, 70–71, 73–86. [Google Scholar] [CrossRef]
- Rostek, K.; Morytko, L.; Jankowska, A. Early detection and prediction of leaks in fluidized-bed boilers using artificial neural networks. Energy 2015, 89, 914–923. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Xiao, F. A statistical fault detection and diagnosis method for centrifugal chillers based on exponentially-weighted moving average control charts and support vector regression. Appl. Thermal Eng. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Samsi, R.; Ray, A.; Mayer, J. Early detection of stator voltage imbalance in three-phase induction motors. Electr. Power Syst. Res. 2009, 79, 239–245. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, C.; Tao, T.L.L. Residual lifetime prediction for lithium-ion battery based on functional principal component analysis and Bayesian approach. Energy 2015, 90, 1983–1993. [Google Scholar] [CrossRef]
- Sankararaman, S. Significance, interpretation, and quantification of uncertainty in prognostics and remaining useful life prediction. Mech. Syst. Signal Process. 2015, 52–53, 228–247. [Google Scholar] [CrossRef]
- Son, S.; Jung, H.; Kwon, T.; Kim, J. Fatigue life prediction of a railway hollow axle with a tapered bore surface. Eng. Fail. Anal. 2015, 58, 44–55. [Google Scholar] [CrossRef]
- Wende, T.I.A.N.; Minggang, H.U.; Chuankun, L.I. Fault Prediction Based on Dynamic Model and Grey Time Series Model in Chemical Processes. Chin. J. Chem. Eng. 2014, 22, 643–650. [Google Scholar]
- Yu, J. Machine health prognostics using the Bayesian-inference-based probabilistic indication and high-order particle filtering framework. J. Sound Vib. 2015, 358, 97–110. [Google Scholar] [CrossRef]
- Peng, T.; Liu, Y.; Saxena, A.; Goebel, K. In-situ fatigue life prognosis for composite laminates based on stiffness degradation. Compos. Struct. 2015, 132, 155–165. [Google Scholar] [CrossRef]
- Wang, W.; Carr, M.; Xu, W.; Kobbacy, K. A model for residual life prediction based on Brownian motion with an adaptive drift. Microelectr. Reliab. 2011, 51, 285–293. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.L. Brownian motion with adaptive drift for remaining useful life prediction: Revisited. Mech. Syst. Signal Process. 2018, 99, 691–701. [Google Scholar] [CrossRef]
- Si, X.; Wang, W.; Hu, C.; Zhou, D.; Pecht, M.G. Remaining Useful Life Estimation Based on a Nonlinear Diffusion Degradation Process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar] [CrossRef]
- Si, X.; Wang, W.; Hu, C.; Zhou, D. Estimating Remaining Useful Life with Three-Source Variability in Degradation Modeling. IEEE Trans. Reliab. 2012, 63, 167–190. [Google Scholar] [CrossRef]
- Hong, A.; Donghua, Z. Fault prediction approach for dynamic system. J. Huazhong Univ. Sci. Technol. 2009, 37 (Suppl. S1), 222–225. [Google Scholar]
- Chakraborty, S.; Gebraeel, N.; Lawley, M.; Wan, H. Residual-life estimation for components with non-symmetric priors. Iie Trans. 2009, 41, 372–387. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual life predictions from vibration-based degradation signals: A neural network approach. IEEE Trans. Ind. Electr. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Kaiser, K.; Gebraeel, N. Predictive Maintenance Management Using Sensor-Based Degradation Models. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2009, 39, 840–849. [Google Scholar] [CrossRef]
- Elwany, A.M.H.; Gebraeel, N. Real-Time Estimation of Mean Remaining Life Using Sensor-Based Degradation Models. J. Manuf. Sci. Eng. 2009, 131, 611–623. [Google Scholar] [CrossRef]
- Jahromi, A.T.; Er, M.J.; Li, X.; Lim, B.S. Sequential fuzzy clustering based dynamic fuzzy neural network for fault diagnosis and prognosis. Neurocomputing 2016, 196, 31–41. [Google Scholar] [CrossRef]
- Sica, F.C.; Guimaraes, F.G.; Duarte, R.D.; Reis, A.J.R. A cognitive system for fault prognosis in power transformers. Electr. Power Syst. Res. 2015, 127, 109–117. [Google Scholar] [CrossRef]
- Chen, B.; Matthews, P.C.; Tavner, P.J. Wind turbine pitch faults prognosis using a-priori knowledge-based ANFIS. Expert Syst. Appl. 2013, 40, 6863–6876. [Google Scholar] [CrossRef]

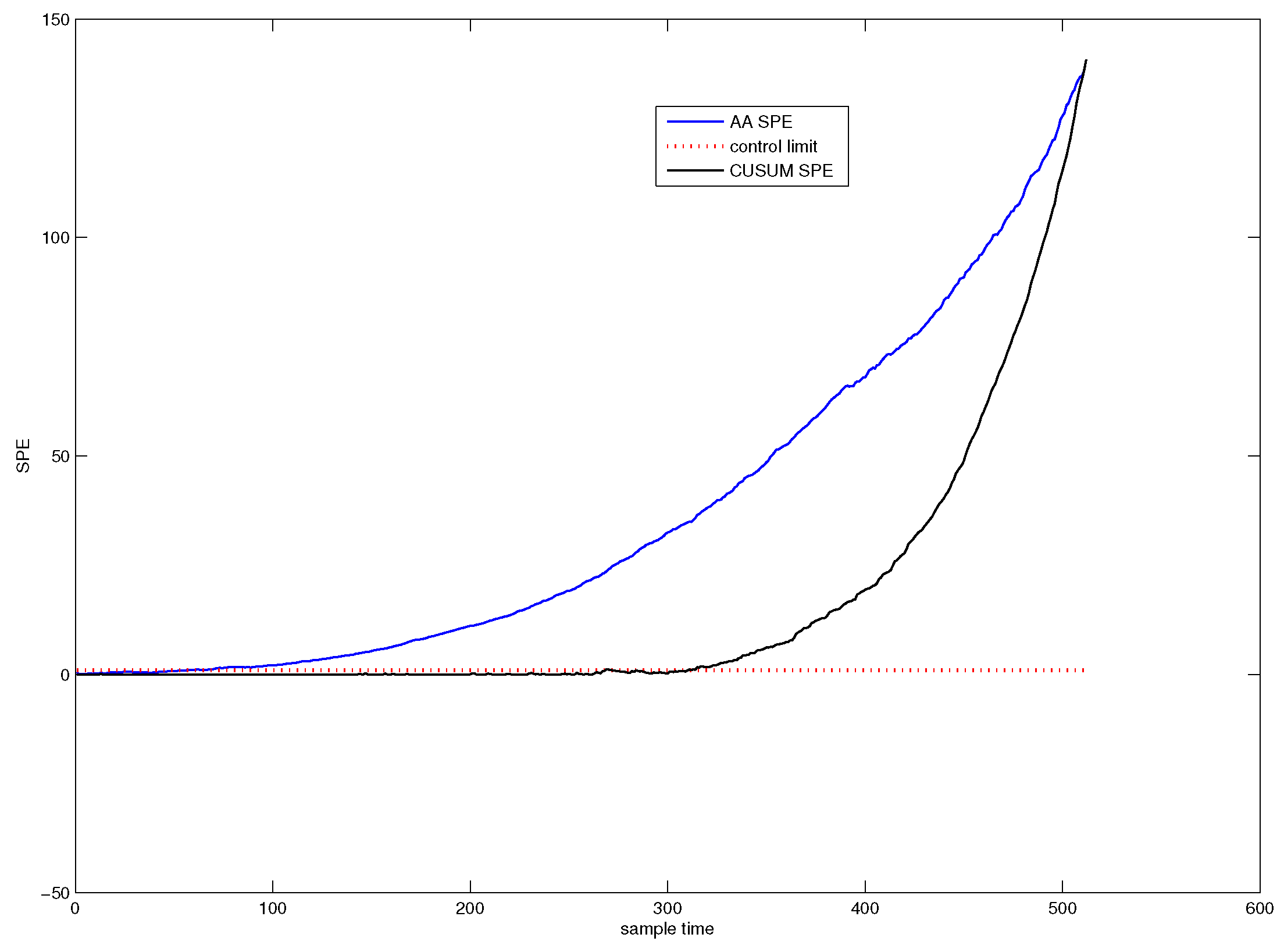

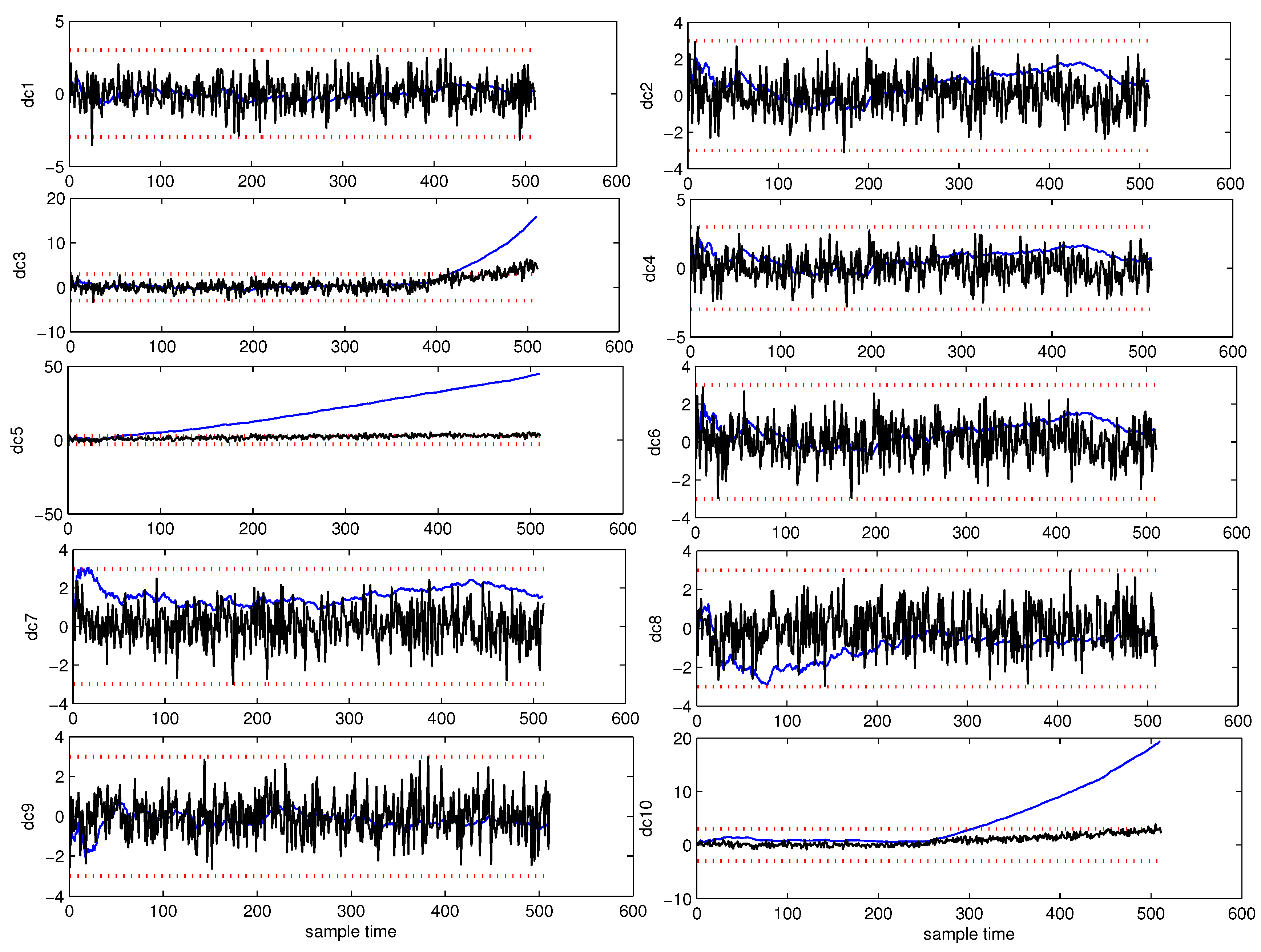
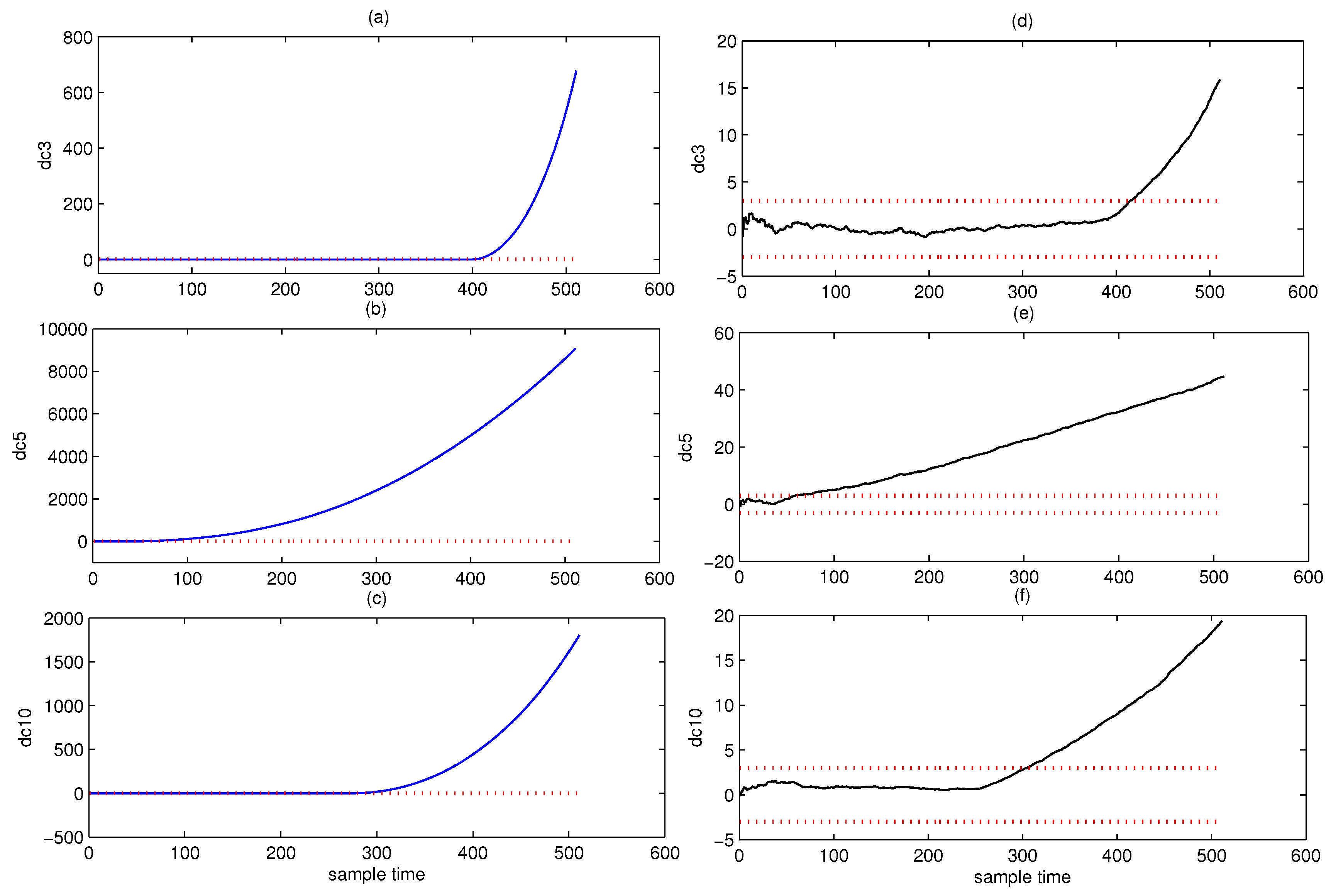

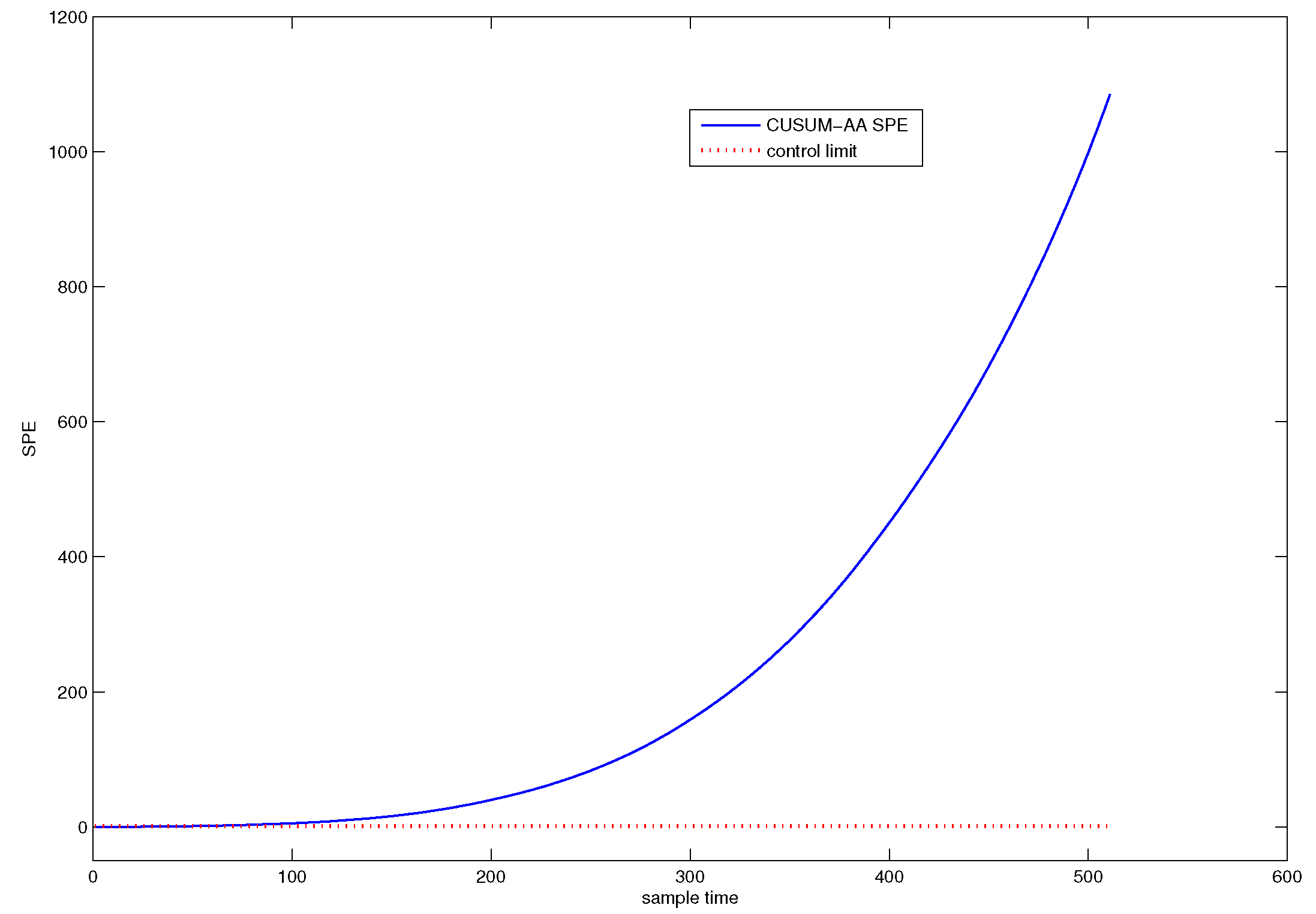

| Method | Detection Point | FDR | MDR |
|---|---|---|---|
| PCA | 421 | 0% | 81.0412% |
| WF-PCA | 281 | 3.125% | 51.875% |
| CUMSUM-PCA | 311 | 0% | 58.125% |
| AA-PCA | 57 | 0% | 5.2083% |
| CUMSUM-AA-PCA | 44 | 0% | 2.5% |
| Statistics | Method | Detection Point | FDR | MDR |
|---|---|---|---|---|
| DCA | 480 | 4.6875% | 75% | |
| CUMSUM-DCA | 419 | 0% | 27.3438% | |
| AA-DCA | 416 | 0% | 25% | |
| CUMSUM-AA-DCA | 403 | 0% | 14.8438% | |
| DCA | 470 | 0.7813% | 91.25 | |
| CUMSUM-DCA | 201 | 0% | 35.2083% | |
| AA-DCA | 60 | 0% | 5.8333% | |
| CUMSUM-AA-DCA | 52 | 0% | 4.1667% | |
| DCA | 512 | 0% | 99.6094 | |
| CUMSUM-DCA | 404 | 0% | 57.8125% | |
| AA-DCA | 305 | 0% | 19.1406% | |
| CUMSUM-AA-DCA | 278 | 0% | 8.5938% |
| Statistics | Exponential Fittting | Auto-Regressive |
|---|---|---|
| SPE | 2.0000 | 9.8084 |
| DC3 | 2.1846 | 2.5500 |
| DC5 | 6.5660 | 6.6320 |
| DC10 | 11.5484 | 19.6766 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Park, J.H.; Wen, C.; Hu, P. Average Accumulative Based Time Variant Model for Early Diagnosis and Prognosis of Slowly Varying Faults. Sensors 2018, 18, 1804. https://doi.org/10.3390/s18061804
Zhou F, Park JH, Wen C, Hu P. Average Accumulative Based Time Variant Model for Early Diagnosis and Prognosis of Slowly Varying Faults. Sensors. 2018; 18(6):1804. https://doi.org/10.3390/s18061804
Chicago/Turabian StyleZhou, Funa, Ju H. Park, Chenglin Wen, and Po Hu. 2018. "Average Accumulative Based Time Variant Model for Early Diagnosis and Prognosis of Slowly Varying Faults" Sensors 18, no. 6: 1804. https://doi.org/10.3390/s18061804
APA StyleZhou, F., Park, J. H., Wen, C., & Hu, P. (2018). Average Accumulative Based Time Variant Model for Early Diagnosis and Prognosis of Slowly Varying Faults. Sensors, 18(6), 1804. https://doi.org/10.3390/s18061804






