Attention-Based Recurrent Temporal Restricted Boltzmann Machine for Radar High Resolution Range Profile Sequence Recognition
Abstract
:1. Introduction
2. Preliminaries
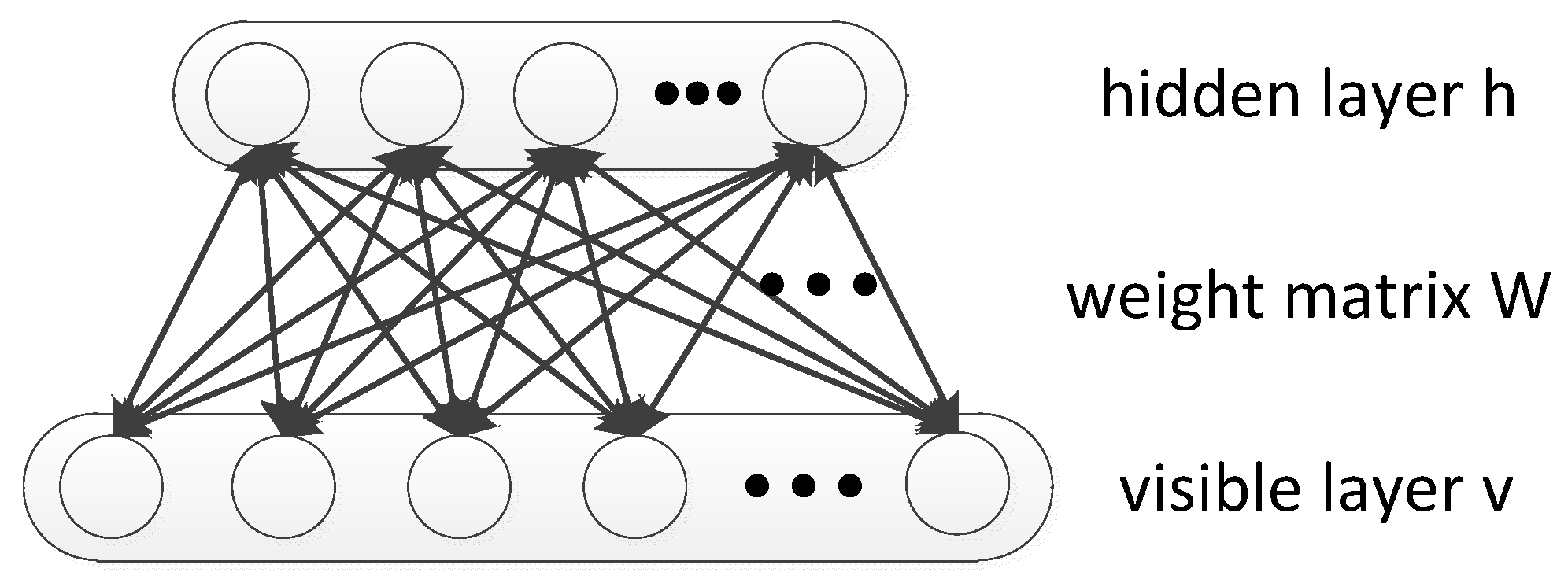
2.1. Restricted Boltzmann Machine
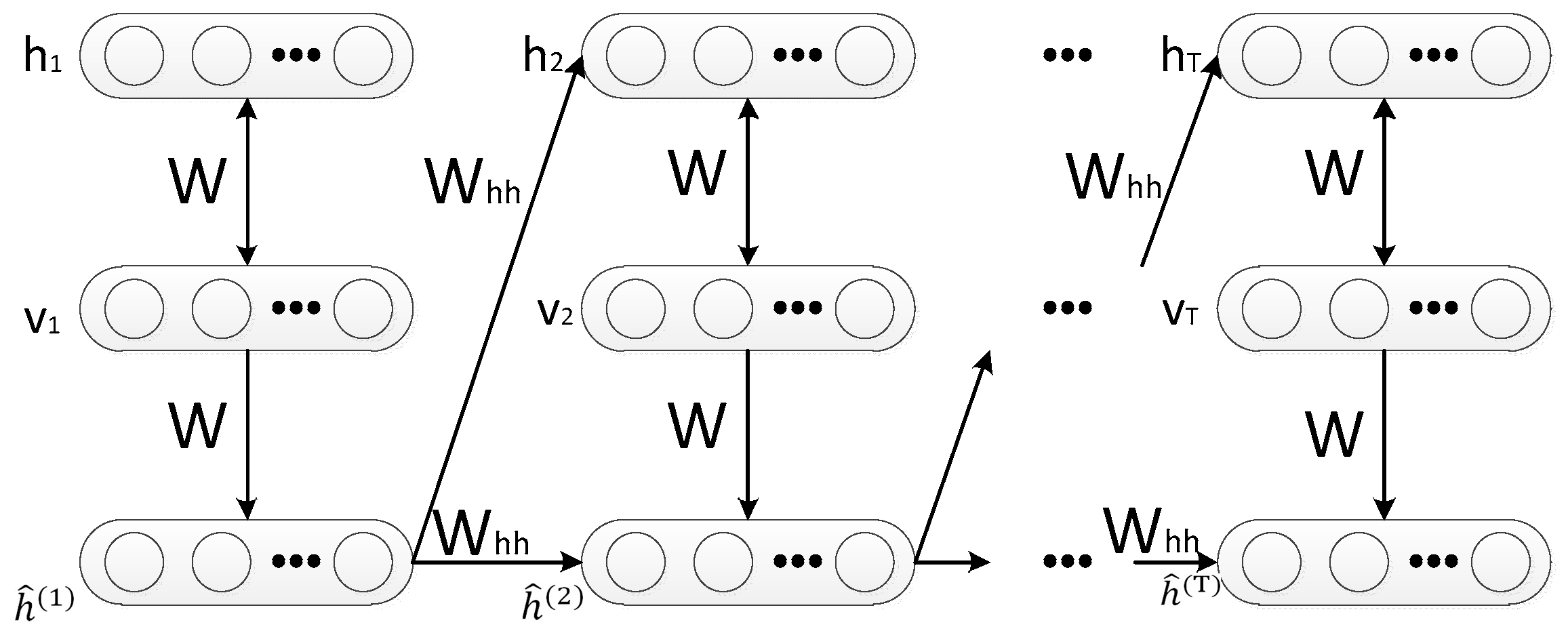
2.2. Recurrent Temporal Restricted Boltzmann Machine
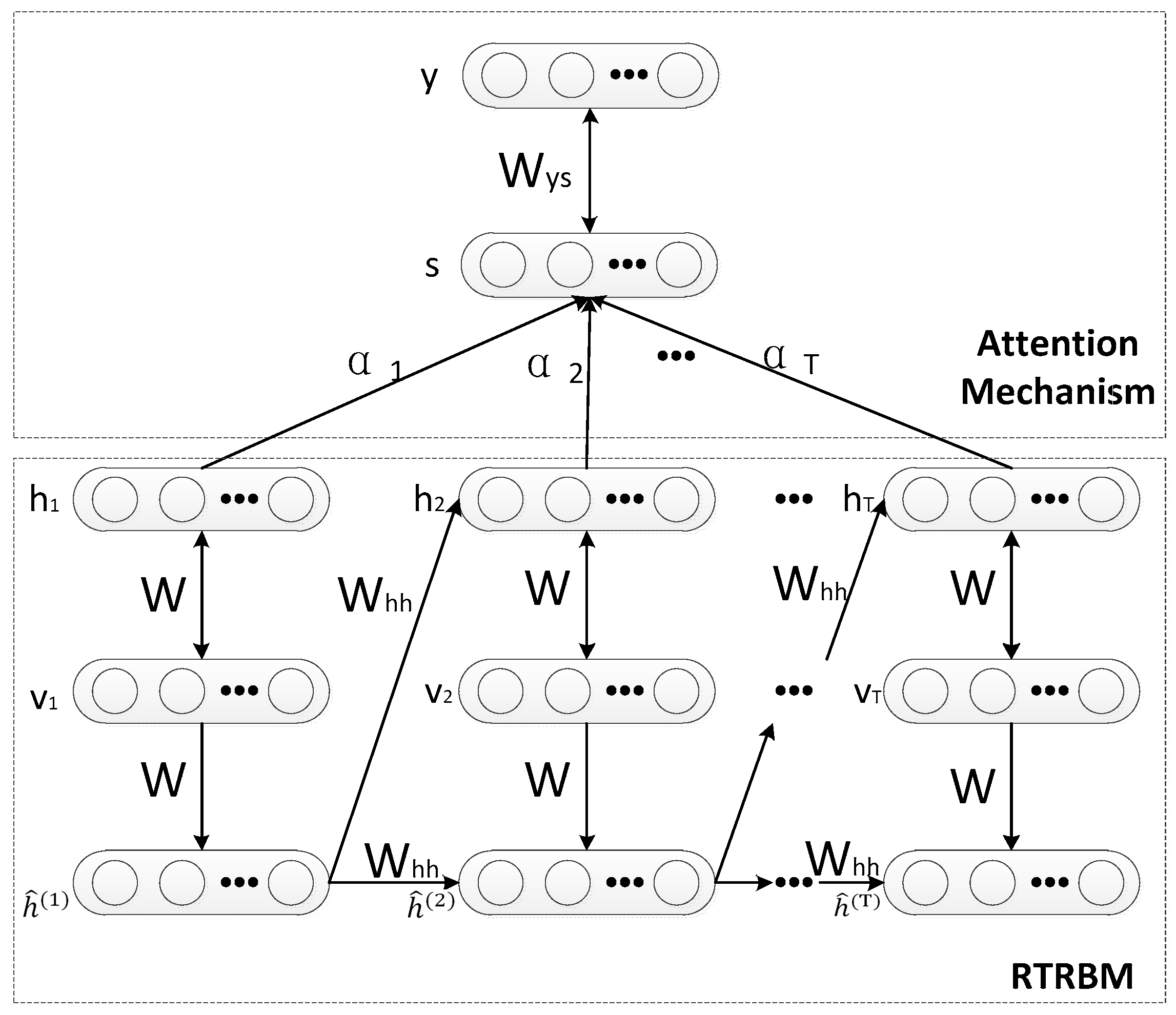
3. The Proposed Model
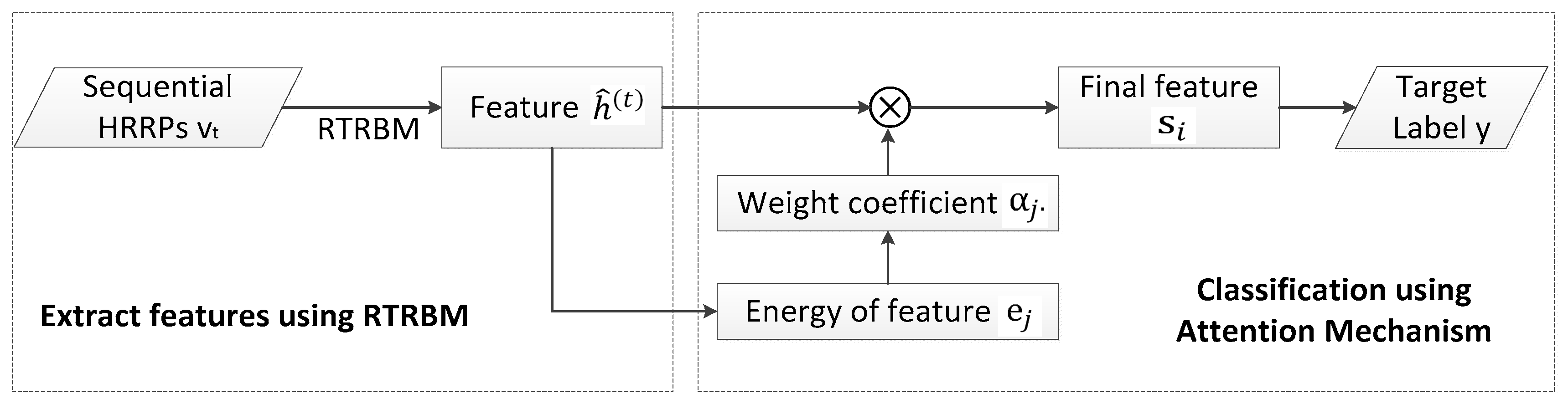
4. Learning the Parameters of the Model
| Algorithm 1. Pseudo code for the learning steps of Attention based RTRBM model |
| Input: training pair: {v_train; y_train}, hidden layer size: dim_h; |
| learning rate: ; momentum: ; and weightcost: . |
| Output: label vector y |
| # Section 1: Extract features using RTRBM |
| (1): Calculate according to Equation (4). |
| (2): Calculate and respectively, |
| according to Equation (5). |
| (3): Calculate the L2 reconstruction error: . |
| (4): Update parameters of this section: , |
| (5): Repeat step (1) to (4) for 1000 epochs and save the trained for test phase. |
| # Section 2: Classification with Attention mechanism |
| (1): Calculate according to Equation (9). |
| (2): Calculate according to Equation (8). |
| (3): Calculate the cross entropy according to Equation (15). |
| (4): Update parameters of this section: |
| (5): Repeat step (1) to (4) for 1000 epochs and save the trained for the test phase. |
5. Experiments
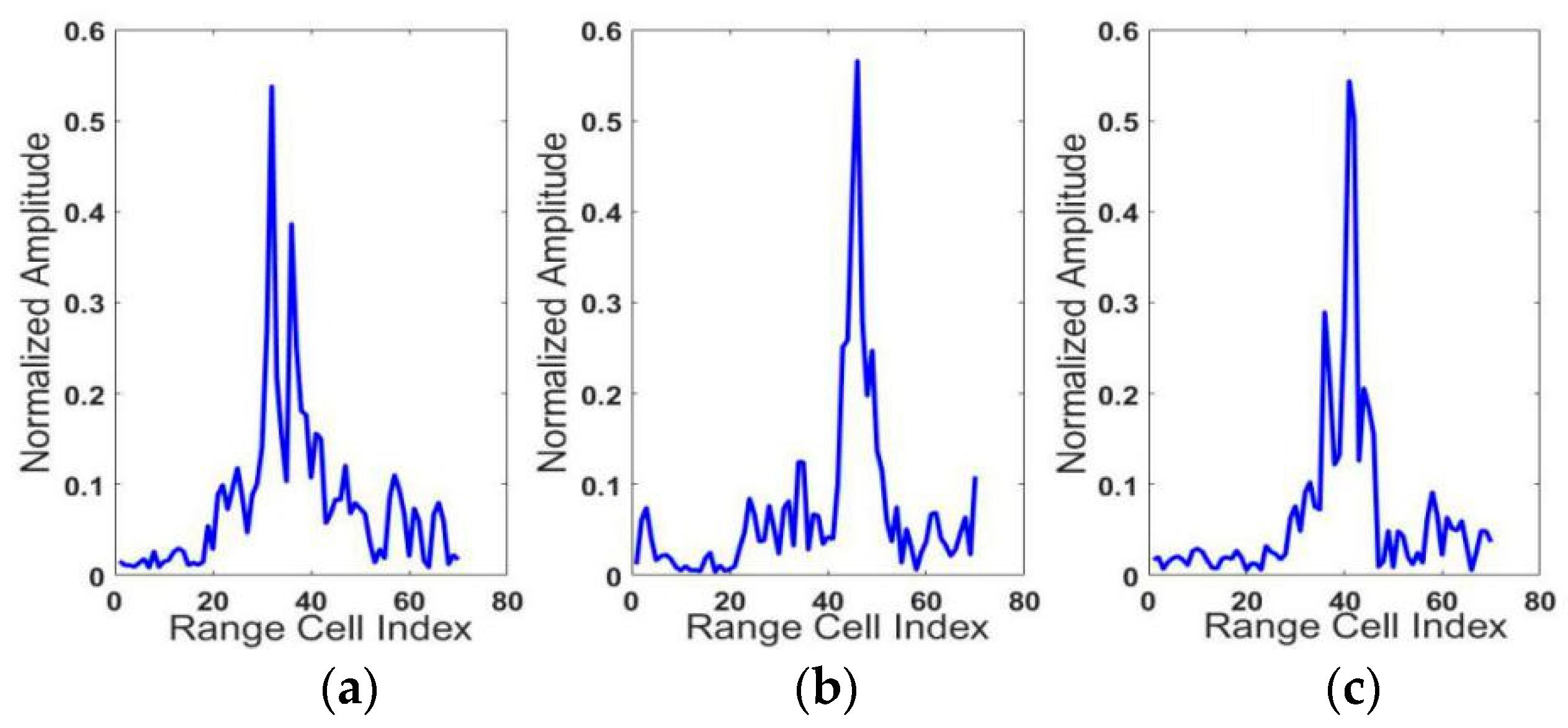
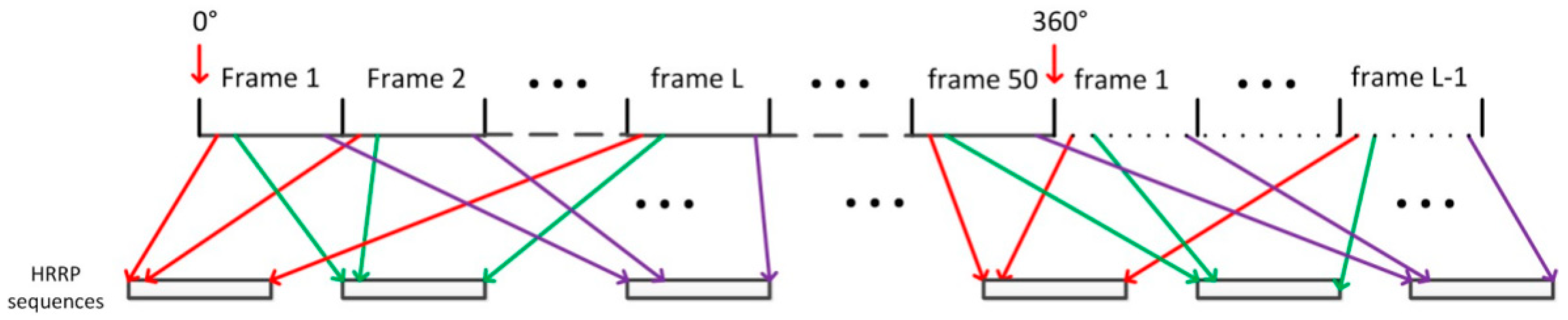
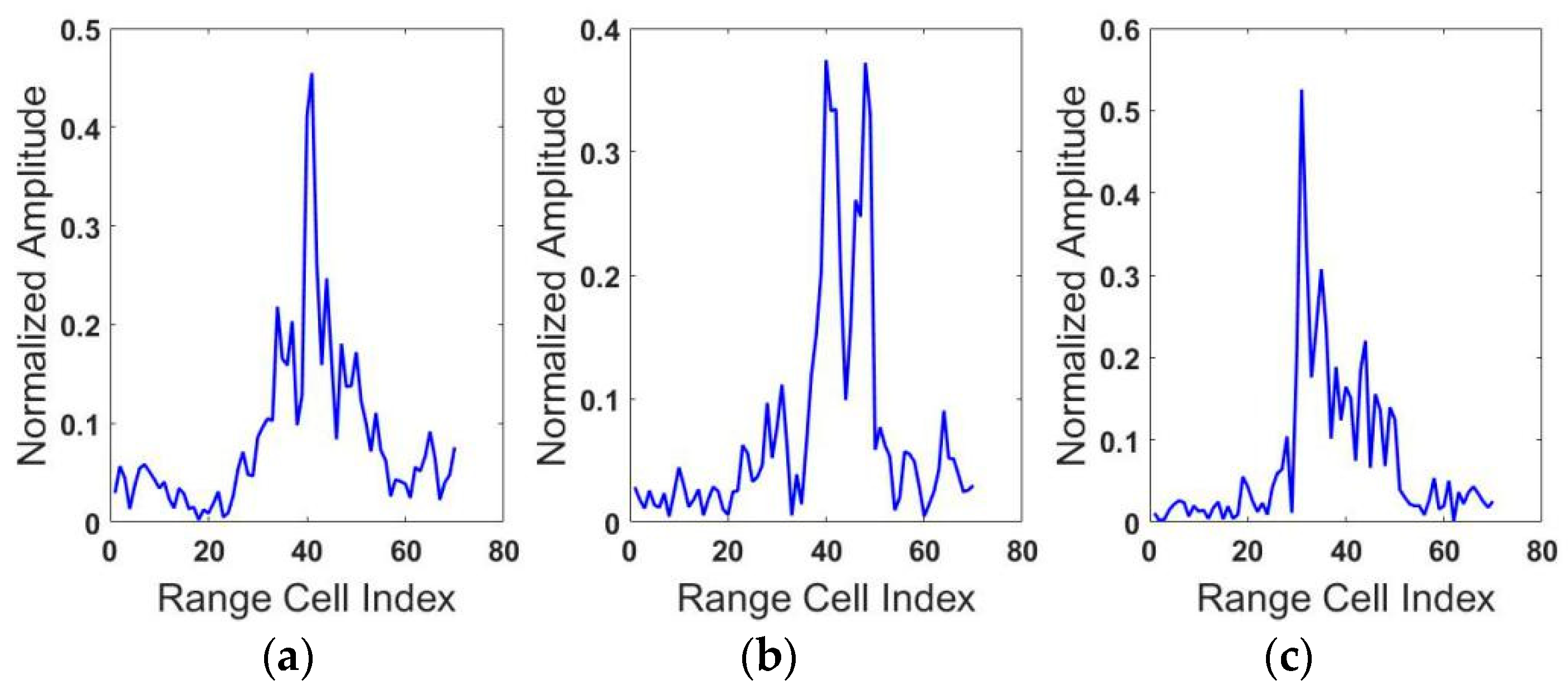
5.1. The Dataset
| Algorithm 2. The composition of the sequential HRRP datasets. |
| Step 1: Start from the aspect frame 1 to L. The first HRRPs in frame 1 to L are chosen to form the first HRRP sequence with length L. Slide one HRRP to the right and the second HRRPs in aspect frame 1 to L are chosen to form the second HRRP sequence. Repeat this algorithm until the end of each frame. |
| Step 2: Slide one frame to the right and repeat step 1 to construct the following sequences. |
| Step 3: Repeat step 2 until the end of all aspect frames. If the remaining frame is less than L, then the first frames are cyclically used one by one to form the remaining sequences. |
5.2. Experiments
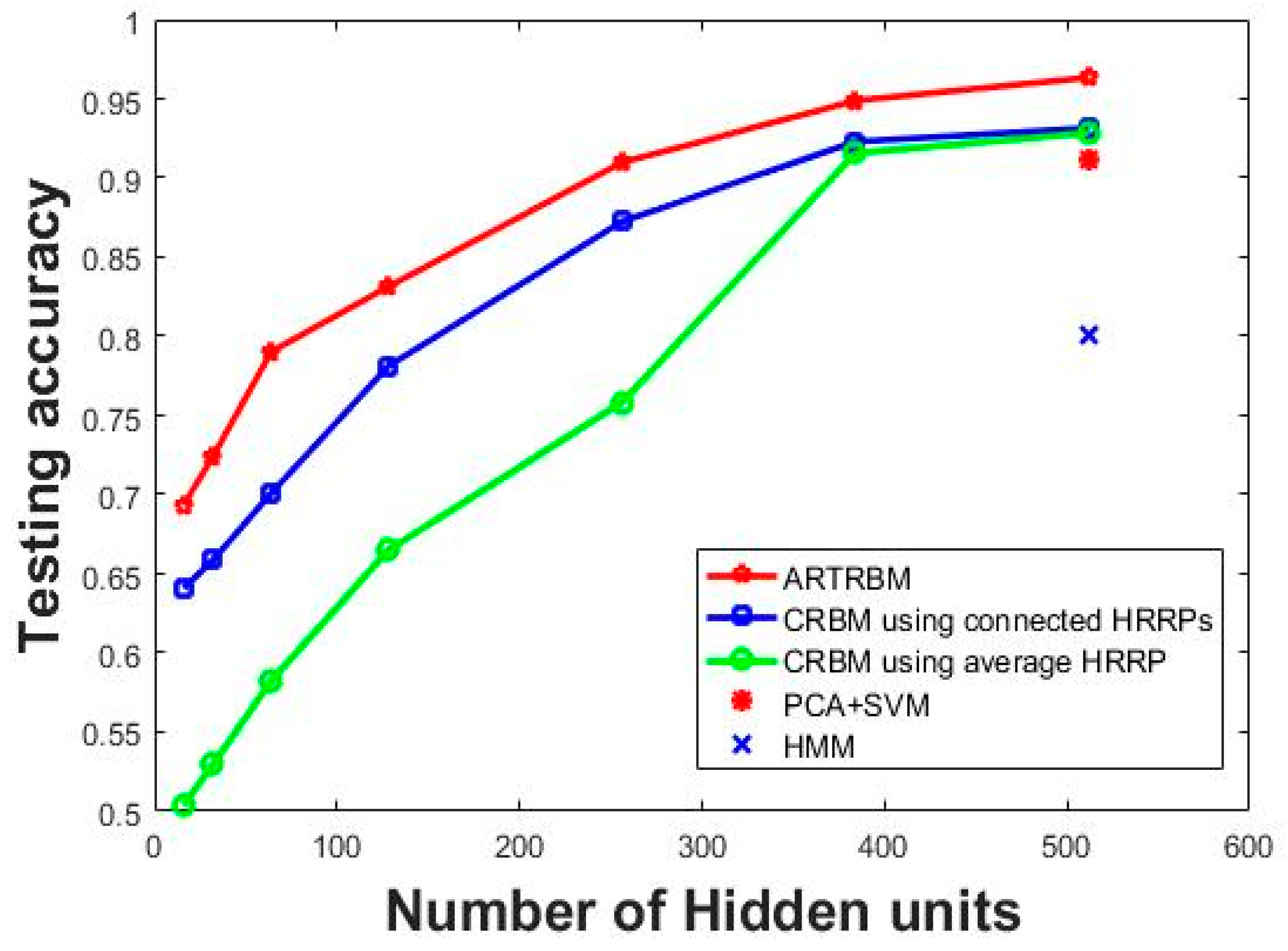
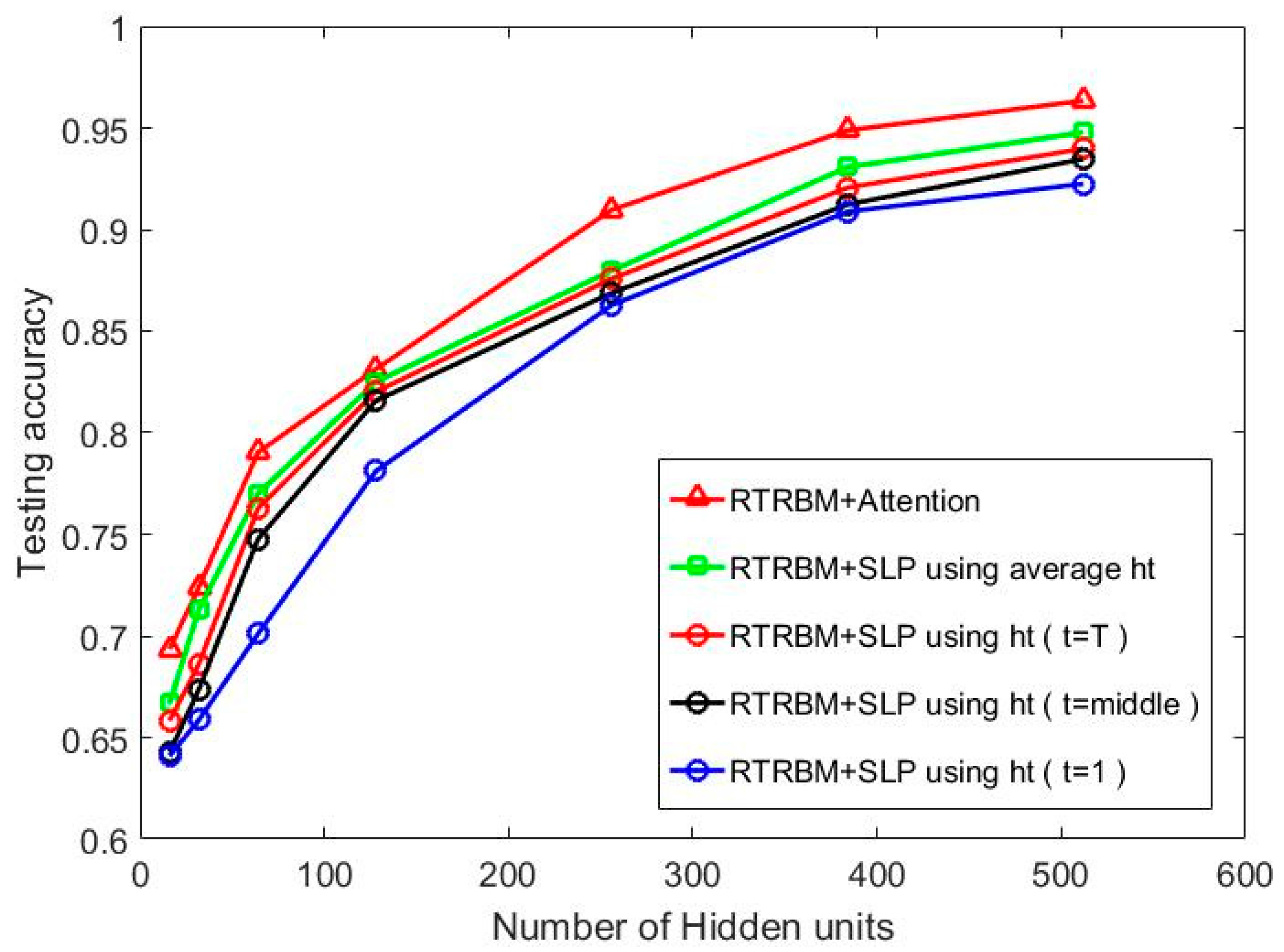
5.2.1. Experiment 1: Investigating the Influence of Hidden Layer Size on Recognition Performance
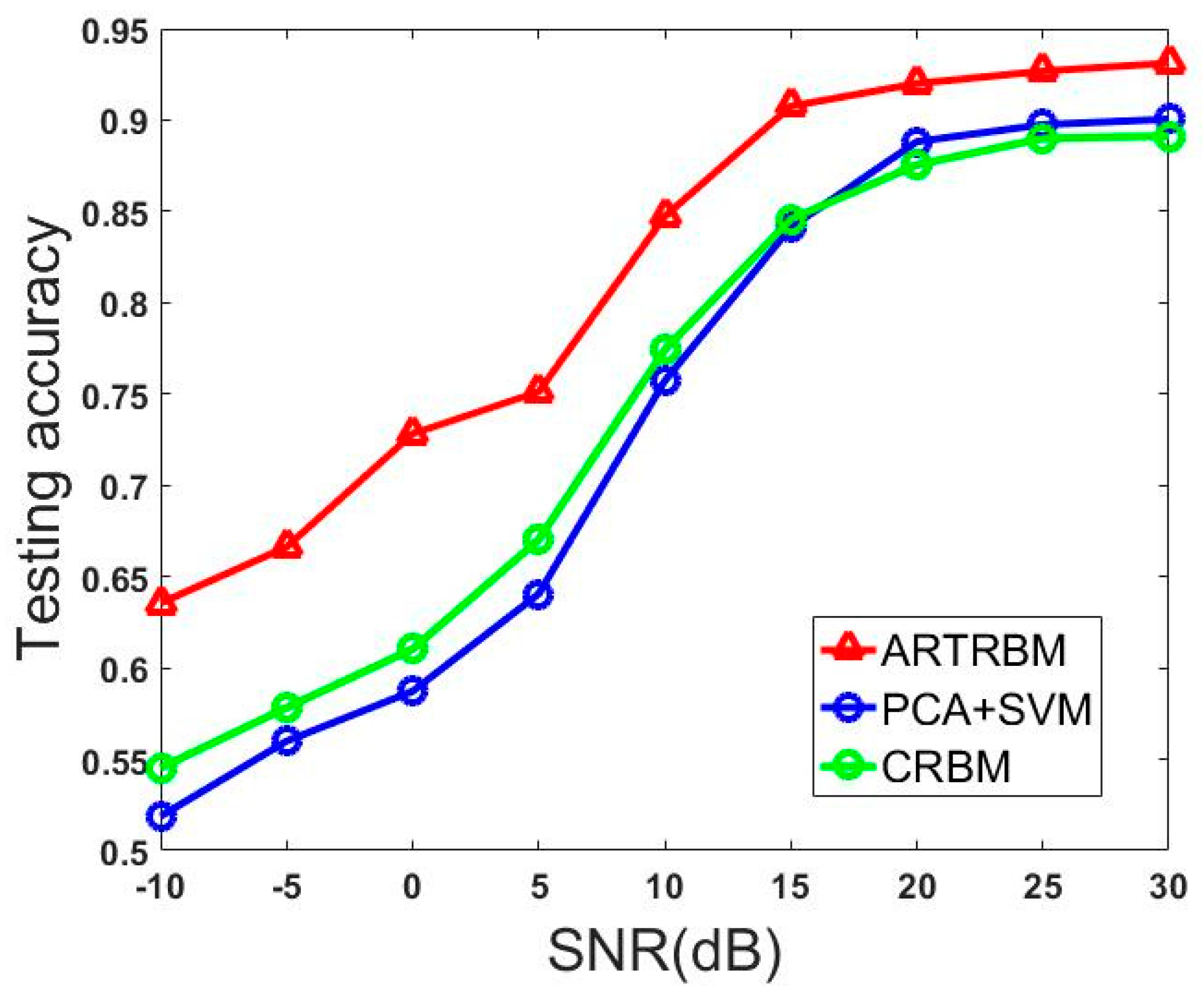
5.2.2. Experiment 2: Investigating the Influence of SNR on Recognition Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Du, L.; Liu, H.; Bao, Z. Radar HRRP statistical recognition: Parametric model and model selection. IEEE Trans. Signal Proc. 2008, 56, 1931–1944. [Google Scholar] [CrossRef]
- Webb, A.R. Gamma mixture models for target recognition. Pattern Recognit. 2000, 33, 2045–2054. [Google Scholar] [CrossRef]
- Du, L.; Wang, P.; Zhang, L.; He, H.; Liu, H. Robust statistical recognition and reconstruction scheme based on hierarchical Bayesian learning of HRR radar target signal. Expert Syst. Appl. 2015, 42, 5860–5873. [Google Scholar] [CrossRef]
- Zhou, D. Orthogonal maximum margin projection subspace for radar target HRRP recognition. Eurasip J. Wirel. Commun. Netw. 2016, 1, 72. [Google Scholar] [CrossRef]
- Zhang, J.; Bai, X. Study of the HRRP feature extraction in radar automatic target recognition. Syst. Eng. Electron. 2007, 29, 2047–2053. [Google Scholar]
- Du, L.; Liu, H.; Bao, Z.; Zhang, J. Radar automatic target recognition using complex high resolution range profiles. IET Radar Sonar Navi. 2007, 1, 18–26. [Google Scholar] [CrossRef]
- Feng, B.; Du, L.; Liu, H.W.; Li, F. Radar HRRP target recognition based on K-SVD algorithm. In Proceedings of the IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; pp. 642–645. [Google Scholar]
- Huether, B.M.; Gustafson, S.C.; Broussard, R.P. Wavelet preprocessing for high range resolution radar classification. IEEE Trans. 2001, 37, 1321–1332. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, X.D.; Hu, Y.F. Gabor Filter Approach to Joint Feature Extraction and Target Recognition. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 17–30. [Google Scholar]
- Hu, P.; Zhou, Z.; Liu, Q.; Li, F. The HMM-based modeling for the energy level prediction in wireless sensor networks. In Proceedings of the IEEE Conference on Industrial Electronics and Applications (ICIEA 2007), Harbin, China, 23–25 May 2007; pp. 2253–2258. [Google Scholar]
- Rossi, S.P.; Ciuonzo, D.; Ekman, T. HMM-based decision fusion in wireless sensor networks with noncoherent multiple access. IEEE Commun. Lett. 2015, 19, 871–874. [Google Scholar] [CrossRef]
- Albrecht, T.W.; Gustafson, S.C. Hidden Markov models for classifying SAR target images. Def. Secur. Int. Soc. Opt. Photonics 2004, 5427, 302–308. [Google Scholar]
- Liao, X.; Runkle, P.; Carin, L. Identification of ground targets from sequential high range resolution radar signatures. IEEE Trans. 2002, 38, 1230–1242. [Google Scholar]
- Zhu, F.; Zhang, X.D.; Hu, Y.F.; Xie, D. Nonstationary hidden Markov models for multiaspect discriminative feature extraction from radar targets. IEEE Trans. Signal Proc. 2007, 55, 2203–2214. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V.; Eldar, Y.C. Cognitive Radar Antenna Selection via Deep Learning. arXiv, 2018; arXiv:1802.09736. [Google Scholar]
- Su, B.; Lu, S. Accurate scene text recognition based on recurrent neural network. In Proceedings of the 12th Asia Conference on Computer Vision, Singapore, 1−5 November 2014; pp. 35–48. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Danvers, MA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Hinton, G.E.; Taylor, G.W. The Recurrent Temporal Restricted Boltzmann Machine. In Proceedings of the 25th International Conference on Machine Learning (ICML), Helsinki, Finland, 5–9 July 2008; pp. 536–543. [Google Scholar]
- Cherla, S.; Tran, S.N.; Garcez, A.D.A.; Weyde, T. Discriminative Learning and Inference in the Recurrent Temporal RBM for Melody Modelling. In Proceedings of the International Joint Coference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–8. [Google Scholar]
- Mittelman, R.; Kuipers, B.; Savarese, S.; Lee, H. Structured Recurrent Temporal Restricted Boltzmann Machines. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1647–1655. [Google Scholar]
- Sutskever, I.; Hinton, G. Learning Multilevel Distributed Representations for High Dimentional Sequences. In Proceedings of the Eleventh International Conference on Artificial Intelegence and Statistics, Toronto, ON, Canada, 21−24 March 2007; pp. 548–555. [Google Scholar]
- Boulanger-Lewandowski, N.; Bengio, Y.; Vincent, P. Modeling Temporal Dependencies in High-Dimensional Sequences: Application to Polyphonic Music Generation and Transcription. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 27 June–3 July 2012. [Google Scholar]
- Martens, J.; Sutskever, I. Learning recurrent neural networks with Hessian-free optimization. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 1033–1040. [Google Scholar]
- Smolensky, P. Information processing in dynamical systems: Foundations of harmony theory. Parallel Distrib. Exp. Microstruct. Found 1986, 1, 194–281. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a620727.pdf (accessed on 5 March 2018).
- Fischer, A.; Igel, C. Training restricted Boltzmann machines: An introduction Pattern Recognition. Pattern Recognit. 2014, 47, 25–39. [Google Scholar] [CrossRef]
- Larochelle, H.; Bengio, Y. Classification using Discriminative Restricted Boltzmann Machines. In Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 5–9 July 2008; pp. 536–543. [Google Scholar]
- Salakhutdinov, R.; Mnih, A.; Hinton, G. Restricted Boltzmann Machines for collaborative filtering. In Proceedings of the 24th international conference on Machine learning, Corvalis, OR, USA, 20–24 June 2007; pp. 791–798. [Google Scholar]
- Chorowski, J.; Bahdanau, D.; Serdyuk, D.; Cho, K.; Bengio, Y. Attention Based Models for Speech Recognition. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Mnih, V.; Heess, N.; Graves, A. Recurrent models of visual attention. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2204–2212. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jiontly to Align and Translate. arXiv, 2014; arXiv:1409.0473. [Google Scholar]
- Luong, M.; Manning, C.D. Effective Approaches to Attention based Machine Translation. arXiv, 2015; arXiv:1508.04025. [Google Scholar]
- Yin, W.; Ebert, S.; Schütze, H. Attention-Based Convolutional Neural Network for Machine Comprehension. arXiv, 2016; arXiv:1602.04341. [Google Scholar]
- Dhingra, B.; Liu, H.; Cohen, W.; Salakhutdinov, R. Gated-Attention Readers for Text Comprehension. arXiv, 2016; arXiv:1606.01549. [Google Scholar]
- Wang, L.; Cao, Z.; De Melo, G.; Liu, Z. Relation Classification via Multi-Level Attention CNNs. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, Berlin, Germany, 7–12 August 2016; pp. 1298–1307. [Google Scholar]
- Zhou, P.; Shi, W.; Tian, J.; Qi, Z.; Li, B.; Hao, H.; Xu, B. Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, Berlin, Germany, 7–12 August 2016; Volume 2, pp. 207–212. [Google Scholar]
- MSTAR (Public) Targets: T-72, BMP-2, BTR-70, SLICY. Available online: http://www.mbvlab.wpafb.af.mil/public/MBVDATA (accessed on 2 March 2018).
- Hinton, G.E. A practical guide to training restricted Boltzmann machines. In Neural Networks: Tricks of the Trade, 2nd ed.; Springer: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2012; pp. 599–619. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Odense, S.; Edwards, R. Universal Approximation Results for the Temporal Restricted Boltzmann Machine and Recurrent Temporal Restricted Boltzmann Machine. J. Mach. Learn. Res. 2016, 17, 1–21. [Google Scholar]
- Tieleman, T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 5–9 July 2008; pp. 1064–1071. [Google Scholar]
- Ghader, H.; Monz, C. What does Attention in Neural Machine Translation Pay Attention to. Available online: https://arxiv.org/pdf/1710.03348 (accessed on 7 March 2018).
- Zhao, F.; Liu, Y.; Huo, K.; Zhang, S.; Zhang, Z. Rarar HRRP Target Recognition Based on Stacked Autoencoder and Extreme Learning Machine. Sensors 2018, 18, 173. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Gao, X.; Zhang, Y.; Li, X. An Adaptive Feature Learning Model for Sequential Radar High Resolution Range Profile Recognition. Sensors 2017, 17, 1675. [Google Scholar] [CrossRef] [PubMed]
- Vaawani, A.; Shazeer, N.; Parmar, N. Attention is all you need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
| Number | Training Set | Size | Testing Set | Size |
|---|---|---|---|---|
| 1 | BMP2 (Sn_C9563) | 2330 | BMP2 (Sn_C9563) | 1950 |
| BMP2 (Sn_C9566) | 1960 | |||
| BMP2 (Sn_C21) | 1960 | |||
| 2 | T72 (Sn_132) | 2320 | T72 (Sn_132) | 1960 |
| T72 (Sn_812) | 1950 | |||
| T72 (Sn_S7) | 1910 | |||
| 3 | BTR70 (Sn_C71) | 2330 | BTR70 (Sn_C71) | 1960 |
| Sum | Training Set | 6980 | Testing Set | 13650 |
| Length of RTRBM | T = 5 | T = 10 | T = 15 | T = 20 | T = 25 | T = 30 |
|---|---|---|---|---|---|---|
| Hidden Units | 128 | 128 | 128 | 128 | 128 | 128 |
| BMP2 | 0.5496 | 0.5556 | 0.6649 | 0.6856 | 0.6900 | 0.6915 |
| T72 | 0.7472 | 0.8345 | 0.8575 | 0.8545 | 0.8723 | 0.8789 |
| BTR70 | 0.7594 | 0.8803 | 0.9368 | 0.9402 | 0.9402 | 0.9428 |
| Average Accuracy | 0.6854 | 0.7535 | 0.8197 | 0.8268 | 0.8341 | 0.8377 |
| Methods | Attention Based RTRBM | CRBM (Connected HRRPs) | CRBM (Average HRRP) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Targets | BMP2 | T72 | BTR70 | BMP2 | T72 | BTR70 | BMP2 | T72 | BTR70 |
| BMP2 | 0.9053 | 0.0717 | 0.0230 | 0.8461 | 0.0821 | 0.0718 | 0.8547 | 0.0819 | 0.0634 |
| T72 | 0.0125 | 0.9758 | 0.0117 | 0.0187 | 0.9726 | 0.0087 | 0.0295 | 0.9516 | 0.0189 |
| BTR70 | 0.0347 | 0 | 0.9653 | 0.0448 | 0.0052 | 0.9500 | 0.0525 | 0.0094 | 0.9381 |
| Av. Acc. | 0.9448 | 0.9229 | 0.9157 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gao, X.; Peng, X.; Ye, J.; Li, X. Attention-Based Recurrent Temporal Restricted Boltzmann Machine for Radar High Resolution Range Profile Sequence Recognition. Sensors 2018, 18, 1585. https://doi.org/10.3390/s18051585
Zhang Y, Gao X, Peng X, Ye J, Li X. Attention-Based Recurrent Temporal Restricted Boltzmann Machine for Radar High Resolution Range Profile Sequence Recognition. Sensors. 2018; 18(5):1585. https://doi.org/10.3390/s18051585
Chicago/Turabian StyleZhang, Yifan, Xunzhang Gao, Xuan Peng, Jiaqi Ye, and Xiang Li. 2018. "Attention-Based Recurrent Temporal Restricted Boltzmann Machine for Radar High Resolution Range Profile Sequence Recognition" Sensors 18, no. 5: 1585. https://doi.org/10.3390/s18051585
APA StyleZhang, Y., Gao, X., Peng, X., Ye, J., & Li, X. (2018). Attention-Based Recurrent Temporal Restricted Boltzmann Machine for Radar High Resolution Range Profile Sequence Recognition. Sensors, 18(5), 1585. https://doi.org/10.3390/s18051585





