Degree-of-Freedom Strengthened Cascade Array for DOD-DOA Estimation in MIMO Array Systems
Abstract
:1. Introduction
- A new array structure named cascade array is designed, which is essentially composed of one ULA and one non-uniform linear array. Through theoretical analysis, the difference co-array of the designed optimal cascade array is hole-free and can provide more DOFs than some state-of-the-art sensor array structures. That is to say, it manifests a strengthened resolving capability.
- We then apply the cascade array into bistatic MIMO array systems to achieve joint direction-of-departure (DOD) and DOA estimation for multiple targets localization. Furthermore, by parameterizing the orthogonal projector onto the null space of the equivalent joint steering matrix, a novel algorithm based on a reduced-dimensional weighted subspace fitting technique is proposed.
- The proposed algorithm transforms a two-dimensional estimation problem into a one-dimensional one. To do so, the DOD information can be acquired by MODE rooting [33,34], and the auto-paired DOA information can be extracted from the estimated receiving array manifold. The proposed algorithm avoids exhausted spectrum searching or tensor decomposition [19,34,35], thus it is computationally efficient.
2. Cascade Array
2.1. Difference Co-Array
2.2. Cascade Array Design
| N | Optimal and | The Number of DOFs |
| Even | ||
| Odd |
3. MIMO Array Systems with Cascade Array
3.1. Data Model
3.2. Two-Dimensional Difference Co-Array
3.3. Identifiability Analysis
4. Joint DOD and DOA Estimation
4.1. Weighted Subspace Fitting
4.2. Angle Estimation
4.3. Computational Complexity
5. Numerical Simulation
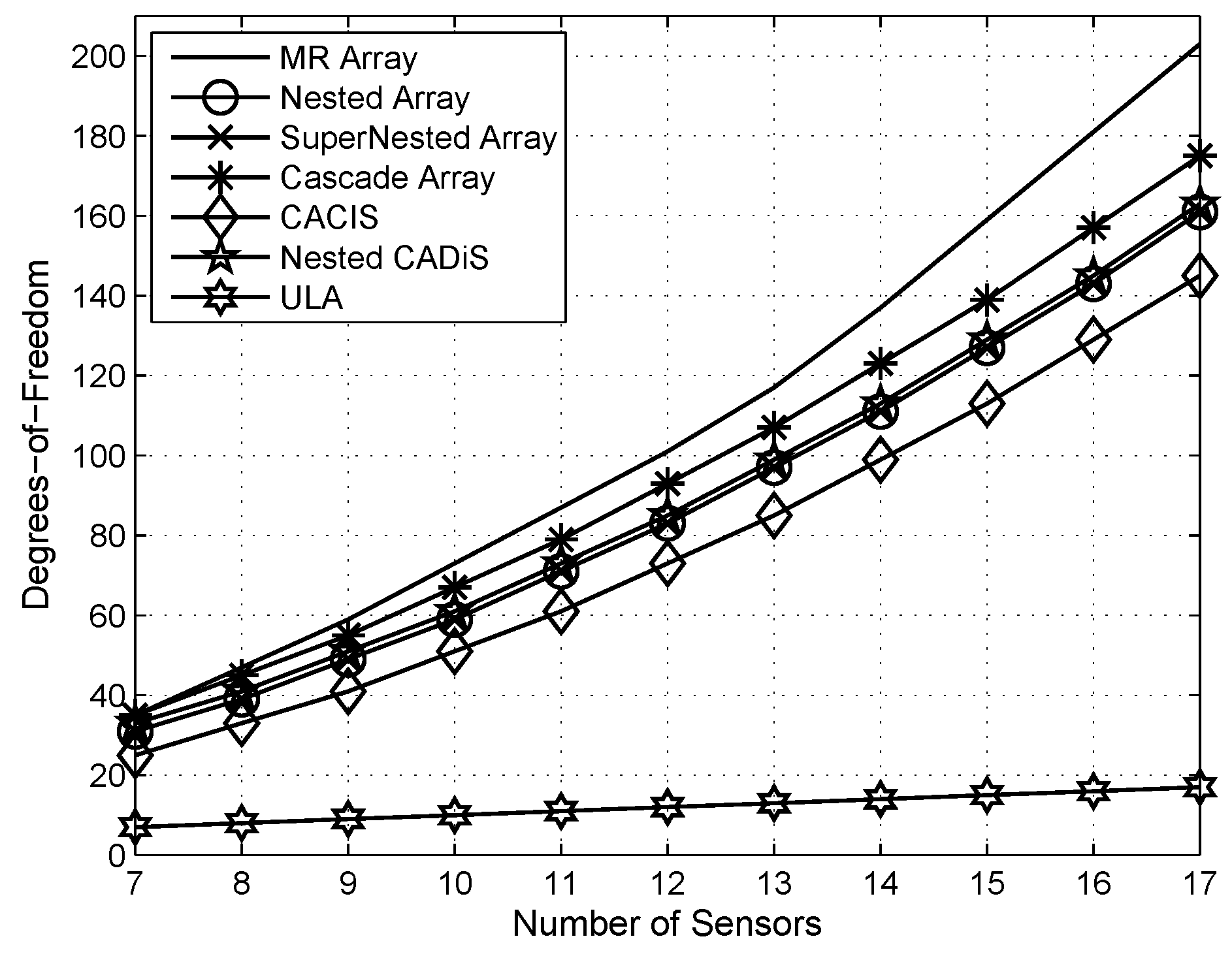
5.1. DOF Comparison
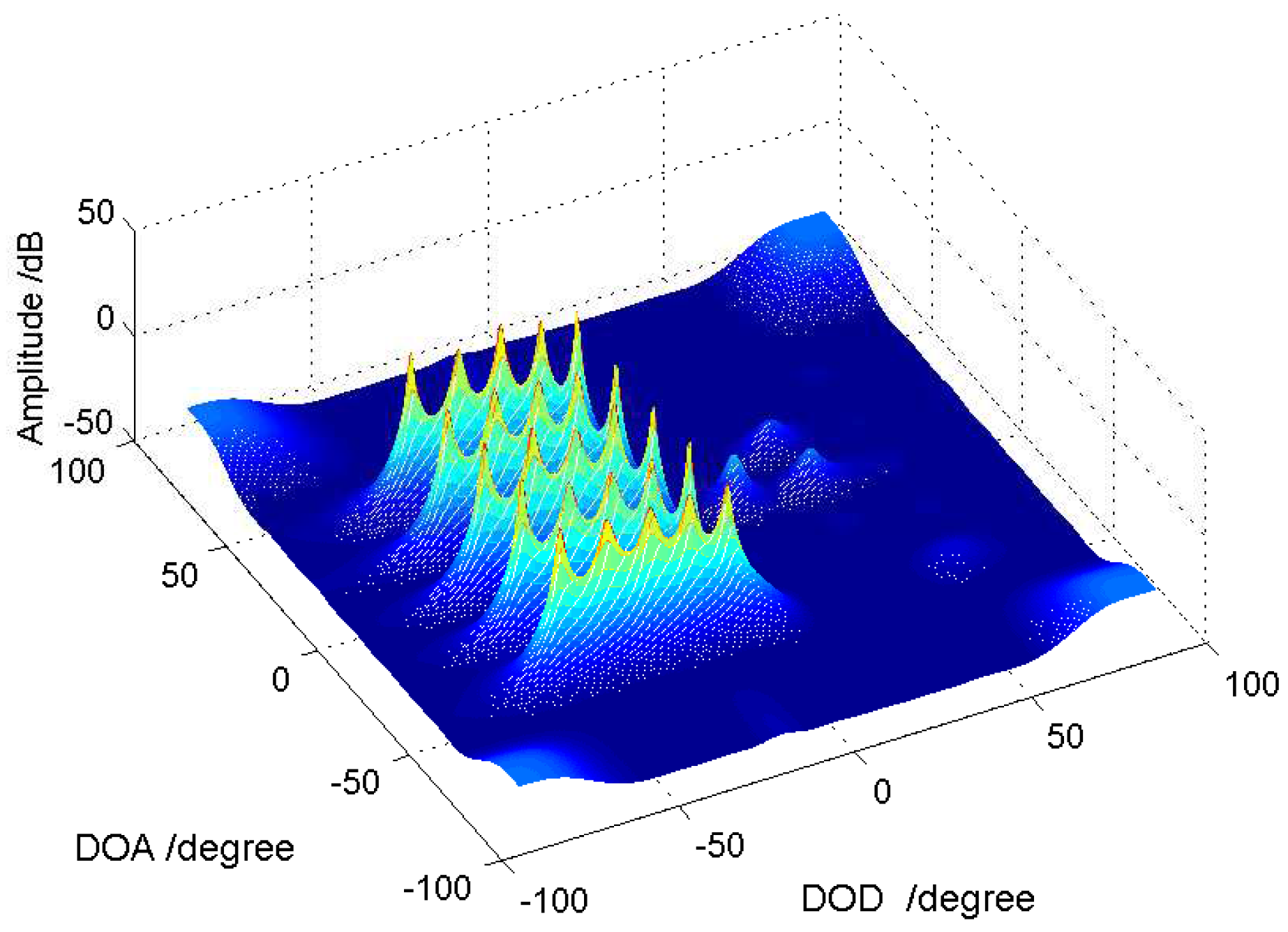
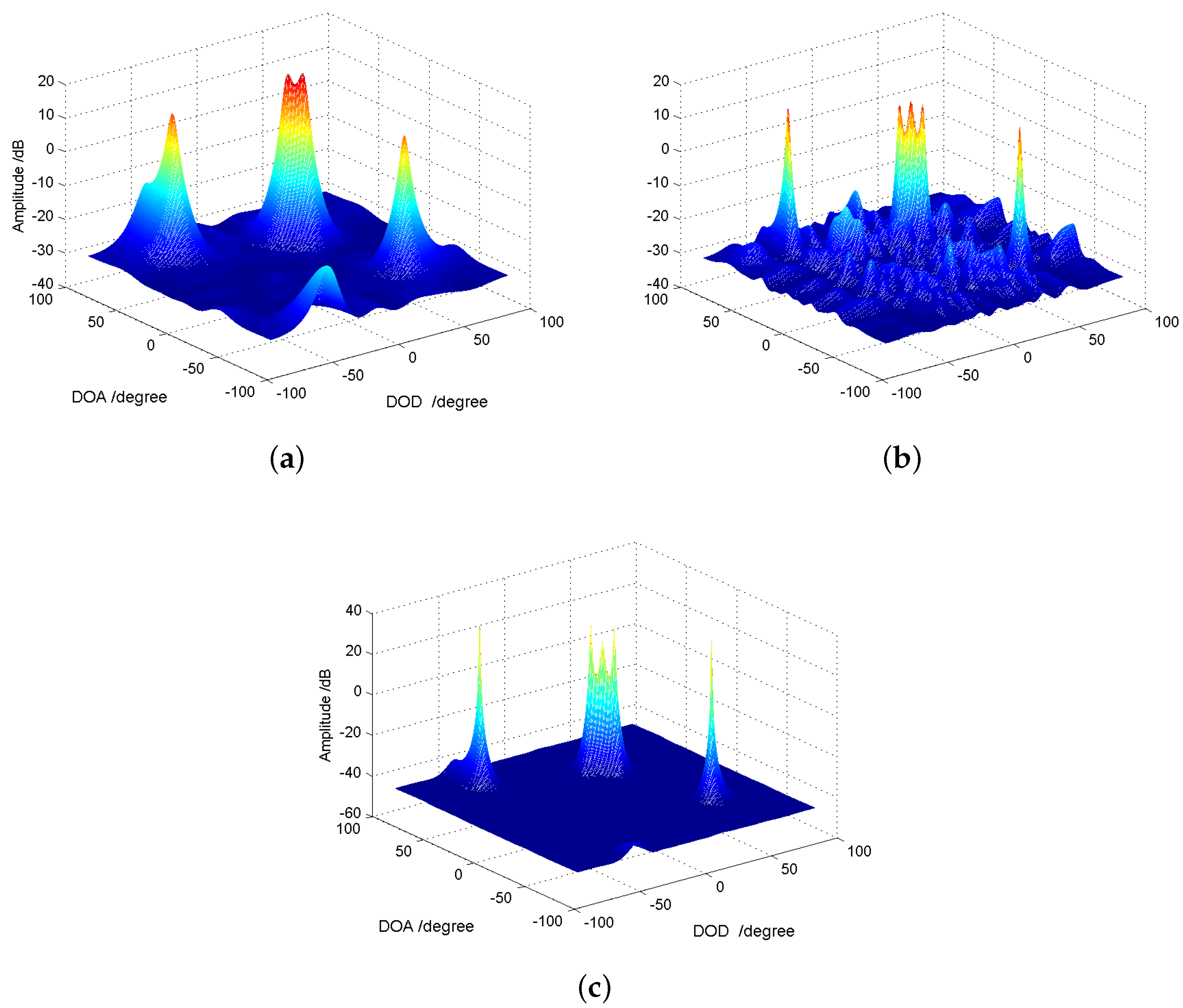
5.2. Identifiability Performance for Cascade Array
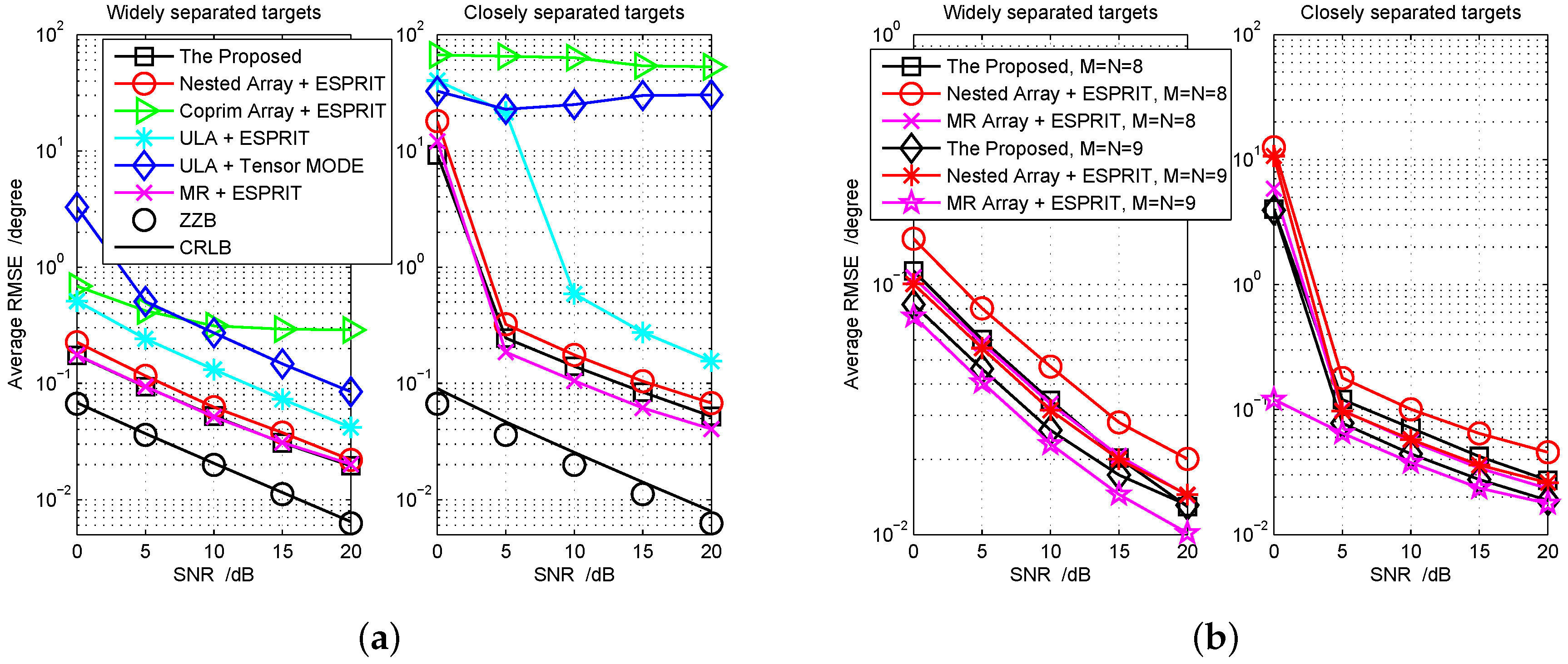
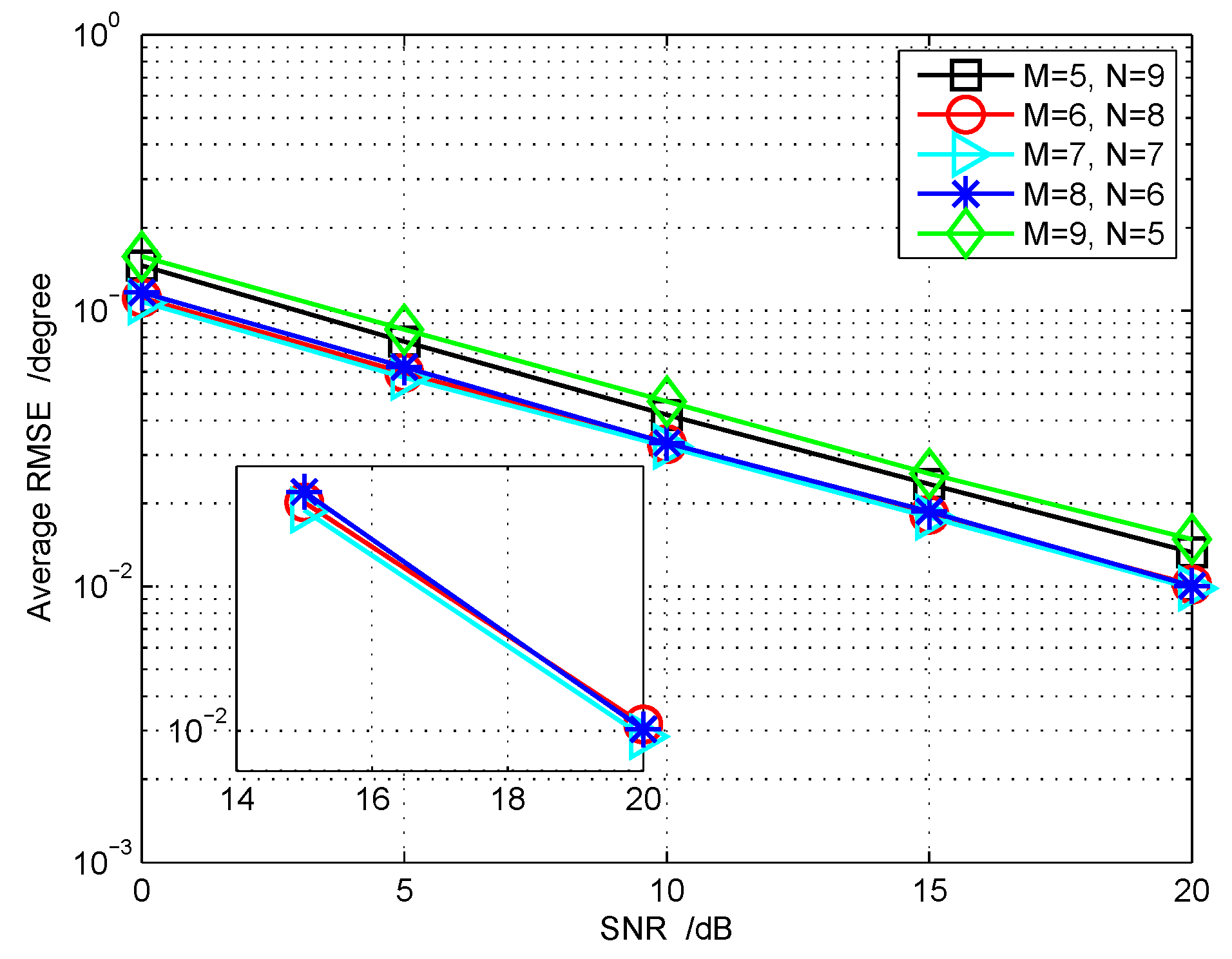
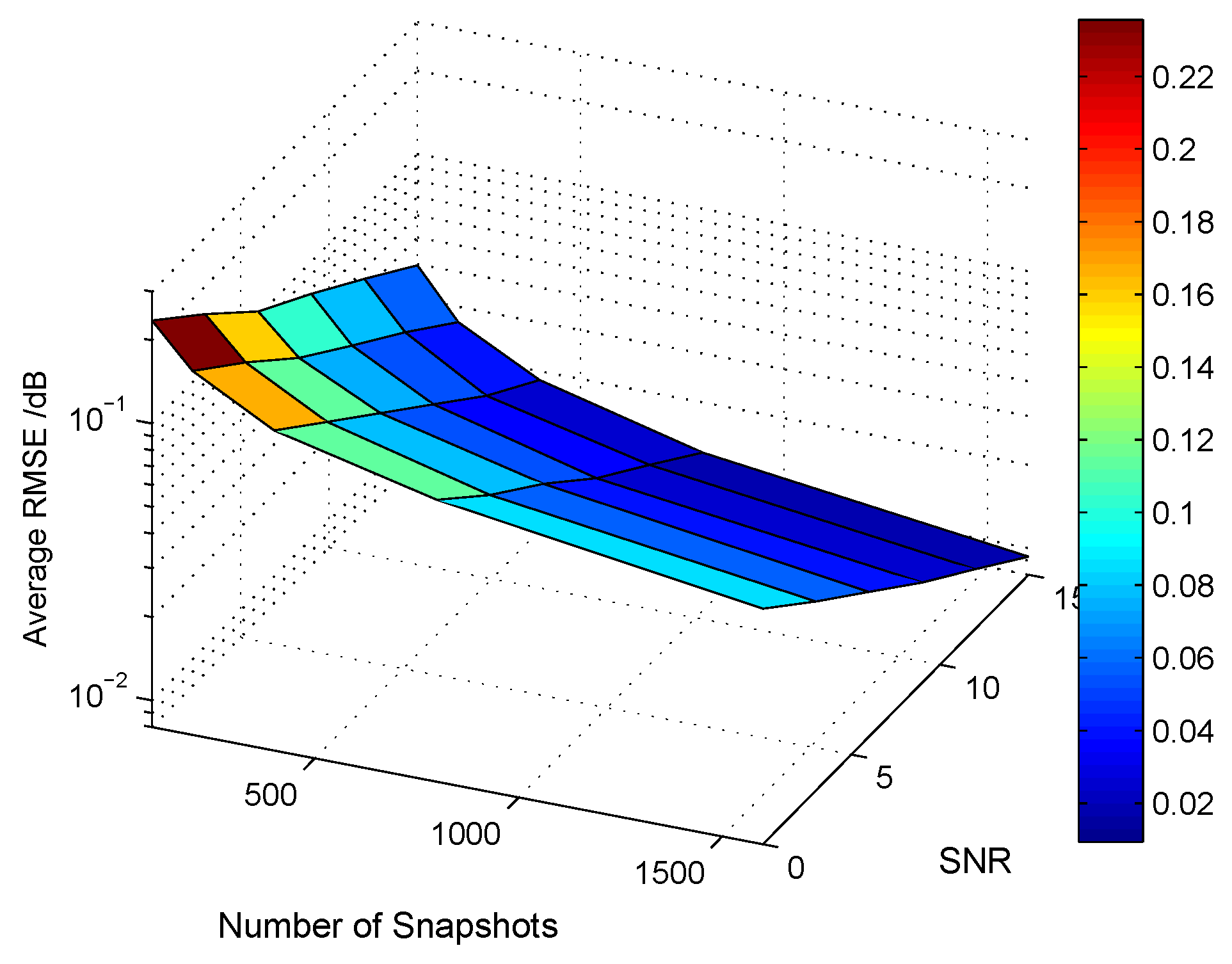
5.3. RMSE Performance for Joint DOD and DOA Estimation
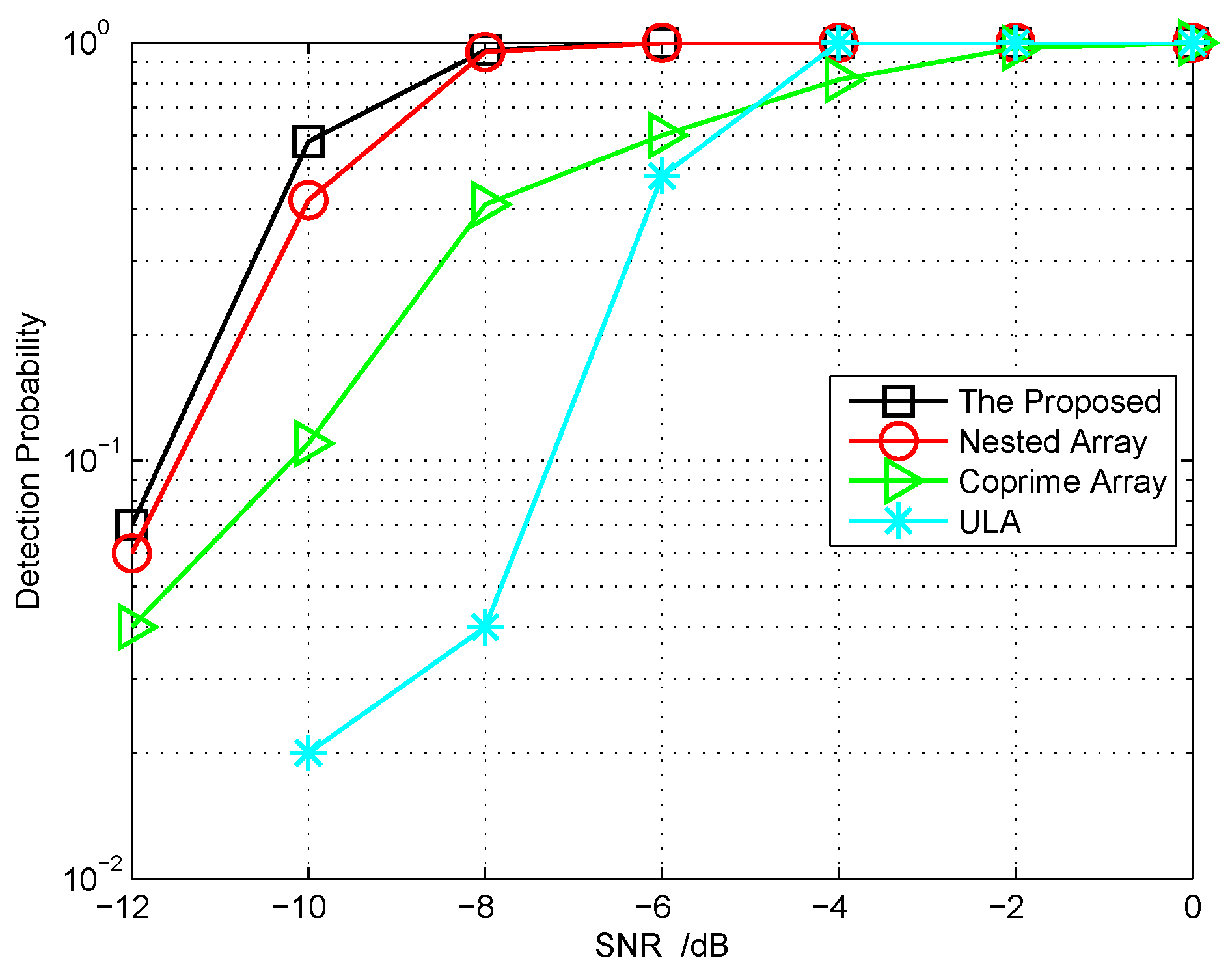
5.4. Other Related Performance
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The DOF of Cascade Co-Array
- If i belongs to the co-array, then its counterpart, i.e., , is also in the same co-array.
- is in the co-array that is determined by the first physical sensor or by the self-difference of any one of the physical sensors.
References
- Van Trees, H.L. Detection, Estimation and Modulation Theory, Part IV, Optimum Array Processing; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Lo, Y.T.; Lee, S.W. A Study of Space-tapered Arrays. IEEE Trans. Antennas Propag. 1966, 14, 22–30. [Google Scholar] [CrossRef]
- Willey, R. Space Tapering of Linear and Planner Arrays. IRE Trans. Antennas Propag. 1962, 10, 369–377. [Google Scholar] [CrossRef]
- Kim, Y.; Jaggard, D.L. The Fractal Random Array. Proc. IEEE 1986, 74, 1278–1280. [Google Scholar] [CrossRef]
- Mishra, K.V.; Shoshan, E.; Namer, M.; Meltsin, M.; Cohen, D.; Madmoni, R.; Dror, S.; Ifraimov, R.; Eldar, Y.C. Cognitive Sub-nyquist Hardware Prototype of a Collocated MIMO Radar. In Proceedings of the 2016 4th International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Aachen, Germany, 19–22 September 2016; pp. 56–60. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Wang, H.; Kaveh, M. Coherent Signal-Subspace Processing for the Detection and Estimation of Angles of Arrival of Multiple Wide-band Sources. IEEE Trans. Acous. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, Y.; Liu, J.; Yu, Z. Underdetermined Wideband DOA Estimation for Off-Grid Sources with Coprime Array Using Sparse Bayesian Learning. Sensors 2018, 18, 253. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.-K.; Hsieh, T.-H.; Chi, C.-Y. DOA Estimation of Quasi-stationary Signals with Less Sensors than Sources and Unknown Spatial Noise Covariance: A Khatri–Rao Subspace Approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Pillai, S.; Haber, F. Statistical Analysis of a High Resolution Spatial Spectrum Estimator Utilizing an Augmented Covariance Matrix. IEEE Trans. Acous. Speech Signal Process. 1987, 35, 1517–1523. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing with Co-prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P.P. Super Nested Arrays: Linear Sparse Arrays with Reduced Mutual Coupling-Part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Li, B.; Li, X.; Zhang, R.; Tang, W.; Li, S. Joint Power Allocation and Adaptive Random Network Coding in Wireless Multicast Networks. IEEE Trans. Commun. 2017, 66, 1520–1533. [Google Scholar] [CrossRef]
- Yao, B.B.; Wang, W.J.; Yin, Q.Y. DOD and DOA Estimation in Bistatic Non-uniform Multiple-input Multiple-output Radar Systems. IEEE Commun. Lett. 2012, 16, 1796–1799. [Google Scholar] [CrossRef]
- Nion, D.; Sidiropoulos, N.D. Tensor Algebra and Multidimensional Harmonic Retrieval in Signal Processing for MIMO Radar. IEEE Trans. Signal Process. 2010, 58, 5693–5705. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy Linear Arrays. IEEE Trans. Antennas Propag. 1986, 16, 172–175. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G.; Zoubir, A.M. Generalized Coprime Sampling of Toeplitz Matrices for Spectrum Estimation. IEEE Trans. Signal Process. 2017, 65, 81–94. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Romano, G.; Solimene, R. Performance Analysis of Time-Reversal MUSIC. IEEE Trans. Signal Proc. 2015, 63, 2650–2662. [Google Scholar] [CrossRef]
- Gruber, F.K.; Marengo, E.A.; Devaney, A.J. Time-reversal Imaging with Multiple Signal Classification Considering Multiple Scattering Between the Targets. J. Acoust. Soc. Am. 2004, 115, 3042–3047. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Salvo Rossi, P. Noncolocated Time-Reversal MUSIC: High-SNR Distribution of Null Spectrum. IEEE Signal Proc. Lett. 2017, 24, 397–401. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P.; Li, J. SPICE: A Sparse Covariance-Based Estimation Method for Array Processing. IEEE Trans. Signal Process. 2011, 59, 629–638. [Google Scholar] [CrossRef]
- Cai, S.; Shi, X.; Zhu, H. Direction-Of-Arrival Estimation and Tracking Based on a Sequential Implementation of C-SPICE with an Off-Grid Model. Sensors 2017, 17, 2718. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.; Eldar, Y.C.; Nehorai, A. Direction of Arrival Estimation Using Co-Prime Arrays: A Super Resolution View point. IEEE Trans. Signal Process. 2014, 62, 5565–5576. [Google Scholar] [CrossRef]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial Compressive Sensing in MIMO Radar with Random Arrays. In Proceedings of the 2012 46th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2012; pp. 1–6. [Google Scholar]
- Mishra, K.V.; Hahane, I.; Jaufmann, A.; Eldar, Y.C. High Spatial Resolution Radar using Thinned Arrays. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1119–1124. [Google Scholar]
- Liu, C.L.; Vaidyanathan, P.P. Tensor MUSIC in Multidimensional Sparse Arrays. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 1783–1787. [Google Scholar]
- Zheng, W.; Zhang, X.; Zhai, H. A Generalized Coprime Planar Array Geometry for Two-dimensional DOA Estimation. IEEE Commun. Lett. 2017, 21, 1075–1078. [Google Scholar] [CrossRef]
- Sun, F.; Gao, B.; Chen, L.; Lan, P. A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays. Sensors 2016, 16, 1367. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Stoica, P.; Liu, Z.S. Comparative Study of IQML and MODE Direction-of-Arrival Estimators. IEEE Trans. Signal Process. 1998, 46, 149–160. [Google Scholar]
- Wen, F.; So, H.C. Tensor-MODE for Multi-dimensional Harmonic Retrieval with Coherent Sources. Signal Process. 2015, 108, 530–534. [Google Scholar] [CrossRef]
- Wen, F.; Liang, C. Improved Tensor-MODE based Direction-of-Arrival Estimation for Massive MIMO system. IEEE Commun. Lett. 2015, 19, 2182–2185. [Google Scholar] [CrossRef]
- Zhang, W.L.; Gao, F.F.; Jin, S.; Lin, H. Frequency Synchronization for Uplink Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2018, 17, 235–249. [Google Scholar] [CrossRef]
- Brewer, J.W. Kronecker Products and Matrix Calculus in System Theory. IEEE Trans. Circuits Syst. 1987, CAS-25, 772–781. [Google Scholar]
- Sidiropoulos, N.D.; Liu, X. Identifiability Results for Blind Beamforming in Incoherent Multipath with Small Delay Spread. IEEE Trans. Signal Process. 2001, 49, 228–236. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X. An Eigenvector-based Approach for Multidimensional Frequency Estimation with Improved Identifiability. IEEE Trans. Signal Process. 2006, 54, 4543–4556. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K.C. Novel Eigenanalysis Method for Direction Estimation. Proc. Inst. Elect. Eng. F 1990, 137, 19–26. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K. Maximum Likelihood Methods for Direction-of-Arrival Estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1132–1143. [Google Scholar] [CrossRef]
- See, C.M.; Gershman, A.B. Direction-of-Arrival Estimation in Partly Calibrated Subarray-based Sensor Arrays. IEEE Trans. Signal Process. 2004, 52, 329–338. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of Departure (DOD) and Direction of Arrival (DOA) Estimation in MIMO Radar with Reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computation, 3rd ed.; John Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Chiriac, V.M.; He, Q.; Haimovich, A.M.; Blum, R.S. Ziv-Zakai Bound for Joint Parameter Estimation in MIMO Radar Systems. IEEE Trans. Signal Process. 2015, 63, 4956–4968. [Google Scholar] [CrossRef]
- Bell, K.L.; Steinberg, Y.; Ephraim, Y.; Van Trees, H.L. Extended Ziv-Zakai lower bound for vector parameter estimation. IEEE Trans. Inf. Theory 1997, 43, 624–637. [Google Scholar] [CrossRef]
- Wang, M.; Nehorai, A. Coarrays, MUSIC, and the Cramer-Rao Bound. IEEE Trans. Signal Process. 2017, 65, 933–946. [Google Scholar] [CrossRef]
- Mishra, K.V.; Eldar, Y.C. Performance of time delay estimation in a cognitive radar. In Proceedings of the 2017 42nd IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 3141–3145. [Google Scholar]
- He, Z.; Cichocke, A.; Xie, S.; Choi, K. Detecting the Number of Clusters in N-way Probabilistic Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2006–2021. [Google Scholar] [PubMed]


| Operation | Dimension Size | Required Flops |
|---|---|---|
| Eigenvalue Decompositon of : and | ||
| Matrix Partition in Label (34) | ||
| Minimization of | ||
| Estimation | ||
| Total flops |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, B.; Dong, Z.; Zhang, W.; Wang, W.; Wu, Q. Degree-of-Freedom Strengthened Cascade Array for DOD-DOA Estimation in MIMO Array Systems. Sensors 2018, 18, 1557. https://doi.org/10.3390/s18051557
Yao B, Dong Z, Zhang W, Wang W, Wu Q. Degree-of-Freedom Strengthened Cascade Array for DOD-DOA Estimation in MIMO Array Systems. Sensors. 2018; 18(5):1557. https://doi.org/10.3390/s18051557
Chicago/Turabian StyleYao, Bobin, Zhi Dong, Weile Zhang, Wei Wang, and Qisheng Wu. 2018. "Degree-of-Freedom Strengthened Cascade Array for DOD-DOA Estimation in MIMO Array Systems" Sensors 18, no. 5: 1557. https://doi.org/10.3390/s18051557
APA StyleYao, B., Dong, Z., Zhang, W., Wang, W., & Wu, Q. (2018). Degree-of-Freedom Strengthened Cascade Array for DOD-DOA Estimation in MIMO Array Systems. Sensors, 18(5), 1557. https://doi.org/10.3390/s18051557





