Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution †
Abstract
:1. Introduction
2. Background
2.1. -Divergence Cost Function
2.1.1. Least Square Distance
2.1.2. Kullback–Liebler Divergence
2.2. Auxiliary Cost Function of Fractional β-Divergence for Matrix Factors Time–Frequency Deconvolution
2.3. Auxiliary Update Function of “Fractional” β-Divergence
2.4. Sparsity-Aware Optimization
2.5. Optimizing the Fractional β
| Algorithm 1. Overview Proposed Algorithm |
|
3. Experiments, Results and Analysis
3.1. Experimental Set-Up
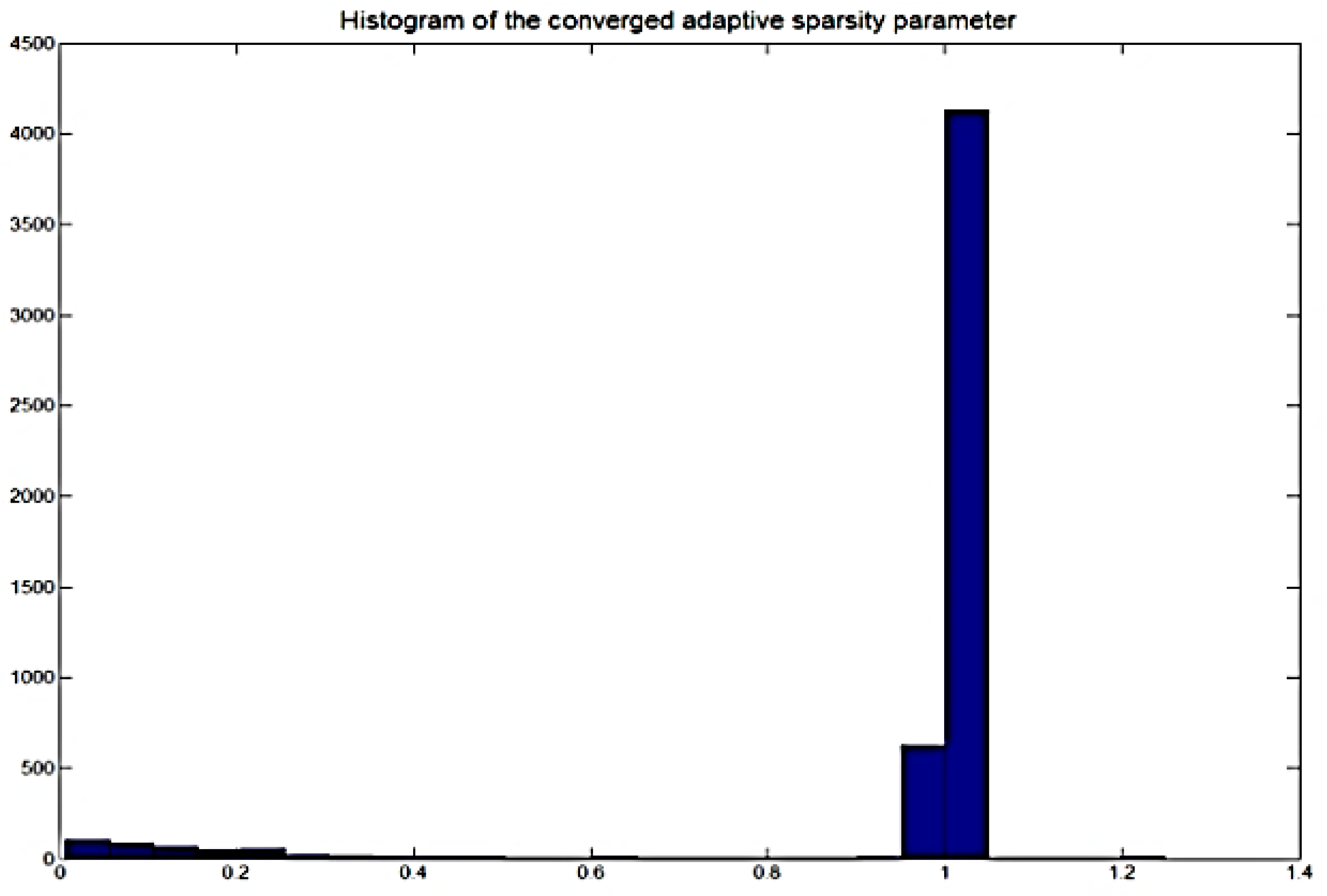
3.2. Analysis of Adaptive and Fixed Sparsity
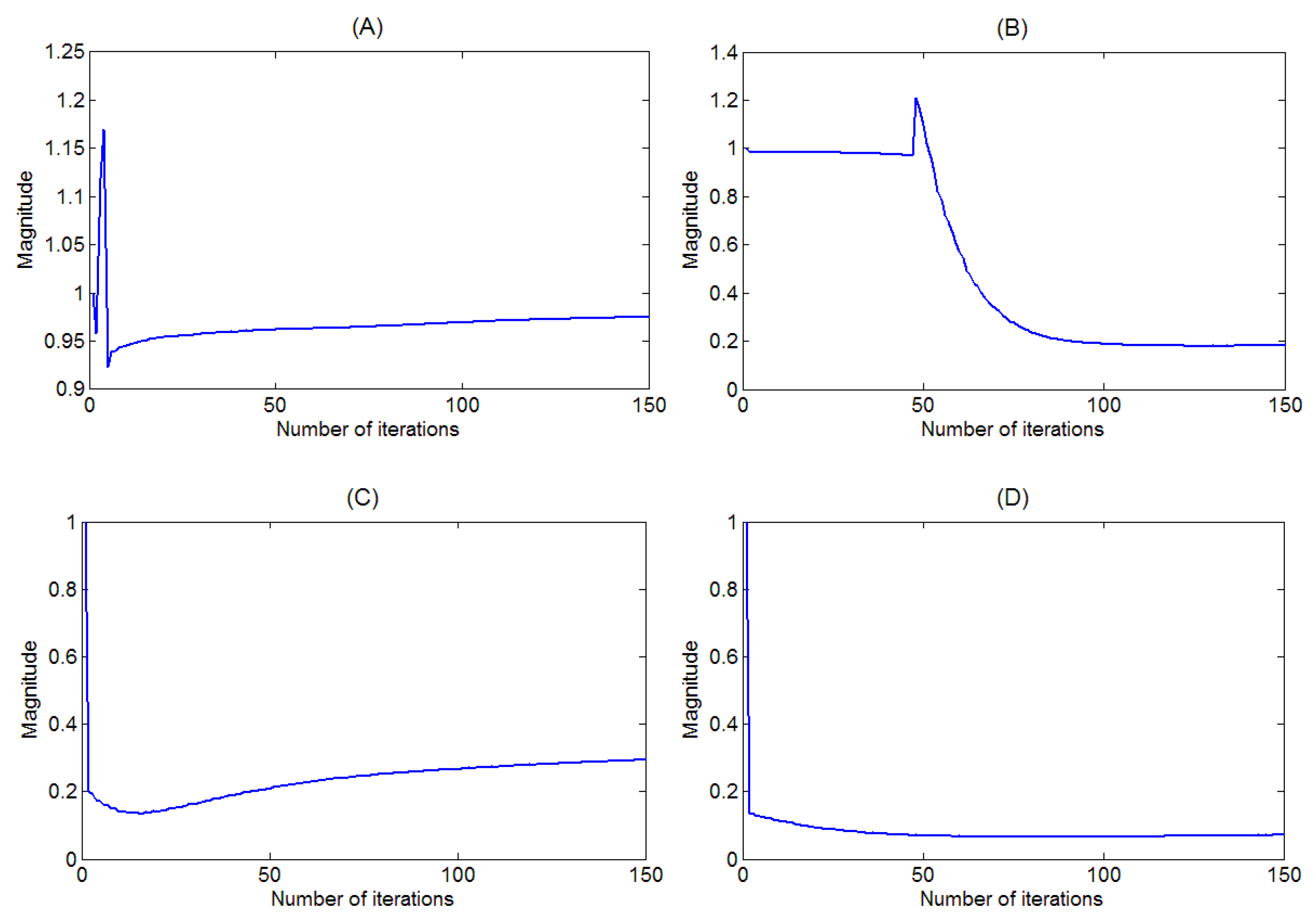
3.3. Adaptive Behavior of Sparsity Parameter
- Case (1):
- No sparseness .
- Case (2):
- Uniform and constant sparseness corresponding to the mean of the first Gaussian distribution of the GMM.
- Case (3):
- Uniform and constant sparseness corresponding to the mean of the second Gaussian distribution of the GMM.
- Case (4):
- Uniform and constant sparseness corresponding to the global mean of the converged adaptive sparsity.
- Case (5):
- Uniform and constant sparseness corresponding to the global mean of the converged adaptive sparsity.
- Case (6):
- Maximum likelihood adaptive sparseness, i.e., Equation (55).
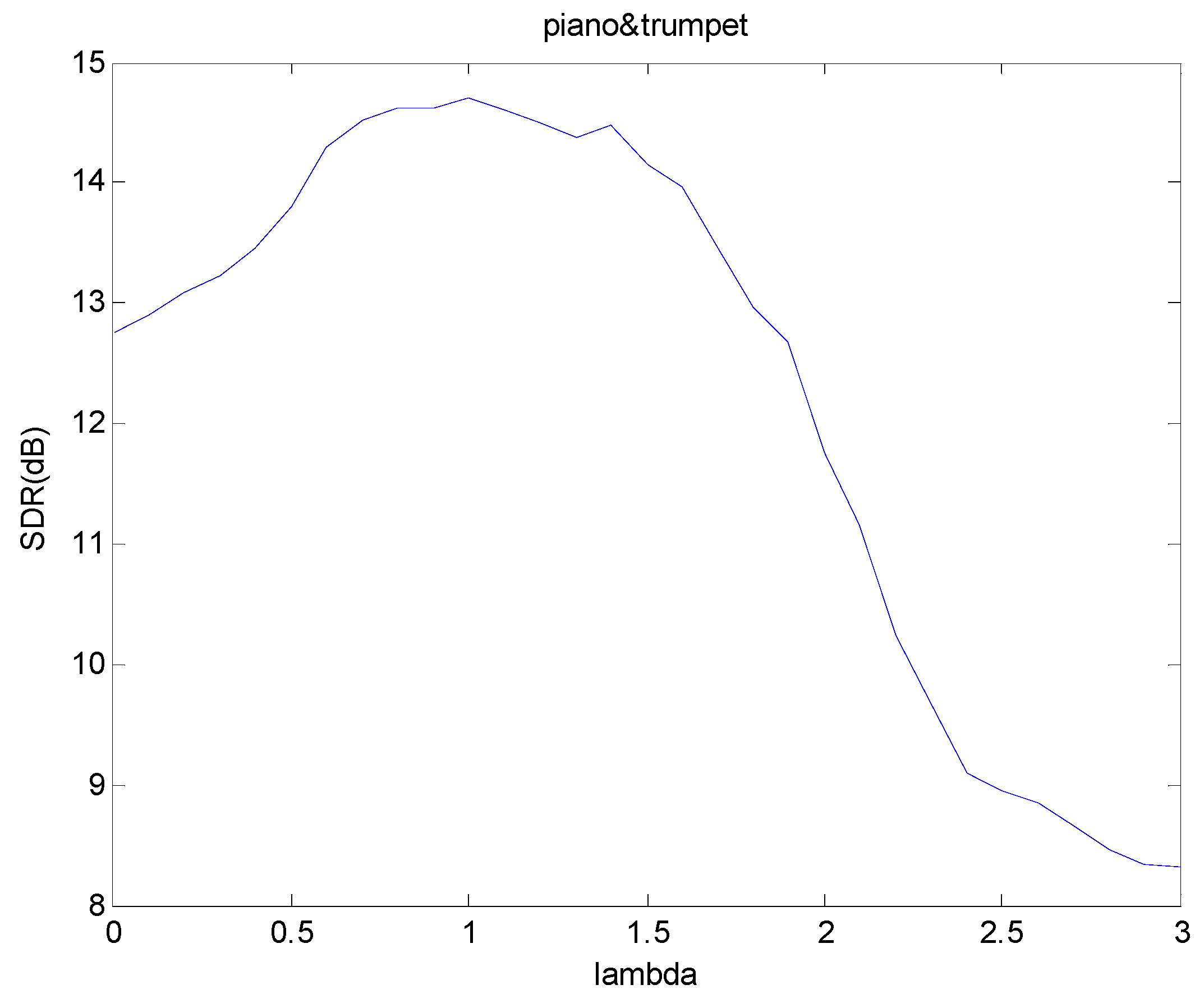
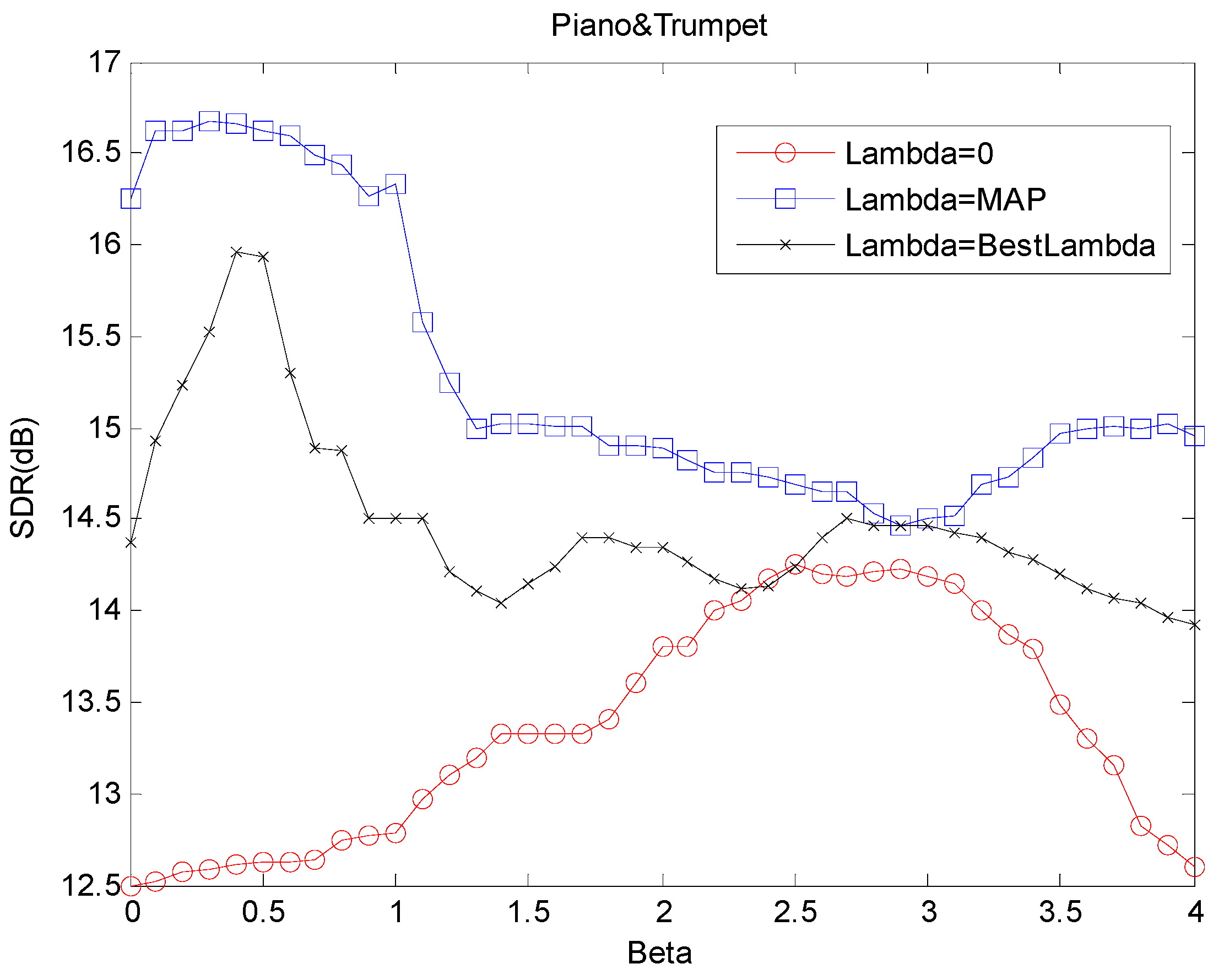
3.4. Analysis of Fractional β-Divergence
3.5. Comparison with Other Nonnegative Factorization Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mitianoudis, N.; Davies, M.E. Audio source separation: Solutions and problems. Int. J. Adapt. Control Signal Process. 2004, 18, 299–314. [Google Scholar] [CrossRef]
- Gao, P.; Woo, W.L.; Dlay, S.S. Nonlinear signal separation for multi-nonlinearity constrained mixing model. IEEE Trans. Neural Netw. 2006, 17, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S.C.; Cichocki, A.; Ribas, L.C. An iterative inversion approach to blind source separation. IEEE Trans. Neural Netw. 2000, 11, 1423–1437. [Google Scholar]
- Gao, B.; Woo, W.L.; Dlay, S.S. Single channel blind source separation using EMD-subband ariable regularized sparse features. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 961–976. [Google Scholar] [CrossRef]
- Zha, D.; Qiu, T. A new blind source separation method based on fractional lower-order statistics. Int. J. Adapt. Control Signal Process. 2006, 20, 213–223. [Google Scholar] [CrossRef]
- Ozerov, A.; Févotte, C. Multichannel nonnegative matrix factorization in convolutive mixtures for audio source separation. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 550–563. [Google Scholar] [CrossRef]
- Zhang, J.; Woo, W.L.; Dlay, S.S. Blind source separation of post-nonlinear convolutive mixture. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 2311–2330. [Google Scholar] [CrossRef]
- Moir, T.J.; Harris, J.I. Decorrelation of multiple non-stationary sources using a multivariable crosstalk-resistant adaptive noise canceller. Int. J. Adapt. Control Signal Process. 2013, 27, 349–367. [Google Scholar] [CrossRef]
- Djendi, M. A new two-microphone Gauss-Seidel pseudo affine projection algorithm for speech quality enhancement. Int. J. Adapt. Control Signal Process. 2017, 31, 1162–1183. [Google Scholar] [CrossRef]
- He, X.; He, F.; Zhu, T. Large-scale super-Gaussian sources separation using Fast-ICA with rational nonlinearities. Int. J. Adapt. Control Signal Process. 2017, 31, 379–397. [Google Scholar] [CrossRef]
- Kemiha, M.; Kacha, A. Complex blind source separation. Circuits Syst. Signal Process. 2017, 36, 1–18. [Google Scholar] [CrossRef]
- Moazzen, I.; Agathoklis, P. A multistage space–time equalizer for blind source separation. Circuits Syst. Signal Process. 2016, 35, 185–209. [Google Scholar] [CrossRef]
- Kumar, V.A.; Rao, C.V.R.; Dutta, A. Performance analysis of blind source separation using canonical correlation. Circuits Syst. Signal Process. 2018, 37, 658–673. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Jing, F. Underdetermined blind source separation of synchronous orthogonal frequency hopping signals based on single source points detection. Sensors 2017, 17, 2074. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Ruan, G.; Liao, Y. A time-frequency domain underdetermined blind source separation algorithm for mimo radar signals. Symmetry 2017, 9, 104. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Zio, E.; Shi, J.; Hong, W. Aliasing signal separation of superimposed abrasive debris based on degenerate unmixing estimation technique. Sensors 2018, 18, 866. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Seung, H. Learning the parts of objects by nonnegative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Donoho, D.; Stodden, V. When Does Non-Negative Matrix Factorisation Give a Correct Decomposition into Parts; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Bertin, N.; Badeau, R.; Vincent, E. Enforcing harmonicity and smoothness in Bayesian non-negative matrix factorization applied to polyphonic music transcription. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 538–549. [Google Scholar] [CrossRef]
- Vincent, E.; Bertin, N.; Badeau, R. Adaptive harmonic spectral decomposition for multiple pitch estimation. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 528–537. [Google Scholar] [CrossRef]
- Smaragdis, P. Non-negative matrix factor deconvolution; extraction of multiple sound sources from monophonic inputs. Int. Conf. Indep. Compon. Anal. Blind Signal Sep. 2004, 3195, 494–499. [Google Scholar]
- Schmidt, M.N.; Morup, M. Nonnegative matrix factor two-dimensional deconvolution for blind single channel source separation. Intl. Conf. Indep. Compon. Anal. Blind Signal Sep. 2006, 3889, 700–707. [Google Scholar]
- Virtanen, T. Monaural sound source separation by nonnegative matrix factorization with temporal continuity and sparseness criteria. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1066–1074. [Google Scholar] [CrossRef]
- Laroche, C.; Papadopoulos, H.; Kowalski, M.; Richard, G. Drum extraction in single channel audio signals using multi-layer non-negative matrix factor deconvolution. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Zhi, R.C.; Flierl, M.; Ruan, Q.; Kleijn, W.B. Graph-preserving sparse nonnegative matrix factorization with application to facial expression recognition. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 38–52. [Google Scholar]
- Okun, O.; Priisalu, H. Unsupervised data reduction. Signal Process. 2007, 87, 2260–2267. [Google Scholar] [CrossRef]
- Kompass, R. A generalized divergence measure for nonnegative matrix factorization. Neural Comput. 2007, 19, 780–791. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Zdunek, R.; Amari, S. Csiszar’s divergences for non-negative matrix factorization: Family of new algorithms. Int. Conf. Indep. Compon. Anal. Blind Signal Sep. 2006, 3889, 32–39. [Google Scholar]
- Gao, B.; Woo, W.L.; Ling, B.W.K. Machine learning source separation using maximum a posteriori nonnegative matrix factorization. IEEE Trans. Cybern. 2014, 44, 1169–1179. [Google Scholar] [PubMed]
- Wu, Z.; Ye, S.; Liu, J.; Sun, L.; Wei, Z. Sparse non-negative matrix factorization on GPUs for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3640–3649. [Google Scholar] [CrossRef]
- Gao, B.; Woo, W.L.; Dlay, S.S. Adaptive sparsity non-negative matrix factorization for single-channel source separation. IEEE J. Sel. Top. Signal Process. 2011, 5, 989–1001. [Google Scholar] [CrossRef]
- Cemgil, A.T. Bayesian inference for nonnegative matrix factorization models. Comput. Intell. Neurosci. 2009. [Google Scholar] [CrossRef] [PubMed]
- Fevotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura-Saito divergence: With application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef] [PubMed]
- Fevotte, C.; Idier, J. Algorithms for nonnegative matrix factorization with the β-divergence. Neural Comput. 2010, 23, 2421–2456. [Google Scholar] [CrossRef]
- Yu, K.; Woo, W.L.; Dlay, S.S. Variational regularized two-dimensional nonnegative matrix factorization with the flexible β-divergence for single channel source separation. In Proceedings of the 2nd IET International Conference in Intelligent Signal Processing (ISP), London, UK, 1–2 December 2015. [Google Scholar]
- Gao, B.; Woo, W.L.; Dlay, S.S. Variational regularized two-dimensional nonnegative matrix factorization. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 703–716. [Google Scholar] [PubMed]
- Parathai, P.; Woo, W.L.; Dlay, S.S. Single-channel blind separation using L1-sparse complex nonnegative matrix factorization for acoustic signals. J. Acoust. Soc. Am. 2015. [Google Scholar] [CrossRef] [PubMed]
- Tengtrairat, N.; Woo, W.L.; Dlay, S.S.; Gao, B. Online noisy single-channel blind separation by spectrum amplitude estimator and masking. IEEE Trans. Signal Process. 2016, 64, 1881–1895. [Google Scholar] [CrossRef]
- Tengtrairat, N.; Gao, B.; Woo, W.L.; Dlay, S.S. Single-channel blind separation using pseudo-stereo mixture and complex 2-D histogram. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1722–1735. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; Hashiguchi, H.; Nishimura, T.; Oka, R. RWC music database: Music genre database and musical instrument sound database. In Proceedings of the International Symposium on Music Information Retrieval, Baltimore, MD, USA, 26–30 October 2003. [Google Scholar]
- Vincent, A.; Gribonval, R.; Fevotte, C. Performance measurement in blind audio source separation. IEEE Trans. Speech Audio Process. 2005, 14, 1462–1469. [Google Scholar] [CrossRef]
- Signal Separation Evaluation Campaign (SiSEC 2018). 2018. Available online: http://sisec.wiki.irisa.fr (accessed on 22 April 2018).
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Mørup, M.; Hansen, K.L. Tuning pruning in sparse non-negative matrix factorization. In Proceedings of the 17th European Signal Processing Conference (EUSIPCO’09), Glasgow, Scotland, 24–28 August 2009. [Google Scholar]
- Al-Tmeme, A.; Woo, W.L.; Dlay, S.S.; Gao, B. Underdetermined convolutive source separation using GEM-MU with variational approximated optimum model order NMF2D. IEEE Trans. Audio Speech Lang. Process. 2017, 25, 35–49. [Google Scholar] [CrossRef]



| Range | |||
|---|---|---|---|
| and | |||
| Mixtures | SDR (dB) | β |
|---|---|---|
| Piano + trumpet | 16.11 | 2.11 |
| 9.19 | 2.13 | |
| 9.43 | 1.93 | |
| 7.73 | 1.82 | |
| 12.21 | 2.09 | |
| Piano + violin | 13.07 | 1.07 |
| 8.15 | 1.23 | |
| 6.25 | 0.92 | |
| 9.33 | 1.20 | |
| 8.19 | 0.89 | |
| Trumpet + violin | 14.63 | 0.68 |
| 8.14 | 0.62 | |
| 7.81 | 0.67 | |
| 9.81 | 0.51 | |
| 7.55 | 0.52 |
| Methods | SDR (dB) |
|---|---|
| Case (1) | 12.77 |
| Case (2) | 13.01 |
| Case (3) | 14.60 |
| Case (4) | 14.62 |
| Case (5) | 14.70 |
| Case (6) | 15.60 |
| Mixtures | SDR (dB) Using Adaptive β | SDR (dB) Using β = 1 | SDR (dB) Using β = 2 |
|---|---|---|---|
| Piano + Trumpet | 16.85 | 14.11 | 15.93 |
| 10.74 | 7.95 | 9.01 | |
| 9.93 | 8.12 | 9.11 | |
| 8.95 | 6.57 | 7.44 | |
| 13.64 | 10.26 | 12.03 | |
| Piano + Violin | 14.17 | 12.12 | 11.67 |
| 9.04 | 7.95 | 7.11 | |
| 8.13 | 6.09 | 5.81 | |
| 10.4 | 9.08 | 8.71 | |
| 9.59 | 7.85 | 7.19 | |
| Trumpet + Violin | 15.40 | 12.49 | 12.13 |
| 8.87 | 6.23 | 6.31 | |
| 9.14 | 6.87 | 7.17 | |
| 10.51 | 7.92 | 8.11 | |
| 9.17 | 7.77 | 7.95 |
| Algorithm | SDR (dB) |
|---|---|
| NMF-LS | 4.17 |
| NMF-KLD | 3.47 |
| NMF-TCS | 5.12 |
| NMF-ARD | 3.98 |
| NMF using proposed method | 7.63 |
| Proposed method using matrix factor time–frequency deconvolution | 12.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, W.L.; Gao, B.; Bouridane, A.; Ling, B.W.-K.; Chin, C.S. Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution †. Sensors 2018, 18, 1371. https://doi.org/10.3390/s18051371
Woo WL, Gao B, Bouridane A, Ling BW-K, Chin CS. Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution †. Sensors. 2018; 18(5):1371. https://doi.org/10.3390/s18051371
Chicago/Turabian StyleWoo, Wai Lok, Bin Gao, Ahmed Bouridane, Bingo Wing-Kuen Ling, and Cheng Siong Chin. 2018. "Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution †" Sensors 18, no. 5: 1371. https://doi.org/10.3390/s18051371
APA StyleWoo, W. L., Gao, B., Bouridane, A., Ling, B. W.-K., & Chin, C. S. (2018). Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution †. Sensors, 18(5), 1371. https://doi.org/10.3390/s18051371









