Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves
Abstract
:1. Introduction
2. Materials and Methods
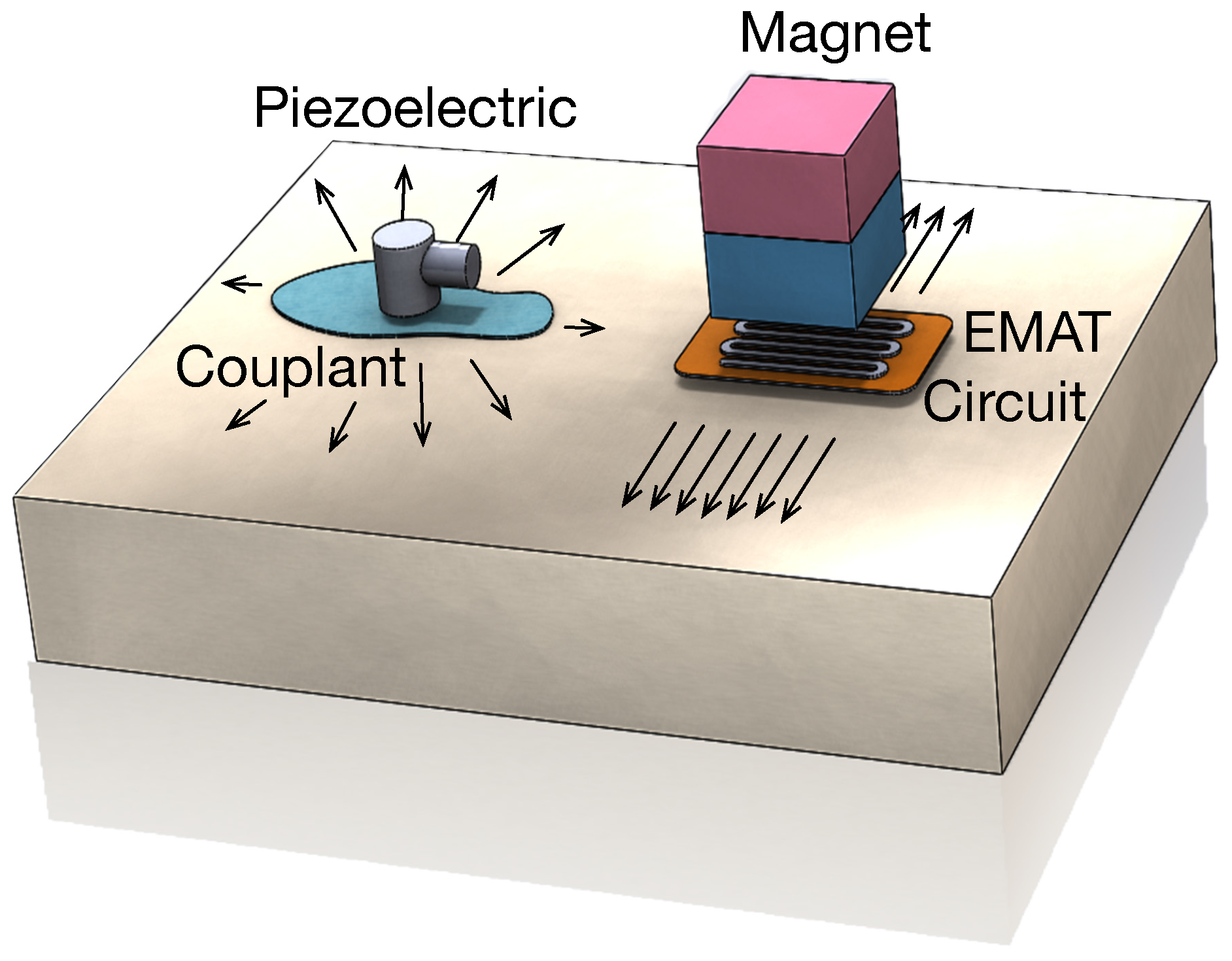
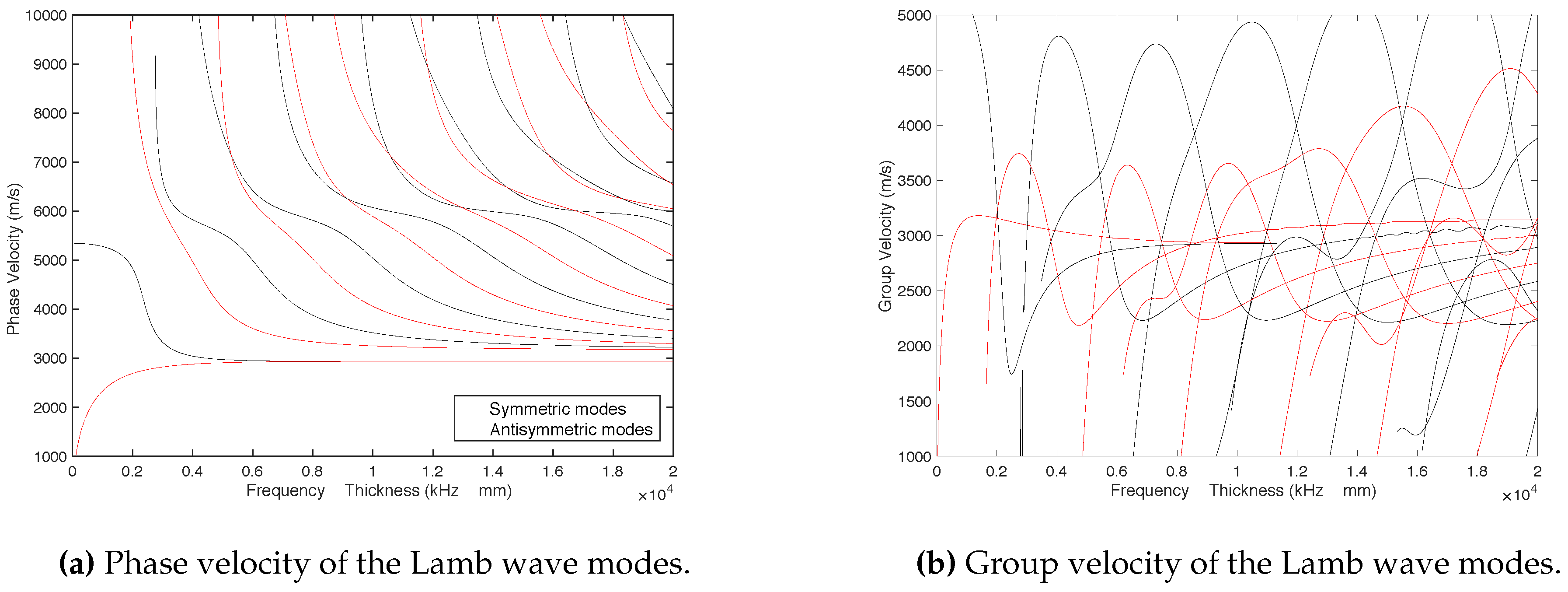
2.1. Lamb Wave Generation Using EMAT Actuators
2.2. Hardware Description
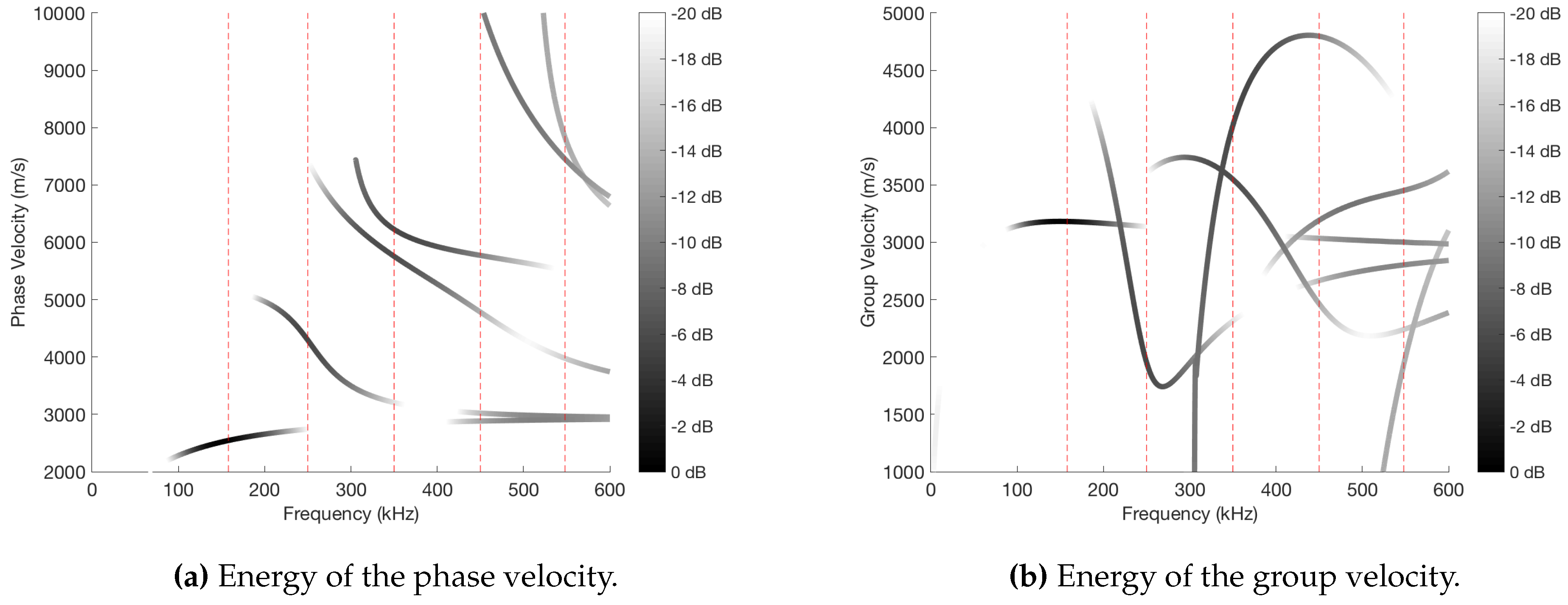
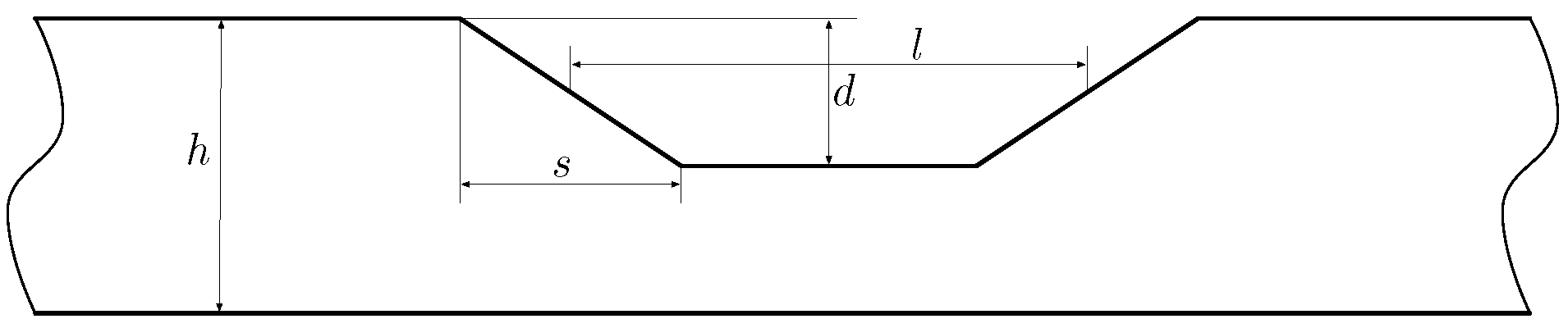
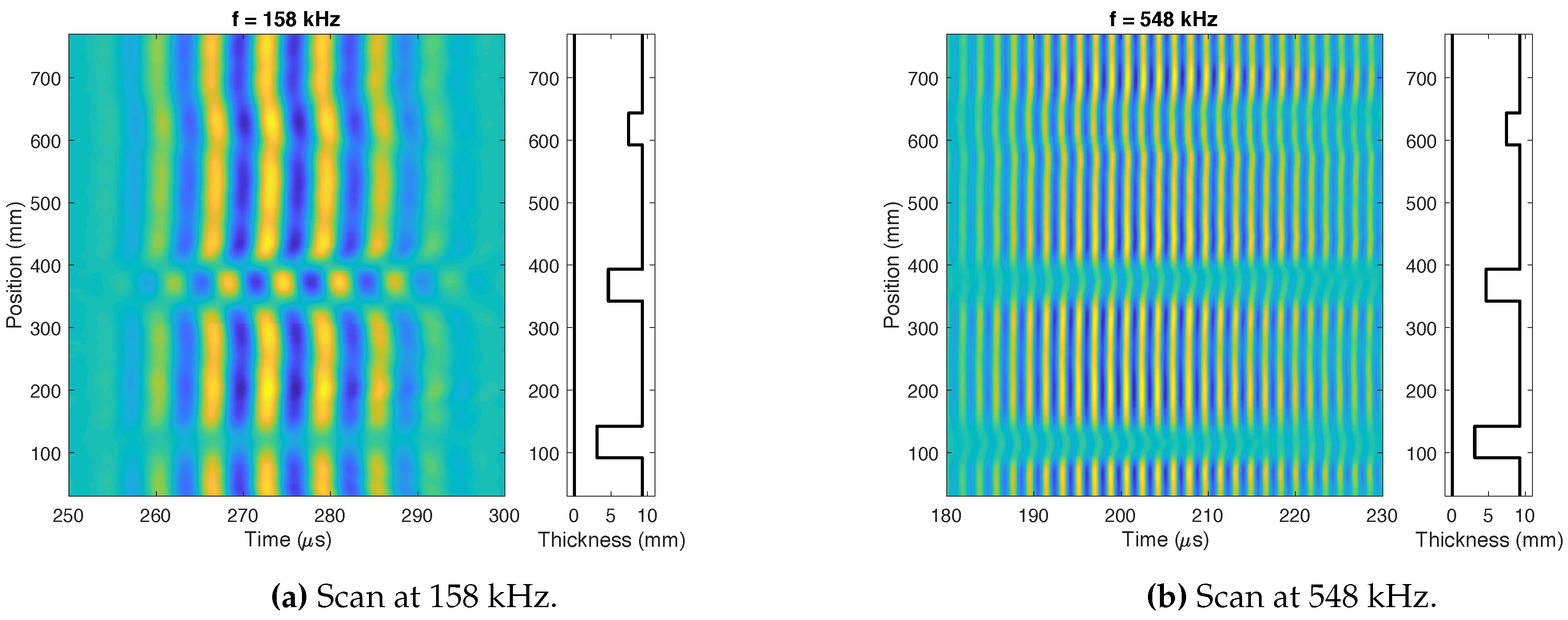
3. Effects of the Defect Over the Lamb Waves
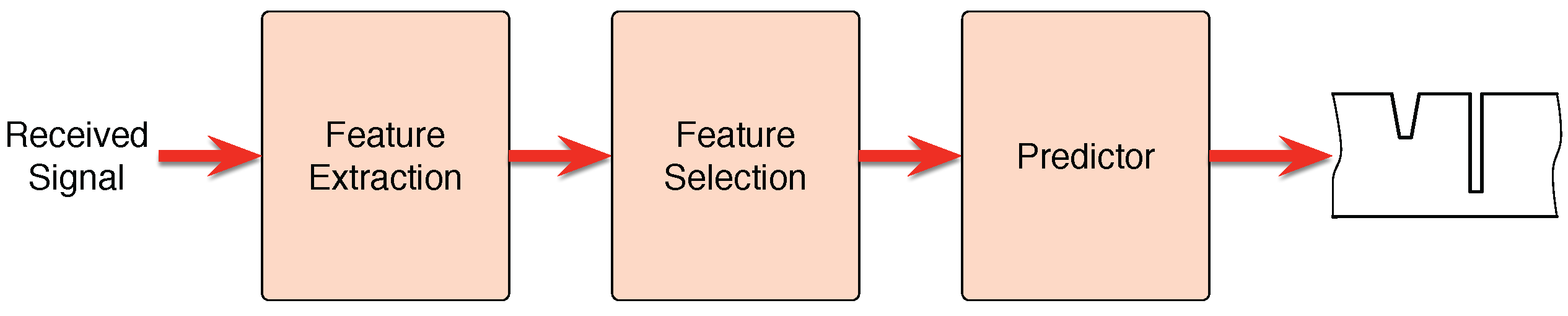
4. Smart Sound Processing (SSP) for Defect Sizing
- Maximum Amplitude (dB). This measure indicates the value of the maximum peak received from the signal. It is determined by looking for the value of the maximum peak around the expected point, which is the position of the maximum of the reference signal form in case of absence of any defects, ).
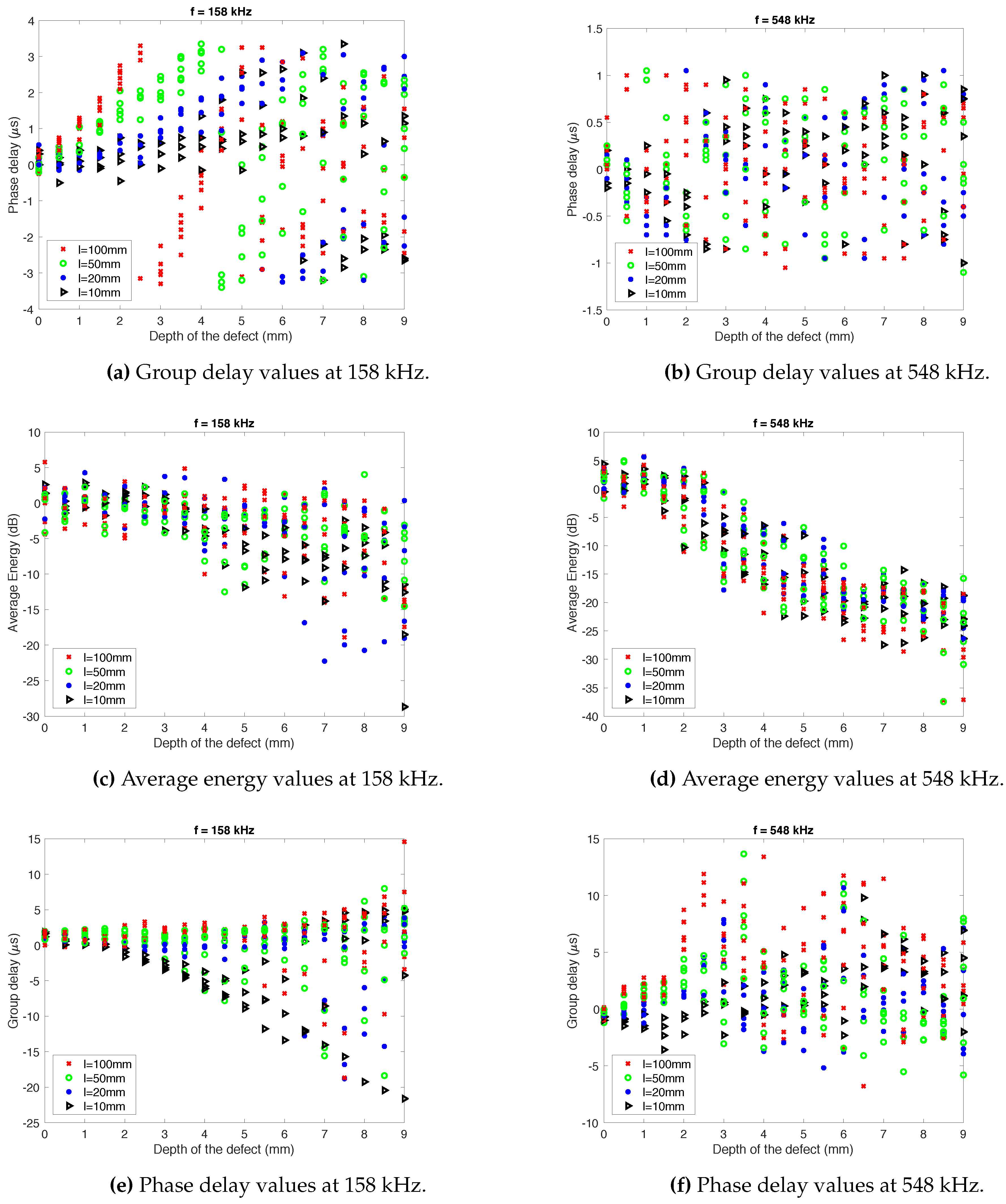
- Phase Delay (s). This measure represents the time taken between the pulse shipment and its reception at the same pipe location. It is determined measuring the time difference between the position of the maximum of the reference signal (signal without defect) and its closest maximum in the sensed signal. There may be considerable uncertainty in this feature if the delay is higher than half the period, since the nearest peak becomes the maximum of the signal.
- Average Energy (dB). It represents the average energy of the pulse. The interval considered for its calculation started 30 s before and ends up 30 s after it.
- Group Delay (s). In order to calculate this measure, the centroid of the average energy of the pulse has been considered. It has been estimated using the centroid of the pulse around the expected maximum (), with Equation (24).
- Maximum Amplitude of the echo (dB).
- Average Energy of the echoes (dB).
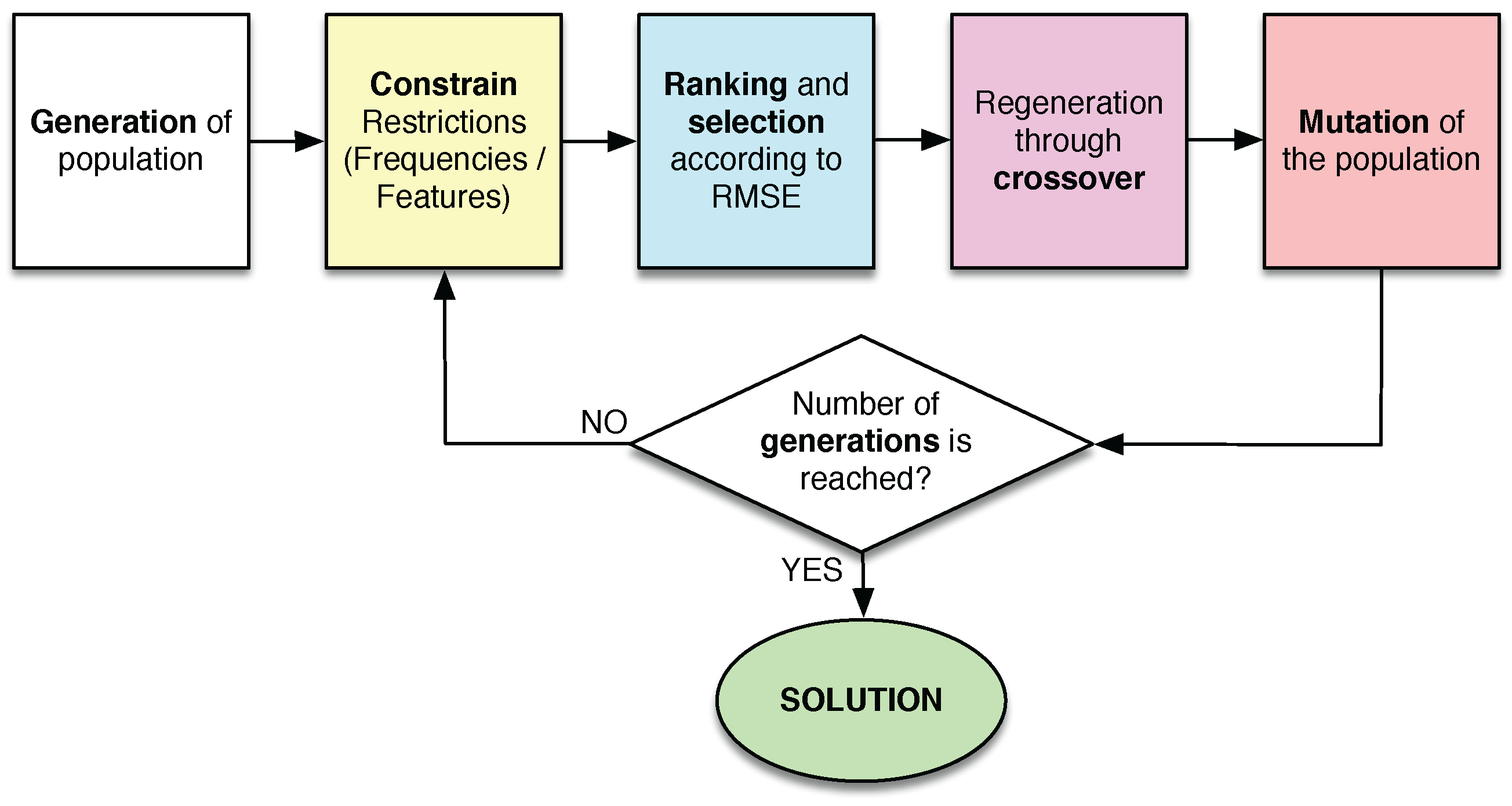
- A population of individuals is generated. Each solution consists of a binary vector with a length equal to the total number of features. Thus, ones indicate the features which are selected in the individual, while zeros indicate the features which remain outside.
- The candidates of the population are restricted to the considered constrains. All of them are modified in order to randomly change the value of some bits until one or the two constrains are fulfilled, depending on the case.
- A LSLD is designed with the subset of features of each candidate solution. The RMSE of the defect depth is calculated, which is the fitness function in this experiment. With this value, the population is ranked, keeping the best individuals in the top of the ranking.
- After that, a selection process is applied, which consists in keeping the best 10% of the solutions, removing the remaining ones.
- The removed solutions (90% of the population) are regenerated by crossover between the best candidates.
- Mutations are applied to the new population. With this step, 1% of the bits is changed. Furthermore, this step is not applied to the best solution in order to ensure the convergence of the algorithm.
- This process is repeated from step 2 during generations. The final best solution will be the best solution obtained in the last iteration.
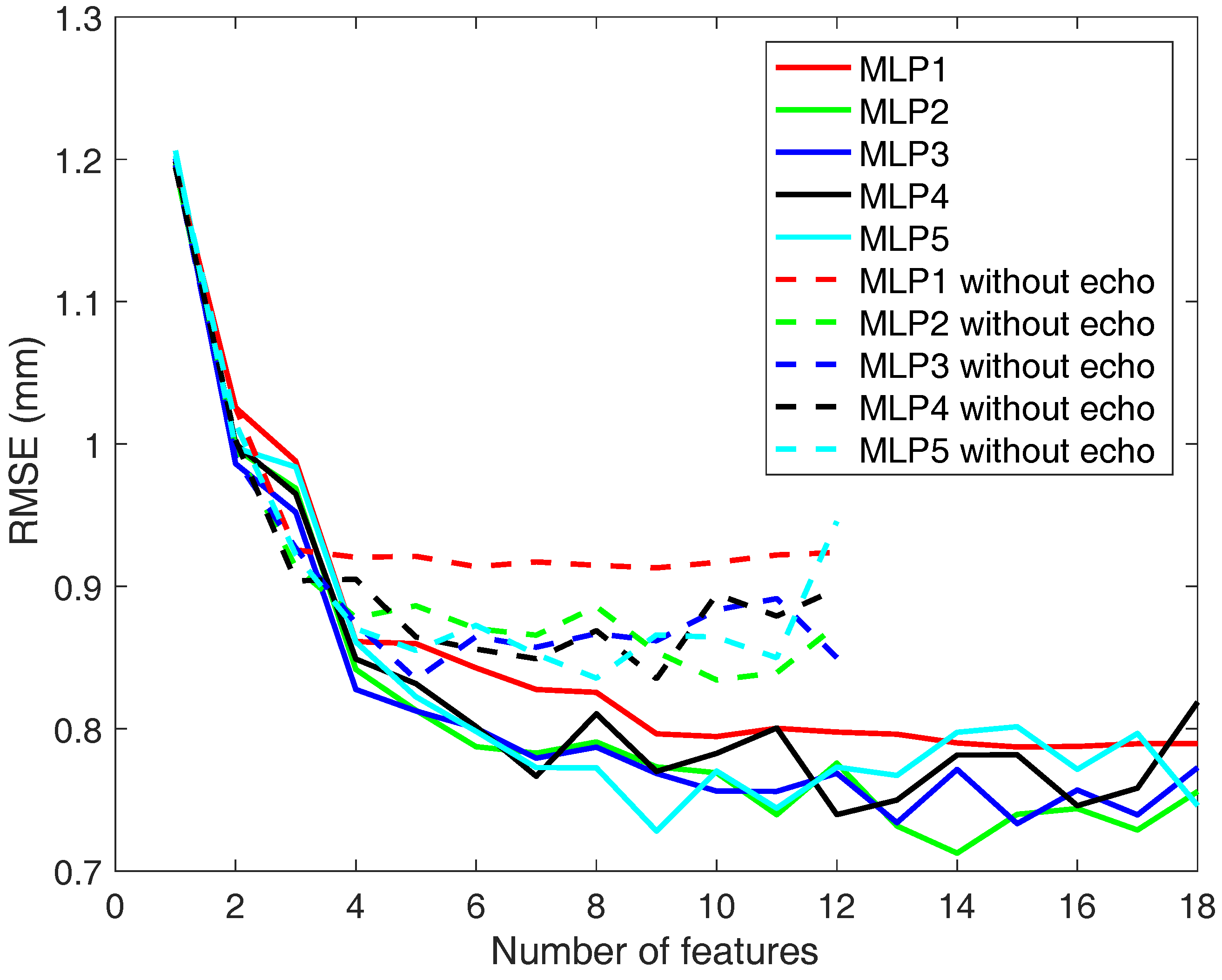
5. Results
5.1. Defect Sizing in Simulated Pipelines
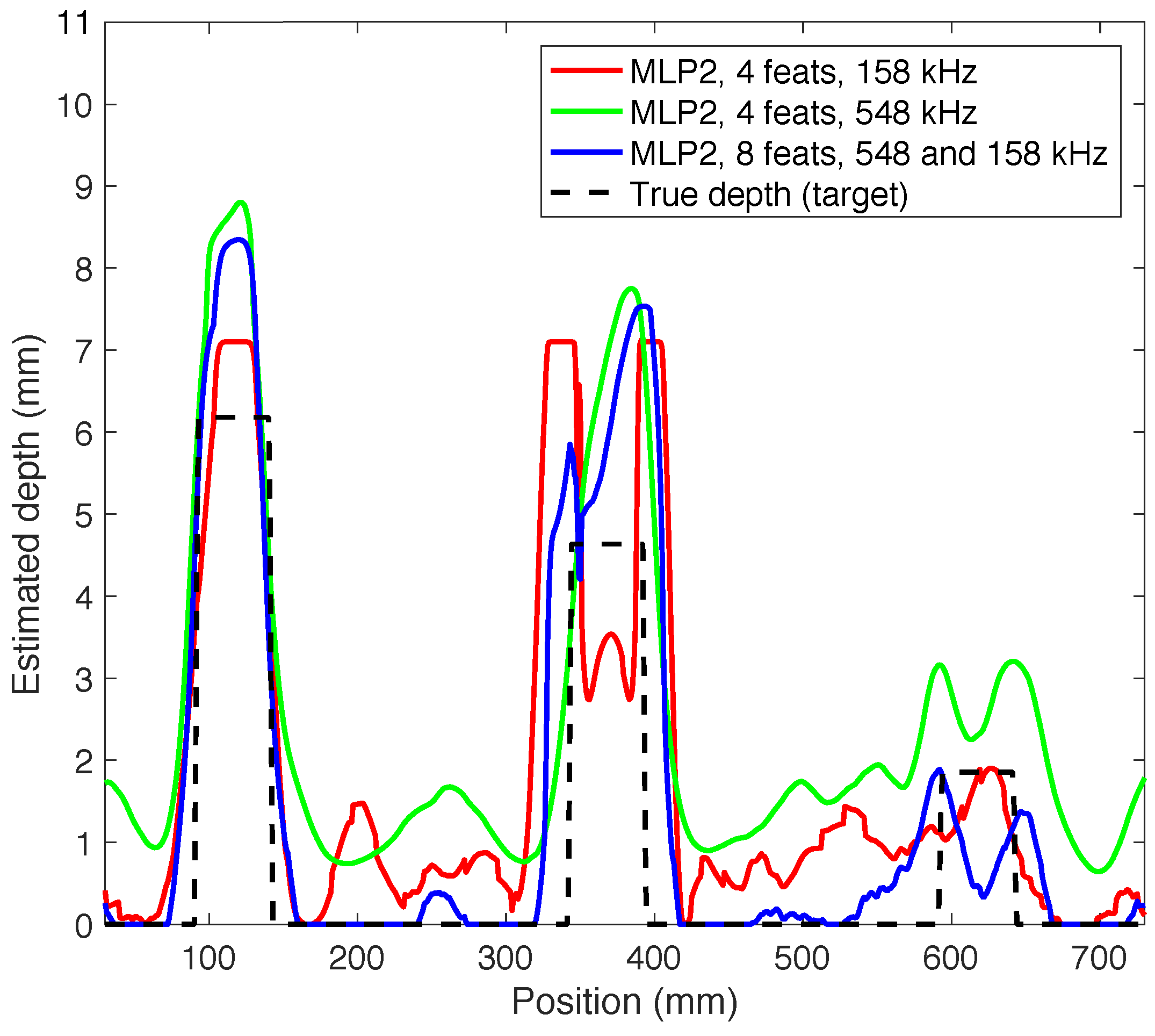
5.2. Defect Sizing in a Real Pipeline
6. Discussion
- The shape of the defect causes differences in the received signal. It is not feasible to obtain an analytical solution for all the cases.
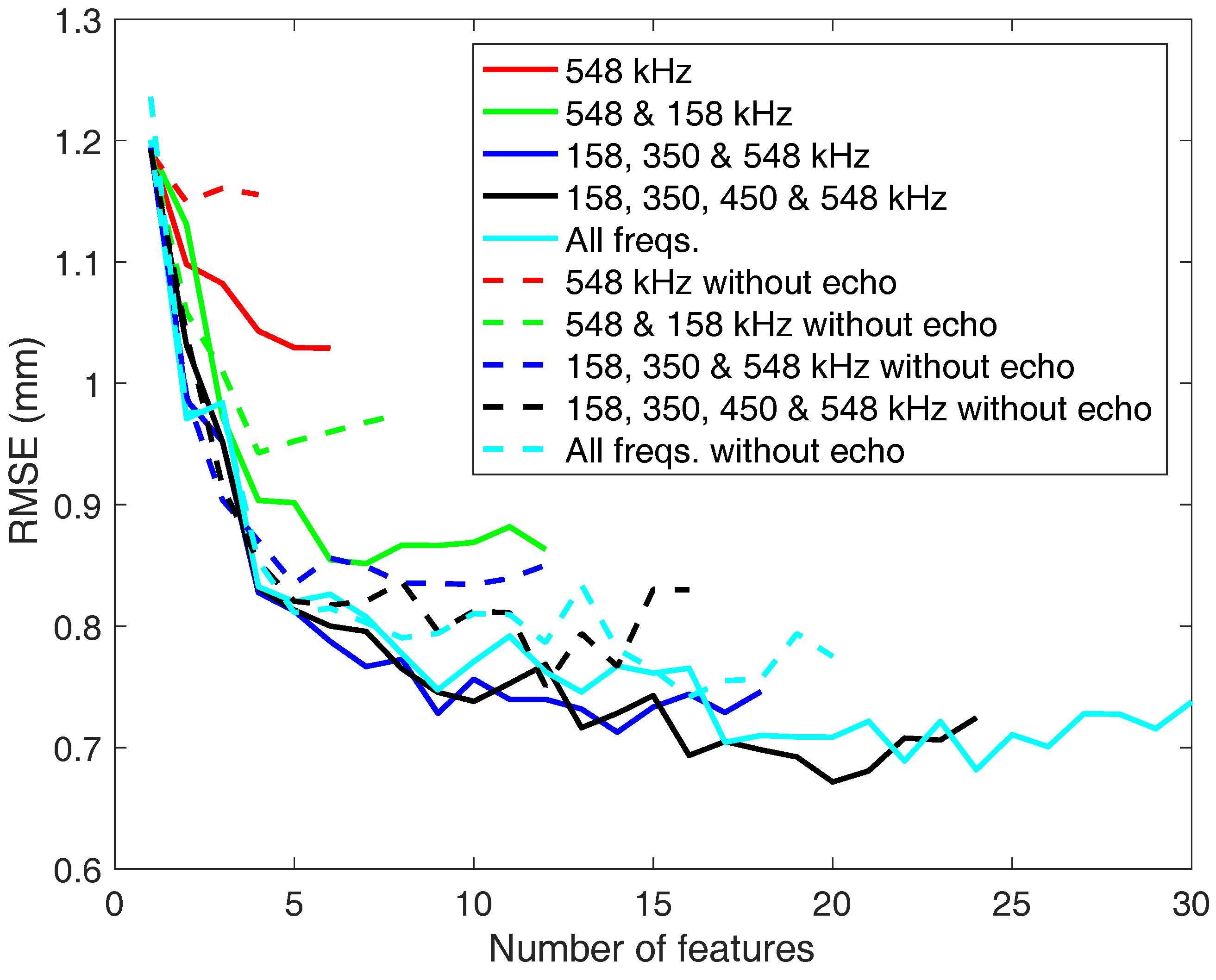
- The extracted features are useful for the pipeline sizing problem, since the results are good in terms of RMSE. The average energy and the maximum amplitude from the signals are particularly relevant for the study.
- It is important to excite the waves at several frequencies because the behavior and velocity of the Lamb modes is totally different depending on this parameter.
- Related to the predictors, a large number of neurons in the MLPs is not required. When it is increased above two or three neurons, the results do not improve significantly.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Springer Science & Business Media: New York, NY, USA, 1995; Volume 2. [Google Scholar]
- Silk, M.G. Ultrasonic Transducers for Nondestructive Testing; CRC Press: Boca Ratón, FL, USA, 1984. [Google Scholar]
- Vanaei, H.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessels Piping 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Green, R.E. Non-contact ultrasonic techniques. Ultrasonics 2004, 42, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Zhai, G.; Jiang, T.; Kang, L. Analysis of multiple wavelengths of Lamb waves generated by meander-line coil EMATs. Ultrasonics 2014, 54, 632–636. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Kim, D.K.; Kim, H.j.; Song, S.J.; Cho, S.H. Development of EMA transducer for inspection of pipelines. J. Mech. Sci. Technol. 2017, 31, 5209–5218. [Google Scholar] [CrossRef]
- Salzburger, H.J.; Niese, F.; Dobmann, G. EMAT pipe inspection with guided waves. Welding World 2012, 56, 35–43. [Google Scholar] [CrossRef]
- Andruschak, N.; Saletes, I.; Filleter, T.; Sinclair, A. An NDT guided wave technique for the identification of corrosion defects at support locations. NDT E Int. 2015, 75, 72–79. [Google Scholar] [CrossRef]
- Clough, M.; Fleming, M.; Dixon, S. Circumferential guided wave EMAT system for pipeline screening using shear horizontal ultrasound. NDT E Int. 2017, 86, 20–27. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Zhao, W.; Wei, Z. 3D modeling of circumferential SH guided waves in pipeline for axial cracking detection in ILI tools. Ultrasonics 2015, 56, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Singh, R. Pipeline Integrity: Management and Risk Evaluation; Gulf Professional Publishing: Houston, TX, USA, 2017. [Google Scholar]
- Demma, A. The Interaction of Guided Waves With Discontinuities in Structures. Ph.D. Thesis, University of London, London, UK, 2003. [Google Scholar]
- Cobb, A.C.; Fisher, J.L. Flaw depth sizing using guided waves. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2016; Volume 1706, p. 030013. [Google Scholar]
- Nurmalia; Nakamura, N.; Ogi, H.; Hirao, M. EMAT pipe inspection technique using higher mode torsional guided wave T (0, 2). NDT E Int. 2017, 87, 78–84. [Google Scholar]
- Hirao, M.; Ogi, H. An SH-wave EMAT technique for gas pipeline inspection. NDT E Int. 1999, 32, 127–132. [Google Scholar] [CrossRef]
- Layouni, M.; Hamdi, M.S.; Tahar, S. Detection and sizing of metal-loss defects in oil and gas pipelines using pattern-adapted wavelets and machine learning. Appl. Soft Comput. 2017, 52, 247–261. [Google Scholar] [CrossRef]
- Mohamed, A.; Hamdi, M.S.; Tahar, S. A machine learning approach for big data in oil and gas pipelines. In Proceedings of the 2015 3rd International Conference on Future Internet of Things and Cloud (FiCloud), Rome, Italy, 24–26 August 2015; pp. 585–590. [Google Scholar]
- Mohamed, A.; Hamdi, M.S.; Tahar, S. An adaptive neuro-fuzzy inference system-based approach for oil and gas pipeline defect depth estimation. In Proceedings of the SAI Intelligent Systems Conference (IntelliSys), London, UK, 10–11 November 2015; pp. 35–42. [Google Scholar]
- Luangvilai, K. Attenuation of Ultrasonic Lamb Waves With Applications To Material Characterization and Condition Monitoring; Georgia Institute of Technology: Atlanta, GA, USA, 2007. [Google Scholar]
- Su, Z.; Ye, L. Identification of Damage Using Lamb Waves: From Fundamentals To Applications; Springer Science & Business Media: New York, NY, USA, 2009; Volume 48. [Google Scholar]
- Garcia, V.; Boyero, C.; Jimenez, J.A. Corrosion detection under pipe supports using EMAT Medium Range Guided Waves. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016; pp. 1–9. [Google Scholar]
- Gil-Pita, R.; García-Gomez, J.; Bautista-Durán, M.; Combarro, E.; Cocana-Fernandez, A. Evolved frequency log-energy coefficients for voice activity detection in hearing aids. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Weisz, L. Pattern Recognition Statistical Structural And Neural Approaches. Pattern Recogn. 2016, 1, 2. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; pp. 532–538. [Google Scholar]



| Parameter | Number of Possible Values | Values |
|---|---|---|
| Frequency (kHz) | 5 | 158, 250, 350, 450, 548 |
| Length (mm) | 4 | 10, 20, 50, 100 |
| Depth (mm) | 19 | 0, 0.5, 1,..., 9 |
| Slope (mm) | 7 | 1, 3, 5, 10, 50, 100 |
| Feature | Frequency (kHz) | ||
|---|---|---|---|
| 158 | 350 | 548 | |
| Maximum Amplitude | 0% | 92% | 0% |
| Phase Delay | 0% | 0% | 0% |
| Average Energy | 100% | 100% | 100% |
| Group Delay | 0% | 0% | 58% |
| Maximum Amplitude of Echo | 8% | 50% | 0% |
| Average Energy of Echos | 92% | 100% | 100% |
| Feature | Frequency (kHz) | ||
|---|---|---|---|
| 158 | 350 | 548 | |
| Maximum Amplitude | 100% | 100% | 92% |
| Phase Delay | 0% | 0% | 0% |
| Average Energy | 100% | 100% | 100% |
| Group Delay | 8% | 100% | 100% |
| Parameter | Value |
|---|---|
| Material | Structural Steel S355NH |
| Thickness (mm) | 9.27 |
| Depth of Defect 1 (mm) | 6.18 |
| Depth of Defect 2 (mm) | 4.63 |
| Depth of Defect 3 (mm) | 1.85 |
| Predictor | Number of feats | Frequency (kHz) | RMSE (mm) |
|---|---|---|---|
| MLP 2 neurons | 4 | 158 | 1.84 |
| 4 | 548 | 1.80 | |
| 8 | 158, 548 | 1.48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Gómez, J.; Gil-Pita, R.; Rosa-Zurera, M.; Romero-Camacho, A.; Jiménez-Garrido, J.A.; García-Benavides, V. Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves. Sensors 2018, 18, 802. https://doi.org/10.3390/s18030802
García-Gómez J, Gil-Pita R, Rosa-Zurera M, Romero-Camacho A, Jiménez-Garrido JA, García-Benavides V. Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves. Sensors. 2018; 18(3):802. https://doi.org/10.3390/s18030802
Chicago/Turabian StyleGarcía-Gómez, Joaquín, Roberto Gil-Pita, Manuel Rosa-Zurera, Antonio Romero-Camacho, Jesús Antonio Jiménez-Garrido, and Víctor García-Benavides. 2018. "Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves" Sensors 18, no. 3: 802. https://doi.org/10.3390/s18030802
APA StyleGarcía-Gómez, J., Gil-Pita, R., Rosa-Zurera, M., Romero-Camacho, A., Jiménez-Garrido, J. A., & García-Benavides, V. (2018). Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves. Sensors, 18(3), 802. https://doi.org/10.3390/s18030802








