Three-Dimensional Reconstruction from Single Image Base on Combination of CNN and Multi-Spectral Photometric Stereo
Abstract
:1. Introduction
2. Related Work
2.1. Photometric Stereo
2.2. Machine Learning in Depth Estimation
3. Methods
3.1. Multi-Spectral Photometric Stereo
3.2. Deep Convolutional Neural Network
3.2.1. Architecture
3.2.2. Training
3.3. Combination of Deep Convolution Neural Network and Multi-Spectral PS
4. Experiments
4.1. The Synthesis Dataset Rendered from ShapeNet
4.2. Result of Our Network
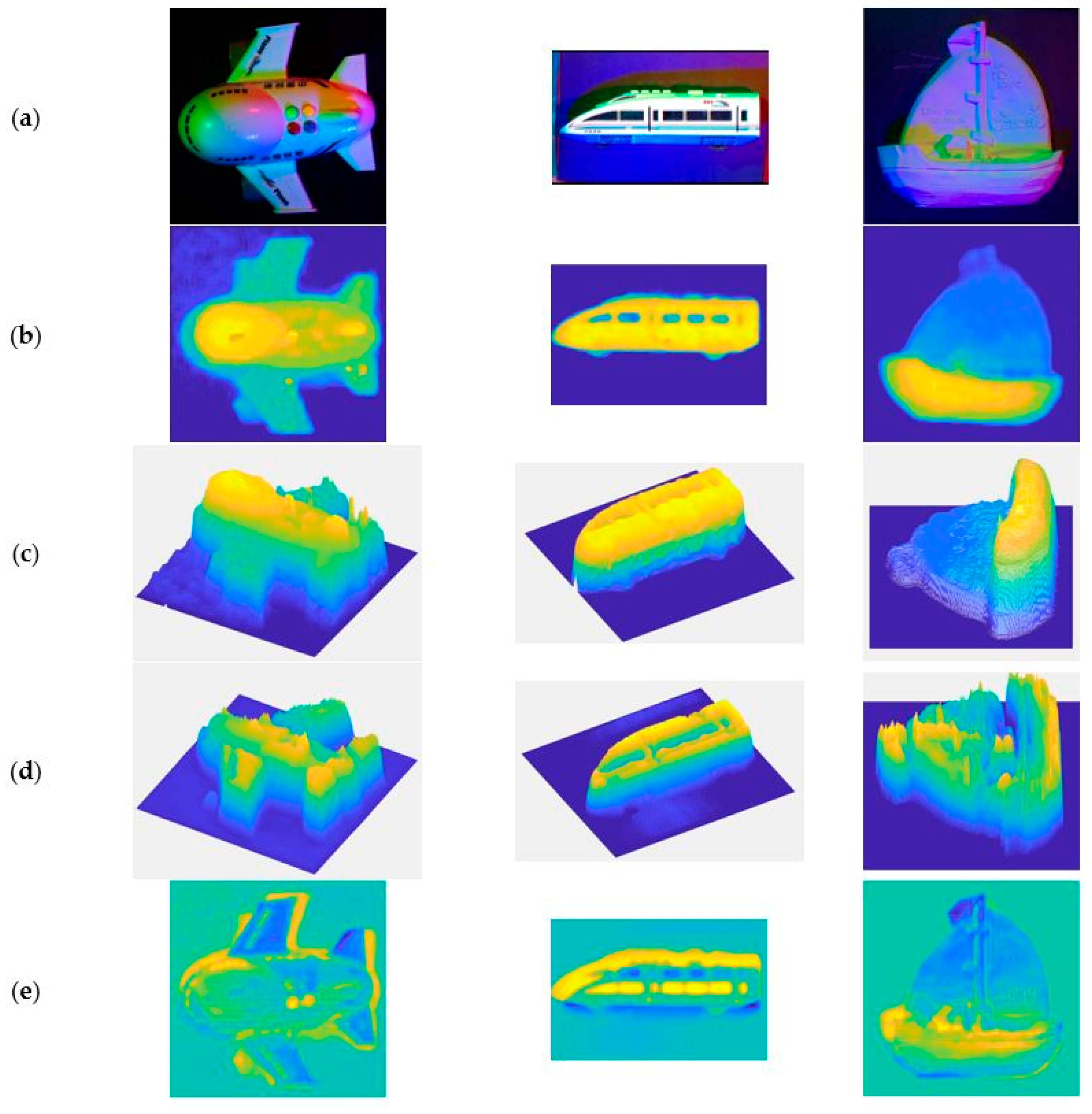
4.2.1. Experiment Results
4.2.2. Quantitative Analysis
- Mean relative error (rel), which can be calculated according to Equation (7):
- Root mean squared error (rms), which can be calculated according to Equation(8):
- Accuracy with threshold t (δ), this is a statistical parameter that is used to count the percentage of pixels matching a certain condition in the image with respect to the total number of pixels in the image. According to the different values of t, the result is divided into three grades, that is, when t is 1.25, the result is δ1, when t is 1.252, the result is δ2, and when t is 1.253, the result is δ3. It can be calculated according to Equation (9):
4.3. Result of Combination of Deep Convolution Neural Network and Multi-Spectral PS
4.3.1. Experiment Results
4.3.2. Quantitative Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ti, C.; Xu, G.; Guan, Y.; Teng, Y. Depth Recovery for Kinect Sensor Using Contour-Guided Adaptive Morphology Filter. IEEE Sens. J. 2017, 17, 4534–4543. [Google Scholar] [CrossRef]
- Ikeuchi, K.; Horn, B.K. Numerical shape from shading and occluding boundaries. Artif. Intell. 1981, 17, 141–184. [Google Scholar] [CrossRef]
- Lee, K.M.; Kuo, C.-C. Shape from shading with a linear triangular element surface model. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 815–822. [Google Scholar] [CrossRef]
- Woodham, R.J. Photometric method for determining surface orientation from multiple images. Opt. Eng. 1980, 19, 139–144. [Google Scholar] [CrossRef]
- Drew, M.S.; Kontsevich, L.L. Closed-form Attitude Determination under Spectrally Varying Illumination; Technical Report CSS/LCCR TR 94-02; Simon Fraser University, Centre for Systems Science: Burnaby, BC, Canada, 1994. [Google Scholar]
- Thomas, A.; Ferrar, V.; Leibe, B.; Tuytelaars, T.; Schiel, B.; van Gool, L. Towards multi-view object class detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 2, pp. 1589–1596. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multiview stereo reconstruction algorithms. In Proceedings of the IEEE Computer Society Conference on Computer vision and pattern recognition, New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Bolles, R.C.; Baker, H.H.; Marimont, D.H. Epipolar-plane image analysis: An approach to determining structure from motion. Int. J. Comput. Vis. 1987, 1, 7–55. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring photo collections in 3d. ACM Trans. Graph. 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Kontsevich, L.; Petrov, A.; Vergelskaya, I. Reconstruction of shape from shading in color images. JOSA A 1994, 11, 1047–1052. [Google Scholar] [CrossRef]
- Woodham, R.J. Gradient and Curvature from Photometric Stereo Including Local Confidence Estimation. J. Opt. Soc. Am. 1994, 11, 3050–3068. [Google Scholar] [CrossRef]
- Tsiotsios, C.; Angelopoulou, M.; Kim, T.K.; Davison, A. Backscatter Compensated Photometric Stereo with 3 Sources. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2259–2266. [Google Scholar]
- Anderson, R.; Stenger, B.; Cipolla, R. Color Photometric Stereo for Multicolored Surfaces. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; Volume 58, pp. 2182–2189. [Google Scholar]
- Decker, D.; Kautz, J.; Mertens, T.; Bekaert, P. Capturing multiple illumination conditions using time and color multiplexing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2009, Miami, FL, USA, 20–25 June 2009; pp. 2536–2543. [Google Scholar]
- Kim, H.; Wilburn, B.; Ben-Ezra, M. Photometric Stereo for Dynamic Surface Orientations. In Computer Vision —ECCV 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 59–72. [Google Scholar]
- Janko, Z.; Delaunoy, A.; Prados, E. Colour dynamic photometric stereo for textured surfaces. In Computer Vision—ACCV 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 55–66. [Google Scholar]
- Hernandez, C.; Vogiatzis, G.; Brostow, G.J.; Stenger, B.; Cipolla, R. Non-rigid Photometric Stereo with Colored Lights. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Narasimhan, S.; Nayar, S. Structured Light Methods for Underwater Imaging: Light Stripe Scanning and Photometric Stereo. In Proceedings of the MTS/IEEE Oceans, Washington, DC, USA, 18–23 September 2005; pp. 1–8. [Google Scholar]
- Petrov. Light, Color and Shape. Cognitive Processes and their Simulation; Velikhov, E.P., Ed.; Nauka: Moscow, Russia, 1987; Volume 2, pp. 350–358. (In Russian) [Google Scholar]
- Ma, W.; Jones, A.; Chiang, J.; Hawkins, T.; Frederiksen, S.; Peers, P.; Vukovic, M.; Ouhyoung, M.; Debevec, P. Facial performance synthesis using deformation-driven polynomial displacement maps. In Proceedings of the ACM SIGGRAPH Asia2008, Los Angeles, CA, USA, 11–15 August 2008; Volume 27, p. 2. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the Neural Information Processing Systems Conference, Montreal, QC, Canada, 8–13 December 2014; pp. 2366–2374. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G. Deep convolutional neural fields for depth estimation from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, Boston, MA, USA, 8–10 June 2015; pp. 5162–5170. [Google Scholar]
- Cipolla, R.; Battiato, S.; Farinella, G.M. Computer Vision: Detection, Recognition and Reconstruction; Springer: Berlin, Germany, 2010; Volume 285. [Google Scholar]
- Coleman, E.N.; Jain, R. Obtaining 3-dimensional shape of textured and specular surfaces using foursource photometry. Comput. Graph. Image Process. 1982, 18, 309–328. [Google Scholar] [CrossRef]
- Nayar, S.K.; Ikeuchi, K.; Kanade, T. Surface Reflection: Physical and Geometrical Perspectives; Technical Reports; DTIC Document: Fort Belvoir, VA, USA, 1989. [Google Scholar]
- Lin, S.; Lee, S.W. Estimation of diffuse and specular appearance. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 855–860. [Google Scholar]
- Jensen, H.W.; Marschner, S.R.; Levoy, M.; Hanrahan, P. A practical model for subsurface light transport. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 2001; pp. 511–518. [Google Scholar]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J. Geometrical Considerations and Nomenclature for Reflectance; National Bureau of Standards, US Department of Commerce: Washington, DC, USA, 1977; Volume 160. [Google Scholar]
- Hernández, C.; Vogiatzis, G.; Cipolla, R. Shadows in three-source photometric stereo. In Computer Vision—ECCV 2008. ECCV 2008. Lecture Notes in Computer Science; Forsyth, D., Torr, P., Zisserman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5302, pp. 290–303. [Google Scholar]
- Zhang, Q.; Ye, M.; Yang, R.; Matsushita, Y.; Wilburn, B.; Yu, H. Edge-preserving photometric stereo via depth fusion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2472–2479. [Google Scholar]
- Yu, L.-F.; Yeung, S.-K.; Tai, Y.-W.; Lin, S. Shading based shape refinement of rgb-d images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1415–1422. [Google Scholar]
- Xiong, S.; Zhang, J.; Zheng, J.; Cai, J.; Liu, L. Robust surface reconstruction via dictionary learning. ACM Trans. Graph. 2014, 33, 201. [Google Scholar] [CrossRef]
- Liu, F.; Chung, S.; Ng, A.Y. Learning depth from single monocular images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 18, 1–8. [Google Scholar]
- Ladicky, L.; Shi, J.; Pollefeys, M. Pulling things out of perspective. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 89–96. [Google Scholar]
- Yoon, Y.; Choe, G.; Kim, N.; Lee, J.-Y.; Kweon, I.S. Fine-scale surface normal estimation using a single nir image. In Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, UK, 2016; Volume 9907, pp. 486–500. [Google Scholar]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Multiview 3d models from single images with a convolutional network. In Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, UK, 2016; Volume 9911, pp. 322–337. [Google Scholar]
- Mousavian, A.; Pirsiavash, H. Joint Semantic Segmentation and Depth Estimation with Deep Convolutional Networks. In Proceedings of the Fourth International Conference on 3D Vision, Stanford, CA, USA, 25–28 October 2016; pp. 611–619. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V. Deeper Depth Prediction with Fully Convolutional Residual Networks. In Proceedings of the Fourth International Conference on 3D Vision, Stanford, CA, USA, 25–28 October 2016; pp. 239–248. [Google Scholar]
- Roy, A.; Todorovic, S. Monocular Depth Estimation Using Neural Regression Forest. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5506–5514. [Google Scholar]
- Xu, D.; Ricci, E.; Ouyang, W.; Wang, X.; Sebe, N. Multi-Scale Continuous CRFs as Sequential Deep Networks for Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 161–169. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G.; Reid, I. Learning Depth from Single Monocular Images Using Deep Convolutional Neural Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2024–2039. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Xiang, D.; Deng, J. Surface Normals in the Wild. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1566–1575. [Google Scholar]
- Li, J.; Klein, R.; Yao, A. A Two-Streamed Network for Estimating Fine-Scaled Depth Maps from Single RGB Images. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3392–3400. [Google Scholar]
- Savva, M.; Chang, A.X.; Hanrahan, P. Semantically-enriched 3d models for common-sense knowledge. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 24–31. [Google Scholar]
- GirHub. Available online: https://github.com/panmari/stanford-shapenet-renderer (accessed on 27 February 2018).

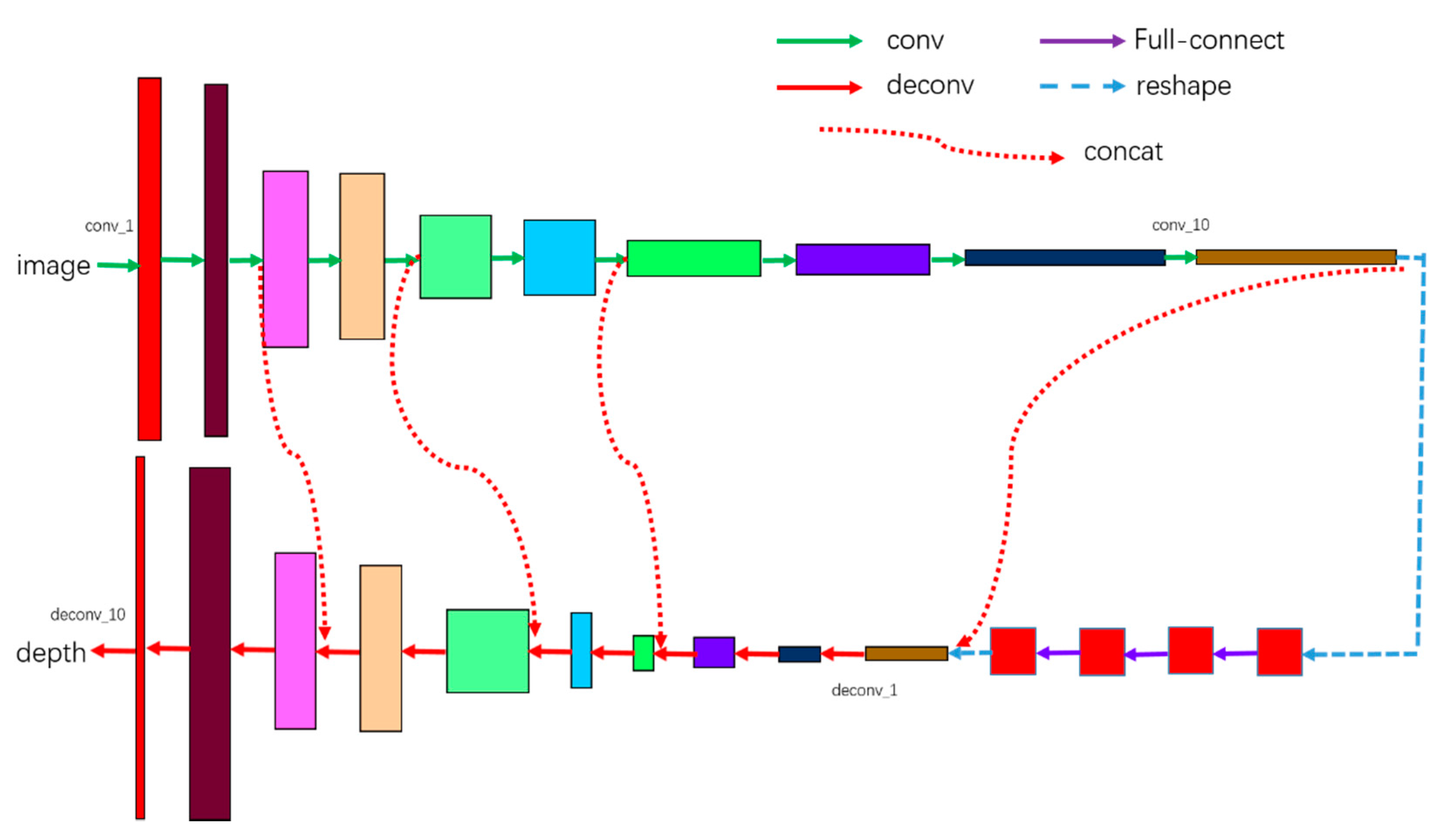





| Name | Input | Weights | Output Layers | Remarks |
|---|---|---|---|---|
| conv_1 | image | (5,5,2,2) | 32 | padding=’VALID |
| conv_2 | conv_1 | (5,5,1,1) | 32 | padding=’VALID |
| conv_3 | conv_2 | (5,5,2,2) | 64 | padding=’VALID |
| conv_4 | conv_3 | (5,5,1,1) | 64 | padding=’VALID |
| conv_5 | conv_4 | (5,5,2,2) | 128 | padding=’VALID |
| conv_6 | conv_5 | (5,5,1,1) | 128 | padding=’VALID |
| conv_7 | conv_6 | (5,5,2,2) | 256 | padding=’VALID |
| conv_8 | conv_7 | (5,5,1,1) | 256 | padding=’VALID |
| conv_9 | conv_8 | (5,5,2,2) | 256 | padding=’VALID |
| conv_10 | conv_9 | (5,5,1,1) | 256 | padding=’VALID |
| reshape | reshape conv_10 to 1×N | |||
| fc_1 | conv_10 | N×4096 | / | keep_prob=0.5 |
| fc_2 | fc1 | 4096×4096 | / | keep_prob=0.5 |
| fc_3 | fc2 | 4096×4096 | / | keep_prob=0.5 |
| fc_4 | fc3 | 4096×N | / | keep_prob=0.5 |
| reshape | reshape fc_4 to the shape of conv_10 | |||
| deconv_1 | fc4+conv10 | (5,5,1,1) | 128 | padding=’VALID |
| deconv_2 | deconv_1 | (5,5,2,2) | 64 | padding=’VALID |
| deconv_3 | deconv_2 | (5,5,1,1) | 64 | padding=’VALID |
| deconv_4 | deconv_3+conv_7 | (5,5,2,2) | 32 | padding=’VALID |
| deconv_5 | deconv_4 | (5,5,1,1) | 32 | padding=’VALID |
| deconv_6 | deconv_5+conv_5 | (5,5,2,2) | 16 | padding=’VALID |
| deconv_7 | deconv_6 | (5,5,1,1) | 16 | padding=’VALID |
| deconv_8 | deconv_7+conv_3 | (5,5,2,2) | 8 | padding=’VALID |
| deconv_9 | deconv_8 | (5,5,1,1) | 8 | padding=’VALID |
| deconv_10 | deconv_9 | (5,5,2,2) | 1 | padding=’VALID |
| Image | rel 1 | rms 1 | δ1 2 | δ2 2 | δ3 2 |
|---|---|---|---|---|---|
| Figure 4a | 0.5935 | 0.5083 | 0.0672 | 0.2120 | 0.4736 |
| Figure 4b | 0.5738 | 0.5083 | 0.0310 | 0.2215 | 0.5116 |
| Figure 4c | 0.5836 | 0.5070 | 0.0693 | 0.2339 | 0.4447 |
| Figure 4d | 0.6497 | 0.6010 | 0.0410 | 0.1205 | 0.2748 |
| Figure 4e | 0.8300 | 0.7292 | 0.0167 | 0.0591 | 0.1224 |
| Figure 4f | 0.7302 | 0.6282 | 0.0133 | 0.0771 | 0.2094 |
| Figure 5a | 0.4225 | 0.2899 | 0.3824 | 0.6693 | 0.7788 |
| Figure 5b | 0.6329 | 0.5032 | 0.1700 | 0.3004 | 0.3848 |
| Figure 5c | 0.6829 | 0.6607 | 0.0381 | 0.1571 | 0.2502 |
| Figure 5d | 0.6358 | 0.4792 | 0.1272 | 0.2744 | 0.4166 |
| Figure 5e | 0.4741 | 0.2979 | 0.3527 | 0.6156 | 0.7533 |
| Figure 5f | 0.3473 | 0.3353 | 0.1949 | 0.6677 | 0.8589 |
| Image | rel 1 | rms 1 | δ1 2 | δ2 2 | δ3 2 | |
|---|---|---|---|---|---|---|
| aircraft | DCNN | 0.5716 | 0.2928 | 0.1262 | 0.2667 | 0.4165 |
| MS-PS | 2.6899 | 0.6273 | 0.5221 | 0.5746 | 0.6315 | |
| DCNN+MS-PS | 2.8001 | 0.4118 | 0.5832 | 0.7078 | 0.8007 | |
| train | DCNN | 0.8165 | 0.5204 | 0.2237 | 0.3637 | 0.4502 |
| MS-PS | 1.8237 | 0.7501 | 0.0607 | 0.0915 | 0.1266 | |
| DCNN+MS-PS | 0.7368 | 0.5831 | 0.2300 | 0.4407 | 0.4979 | |
| ship | DCNN | 2.1245 | 0.3684 | 0.2371 | 0.3756 | 0.4887 |
| MS-PS | 1.1393 | 0.3393 | 0.1560 | 0.2689 | 0.3621 | |
| DCNN+MS-PS | 1.2453 | 0.3089 | 0.2184 | 0.4048 | 0.5548 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Qi, L.; Luo, Y.; Jiao, H.; Dong, J. Three-Dimensional Reconstruction from Single Image Base on Combination of CNN and Multi-Spectral Photometric Stereo. Sensors 2018, 18, 764. https://doi.org/10.3390/s18030764
Lu L, Qi L, Luo Y, Jiao H, Dong J. Three-Dimensional Reconstruction from Single Image Base on Combination of CNN and Multi-Spectral Photometric Stereo. Sensors. 2018; 18(3):764. https://doi.org/10.3390/s18030764
Chicago/Turabian StyleLu, Liang, Lin Qi, Yisong Luo, Hengchao Jiao, and Junyu Dong. 2018. "Three-Dimensional Reconstruction from Single Image Base on Combination of CNN and Multi-Spectral Photometric Stereo" Sensors 18, no. 3: 764. https://doi.org/10.3390/s18030764
APA StyleLu, L., Qi, L., Luo, Y., Jiao, H., & Dong, J. (2018). Three-Dimensional Reconstruction from Single Image Base on Combination of CNN and Multi-Spectral Photometric Stereo. Sensors, 18(3), 764. https://doi.org/10.3390/s18030764





