A New Black Carbon Sensor for Dense Air Quality Monitoring Networks
Abstract
1. Introduction
2. Materials and Methods
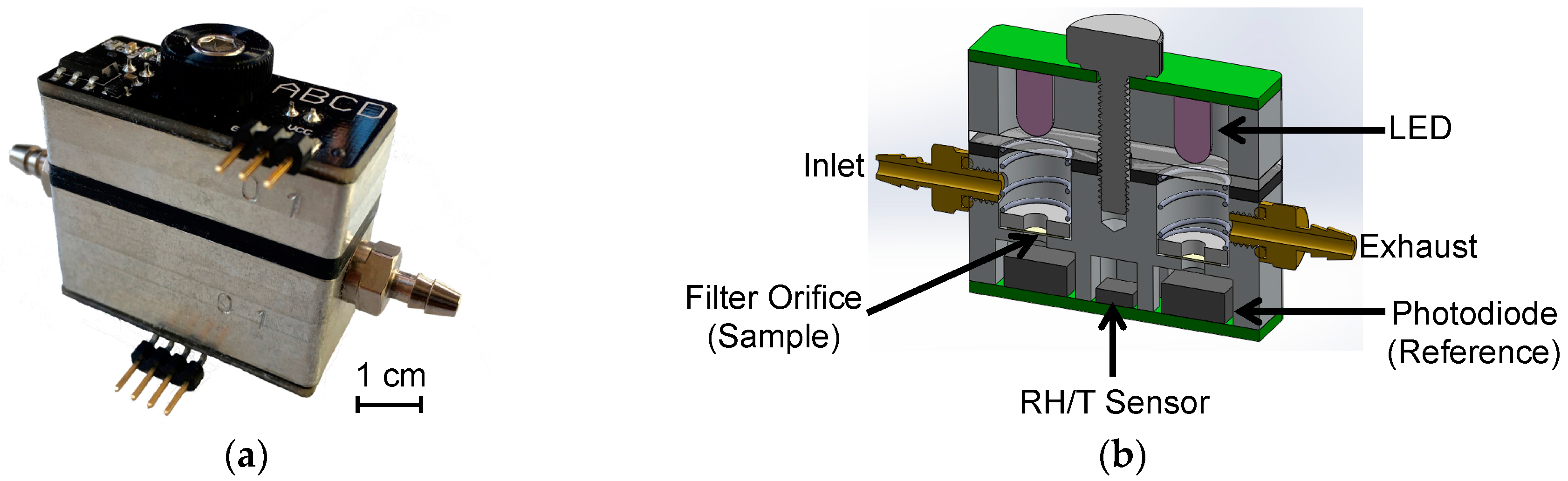
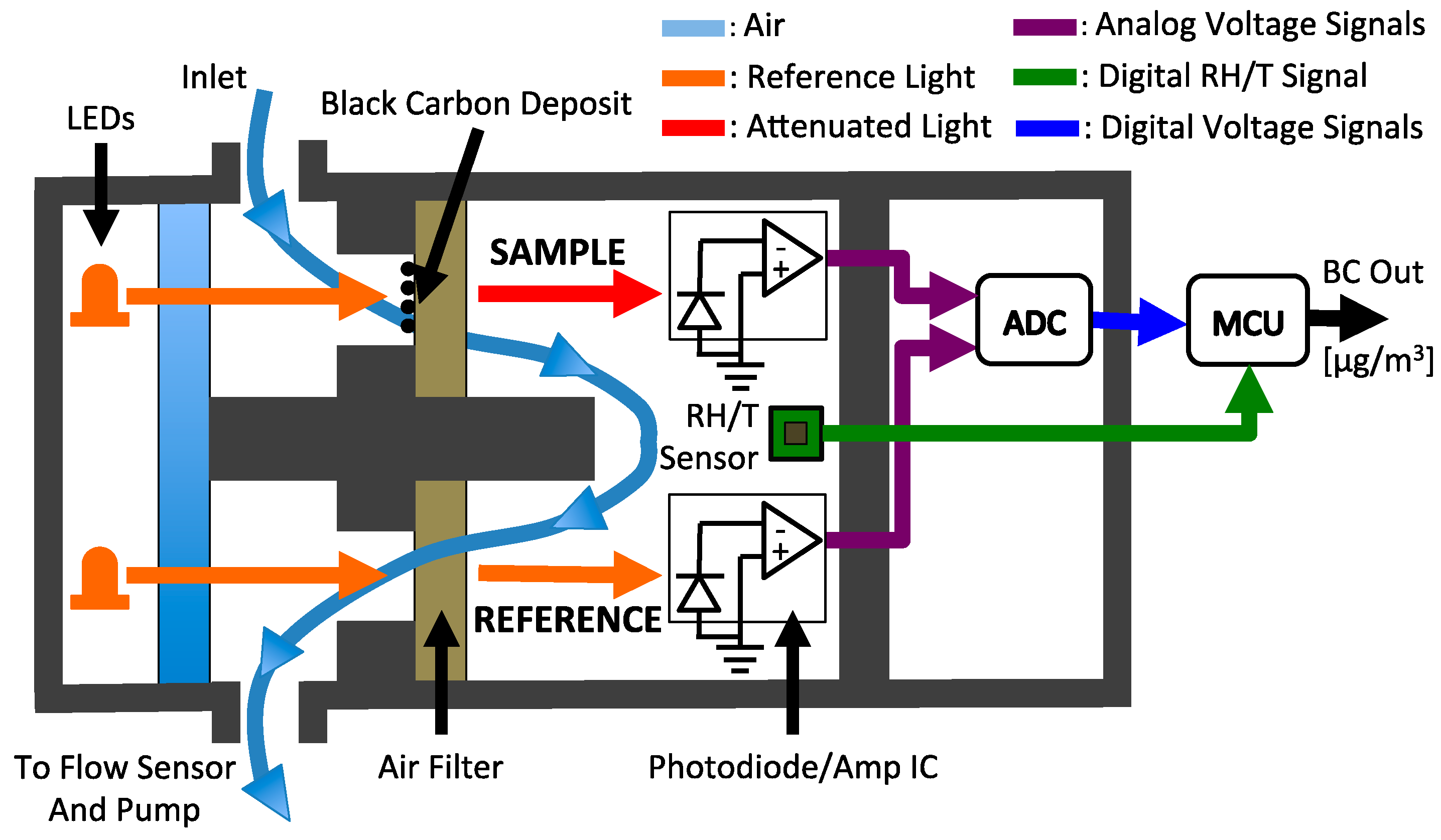
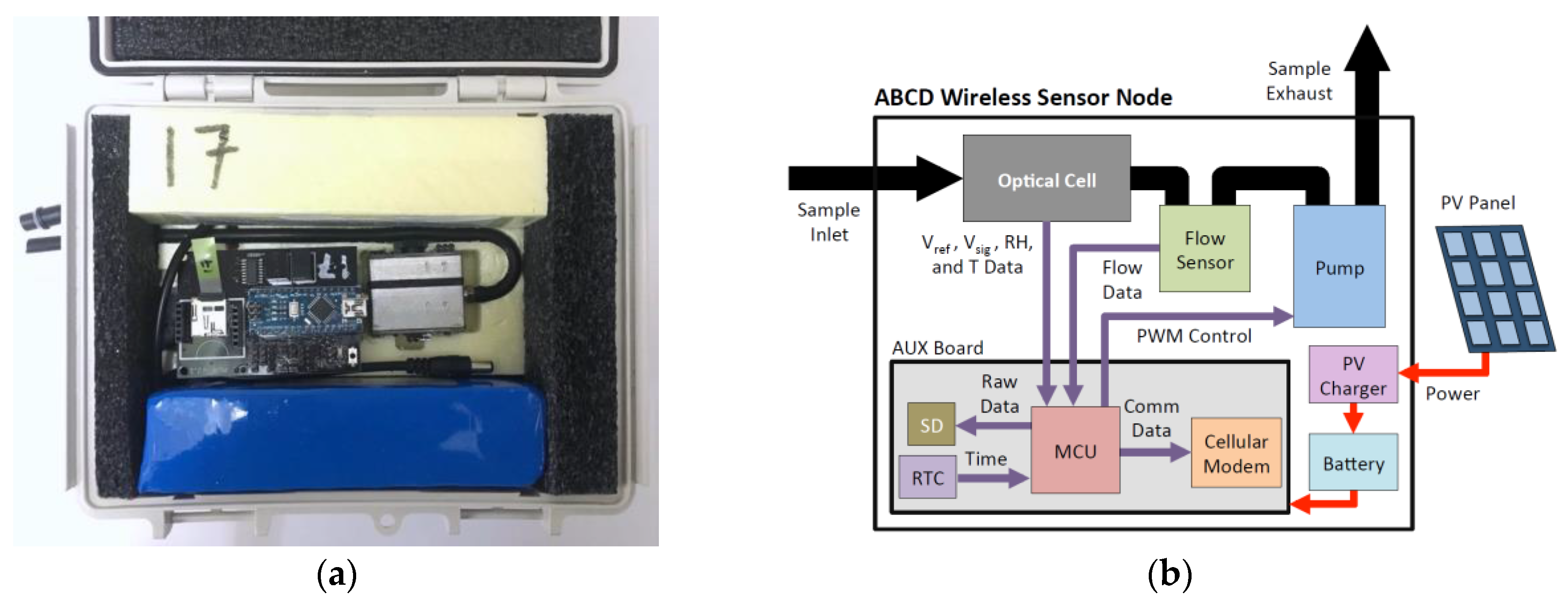
2.1. Aerosol Black Carbon Detector (ABCD)
2.2 Field Validation
3. Results
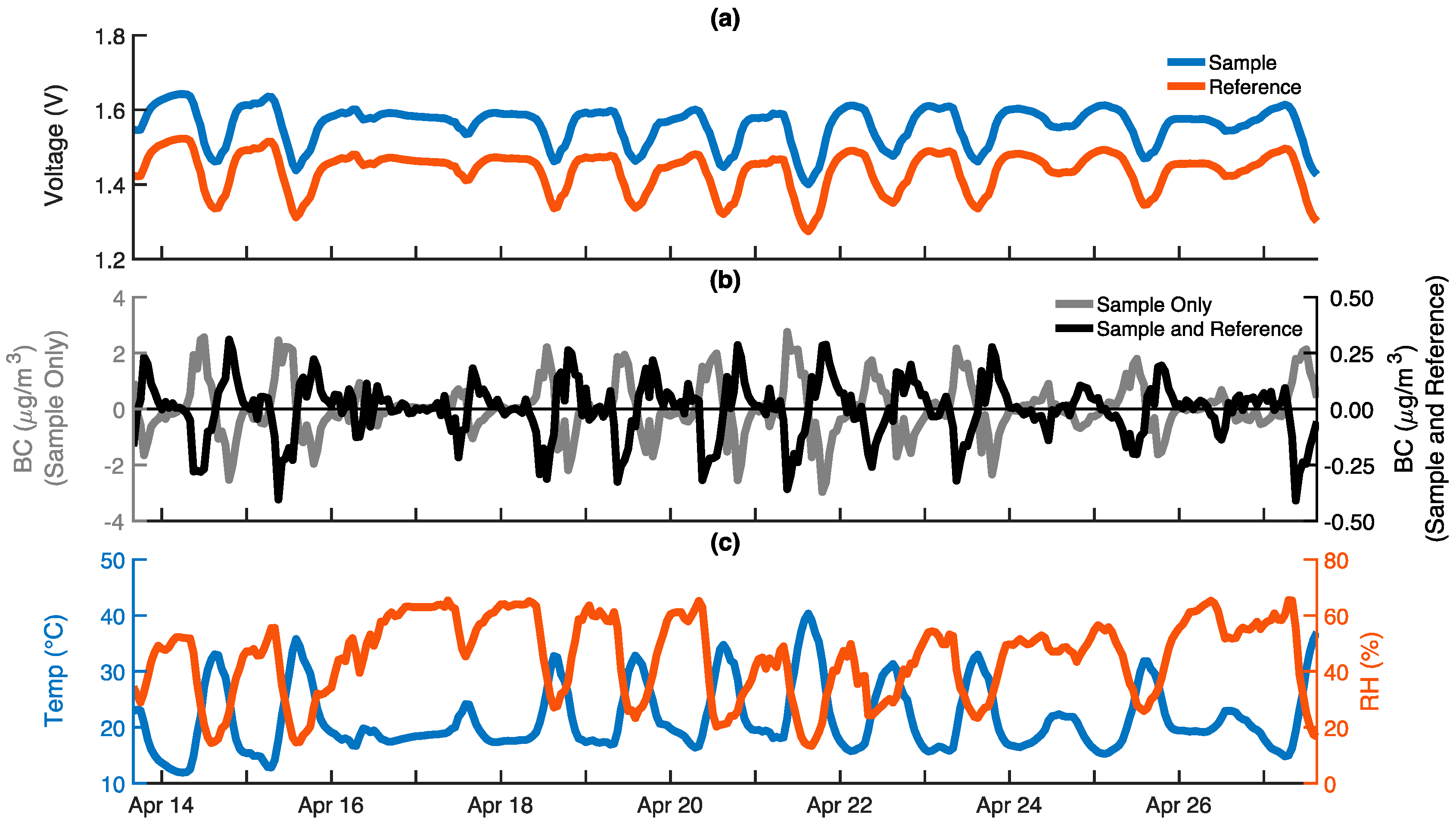
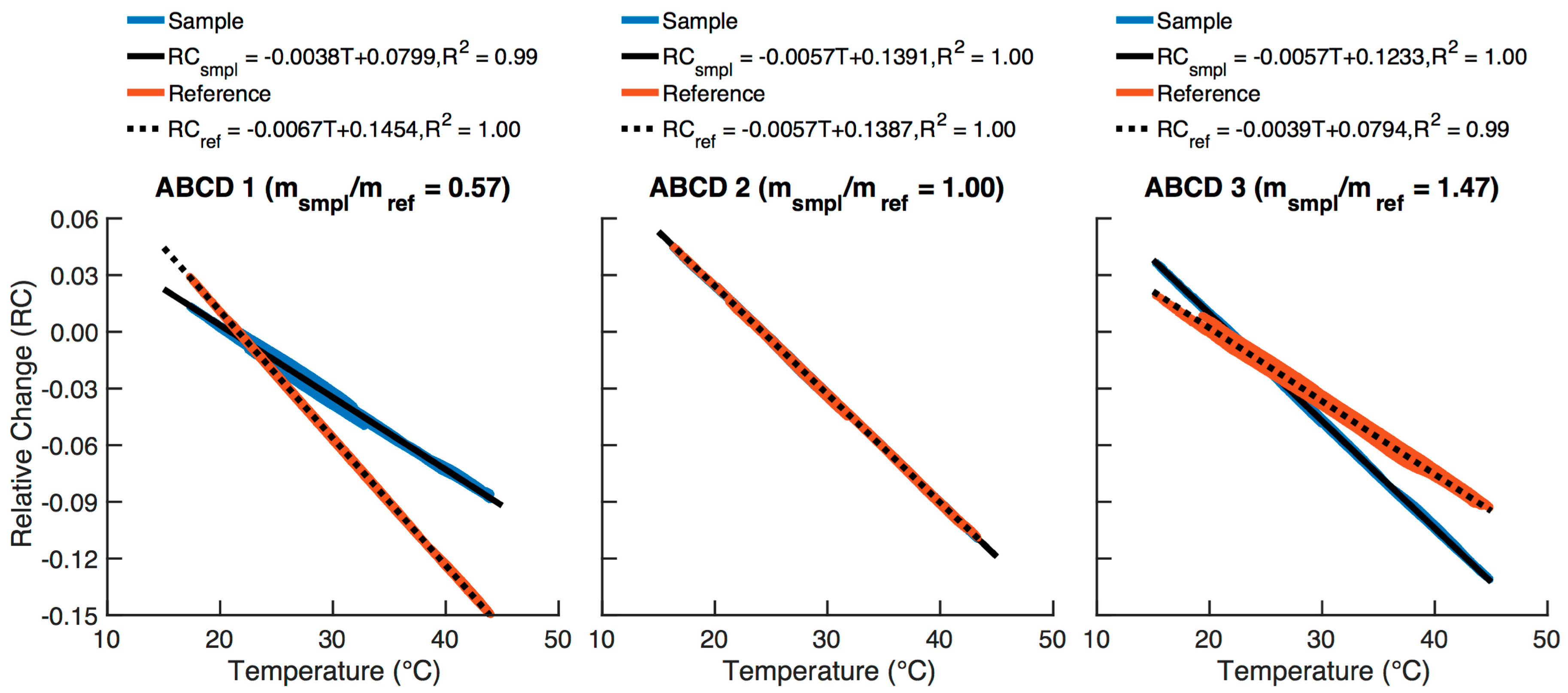
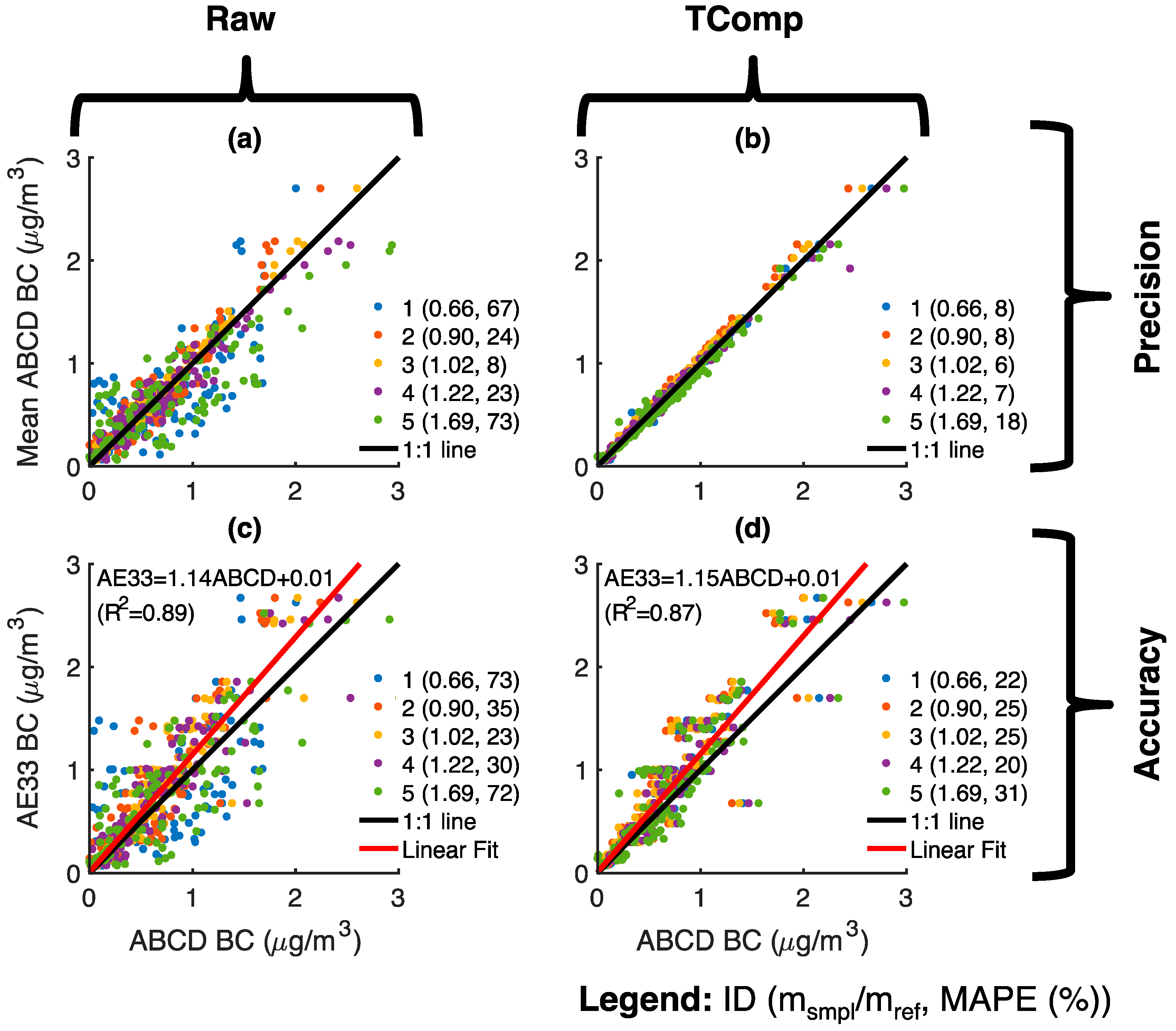
3.1. Measurement Bias from Environmental Fluctuations
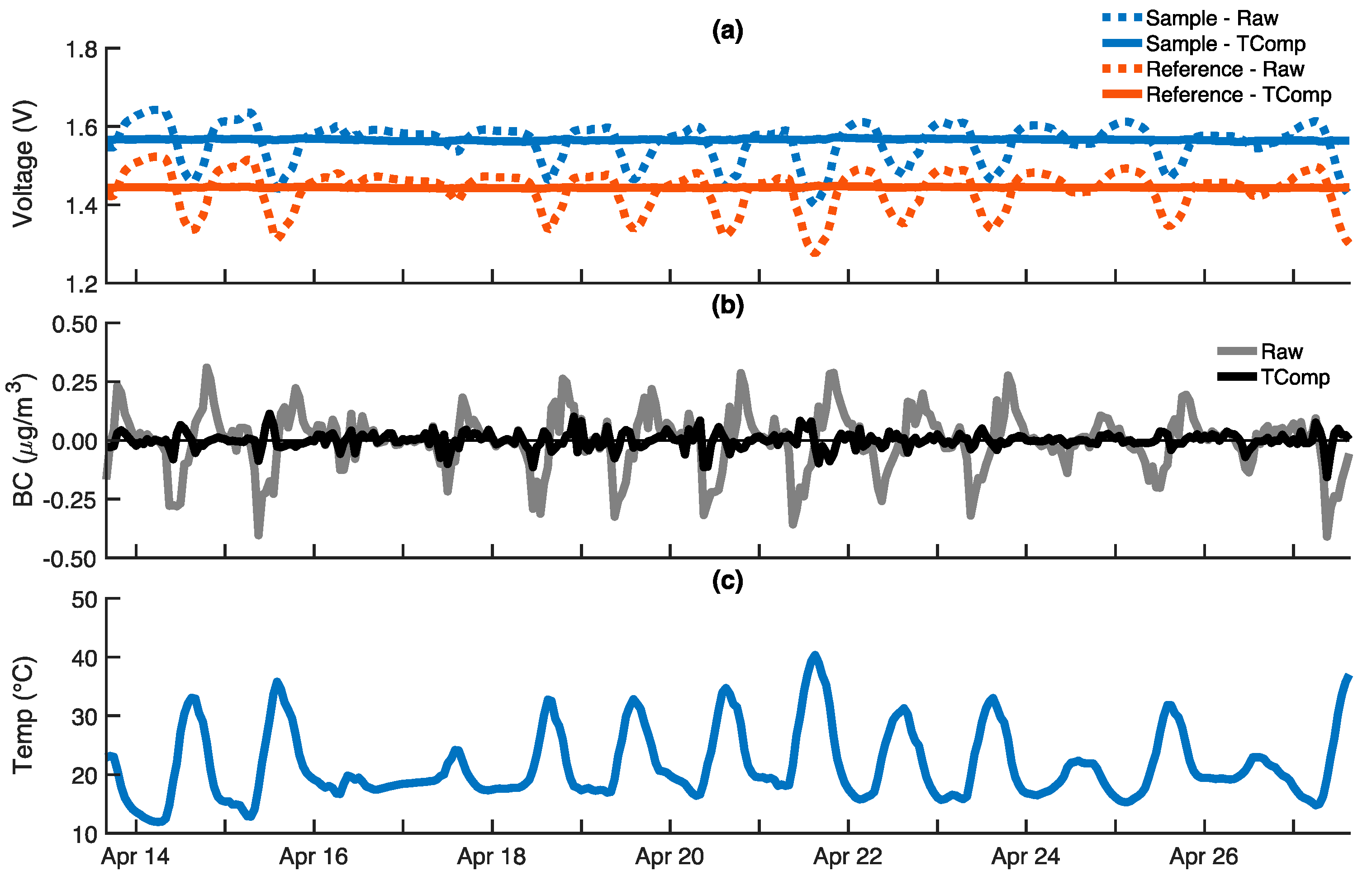
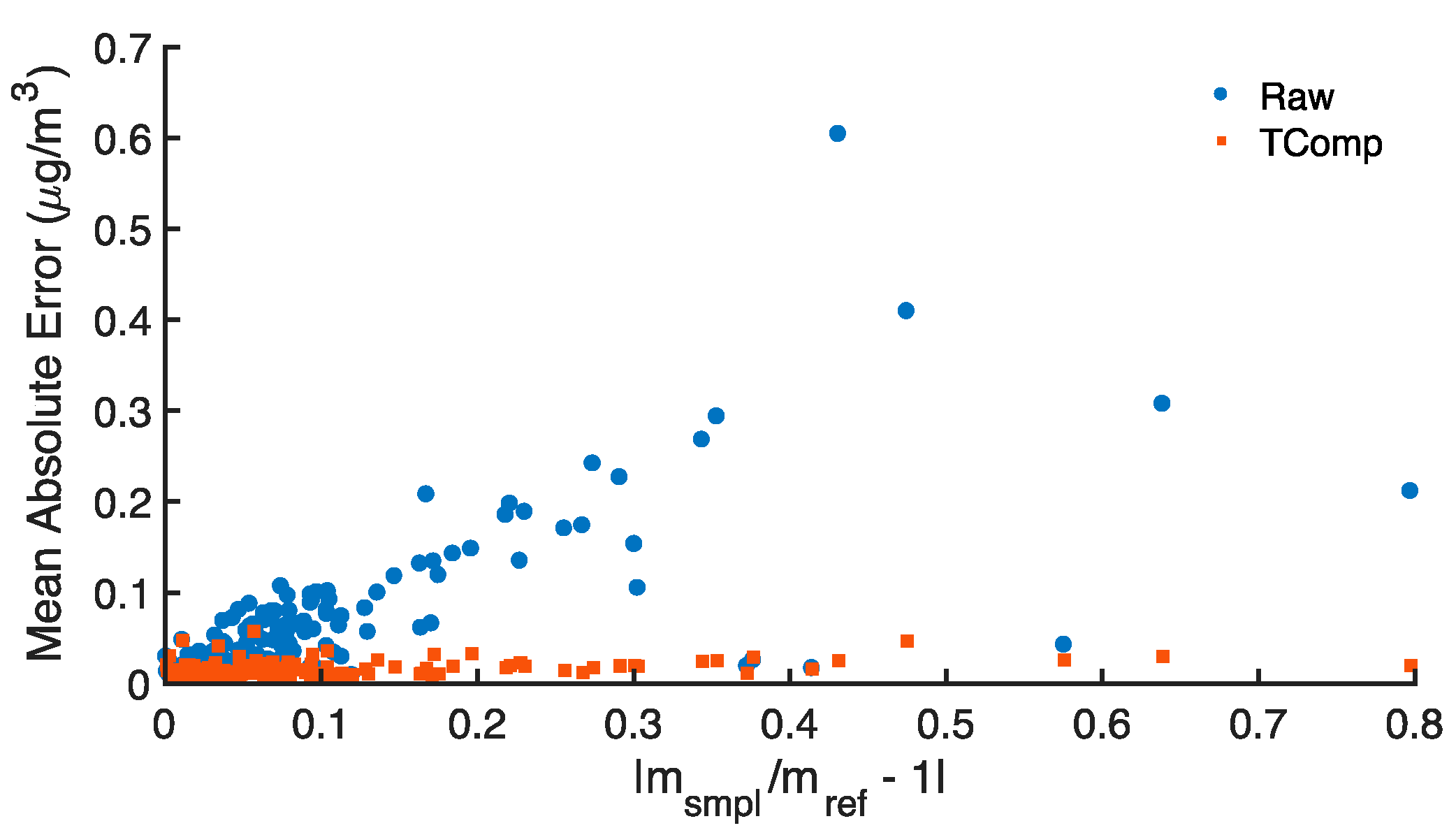
3.2. Temperature Compensation
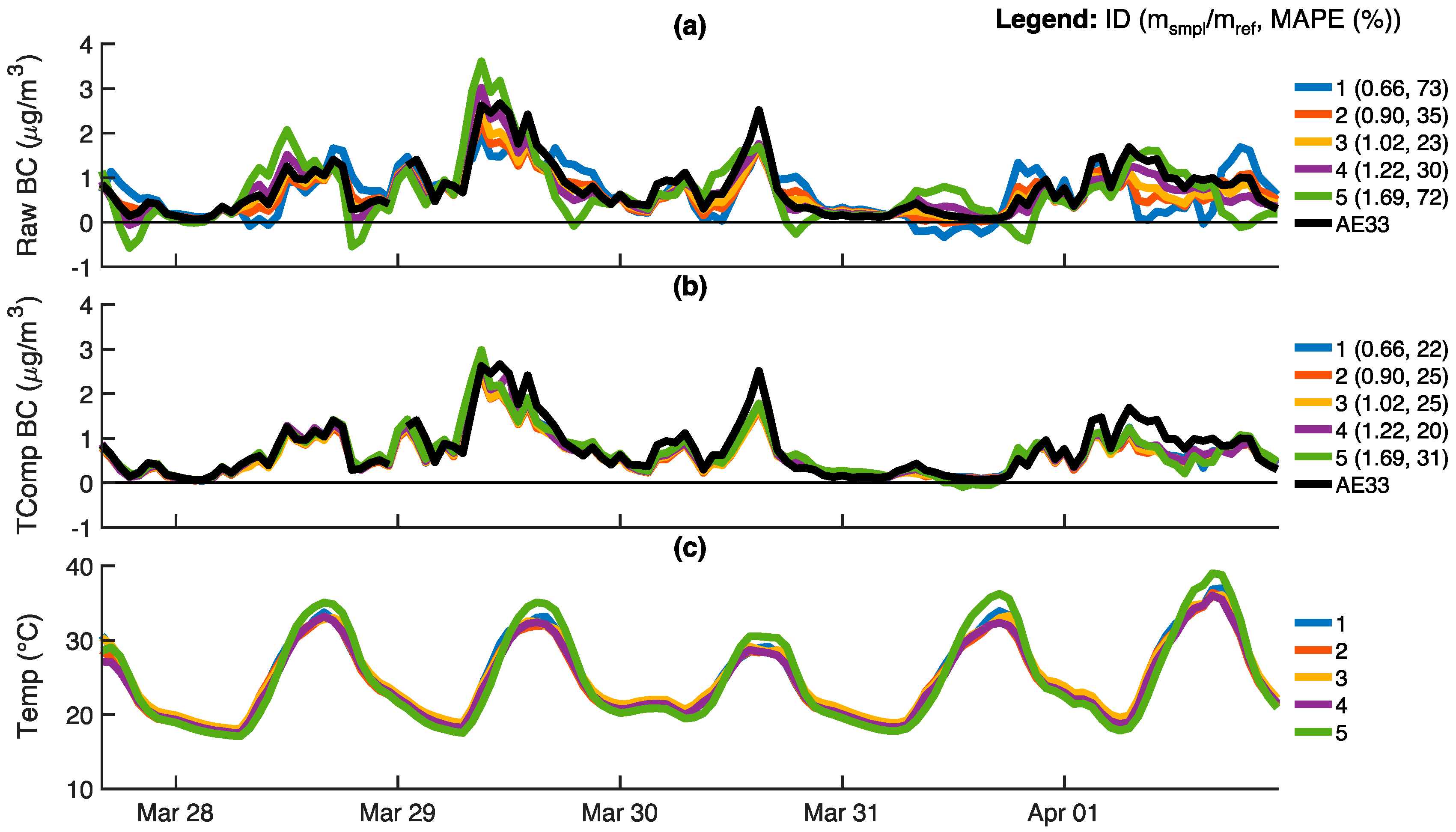
3.3. Field Validation
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B

Appendix C
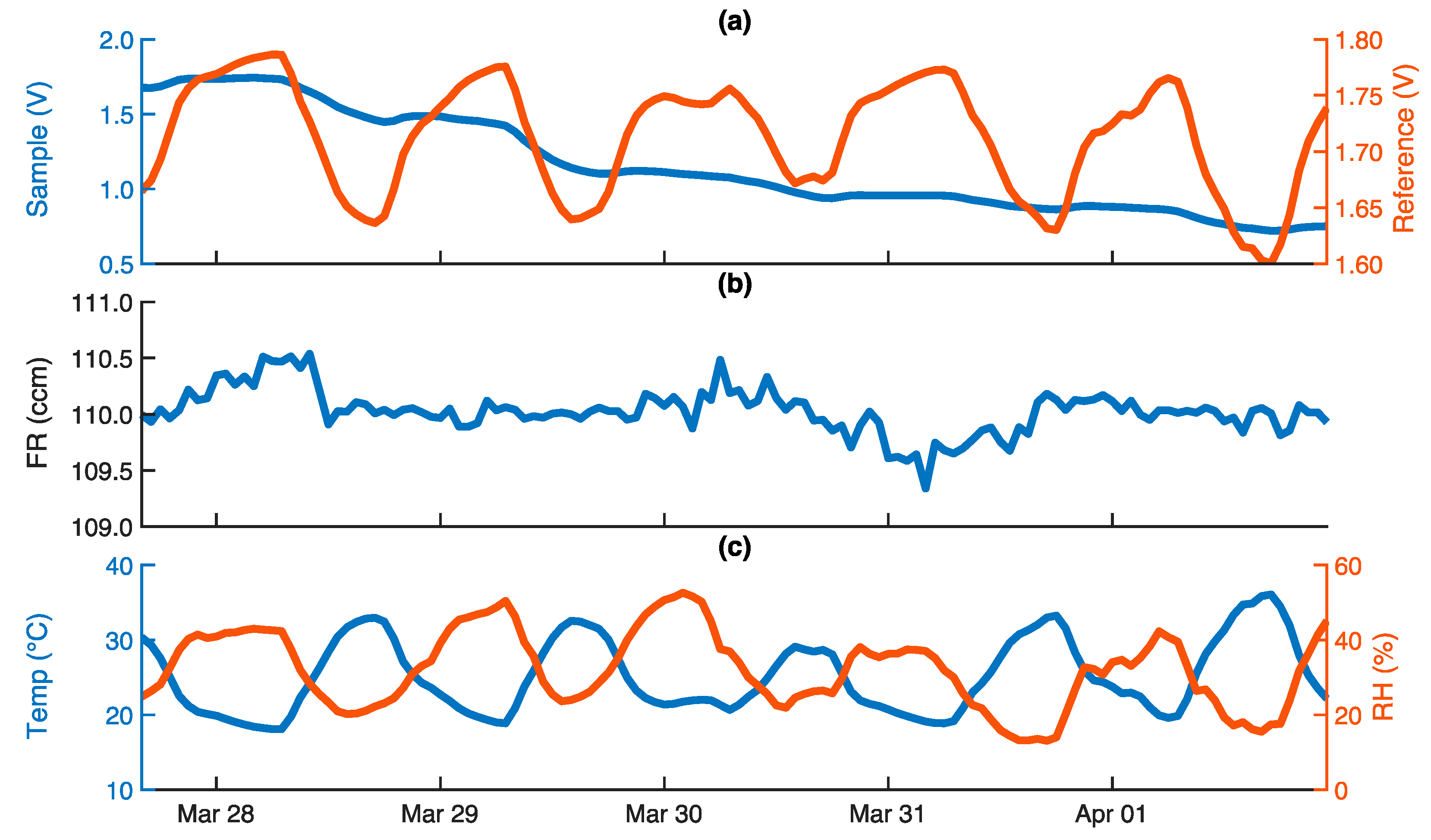
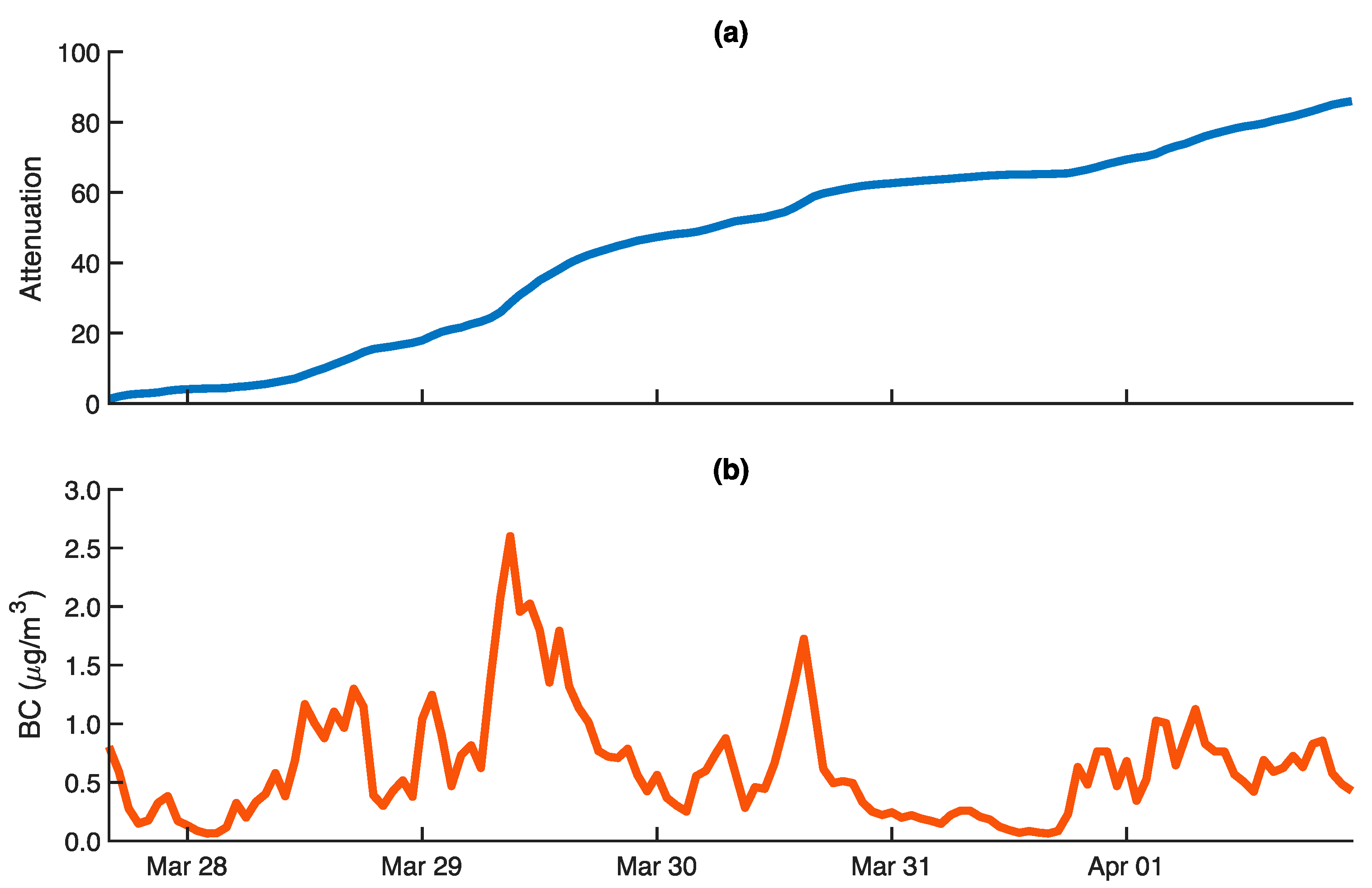
Appendix D
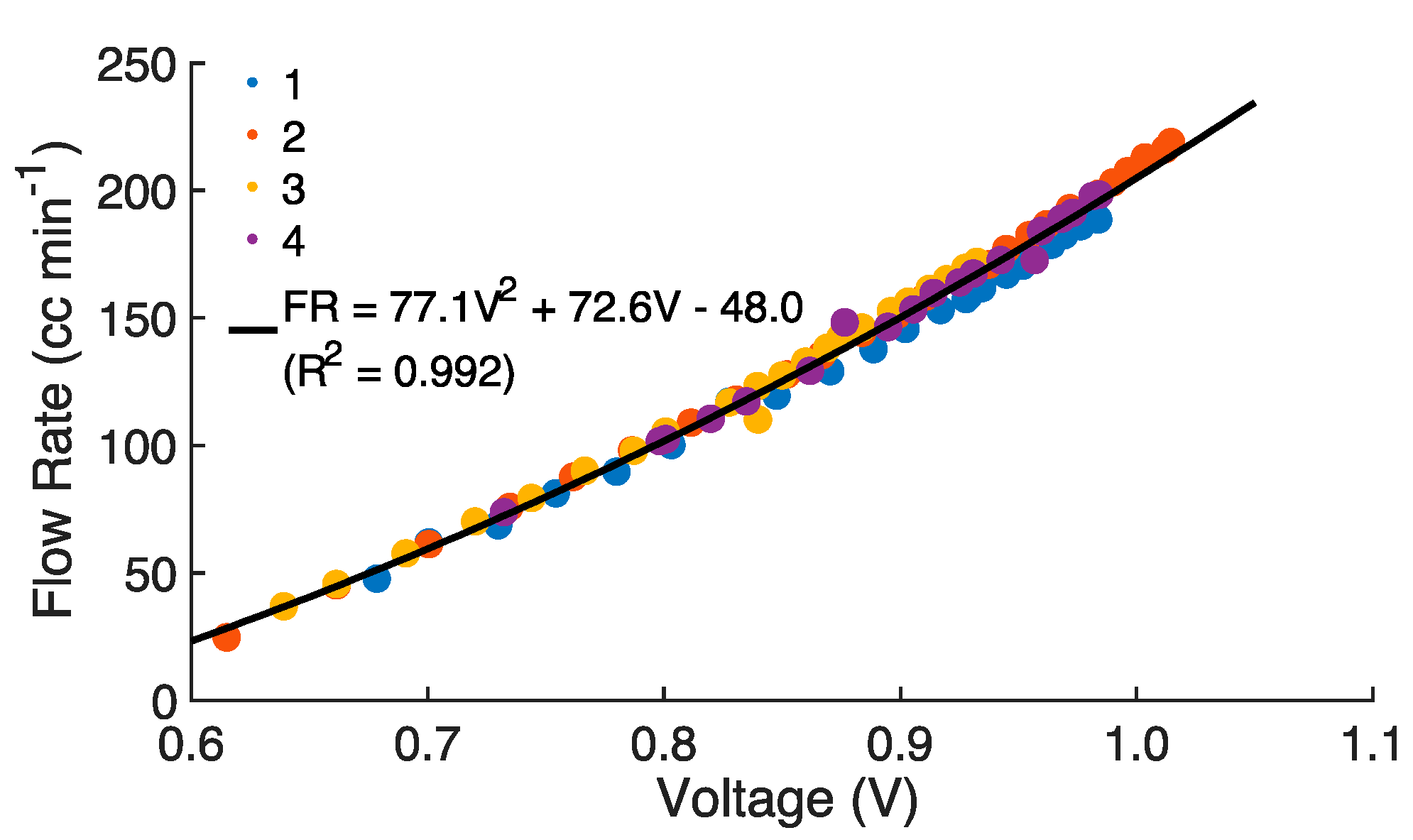
Appendix E
| Component | Manufacturer/Model | Approximate Material Cost (USD) |
|---|---|---|
| Optical Cell | N/A | 100 |
| AUX Board | N/A | 80 |
| Pump | Schwartzer/135 FZ | 125 |
| Flow Sensor | Omron/D6F | 40 |
| Battery | KXD/12 V, 10 AH | 35 |
| Photovoltaic Panel | Shine Solar/18 V, 8 W | 20 |
| Packaging | BUD Industries/NBF-32002 | 20 |
| Miscellaneous 1 | N/A | 10 |
Appendix F
- BC Outlier Filter: Remove all data points where the absolute value of the BC measurement is greater than 100 μg m−3. BC concentrations on this order of magnitude are improbable while sampling ambient air, and instead usually result from hardware errors, such as disconnection or disturbance of the optical cell during field maintenance (changing of filters or batteries).
- High Attenuation Filter: Remove data when measured optical attenuation is greater than 100 units to avoid possible optical saturation effects.
- Flow Rate Filter: Remove all data generated when the ABCD is operating at a flow rate that deviates by more than 5 cc min−1 from the nominal set point (usually 110 cc min−1). It was found that some rotary vane pumps failed during deployment, so the flow rate through the ABCD could not be steadily maintained. Consequently, all data with non-nominal sample flow is discarded to account for pump failures and potentially inaccurate flow rate measurements.
Appendix G
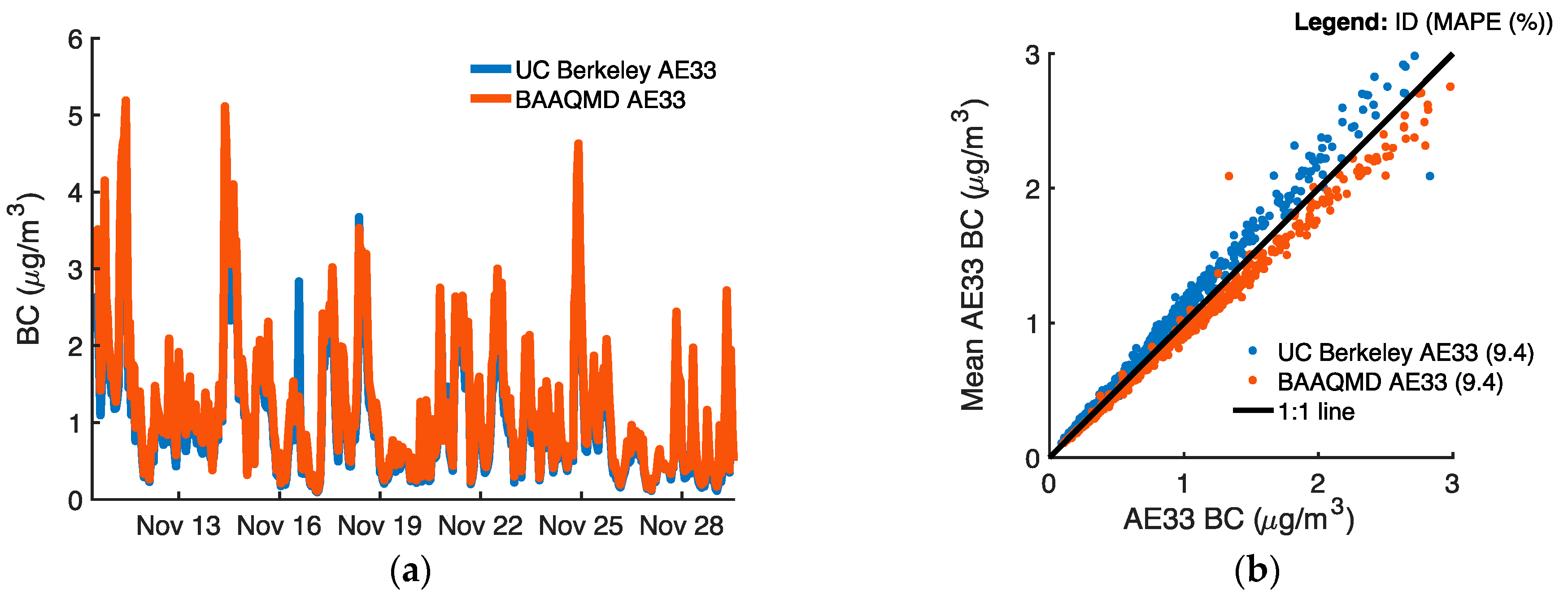
References
- European Parliament. Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe; European Parliament: Brussels, Belgium, 2008.
- Chow, J.C. Measurement Methods to Determine Compliance with Ambient Air Quality Standards for Suspended Particles. J. Air Waste Manag. Assoc. 1995, 45, 320–382. [Google Scholar] [CrossRef] [PubMed]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.W.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The Changing Paradigm of Air Pollution Monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef] [PubMed]
- US Environmental Protection Agency EPA. DRAFT Roadmap for Next Generation Air Monitoring; EPA: Washington, DC, USA, 2013.
- Steinle, S.; Reis, S.; Sabel, C.E. Quantifying human exposure to air pollution—Moving from static monitoring to spatio-temporally resolved personal exposure assessment. Sci. Total Environ. 2013, 443, 184–193. [Google Scholar] [CrossRef] [PubMed]
- De Nazelle, A.; Seto, E.; Donaire-Gonzalez, D.; Mendez, M.; Matamala, J.; Nieuwenhuijsen, M.J.; Jerrett, M. Improving estimates of air pollution exposure through ubiquitous sensing technologies. Environ. Pollut. 2012, 176, 92–99. [Google Scholar] [CrossRef] [PubMed]
- Janssen, N.A.H.; van Vliet, P.H.N.; Arts, F.; Harssema, H.; Brunekreef, B. Assessment of exposure to traffic related air pollution of children attending schools near motorways. Atmos. Environ. 2001, 35, 3875–3884. [Google Scholar] [CrossRef]
- Van Roosbroeck, S.; Wichmann, J.; Janssen, N.A.H.; Hoek, G.; van Wijnen, J.H.; Lebret, E.; Brunekreef, B. Long-term personal exposure to traffic-related air pollution among school children, a validation study. Sci. Total Environ. 2006, 368, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Cross, E.S.; Williams, L.R.; Lewis, D.K.; Magoon, G.R.; Onasch, T.B.; Kaminsky, M.L.; Worsnop, D.R.; Jayne, J.T. Use of electrochemical sensors for measurement of air pollution: Correcting interference response and validating measurements. Atmos. Meas. Tech. 2017, 10, 3575–3588. [Google Scholar] [CrossRef]
- Masson, N.; Piedrahita, R.; Hannigan, M. Quantification Method for Electrolytic Sensors in Long-Term Monitoring of Ambient Air Quality. Sensors 2015, 15, 27283–27302. [Google Scholar] [CrossRef] [PubMed]
- Lewis, A.C.; Lee, J.D.; Edwards, P.M.; Shaw, M.D.; Evans, M.J.; Moller, S.J.; Smith, K.R.; Buckley, J.W.; Ellis, M.; Gillot, S.R.; White, A. Evaluating the performance of low cost chemical sensors for air pollution research. Faraday Discuss. 2016, 189, 85–103. [Google Scholar] [CrossRef] [PubMed]
- Tsujita, W.; Yoshino, A.; Ishida, H.; Moriizumi, T. Gas sensor network for air-pollution monitoring. Sens. Actuators B Chem. 2005, 110, 304–311. [Google Scholar] [CrossRef]
- Budde, M.; Busse, M.; Beigl, M. Investigating the Use of Commodity Dust Sensors for the Embedded Measurement of Particulate Matter. In Proceedings of the Ninth International Conference on Networked Sensing Systems (INSS), Antwerp, Belgium, 11–14 June 2012; pp. 1–4. [Google Scholar]
- Kuula, J.; Mäkelä, T.; Hillamo, R.; Timonen, H. Response Characterization of an Inexpensive Aerosol Sensor. Sensors 2017, 17, 2915. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Kaufman, A.; Hanley, T.; Rice, J.; Garvey, S. Evaluation of Field-Deployed Low Cost PM Sensors; US Environmental Protection Agency (EPA): Washington, DC, USA, 2014.
- Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.J.; McLeod, M.W.; Hodgson, T.F.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atmos. Environ. 2012, 70, 186–203. [Google Scholar] [CrossRef]
- Jiao, W.; Hagler, G.; Williams, R.; Sharpe, R.; Brown, R.; Garver, D.; Judge, R.; Caudill, M.; Rickard, J.; Davis, M.; et al. Community Air Sensor Network (CAIRSENSE) project: Evaluation of low-cost sensor performance in a suburban environment in the southeastern United States. Atmos. Meas. Tech. 2016, 9, 5281–5292. [Google Scholar]
- Gao, M.; Cao, J.; Seto, E. A distributed network of low-cost continuous reading sensors to measure spatiotemporal variations of PM2.5 in Xi’an, China. Environ. Pollut. 2015, 199, 56–65. [Google Scholar] [PubMed]
- Heimann, I.; Bright, V.B.; McLeod, M.W.; Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Jones, R.L. Source attribution of air pollution by spatial scale separation using high spatial density networks of low cost air quality sensors. Atmos. Environ. 2015, 113, 10–19. [Google Scholar] [CrossRef]
- Kanaroglou, P.S.; Jerrett, M.; Morrison, J.; Beckerman, B.; Arain, M.A.; Gilbert, N.L.; Brook, J.R. Establishing an air pollution monitoring network for intra-urban population exposure assessment: A location-allocation approach. Atmos. Environ. 2005, 39, 2399–2409. [Google Scholar]
- Sasser, E.; Hernby, J. Report to Congress on Black Carbon; US Environmental Protection Agency (EPA): Washington, DC, USA, 2012.
- Kim, J.J.; Smorodinsky, S.; Lipsett, M.; Singer, B.C.; Hodgson, A.T.; Ostro, B. Traffic-related Air Pollution near Busy Roads. Am. J. Respir. Crit. Care Med. 2004, 170, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Landrigan, P.J.; Fuller, R.; Adeyi, O.; Arnold, R.; Boufford, J.I. The Lancet Commission on pollution and health. Lancet 2018, 391, 462–512. [Google Scholar] [CrossRef]
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2007; Solomon, S., Qin, D., Manning, M., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 1–1007. [Google Scholar]
- Watson, J.G.; Chow, J.C.; Chen, L.W.A. Summary of Organic and Elemental Carbon/Black Carbon Analysis Methods and Intercomparisons. Aerosol Air Qual. Res. 2005, 5, 65–102. [Google Scholar]
- Lack, D.A.; Moosmüller, H.; McMeeking, G.R.; Chakrabarty, R.K.; Baumgardner, D. Characterizing elemental, equivalent black, and refractory black carbon aerosol particles: A review of techniques, their limitations and uncertainties. Anal. Bioanal Chem. 2013, 406, 99–122. [Google Scholar] [CrossRef] [PubMed]
- Cai, J. Validation of MicroAeth® as a Black Carbon Monitor for Fixed-Site Measurement and Optimization for Personal Exposure Characterization. Aerosol Air Qual. Res. 2014, 14, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Arnott, W.P. Photoacoustic and filter-based ambient aerosol light absorption measurements: Instrument comparisons and the role of relative humidity. J. Geophys. Res. 2003, 108, 15-1–15-11. [Google Scholar] [CrossRef]
- Springston, S. Particle Soot Absorption Photometer Instrument Handbook; US Department of Energy: Washington, DC, USA, 2016; pp. 1–28.
- Hansen, A.D.A.; Rosen, H.; Novakov, T. The Aethalometer—An Instrument for the Real-Time Measurement of Optical Absorption by Aerosol Particles. Sci. Total Environ. 1984, 36, 191–196. [Google Scholar] [CrossRef]
- Petzold, A.; Schönlinner, M. Multi-angle absorption photometry—A new method for the measurement of aerosol light absorption and atmospheric black carbon. J. Aerosol Sci. 2004, 35, 421–441. [Google Scholar] [CrossRef]
- Kirchstetter, T.W.; Thatcher, T.L. Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation. Atmos. Chem. Phys. 2012, 12, 6067–6072. [Google Scholar] [CrossRef]
- Ramachandran, S.; Rajesh, T.A. Black carbon aerosol mass concentrations over Ahmedabad, an urban location in western India: Comparison with urban sites in Asia, Europe, Canada, and the United States. J. Geophys. Res. 2007, 112, 817–819. [Google Scholar] [CrossRef]
- Bodhaine, B.A. Aerosol Absorption Measurements at Barrow, Mauna Loa and the South Pole. J. Geophys. Res. 1995, 100, 8967–8975. [Google Scholar] [CrossRef]
- Yang, M.; Howell, S.G.; Huebert, B.J. Attribution of aerosol light absorption to black carbon, brown carbon, and dust in China—Interpretations of atmospheric measurements during EAST-AIRE. Atmos. Chem. Phys. 2009, 9, 1–16. [Google Scholar] [CrossRef]
- Pall Life Sciences. Pallflex® Filters: Emfab™, Fiberfilm™, and Tissuquartz™ Filters; Pall Life Sciences: Ann Arbor, MI, USA, 2002. [Google Scholar]
- Jimenez, J.; Claiborn, C.; Larson, T.; Gould, T.; Kirchstetter, T.; Gundel, L. Loading Effect Correction for Real-Time Aethalometer Measurements of Fresh Diesel Soot. J. Air Waste Manag. Assoc. 2007, 57, 868–873. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.H.; Yang, L.S. Correcting aethalometer black carbon data for measurement artifacts by using inter-comparison methodology based on two different light attenuation increasing rates. Atmos. Meas. Tech. Discuss. 2015, 8, 2851–2879. [Google Scholar] [CrossRef]
- Virkkula, A.; Mäkelä, T.; Hillamo, R.; Yli-Tuomi, T.; Hirsikko, A.; Hämeri, K.; Koponen, I.K. A Simple Procedure for Correcting Loading Effects of Aethalometer Data. J. Air Waste Manag. Assoc. 2007, 57, 1214–1222. [Google Scholar] [CrossRef] [PubMed]
- Fairchild Semiconductor Corporation. QED121, QED122, QED123 Plastic Infrared Light Emitting Diode; Fairchild Semiconductor Corporation: Sunnyvale, CA, USA, 2008; pp. 1–8. [Google Scholar]
- Texas Instruments. OPT101 Monolithic Photodiode and Single-Supply Transimpedance Amplifier; Texas Instruments: Dallas, TX, USA, 2015. [Google Scholar]
- Drinovec, L.; Močnik, G.; Zotter, P.; Prévôt, A.S.H.; Ruckstuhl, C.; Coz, E.; Rupakheti, M.; Sciare, J.; Müller, T.; Wiedensohler, A.; et al. The “dual-spot” Aethalometer: An improved measurement of aerosol black carbon with real-time loading compensation. Atmos. Meas. Tech. 2015, 8, 1965–1979. [Google Scholar] [CrossRef]
- Cheng, Y.-H. Real-Time Performance of the microAeth® AE51 and the Effects of Aerosol Loading on Its Measurement Results at a Traffic Site. Aerosol Air Qual. Res. 2013, 13, 1853–1863. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caubel, J.J.; Cados, T.E.; Kirchstetter, T.W. A New Black Carbon Sensor for Dense Air Quality Monitoring Networks. Sensors 2018, 18, 738. https://doi.org/10.3390/s18030738
Caubel JJ, Cados TE, Kirchstetter TW. A New Black Carbon Sensor for Dense Air Quality Monitoring Networks. Sensors. 2018; 18(3):738. https://doi.org/10.3390/s18030738
Chicago/Turabian StyleCaubel, Julien J., Troy E. Cados, and Thomas W. Kirchstetter. 2018. "A New Black Carbon Sensor for Dense Air Quality Monitoring Networks" Sensors 18, no. 3: 738. https://doi.org/10.3390/s18030738
APA StyleCaubel, J. J., Cados, T. E., & Kirchstetter, T. W. (2018). A New Black Carbon Sensor for Dense Air Quality Monitoring Networks. Sensors, 18(3), 738. https://doi.org/10.3390/s18030738




