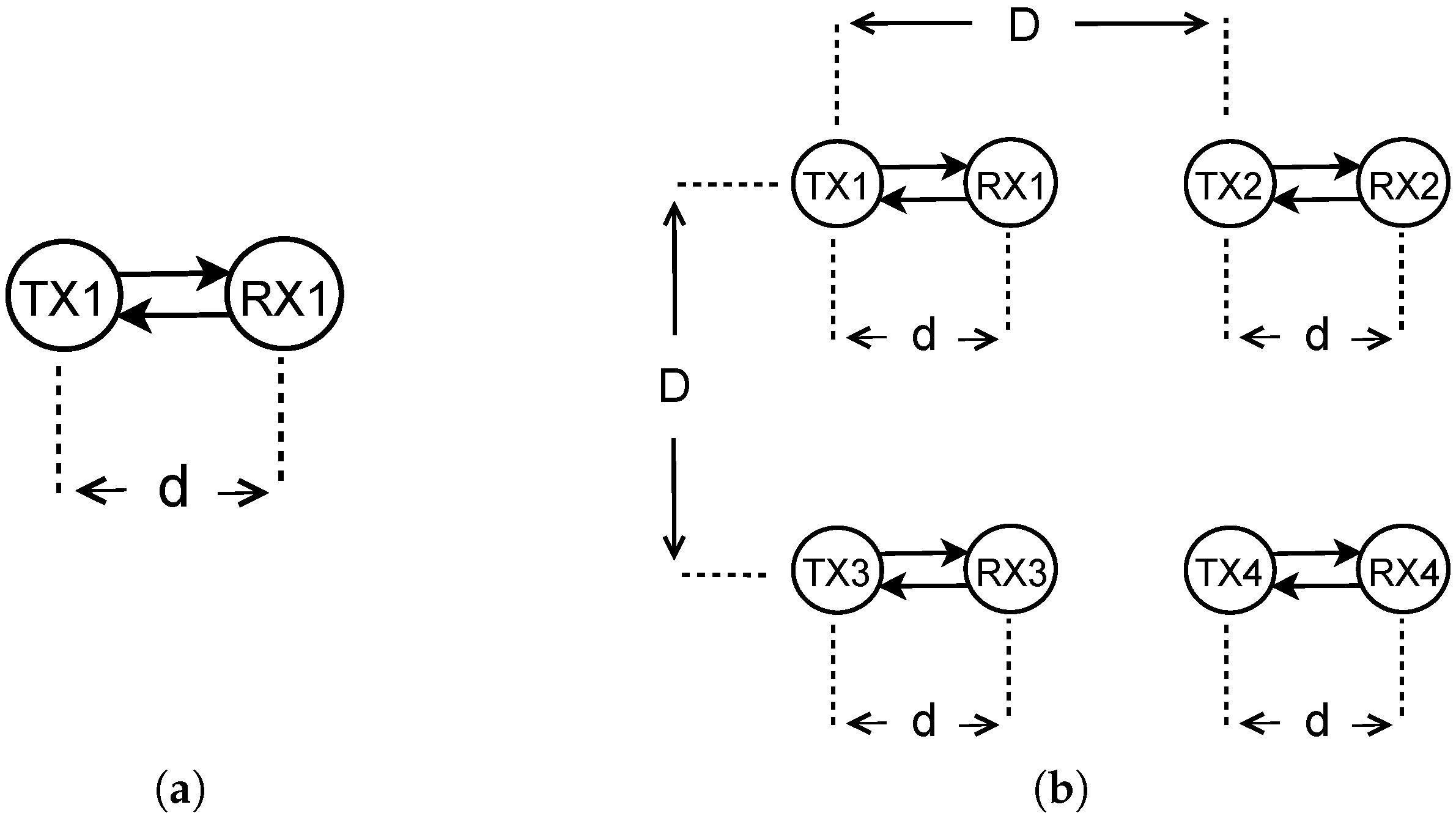
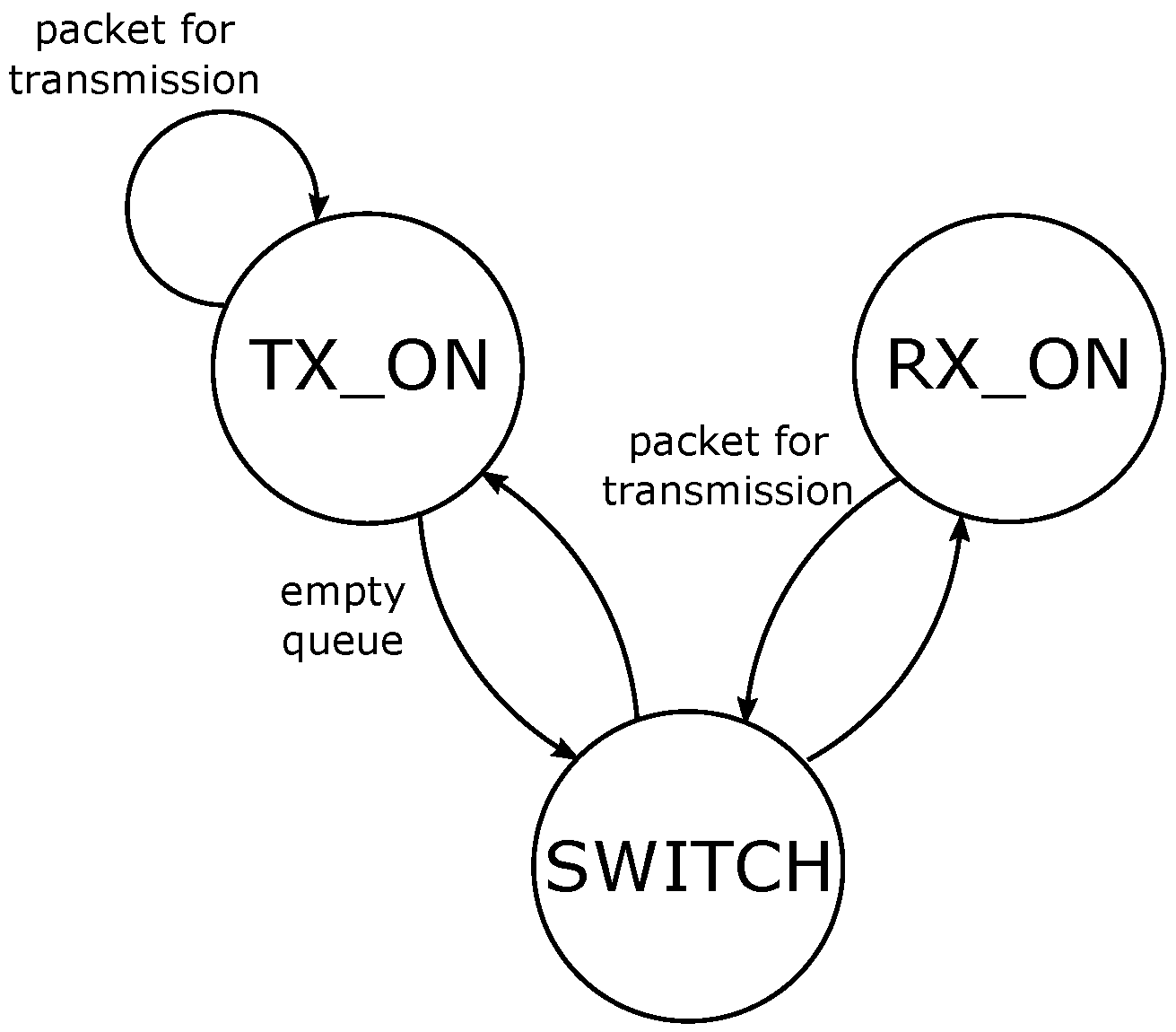
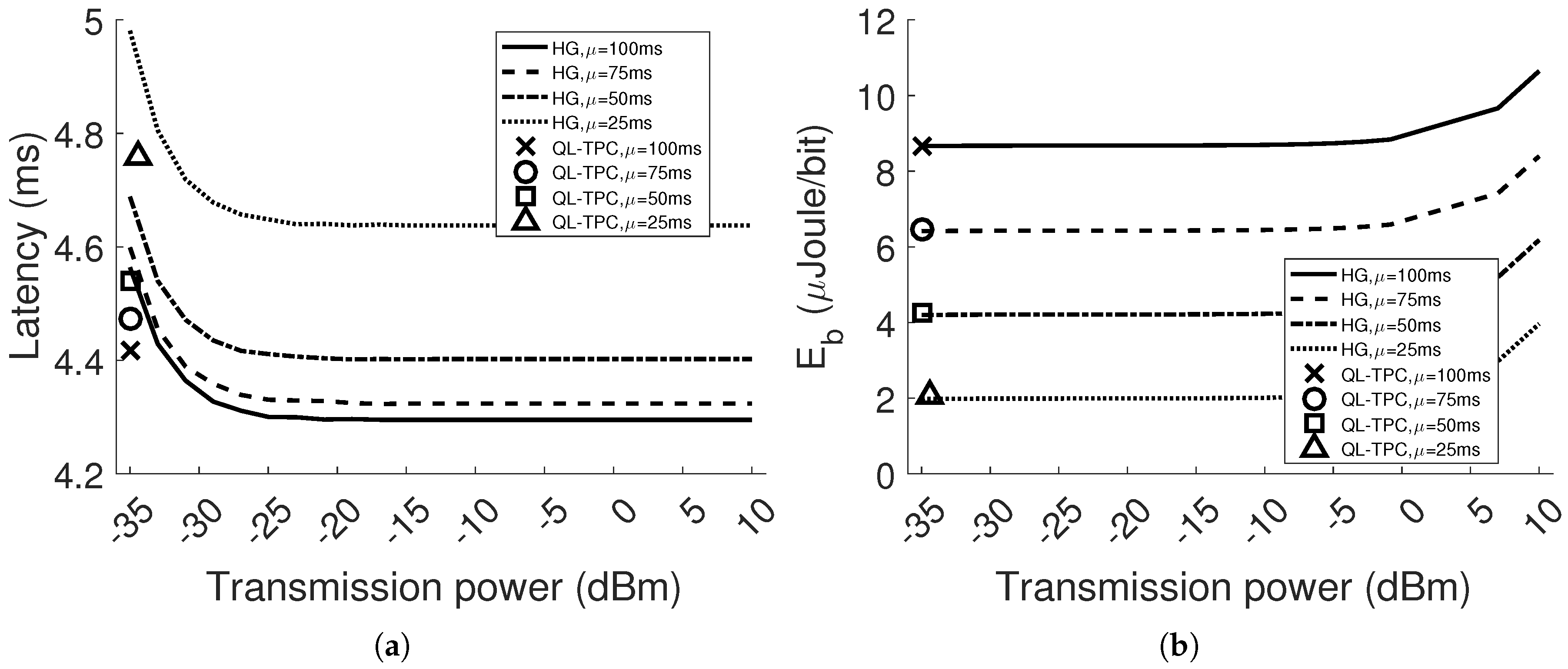
1. Introduction
Wireless Sensor Networks (WSNs) are dense mesh networks, thus techniques of multiple access to the medium are necessary to manage the communications among the nodes [
1]. Such techniques suggest multiple transmissions from different sources, which should not interfere with one another. The transmissions can be scheduled in various dimensions. For instance, in the case of Time Division Multiple Access (TDMA), the time is divided in slots, which are assigned to each source for transmission. Only one stream of information can occur per slot, so multiple transmissions are serialized. In Frequency Division Multiple Access (FDMA), the traffic of the sources are parallelized in frequency per allocated channel. Simultaneous communications can happen, proportionally to the number of channels available. In Code Division Multiple Access (CDMA), transmitters can send packets at the same time, using orthogonal codes multiplied to the symbols that are transmitted/received. In this case, the number of simultaneous transmissions is limited to the number of orthogonal codes. In addition, two more techniques allow concurrent transmissions: Space Division Multiple Access (SDMA) and Carrier Sense Multiple Access (CSMA). These techniques are very sensitive to the dynamics of the network. In SDMA, the communications are confined in zones of the network to reduce contention, while maintaining the connectivity of the network. Using CSMA, the spectrum is scanned and analysed to discover the interested carrier. Both SDMA and CSMA are regulated by either a standard or a de facto protocol. Their advantage is that communications are flexible and decentralized, without the need of synchronization as in TDMA and FDMA. The drawback is that they do not ensure a network free of collision. Thus, the design of the regulations is important for the minimization of the collisions.
Spatial reuse and contention mitigation in SDMA are obtained by dimming the transmission power of the nodes in a network. The decision of the transmission power is dependent on many factors: distance between transmitter and receiver, density of the network, energy available by the nodes, fading of the channel, mobility and performance constraints. In particular, two fields of protocols can be considered for transmission power decision, namely Topology Control (TC) and Transmission Power Control (TPC) [
2]. The former acts at the network layer, thus the value of transmission power per node is chosen with respect to the routing path that the traffic can take to reach the destination. The path can either be point-to-point or multi-hop with variable number of hops. Unlike TC, TPC is link-based, used only for point-to-point communications by means of link quality monitoring.
TPC is used in WSNs, whereby energy and spectrum efficiency are particularly critical. Energy consumption is a typical problem, given the constrained resources of the sensor nodes, including limited battery capacity [
3]. The latter should guarantee a long period of lifetime, more than a decade, where the sensor nodes operate without human intervention [
4]. For this reason, sleeping techniques for energy efficiency are proposed in the literature to carefully allocate operational time and reduce idle periods [
5,
6].
WSNs were initially developed as independent, isolated entities for Machine to Machine (M2M) communications, providing simple operations, such as the monitoring of physical phenomena and executing actions. Therefore, the energy efficiency was prioritized by researchers, neglecting the Quality of Service (QoS). Instead, in the context of Internet of Things (IoT), WSNs are interconnected with other networks, providing services to users through Internet (e.g., smart meters [
7]). Hence, QoS becomes more relevant, with regard to network reliability, to respect performance requirements of various applications [
8].
TPC is a widely studied topic [
9], but all the solutions provided up to now are not sufficient for predicting the link quality required to adapt the transmission power to any environment [
10,
11]. In literature, most of the protocols can be categorized in proactive and reactive classes [
12]. In the former case, they use algorithms that are either based on empirical studies or analytical models [
13,
14,
15,
16]. In empirical studies, the devices evaluate the link quality of the wireless channel, which is used as a metric for the transmission power selection. The drawback in this approach is that unexpected changes in the environment are not considered, thus the nodes are unprepared and may take wrong actions, sacrificing the network performance. Instead, the algorithms based on analytical models are founded on theoretical basis. In the reactive case, the link quality is continuously monitored and compared with a threshold to adjust the transmission power, adapting to changes in the environment only after these have been sensed [
17,
18,
19,
20]. Past events are not accounted for and the result is that transmission power is left to oscillate due to the variability of the channel conditions. This is particularly so, because the link quality varies often in space and time.
To overcome the disadvantages of the proactive and reactive techniques, machine learning represents an attractive solution [
21] to reach a defined goal by learning the dynamics of the WSNs [
22,
23], predicting and adapting the transmission power values in different conditions. The objective is making WSNs autonomous without the intervention of developers and users to set the transmission power. To the best of our knowledge, only few contributions have applied machine learning in TPC, mainly Reinforcement Learning (RL) and fuzzy logic [
12]. RL in WSNs has been used in literature but mainly for path selection in routing protocols and sleeping techniques, maintaining constant learning factors [
24,
25,
26]. Static values would either bring the system slowly to convergence or make the system too reactive if the learning factor is constantly low or high respectively. In parallel, a wrong calibration of the explorative policy influences again the speed of convergence and the optimality of the reached value.
Given the density of WSNs and the unreliability of the wireless channel, a centralized approach would be inefficient and resource consuming, with waste of bandwidth for the transfer of information to a central node, risk of packet loss, long packet delay and energy consumption for the nodes involved in the routing process [
27]. For this reason, we are interested in developing a distributed TPC protocol. In such a context, the nodes have to coordinate among each other to efficiently allocate the resources [
28,
29]. Otherwise, if hundreds of smart objects compete for wireless spectrum, it is unimaginable for them to employ aggressive and power-raising policies in face of channel congestion [
30]. Nodes should rather cooperate with one another, which requires them to strive for minimum transmission power. In a cooperative approach, every node tunes its transmission power towards a global goal (e.g., interference mitigation and energy savings by transmission power minimization) [
31].
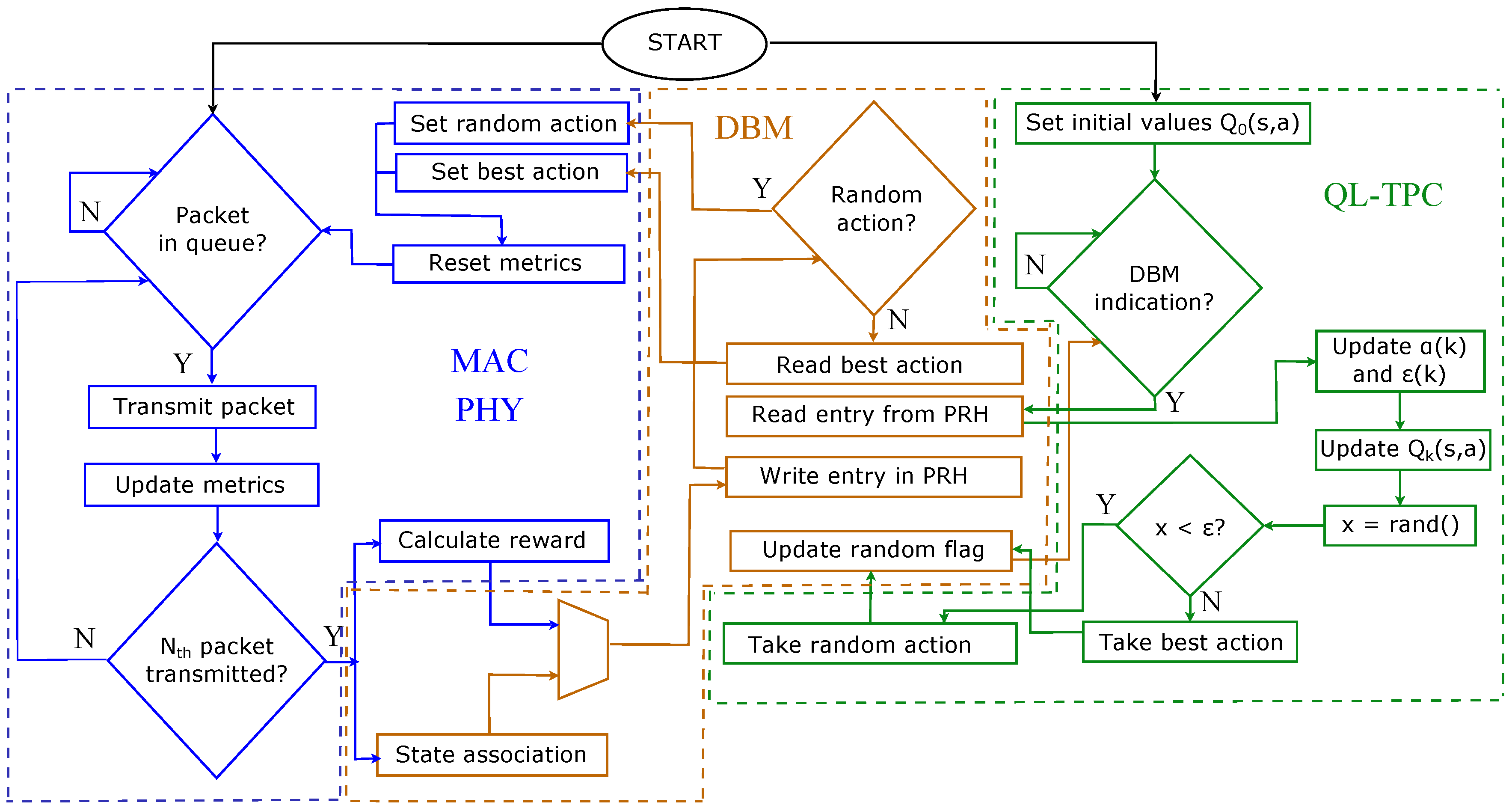
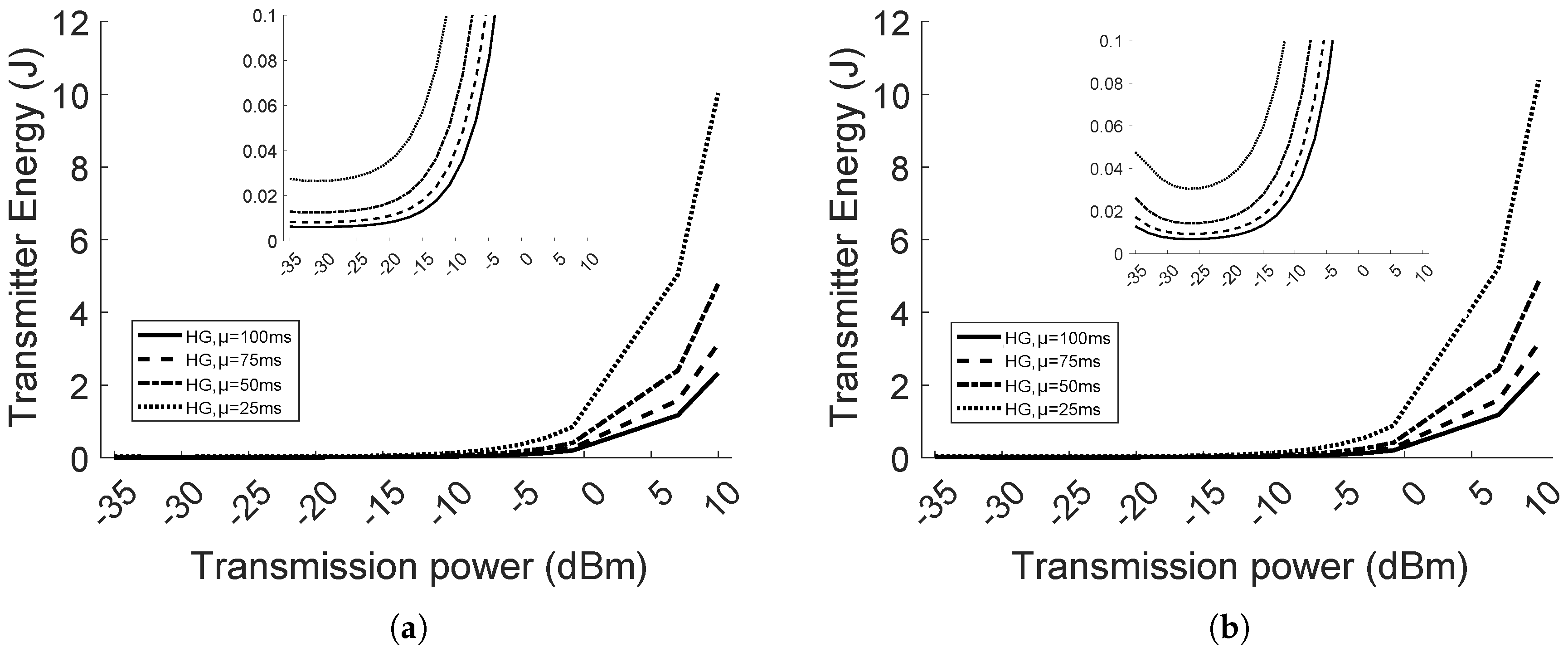
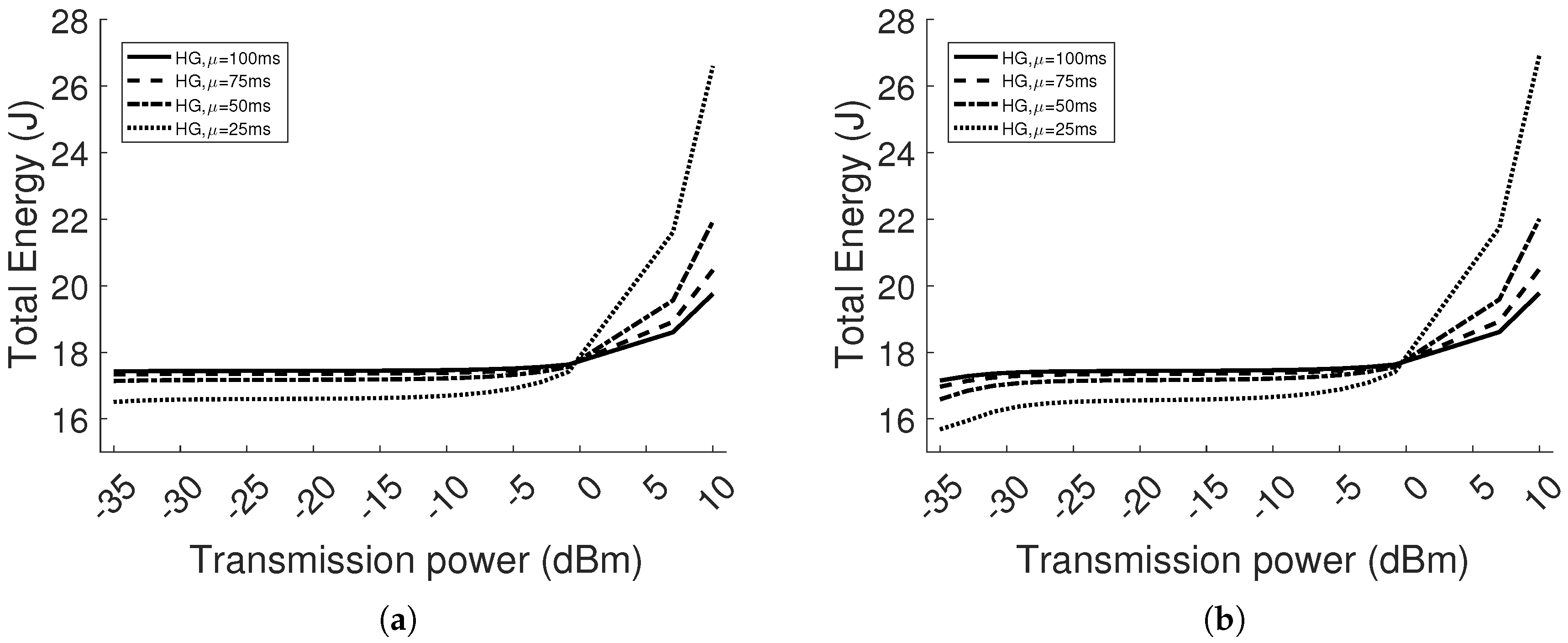
In this paper, we propose a smart protocol, as the result of a RL algorithm (i.e., Q-learning) and TPC integration. The protocol is implemented in both the NS3 network simulator and Contiki OS for sensor devices. In NS3, we test the protocol in two scenarios: single agent and multi-agent WSNs, where one agent is the transmitter in a point-to-point communication. For each scenario, the traffic load and the distance between one transmitter and its receiver vary. A comparison is performed with Homogeneous networks (HG), in which nodes transmit at one constant power level, considering all available power levels. In each case, network performance is evaluated in terms of Packet Reception Ratio (PRR), packet delay and energy per bit. The comparison is meant to show the benefits of the learning protocol with respect to choosing an arbitrary transmission power. HG is also considered the reference for the performance of the network, indicating the transmission power levels at which the nodes should learn to set.
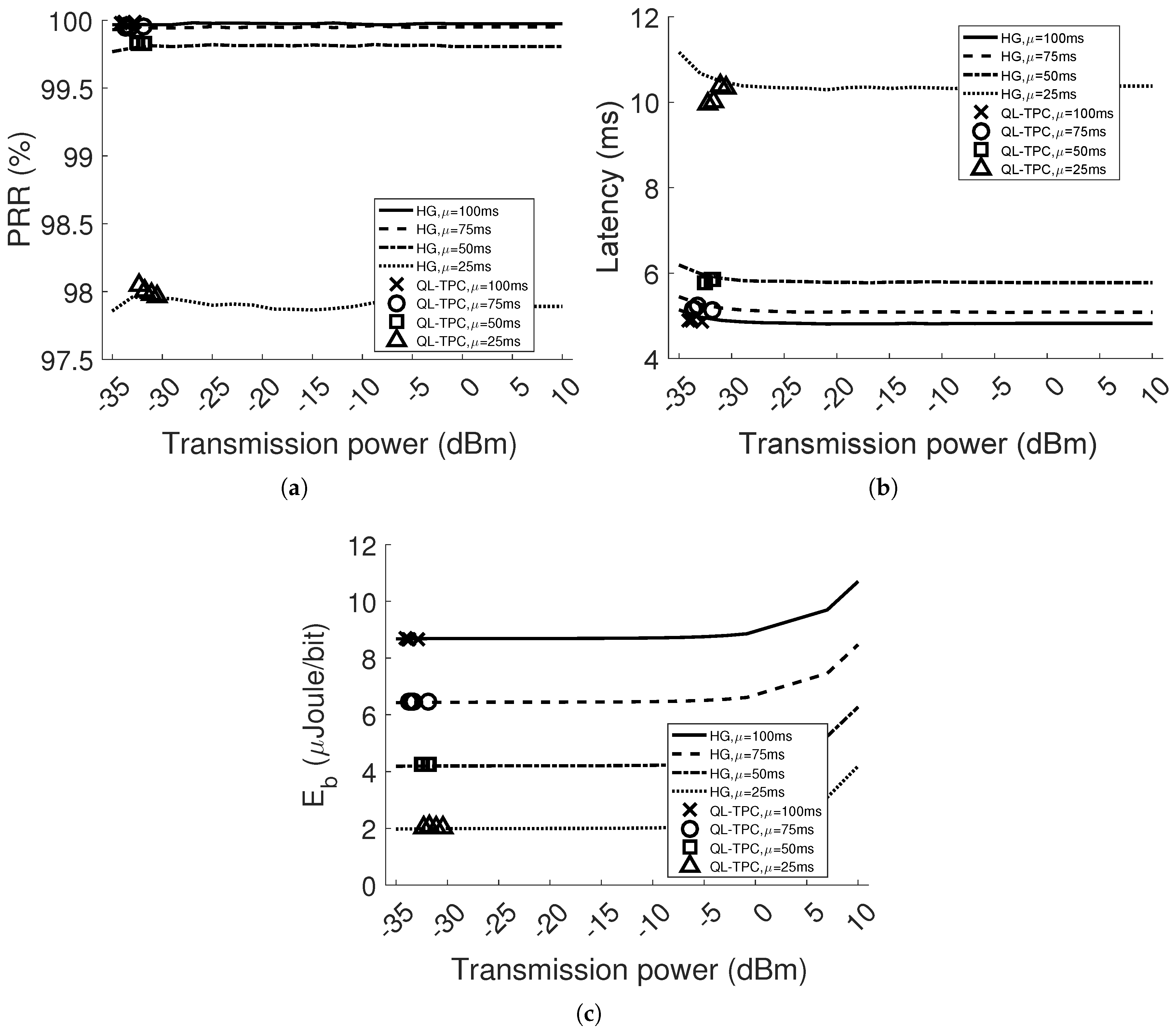
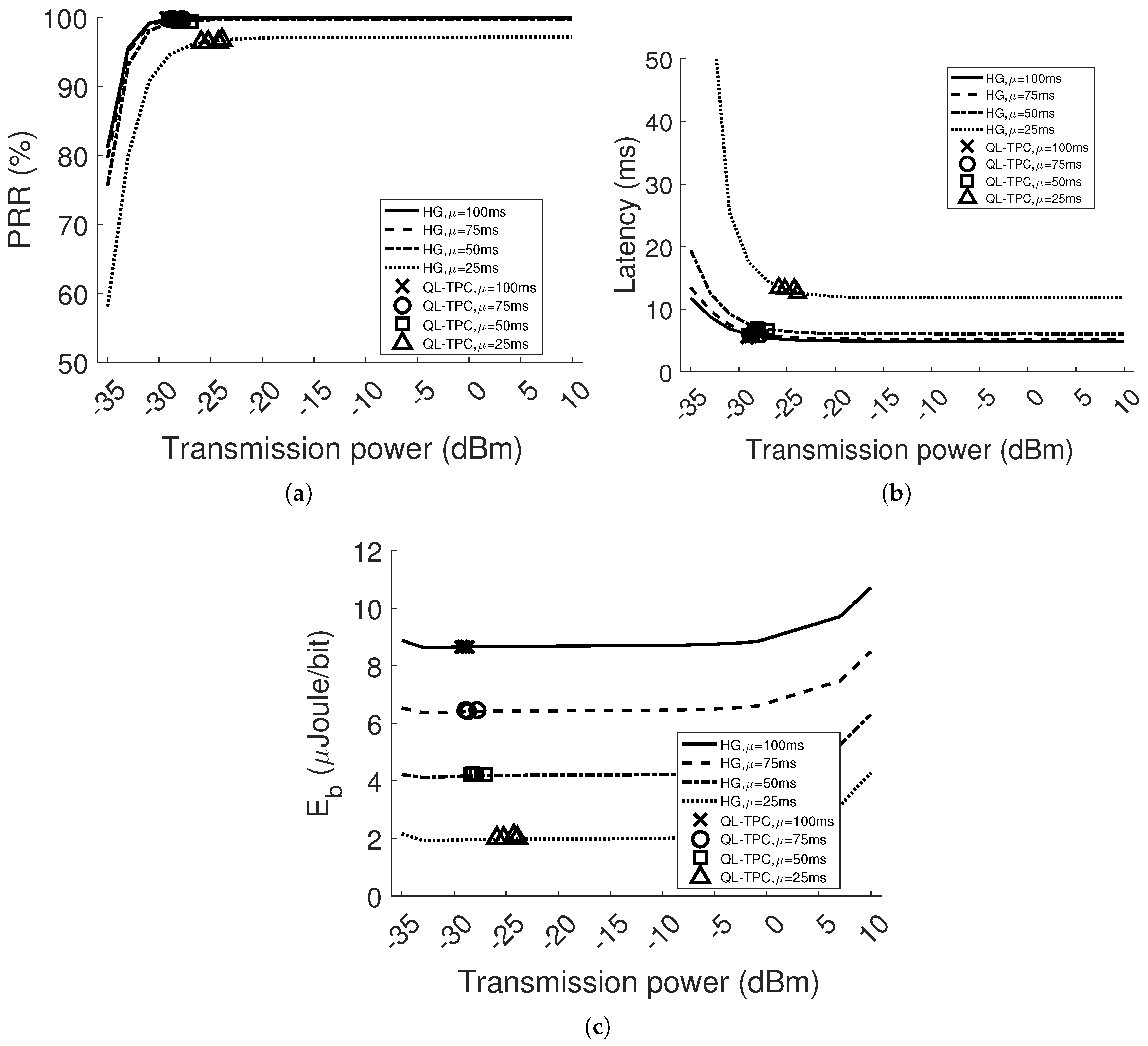
This paper shows that for different network conditions, there exists a trade-off among the performance obtained using different transmission power levels. For instance, we see that using high transmission power in the homogeneous network, PRR and latency either stay constant or are only improved by a decimal factor with respect to transmitting at lower power levels, thus extra energy is wasted. However, using low transmission power, in network conditions of detrimental path loss and interference, the nodes have the counter-effect of consuming more energy and performing worse than at higher power because of retransmissions. Through our protocol, we discover a near-optimal equilibrium in the system that provides a balance between reliability, in the sense of packet reception, and energy efficiency.
To summarise, we explore the principles of cooperation, distribution and machine learning applied to WSNs. Our contributions are:
Investigate Q-learning for TPC and analysis of the algorithm convergence by varying the learning factors in time.
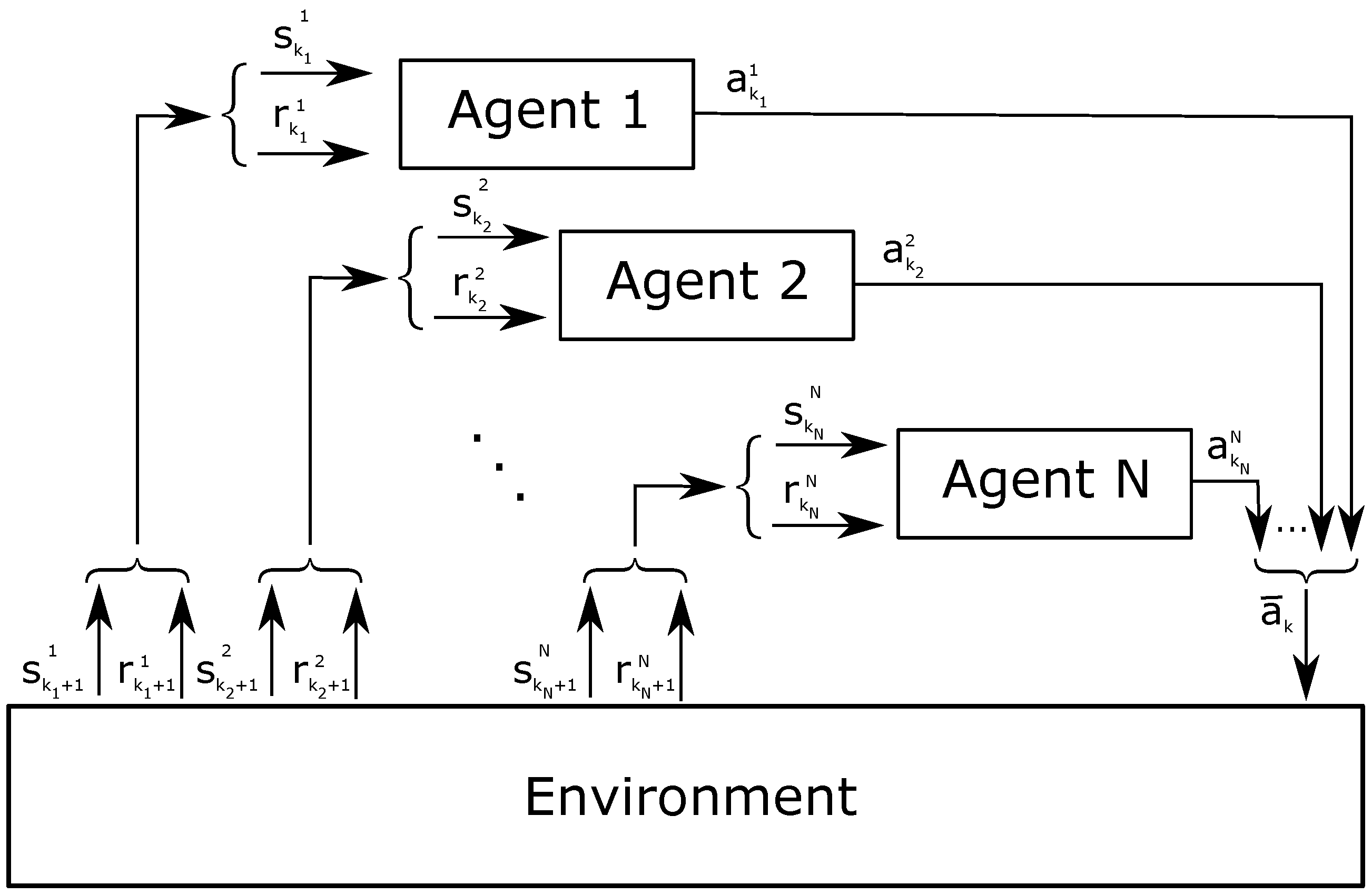
RL based on a Decentralized Partially Observable Markov Decision Process (Dec-POMDP): To the best of our knowledge, this is the first work that applies such method to TPC in WSNs [
32]. The nodes of the network learn from past observations by memorizing only the last values of the observed parameters, by using a Markov Decision Process (MDP). Each node is independent and relies on its own local information. Therefore, the system is decentralized and partially observable. To this end, the bandwidth is not spent for the exchange of information with a central node for the purpose of handling a network protocol.
Indirect collaboration among the devices without the exchange of information: This is possible through the application of the common interest game in Game Theory. The agents in RL are also the players of the game, cooperating towards a common goal that leads to a global benefit by minimizing the transmission power.
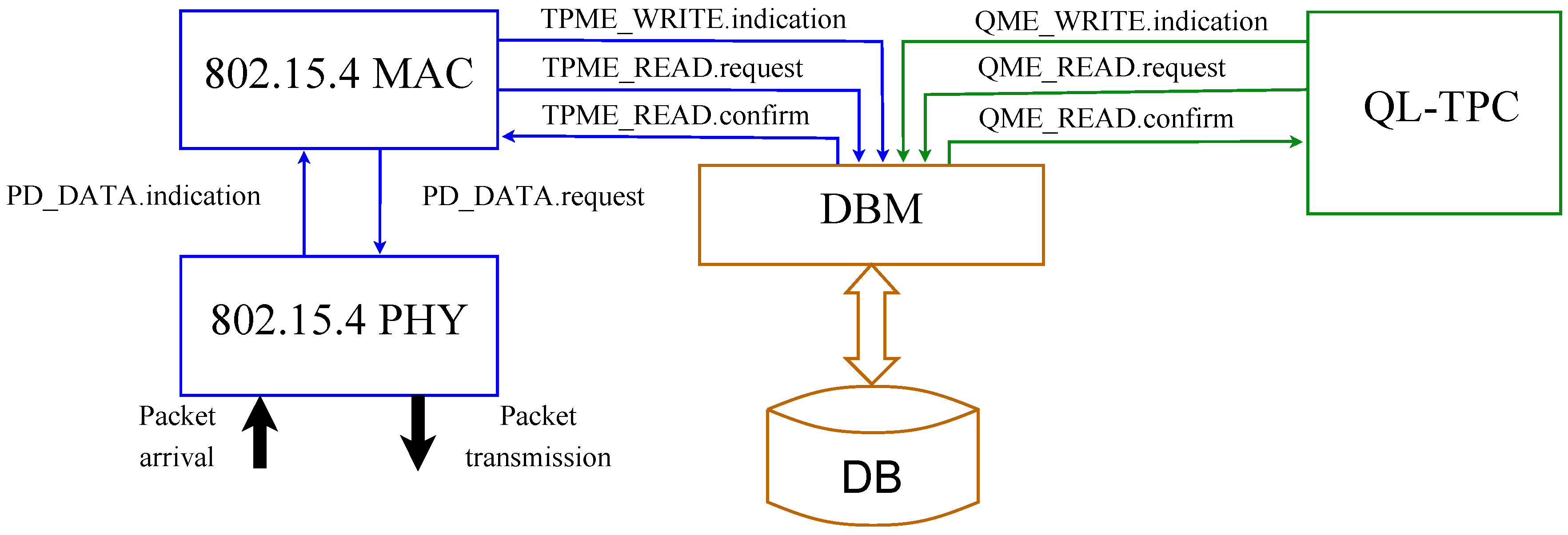
Design and implementation of new modules in NS3 related to TPC. New modules are generated and linked to the physical and MAC layers modules, which are already included in the NS3 open source release. We provide more realistic and reliable results, when compared with other tools used in the literature [
33,
34,
35,
36], since NS3 offers the opportunity to analyse many aspects involved in the wireless communications.
Commercial applicability: To the best of our knowledge, it is the first time that a smart protocol is implemented in sensor devices for TPC. The design of our protocol takes into consideration the industrial application, aiming at putting in practice the concept of autonomic networks. Our protocol is lightweight and suitable for constrained devices having limited memory, processing and energy capabilities. A section of this paper is dedicated to the implementation of our protocol in Contiki OS, for real-world sensor devices, experiments and the discussion of the results.
The remaining part of the paper proceeds as follows:
Section 2 provides an overview of reinforcement learning. In
Section 3, we identify the works related to our research.
Section 4 introduces the Q-learning algorithm, the approach to single-agent and multi-agent systems, the detailed implementation of Q-learning and its integration in a TPC protocol. The simulation setup and the results are explained in
Section 5. The experimental setup and results follow in
Section 6. Finally, the paper ends with discussions in
Section 7 and conclusions and future works in
Section 8.
2. Background
RL is one of the three big groups in Machine Learning together with supervised learning and unsupervised learning. In supervised learning, the system learns from labelled data, providing a map between input and known output in order to make associations for future data. In unsupervised learning, the data is unlabelled and the system learns how to classify it. Each class is defined by features that help the system to distinguish coming data. Instead, RL is used for self-learning systems in an unknown environment. The training is done either on a batch of stored data [
37] or online, using real-time data [
38]. In both manners, the data is obtained through observations, taking certain actions. Our protocol lies in the group of RL. Initially the devices do not have information about the environment, thus they adapt to any kind of scenario, learning through real-time data.
RL is a solution to an MDP, whenever the environment respects the Markovian properties. The MDP is a framework of sequential tasks in instants of time, which are required to make decisions. Solutions of MDPs are obtained through different methods that depend on the time horizon of the system. If the system is operative only for a fixed period, the time horizon is finite and the MDPs can be solved by the Bellman optimality equation using either the dynamic programming approach or the value iteration approach. Otherwise, if the system is operative on an infinite time horizon, the solution methods are: value iteration, policy iteration, linear programming, approximation method and online learning [
32]. The latter includes RL.
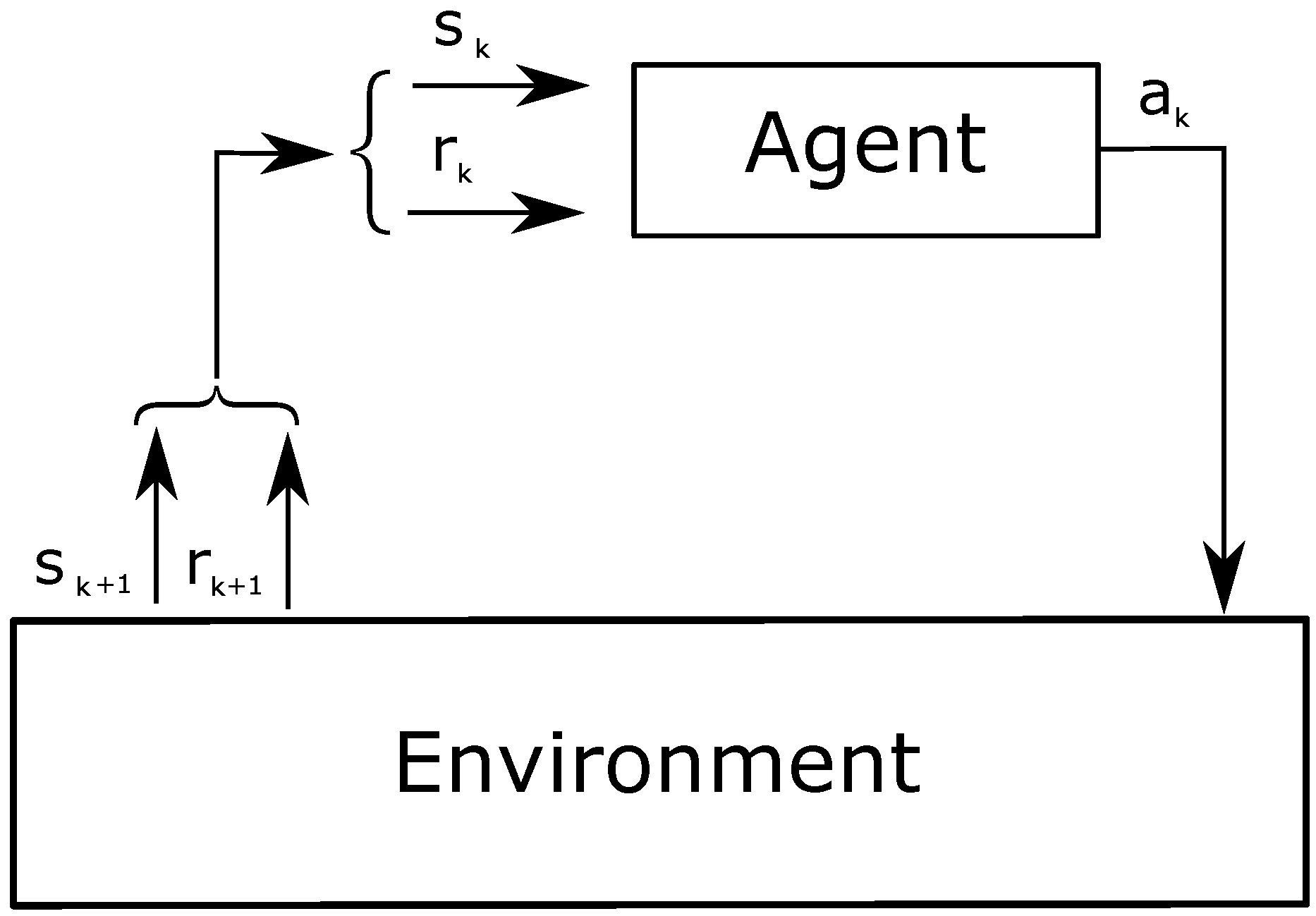
RL involves two main entities: an agent and the environment (
Figure 1). The agent is the learner and decision-maker, while the environment is an unknown entity that influences the agent’s performance. The system strives to achieve a specific target; thus, the agent iteratively learns the actions to pursue such target, adapting to various circumstances. Particular attention is required for the definition of the agent and the environment, based on the target. For instance, the environment can be represented as anything that the agent cannot control. The latter observes the environment on an episodic basis, where the episodes are defined by the developer. At a given
k-th episode, the status of the environment is represented by the value
, where
S is a set of states. The agent interacts with the environment by taking decisions, called actions
, where
A is a set of actions. The succession of state–action–state is formulated by transition probabilities. The system decides to select an action under a certain state following a policy,
. Actions can have either a positive or negative impact on the system in order to accomplish the target. Thus, the system provides a feedback or reward
to evaluate the effect of the actions, where
R is a set of rewards. The reward is both a quality value and the goal of the agent.
Given the fundamental parameters of the system, the Markovian property is defined as follows:
Only the last state and action are necessary to know the probability of getting certain states and rewards in the next episode. Hence, it is not necessary to memorize all the past values but only the ones that happened in the last event.
The total reward in the long term, or return of the system, knowing all the values obtained per episode, is calculated by a sum of rewards. To avoid the divergence of the series, the return is multiplied with the discount factor,
, obtaining the discounted return
D:
The discounted return can be calculated only after getting the rewards. Therefore, to predict the return in advance, we have to calculate the expectation of
D knowing the current state and action, which is called the action-value function,
, under the policy
:
The target of the system is to maximize the action-value function, thus the agent has to define the optimal policy,
, and solve the Bellman optimality equation, as follows:
given that
and
,
. Maximal action values are discovered by pursuing an additive strategy, such as
-greedy,
-soft and softmax.
In this section, we have described RL based on MDP, expressed by the interaction between one agent and the environment, which is entirely observable by the agent. However, in some systems, the environment is not always completely observable; therefore, these systems are based on Partially Observable Markov Decision Process (POMDP). In other cases, systems are based on Multi-Agent Markov Decision Process (MMDP), when they are composed by multiple agents that have a global view of the environment and influence it simultaneously in a cooperative matter. In the same situation but with agents that have a partial view of the environment, the extension of MDP is called Decentralized POMPD (Dec-POMPD). Finally, if multiple agents do not cooperate, systems are based on Stochastic Games (SGs) [
32].
3. Related Work
As explained in the previous section, RL is one of the possible solutions to MDP. Therefore, we firstly provide a deep investigation to all the works that have addressed MDP for power control with offline solutions, and then we focus only on those that have considered RL. Alsheikh et al. categorize works in the literature per MDP extension and application in WSNs [
32]. Among the applications considered in their survey, the one that is related to our work is resource and power optimization. Within the group of works under such application class, the methods use the classic MDP, except for few that are based either on SG or POMDP [
39,
40]. Furthermore, only one approach based on online learning (i.e., RL) [
33] is reported, where the difference against the other solutions is that the system does not know the environment.
For instance, Krishnamurthy et al. apply SG to CDMA ALOHA networks for the selection of the Signal Noise Ratio (SNR) threshold, in order to decide whether to transmit or wait in a determined time slot [
39]. The nodes know in advance the channel status before transmitting. The results show the variation of the threshold and throughput with respect to the number of nodes in the network. The proposed method is compared with two cases where there is no control and no channel information respectively. Instead, Udenze et al. apply POMDP in their system, which is formed by one transmitter node (i.e., the agent) that interacts with a static environment [
40]. The wireless channel is without a fading model, and the interferers have only one power level available for transmission. Since the agent observes partially the environment, it creates belief states as an estimation of the environment status (i.e., the interferers are either idle or transmitting). The actions that the agent can take are either a transmission with low power or high power, wait idle or listen to the channel. The policy to take one action under one belief state is set by fixed transition probabilities. The agent gets either a positive reward, if a packet is received, or a negative one otherwise. The authors show how the computational time varies by increasing the number of states and actions. Other works presented in the survey [
32] use MDP [
34,
35,
36,
41]. An industrial application is studied by Gatsis et al., where the state information of one plant is transmitted by a sensor node to a controller [
34]. The goal is to minimize the transmission power and the state estimation error at the controller side. The optimal power is obtained following an MDP formulation and solving the Bellman equation. However, given the onerous calculations that are needed to solve the Bellman equation, only the expression of the optimal power is provided. Then, the approximate dynamic programming is used to define the suboptimal power policy, which is evaluated through numerical simulations. The results show the transmission decision (transmit or not) with respect to two plant states and the channel gain.
TPC is also used for neighbour discovery, minimizing the energy consumption [
35,
36]. Unlike the work of Madan et al. [
35], the one of Stabellini [
36] considers the energy also in listening mode for the energy consumption calculation. Both approaches model the problem as MDP and they solve it offline via linear and dynamic programming. In the results, the authors analyse through numerical simulations the average energy consumption to discover the neighbours related to the density of nodes in the network. Madan’s results are compared against two schemas: an ideal schema of perfect knowledge and a simple one, where the power is doubled [
35]. Instead, Stabellini’s results are compared against the optimal and suboptimal cases [
36].
A centralized approach for energy savings is introduced in the literature, preventing the use of certain transmission power levels while a device is in a specific battery level range [
41]. The problem is formulated as a discrete finite horizon MDP and is solved in a central node that collects all the needed information from the sensors. The central node calculates the optimal policy through the Bellman optimality equation. The battery lifetime of a sensor node is analysed and compared with other simpler policies, such as: not transmitting; transmitting with the highest available power; or transmitting with low and high power in the first and second half period, respectively.
Other solutions use MDP for harvesting energy protocols, where the transmission power is adjusted to get certain information [
42,
43,
44].
RL has already been applied to WSNs for solving different aspects, as discussed in the survey of Kulkarni et al. [
24]. Examples of these are the design and deployment of sensor nodes, routing and scheduling of sleeping time for energy saving techniques. In the survey, none of the contributions in RL have targeted QoS in WSNs, since energy efficiency is always prioritized. In addition, only one research direction uses RL for power control [
33]. The work presents the actor/critic algorithm to maximize the ratio between throughput and energy consumption. The nodes learn the transmission power and modulation level to use based on the channel gain of the previous transmission and number of packets in the queue. Both the reward and the discounted return are iteratively averaged. The authors choose the Gibbs softmax as action decision strategy, which considers the probability of choosing an action knowing the state. The probability is also adjusted at every iteration. In the case of multi-node scenarios, the authors consider the interference in their model, which is an argument of the reward function. However, the nodes do not cooperate to reduce the interference. Furthermore, the interference is used as an input sequence of discrete values for numerical simulations. Similarly, also the other parameters, such as SNR, Signal to Interference plus Noise Ratio (
SINR), buffer cost, distance between the nodes, are treated as a set of numbers to feed in the learning algorithm, instead of obtaining them as a result of stochastic models (e.g., localization, capture effect and fading) at every iteration. The network performance is compared with a simple policy, where the nodes transmit with the highest modulation possible, keeping a predefined SNR/
SINR constant.
Another classification of RL considers the following schemes: MAC, cooperative communications, routing, rate control, sensing coverage and task scheduling [
26]. Compared to the previous survey [
24], MAC, rate control and task scheduling can be associated to the group of scheduling; routing and cooperative communications to the group of routing; and sensing coverage to the group of design and deployment. Two protocols apply RL to TPC [
45,
46]. In one work, the authors implement a collaborative routing protocol to deliver traffic flows from a source to a destination [
45]. Whether the direct communication is not successful, relay communications are considered. The goal is to find the optimal routing path that provides certain performance, in terms of packet delivery ratio, delay and energy consumption. The nodes learn to take actions, such as transmitting with a variable transmission power or not transmitting. The strategy to choose the transmission power and the learning curve that brings the system to convergence are unfortunately not provided. In the other research track, RL is used for a completely different case, namely accessing the channel through either a short-range or a long-range radio transceiver, by selecting one of the four total transmit power levels [
46]. The authors aim at reducing the energy consumption, which is the argument in the reward function when a packet is received, and packet loss, rewarding the system with a high negative value when a packet is lost. Both the methods use Q-learning as RL algorithm [
45,
46].
Few other solutions have used RL in WSNs for TPC. One of them is focused on delay sensitive applications for multi-hop communications [
47]. The authors compare the network performance among the optimal policy, the centralized and the distributed systems. The centralized system considers the joint state and action of all the nodes involved, that are controlled at a central node. Instead, in the distributed system, the MDP is factorized and integrated in all the nodes. Each hop has its own tuple state–action–reward and value function that are updated at each epoch as defined in the work. The update at each node is calculated with the information of the value function from the other nodes. This information is transferred by the nodes themselves at a certain rate in packets with a variable length. Increasing the length and/or lowering the rate, the system is closer to obtain an optimal solution, but the overhead in the network increases as well, affecting the performance. Thus, the authors have considered a trade-off by considering an approximation of the exact value function, by reducing the transfer of information. The target of the system is to provide the delivery of the traffic flow under a certain delay constraint by defining the transmission power and the routing path. The MDP is solved through the actor and critic, RL algorithm. The performance shows that the distributed system performs better than the centralized.
The method on POMDP by Udenze et al. [
40] is extended to RL [
48]. Udenze et al. improve their previous work [
40] by considering a more realistic environment in WSNs, which is initially unknown [
48]. The main focus of the results is the comparison among the convergence time of three different solutions for an unknown environment, namely Monte Carlo, one step Temporal Difference (TD0) and Temporal Difference
(TD
), where the
value averages the long term returns. Although the authors claim to study an unknown environment, they use a data set for the state transition probability. Similarly, the states of the environment correspond to the combination of transmission activity by the nodes in the network during a range of time slots. Hence, the number of states increases proportionally to the number of nodes and time slots. In addition, the number of nodes in the network must be known in advance to design the states. From a state, the agent can take three actions, specifically either transmitting at low or high power, or wait and transmit in the next time slot. The goal of the agent is to spend energy efficiently and avoid packet loss.
Le et al. [
49] use Q-learning for topology control, applied to sensor nodes in order to keep the connectivity of the network with
k-degree. The nodes exchange information regarding the transmission power used and communication range. Simulations in Matlab show energy, communication range and connectivity, comparing the method with spanning tree and fuzzy logic topology control, as well as with a network without topology control. The topology control with Q-learning is able to save energy, while keeping the desired grade of connectivity, with respect to the other schemes.
In addition, in the studies of Sung et al., Q-learning is used for ensuring the connectivity by adjusting the transmission power [
50]. However, this work is specifically focused on improving the learning time of the Q-learning using a reward propagation method. In such a way, not only the Q-value of the observed state and executed action is updated, but also the Q-values of other state-action combinations are updated at the same time.
Q-learning applied to Wireless Body Area Networks (WBANs), to mitigate inter-network interference, increases the throughput and minimizes the energy consumption [
51]. Kazemi et al. compare an approximated Q-learning, using radial basis functions, with two of their approaches that use fuzzy logic and game theory, respectively. The results, obtained through simulations, show that the RL approach outperforms the other techniques.
To summarize, different research tracks have studied the problem of TPC in WSNs through the formulation of MDP, but only few have solved MDP with online learning. Systems based on the offline approach are unrealistic and unfeasible for embedded systems because these are based on assumptions and statistical models. Indeed, the methods are evaluated either through theoretical work or numerical simulations. Most of the methods consider only one agent in one-to-one communications [
34,
42,
46,
51]. Instead, in the methods that study the network with multiple nodes, the system is designed in a fully joint state-action space. The coexistence of multiple links is taken into account only in the state and reward definition, considering either each node’s transmission mode combination (i.e., idle, transmitting with a power level) or the level of interference that is detected at the reception [
33,
40,
41,
48]. Such approach is also adopted for MDP and POMDP frameworks that are solved with online learning. This is implementable either in a centralized architecture, where all the components of the network transmit their local information to a central node, or by exchanging information among the nodes. However, in reality, the amount of data to be exchanged is unfeasible for dense wireless networks. The nodes deal with an unreliable environment. For this reason, we propose a TPC protocol that is defined as a Dec-POMDP solved with RL. Each node has its own local perception of the environment status, is independent, and does not require tight synchronization with the other nodes. Moreover, to the best of our knowledge, our protocol is the first one to consider cooperation in a multi-agent system for interference mitigation, providing connectivity in point-to-point communications, without exchange of information. The nodes cooperate indirectly to satisfy a common goal, equivalent to the same QoS requirements. Cooperation is possible thanks to a theoretical game approach, whose rules are taken into consideration in the reward calculations. In literature, Liang et al. use the collaboration for the routing protocol, focusing on the exchange of packets for the routing path decision [
45]. Instead in the method of Lin et al., the nodes individually solve the MDP and exchange their local returns in the network, in order to decide the most efficient transmission power and routing path [
47]. However, the work does not take into consideration simultaneous end-to-end communications, thus interference.
Unlike other related works, we test our protocol in a detailed, modular simulator and in real nodes. We analyse the convergence procedure in Q-learning by varying the factors of exploration and learning in time, as recommended in theory [
38]. In all research literature using Q-learning, the parameters are set to a constant value. The results in each method are generally a comparison between optimal and suboptimal solutions (using the approximation method), or between the network performance using the specific method and constant transmission power. The problem formulation, the model of the environment, the goal of the system and the evaluated performance are different for every work. For this reason, the various methods presented in the literature have not been compared against each other.
6. Experiments
In this section, we provide the experimental setup and results of QL-TPC for a point-to-point communication. The system is the same as in
Section 4.1, but the setup is different than the one used for the simulations. We use TelosB sensor nodes with Contiki OS. TelosB has 48 kB of program flash, 10 kB of data RAM and 1 MB of external flash. The nodes are connected to a cabled test-bed, which is formed by BeagleBone Black (BBB) devices linked via Ethernet to a server, through a Virtual Private Network (VPN). Each node is connected via USB to one BBB. Using the test-bed, we are able to store and analyse reliably the traffic that is generated, transmitted, received and lost through the ether. The TelosB nodes run the Contiki program that implements the QL-TPC protocol. In Contiki, we use the unicast routing protocol in the network layer, and Contiki-MAC in the MAC layer. The latter is an asynchronous radio duty cycling protocol, which has been created following the characteristic of the IEEE 802.15.4 standard. In Contiki-MAC, the radio is in sleeping mode by default (i.e., the radio is off) and it turns on every 0.5 ms for 0.192 ms. The transmitter sends copies of the same packet every 0.4 ms. Using this procedure, the nodes save energy and, at the same time, are able to communicate [
59]. The program allocates memory in the device as follows: around 28 kB for the executable code, 118 bytes for the initialized data and 6.8 kB reserved for uninitialized data. The former is written in the ROM, the second in the EEPROM and the latter in the RAM. The BBBs use a Python program that reads the data from the TelosB and forwards it to a central server via a RabbitMQ messaging system. The format of the data from the TelosB to the server is JSON. The server runs a Python application that parses the JSON data and makes a CSV file, which is used for data analysis in MATLAB. The experiments are performed in the lab. The nodes are distant 8 m between each other. The choice of
in time follows an exponential function
with
. The value for
and
is constant and set to 0.8. The number of actions are 8, which correspond to the transmit power levels of the TelosB. The state is determined based on the number of retransmissions, number of CCA attempts and the latency as follows:
with
the number of quantization levels,
,
and
the average quantized number of CCA attempts, retransmissions and latency of the
k-th episode, respectively. The quantization association is shown in
Table 4. The latency is classified in low, medium and high, based on the values obtained during the experiments. They are associated to the range equal to the cumulative difference between the maximum and the minimum, divided by 3. When a packet is lost, the latency is NA and is ignored for the average in the window
W.
Finally, the reward is calculated as the PRR over
W, in its continuous form. The experiment is 750 min long. The inter-arrival time of the packet generation is equal to 3 s. The power level used to send ACKs is constant and set to 7. The size of the Q-matrix is equal to 2.048 kB, given that the matrix contains an amount of float numbers equivalent to the multiplication of
. The values of the parameters involved in the experiments are listed in
Table 5.
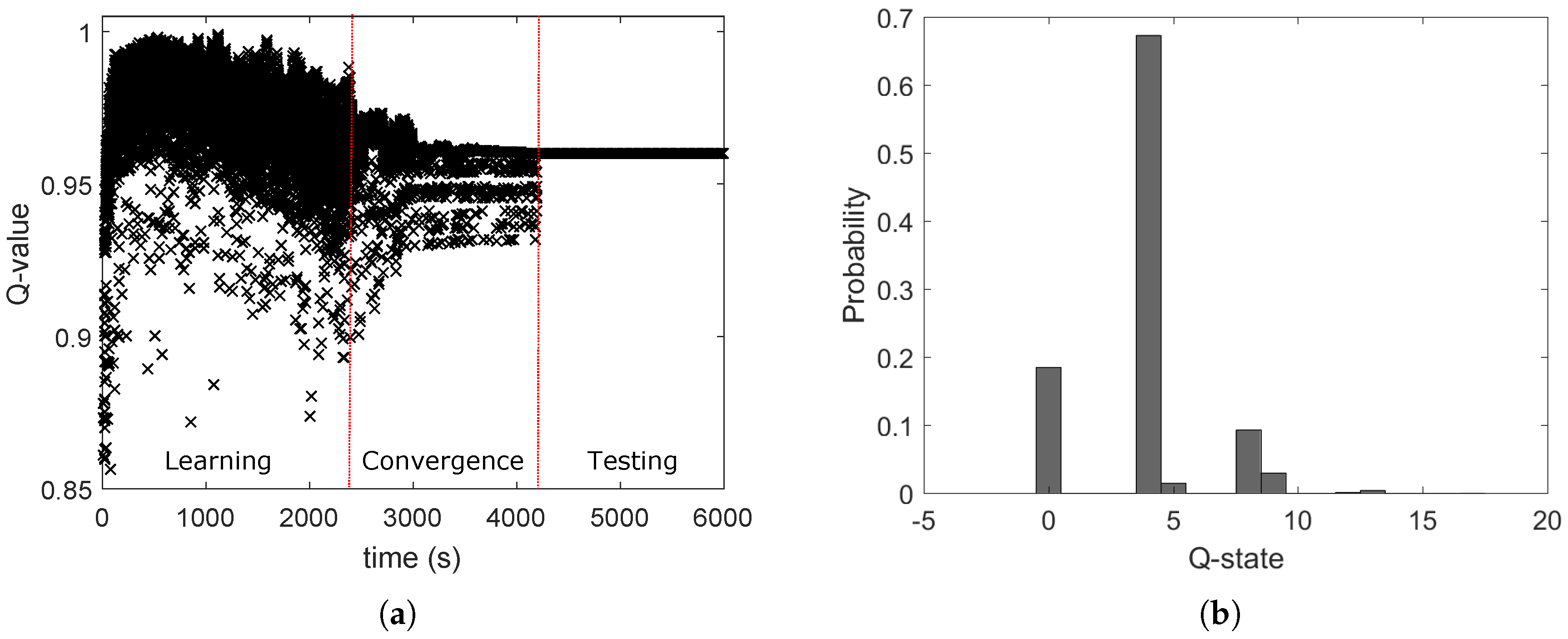
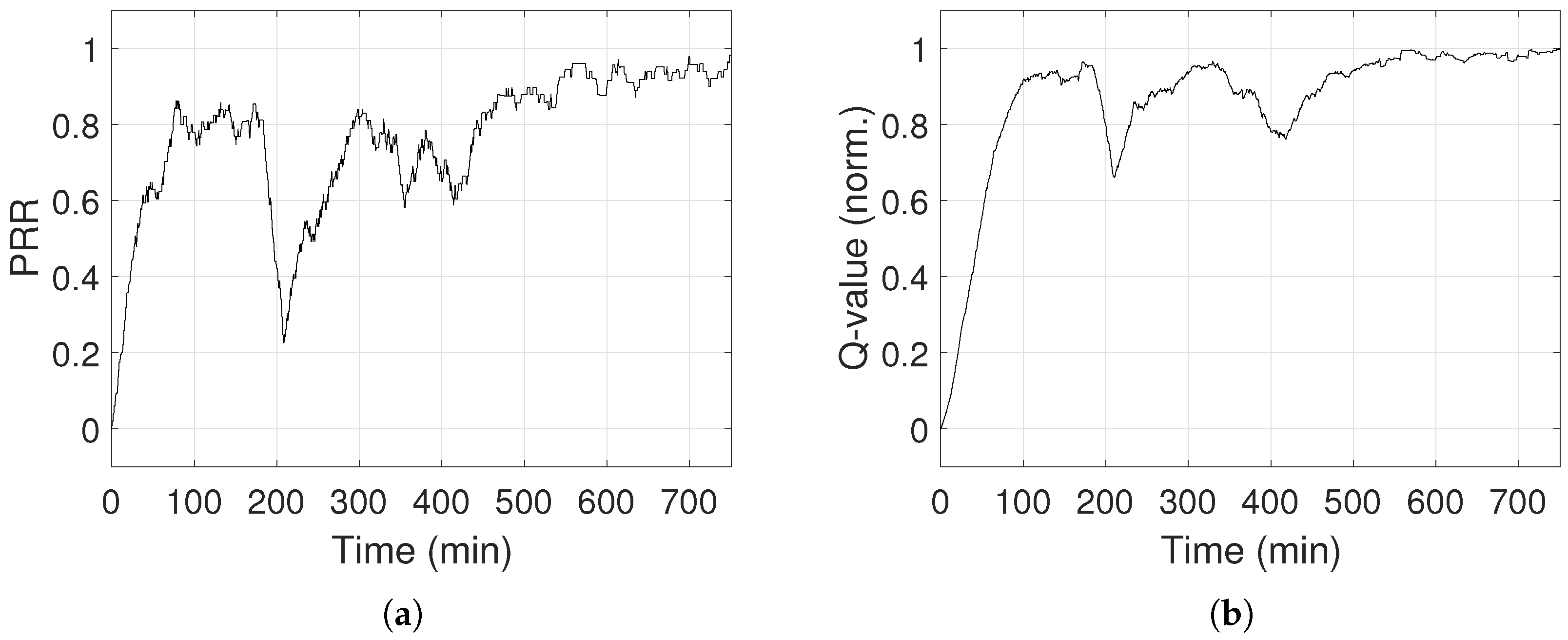
In
Figure 16, PRR and Q-values rise over time, showing that the system learns and improves its performance. When the system is mostly exploring (i.e.,
), PRR is unstable, but as
drops, PRR stabilizes between 90% and 98%. PRR never reaches 100%, because the system keeps exploring, since
never reaches 0. Exploring gives the possibility to choose power levels that result in low PRR and low Q-values. When
drops below 0.1 (i.e., after 550 min), PRR remains above 87%. As a last note, PRR and Q-value drop in
Figure 16 after 200 min, which is explained by the fact that someone entered in the lab. The environment changed and its representation in the system moved into a new state that was not explored previously, causing the drop and a new learning curve. Differently from
Section 5, the convergence is longer because the inter-arrival time of packet generation is 3 s, thus the PRR is calculated around every 30 s. We also analyse the energy consumption of the transmitter node and compared it to the homogeneous case, when the maximum transmission power is set. The values of the parameters for the energy calculation are taken from the datasheet of the transceiver CC2420 [
60]. The nodes can be in four different operational modes: sleep, idle, transmission and reception. In the sleep mode, the power supply is turned off. The idle mode in TelosB is equivalent to the power down mode in CC2420 where the crystal oscillator, FIFO buffer and RAM access are disabled. During the transmission and reception mode, the node transmits and receives, respectively. The nodes are in sleep mode for
of the time. The transmitter sends the data every 3 s, with a payload of 8 bytes added to 6 bytes of header. The time in the transmitting mode,
, is calculated by the number of packets that are transmitted and retransmitted during the entire time of the experiments (i.e., 750 min), at the data rate of 250 kbit/s. Similarly, the time in reception mode,
, is calculated by the number of ACKs (i.e., 11 bytes long) that are received. The remaining time is spent idle. Therefore, the total energy spent is equal to:
. The current draw per mode is given in
Table 5. Specifically, the current draw in the transmission mode,
, is provided in the CC2420 datasheet for some transmission power levels, while the other values are evaluated through a quadratic fitting curve. In
Table 5, the values of the current in the transmission mode are ordered accordingly to the list of power levels. The total energy consumption is equal to 1.78 Joule. Considering that TelosB nodes are supplied by 2 AA alkaline batteries, the capacity is twice 3000 mAh. Thus, the energy consumed by the transmitter over 750 min is
of the available supply. In comparison, if we assume that the same amount of transmissions would have been executed by the highest transmission power level (i.e., 0 dBm), the energy consumption is 1.88 Joule, equal to
of the energy supply.
7. Discussion
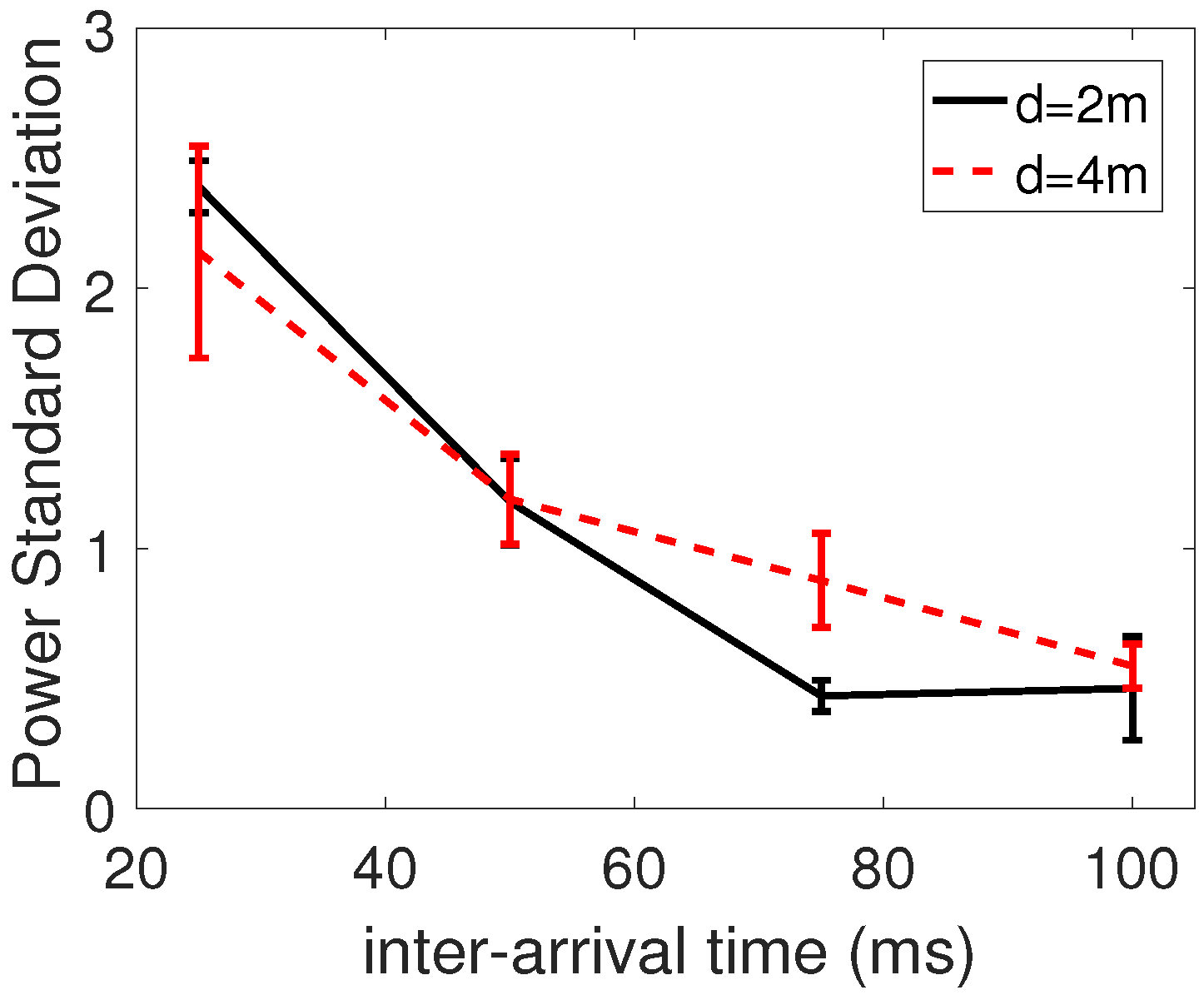
Our nodes are able to automatically adapt their transmission power to the varying conditions of the environment. The conditions have been changed per scenario by means of the distance between the transmitter and receiver of each node’s pair, the number of simultaneous transmitters and the traffic load. We have seen that increasing the value of the variables, the nodes raise their power. For each scenario, the QoS requirement of the system is the same: PRR higher than 95% using the minimum transmission power. The research question of this paper is about the transmission power that should be used to fulfill the QoS constraints, while minimizing the interference to the neighbours. Measurements and analysis per link at the network’s installation phase may provide useful hints, but then it is legitimate to ask ourselves whether users, or someone on their behalf, want to make measurements before using their products within the IoT market. Initial measurements would only be relevant for the static conditions tested at deployment time. However, the environment is influenced by changes (e.g., moving objects, new objects, variable number of people, variable number of sensor nodes), thus the power should be adaptive and autonomous (no user intervention). For instance, if the transmitter is moved further away from its recipient, it causes an increment on the transmitted signals’ attenuation and a drop on the received signal power. Hence, the transmission power needs to increase. Yet, if the number of transmitters in the network increases, a receiver will detect more interference. In both the cases, the receivers’ SINR worsens, affecting the QoS. The solution is either lowering the interferers power or boosting the transmitting signal. However, the limitation is that decreasing other nodes’ power influences their own network performance, whereas increasing one transmitter’s power produces more interference to the neighbours. There might be a trade-off that allows each node to satisfy their own performance constraints. A typical industrial solution is to set the transmission power to its maximum. This would be the easiest and apparently the most conservative approach, which would however consume energy excessively and waste spectrum, issues that become unsurmountable in high-density scenarios.
The benefit of our approach is that the nodes learn the minimum power they can use, without having to rely on any previous knowledge about the environment. Additionally, our self-learning process can take QoS requirements into account. Even though, in this paper, we have addressed only PRR, our method could consider any other features during the self-learning process, by modifying the nodes reward function. We could also set different goals for different nodes or subnetworks; there is no need to set up the learning process uniformly. In our work, we adopt the Manhattan grid topology, which is symmetric in the node disposition. Each transmitter in the multi-agent system has the same target, namely the QoS requirements. Therefore, as expected, the nodes learn similar transmission power levels, which are within a range smaller than 4 dBm. As future work, it would also be straightforward to study our protocol in asymmetric topologies, with dissimilar QoS constraints per node, whereby the transmission power varies across nodes.
8. Conclusion and future work
We have proposed a protocol that controls the effects that transmission power has on wireless sensor communications. The environment is formulated for the first time in WSNs as a Decentralized Partially Observable Markov Decision Process (Dec-POMDP), which is solved by an online reinforcement learning algorithm. Such formulation is realistic for a wireless network with a distributed architecture and composed by multiple nodes. Each node exploits its own local information of the environment in the algorithm. Such information is not transferred to other nodes, thus we avoid overheads in the network. The nodes are independent learners by observing the environment during packet transmissions, and players of a common interest theoretical game. The node’s cooperation is beneficial to the global network in terms of power reduction, such as to minimize the interference and prolong their battery lifetime.
Our TPC protocol is compared to the case of constant transmission power (i.e., homogeneous network). The results show that the system is adaptive to different scenarios, varying the interference and path loss, in a dynamic environment. The PRR is always higher than , satisfying the requirement range 95–100%. The packet delay difference between the TPC protocol and the minimum value in the homogeneous case is lower than . The maximum energy saving is with respect to the homogeneous case. Finally, we have implemented the protocol in real sensor devices and shown the learning curve and performance improvement for one point-to-point communication.
Although our prototype and simulation work suggest great potential in self-controlled WSN based on learning, there are various ways in which our method may be further improved. First, we consider a deterministic time scheduling for the phases of learning and converging, followed by a testing period. It will be interesting to explore how time may be adjusted in face of different scenarios and conditions, for instance with different traffic patterns and traffic rates. We intend to study ways to consider together the scheduling time, the learning, discount and exploration factors with the action-value learning in time (i.e., the difference between two consecutive values is lower than a constant). Based on the stochastic analysis, the system switches between phases autonomously. In addition, the learning, converging and testing phases should take into account topology changes, such as either new nodes join the network or the existing nodes move or the environment changes (e.g. new obstacles, people activity). Such changes are represented by states that may have not been previously explored, thus the action-value is still equal to the initial value. A solution could be the use of transfer learning at the end of each phase, where the knowledge of the explored states is transferred to the unexplored ones [
61]. In this way, convergence may get faster and the system would be able to adjust to a range of environmental conditions. Our protocol has been designed for real devices. Therefore, we have also presented an experimental work with sensor nodes that learn which transmission power to use in a real environment, aiming to maximize the PRR. It would be interesting to extend our work to carry out a more extensive comparative analysis and, in turn, address any deficiencies in the simulator.