A Polarization Independent Quasi-TEM Metamaterial Absorber for X and Ku Band Sensing Applications
Abstract
1. Introduction
2. Design Methodology
- where, l = length of microstrip line
- w = width of microstrip line
- t = thickness of microstrip line
- correction factor =
- = substrate width
- = substrate thickness
- = dielectric constant of dielectric film
- d = distance between mutual overlapping stripline
3. Absorption and Pressure Sensor Results and Discussion
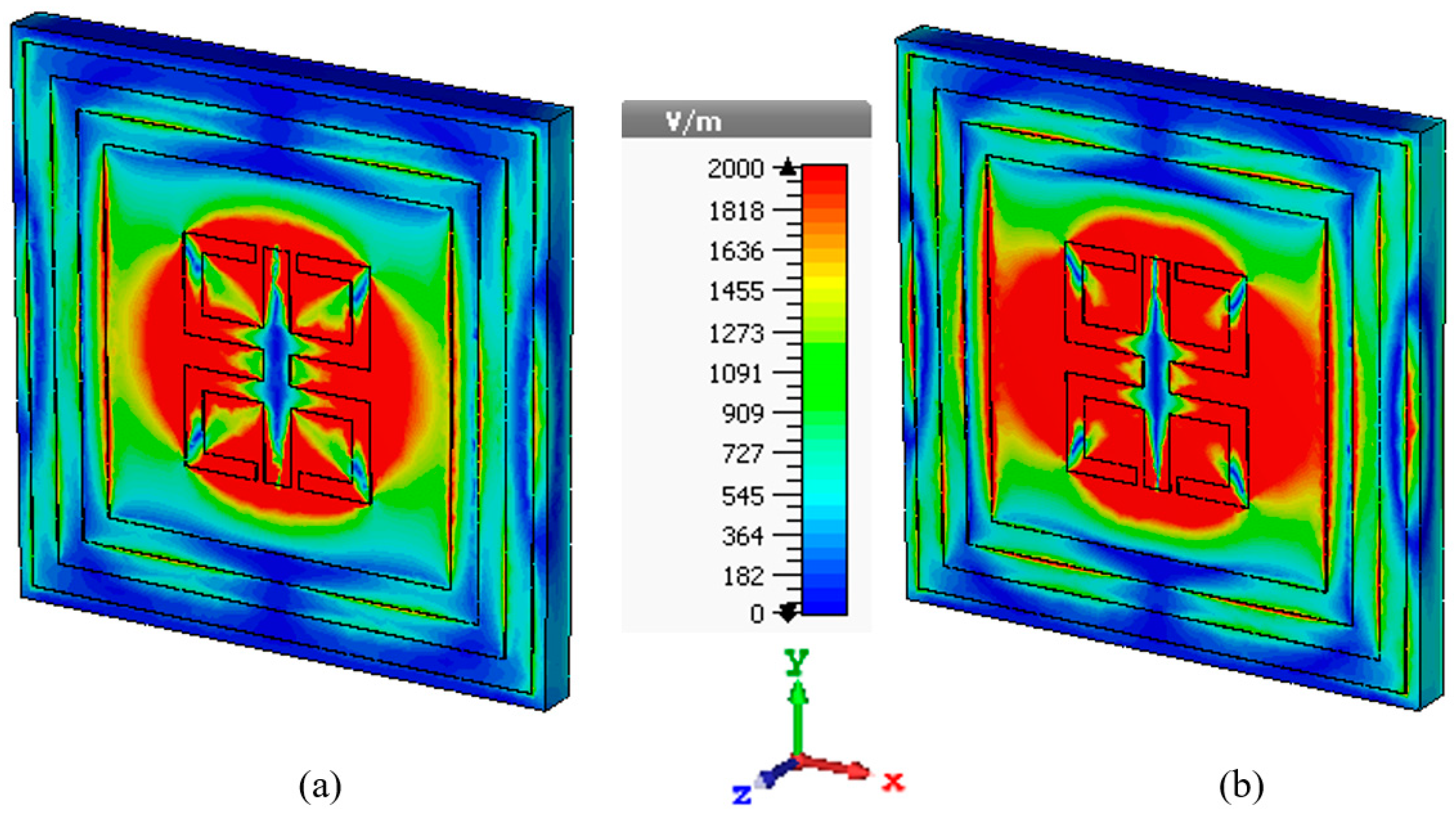
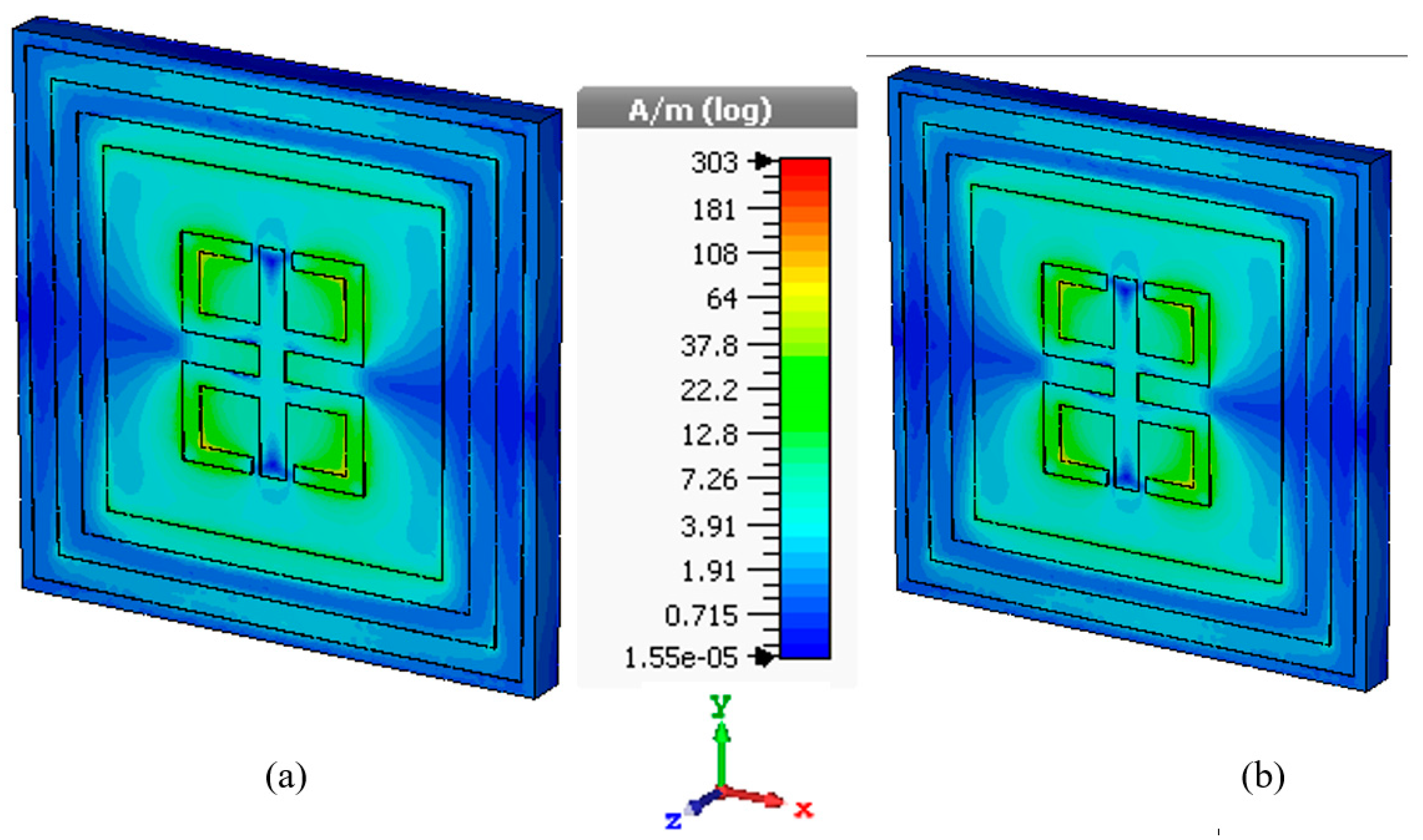
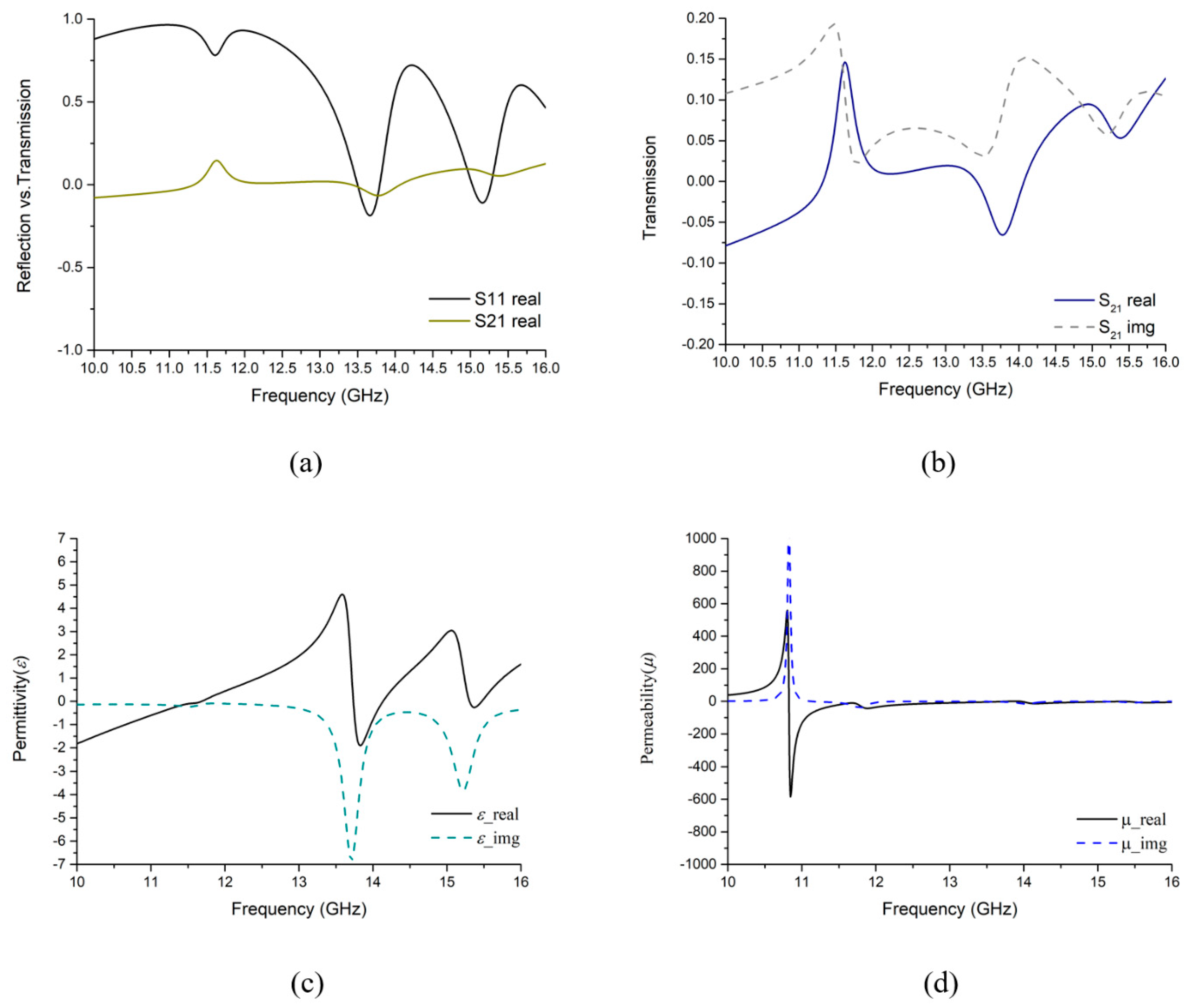
3.1. E-Field, H-Field and Surface Current Analysis
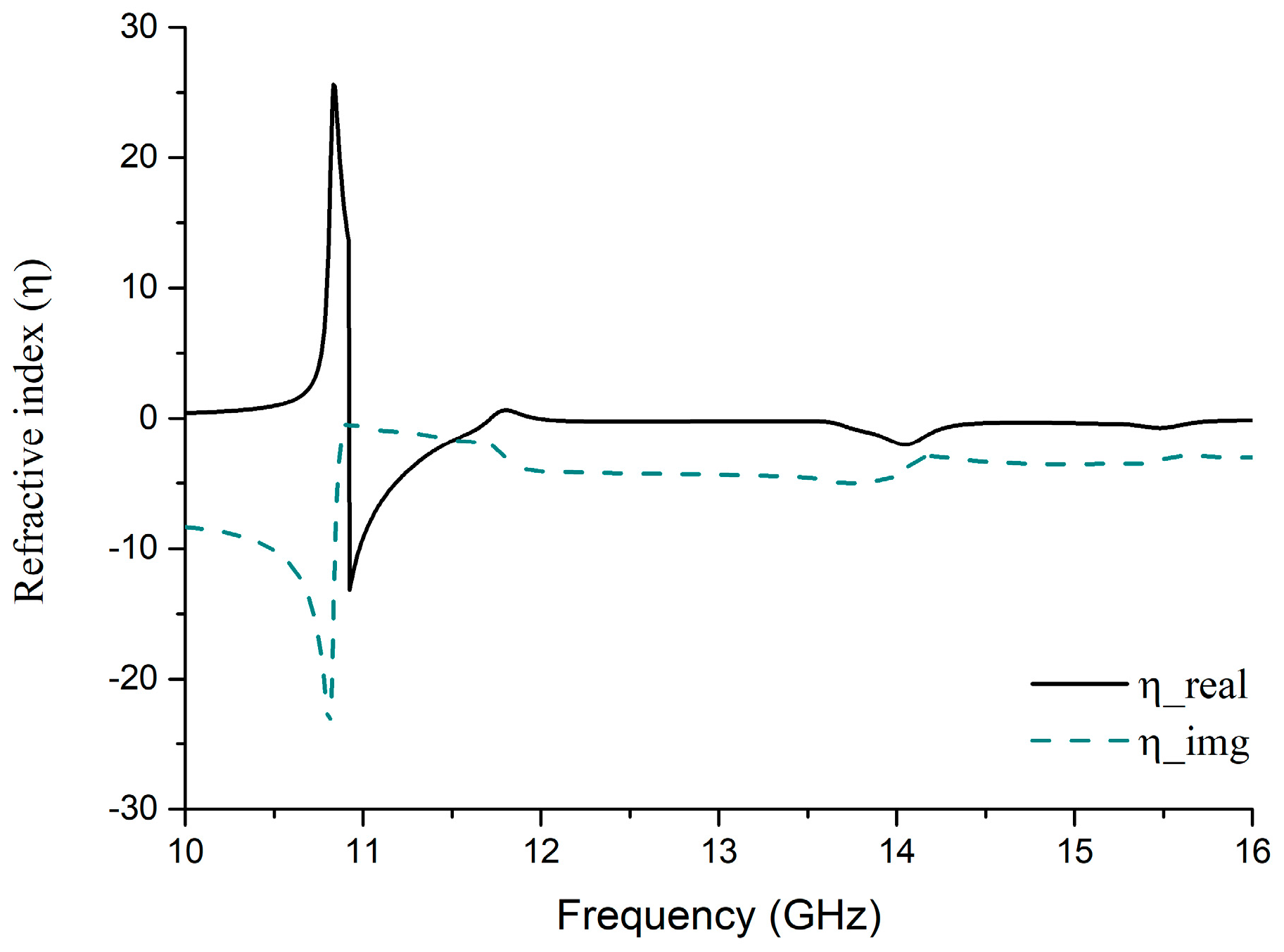
3.2. Quasi-TEM Polarization Independence Regarding Maxwell Equations
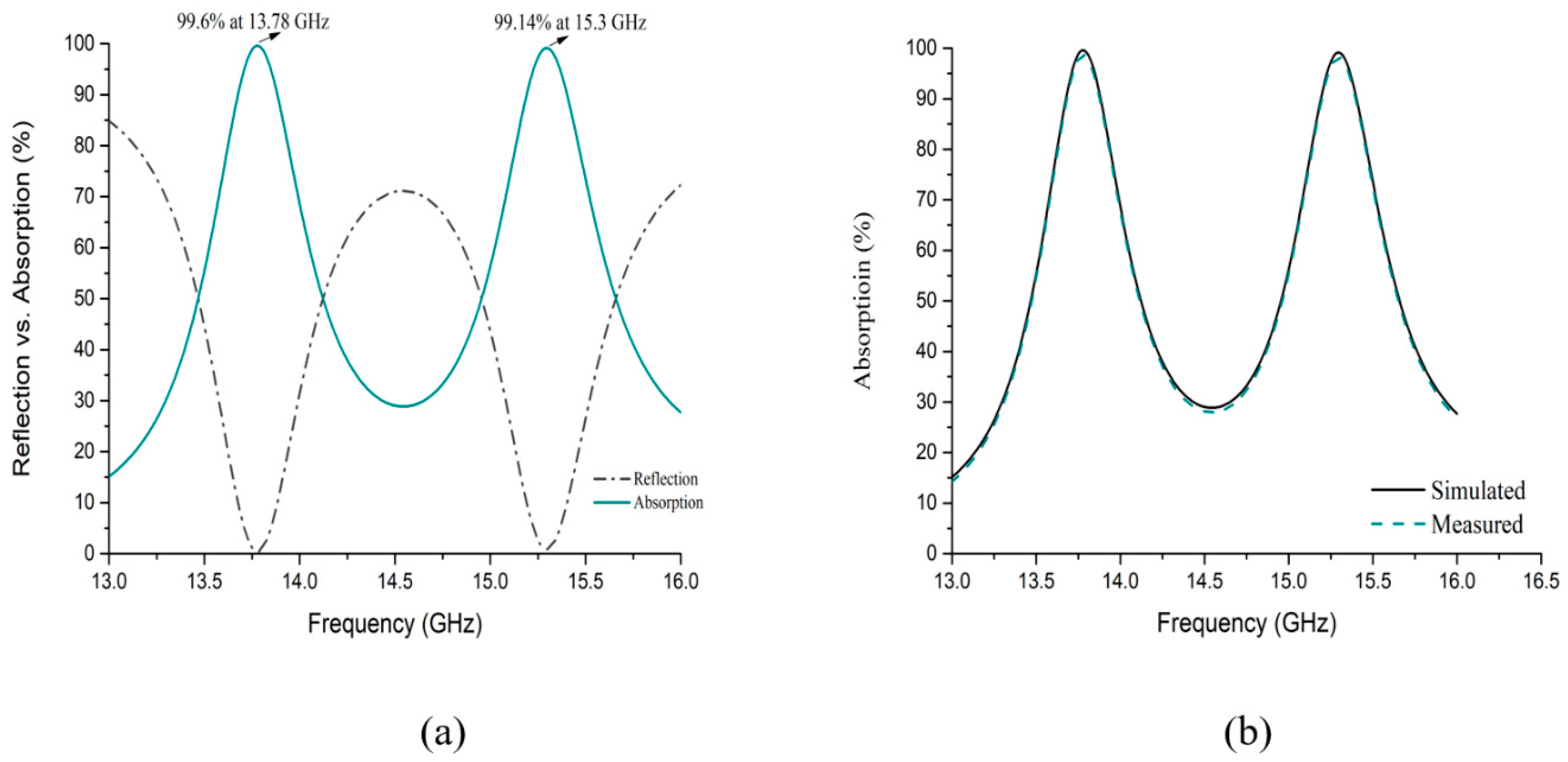
3.3. Absorption Based on Simulation
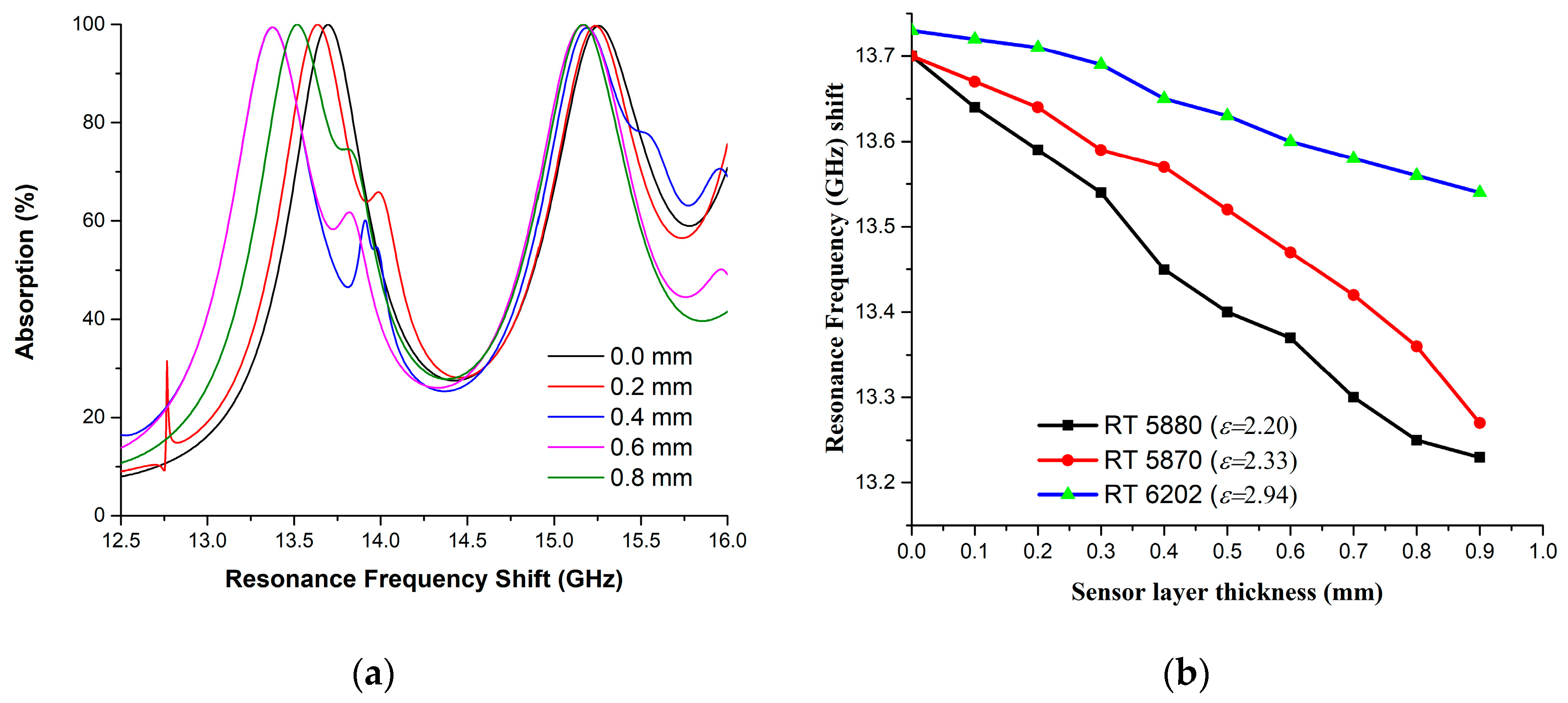
3.4. Pressure Sensor on Simulation Environment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, Y.; Kim, S.-J.; Park, H.; Lee, B. Metamaterials and metasurfaces for sensor applications. Sensors 2017, 17, 1726. [Google Scholar] [CrossRef] [PubMed]
- Namai, A.; Sakurai, S.; Nakajima, M.; Suemoto, T.; Matsumoto, K.; Goto, M.; Sasaki, S.; Ohkoshi, S.-I. Synthesis of an electromagnetic wave absorber for high-speed wireless communication. J. Am. Chem. Soc. 2008, 131, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Padilla, W.; Aronsson, M.; Highstrete, C.; Lee, M.; Taylor, A.; Averitt, R. Electrically resonant terahertz metamaterials: Theoretical and experimental investigations. Phys. Rev. B 2007, 75, 041102. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef] [PubMed]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef] [PubMed]
- La Spada, L.; Vegni, L. Electromagnetic nanoparticles for sensing and medical diagnostic applications. Materials 2018, 11, 603. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.; Justice, B.; Cummer, S.A.; Pendry, J.B.; Starr, A.; Smith, D. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Grant, J.; Ma, Y.; Saha, S.; Khalid, A.; Cumming, D.R. Polarization insensitive, broadband terahertz metamaterial absorber. Opt. Lett. 2011, 36, 3476–3478. [Google Scholar] [CrossRef] [PubMed]
- Sabah, C. Tunable graphene integrated perfect metamaterial absorber for energy harvesting and visible light communication. In Proceedings of the 2018 Global LIFI Congress (GLC), Paris, France, 8–9 February 2018; pp. 1–4. [Google Scholar]
- Ishii, S.; Uchida, K.-I.; Dao, T.D.; Wada, Y.; Saitoh, E.; Nagao, T. Generating spin current from mid infrared plasmonic metamaterial absorbers. In CLEO: QELS Fundamental Science; Optical Society of America: San Jose, CA, USA, 2018. [Google Scholar]
- Nguyen, T.T.; Lim, S. Angle-and polarization-insensitive broadband metamaterial absorber using resistive fan-shaped resonators. Appl. Phys. Lett. 2018, 112, 021605. [Google Scholar] [CrossRef]
- Zhou, Q.; Yin, X.; Ye, F.; Liu, X.; Cheng, L.; Zhang, L. A novel two-layer periodic stepped structure for effective broadband radar electromagnetic absorption. Mater. Des. 2017, 123, 46–53. [Google Scholar] [CrossRef]
- Shang, Y.; Shen, Z.; Xiao, S. On the design of single-layer circuit analog absorber using double-square-loop array. IEEE Trans. Antennas Propag. 2013, 61, 6022–6029. [Google Scholar] [CrossRef]
- Xiong, H.; Hong, J.-S.; Luo, C.-M.; Zhong, L.-L. An ultrathin and broadband metamaterial absorber using multi-layer structures. J. Appl. Phys. 2013, 114, 064109. [Google Scholar] [CrossRef]
- Sugimoto, S.; Kondo, S.; Okayama, K.; Nakamura, H.; Book, D.; Kagotani, T.; Homma, M.; Ota, H.; Kimura, M.; Sato, R. M-Type ferrite composite as a microwave absorber with wide bandwidth in the GHz range. IEEE Trans. Magn. 1999, 35, 3154–3156. [Google Scholar] [CrossRef]
- Park, M.-J.; Choi, J.; Kim, S.-S. Wide bandwidth pyramidal absorbers of granular ferrite and carbonyl iron powders. IEEE Trans. Magn. 2000, 36, 3272–3274. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y. Ultrabroadband microwave metamaterial absorber based on electric SRR loaded with lumped resistors. J. Electron. Mater. 2016, 45, 5033–5039. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, S.; Da, X.; Fang, Y.; Ma, J.; Li, W.; Zhu, Z. Triple-band low frequency ultra-compact metamaterial absorber. J. Appl. Phys. 2015, 117, 184503. [Google Scholar] [CrossRef]
- Dincer, F.; Karaaslan, M.; Sabah, C. Design and analysis of perfect metamaterial absorber in GHz and THz frequencies. J. Electromagn. Waves Appl. 2015, 29, 2492–2500. [Google Scholar] [CrossRef]
- Hossain, M.J.; Faruque, M.R.I.; Islam, M.T. Design and analysis of a new composite double negative metamaterial for multi-band communication. Curr. Appl. Phys. 2017, 17, 931–939. [Google Scholar] [CrossRef]
- Islam, S.S.; Faruque, M.R.I.; Islam, M.T. Design and absorption analysis of a new multiband split-s-shaped metamaterial. Sci. Eng. Compos. Mater. 2017, 24, 139–148. [Google Scholar] [CrossRef]
- Kim, Y.; Yoo, Y.; Hwang, J.; Lee, Y. Ultra-broadband microwave metamaterial absorber based on resistive sheets. J. Opt. 2016, 19, 015103. [Google Scholar] [CrossRef]
- Bakır, M.; Karaaslan, M.; Dincer, F.; Delihacioglu, K.; Sabah, C. Tunable perfect metamaterial absorber and sensor applications. J. Mater. Sci. Mater. Electron. 2016, 27, 12091–12099. [Google Scholar] [CrossRef]
- Xu, G.; Huang, J.; Ju, Z.; Wei, Z.; Li, J.; Zhao, Q. A novel six-band polarization-insensitive metamaterial absorber with four multiple-mode resonators. Prog. Electromagn. Res. 2017, 77, 133–144. [Google Scholar] [CrossRef]
- Akgol, O.; Karaaslan, M.; Unal, E.; Sabah, C. Implementation of a perfect metamaterial absorber into multi-functional sensor applications. Mod. Phys. Lett. B 2017, 31, 1750176. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.-Y.; Xie, J. High sensitivity refractive index sensor based on metamaterial absorber. Prog. Electromagn. Res. 2018, 71, 107–115. [Google Scholar] [CrossRef]
- Altintas, O.; Aksoy, M.; Akgol, O.; Unal, E.; Karaaslan, M.; Sabah, C. Fluid, strain and rotation sensing applications by using metamaterial based sensor. J. Electrochem. Soc. 2017, 164, B567–B573. [Google Scholar] [CrossRef]
- Wu, J.; Wang, P.; Huang, X.; Rao, F.; Chen, X.; Shen, Z.; Yang, H. Design and validation of liquid permittivity sensor based on rcrr microstrip metamaterial. Sens. Actuators A Phys. 2018, 280, 222–227. [Google Scholar] [CrossRef]
- Salim, A.; Memon, M.U.; Lim, S. Simultaneous detection of two chemicals using a te20-mode substrate-integrated waveguide resonator. Sensors 2018, 18, 811. [Google Scholar] [CrossRef] [PubMed]
- Dassault Systèmes. CST Microwave Studio. Available online: https://www.cst.com (accessed on 12 October 2018).
- Padooru, Y.R.; Yakovlev, A.B.; Kaipa, C.S.; Hanson, G.W.; Medina, F.; Mesa, F.; Glisson, A.W. New absorbing boundary conditions and analytical model for multilayered mushroom-type metamaterials: Applications to wideband absorbers. IEEE Trans. Antennas Propag. 2012, 60, 5727–5742. [Google Scholar] [CrossRef]
- Tarparelli, R.; Iovine, R.; La Spada, L.; Vegni, L. Surface plasmon resonance of nanoshell particles with pmma-graphene core. COMPEL 2014, 33, 2016–2029. [Google Scholar] [CrossRef]
- La Spada, L.; Vegni, L. Metamaterial-based wideband electromagnetic wave absorber. Opt. Express 2016, 24, 5763–5772. [Google Scholar] [CrossRef] [PubMed]
- Gopinath, A.; Silvester, P. Calculation of inductance of finite-length strips and its variation with frequency. IEEE Trans. Microw. Theory Tech. 1973, 21, 380–386. [Google Scholar] [CrossRef]
- Bahl, I.J.; Bhartia, P. Microwave Solid State Circuit Design; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Qin, F.; Ding, L.; Zhang, L.; Monticone, F.; Chum, C.C.; Deng, J.; Mei, S.; Li, Y.; Teng, J.; Hong, M. Hybrid bilayer plasmonic metasurface efficiently manipulates visible light. Sci. Adv. 2016, 2, e1501168. [Google Scholar] [CrossRef] [PubMed]
- La Spada, L.; Haq, S.; Hao, Y. Modeling and design for electromagnetic surface wave devices. Radio Sci. 2017, 52, 1049–1057. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184. [Google Scholar] [CrossRef] [PubMed]
- Sadiku, M.N. Elements of Electromagnetics; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Caloz, C.; Itoh, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- In, S.; Park, N. Effects of optical joule heating in metamaterial absorber: A non-linear recursive feedback optical-thermodynamic multiphysics study. In Proceedings of the IEEE 2015 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (METAMATERIALS), Oxford, UK, 7–12 September 2015; pp. 121–123. [Google Scholar]
- Rothwell, E.J.; Frasch, J.L.; Ellison, S.M.; Chahal, P.; Ouedraogo, R.O. Analysis of the nicolson-ross-weir method for characterizing the electromagnetic properties of engineered materials. Prog. Electromagn. Res. 2016, 157, 31–47. [Google Scholar] [CrossRef]
- Islam, S.S.; Faruque, M.R.I.; Islam, M.T. A new direct retrieval method of refractive index for the metamaterial. Curr. Sci. 2015, 109, 337–342. [Google Scholar]
- Iovine, R.; La Spada, L.; Vegni, L. Nanoparticle device for biomedical and optoelectronics applications. COMPEL 2013, 32, 1596–1608. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Y.; Li, K.; Gong, S. Radar cross section reduction of a microstrip antenna based on polarization conversion metamaterial. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 80–83. [Google Scholar] [CrossRef]
- Iovine, R.; La Spada, L.; Vegni, L. Optical properties of modified nanorod particles for biomedical sensing. IEEE Trans. Magn. 2014, 50, 169–172. [Google Scholar] [CrossRef]
- Engheta, N. Circuits with light at nanoscales: Optical nanocircuits inspired by metamaterials. Science 2007, 317, 1698–1702. [Google Scholar] [CrossRef] [PubMed]
- La Spada, L.; McManus, T.; Dyke, A.; Haq, S.; Zhang, L.; Cheng, Q.; Hao, Y. Surface wave cloak from graded refractive index nanocomposites. Sci. Rep. 2016, 6, 29363. [Google Scholar] [CrossRef] [PubMed]
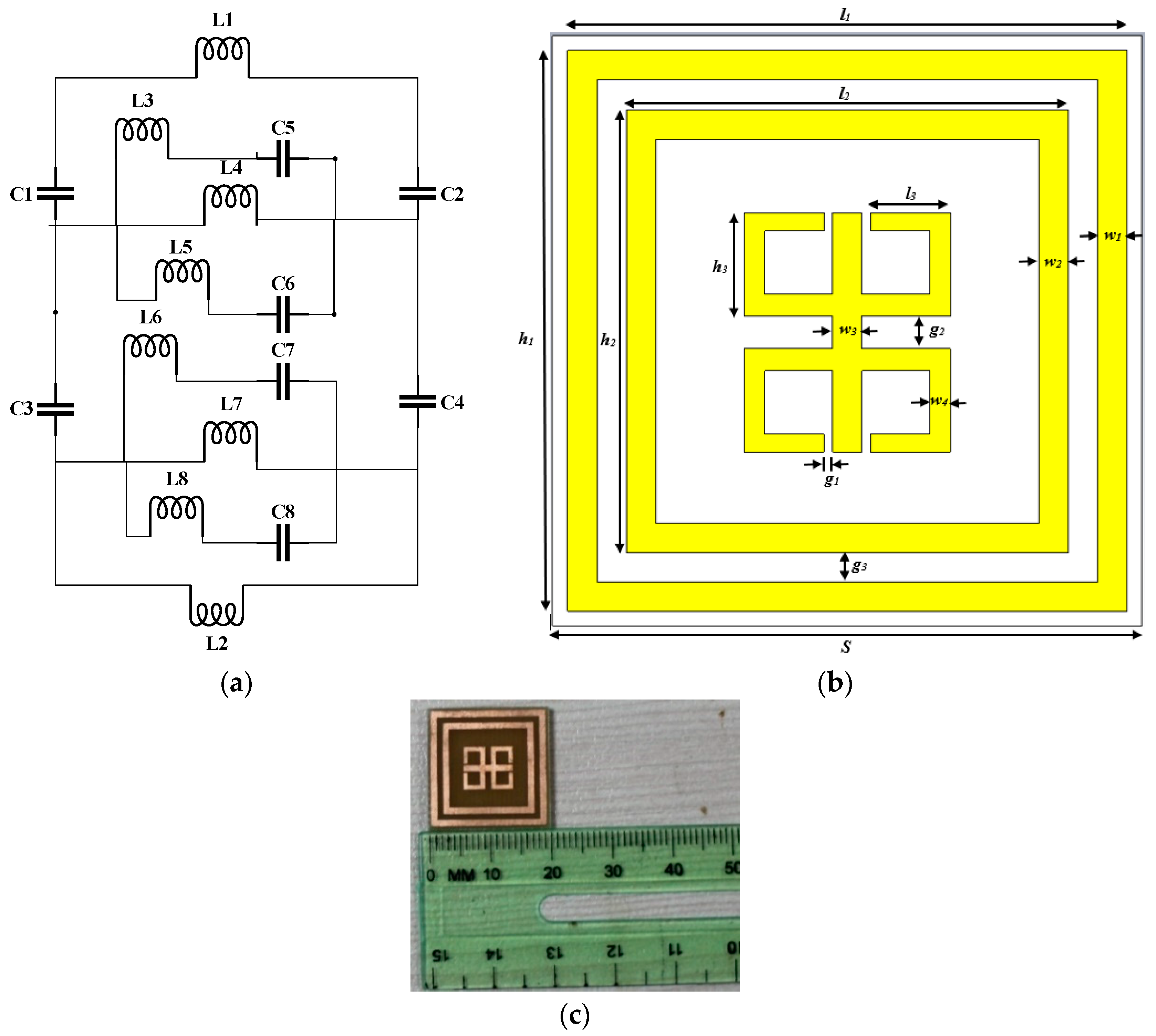
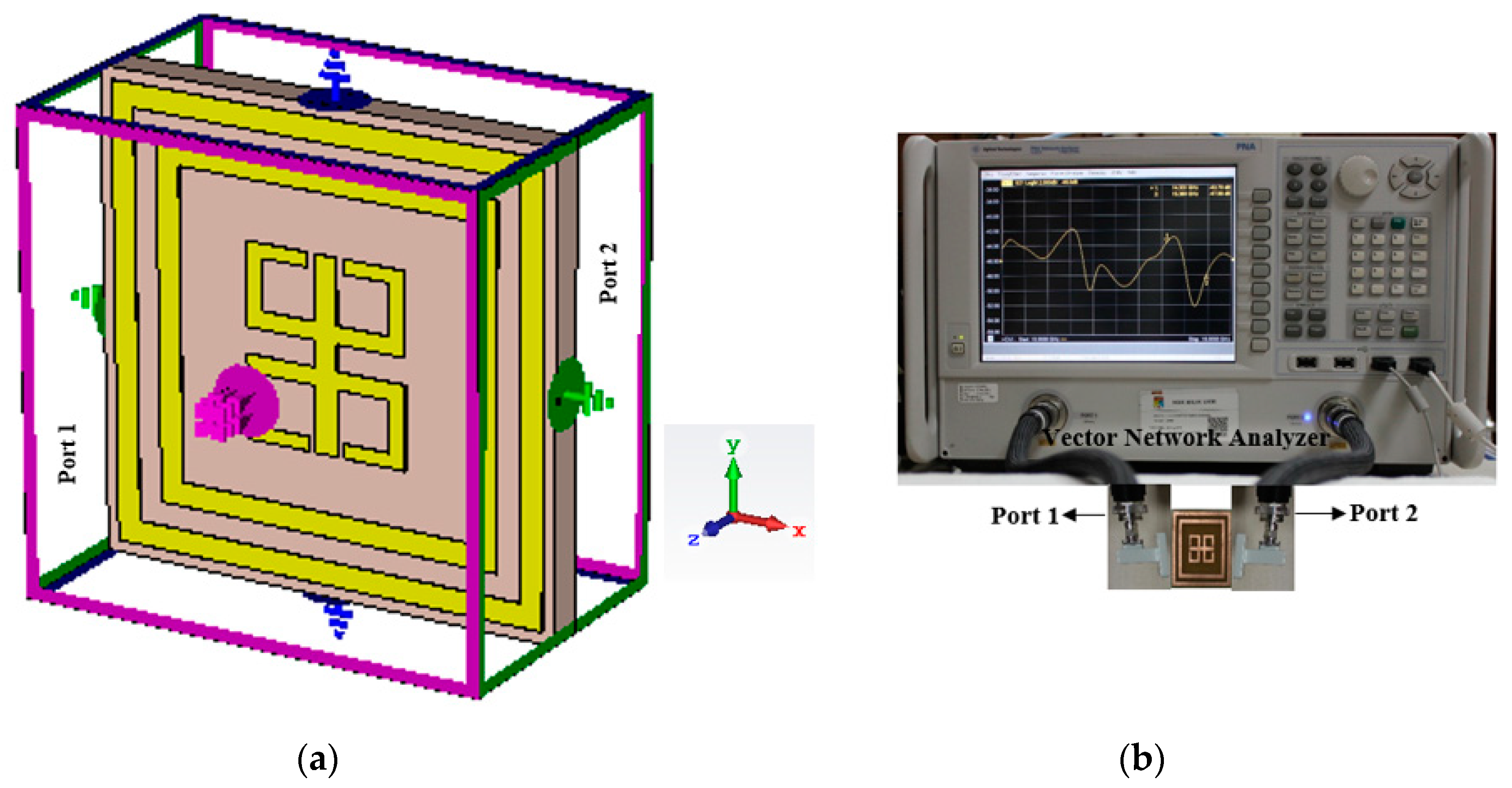


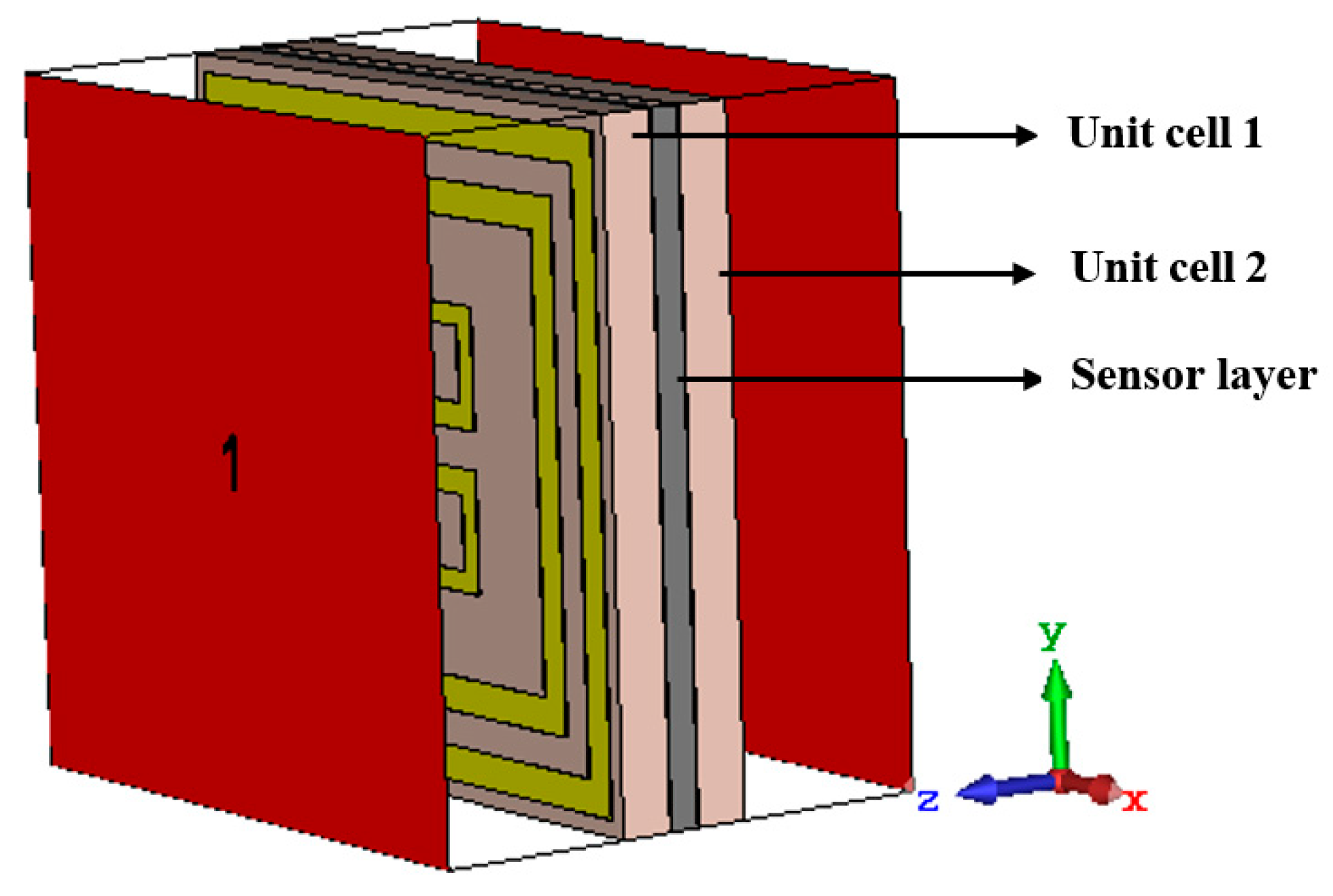
| Parameter | l1 | l2 | l3 | h1 | h2 | h3 | w1 | w2 | w3 | w4 | g1 | g2 | g3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (mm) | 19 | 15 | 2.70 | 19 | 15 | 3.50 | 1 | 1 | 1 | 0.70 | 0.30 | 1.10 | 1 |
| Substrate length & width, S | |||||||||||||
| 20 | |||||||||||||
| Resonance Frequency (GHz) | Permittivity, ε | Permeability, µ | Reflection Co-Efficient, η |
|---|---|---|---|
| 13.78 | −1.484 | −0.362 | −0.887 |
| 15.3 | −0.048 | −1.054 | −0.460 |
| Polarization Angle (φ) | Resonance Frequency (GHz) | Max Absorption (%) | ε | µ | EM Mode | Substrate | Dielectric Constant (εr) | |
|---|---|---|---|---|---|---|---|---|
| 0 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 10 | 13.74 | 99.52 | −1.601 | −0.343 | −0.885 | TEM | FR-4 (lossy) | 4.6 |
| 15.27 | 99.1 | 0.073 | −1.114 | −0.4466 | ||||
| 20 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 30 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 40 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 50 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 60 | 13.78 | 99.6 | −1.484 | −0.361 | −0.887 | TEM | FR-4 (lossy) | 4.6 |
| 15.3 | 99.14 | 0.002 | −1.054 | −0.460 | ||||
| 0 | 12.95 | 91.39 (very narrow band) | −1.327 | −4.437 | −1.515 | TEM | RT-5880 (lossy) | 2.2 |
| 10 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| 20 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| 30 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| 40 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| 50 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| 60 | 12.95 | 91.39 | −1.327 | −4.437 | −1.515 | TEM | RT-5880 | 2.2 |
| Ref. # | Size (mm) | Substrate Material | Operating Frequency [GHz] | Application | Remarks |
|---|---|---|---|---|---|
| [25] | 24 × 30 | FR-4 | 3–6 | Temperature sensor | Absorption rate can be tuned |
| [26] | 20 × 20 | FR-4 | 2–17 | No sensing application | Six-band metamaterial absorber |
| [27] | 36 × 36 | FR-4 | 2–6 | Permittivity sensor | Perfect absorption |
| [29] | 28 × 35 | FR-4 | 3–5 | Micro-fluid sensor | Metamaterial based sensing no absorption |
| [30] | 40 × 20 | F4B | Less than 1 | Permittivity sensor | Metamaterial based sensing no absorption |
| [28] | 24 × 24 | FR-4 | 3–5 | Refractive index sensor | Ring resonant absorber |
| [31] | 60 × 40 | RT 5880 | 7–8 | Chemical sensor | Single band with same liquid loading system |
| Proposed | 20 × 20 | FR-4 | X and Ku Band | Pressure sensor | Dual-band Perfect Absorber and sensing simultaneously |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoque, A.; Tariqul Islam, M.; Almutairi, A.F.; Alam, T.; Jit Singh, M.; Amin, N. A Polarization Independent Quasi-TEM Metamaterial Absorber for X and Ku Band Sensing Applications. Sensors 2018, 18, 4209. https://doi.org/10.3390/s18124209
Hoque A, Tariqul Islam M, Almutairi AF, Alam T, Jit Singh M, Amin N. A Polarization Independent Quasi-TEM Metamaterial Absorber for X and Ku Band Sensing Applications. Sensors. 2018; 18(12):4209. https://doi.org/10.3390/s18124209
Chicago/Turabian StyleHoque, Ahasanul, Mohammad Tariqul Islam, Ali F. Almutairi, Touhidul Alam, Mandeep Jit Singh, and Nowshad Amin. 2018. "A Polarization Independent Quasi-TEM Metamaterial Absorber for X and Ku Band Sensing Applications" Sensors 18, no. 12: 4209. https://doi.org/10.3390/s18124209
APA StyleHoque, A., Tariqul Islam, M., Almutairi, A. F., Alam, T., Jit Singh, M., & Amin, N. (2018). A Polarization Independent Quasi-TEM Metamaterial Absorber for X and Ku Band Sensing Applications. Sensors, 18(12), 4209. https://doi.org/10.3390/s18124209







