Conformal and Disposable Antenna-Based Sensor for Non-Invasive Sweat Monitoring
Abstract
1. Introduction
2. Materials and Methods
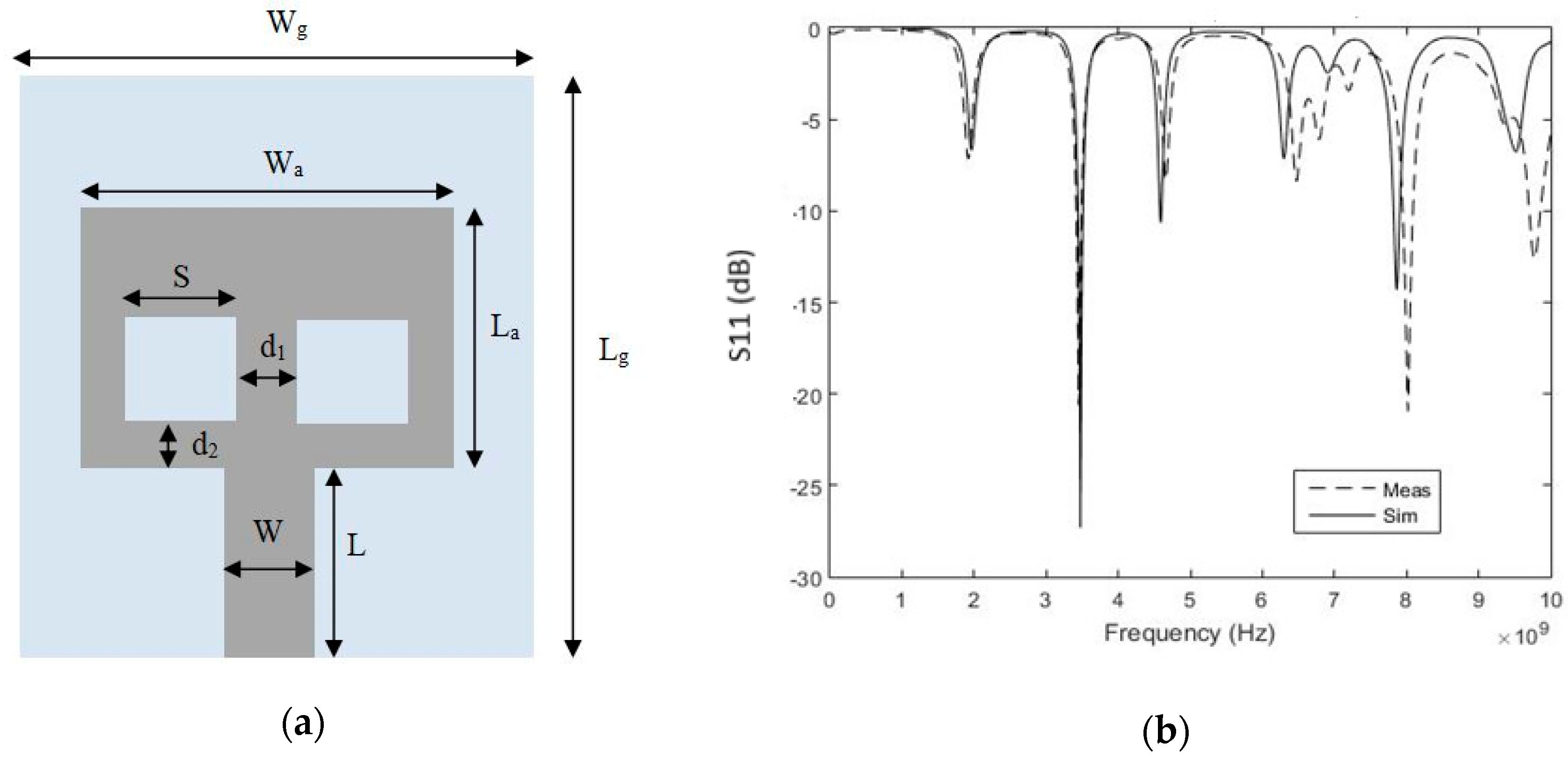
2.1. Sensor Design
2.2. Sensing Methodology and Test Solutions
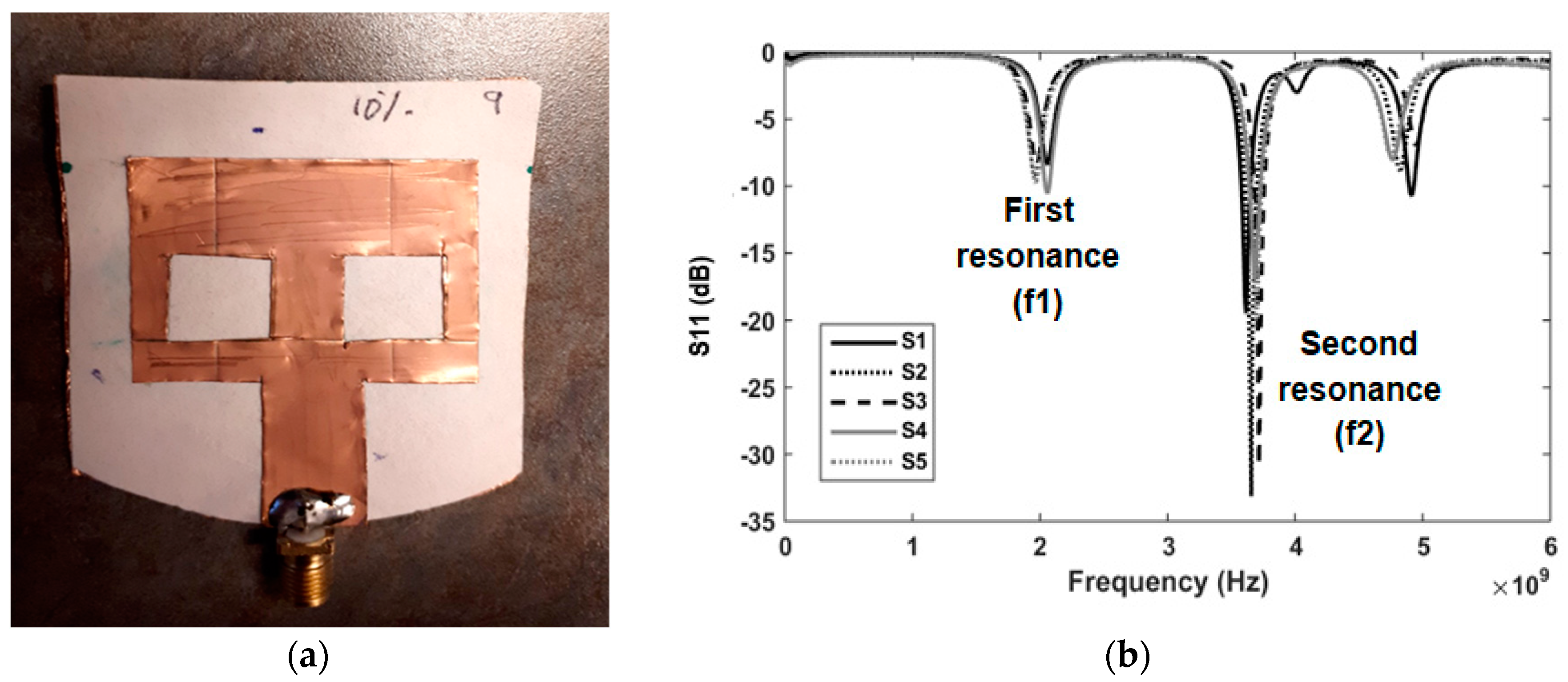
3. Results
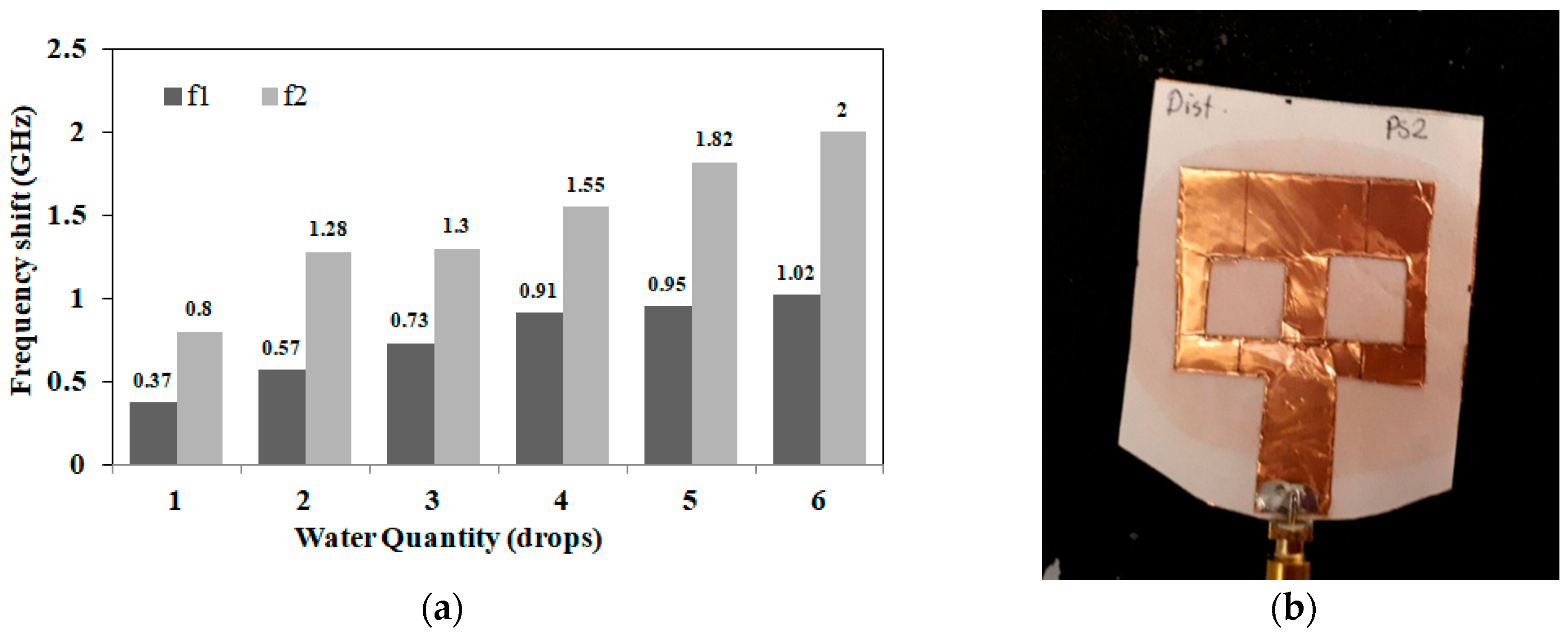
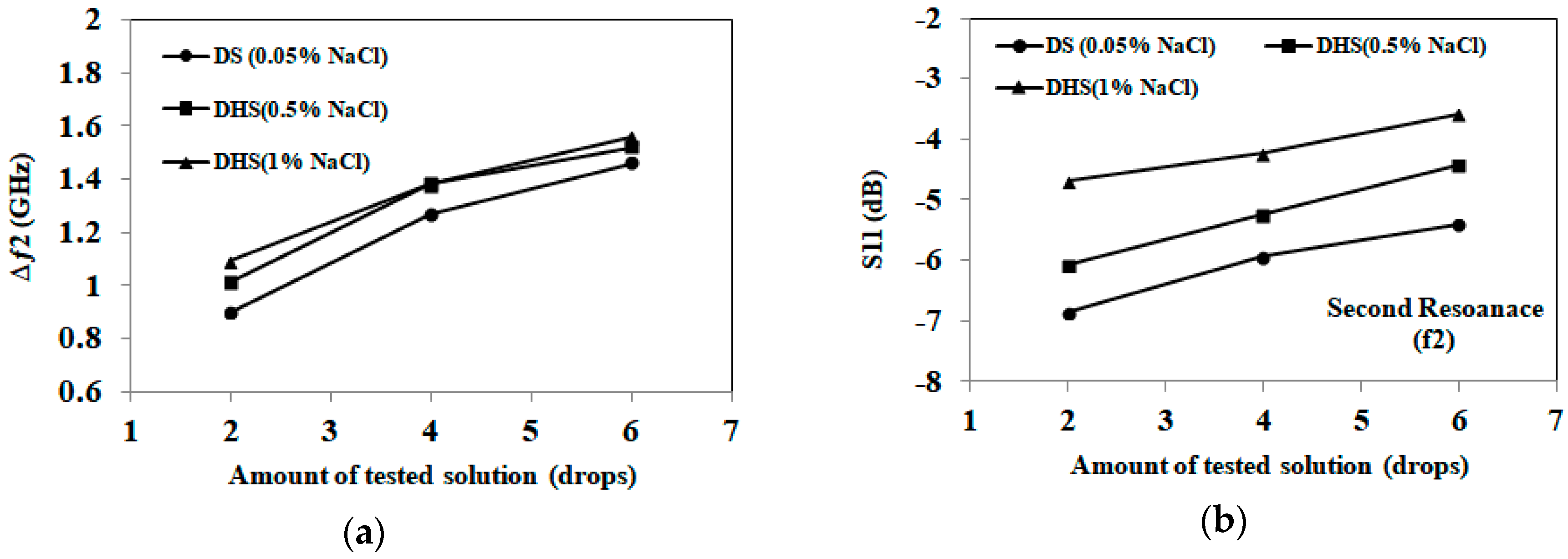
3.1. Detection of Applied Solution Quantity
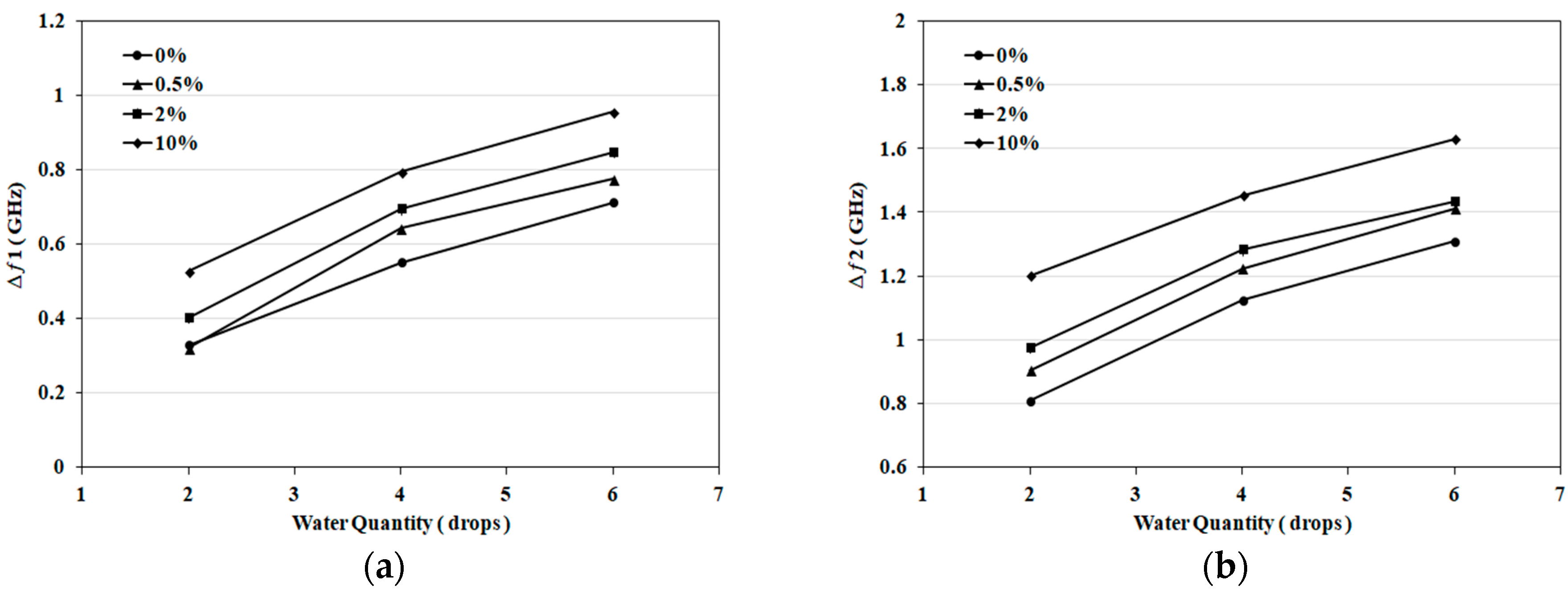
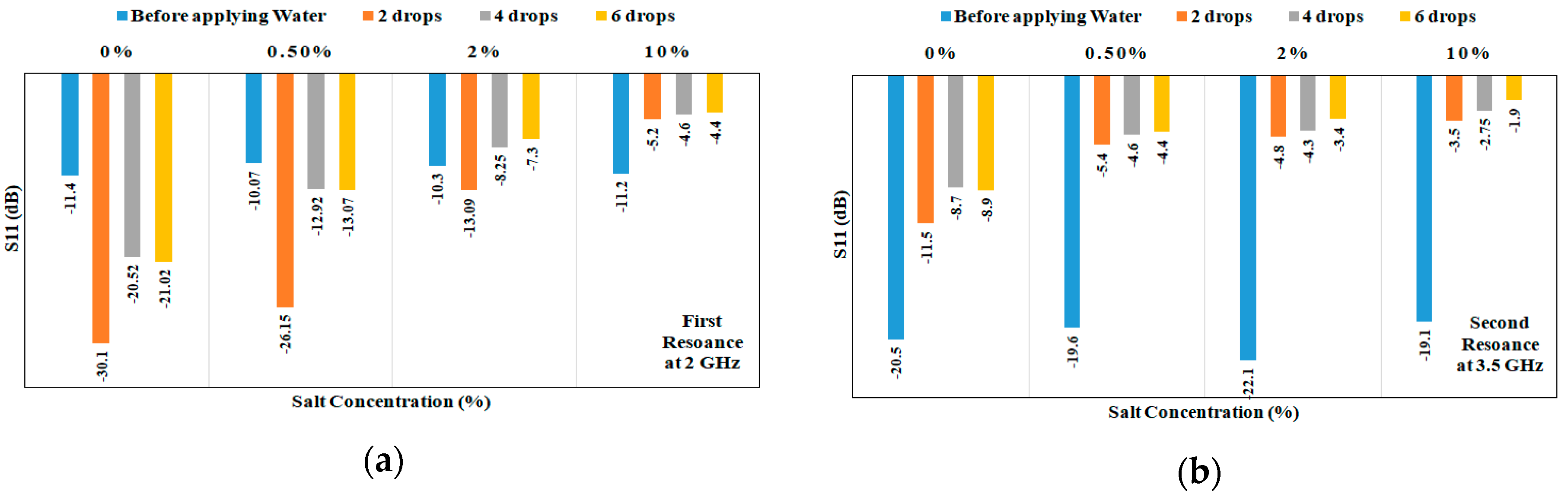
3.2. Detection of Salt Concentrations
3.3. Case Studies: NaCl Solutions
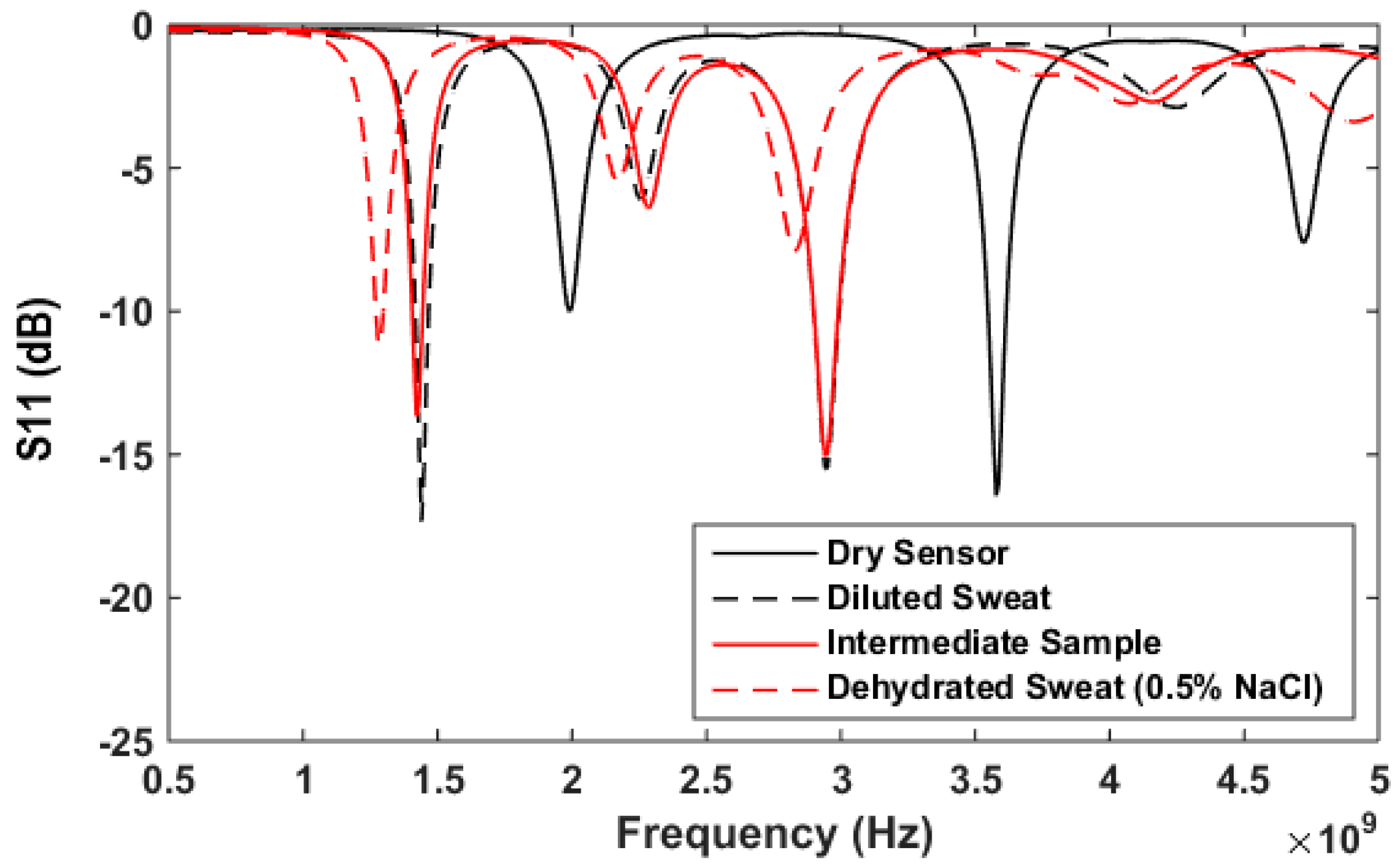
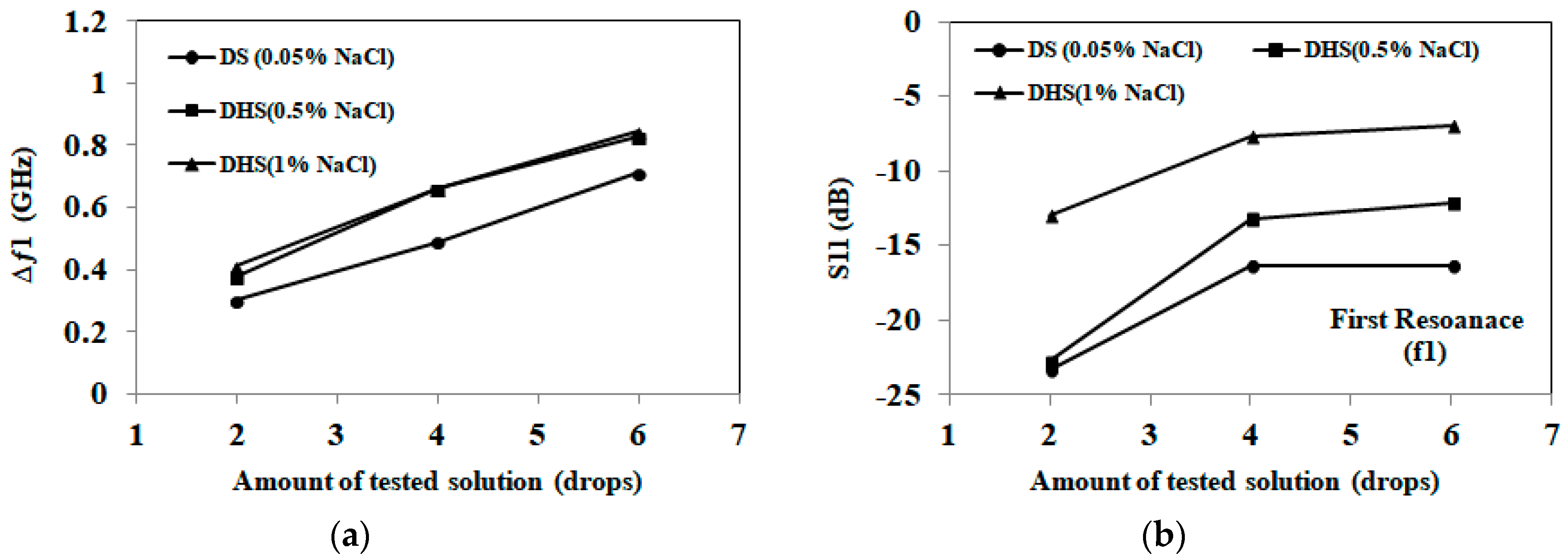
3.4. Artificial Sweat Trials
4. Discussion
5. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nag, A.; Mukhopadhyay, S.C.; Kosel, J. Wearable Flexible Sensors: A Review. IEEE Sens. J. 2017, 17, 3949–3960. [Google Scholar] [CrossRef]
- Mosenia, A.; Sur-Kolay, S.; Raghunathan, A.; Jha, N.K. Wearable Medical Sensor-Based System Design: A Survey. IEEE Trans. Multi-Scale Comput. Syst. 2017, 3, 124–138. [Google Scholar] [CrossRef]
- Wearable Sweat Sensor Could Monitor Dehydration, Fatigue. Available online: https://www.medicalnewstoday.com/articles/305751.php (accessed on 8 March 2018).
- Kurdak, S.S.; Shirreffs, S.M.; Maughan, R.J.; Ozgünen, K.T.; Zeren, C.; Korkmaz, S.; Yazici, Z.; Ersöz, G.; Binnet, M.S.; Dvorak, J. Hydration and sweating responses to hot-weather football competition. Scand. J. Med. Sci. Sports 2010, 20, 133–139. [Google Scholar] [CrossRef] [PubMed]
- Warren, J.L.; Bacon, W.E.; Harris, T.; McBean, A.M.; Foley, D.; Phillips, C. The burden and outcomes associated with dehydration among US elderly, 1991. Am. J. Public Health 1994, 84, 1265–1269. [Google Scholar] [CrossRef] [PubMed]
- Benelam, B.; Wyness, L. Hydration and health: A review. Nutr. Bull. 2010, 35, 3–25. [Google Scholar] [CrossRef]
- Garrett, D.C.; Rae, N.; Fletcher, J.R.; Zarnke, S.; Thorson, S.; Hogan, D.B.; Fear, E.C. Engineering Approaches to Assessing Hydration Status. IEEE Rev. Biomed. Eng. 2018, 11, 234–248. [Google Scholar] [CrossRef] [PubMed]
- Thomas, D.R.; Cote, T.R.; Lawhorne, L.; Levenson, S.A.; Rubenstein, L.Z.; Smith, D.A.; Stefanacci, R.G.; Tangalos, E.G.; Morley, J.E.; Council, D. Understanding clinical dehydration and its treatment. J. Am. Med. Dir. Assoc. 2008, 9, 292–301. [Google Scholar] [CrossRef] [PubMed]
- Brendtke, R.; Wiehl, M.; Groeber, F.; Schwarz, T.; Walles, H.; Hansmann, J. Feasibility Study on a Microwave-Based Sensor for Measuring Hydration Level Using Human Skin Models. PLoS ONE 2016, 11, e0153145. [Google Scholar] [CrossRef] [PubMed]
- Daggett, P.; Deanfield, J.; Moss, F.; Reynolds, D. Severe hypernatraemia in adults. Br. Med. J. 1979, 1, 1177–1180. [Google Scholar] [CrossRef] [PubMed]
- Gonzalo-Ruiz, J.; Mas, R.; de Haro, C.; Cabruja, E.; Camero, R.; Alonso-Lomillo, M.A.; Muñoz, F.J. Early determination of cystic fibrosis by electrochemical chloride quantification in sweat. Biosens. Bioelectron. 2009, 24, 1788–1791. [Google Scholar] [CrossRef] [PubMed]
- Sterns, R.H.; Silver, S.M.; Hix, J.K. Treatment of Hyponatremia. In Hyponatremia; Springer: New York, NY, USA, 2013; pp. 221–250. ISBN 978-1-4614-6644-4. [Google Scholar]
- De Guzman, K.; Morrin, A. Screen-printed Tattoo Sensor towards the Non-invasive Assessment of the Skin Barrier. Electroanalysis 2017, 29, 188–196. [Google Scholar] [CrossRef]
- Walsh, N.P.; Laing, S.J.; Oliver, S.J.; Montague, J.C.; Walters, R.; Bilzon, J.L. Saliva parameters as potential indices of hydration status during acute dehydration. Med. Sci. Sports Exerc. 2004, 36, 1535–1542. [Google Scholar] [CrossRef] [PubMed]
- Morgan, R.M.; Patterson, M.J.; Nimmo, M.A. Acute effects of dehydration on sweat composition in men during prolonged exercise in the heat. Acta Physiol. 2004, 182, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Coyle, S.; Lau, K.-T.; Moyna, N.; O’Gorman, D.; Diamond, D.; Di Francesco, F.; Costanzo, D.; Salvo, P.; Trivella, M.G.; De Rossi, D.E. BIOTEX—Biosensing textiles for personalised healthcare management. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 364–370. [Google Scholar] [CrossRef] [PubMed]
- Schazmann, B.; Morris, D.; Slater, C.; Beirne, S.; Fay, C.; Reuveny, R.; Moyna, N.; Diamond, D. A wearable electrochemical sensor for the real-time measurement of sweat sodium concentration. Anal. Methods 2010, 2, 342–348. [Google Scholar] [CrossRef]
- Faulkner, S.H.; Spilsbury, K.L.; Harvey, J.; Jackson, A.; Huang, J.; Platt, M.; Tok, A.; Nimmo, M.A. The detection and measurement of interleukin-6 in venous and capillary blood samples, and in sweat collected at rest and during exercise. Eur. J. Appl. Physiol. 2014, 114, 1207–1216. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Ho, C.; Slappey, N.; Zhou, Z.; Snelgrove, S.E.; Brown, M.; Grabinski, A.; Guo, X.; Chen, Y.; Miller, K. A wearable conductivity sensor for wireless real-time sweat monitoring. Sens. Actuators B Chem. 2016, 227, 35–42. [Google Scholar] [CrossRef]
- Bandodkar, A.J.; Molinnus, D.; Mirza, O.; Guinovart, T.; Windmiller, J.R.; Valdés-Ramírez, G.; Andrade, F.J.; Schöning, M.J.; Wang, J. Epidermal tattoo potentiometric sodium sensors with wireless signal transduction for continuous non-invasive sweat monitoring. Biosens. Bioelectron. 2014, 54, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Emaminejad, S.; Nyein, H.Y.Y.; Challa, S.; Chen, K.; Peck, A.; Fahad, H.M.; Ota, H.; Shiraki, H.; Kiriya, D. Fully integrated wearable sensor arrays for multiplexed in situ perspiration analysis. Nature 2016, 529, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Anastasova, S.; Crewther, B.; Bembnowicz, P.; Curto, V.; Ip, H.M.; Rosa, B.; Yang, G.-Z. A wearable multisensing patch for continuous sweat monitoring. Biosens. Bioelectron. 2017, 93, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.K.; Kenney, W.L. Effect of age on heat-activated sweat gland density and flow during exercise in dry heat. J. Appl. Physiol. 1987, 63, 1089–1094. [Google Scholar] [CrossRef] [PubMed]
- Kenney, W.L.; Anderson, R.K. Responses of older and younger women to exercise in dry and humid heat without fluid replacement. Med. Sci. Sports Exerc. 1988, 20, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Tankersley, C.G.; Smolander, J.; Kenney, W.L.; Fortney, S.M. Sweating and skin blood flow during exercise: Effects of age and maximal oxygen uptake. J. Appl. Physiol. 1991, 71, 236–242. [Google Scholar] [CrossRef] [PubMed]
- Inoue, Y.; Nakao, M.; Okudaira, S.; Ueda, H.; Araki, T. Seasonal variation in sweating responses of older and younger men. Eur. J. Appl. Physiol. Occup. Physiol. 1995, 70, 6–12. [Google Scholar] [CrossRef] [PubMed]
- Inbar, O.; Morris, N.; Epstein, Y.; Gass, G. Comparison of thermoregulatory responses to exercise in dry heat among prepubertal boys, young adults and older males. Exp. Physiol. 2004, 89, 691–700. [Google Scholar] [CrossRef] [PubMed]
- Taylor, N.A.; Machado-Moreira, C.A. Regional variations in transepidermal water loss, eccrine sweat gland density, sweat secretion rates and electrolyte composition in resting and exercising humans. Extrem. Physiol. Med. 2013, 2, 4. [Google Scholar] [CrossRef] [PubMed]
- Brueck, A.; Iftekhar, T.; Stannard, A.B.; Yelamarthi, K.; Kaya, T. A Real-Time Wireless Sweat Rate Measurement System for Physical Activity Monitoring. Sensors 2018, 18, 533. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, K.; Hattori, K.; Ota, Y.; Kanai, T.; Shimizu, M.; Kobayashi, H.; Tokuda, Y. The measurement of axillary moisture for the assessment of dehydration among older patients: A pilot study. Exp. Gerontol. 2013, 48, 255–258. [Google Scholar] [CrossRef] [PubMed]
- Bak, A.; Tsiami, A.; Greene, C. Methods of Assessment of Hydration Status and their Usefulness in Detecting Dehydration in the Elderly. Curr. Res. Nutr. Food Sci. J. 2017, 5, 43–54. [Google Scholar] [CrossRef]
- Huang, J.; Harvey, J.; Fam, W.H.D.; Nimmo, M.A.; Tok, I.Y.A. Novel Biosensor for InterLeukin-6 Detection. Procedia Eng. 2013, 60, 195–200. [Google Scholar] [CrossRef]
- Rose, D.P.; Ratterman, M.E.; Griffin, D.K.; Hou, L.; Kelley-Loughnane, N.; Naik, R.R.; Hagen, J.A.; Papautsky, I.; Heikenfeld, J.C. Adhesive RFID sensor patch for monitoring of sweat electrolytes. IEEE Trans. Biomed. Eng. 2015, 62, 1457–1465. [Google Scholar] [CrossRef] [PubMed]
- Moran, D.S.; Heled, Y.; Margaliot, M.; Shani, Y.; Laor, A.; Margaliot, S.; Bickels, E.E.; Shapiro, Y. Hydration status measurement by radio frequency absorptiometry in young athletes—A new method and preliminary results. Physiol. Meas. 2004, 25, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Butterworth, I.; Serallés, J.; Mendoza, C.S.; Giancardo, L.; Daniel, L. A wearable physiological hydration monitoring wristband through multi-path non-contact dielectric spectroscopy in the microwave range. In Proceedings of the 2015 IEEE MTT-S 2015 International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-BIO), Taipei, Taiwan, 21–23 September 2015; pp. 60–61. [Google Scholar]
- Trenz, F.; Weigel, R.; Kissinger, D. Evaluation of a reflection based dehydration sensing method for wristwatch integration. In Proceedings of the 2016 21st International Conference on Microwave, Radar and Wireless Communications (MIKON), Krakow, Poland, 9–11 May 2016; pp. 1–3. [Google Scholar]
- Khaleel, H.R.; Al-Rizzo, H.M.; Abbosh, A.I. Design, Fabrication, and Testing of Flexible Antennas; InTech: Rijeka, Croatia, 2013. [Google Scholar]
- Raad, H.K.; Al-Rizzo, H.M.; Abbosh, A.I.; Hammoodi, A.I. A compact dual band polyimide based antenna for wearable and flexible telemedicine devices. Progress Electromagn. Res. C 2016, 63, 153–161. [Google Scholar] [CrossRef]
- Hassan, A.; Ali, S.; Hassan, G.; Bae, J.; Lee, C.H. Inkjet-printed antenna on thin PET substrate for dual band Wi-Fi communications. Microsyst. Technol. 2017, 23, 3701–3709. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Coupez, J.P.; Castel, V.; Person, C.; Delattre, A.; Crowther-Alwyn, L.; Borel, P. RF characterization of flexible substrates for new conformable antenna systems. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar]
- Anagnostou, D.E. Organic Paper-Based Antennas; WIT Press: Billerica, MA, USA, 2014. [Google Scholar]
- Killard, A.J. Disposable sensors. Curr. Opin. Electrochem. 2017. [Google Scholar] [CrossRef]
- Moscato, S.; Moro, R.; Pasian, M.; Bozzi, M.; Perregrini, L. Innovative manufacturing approach for paper-based substrate integrated waveguide components and antennas. IET Microw. Antennas Propag. 2016, 10, 256–263. [Google Scholar] [CrossRef]
- Palazzi, V.; Mezzanotte, P.; Roselli, L. Design of a novel antenna system intended for harmonic RFID tags in paper substrate. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–4. [Google Scholar]
- Alimenti, F.; Mezzanotte, P.; Dionigi, M.; Virili, M.; Roselli, L. Microwave circuits in paper substrates exploiting conductive adhesive tapes. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 660–662. [Google Scholar] [CrossRef]
- Baker, L.B. Sweating Rate and Sweat Sodium Concentration in Athletes: A Review of Methodology and Intra/Interindividual Variability. Sports Med. 2017, 47, 111–128. [Google Scholar] [CrossRef] [PubMed]
- Callewaert, C.; Buysschaert, B.; Vossen, E.; Fievez, V.; Van de Wiele, T.; Boon, N. Artificial sweat composition to grow and sustain a mixed human axillary microbiome. J. Microbiol. Methods 2014, 103, 6–8. [Google Scholar] [CrossRef] [PubMed]
- Midander, K.; Julander, A.; Kettelarij, J.; Lidén, C. Testing in artificial sweat—Is less more? Comparison of metal release in two different artificial sweat solutions. Regul. Toxicol. Pharmacol. 2016, 81, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Alomari, M.; Sahin, B.; Snelgrove, S.E.; Edwards, J.; Mellinger, A.; Kaya, T. Real-time sweat analysis via alternating current conductivity of artificial and human sweat. Appl. Phys. Lett. 2015, 106, 133702. [Google Scholar] [CrossRef]
- Hoekstra, R.; Blondeau, P.; Andrade, F.J. IonSens: A Wearable Potentiometric Sensor Patch for Monitoring Total Ion Content in Sweat. Electroanalysis 2018, 30, 1536–1544. [Google Scholar] [CrossRef]
- Buchner, R.; Hefter, G.T.; May, P.M. Dielectric Relaxation of Aqueous NaCl Solutions. J. Phys. Chem. A 1999, 103, 1–9. [Google Scholar] [CrossRef]
- Chen, T.; Hefter, G.; Buchner, R. Dielectric Spectroscopy of Aqueous Solutions of KCl and CsCl. J. Phys. Chem. A 2003, 107, 4025–4031. [Google Scholar] [CrossRef]
- Gulich, R.; Köhler, M.; Lunkenheimer, P.; Loidl, A. Dielectric spectroscopy on aqueous electrolytic solutions. Radiat. Environ. Biophys. 2009, 48, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Romanov, A.N. Dielectric properties of human sweat fluid in the microwave range. Biophysics 2010, 55, 473–476. [Google Scholar] [CrossRef]

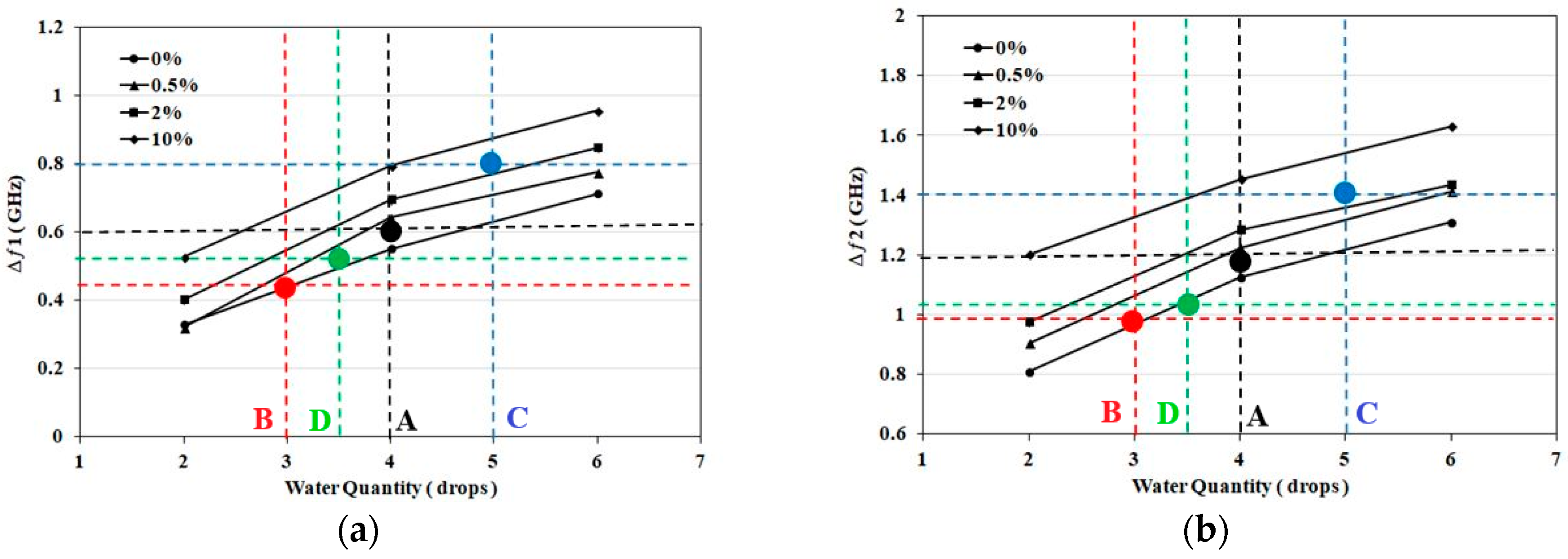

| Samples | First Band (GHZ) | Second Band (GHZ) | Detection Decision |
|---|---|---|---|
| Sample. A (4 drops, 0.5%) | Δƒ1=0.58 | Δƒ2=1.14 | Navg=4 (0–0.5%) |
| Sample. B (2 drops, 0%) | Δƒ1=0.44 | Δƒ2=0.97 | Navg=3 (0–0.5%) |
| Sample. C (4 drops, 10%) | Δƒ1=0.8 | Δƒ2=1.4 | Navg=5 (2–10%) |
| Sample. D (3 drops, 0%) | Δƒ1=0.51 | Δƒ2=1.03 | Navg=3.5 (0–0.5%) |
| Sample. E (6 drops, 2%) | Δƒ1=0.92 | Δƒ2=1.43 | Navg=7 (2–10%) |
| Sample. F (5 drops, 2%) | Δƒ1=0.8 | Δƒ2=1.39 | Navg= 5 (2–10%) |
| Sample. G (6 drops, 0%) | Δƒ1=0.72 | Δƒ2=1.33 | Navg=6 (0–0.5%) |
| Sample. H (3 drops, 0.5%) | Δƒ1=0.47 | Δƒ2=1.14 | Navg=3.5 (0–0.5%) |
| Sample. I (5 drops, 10%) | Δƒ1=0.9 | Δƒ2=1.51 | Navg=6 (2–10%) |
| Sample. J (4 drops, 2%) | Δƒ1=0.62 | Δƒ2=1.2 | Navg=4 (0.5–2%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eldamak, A.R.; Fear, E.C. Conformal and Disposable Antenna-Based Sensor for Non-Invasive Sweat Monitoring. Sensors 2018, 18, 4088. https://doi.org/10.3390/s18124088
Eldamak AR, Fear EC. Conformal and Disposable Antenna-Based Sensor for Non-Invasive Sweat Monitoring. Sensors. 2018; 18(12):4088. https://doi.org/10.3390/s18124088
Chicago/Turabian StyleEldamak, Angie R., and Elise C. Fear. 2018. "Conformal and Disposable Antenna-Based Sensor for Non-Invasive Sweat Monitoring" Sensors 18, no. 12: 4088. https://doi.org/10.3390/s18124088
APA StyleEldamak, A. R., & Fear, E. C. (2018). Conformal and Disposable Antenna-Based Sensor for Non-Invasive Sweat Monitoring. Sensors, 18(12), 4088. https://doi.org/10.3390/s18124088






