Segmentation and Multi-Scale Convolutional Neural Network-Based Classification of Airborne Laser Scanner Data
Abstract
1. Introduction
- -
- We propose a three-step region-growing segmentation method for segment-based classification. We divide the segmentation into three steps in order to provide a good starting point for the following procedure.
- -
- We also develop our convolutional neural network. A multi-scale convolutional neural network is trained to automatically learn deep features of each point from the generated feature images across multiple scales.
2. Related Work
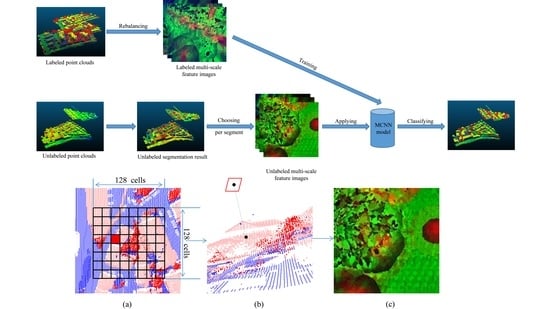
3. Methodology
3.1. Three-Step Region-Growing Segmentation
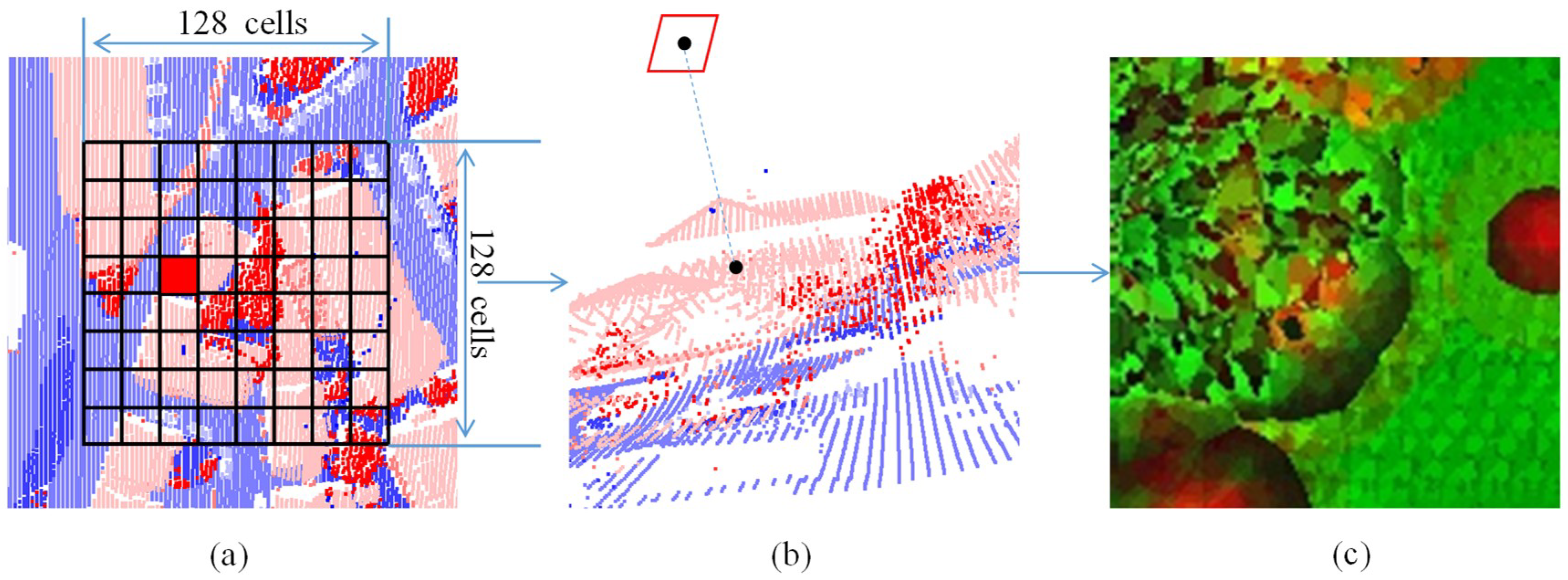
3.2. Feature Image Generation
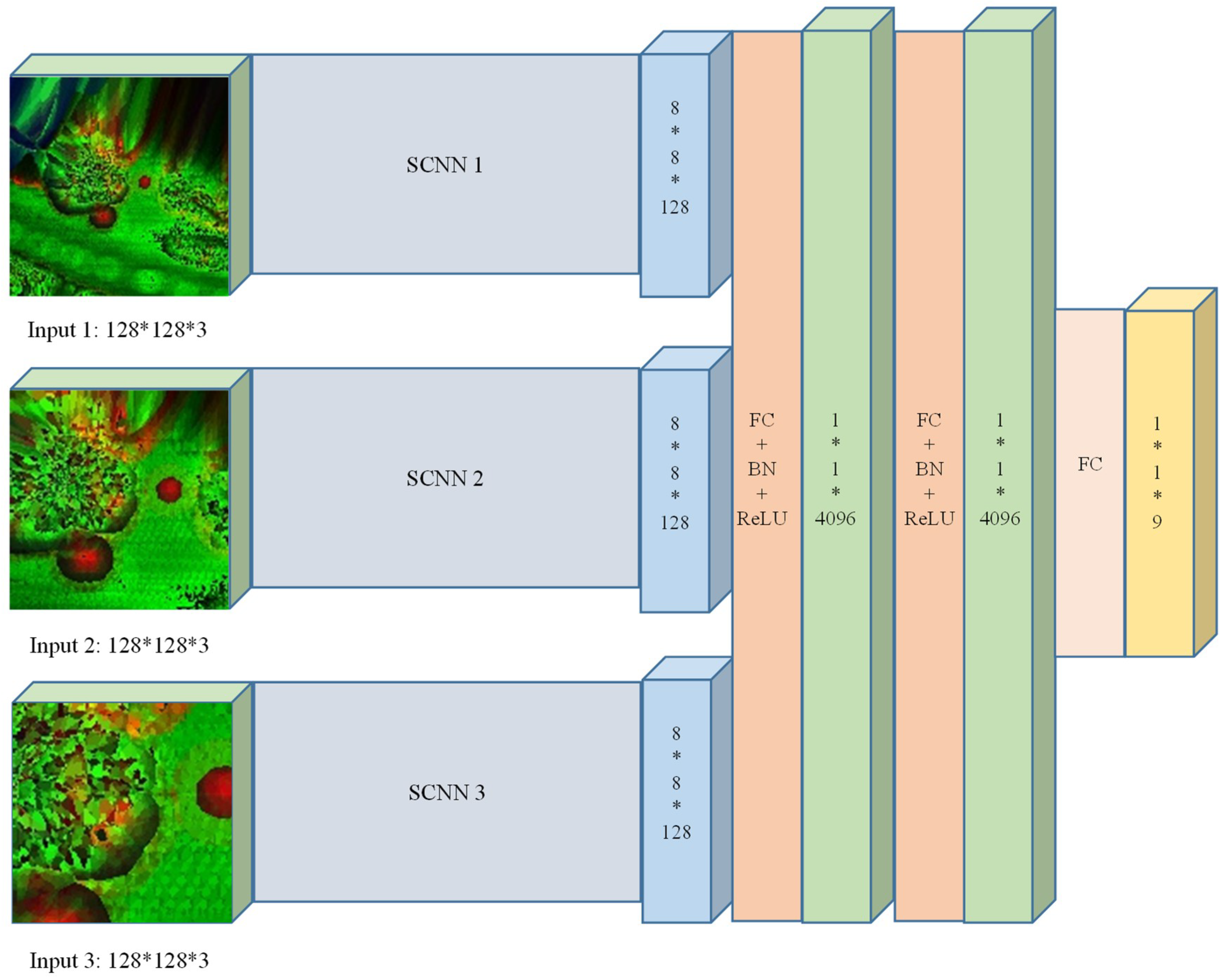
3.3. The Multi-Scale Convolutional Neural Network (MCNN)
3.4. Workflow
4. Experimental Results
4.1. Test Data
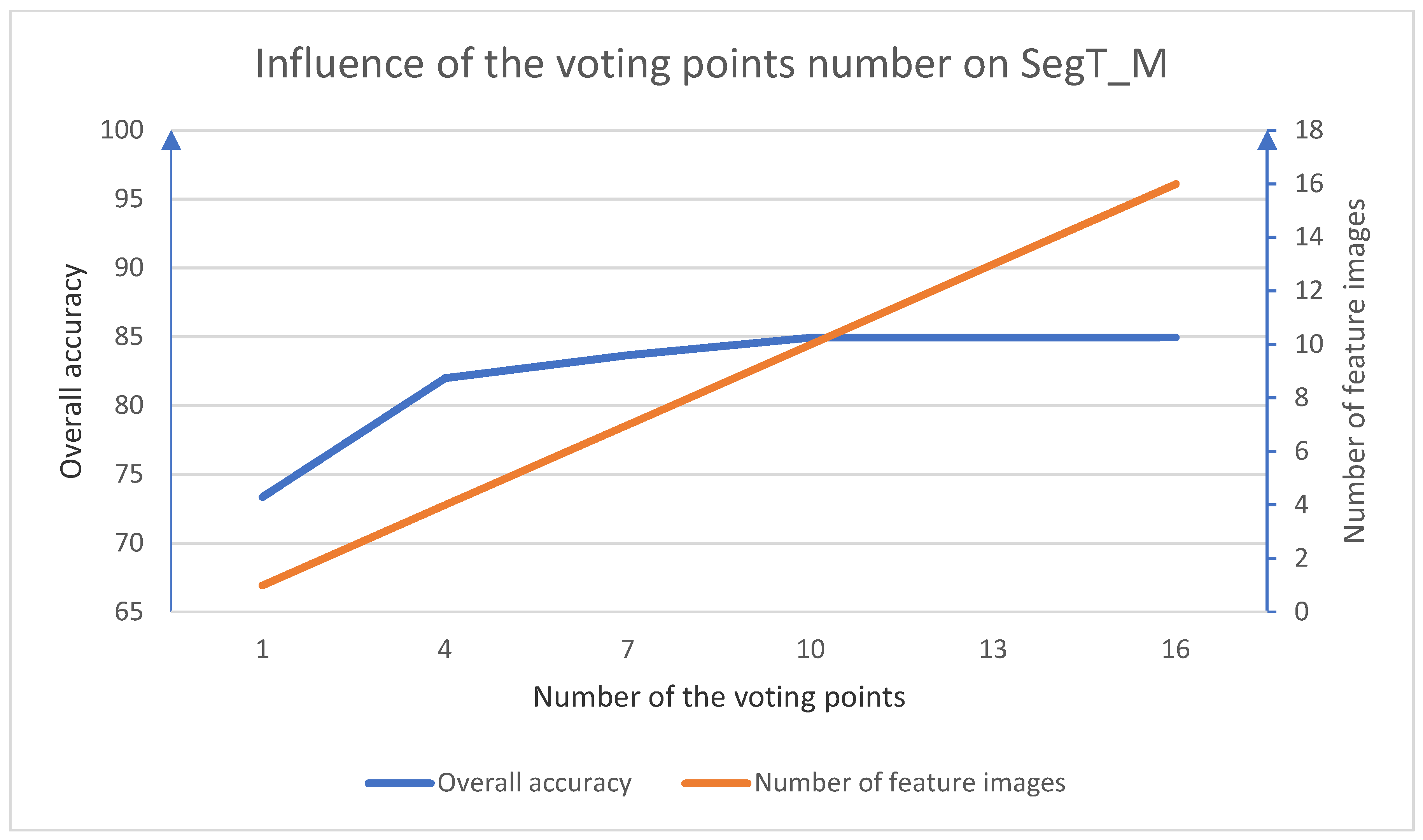
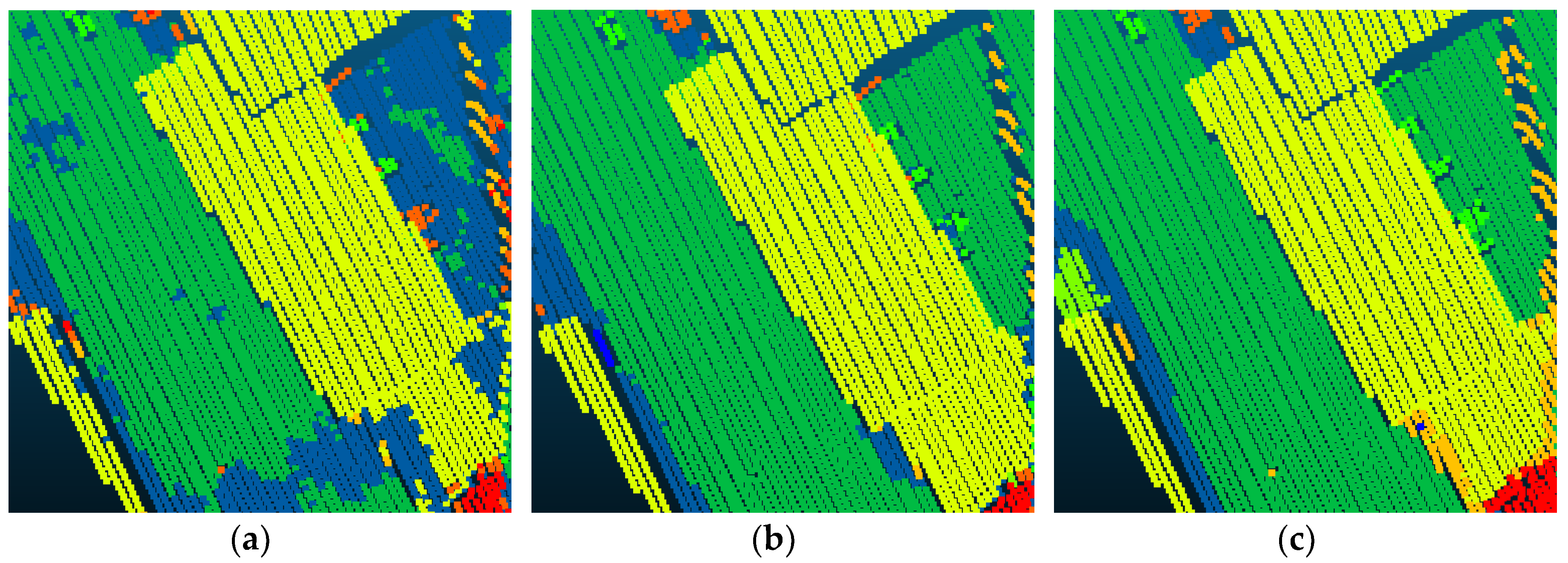
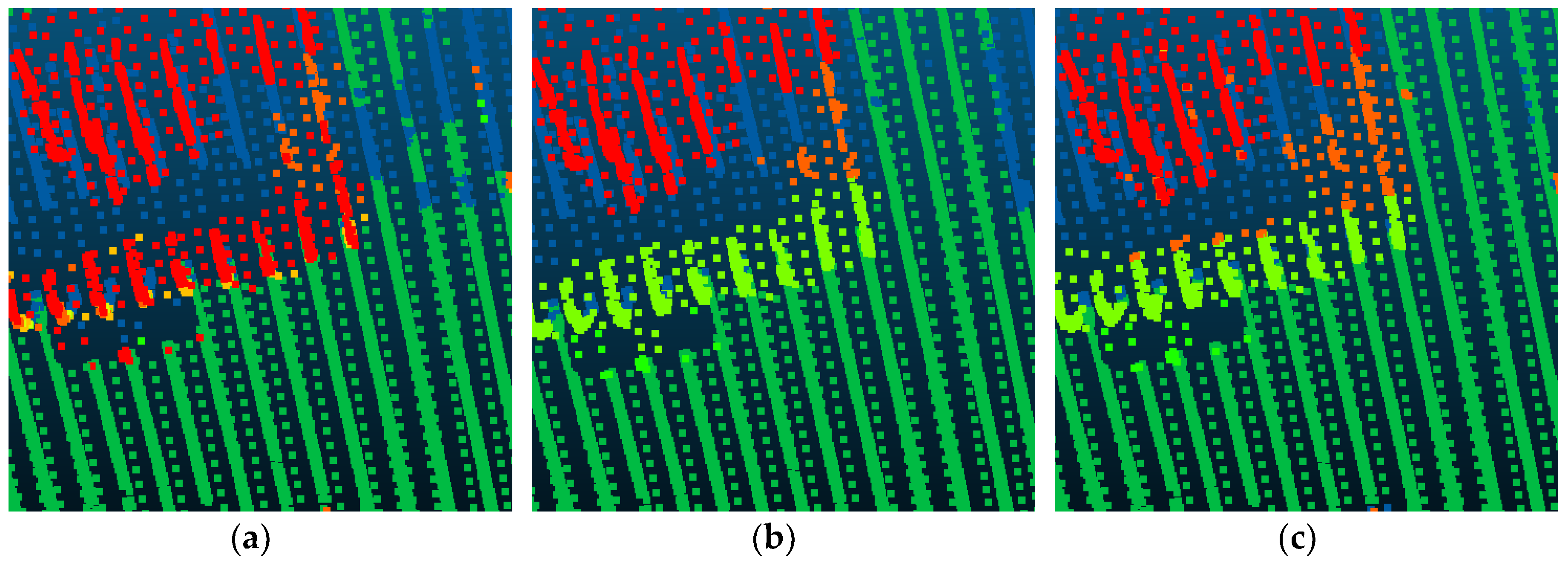
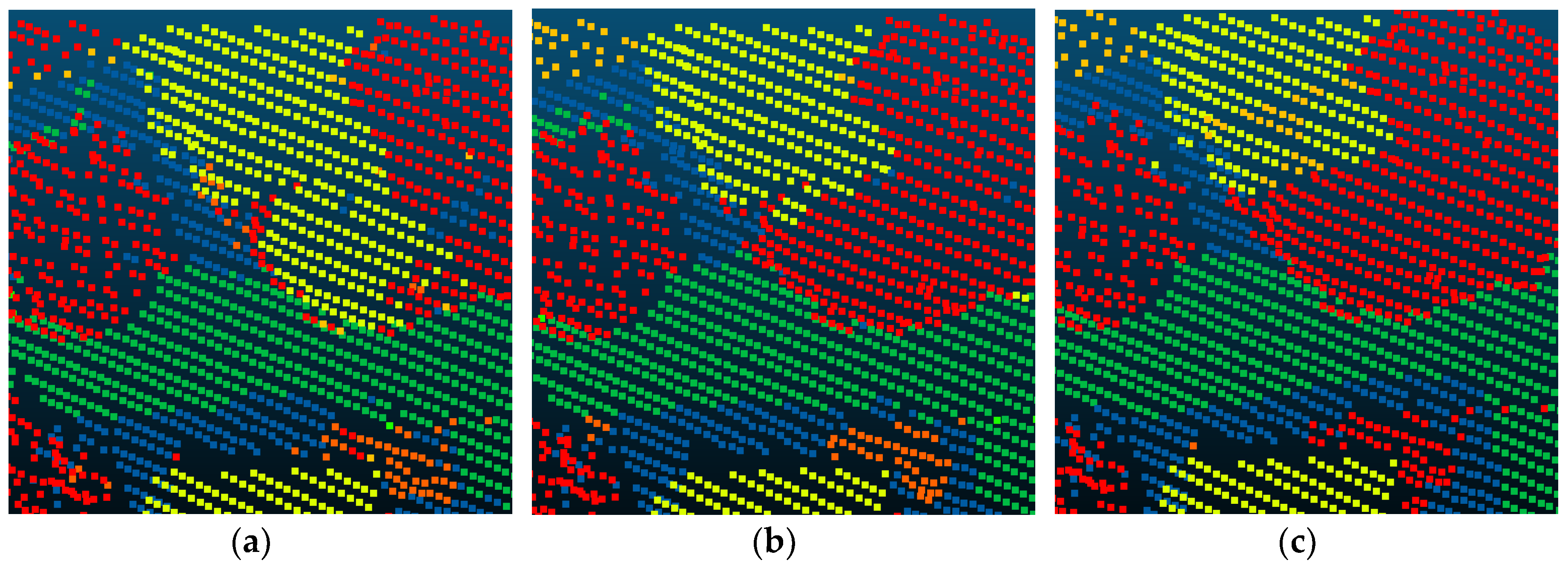
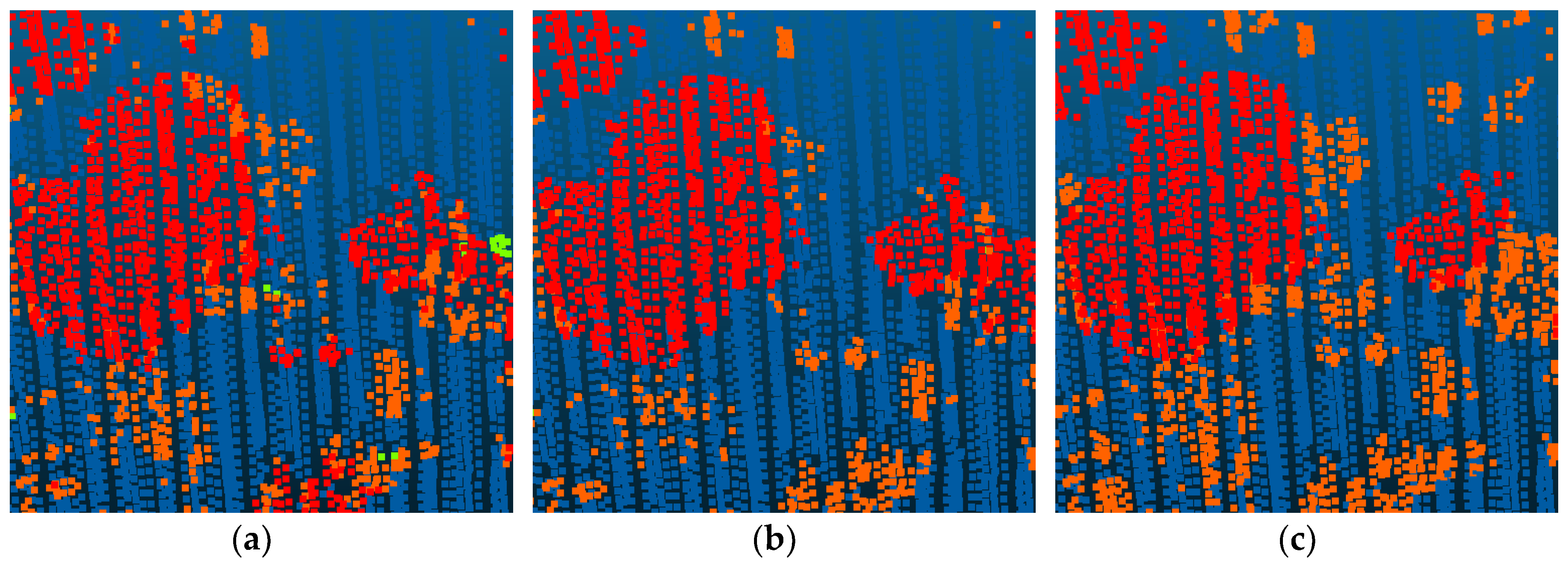
4.2. Experiment Results
- Point_S indicates the method used in [6]. It is a point-based method and uses the SCNN for semantic labeling.
- Point_M replaces the SCNN in Point_C with the MCNN.
- SegS_M adds the simple normal vector-based region-growing segmentation strategy into Point_M.
- SegT_M adds our three-step region growing segmentation strategy into Point_M.
- SegT_S replaces the MCNN in SegT_M with the SCNN.
4.3. ISPRS Benchmark Testing Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3d approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar] [CrossRef] [PubMed]
- Sithole, G.; Vosselman, G. Automatic structure detection in a point-cloud of an urban landscape. In Proceedings of the 2003 2nd GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003; pp. 67–71. [Google Scholar]
- Pepe, M.; Prezioso, G. Two approaches for dense dsm generation from aerial digital oblique camera system. In Proceedings of the 2nd International Conference on Geographical Information Systems Theory, Applications and Management, Rome, Italy, 26–27 April 2016; pp. 63–70. [Google Scholar]
- Xu, S.; Oude Elberink, S.; Vosselman, G. Entities and features for classifcation of airborne laser scanning data in urban area. Anal. Chim. Acta 2012, I-4, 257–262. [Google Scholar] [CrossRef]
- Vosselman, G.; Coenen, M.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, W.; Xu, B.; Zhu, Q.; Jiang, S.; Huang, W. A convolutional neural network-based 3d semantic labeling method for als point clouds. Remote Sens. 2017, 9, 936. [Google Scholar] [CrossRef]
- Rätsch, G.; Onoda, T.; Müller, K.-R. Soft margins for adaboost. Mach. Learn. 2001, 42, 287–320. [Google Scholar]
- Joachims, T. Making Large-Scale Svm Learning Practical; Technical Report, SFB 475: Komplexitätsreduktion in Multivariaten Datenstrukturen; Universität Dortmund: Dortmund, Germany, 1998. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Lafferty, J.; McCallum, A.; Pereira, F.C. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, San Francisco, CA, USA, 28 June–1 July 2001; pp. 282–289. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Lodha, S.K.; Fitzpatrick, D.M.; Helmbold, D.P. Aerial lidar data classification using adaboost, 3-D Digital Imaging and Modeling. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling (3DIM 2007), Montreal, QC, Canada, 21–23 August 2007; pp. 435–442. [Google Scholar]
- Mallet, C.; Bretar, F.; Roux, M.; Soergel, U.; Heipke, C. Relevance assessment of full-waveform lidar data for urban area classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, S71–S84. [Google Scholar] [CrossRef]
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, W8. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Niemeyer, J.; Wegner, J.D.; Mallet, C.; Rottensteiner, F.; Soergel, U. Conditional random fields for urban scene classification with full waveform lidar data. In Photogrammetric Image Analysis; Springer: Berlin, Germany, 2011; pp. 233–244. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Luo, C.; Sohn, G. Scene-layout compatible conditional random field for classifying terrestrial laser point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 79. [Google Scholar] [CrossRef]
- Xiong, X.; Munoz, D.; Bagnell, J.A.; Hebert, M. 3-d scene analysis via sequenced predictions over points and regions. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2609–2616. [Google Scholar]
- Kohli, P.; Torr, P.H. Robust higher order potentials for enforcing label consistency. Int. J. Comput. Vision 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Boulch, A.; Le Saux, B.; Audebert, N. Unstructured point cloud semantic labeling using deep segmentation networks. In Proceedings of the the Eurographics Workshop on 3D Object Retrieval, Lyon, France, 23–24 April 2017. [Google Scholar]
- Caltagirone, L.; Scheidegger, S.; Svensson, L.; Wahde, M. Fast lidar-based road detection using fully convolutional neural networks. arXiv, 2017; arXiv:1703.03613. [Google Scholar]
- Yousefhussien, M.; Kelbe, D.J.; Ientilucci, E.J.; Salvaggio, C. A fully convolutional network for semantic labeling of 3d point clouds. arXiv, 2017; arXiv:1710.01408. [Google Scholar]
- Golovinskiy, A.; Kim, V.G.; Funkhouser, T. Shape-based recognition of 3d point clouds in urban environments. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2154–2161. [Google Scholar]
- Shapovalov, R.; Velizhev, E.; Barinova, O. Nonassociative markov networks for 3d point cloud classification. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences XXXVIII, Part 3A, Saint Mandé, France, 1–3 September 2010. [Google Scholar]
- Niemeyer, J.; Rottensteiner, F.; Sörgel, U.; Heipke, C. Hierarchical higher order crf for the classification of airborne lidar point clouds in urban areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 655–662. [Google Scholar] [CrossRef]
- Guinard, S.; Landrieu, L. Weakly supervised segmentation-aided classification of urban scenes from 3d lidar point clouds. In Proceedings of the International Society for Photogrammetry and Remote Sensing, Hannover, Germany, 6–9 June 2017. [Google Scholar]
- Rabbani, T.; Heuvel, F.A.V.D.; Vosselman, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Xu, G.; Zhang, Z. Epipolar Geometry in Stereo, Motion and Object Recognition: A Unified Approach; Springer Science & Business Media Press: Berlin, Germany, 2013; Volume 6. [Google Scholar]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3d lidar point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, W12. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM international conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv, 2015; arXiv:1502.03167. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Buyssens, P.; Elmoataz, A.; Lézoray, O. Multiscale convolutional neural networks for vision–based classification of cells. In Proceedings of the 11th Asian Conference on Computer Vision, Daejeon, Korea, 5–9 November 2012; pp. 342–352. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Boer, P.T.D.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Cramer, M. The dgpf-test on digital airborne camera evaluation–overview and test design. Photogramm. Fernerkund. Geoinform. 2010, 2010, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Ramiya, A.M.; Nidamanuri, R.R.; Ramakrishnan, K. A supervoxel-based spectro-spatial approach for 3d urban point cloud labelling. Int. J. Remote Sens. 2016, 37, 4172–4200. [Google Scholar] [CrossRef]
- Horvat, D.; Žalik, B.; Mongus, D. Context-dependent detection of non-linearly distributed points for vegetation classification in airborne lidar. ISPRS J. Photogramm. Remote Sens. 2016, 116, 1–14. [Google Scholar] [CrossRef]
- Steinsiek, M.; Polewski, P.; Yao, W.; Krzystek, P. Semantische analyse von als-und mls-daten in urbanen gebieten mittels conditional random fields. Tagungsband 2017, 37, 521–531. [Google Scholar]




| Type | Symbol | Feature |
|---|---|---|
| Height features | Height above DTM | |
| Echo features | Intensity | |
| Eigenvalue features | Planarity | |
| Sphericity | ||
| Local plane features | Variance of deviation angles |
| Class | Training Set | Rebalancing Result | Test Set |
|---|---|---|---|
| Powerline | 546 | 546 | N/A |
| Low Vegetation | 180,850 | 18,005 | N/A |
| Impervious Surfaces | 193,723 | 19,516 | N/A |
| Car | 4614 | 4614 | N/A |
| Fence/Hedge | 12,070 | 12,070 | N/A |
| Roof | 152,045 | 15,235 | N/A |
| Facade | 27,250 | 13,731 | N/A |
| Shrub | 47,605 | 11,850 | N/A |
| Tree | 135,173 | 13,492 | N/A |
| ∑ | 753,876 | 109,059 | 411,722 |
| Method | Power | Low Vegetation | Impervious Surface | Car | Fence/Hedge | Roof | Facade | Shrub | Tree | OA |
|---|---|---|---|---|---|---|---|---|---|---|
| Point_S | 24.7 | 81.8 | 91.9 | 69.3 | 14.7 | 95.4 | 40.9 | 38.2 | 78.5 | 82.3 |
| Point_M | 25.2 | 83.1 | 92.1 | 71.2 | 19.3 | 95.5 | 42.1 | 39.2 | 79.3 | 83.0 |
| SegS_M | 28.3 | 84.7 | 92.5 | 69.5 | 18.7 | 95.5 | 40.7 | 38.3 | 78.4 | 83.3 |
| SegT_S | 26.8 | 84.3 | 91.2 | 71.2 | 33.7 | 95.4 | 43.3 | 43.6 | 81.2 | 83.6 |
| SegT_M | 31.2 | 85.0 | 92.4 | 78.9 | 42.5 | 95.6 | 46.5 | 42.4 | 83.7 | 84.9 |
| Point_S | Point_M | SegS_M | SegT_S | SegT_M | |
|---|---|---|---|---|---|
| Segmentation time (min) | 0 | 0 | 4:20 | 7:40 | 7:40 |
| Number of training feature images | 109,059 | 327,177 | 327,177 | 109,059 | 327,177 |
| Training feature images generation time (h) | 0.4 | 1.3 | 1.3 | 0.4 | 1.3 |
| Number of testing feature images | 411,722 | 1,235,166 | 538,398 | 39,430 | 118,290 |
| Testing feature images generation time (h) | 1.6 | 4.7 | 2.0 | 0.2 | 0.5 |
| Training time (h) | 6.5 | 20.0 | 20.0 | 6.5 | 20.1 |
| Testing time (s) | 70.4 | 172.8 | 83.8 | 10.4 | 30.7 |
| Overall Accuracy (%) | 82.3 | 83.0 | 83.3 | 83.6 | 84.9 |
| Average F1 (%) | 61.6 | 63.7 | 65.7 | 64.3 | 69.2 |
| Method | Power | Low Vegetation | Impervious Surface | Car | Fence/Hedge | Roof | Facade | Shrub | Tree | OA |
|---|---|---|---|---|---|---|---|---|---|---|
| ISS_7 | 40.8 | 49.9 | 96.5 | 46.7 | 39.5 | 96.2 | - | 52.0 | 68.8 | 76.2 |
| UM | 33.3 | 79.5 | 90.3 | 32.5 | 2.9 | 90.5 | 43.7 | 43.3 | 85.2 | 80.8 |
| HM_1 | 82.8 | 65.9 | 94.2 | 67.1 | 25.2 | 91.5 | 49.0 | 62.7 | 82.6 | 80.5 |
| WhuY3 | 24.7 | 81.8 | 91.9 | 69.3 | 14.7 | 95.4 | 40.9 | 38.2 | 78.5 | 82.3 |
| LUH | 53.2 | 72.7 | 90.4 | 63.3 | 25.9 | 91.3 | 60.7 | 73.4 | 79.1 | 81.6 |
| RIT_1 | 29.8 | 69.8 | 93.6 | 77.0 | 10.4 | 92.9 | 47.4 | 73.4 | 79.3 | 81.6 |
| Ours | 31.2 | 85.0 | 92.4 | 78.9 | 42.5 | 95.6 | 46.5 | 42.4 | 83.7 | 84.9 |
| Method | Power | Low Vegetation | Impervious Surface | Car | Fence/Hedge | Roof | Facade | Shrub | Tree | Avg. F1 |
|---|---|---|---|---|---|---|---|---|---|---|
| ISS_7 | 54.4 | 65.2 | 85.0 | 57.9 | 28.9 | 90.9 | - | 39.5 | 75.6 | 55.27 |
| UM | 46.1 | 79.0 | 89.1 | 47.7 | 5.2 | 92.0 | 52.7 | 40.9 | 77.9 | 58.96 |
| HM_1 | 69.8 | 73.8 | 91.5 | 58.2 | 29.9 | 91.6 | 54.7 | 47.8 | 80.2 | 66.39 |
| WhuY3 | 37.1 | 81.4 | 90.1 | 63.4 | 23.9 | 93.4 | 47.5 | 39.9 | 78.0 | 61.63 |
| LUH | 59.6 | 77.5 | 91.1 | 73.1 | 34.0 | 94.2 | 56.3 | 46.6 | 83.1 | 68.39 |
| RIT_1 | 37.5 | 77.9 | 91.5 | 73.4 | 18.0 | 94.0 | 49.3 | 45.9 | 82.5 | 63.33 |
| Ours | 42.5 | 82.7 | 91.4 | 74.7 | 53.7 | 94.3 | 53.1 | 47.9 | 82.8 | 69.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Tan, B.; Pei, H.; Jiang, W. Segmentation and Multi-Scale Convolutional Neural Network-Based Classification of Airborne Laser Scanner Data. Sensors 2018, 18, 3347. https://doi.org/10.3390/s18103347
Yang Z, Tan B, Pei H, Jiang W. Segmentation and Multi-Scale Convolutional Neural Network-Based Classification of Airborne Laser Scanner Data. Sensors. 2018; 18(10):3347. https://doi.org/10.3390/s18103347
Chicago/Turabian StyleYang, Zhishuang, Bo Tan, Huikun Pei, and Wanshou Jiang. 2018. "Segmentation and Multi-Scale Convolutional Neural Network-Based Classification of Airborne Laser Scanner Data" Sensors 18, no. 10: 3347. https://doi.org/10.3390/s18103347
APA StyleYang, Z., Tan, B., Pei, H., & Jiang, W. (2018). Segmentation and Multi-Scale Convolutional Neural Network-Based Classification of Airborne Laser Scanner Data. Sensors, 18(10), 3347. https://doi.org/10.3390/s18103347