3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras
Abstract
:1. Introduction
2. Ultrasonic and Range Imaging Indoor Positioning
2.1. Ultrasonic Positioning
2.2. Range Imaging Positioning
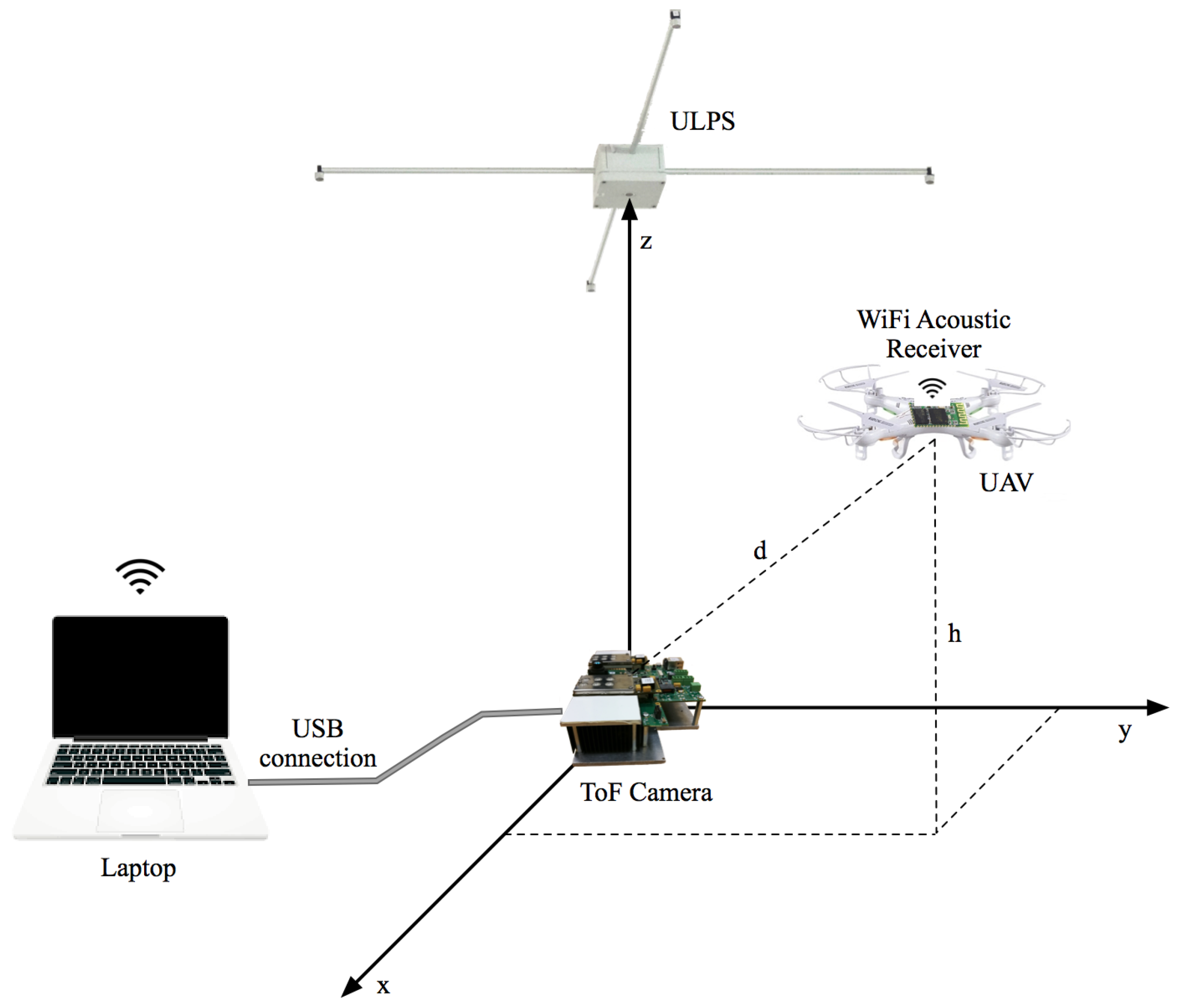
3. Proposed Indoor Positioning System
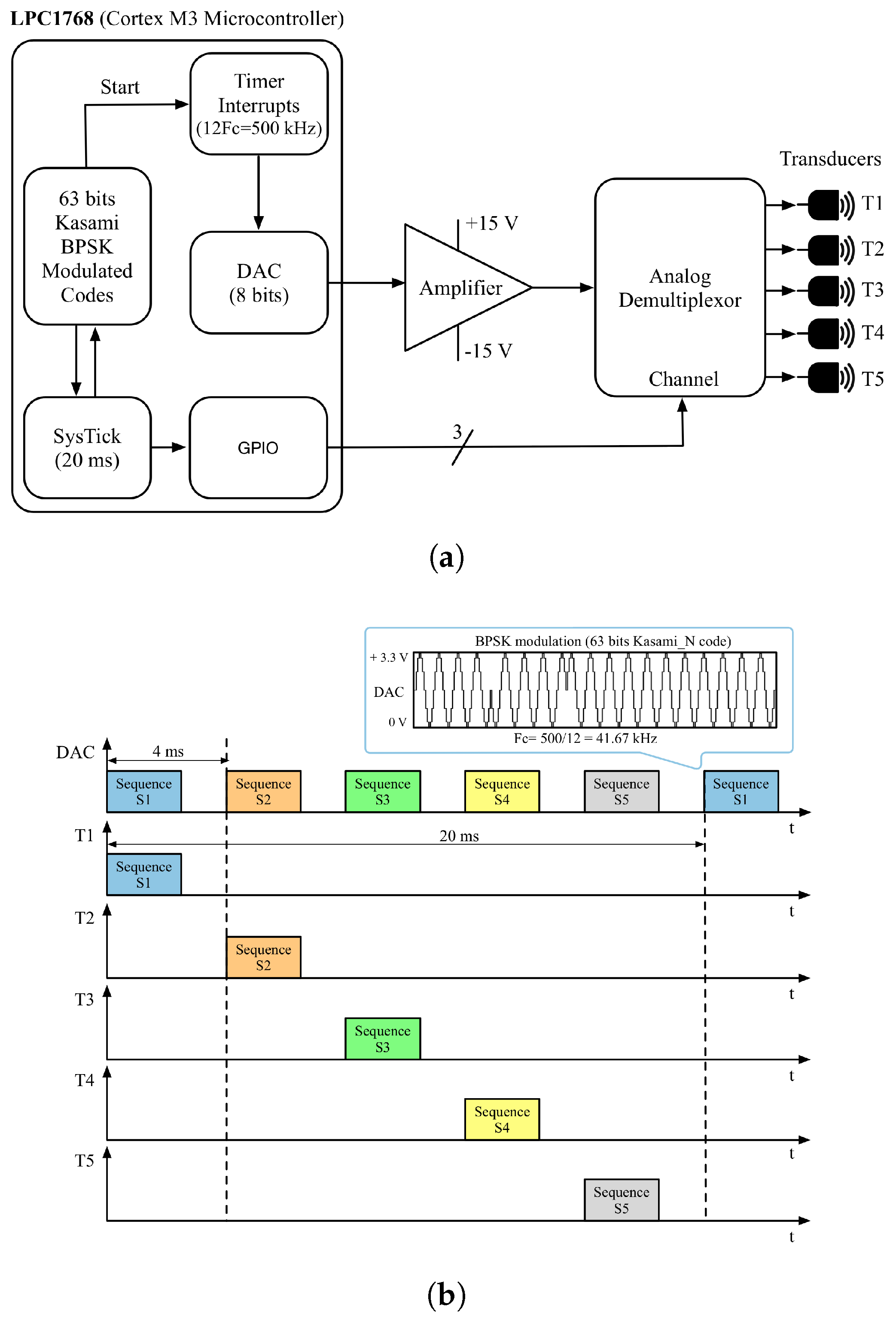
3.1. Ultrasonic Module
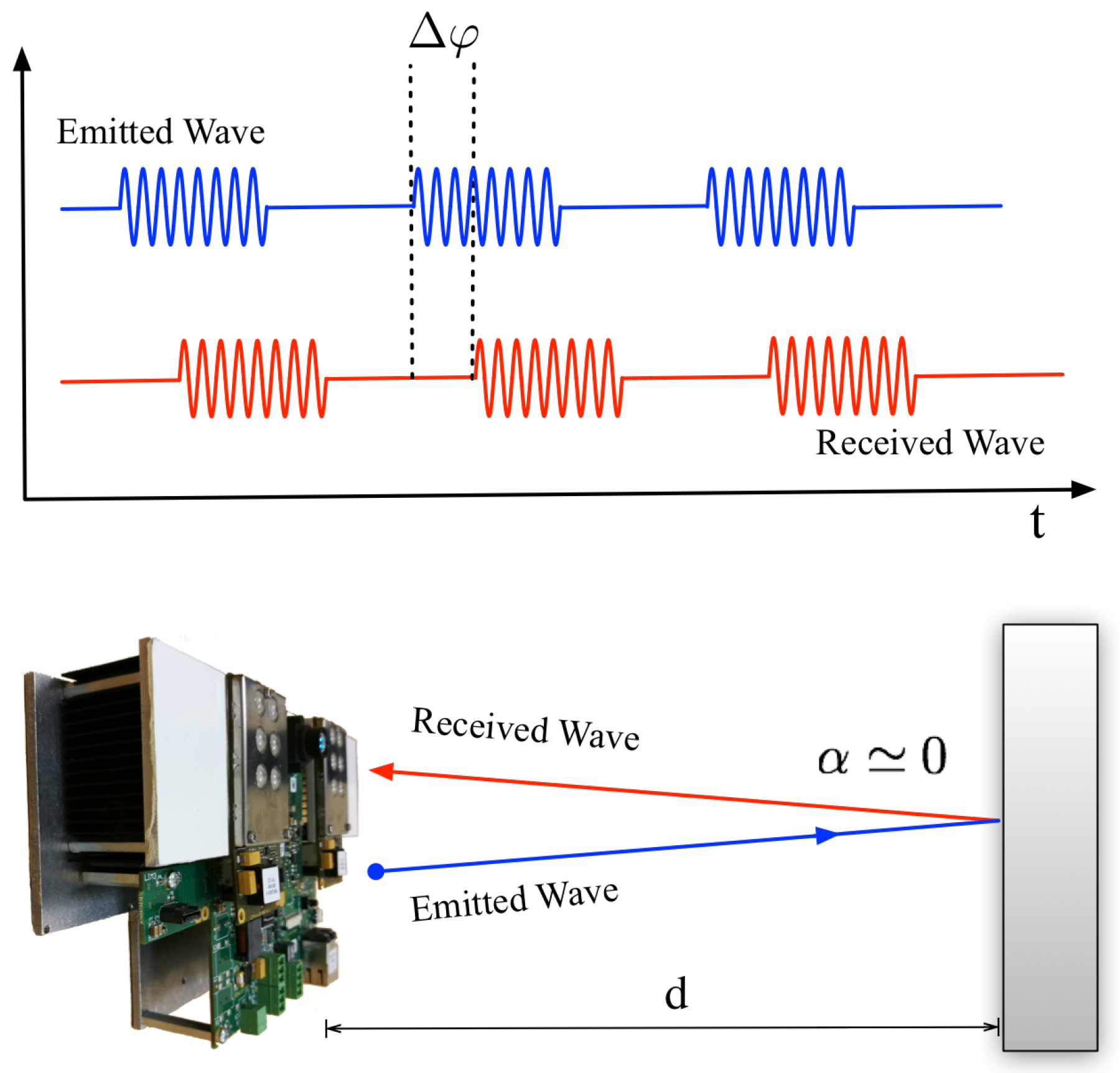
3.2. ToF Camera
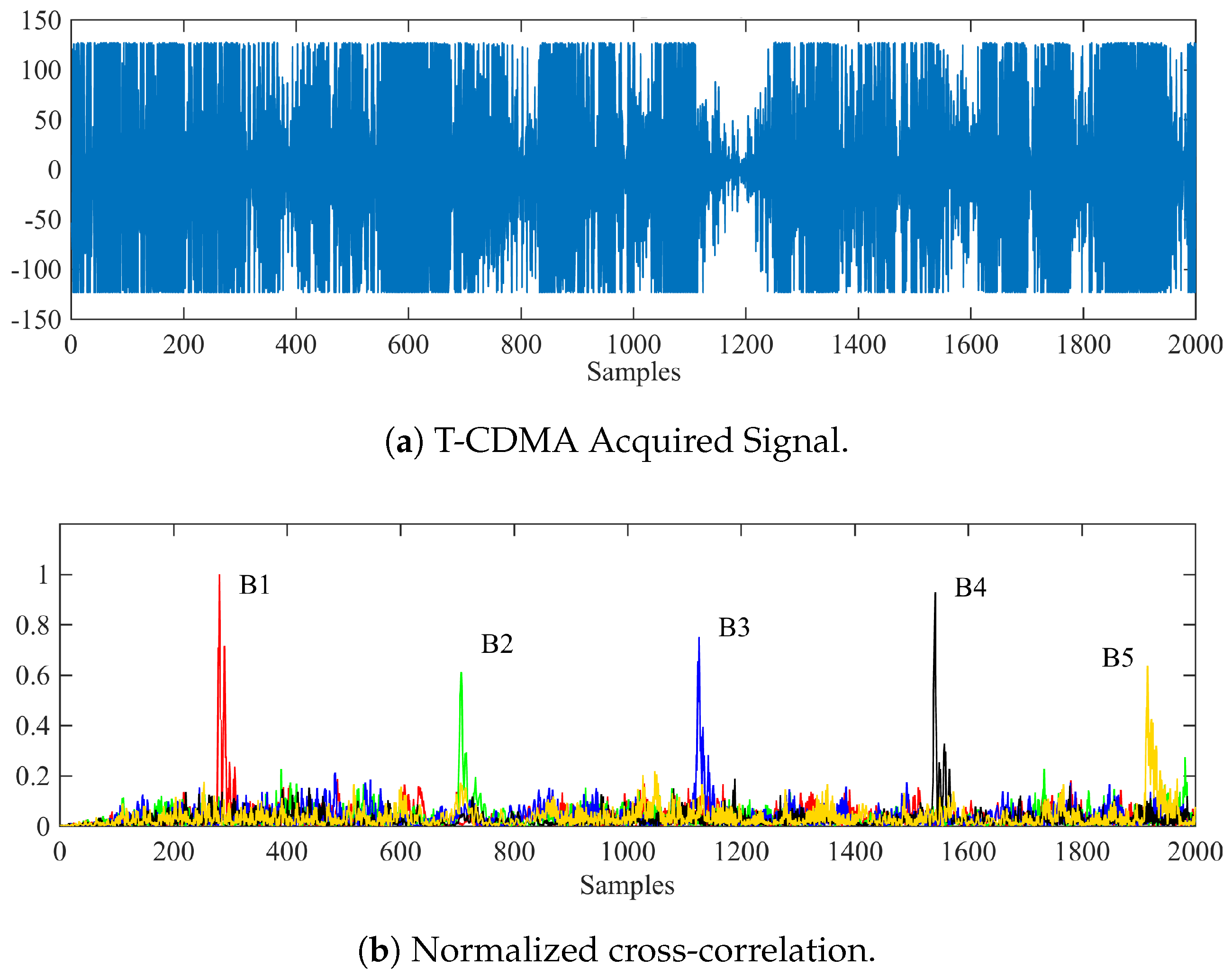
3.3. Positioning Strategy
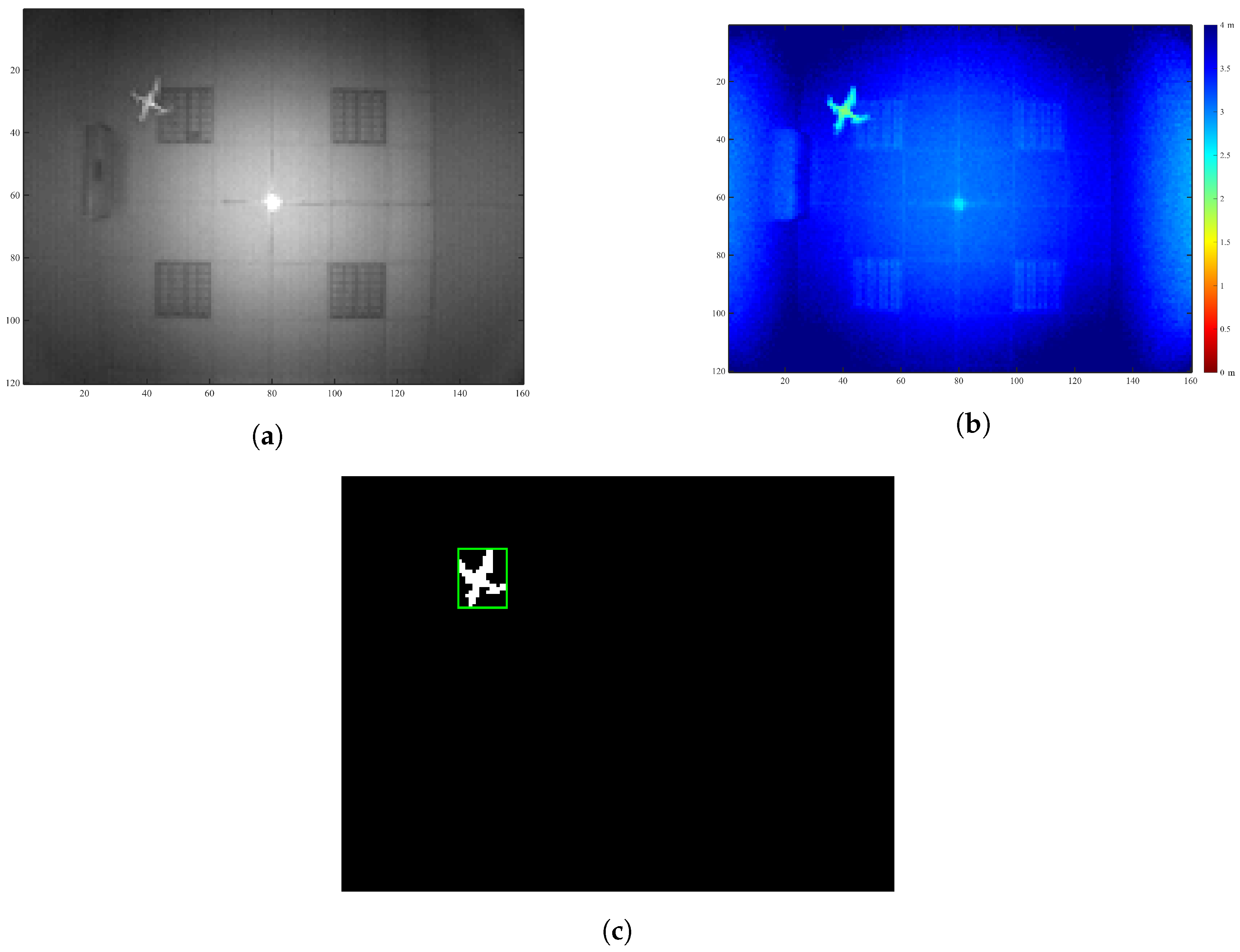
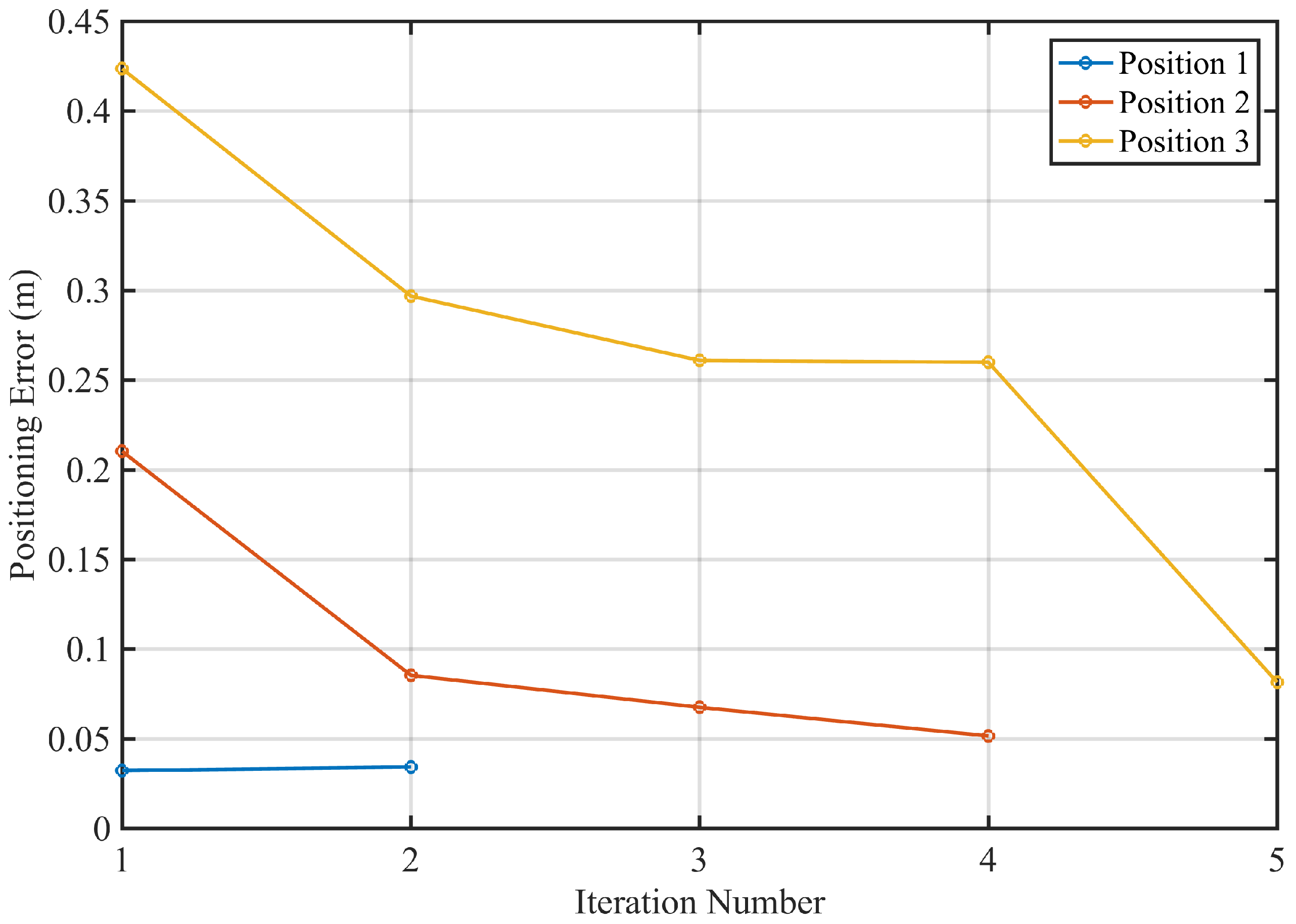
4. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tiemann, J.; Schweikowski, F.; Wietfeld, C. Design of an UWB indoor-positioning system for UAV navigation in GNSS-denied environments. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–7. [Google Scholar]
- Grzonka, S.; Grisetti, G.; Burgard, W. A Fully Autonomous Indoor Quadrotor. IEEE Trans. Robot. 2012, 28, 90–100. [Google Scholar] [CrossRef]
- Otsason, V.; Varshavsky, A.; LaMarca, A.; De Lara, E. Accurate GSM indoor localization. In Proceedings of the International Conference on Ubiquitous Computing (UbiComp), Tokyo, Japan, 11–14 September 2005; p. 903. [Google Scholar]
- Teulière, C.; Eck, L.; Marchand, E.; Guénard, N. 3D model-based tracking for UAV position control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1084–1089. [Google Scholar]
- Deris, A.; Trigonis, I.; Aravanis, A.; Stathopoulou, E.K. Depth Cameras on UAVs: A First Approach. In Proceedings of the ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Nafplio, Greece, 1–3 March 2017; Volume XLII-2/W3, pp. 231–236. [Google Scholar]
- Mustafah, Y.M.; Azman, A.W.; Akbar, F. Indoor UAV Positioning Using Stereo Vision Sensor. Procedia Eng. 2012, 41, 575–579. [Google Scholar] [CrossRef]
- Wang, F.; Cui, J.; Phang, S.K.; Chen, B.M.; Lee, T.H. A mono-camera and scanning laser range finder based UAV indoor navigation system. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 694–701. [Google Scholar]
- Wang, C.; Li, K.; Liang, G.; Chen, H.; Huang, S.; Wu, X. A Heterogeneous Sensing System-Based Method for Unmanned Aerial Vehicle Indoor Positioning. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Kumar, G.A.; Patil, A.K.; Patil, R.; Park, S.S.; Chai, Y.H. A LiDAR and IMU Integrated Indoor Navigation System for UAVs and Its Application in Real-Time Pipeline Classification. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- López, E.; García, S.; Barea, R.; Bergasa, L.M.; Molinos, E.J.; Arroyo, R.; Romera, E.; Pardo, S. A Multi-Sensorial Simultaneous Localization and Mapping (SLAM) System for Low-Cost Micro Aerial Vehicles in GPS-Denied Environments. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Mautz, R. Indoor Positioning Technologies. Ph.D. Thesis, Institute of Geodesy and Photogrammetry, Department of Civil, Environmental and Geomatic Engineering, ETH Zurich, Zürich, Switzerland, 2012. [Google Scholar]
- Mainetti, L.; Patrono, L.; Sergi, I. A survey on indoor positioning systems. In Proceedings of the 22nd International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2014; pp. 111–120. [Google Scholar]
- Ward, A.; Jones, A.; Hopper, A. A new location technique for the active office. IEEE Pers. Commun. 1997, 4, 42–47. [Google Scholar] [CrossRef]
- Addlesee, M.; Curwen, R.; Hodges, S.; Newman, J.; Steggles, P.; Ward, A.; Hopper, A. Implementing a sentient computing system. Computer 2001, 34, 50–56. [Google Scholar] [CrossRef]
- Foxlin, E.; Harrington, M. Constellation: A wide-range wireless motion-tracking system for augmented reality and virtual set applications. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; pp. 371–378. [Google Scholar]
- Priyantha, N.B.; Chakraborty, A.; Balakrishnan, H. The Cricket Location-support System. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MobiCom’00), Boston, MA, USA, 6–11 August 2000; ACM: New York, NY, USA, 2000; pp. 32–43. [Google Scholar]
- Priyantha, N.B. The Cricket Indoor Location System. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Skolnik, M.I. Introduction to Radar Systems, 2nd ed.; McGraw Hill Book Co.: New York, NY, USA, 1980. [Google Scholar]
- Peremans, H.; Audenaert, K.; Campenhout, J.M.V. A high-resolution sensor based on tri-aural perception. IEEE Trans. Robot. Autom. 1993, 9, 36–48. [Google Scholar] [CrossRef]
- Jörg, K.W.; Berg, M. Sophisticated mobile robot sonar sensing with pseudo-random codes. Robot. Auton. Syst. 1998, 25, 241–251. [Google Scholar] [CrossRef]
- Ureña, J.; Mazo, M.; García, J.J.; Hernández, Á.; Bueno, E. Classification of reflectors with an ultrasonic sensor for mobile robot applications. Robot. Auton. Syst. 1999, 29, 269–279. [Google Scholar] [CrossRef]
- Hazas, M.; Ward, A. A Novel Broadband Ultrasonic Location System. In Proceedings of the 4th International Conference on Ubiquitous Computing, Göteborg, Sweden, 29 September–1 October 2002; Borriello, G., Holmquist, L.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 264–280. [Google Scholar]
- Hazas, M.; Ward, A. A high performance privacy-oriented location system. In Proceedings of the First IEEE International Conference on Pervasive Computing and Communications (PerCom 2003), Fort Worth, TX, USA, 26 March 2003; pp. 216–223. [Google Scholar]
- Villadangos, J.M.; Urena, J.; Mazo, M.; Hernandez, A.; Alvarez, F.; Garcia, J.J.; Marziani, C.D.; Alonso, D. Improvement of ultrasonic beacon-based local position system using multi-access techniques. In Proceedings of the IEEE International Workshop on Intelligent Signal Processing, Faro, Portugal, 1–3 September 2005; pp. 352–357. [Google Scholar]
- Álvarez, F.J.; Hernández, Á.; Moreno, J.A.; Pérez, M.C.; Ureña, J.; Marziani, C.D. Doppler-tolerant receiver for an ultrasonic LPS based on Kasami sequences. Sens. Actuators A Phys. 2013, 189, 238–253. [Google Scholar] [CrossRef]
- Álvarez, F.J.; Aguilera, T.; López-Valcarce, R. CDMA-based acoustic local positioning system for portable devices with multipath cancellation. Digit. Signal Process. 2017, 62, 38–51. [Google Scholar] [CrossRef]
- Seco, F.; Prieto, J.C.; Ruiz, A.R.J.; Guevara, J. Compensation of Multiple Access Interference Effects in CDMA-Based Acoustic Positioning Systems. IEEE Trans. Instrum. Meas. 2014, 63, 2368–2378. [Google Scholar] [CrossRef]
- Aguilera, T.; Paredes, J.A.; Álvarez, F.J.; Suárez, J.I.; Hernández, A. Acoustic local positioning system using an iOS device. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard-Belfort, France, 28–31 October 2013; pp. 1–8. [Google Scholar]
- Pérez, M.C.; Gualda, D.; Villadangos, J.M.; Ureña, J.; Pajuelo, P.; Díaz, E.; García, E. Android application for indoor positioning of mobile devices using ultrasonic signals. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–7. [Google Scholar]
- Kohoutek, T.K.; Mautz, R.; Donaubauer, A. Real-time indoor positioning using range imaging sensors. In Real-Time Image and Video Processing; SPIE: Bellingham, WA, USA, 2010; Volume 7724. [Google Scholar]
- Kohoutek, T.K.; Droeschel, D.; Mautz, R.; Behnke, S. Indoor Positioning and Navigation Using Time-of-Flight Cameras. In TOF Range-Imaging Cameras; Remondino, F., Stoppa, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 165–176. [Google Scholar]
- Cunha, J.; Pedrosa, E.; Cruz, C.; Neves, A.J.; Lau, N. Using a Depth Camera for Indoor Robot Localization and Navigation. In Proceedings of the Robotics Science and Systems Conference, Los Angeles, CA, USA, 27–30 June 2011. [Google Scholar]
- Biswas, J.; Veloso, M. Depth camera based indoor mobile robot localization and navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1697–1702. [Google Scholar]
- Vaz, M.; Ventura, R. Real-time ground-plane based mobile localization using depth camera in real scenarios. In Proceedings of the IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Espinho, Portugal, 14–15 May 2014; pp. 187–192. [Google Scholar]
- Jia, L.; Radke, R.J. Using Time-of-Flight Measurements for Privacy-Preserving Tracking in a Smart Room. IEEE Trans. Ind. Inform. 2014, 10, 689–696. [Google Scholar] [CrossRef]
- Stahlschmidt, C.; Gavriilidis, A.; Velten, J.; Kummert, A. People Detection and Tracking from a Top-View Position Using a Time-of-Flight Camera. In Proceedings of the 6th International Conference on Multimedia Communications, Services and Security (MCSS 2013), Krakow, Poland, 6–7 June 2013; Dziech, A., Czyżewski, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 213–223. [Google Scholar]
- Kasami, T. Weigh Distribution Formula for Some Class of Cyclic Codes; Technical Report R-285; Coordinated Science Laboratory: Urbana, IL, USA, 1968. [Google Scholar]
- Pro-Wave Electronics Corporation. Air Ultrasonic Ceramic Transducers 328ST/R160, Product Specification; Pro-Wave Electronics Corporation: New Taipei City, Taiwan, 2014. [Google Scholar]
- Knowles Acoustics. SiSonic Design Guide, Application Note rev. 3.0; Knowles Acoustics: Itasca, IL, USA, 2011. [Google Scholar]
- STMicroelectronics 32-bit ARM Cortex M3 Microcontroller. 2017. Available online: http://www.st.com/en/microcontrollers/stm32f103cb.html (accessed on 29 December 2017).
- DT-06 Wireless WiFi Serial Port Transparent Transmission Module. Shenzhen Doctors of Intelligence & Technology Co., Ltd. 2017. Available online: ttl.doit.am (accessed on 29 December 2017). (In Chinese).
- Prieto, J.C.; Jimenez, A.R.; Guevara, J.; Ealo, J.L.; Seco, F.; Roa, J.O.; Ramos, F. Performance Evaluation of 3D-LOCUS Advanced Acoustic LPS. IEEE Trans. Instrum. Meas. 2009, 58, 2385–2395. [Google Scholar] [CrossRef]
- Álvarez, F.J.; Esteban, J.; Villadangos, J.M. High Accuracy APS for Unmanned Aerial Vehicles. In Proceedings of the 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS), Niš, Serbia, 18–20 October 2017; pp. 217–223. [Google Scholar]
- Lange, R. 3D Time-of-Flight Distance Measurement with Custom Solid-State Image Sensors in CMOS/CCD-Technology. Ph.D. Thesis, University of Siegen, Siegen, Germany, 2000. [Google Scholar]
- Langmann, B. Wide Area 2D/3D Imaging. Development, Analysis and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Hussmann, S.; Edeler, T.; Hermanski, A. Machine Vision-Applications and Systems; InTech: Rijeka, Croatia, 2012; Chapter 4: Real-Time Processing of 3D-ToF Data; pp. 1–284. [Google Scholar]
- Chiabrando, F.; Chiabrando, R.; Piatti, D.; Rinaudo, F. Sensors for 3D Imaging: Metric Evaluation and Calibration of a CCD/CMOS Time-of-Flight Camera. Sensors 2009, 9, 10080–10096. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Schiller, I.; Kolb, A.; Koch, R. Time-of-Flight Sensor Calibration for Accurate Range Sensing. Comput. Vis. Image Underst. 2010, 114, 1318–1328. [Google Scholar] [CrossRef]
- Matheis, F.; Brockherde, W.; Grabmaier, A.; Hosticka, B.J. Modeling and calibration of 3D-Time-of-Flight pulse-modulated image sensors. In Proceedings of the 20th European Conference on Circuit Theory and Design (ECCTD), Linkoping, Sweden, 29–31 August 2011; pp. 417–420. [Google Scholar]
- MTK USB Evaluation KIT for TIM-UP-19k-S3-Spartan6. Bluetechnix Lab GmbH. Bluetechnix (Wien, Austria) 2017. Available online: https://support.bluetechnix.at/wiki/MTK_USB_Evaluation_KIT_for_TIM-UP-19k-S3-Spartan6 (accessed on 29 December 2017).




| (m) | Position 1 | Position 2 | Position 3 | |||
|---|---|---|---|---|---|---|
| Acoustic System | 0.140 | (0.089) | 0.350 | (0.032) | 0.303 | (0.257) |
| Hybrid System | 0.037 | (0.009) | 0.067 | (0.017) | 0.081 | (0.061) |
| MSE | SD | MSE | SD | MSE | SD | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paredes, J.A.; Álvarez, F.J.; Aguilera, T.; Villadangos, J.M. 3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras. Sensors 2018, 18, 89. https://doi.org/10.3390/s18010089
Paredes JA, Álvarez FJ, Aguilera T, Villadangos JM. 3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras. Sensors. 2018; 18(1):89. https://doi.org/10.3390/s18010089
Chicago/Turabian StyleParedes, José A., Fernando J. Álvarez, Teodoro Aguilera, and José M. Villadangos. 2018. "3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras" Sensors 18, no. 1: 89. https://doi.org/10.3390/s18010089
APA StyleParedes, J. A., Álvarez, F. J., Aguilera, T., & Villadangos, J. M. (2018). 3D Indoor Positioning of UAVs with Spread Spectrum Ultrasound and Time-of-Flight Cameras. Sensors, 18(1), 89. https://doi.org/10.3390/s18010089







