A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks †
Abstract
1. Introduction
- Unlike other approaches that rely on planar calibration objects, our usage of a spherical object overcomes the problem of limited scene features shared by sparsely-placed cameras. Specifically, the location of the sphere center can be robustly estimated from any viewpoint as long as a small part of the sphere surface can be observed.
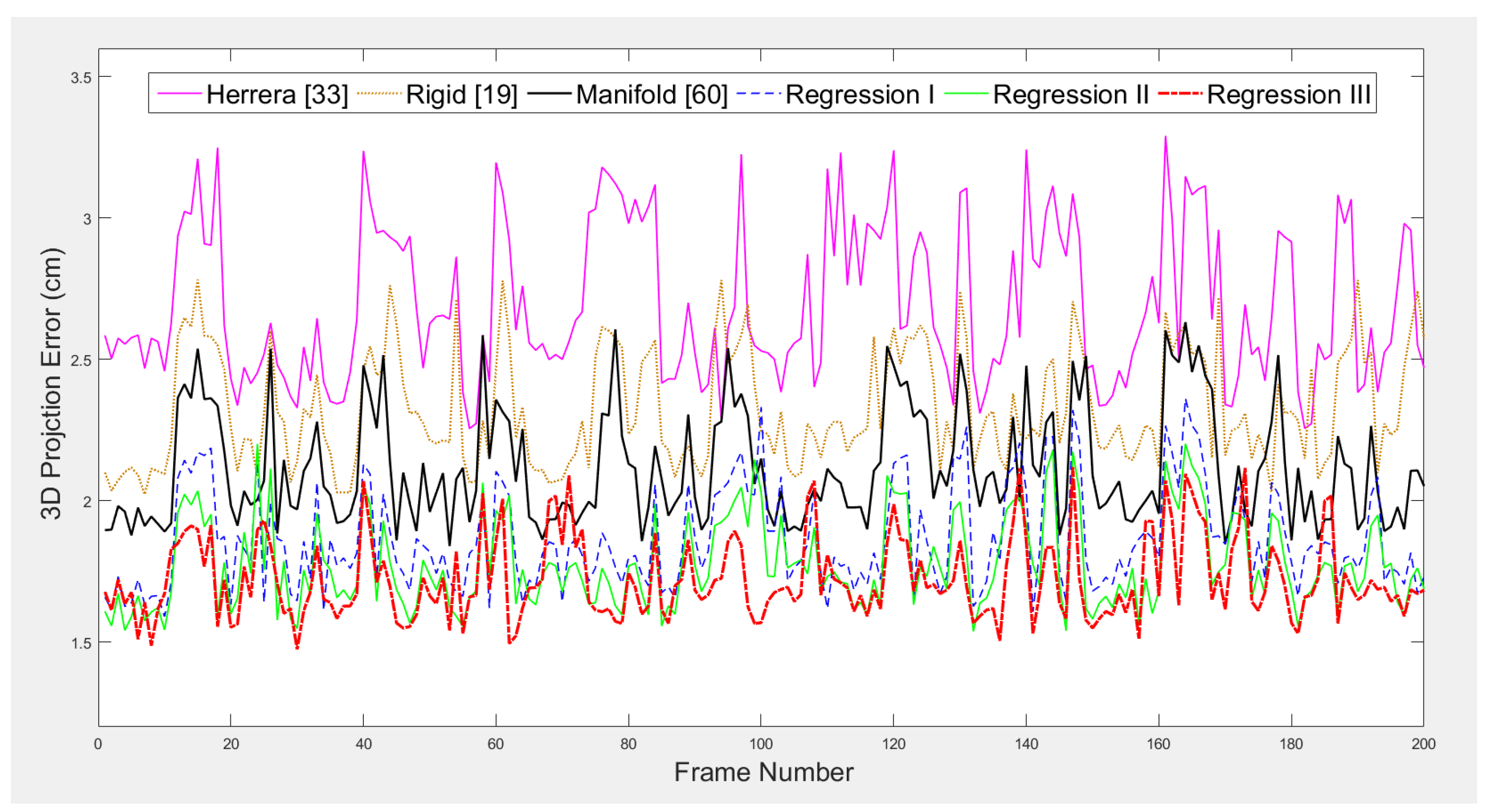
- Rigid transformation is typically used to represent camera extrinsic calibration and has been shown to be optimal for the pinhole camera model. However, real cameras have imperfections, and a more flexible transformation could provide higher fidelity in aligning 3D point clouds from different cameras. We systematically compare a broad range of transformation functions including rigid transformation, intrinsic-extrinsic factorization, polynomial regression and manifold regression. Our experiments demonstrate that linear regression produces the most accurate calibration results.
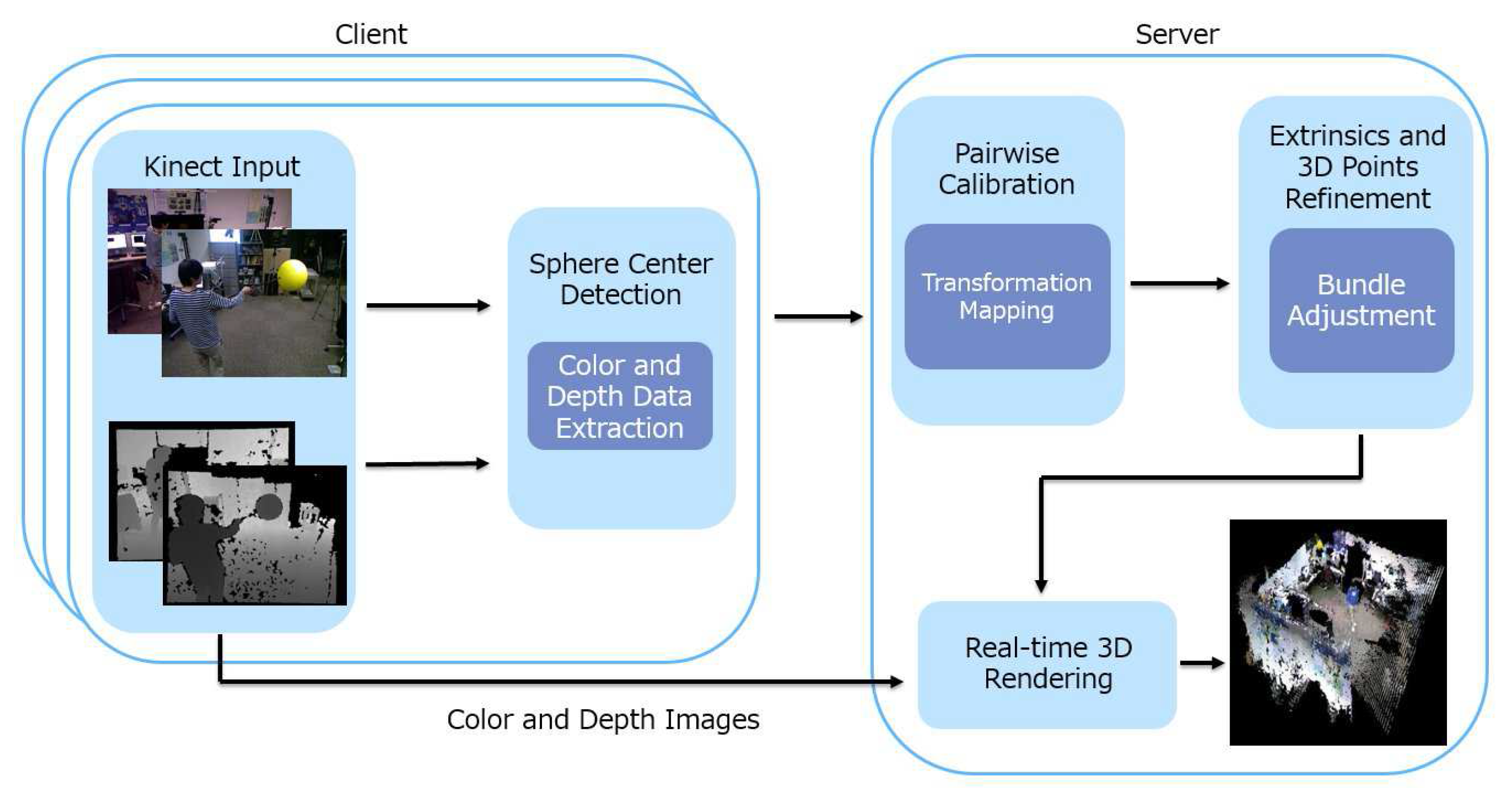
- In order to provide an efficient calibration procedure and to support real-time 3D rendering and dynamic viewpoints, our proposed algorithm is implemented in a client-and-server architecture where data capturing and much of the 3D processing are carried out at the clients.
2. Related Work
3. Proposed Method
- Sphere center detection: The 3D locations of the center of a moving sphere are estimated from the color and depth images. They are used as visual correspondences across different camera views. There are two reasons for choosing a sphere as a calibration object. First, it is suitable for a wide baseline: any small surface patch on the sphere is sufficient to estimate the location of its center. As such, two cameras capturing different sides of the sphere can still use the sphere center as a correspondence. Second, instead of using the error-prone point or edge features as correspondences, depth measurements of the sphere surface are mostly accurate, and the spherical constraint can be used to provide a robust estimate of the center location. This step is independently executed at each camera client. The details of the procedure can be found in Section 3.2.
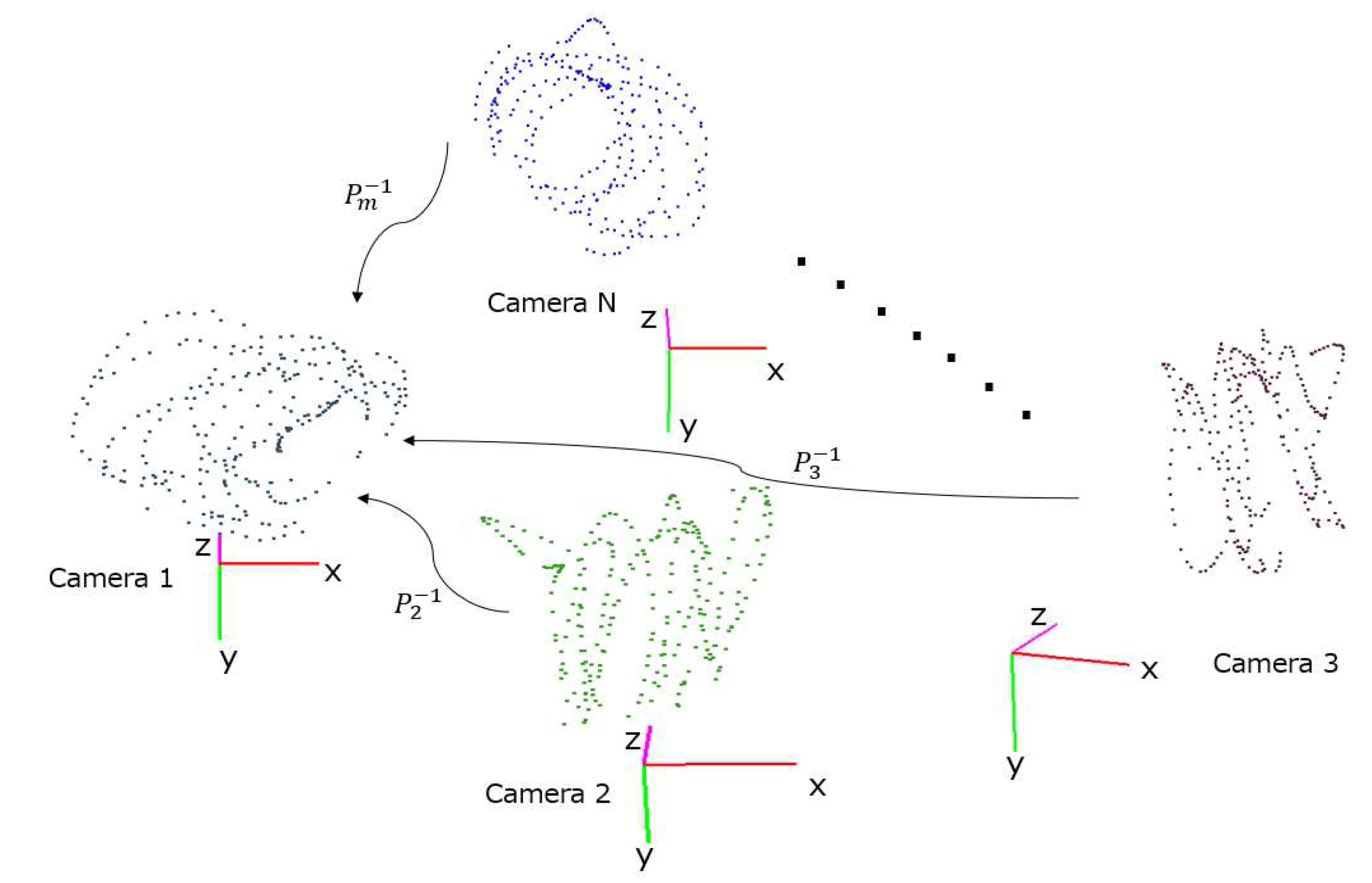
- Pairwise calibration: To provide an initial estimate of the extrinsic parameters of each camera, we perform pairwise calibration to find the view transformation function from each camera to an arbitrarily-chosen reference coordinate system. The server receives from each client the estimated sphere center locations and the associated time-stamps. Correspondences are established by grouping measurements from different cameras that are collected within the time synchronization error tolerance. Then, a system of equations with all correspondences as data terms and parameters of the view transformations as unknowns are solved at the server to provide an initial guess of the transformation functions. Details of this step can be found in Section 3.3.
- Simultaneous optimization: The estimated view transformations are then used to bootstrap a pseudo bundle adjustment procedure. This procedure simultaneously adjusts all the extrinsic parameters and the true 3D locations of the sphere center so as to minimize the sum of 3D projection errors across the entire network. Details of this step can be found in Section 3.4.
3.1. Problem Formulation
3.2. Sphere Detection by Joint Color and Depth Information
3.3. Extrinsic Calibration between Pairwise Cameras
3.3.1. Rigid Transformation
3.3.2. Polynomial Regression
3.3.3. Manifold Alignment
3.4. Simultaneous Optimization
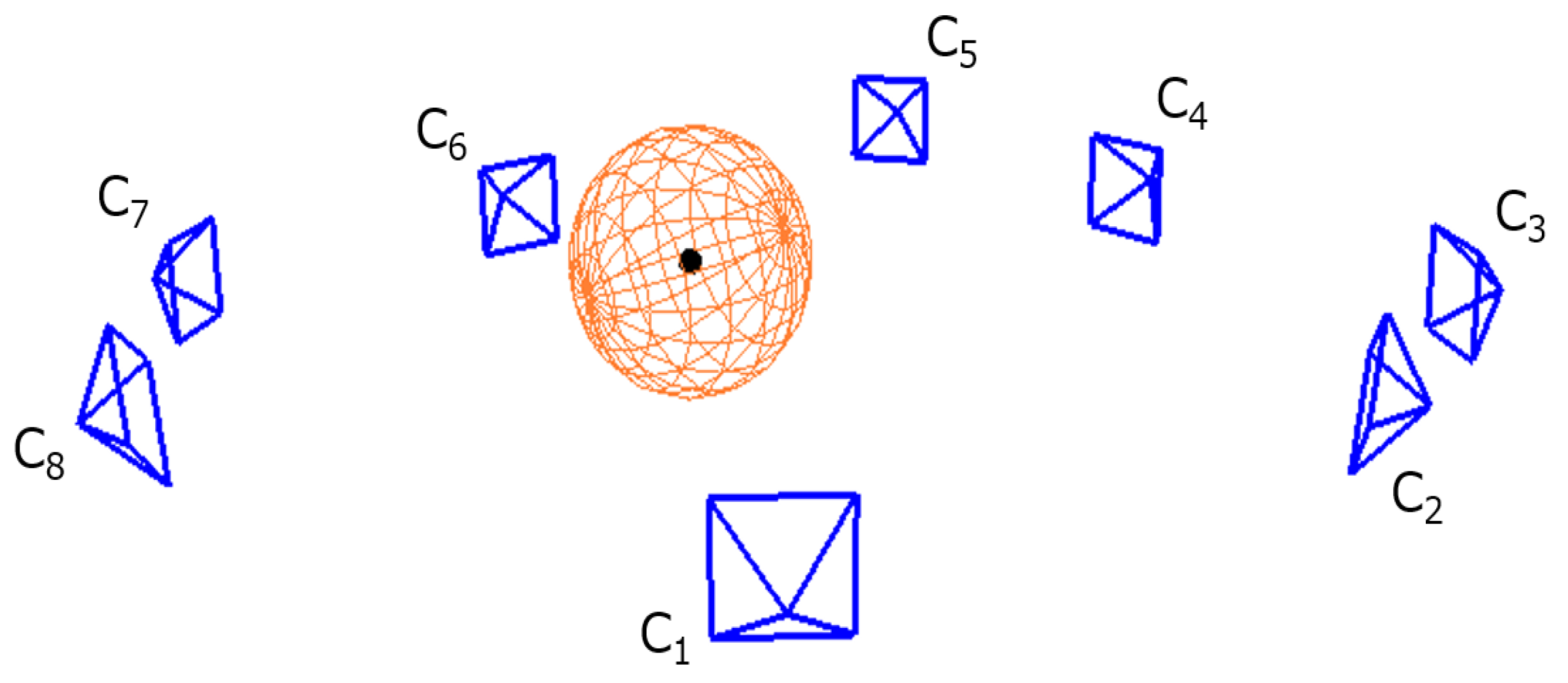
4. Experiments
4.1. Quantitative Evaluation
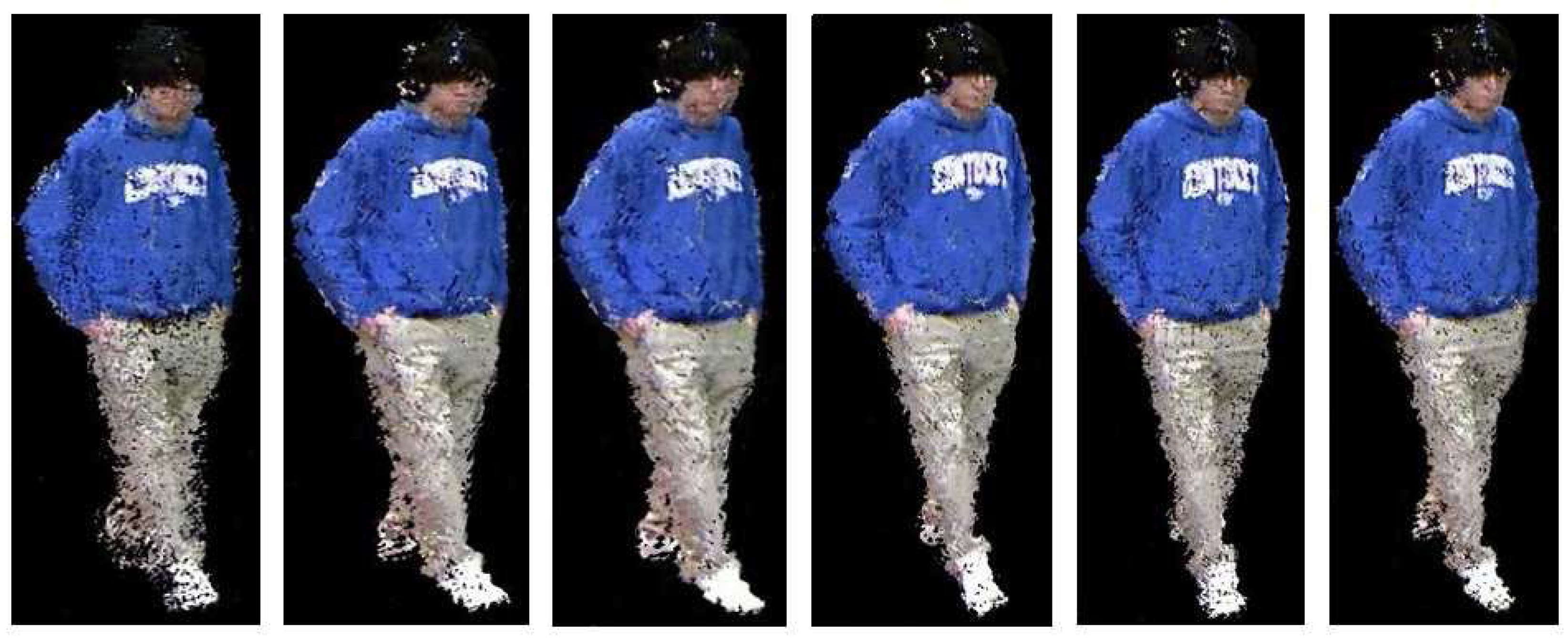
4.2. Qualitative Evaluation
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Konolige, K.; Agrawal, M. FrameSLAM: From Bundle Adjustment to Real-Time Visual Mapping. IEEE Trans. Robot. 2008, 24, 1066–1077. [Google Scholar] [CrossRef]
- Izadi, S.; Kim, D.; Hilliges, O.; Molyneaux, D.; Newcombe, R.; Kohli, P.; Shotton, J.; Hodges, S.; Freeman, D.; Davison, A.; et al. KinectFusion: Real-time 3D Reconstruction and Interaction Using a Moving Depth Camera. In Proceedings of the 24th Annual ACM Symposium on User Interface Software and Technology, Santa Barbara, CA, USA, 16–19 October 2011; ACM: New York, NY, USA, 2011; pp. 559–568. [Google Scholar]
- Kerl, C.; Sturm, J.; Cremers, D. Dense Visual SLAM for RGB-D Cameras. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Kahlesz, F.; Lilge, C.; Klein, R. Easy-to-use calibration of multiple-camera setups. In Proceedings of the Workshop on Camera Calibration Methods for Computer Vision Systems (CCMVS), Bielefeld, Germany, 21–24 March 2007. [Google Scholar]
- Puwein, J.; Ziegler, R.; Vogel, J.; Pollefeys, M. Robust multi-view camera calibration for wide-baseline camera networks. In Proceedings of the IEEE Workshop on Applications of Computer Vision (WACV), Kona, HI, USA, 5–7 January 2011; pp. 321–328. [Google Scholar]
- Kuo, T.; Ni, Z.; Sunderrajan, S.; Manjunath, B. Calibrating a wide-area camera network with non-overlapping views using mobile devices. ACM Trans. Sens. Netw. 2014, 10. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Yang, R.; Davis, J.; Pan, Z. Reliability fusion of time-of-flight depth and stereo geometry for high quality depth maps. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1400–1414. [Google Scholar] [PubMed]
- Shim, H.; Adelsberger, R.; Kim, J.D.; Rhee, S.M.; Rhee, T.; Sim, J.Y.; Gross, M.; Kim, C. Time-of-flight sensor and color camera calibration for multi-view acquisition. Vis. Comput. 2012, 28, 1139–1151. [Google Scholar] [CrossRef]
- Hansard, M.; Evangelidis, G.; Pelorson, Q.; Horaud, R. Cross-calibration of time-of-flight and colour cameras. Comput. Vis. Image Underst. 2015, 134, 105–115. [Google Scholar] [CrossRef]
- Su, P.C.; Shen, J.; Cheung, S.C.S. A robust RGB-D SLAM system for 3D environment with planar surfaces. In Proceedings of the 20th IEEE International Conference on Image Processing (ICIP), Melbourne, VIC, Australia, 15–18 September 2013; pp. 275–279. [Google Scholar]
- Shen, J.; Su, P.C.; Cheung, S.C.S.; Zhao, J. Virtual Mirror Rendering with Stationary RGB-D Cameras and Stored 3D Background. IEEE Trans. Image Process. 2013, 22, 3433–3448. [Google Scholar] [CrossRef] [PubMed]
- Tran, A.T.; Harada, K. Depth-aided tracking multiple objects under occlusion. J. Signal Inf. Process. 2013, 4, 299–307. [Google Scholar] [CrossRef]
- Macknojia, R.; Chavez-Aragon, A.; Payeur, P.; Laganiere, R. Calibration of a network of Kinect sensors for robotic inspection over a large workspace. In Proceedings of the IEEE Workshop on Robot Vision (WORV), Clearwater Beach, FL, USA, 15–17 January 2013; pp. 184–190. [Google Scholar]
- Vemulapalli, R.; Arrate, F.; Chellappa, R. Human Action Recognition by Representing 3D Skeletons as Points in a Lie Group. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 588–595. [Google Scholar]
- Afzal, H.; Aouada, D.; Foni, D.; Mirbach, B.; Ottersten, B. RGB-D Multi-view System Calibration for Full 3D Scene Reconstruction. In Proceedings of the 22nd International Conference on Pattern Recognition (ICPR), Stockholm, Sweden, 24–28 August 2014; pp. 2459–2464. [Google Scholar]
- Ruan, M.; Huber, D. Calibration of 3D Sensors Using a Spherical Target. In Proceedings of the 2nd International Conference on 3D Vision (3DV), Tokyo, Japan, 8–11 December 2014; pp. 187–193. [Google Scholar]
- Kumara, W.; Yen, S.H.; Hsu, H.H.; Shih, T.K.; Chang, W.C.; Togootogtokh, E. Real-time 3D human objects rendering based on multiple camera details. Multimed. Tools Appl. 2017, 76, 11687–11713. [Google Scholar] [CrossRef]
- Shen, J.; Xu, W.; Luo, Y.; Su, P.C.; Cheung, S.C. Extrinsic calibration for wide-baseline RGB-D camera network. In Proceedings of the 2014 IEEE 16th International Workshop on Multimedia Signal Processing (MMSP), Jakarta, Indonesia, 22–24 September 2014; pp. 1–6. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Ahmed, N.; Junejo, I.N. A System for 3D Video Acquisition and Spatio-Temporally Coherent 3D Animation Reconstruction using Multiple RGB-D Cameras. Proc. IJSIP 2013, 6, 113–128. [Google Scholar]
- Lemkens, W.; Kaur, P.; Buys, K.; Slaets, P.; Tuytelaars, T.; Schutter, J.D. Multi RGB-D camera setup for generating large 3D point clouds. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 1092–1099. [Google Scholar]
- Chen, X.; Davis, J. Wide Area Camera Calibration Using Virtual Calibration Objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 15 June 2000; pp. 520–527. [Google Scholar]
- Svoboda, T.; Martinec, D.; Pajdla, T. A Convenient Multicamera Self-calibration for Virtual Environments. Presence 2005, 14, 407–422. [Google Scholar] [CrossRef]
- Alexiadis, D.S.; Zarpalas, D.; Daras, P. Real-Time, Full 3-D Reconstruction of Moving Foreground Objects From Multiple Consumer Depth Cameras. IEEE Trans. Multimed. 2013, 15, 339–358. [Google Scholar] [CrossRef]
- Irschara, A.; Zach, C.; Bischof, H. Towards Wiki-based Dense City Modeling. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Kuster, C.; Popa, T.; Zach, C.; Gotsman, C.; Gross, M.H.; Eisert, P.; Hornegger, J.; Polthier, K. FreeCam: A Hybrid Camera System for Interactive Free-Viewpoint Video. In Proceedings of the Vision, Modeling, and Visualization (VMV), Berlin, Germany, 4–6 October 2011; pp. 17–24. [Google Scholar]
- Kumar, R.K.; Ilie, A.; Frahm, J.M.; Pollefeys, M. Simple calibration of non-overlapping cameras with a mirror. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–7. [Google Scholar]
- Kim, J.H.; Koo, B.K. Convenient calibration method for unsynchronized camera networks using an inaccurate small reference object. Opt. Express 2012, 20, 25292–25310. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, H.; Tai, Y.W.; Brown, M.; Kweon, I. High quality depth map upsampling for 3D-TOF cameras. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 1623–1630. [Google Scholar]
- Herrera, C.; Kannala, J.; Heikkil, J. Accurate and practical calibration of a depth and color camera pair. In Computer Analysis of Images and Patterns; Springer: Berlin/Heidelberg, Germany, 2011; pp. 437–445. [Google Scholar]
- Liu, W.; Fan, Y.; Zhong, Z.; Lei, T. A new method for calibrating depth and color camera pair based on Kinect. In Proceedings of the International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 16–18 July 2012; pp. 212–217. [Google Scholar]
- Herrera, C.; Kannala, J.; Heikkil, J. Joint Depth and Color Camera Calibration with Distortion Correction. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2058–2064. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Chan, D.; Theobalt, C.; Thrun, S. Design and calibration of a multi-view TOF sensor fusion system. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008; pp. 1–7. [Google Scholar]
- Zhang, C.; Zhang, Z. Calibration between depth and color sensors for commodity depth cameras. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Barcelona, Spain, 11–15 July 2011; pp. 1–6. [Google Scholar]
- Sinha, S.N.; Pollefeys, M.; McMillan, L. Camera network calibration from dynamic silhouettes. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. I-195–I-202. [Google Scholar]
- Carrera, G.; Angeli, A.; Davison, A.J. SLAM-based automatic extrinsic calibration of a multi-camera rig. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2652–2659. [Google Scholar]
- Miller, S.; Teichman, A.; Thrun, S. Unsupervised extrinsic calibration of depth sensors in dynamic scenes. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 2695–2702. [Google Scholar]
- Li, S.; Pathirana, P.N.; Caelli, T. Multi-kinect skeleton fusion for physical rehabilitation monitoring. Conf. Proc. Eng. Med. Biol. Soc. 2014, 2014, 5060–5063. [Google Scholar]
- Prasad, T.D.A.; Hartmann, K.; Wolfgang, W.; Ghobadi, S.E.; Sluiter, A. First steps in enhancing 3D vision technique using 2D/3D sensors. In Proceedings of the Computer Vision Winter Workshop 2006, Telč, Czech Republic, 6–8 February 2006. [Google Scholar]
- OpenNI. Open Natural Interaction. Available online: http://structure.io/openni (accessed on 9 January 2018).
- Ly, D.S.; Demonceaux, C.; Vasseur, P.; Pegard, C. Extrinsic calibration of heterogeneous cameras by line images. Mach. Vis. Appl. 2014, 25, 1601–1614. [Google Scholar] [CrossRef]
- Bruckner, M.; Bajramovic, F.; Denzler, J. Intrinsic and extrinsic active self-calibration of multi-camera systems. Mach. Vis. Appl. 2014, 25, 389–403. [Google Scholar] [CrossRef]
- Fernandez-Moral, E.; Gonzalez-Jimenez, J.; Rives, P.; Arevalo, V. Extrinsic calibration of a set of range cameras in 5 seconds without pattern. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 429–435. [Google Scholar]
- Yang, R.S.; Chan, Y.H.; Gong, R.; Nguyen, M.; Strozzi, A.G.; Delmas, P.; Gimel’farb, G.; Ababou, R. Multi-Kinect scene reconstruction: Calibration and depth inconsistencies. In Proceedings of the IEEE 28th International Conference of Image and Vision Computing New Zealand (IVCNZ), Wellington, New Zealand, 27–29 November 2013; pp. 47–52. [Google Scholar]
- Lee, J.H.; Kim, E.S.; Park, S.Y. Synchronization Error Compensation of Multi-view RGB-D 3D Modeling System. In Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 162–174. [Google Scholar]
- Staranowicz, A.N.; Brown, G.R.; Morbidi, F.; Mariottini, G.L. Practical and Accurate Calibration of RGB-D Cameras Using Spheres. Comput. Vis. Image Underst. 2015, 137, 102–114. [Google Scholar] [CrossRef]
- Staranowicz, A.N.; Ray, C.; Mariottini, G.L. Easy-to-use, general, and accurate multi-Kinect calibration and its application to gait monitoring for fall prediction. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4994–4998. [Google Scholar]
- NTP. The Network Time Protocol. Available online: http://www.ntp.org/ (accessed on 9 January 2018).
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Smisek, J.; Jancosek, M.; Pajdla, T. 3D with Kinect. In Consumer Depth Cameras for Computer Vision. Advances in Computer Vision and Pattern Recognition; Fossati, A., Gall, J., Grabner, H., Ren, X., Konolige, K., Eds.; Springer: London, UK, 2013. [Google Scholar]
- Burrus, N. Kinect Calibration. Available online: http://nicolas.burrus.name/index.php/Research/KinectCalibration (accessed on 9 January 2018).
- Butler, D.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Hodges, S.; Kim, D. Shake’n’sense: Reducing interference for overlapping structured light depth cameras. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Austin, Texas, USA, 5–10 May 2012; ACM: New York, NY, USA, 2012; pp. 1933–1936. [Google Scholar]
- Maimone, A.; Fuchs, H. Reducing interference between multiple structured light depth sensors using motion. In Proceedings of the IEEE Virtual Reality Short Papers and Posters (VRW), Costa Mesa, CA, USA, 4–8 March 2012; pp. 51–54. [Google Scholar]
- Berger, K.; Ruhl, K.; Albers, M.; Schröder, Y.; Scholz, A.; Kokemüller, J.; Guthe, S.; Magnor, M. The capturing of turbulent gas flows using multiple kinects. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 1108–1113. [Google Scholar]
- Maimone, A.; Fuchs, H. Encumbrance-free telepresence system with real-time 3D capture and display using commodity depth cameras. In Proceedings of the 10th IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Basel, Switzerland, 26–29 October 2011; pp. 137–146. [Google Scholar]
- Mallick, T.; Das, P.P.; Majumdar, A.K. Study of Interference Noise in multi-Kinect set-up. In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP), Lisbon, Portugal, 5–8 January 2014; pp. 173–178. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Mahadevan, S. A general framework for manifold alignment. In AAAI Fall Symposium on Manifold Learning and its Applications; AAAI Publications: Palo Alto, CA, USA, 2009; pp. 53–58. [Google Scholar]
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment - A Modern Synthesis. In Vision Algorithms: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for the least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Sarbolandi, H.; Lefloch, D.; Kolb, A. Kinect range sensing: Structured-light versus Time-of-Flight Kinect. Comput. Vis. Image Underst. 2015, 139, 1–20. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical methods and scientific inference. Math. Gaz. 1956, 58, 297. Available online: http://psycnet.apa.org/record/1957-00078-000 (accessed on 9 January 2018).






| Task | Processing Time |
|---|---|
| Sphere center detection | 44 ms (per frame) |
| Pairwise calibration | 60 ms |
| Simultaneous optimization | 2.2 s |
| Local Coordinate | Herrera [33] | Rigid [19] | Manifold [60] | Regression I | Regression II | Regression III |
|---|---|---|---|---|---|---|
| Camera 1 | 2.74 ± 0.23 | 2.40 ± 0.2 | 2.24 ± 0.22 | 1.98 ± 0.19 | 1.87 ± 0.17 | 1.80 ± 0.15 |
| Camera 2 | 2.73 ± 0.22 | 2.36 ± 0.21 | 2.01 ± 0.23 | 2.01 ± 0.15 | 1.94 ± 0.16 | 1.88 ± 0.18 |
| Camera 3 | 4.94 ± 0.54 | 4.56 ± 0.42 | 2.29 ± 0.22 | 2.12 ± 0.2 | 1.90 ± 0.16 | 1.85 ± 0.2 |
| Camera 4 | 2.86 ± 0.22 | 2.29 ± 0.18 | 1.56 ± 0.12 | 1.44 ± 0.11 | 1.40 ± 0.1 | 1.49 ± 0.12 |
| Camera 5 | 1.86 ± 0.17 | 2.33 ± 0.2 | 2.27 ± 0.17 | 2.05 ± 0.19 | 1.88 ± 0.17 | 1.84 ± 0.17 |
| Average (cm) | 3.03 | 2.79 | 2.07 | 1.92 | 1.80 | 1.77 |
| Local Coordinate | R. III - Herrera [33] | R. III - Rigid [19] | R. III - Manifold [60] | R. III - R. I | R. III - R. II | R. II - R. I |
|---|---|---|---|---|---|---|
| Camera 1 | 0.0001 | 0.0001 | 0.0001 | 0.0905 | 0.9996 | 0.9999 |
| Camera 2 | 0.0001 | 0.0001 | 0.9998 | 0.9952 | 0.9999 | 0.9999 |
| Camera 3 | 0.0001 | 0.0001 | 0.0001 | 0.1302 | 0.9999 | 0.9999 |
| Camera 4 | 0.0001 | 0.0001 | 0.0001 | 0.1517 | 0.9989 | 0.9999 |
| Camera 5 | 0.0001 | 0.0001 | 0.0001 | 0.8743 | 0.9999 | 0.9999 |
| Camera | C1 | C2 | C3 | C4 | C5 | Camera | C1 | C2 | C3 | C4 | C5 | |
| C1 | 2.98 | 5.39 | 3.08 | 3.01 | C1 | 2.36 | 5.02 | 2.57 | 3.03 | |||
| C2 | 2.98 | 5.69 | 2.85 | 2.77 | C2 | 2.36 | 5.57 | 2.32 | 2.95 | |||
| C3 | 5.39 | 5.69 | 6.05 | 4.73 | C3 | 5.02 | 5.57 | 5.89 | 4.52 | |||
| C4 | 3.08 | 2.85 | 6.05 | 2.46 | C4 | 2.57 | 2.32 | 5.89 | 2.99 | |||
| C5 | 3.01 | 2.77 | 4.73 | 2.46 | C5 | 3.03 | 2.95 | 4.52 | 2.99 | |||
| (c) Manifold [60] | (d) Regression I | |||||||||||
| Camera | C1 | C2 | C3 | C4 | C5 | Camera | C1 | C2 | C3 | C4 | C5 | |
| C1 | 2.42 | 2.67 | 2.33 | 2.75 | C1 | 2.23 | 2.64 | 2.0 | 2.46 | |||
| C2 | 2.42 | 3.02 | 2.48 | 2.39 | C2 | 2.23 | 2.37 | 2.07 | 2.25 | |||
| C3 | 2.67 | 3.02 | 2.33 | 2.95 | C3 | 2.64 | 2.37 | 2.07 | 2.34 | |||
| C4 | 2.33 | 2.48 | 2.33 | 2.0 | C4 | 2.0 | 2.07 | 2.07 | 1.79 | |||
| C5 | 2.75 | 2.39 | 2.95 | 2.0 | C5 | 2.46 | 2.25 | 2.34 | 1.79 | |||
| (e) Regression II | (f) Regression III | |||||||||||
| Camera | C1 | C2 | C3 | C4 | C5 | Camera | C1 | C2 | C3 | C4 | C5 | |
| C1 | 2.27 | 2.6 | 1.95 | 2.26 | C1 | 2.19 | 2.43 | 2.05 | 2.24 | |||
| C2 | 2.27 | 2.43 | 2.17 | 2.24 | C2 | 2.19 | 2.38 | 2.11 | 2.13 | |||
| C3 | 2.6 | 2.43 | 2.07 | 2.18 | C3 | 2.43 | 2.38 | 2.27 | 2.17 | |||
| C4 | 1.95 | 2.17 | 2.07 | 1.7 | C4 | 2.05 | 2.11 | 2.27 | 1.75 | |||
| C5 | 2.26 | 2.24 | 2.18 | 1.7 | C5 | 2.24 | 2.13 | 2.17 | 1.75 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, P.-C.; Shen, J.; Xu, W.; Cheung, S.-C.S.; Luo, Y. A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks. Sensors 2018, 18, 235. https://doi.org/10.3390/s18010235
Su P-C, Shen J, Xu W, Cheung S-CS, Luo Y. A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks. Sensors. 2018; 18(1):235. https://doi.org/10.3390/s18010235
Chicago/Turabian StyleSu, Po-Chang, Ju Shen, Wanxin Xu, Sen-Ching S. Cheung, and Ying Luo. 2018. "A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks" Sensors 18, no. 1: 235. https://doi.org/10.3390/s18010235
APA StyleSu, P.-C., Shen, J., Xu, W., Cheung, S.-C. S., & Luo, Y. (2018). A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks. Sensors, 18(1), 235. https://doi.org/10.3390/s18010235





