Optical Fiber Demodulation System with High Performance for Assessing Fretting Damage of Steam Generator Tubes
Abstract
:1. Introduction
2. Theory and Simulation of the Modulation System
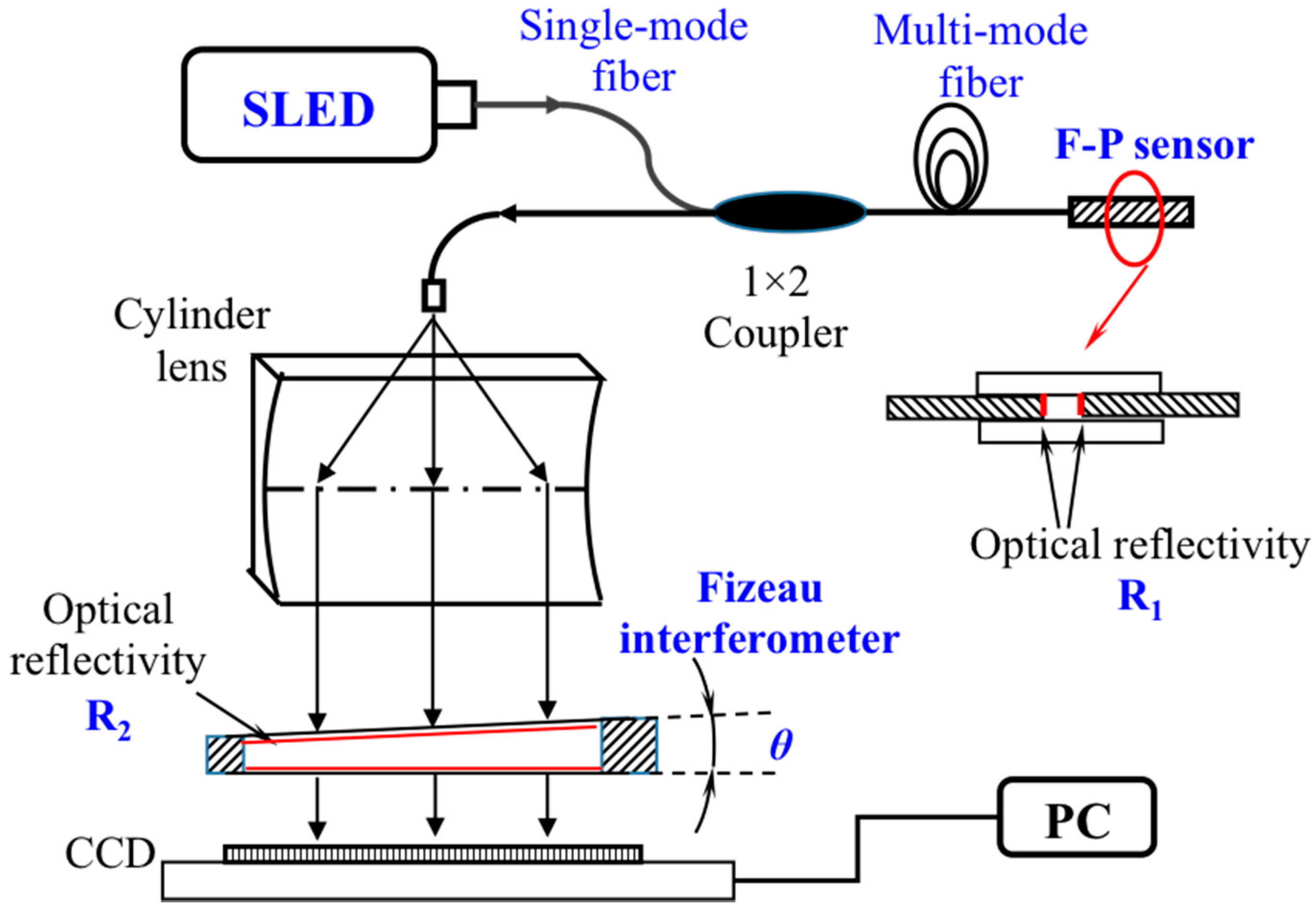
2.1. The Principle of the Non-Scanning Correlation Demodulation System
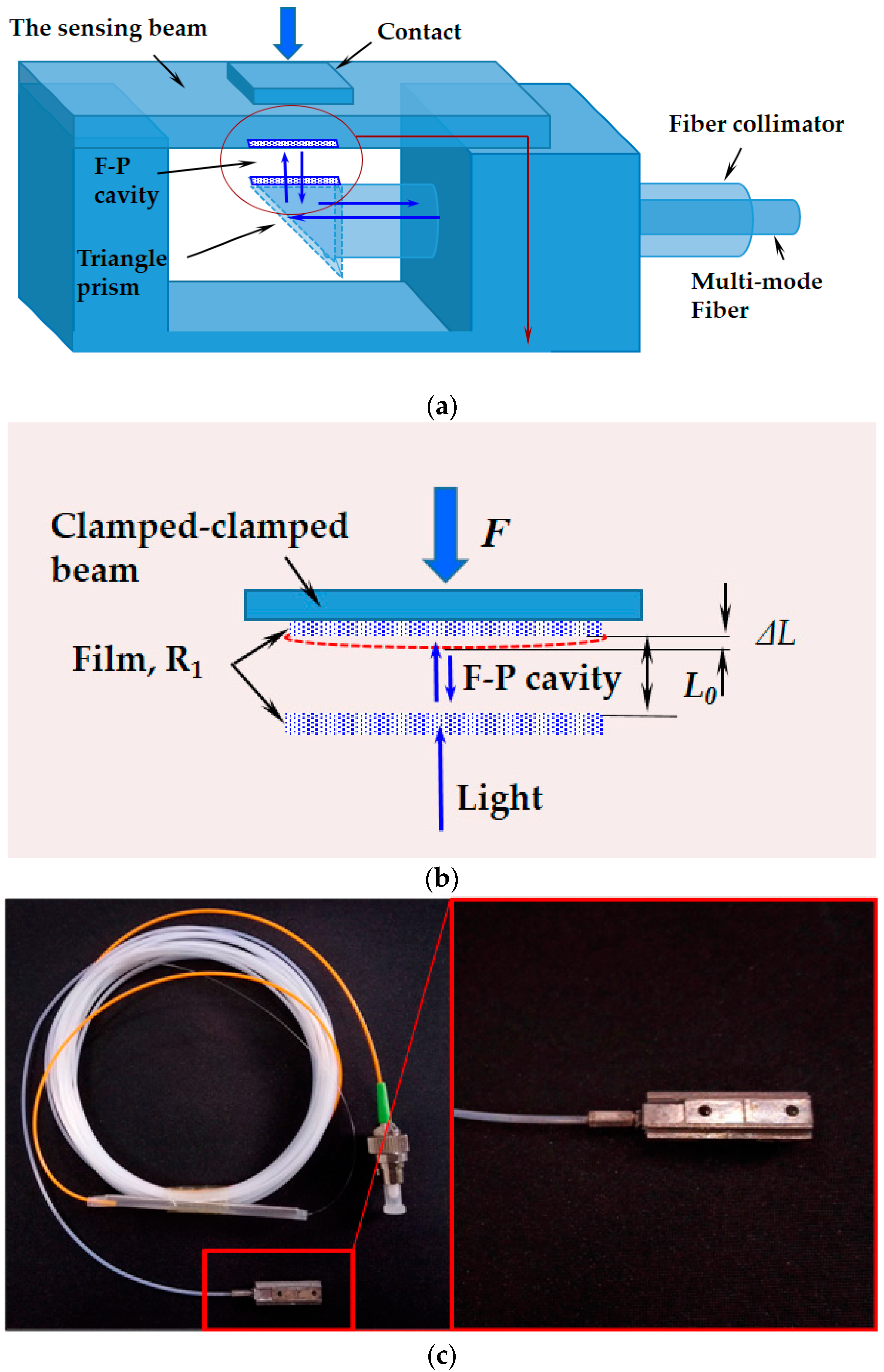
2.2. The Principle of the F-P Force Sensor
3. The Parameters Calculation of Non-Scanning Demodulation System
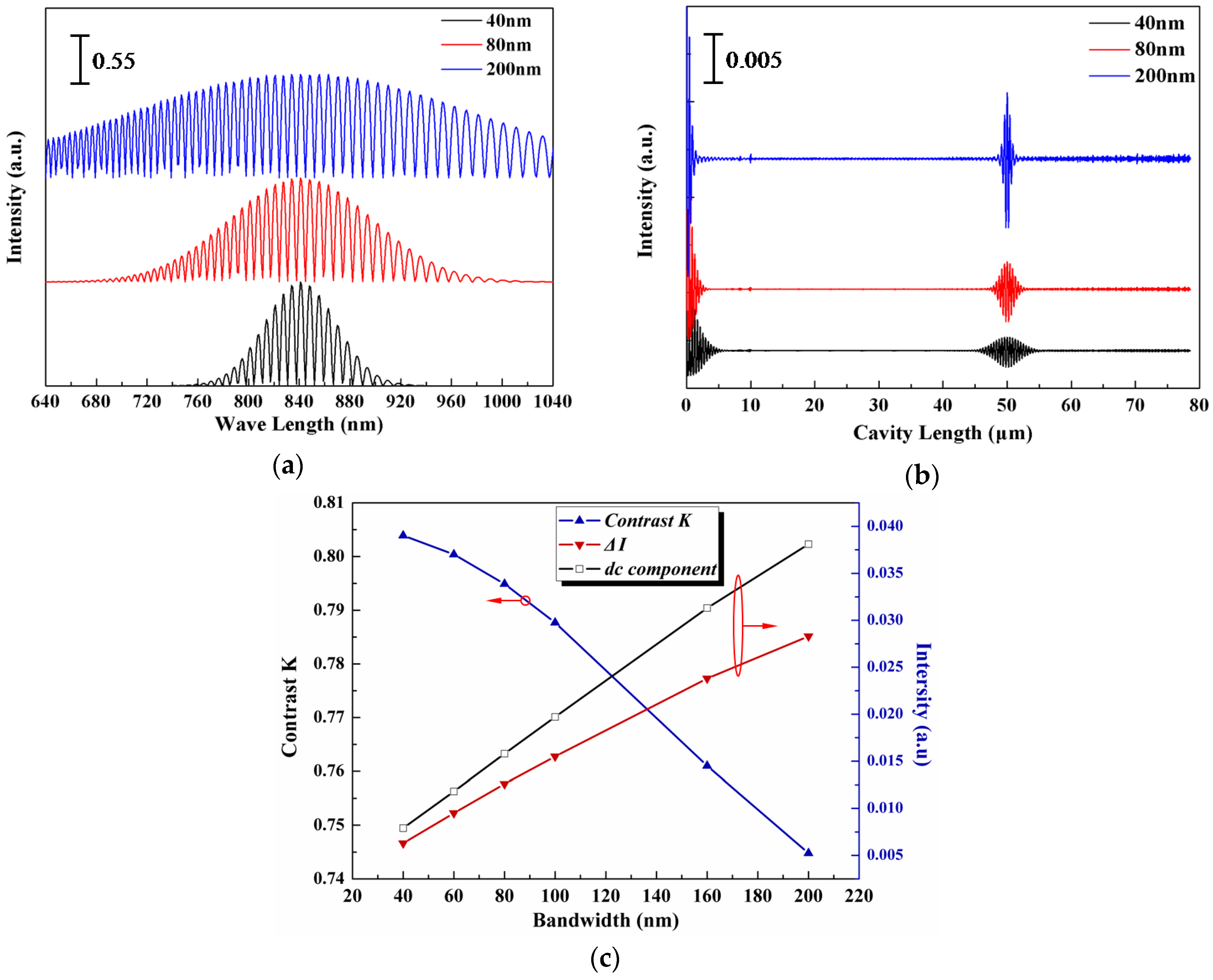
3.1. Effects of Light Source
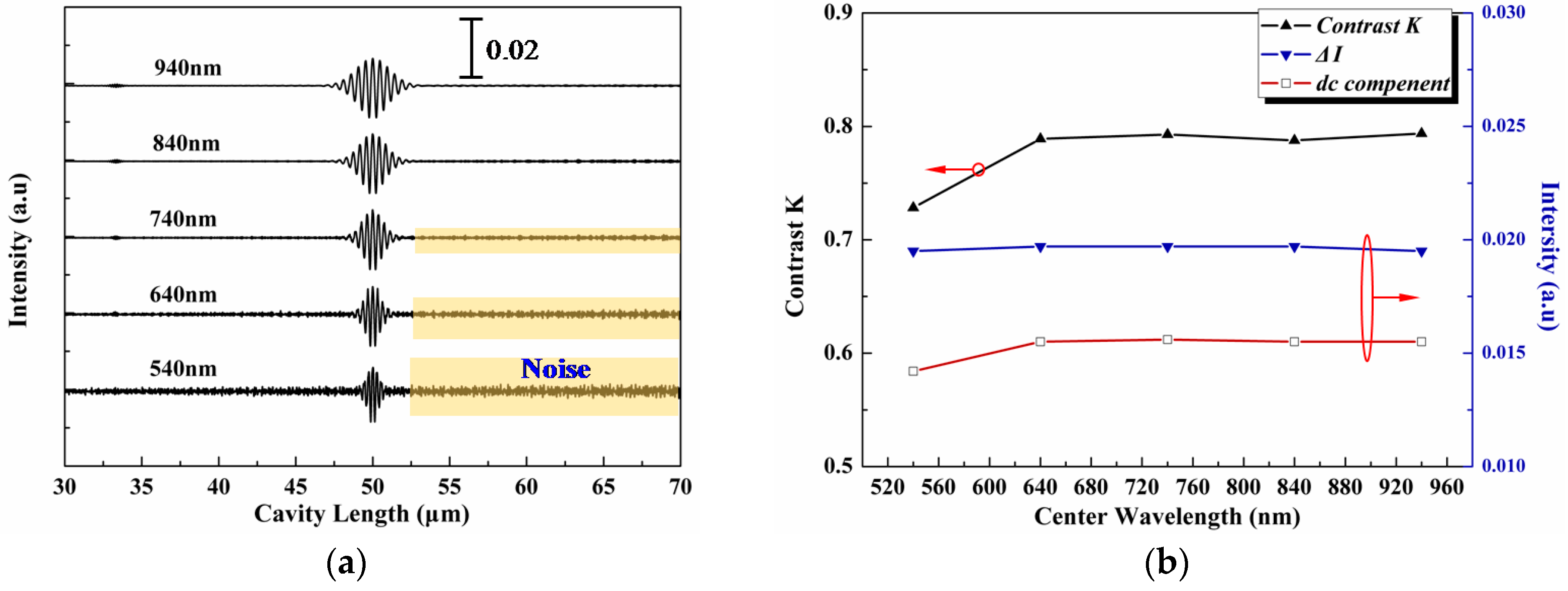
3.1.1. Effects of Wavelength Width
3.1.2. Effects of Central Wavelength
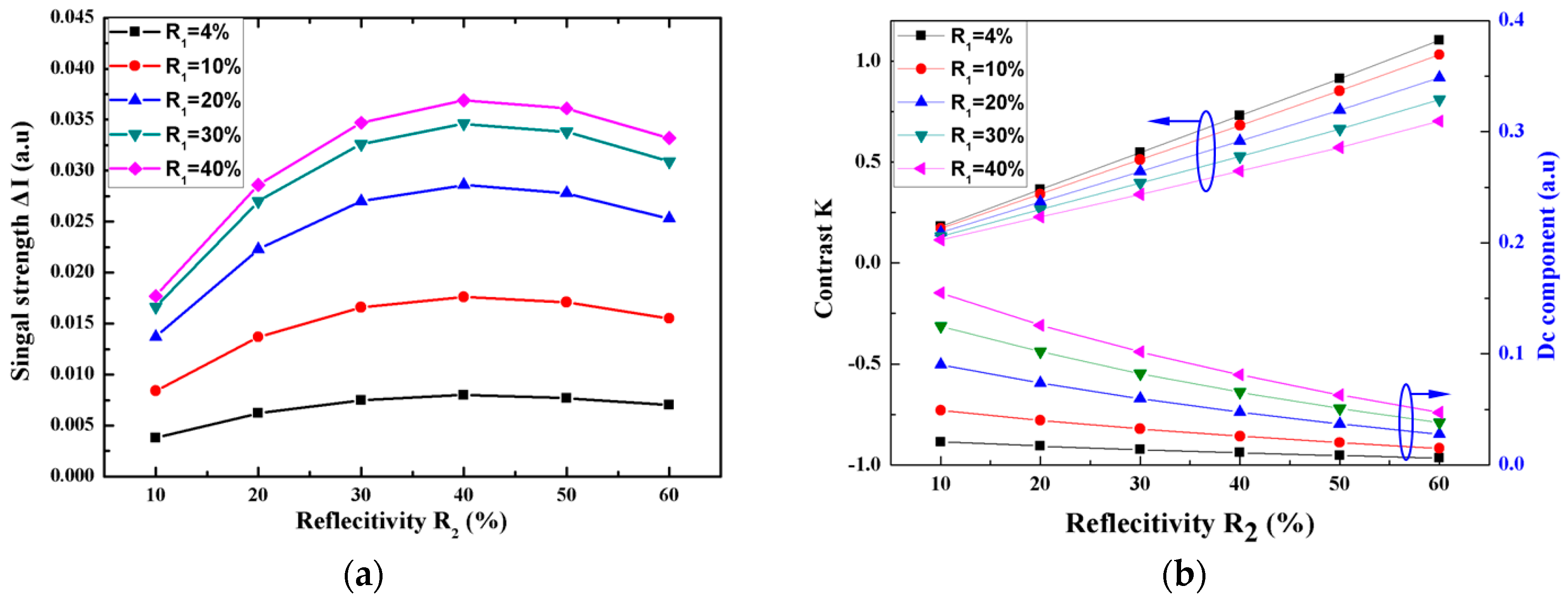
3.2. Reflectivity of F-P Sensor and Optical Wedge
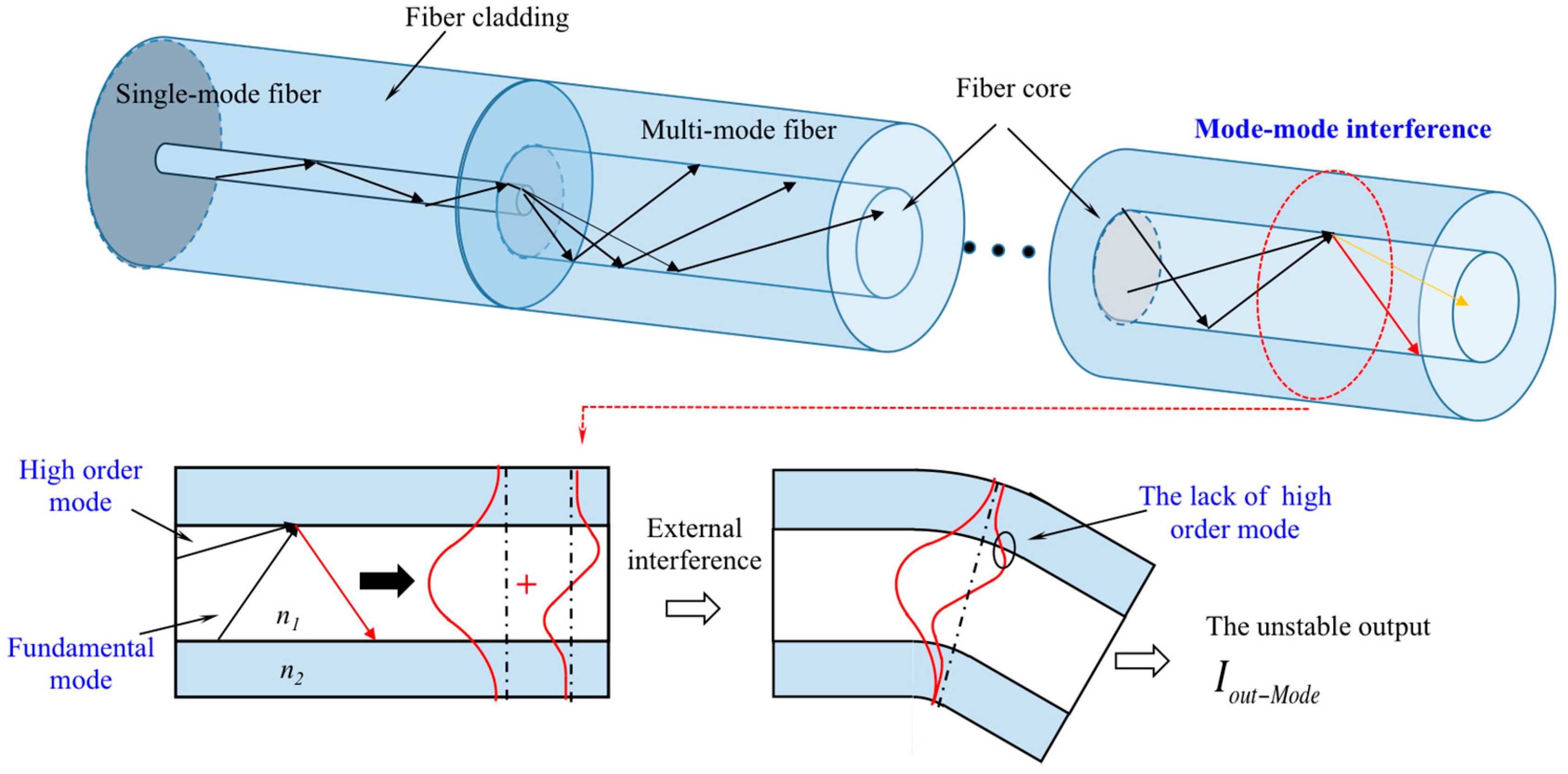
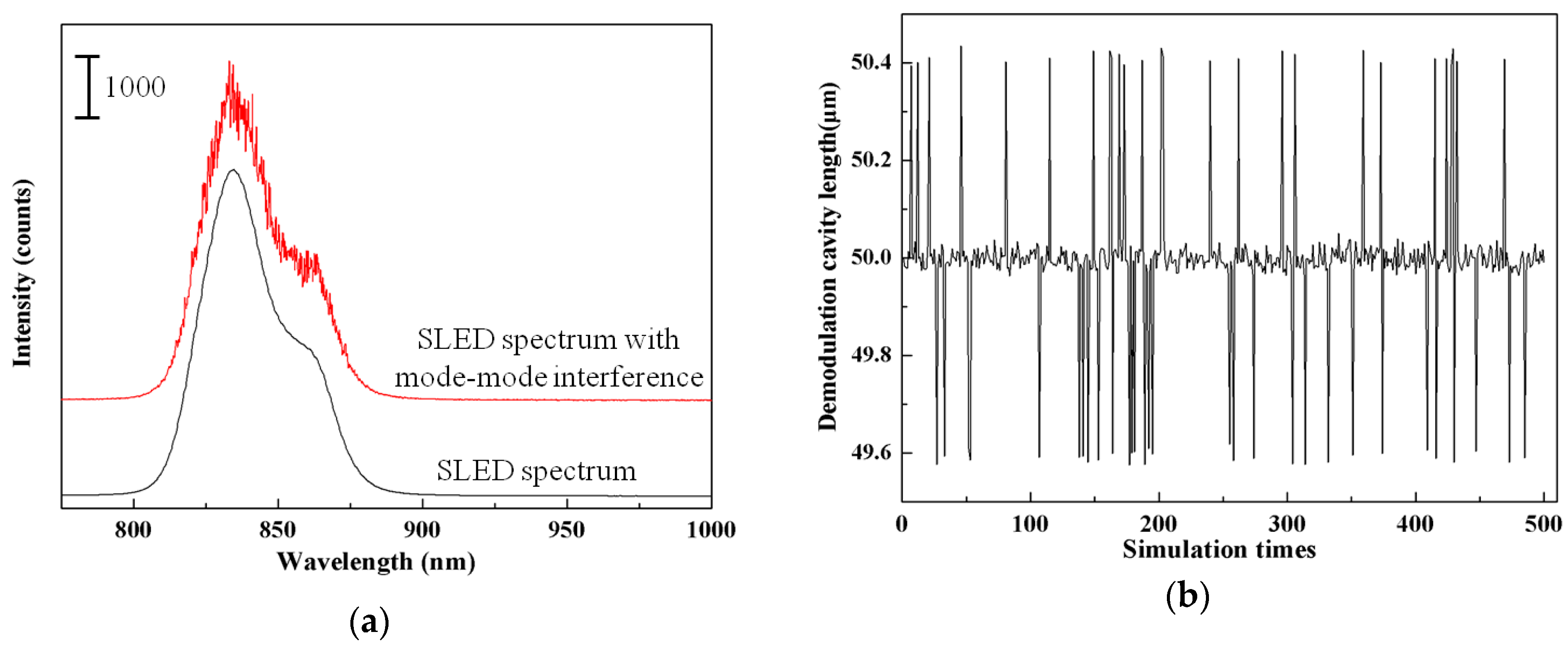
3.3. Effects of Mode-Mode Interference
4. Experiment and Calibration
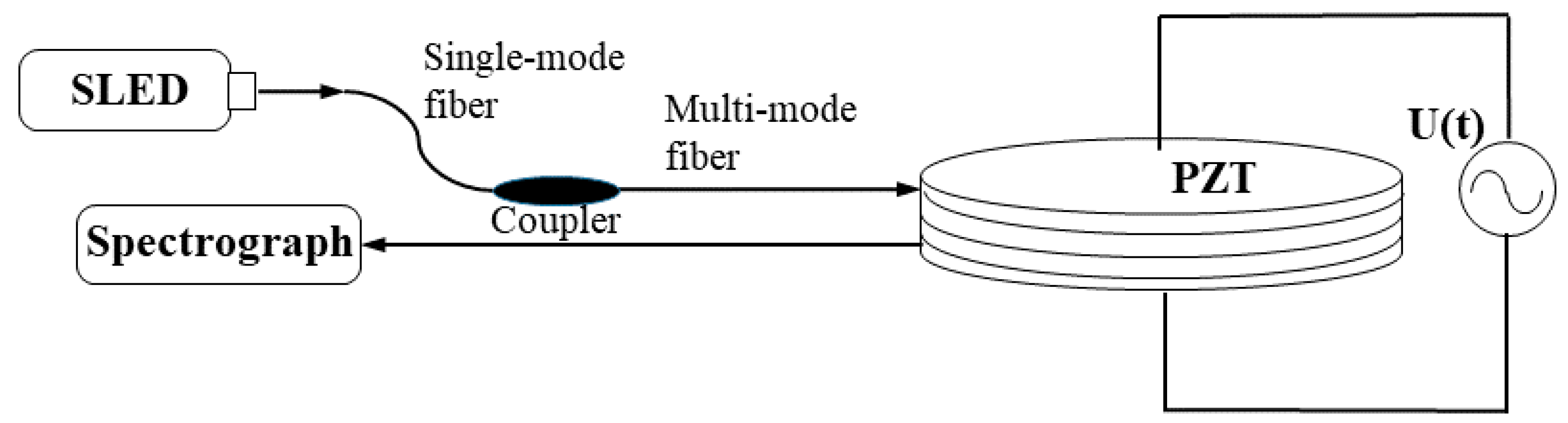
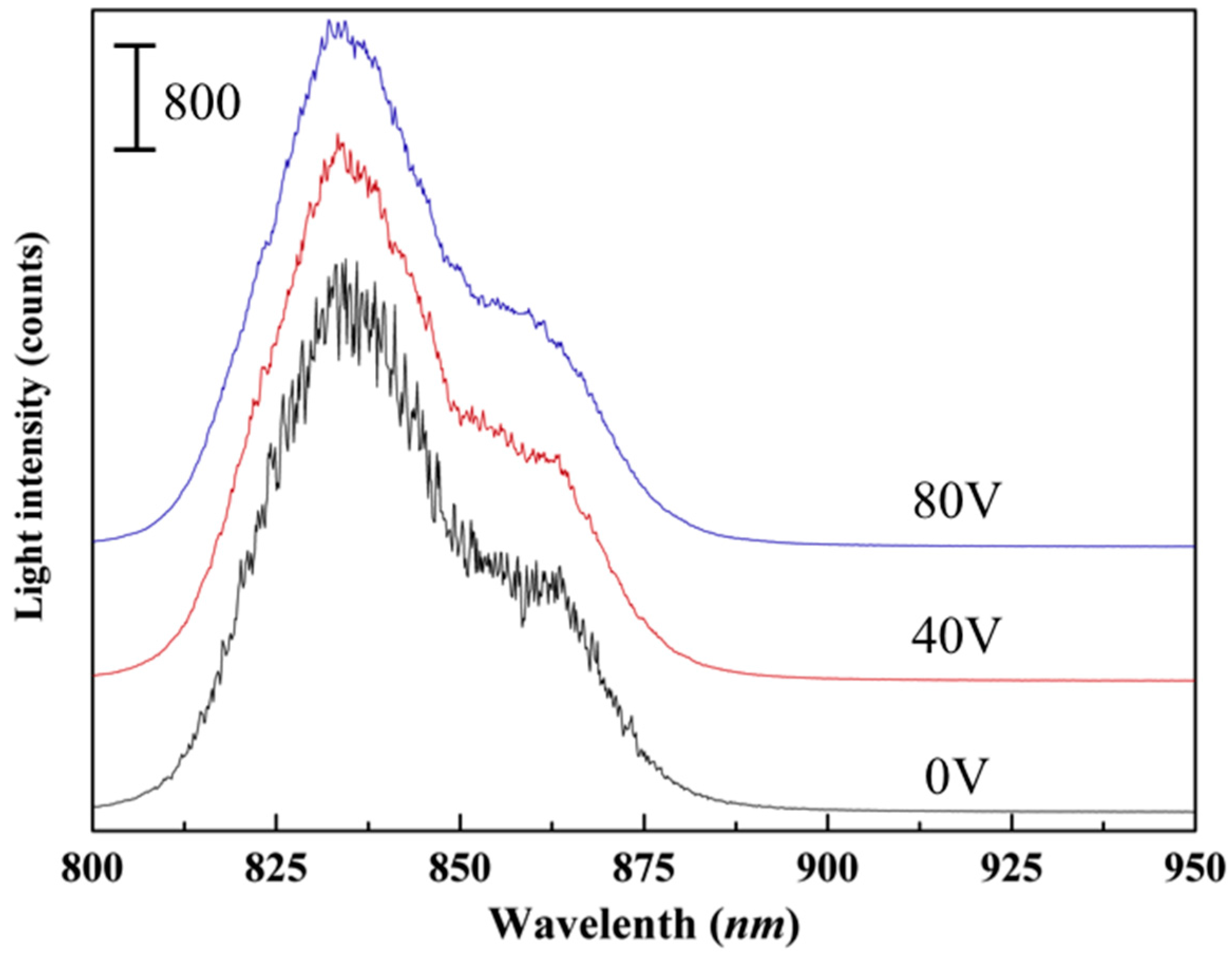
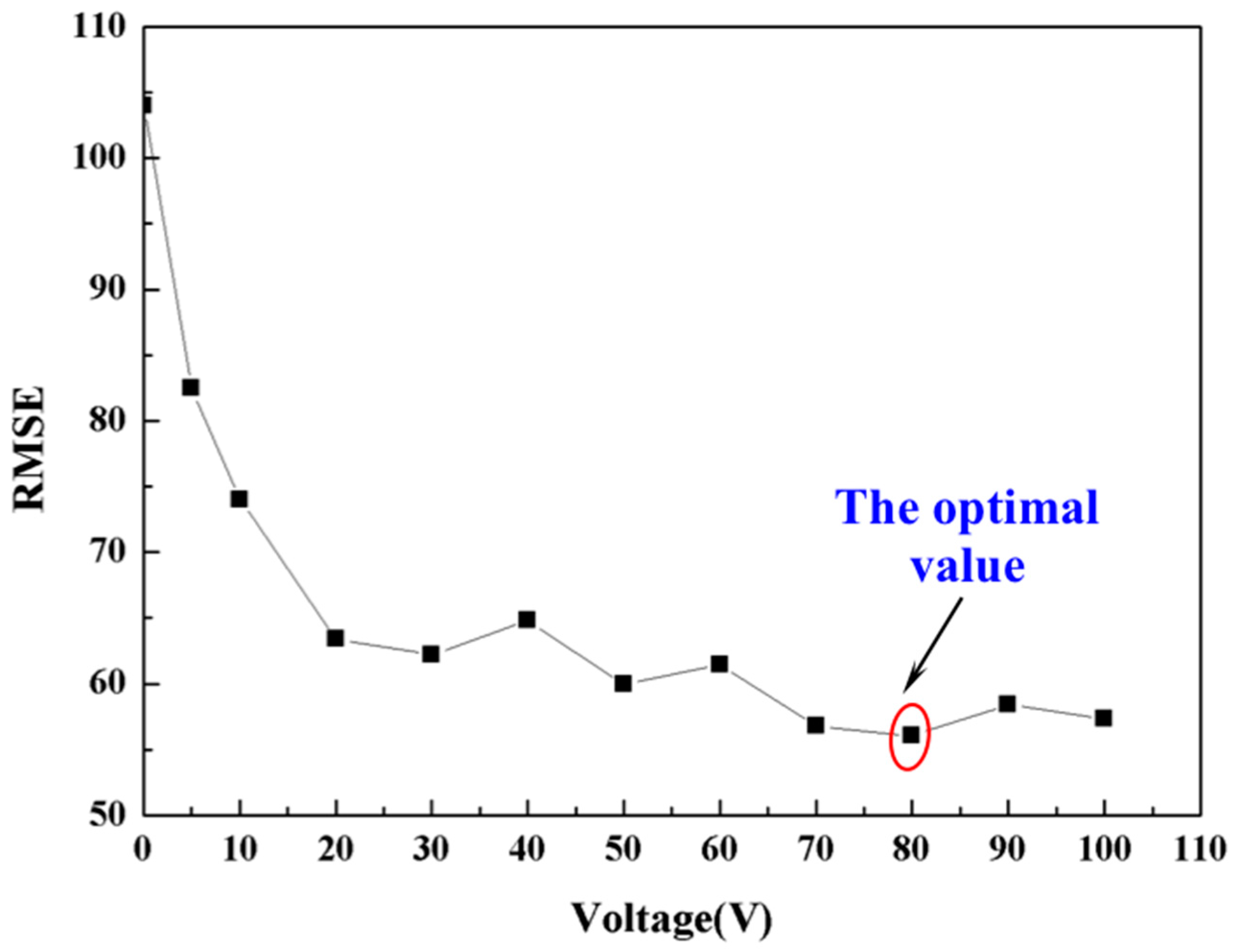
4.1. Solution to Fiber Mode-Mode Interference
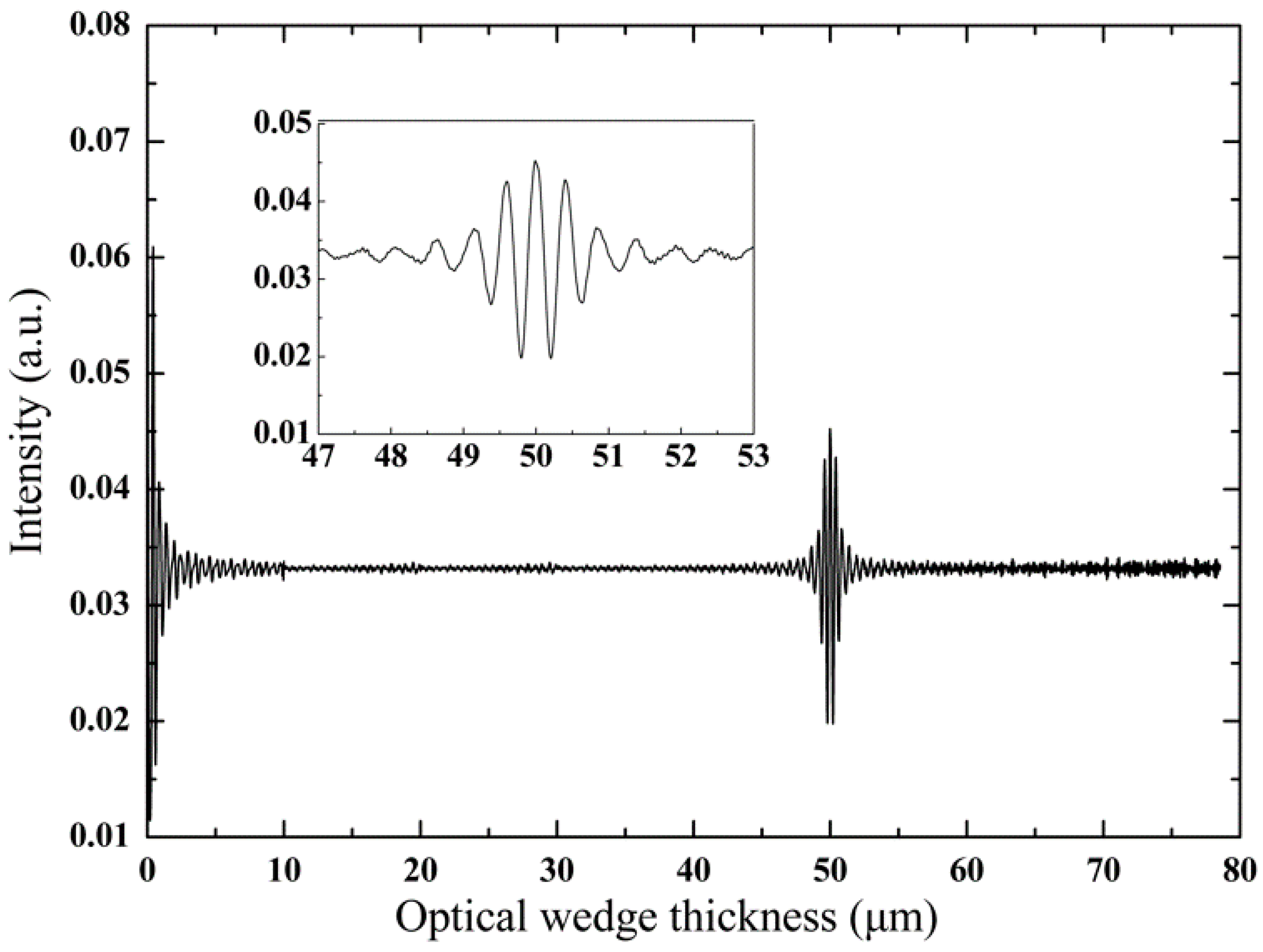
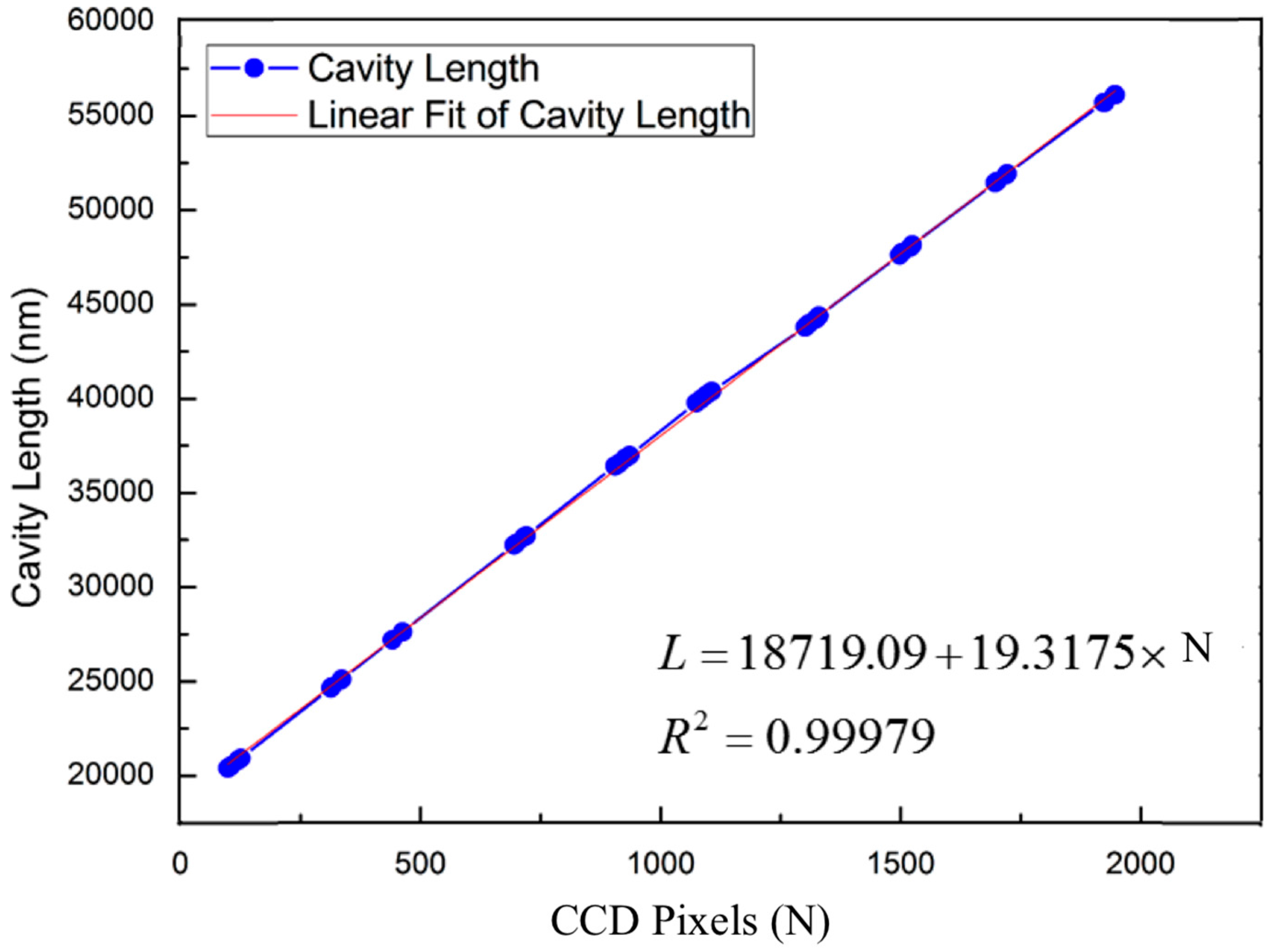
4.2. Calibration of Optical System
4.3. Experiments of the Demodulation System
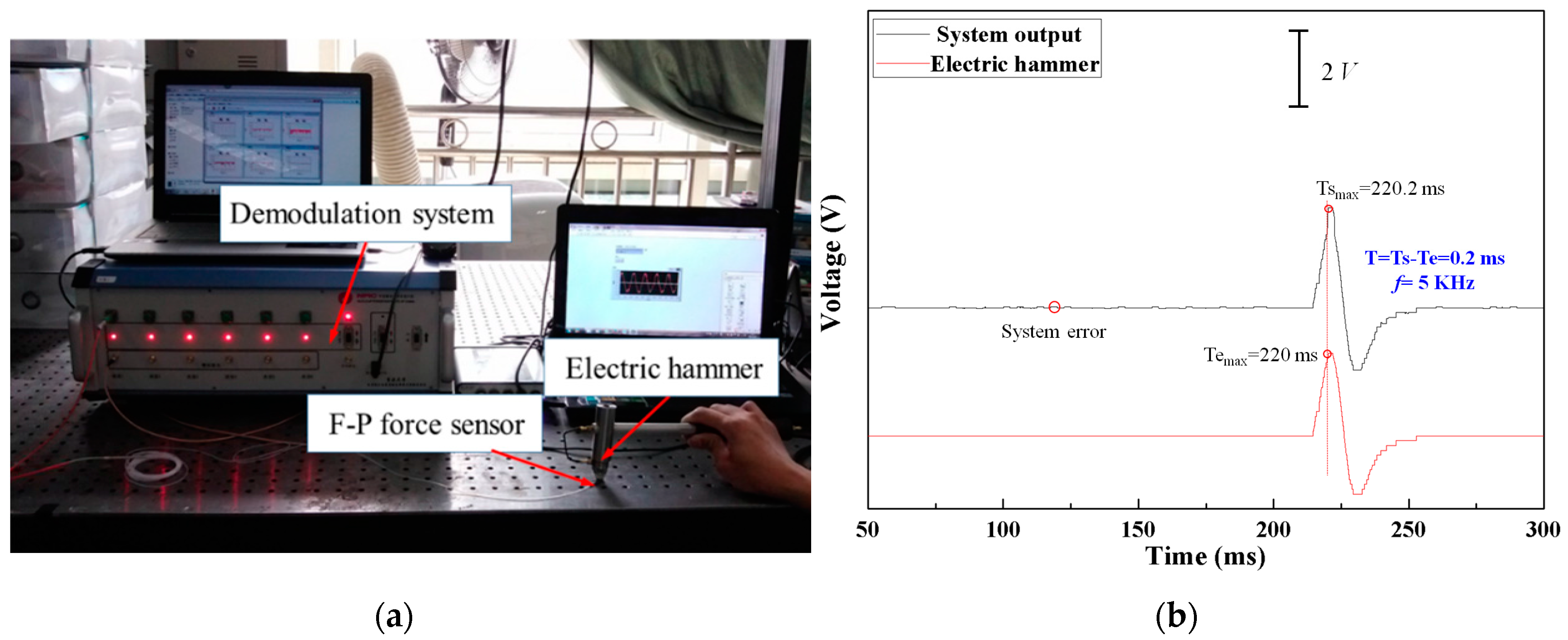
4.3.1. Dynamic Test of the Demodulation System
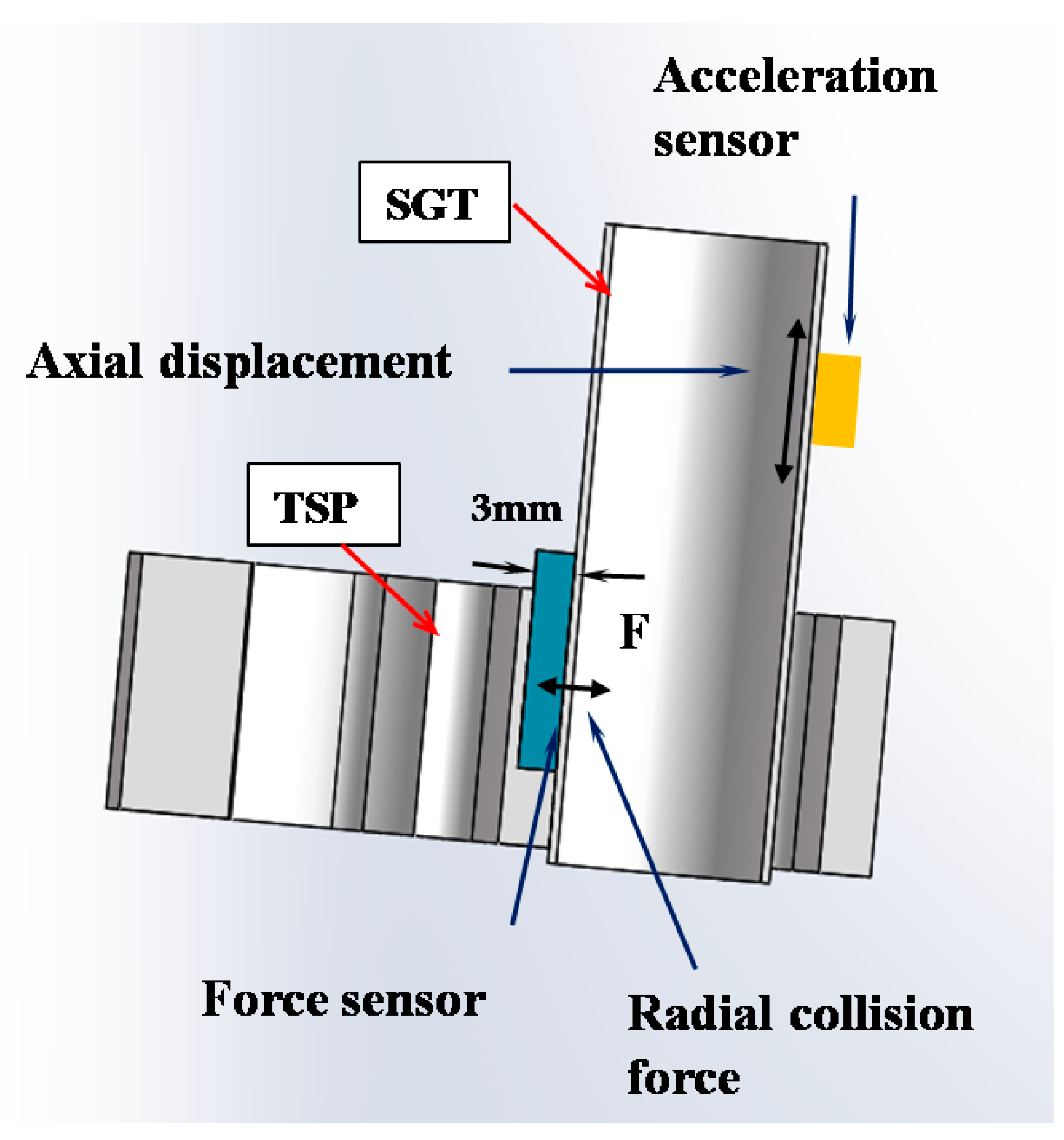
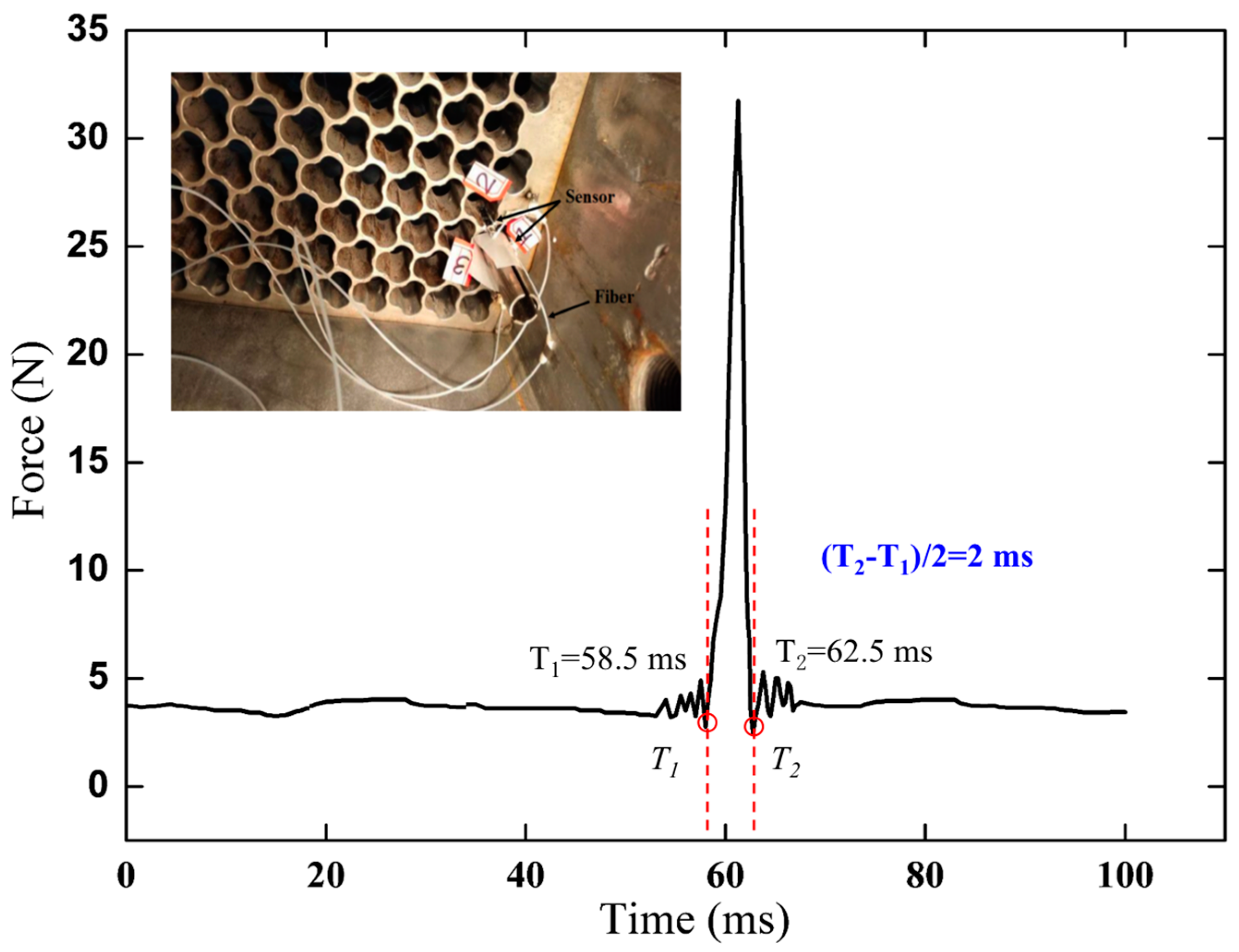
4.3.2. Experiments in the 1:1 Steam Generator Test Loop
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wade, W.C. Steam Generator Degradation and Its Collision on Continued Operation of Pressurized Water Reactors in the United States. In Energy Information Administration/Electric Power Monthly; Energy Information Administration: Washington, DC, USA, 1995. [Google Scholar]
- Soria, S.R.; Tolley, A.; Yawny, A. Characterization of damage and triboparticles resulting from fretting of incoloy 800 steam generator tubes against different materials. Wear 2017, 390–391, 198–208. [Google Scholar] [CrossRef]
- Jong, C.J.; Myung, J.J.; Woong, S.K.; Young, H.C.; Hho, J.K. Fretting-wear characteristics of steam generator tubes by foreign object. Nucl. Eng. Technol. 2003, 35, 442–453. [Google Scholar]
- Frick, T.M.; Sobek, T.E.; Reavis, J.R. Overview on the Development and Implementation of Methodologies to Compute Vibration and Wear of Steam Generator Tubes. In Symposium on Flow-Induced Vibrations, Volume 6: Computational Aspects of Flow-Induced Vibration, Proceedings of the 1984 ASME Winter Annual Meeting, New York, NY, USA, 9–14 December 1984; American Society of Mechanical Engineers: New York, NY, USA, 1984; pp. 149–161. [Google Scholar]
- Attia, M.H.; Magel, E. Experimental investigation of long-term fretting wear of multi-span steam generator tubes with u-bend sections. Wear 1999, 225–229, 563–574. [Google Scholar] [CrossRef]
- Attia, H. A Generalized fretting wear theory. Tribol. Int. 2009, 42, 1380–1388. [Google Scholar] [CrossRef]
- Berthold, J.W.; Jeffers, L.A.; Lopushansky, R.L. Fiber Optic Sensors for the Refinery of the Future. In Proceedings of the ISA/IEEE Sensors for Industry Conference, Houston, TX, USA, 19–21 November 2002; Volume 40, pp. 40–43. [Google Scholar]
- Huang, P.; Wang, N.; Li, J.; Zhu, Y.; Zhang, J. Fiber fabry-perot force sensor with small volume and high performance for assessing fretting damage of steam generator tubes. Sensors 2017, 17, 2899. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Zhao, Y.; Li, X.; Chen, J.; Lv, Z. Novel optical fiber current sensor based on magnetic fluid. Chin. Opt. Lett. 2010, 8, 1–4. [Google Scholar]
- Ge, Y.; Wang, M.; Chen, X.; Rong, H. An Optical MEMS pressure sensor based on a phase demodulation method. Sens. Actuators A Phys. 2008, 143, 224–229. [Google Scholar] [CrossRef]
- Lu, E.; Ran, Z.; Peng, F.; Liu, Z.; Xu, F. Demodulation of micro fiber-optic Fabry–Perot interferometer using subcarrier and dual-wavelength method. Opt. Commun. 2012, 285, 1087–1090. [Google Scholar] [CrossRef]
- Ran, Z.; Rao, Y.; Zhang, J.; Liu, Z.; Xu, B. A Miniature fiber-optic refractive-index sensor based on laser-machined fabry–perot interferometer tip. J. Lightwave Technol. 2009, 27, 5426–5429. [Google Scholar]
- Wang, N.; Zhu, Y.; Gong, T. Multichannel fiber optic fabry-perot non-scanning correlation demodulator. Chin. Opt. Lett. 2013, 11, 10–12. [Google Scholar]
- Layton, M.R.; Bucaro, J.A. Optical fiber acoustic sensor utilizing mode-mode interference. Appl. Opt. 1979, 18, 666–670. [Google Scholar] [CrossRef] [PubMed]
- Riedel, M. Piezoelectric Bending Transducer: US. U.S. Patent 6,548,939, 15 April 2003. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Wang, N.; Li, J.; Zhu, Y.; Zhang, J.; Xi, Z. Optical Fiber Demodulation System with High Performance for Assessing Fretting Damage of Steam Generator Tubes. Sensors 2018, 18, 201. https://doi.org/10.3390/s18010201
Huang P, Wang N, Li J, Zhu Y, Zhang J, Xi Z. Optical Fiber Demodulation System with High Performance for Assessing Fretting Damage of Steam Generator Tubes. Sensors. 2018; 18(1):201. https://doi.org/10.3390/s18010201
Chicago/Turabian StyleHuang, Peijian, Ning Wang, Junying Li, Yong Zhu, Jie Zhang, and Zhide Xi. 2018. "Optical Fiber Demodulation System with High Performance for Assessing Fretting Damage of Steam Generator Tubes" Sensors 18, no. 1: 201. https://doi.org/10.3390/s18010201
APA StyleHuang, P., Wang, N., Li, J., Zhu, Y., Zhang, J., & Xi, Z. (2018). Optical Fiber Demodulation System with High Performance for Assessing Fretting Damage of Steam Generator Tubes. Sensors, 18(1), 201. https://doi.org/10.3390/s18010201



