Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors
Abstract
:1. Introduction
2. Methods
2.1. Measurement Periods
2.2. Instruments
2.2.1. Speck Monitors
2.2.2. Tapered Element Oscillating Microbalance (TEOM)
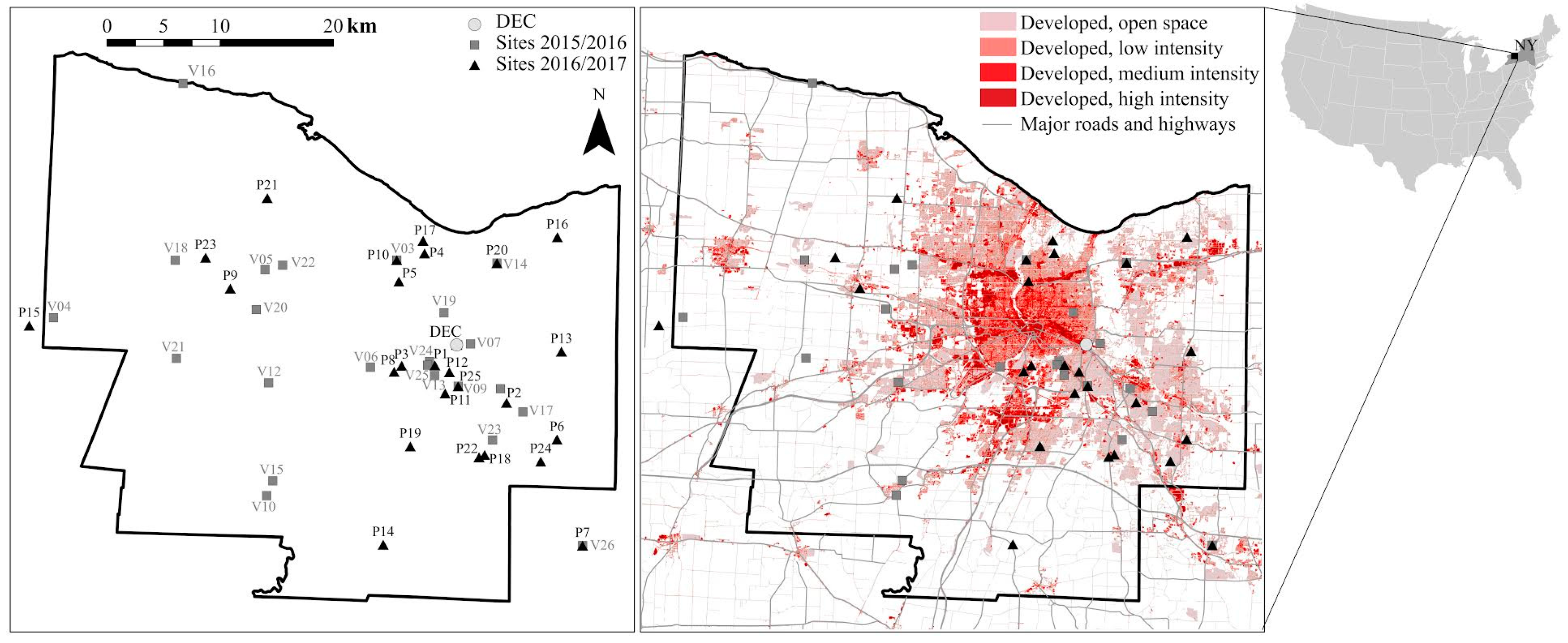
2.3. Study Area
2.4. Measurement Sites
2.5. Meteorological Data
2.6. Data Analyses
2.6.1. Wilcoxon Signed-Rank Test
2.6.2. Correlation Analysis
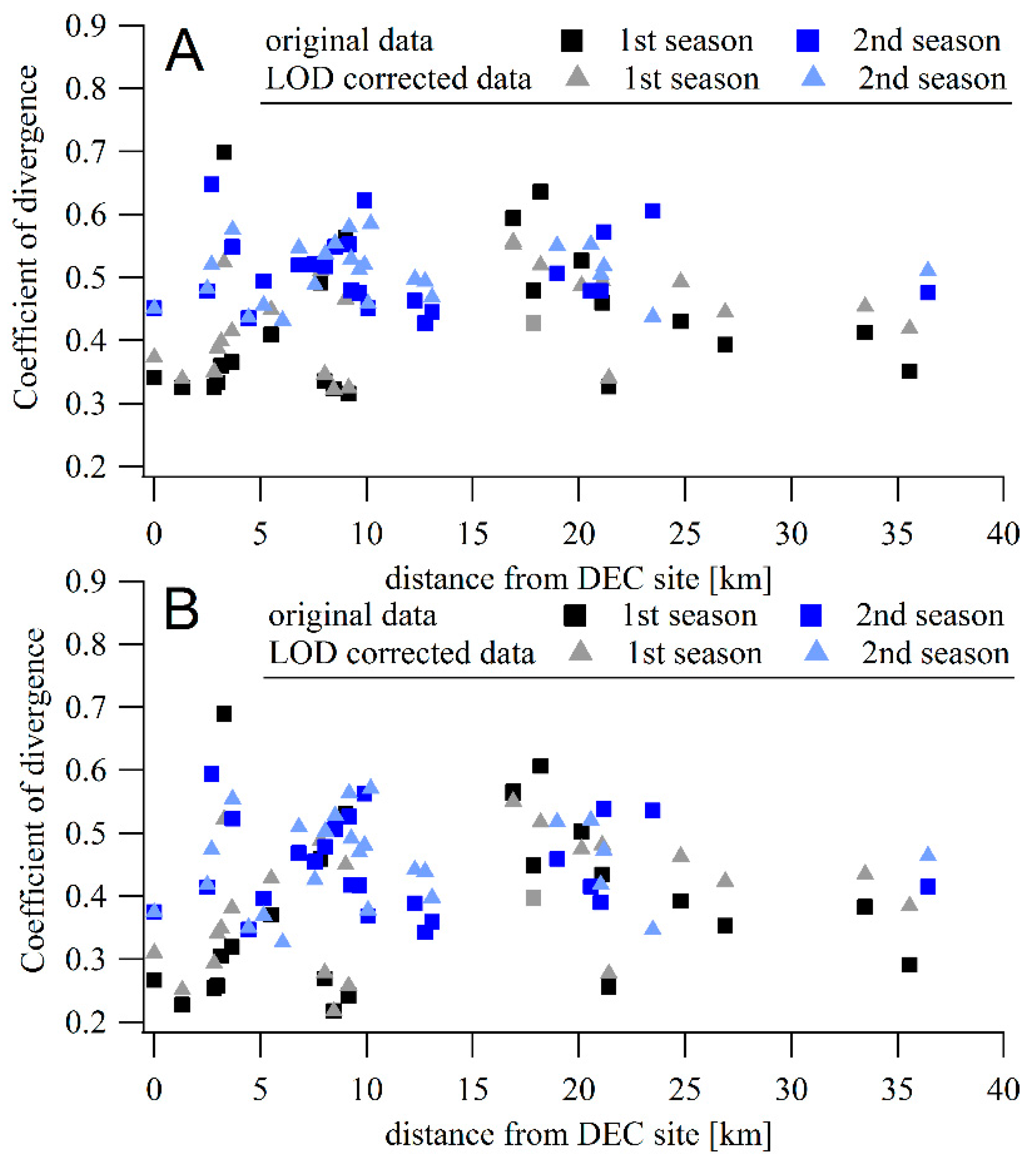
2.6.3. Coefficient of Divergence
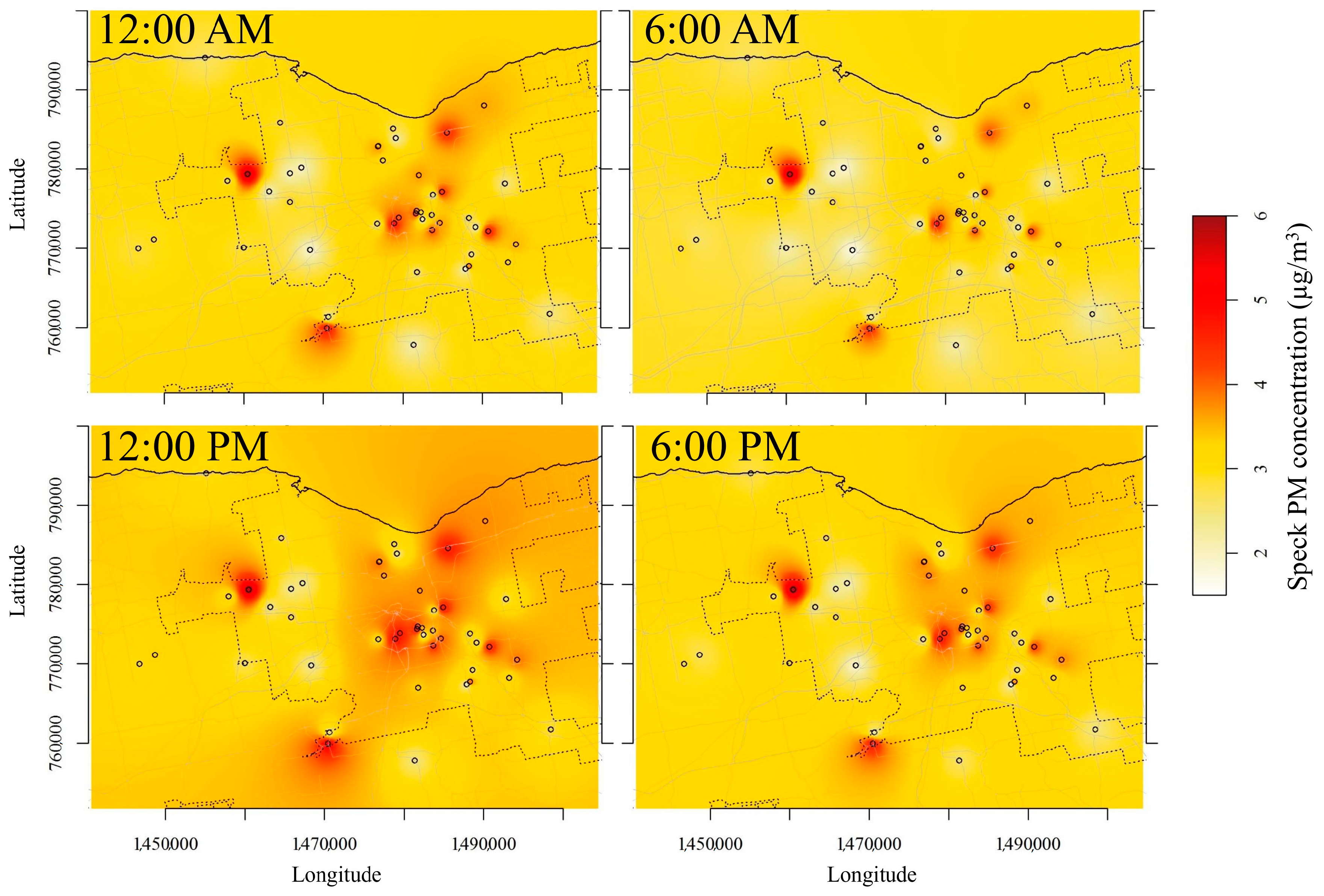
2.6.4. Spatial Interpolations
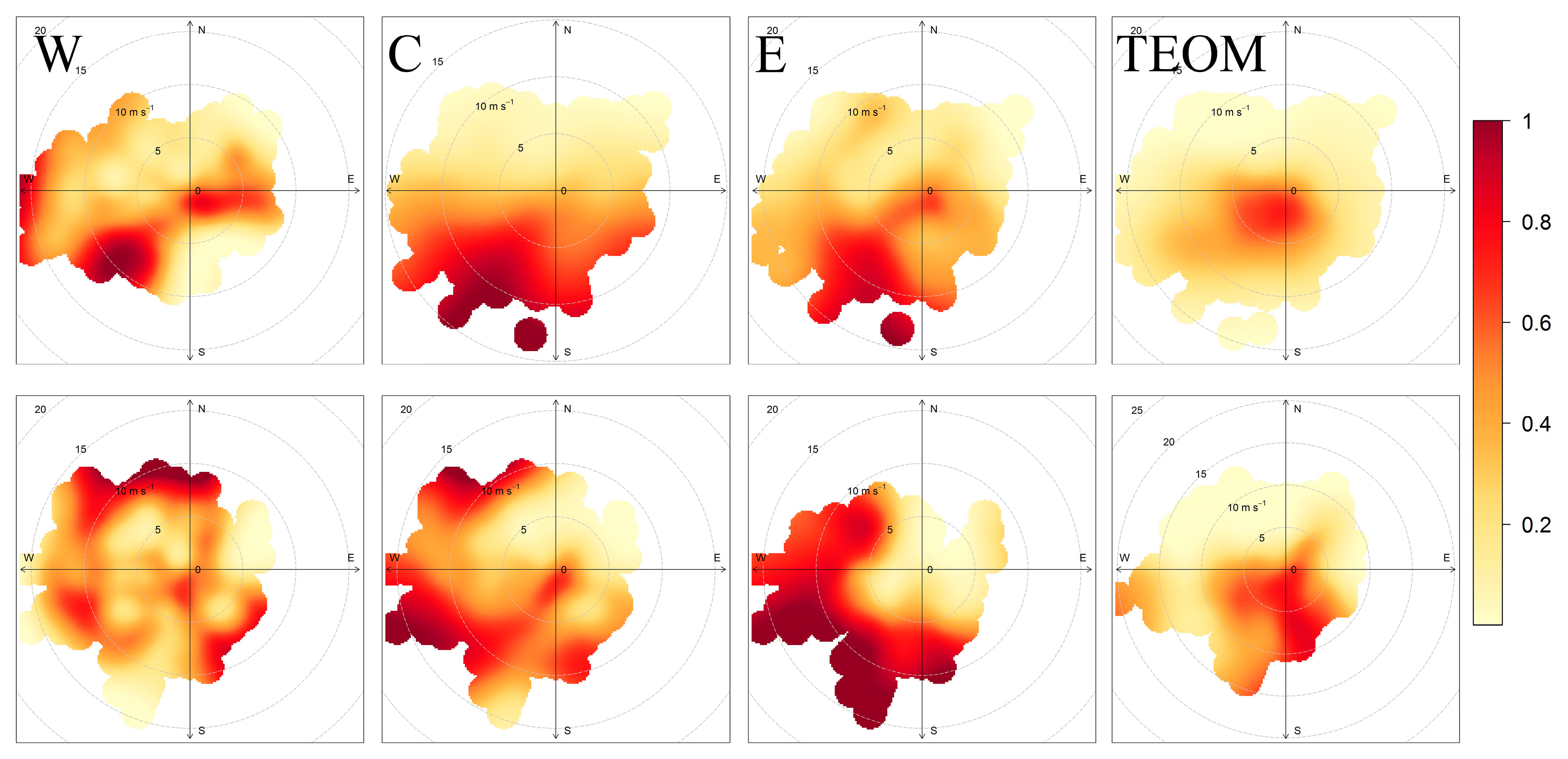
2.6.5. Conditional Bivariate Probability Function
3. Results and Discussion
3.1. Data Availability
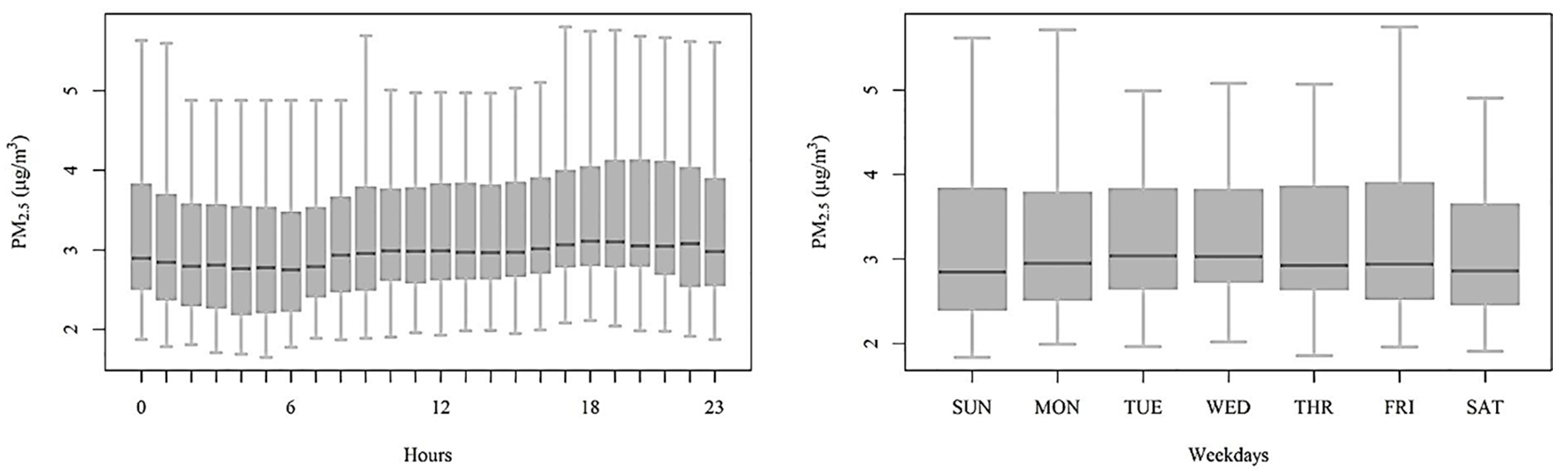
3.2. Mean PM2.5 Concentrations
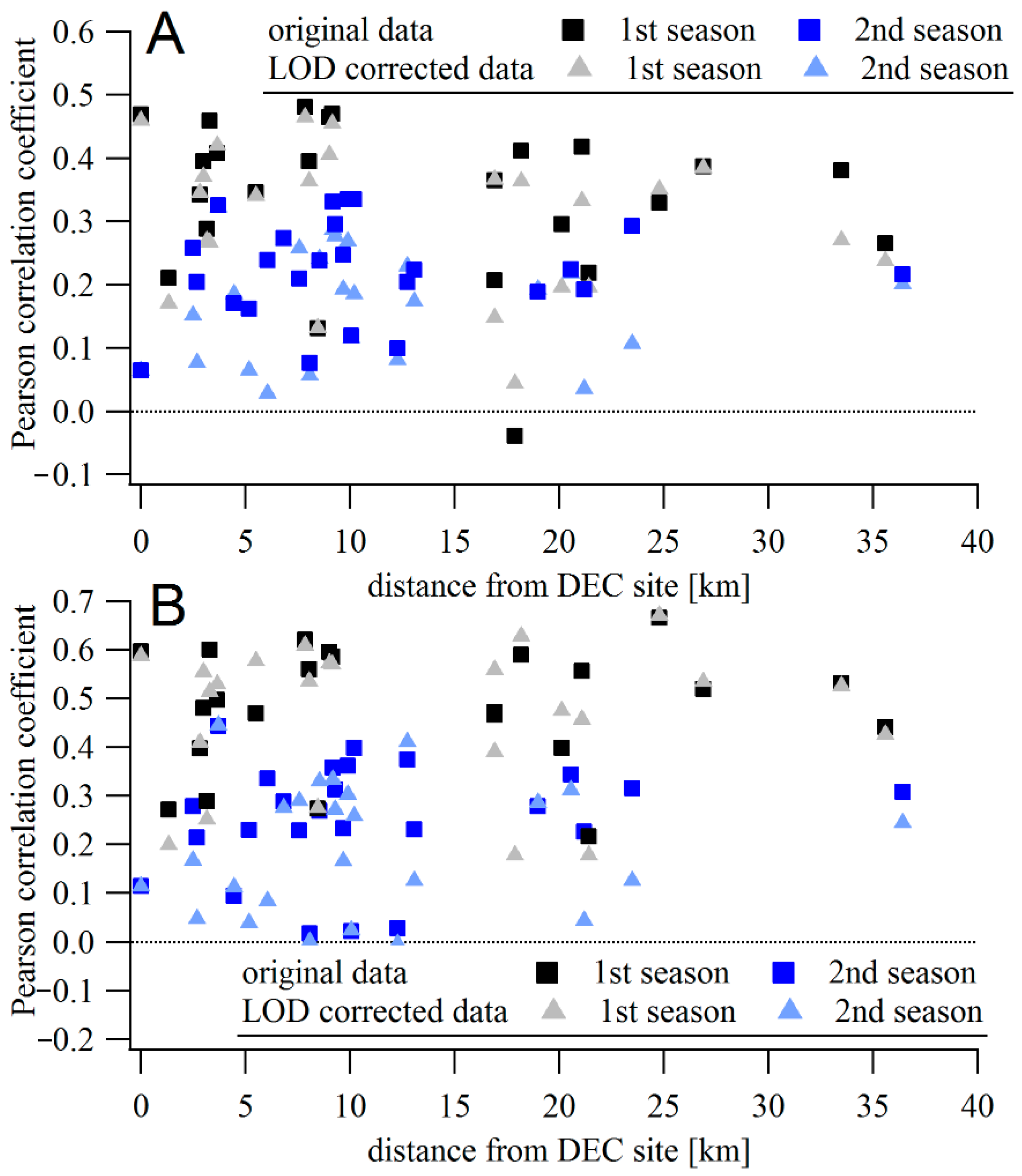
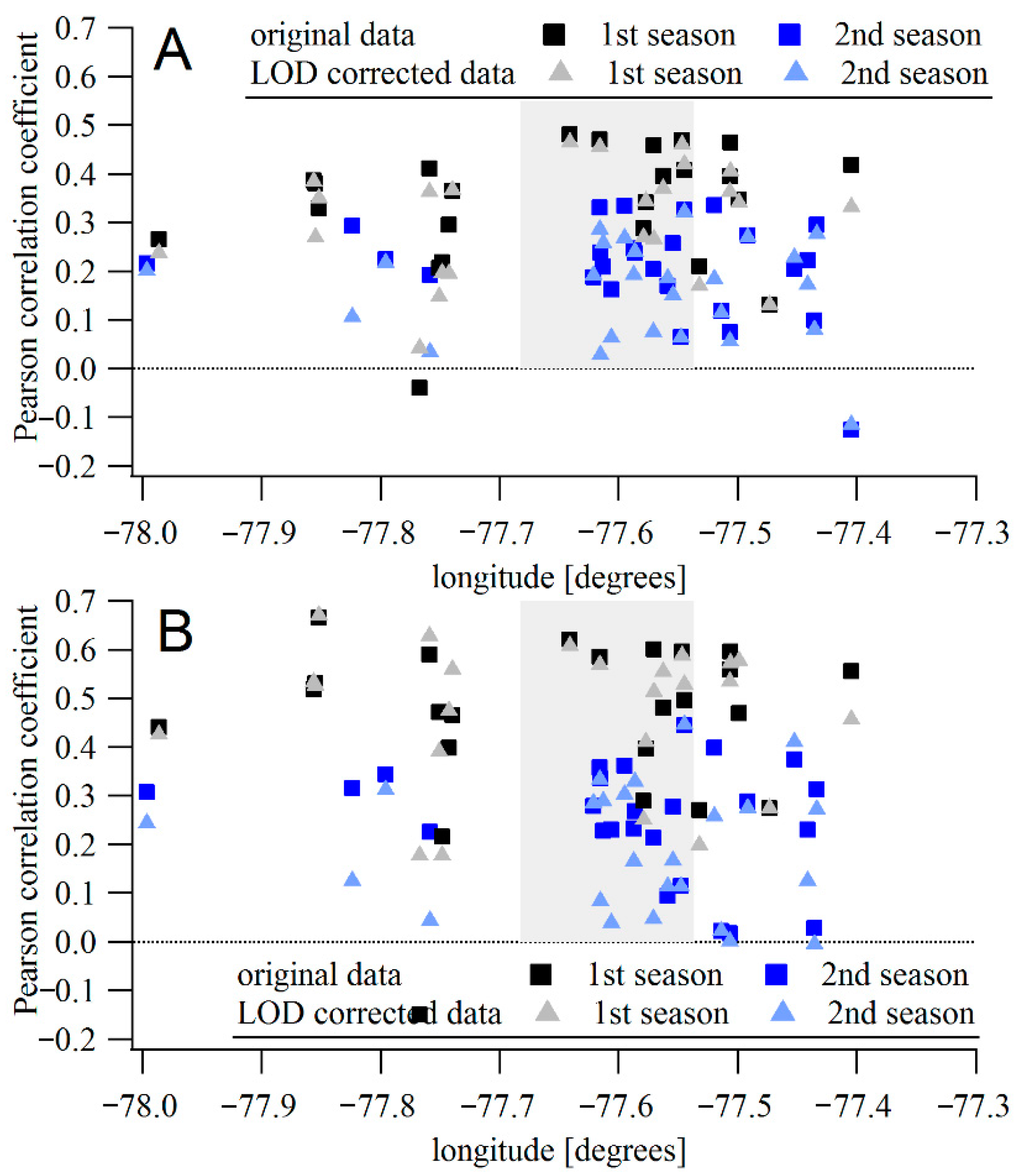
3.3. Temporal Correlations
Speck vs. TEOM Correlations
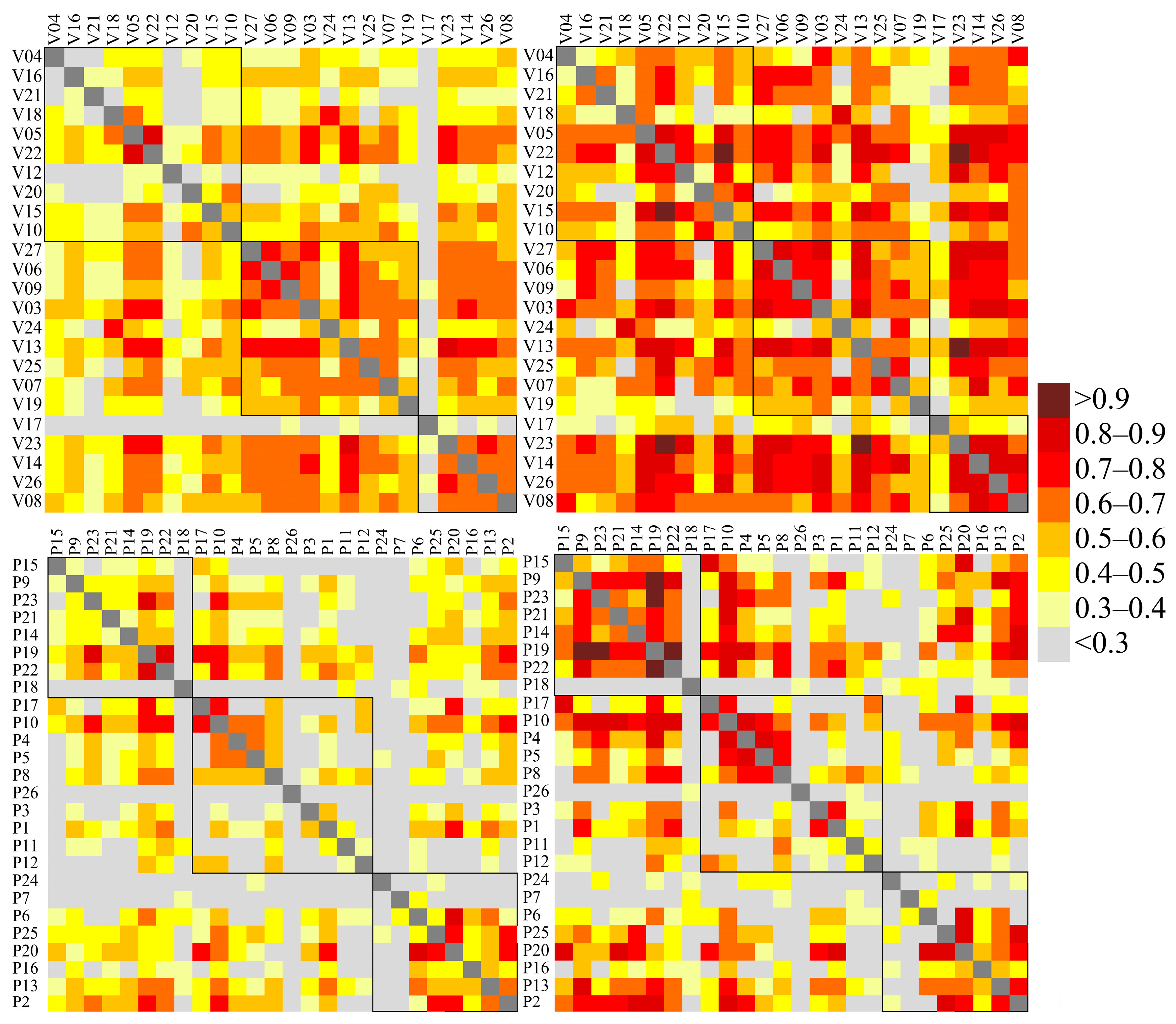
3.4. Correlation Matrixes
3.5. Coefficients of Divergence
3.6. Spatial Interpolation
3.7. CBPF
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, K.H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Solomon, P.A.; Crumpler, D.; Flanagan, J.B.; Jayanty, R.K.M.; Rickman, E.E.; McDade, C.E. U.S. National PM2.5 Chemical Speciation Monitoring Networks—CSN and IMPROVE: Description of networks. J. Air Waste Manag. Assoc. 2014, 64, 1410–1438. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.G.; Chow, J.C.; Dubois, D.; Green, M.; Frank, N. Guidance for the Network Design and Optimum Site Exposure for PM2.5 and PM10. Available online: https://www.osti.gov/scitech/biblio/678946 (accessed on 17 August 2017).
- Watkins, N.; Baldauf, R. Near-Road NO2 Monitoring Technical Assistance Document. Available online: https://trid.trb.org/view.aspx?id=1212411 (accessed on 17 August 2017).
- Apte, J.S.; Messier, K.P.; Gani, S.; Brauer, M.; Kirchstetter, T.W.; Lunden, M.M.; Marshall, J.D.; Portier, C.J.; Vermeulen, R.C.H.; Hamburg, S.P. High-Resolution Air Pollution Mapping with Google Street View Cars : Exploiting Big Data. Environ. Sci. Technol. 2017, 51, 6999–7008. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Liu, T.; Xiao, J.; Zeng, W.; Guo, L.; Li, X.; Xu, Y.; Zhang, Y.; Chang, J.J.; Vaughn, M.G.; et al. Hourly peak PM2.5 concentration associated with increased cardiovascular mortality in Guangzhou, China. J. Expo. Sci. Environ. Epidemiol. 2017, 27, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Northcross, A.L.; Edwards, R.J.; Johnson, M.A.; Wang, Z.-M.; Zhu, K.; Allen, T.; Smith, K.R. A low-cost particle counter as a realtime fine-particle mass monitor. Environ. Sci. Process. Impacts 2013, 15, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Cao, J.; Seto, E. A distributed network of low-cost continuous reading sensors to measure spatiotemporal variations of PM2.5 in Xi’an, China. Environ. Pollut. 2015, 199, 56–65. [Google Scholar] [CrossRef] [PubMed]
- Steinle, S.; Reis, S.; Sabel, C.E. Quantifying human exposure to air pollution-Moving from static monitoring to spatio-temporally resolved personal exposure assessment. Sci. Total Environ. 2013, 443, 184–193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holstius, D.M.; Pillarisetti, A.; Smith, K.R.; Seto, E. Field calibrations of a low-cost aerosol sensor at a regulatory monitoring site in California. Atmos. Meas. Tech. 2014, 7, 1121–1131. [Google Scholar] [CrossRef]
- Budde, M.; Zhang, L.; Beigl, M. Distributed, Low-Cost Particulate Matter Sensing: Scenarios, Challenges, Approaches. In Proceedings of the 1st International Conference on Atmospheric Dust, Castellaneta Marina, Italy, 1–6 June 2014; pp. 230–236. [Google Scholar]
- Lewis, A.; Edwards, P. Validate personal air-pollution sensors. Nature 2016, 535, 29–31. [Google Scholar] [CrossRef] [PubMed]
- Sousan, S.; Koehler, K.; Thomas, G.; Park, J.H.; Hillman, M.; Halterman, A.; Peters, T.M. Inter-comparison of low-cost sensors for measuring the mass concentration of occupational aerosols. Aerosol Sci. Technol. 2016, 50, 462–473. [Google Scholar] [CrossRef]
- Steinle, S.; Reis, S.; Sabel, C.E.; Semple, S.; Twigg, M.M.; Braban, C.F.; Leeson, S.R.; Heal, M.R.; Harrison, D.; Lin, C.; et al. Personal exposure monitoring of PM2.5 in indoor and outdoor microenvironments. Sci. Total Environ. 2015, 508, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Kaufman, A.; Hanley, T.; Rice, J.; Garvey, S. Evaluation of Field-Deployed Low Cost PM Sensors. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?dirEntryId=297517 (accessed on 17 August 2017).
- Manikonda, A.; Zikova, N.; Hopke, P.K.; Ferro, A.R. Laboratory assessment of low-cost PM monitors. J. Aerosol Sci. 2016, 102, 29–40. [Google Scholar] [CrossRef]
- Zikova, N.; Hopke, P.K.; Ferro, A.R. Evaluation of new low-cost particle monitors for PM2.5 concentrations measurements. J. Aerosol Sci. 2017, 105, 24–34. [Google Scholar] [CrossRef]
- Wang, Y.; Hopke, P.K.; Utell, M.J. Urban-scale spatial-temporal variability of black carbon and winter residential wood combustion particles. Aerosol Air Qual. Res. 2011, 11, 473–481. [Google Scholar] [CrossRef]
- Wang, Y.; Hopke, P.K.; Rattigan, O.V.; Chalupa, D.C.; Utell, M.J. Multiple-year black carbon measurements and source apportionment using Delta-C in Rochester, New York. J. Air Waste Manag. Assoc. 2012, 62, 880–887. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hopke, P.K.; Xia, X.; Rattigan, O.V.; Chalupa, D.C.; Utell, M.J. Source apportionment of airborne particulate matter using inorganic and organic species as tracers. Atmos. Environ. 2012, 55, 525–532. [Google Scholar] [CrossRef]
- Emami, F.; Masiol, M.; Hopke, P.K. The Air Pollution at Rochester, NY: Long-Term Trends and Multivariate Analysis of Upwind SO2 Source Impacts. Sci. Total Environ. 2017. submitted. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Wongphatarakul, V.; Friedlander, S.K.; Pinto, J.P. A comparative study of PM2.5 ambient aerosol chemical databases. Environ. Sci. Technol. 1998, 32, 3926–3934. [Google Scholar] [CrossRef]
- Pinto, J.P.; Lefohn, A.S.; Shadwick, D.S. Spatial Variability of PM2.5 in Urban Areas in the United States. J. Air Waste Manag. Assoc. 2004, 54, 440–449. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.G.; Kingham, S.; Pearce, J.; Sturman, A.P. A review of intraurban variations in particulate air pollution: Implications for epidemiological research. Atmos. Environ. 2005, 39, 6444–6462. [Google Scholar] [CrossRef]
- Marshall, J.D.; Nethery, E.; Brauer, M. Within-urban variability in ambient air pollution: Comparison of estimation methods. Atmos. Environ. 2008, 42, 1359–1369. [Google Scholar] [CrossRef]
- Beelen, R.; Hoek, G.; Pebesma, E.; Vienneau, D.; de Hoogh, K.; Briggs, D.J. Mapping of background air pollution at a fine spatial scale across the European Union. Sci. Total Environ. 2009, 407, 1852–1867. [Google Scholar] [CrossRef] [PubMed]
- Dodson, R.; Marks, D. Daily air temperature interpolation at high spatial resolution over a large mountainous region. Clim. Res. 1997, 8, 1–20. [Google Scholar] [CrossRef]
- Uria-Tellaetxe, I.; Carslaw, D.C. Conditional bivariate probability function for source identification. Environ. Model. Softw. 2014, 59, 1–9. [Google Scholar] [CrossRef]
- Ashbaugh, L.L.; Malm, W.C.; Sadeh, W.Z. A residence time probability analysis of sulfur concentrations at Grand Canyon national park. Atmos. Environ. 1985, 19, 1263–1270. [Google Scholar] [CrossRef]
- Wang, Y.; Hopke, P.K.; Utell, M.J. Urban-scale Spatial-Temporal Variability of Ultrafine Particle Number. Water Air Soil Pollut. 2012, 223, 2223–2235. [Google Scholar] [CrossRef]

| Unit # | # Data Points | Coverage [%] | >LOD [%] | Corr. Factor | Unit # | # Data Points | Coverage [%] | >LOD [%] | Corr. Factor |
|---|---|---|---|---|---|---|---|---|---|
| V03 | 171319 | 100 | 83.2 | 0.41 | P01 | 227379 | 100 | 20.0 | 0.18 |
| V04 | 172430 | 100 | 16.3 | 0.47 | P02 | 224369 | 100 | 51.0 | 0.20 |
| V05 | 169578 | 99.5 | 5.5 | 0.40 | P03 | 225808 | 100 | 39.7 | 0.22 |
| V06 | 172710 | 100 | 34.7 | 0.29 | P04 | 215369 | 95.9 | 13.0 | 0.29 |
| V07 | 84731 | 92.3 | 81.6 | 0.41 | P05 | 224224 | 100 | 58.1 | 0.25 |
| V08 | 173872 | 100 | 4.3 | 0.53 | P06 | 224292 | 100 | 37.8 | 0.27 |
| V09 | 172299 | 100 | 51.4 | 0.41 | P07 | 214569 | 100 | 66.7 | 0.27 |
| V10 | 185767 | 100 | 82.8 | 0.41 | P08 | 150726 | 66.7 | 0.8 | 0.72 |
| V12 | 171244 | 100 | 15.2 | 0.31 | P09 | 222425 | 100 | 18.6 | 0.28 |
| V13 | 171412 | 100 | 1.8 | 0.41 | P10 | 138294 | 63.8 | 15.9 | 0.25 |
| V14 | 172625 | 100 | 90.3 | 0.34 | P11 | 220149 | 98.6 | 95.3 | 0.24 |
| V15 | 173688 | 100 | 4 | 0.46 | P12 | 224304 | 100 | 55.8 | 0.36 |
| V16 | 170445 | 100 | 3.8 | 0.52 | P13 | 220931 | 100 | 19.6 | 0.29 |
| V17 | 99435 | 57.8 | 100 | 0.30 | P14 | 221274 | 99.2 | 55.0 | 0.21 |
| V18 | 172537 | 100 | 17.3 | 0.47 | P15 | 202146 | 98.3 | 63.3 | 0.25 |
| V19 | 175178 | 92.9 | 3.7 | 0.67 | P16 | 226502 | 97.1 | 64.5 | 0.27 |
| V20 | 106170 | 94.2 | 0.4 | 0.59 | P17 | 212246 | 97.3 | 59.4 | 0.26 |
| V21 | 172716 | 100 | 39.9 | 0.3 | P18 | 217567 | 100 | 90.9 | 0.24 |
| V22 | 128105 | 71.3 | 13 | 0.35 | P19 | 111800 | 100 | 12.7 | 0.34 |
| V23 | 174482 | 100 | 4.8 | 0.49 | P20 | 102458 | 98.9 | 79.9 | 0.16 |
| V24 | 170041 | 100 | 56.2 | 0.39 | P21 | 216764 | 99.1 | 1.5 | 0.56 |
| V25 | 180491 | 100 | 74.9 | 0.36 | P22 | 216647 | 99.9 | 3.7 | 0.27 |
| V26 | 185397 | 100 | 8.9 | 0.44 | P23 | 214108 | 99.2 | 1.7 | 0.96 |
| V27 | 181548 | 100 | 44.7 | 0.27 | P24 | 187046 | 100 | 27.0 | 0.33 |
| P25 | 159439 | 99.8 | 67.5 | 0.15 | |||||
| P26 | 200203 | 91.5 | 99.9 | 0.17 |
| Hourly | Hourly LOD | Daily | Daily LOD | |
|---|---|---|---|---|
| First period | 2 (1) | 2 (1) | 2 (1) | 8 (5) |
| Second period | 4 (2) | 4 (2) | 11 (4) | 11 (5) |
| Correlation Coefficient | >0.9 | >0.8 | >0.7 | >0.6 | >0.5 | >0.4 | >0.3 | |
|---|---|---|---|---|---|---|---|---|
| First period | hourly | 0.0 | 0.7 | 7.2 | 28.3 | 48.9 | 68.5 | 85.1 |
| hourly LOD | 0.0 | 0.4 | 2.5 | 10.9 | 27.5 | 43.5 | 64.1 | |
| daily | 1.1 | 13.0 | 31.2 | 54.7 | 73.2 | 84.4 | 93.8 | |
| daily LOD | 0.7 | 8.0 | 23.9 | 41.7 | 56.9 | 72.5 | 85.5 | |
| Second period | hourly | 0.0 | 0.9 | 4.6 | 10.2 | 26.2 | 44.3 | 57.5 |
| hourly LOD | 0.0 | 0.9 | 2.2 | 8.3 | 14.8 | 26.5 | 36.0 | |
| daily | 0.9 | 7.1 | 16.0 | 27.7 | 37.5 | 52.3 | 62.2 | |
| daily LOD | 0.0 | 0.0 | 1.8 | 6.8 | 12.9 | 22.8 | 35.1 |
| COD Values | Hour | Hour LOD | Day | Day LOD | |
|---|---|---|---|---|---|
| First period | <0.2 | 22.8 | 30.8 | 37.3 | 50.0 |
| 0.2–0.4 | 49.3 | 64.9 | 46.0 | 47.8 | |
| 0.4–0.6 | 24.6 | 4.3 | 15.6 | 2.2 | |
| 0.6–0.8 | 3.3 | 0 | 1.1 | 0 | |
| >0.8 | 0 | 0 | 0 | 0 | |
| Second period | <0.2 | 25.5 | 23.1 | 33.2 | 35.4 |
| 0.2–0.4 | 37.8 | 69.8 | 43.4 | 58.5 | |
| 0.4–0.6 | 22.5 | 7.1 | 13.8 | 6.2 | |
| 0.6–0.8 | 13.8 | 0 | 9.5 | 0 | |
| >0.8 | 0.3 | 0 | 0 | 0 |
| Group | Hour | Hour LOD | Day | Day LOD | |
|---|---|---|---|---|---|
| First period | West | 0.24 | 0.17 | 0.31 | 0.20 |
| Center | 0.24 (0.16) | 0.21 (0.19) | 0.28 (0.20) | 0.24 (0.22) | |
| East | 0.21 | 0.18 | 0.25 | 0.19 | |
| Second period | West | 0.34 | 0.22 | 0.26 | 0.19 |
| Center | 0.32 | 0.28 | 0.28 | 0.24 | |
| East | 0.28 | 0.21 | 0.23 | 0.19 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zikova, N.; Masiol, M.; Chalupa, D.C.; Rich, D.Q.; Ferro, A.R.; Hopke, P.K. Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors. Sensors 2017, 17, 1922. https://doi.org/10.3390/s17081922
Zikova N, Masiol M, Chalupa DC, Rich DQ, Ferro AR, Hopke PK. Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors. Sensors. 2017; 17(8):1922. https://doi.org/10.3390/s17081922
Chicago/Turabian StyleZikova, Nadezda, Mauro Masiol, David C. Chalupa, David Q. Rich, Andrea R. Ferro, and Philip K. Hopke. 2017. "Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors" Sensors 17, no. 8: 1922. https://doi.org/10.3390/s17081922
APA StyleZikova, N., Masiol, M., Chalupa, D. C., Rich, D. Q., Ferro, A. R., & Hopke, P. K. (2017). Estimating Hourly Concentrations of PM2.5 across a Metropolitan Area Using Low-Cost Particle Monitors. Sensors, 17(8), 1922. https://doi.org/10.3390/s17081922





